为实现过渡段刚度平顺过渡、控制线路沉降及轨面弯折变形,保证过渡段路基的耐久性和长期动力稳定性,国内外许多学者都基于传统的确定性模型研究了过渡段刚度对车辆轨道路基系统动力特性的影响.文献[1-6]将路基等效为支承弹簧,应用车辆轨道耦合动力学方法,分析了路基综合刚度对系统动力特性的影响,然而过渡段路基支承弹簧刚度与填筑材料力学参数的关系并不明确,不能直接考虑分层路基的材料特性,支承弹簧刚度取值的确定也较为困难.因而文献[7-11]建立了三维实体有限元模型,直接对过渡段路基填筑材料的力学参数进行分析.但事实上,由于岩土工程的复杂性、多变性,其物理力学参数存在较大的离散性和不确定性.在过渡段施工过程中,桥梁往往作为节点工程先期施工,过渡段则在普通路基施工完成后再分层压实填筑,施工作业面相对狭小,大型施工机具难以充分发挥作用,再加上填筑碎石级配不合理、压实质量管控不严等影响,以致过渡段路基的施工质量比普通路基段更难以控制,过渡段路基刚度往往会较大程度地随机偏离最初设计.路桥过渡段是线路病害高发区,因而对过渡段主要不确定性因素加以定量考虑,利用随机力学方法分析参数变异性对系统动力响应的影响,对过渡段结构设计的安全评估及参数优化具有重要的理论意义.
自20世纪80年代以来,随机有限元在工程结构可靠性、安全性分析领域以及在各种随机激励下结构响应变异研究领域中广为应用.蒙特卡罗随机有限元(Monte -Carlo SFEM)[12]将蒙特卡罗模拟与有限元力学分析相结合,利用统计学方法分析有限元求解变量的分布特性,回避了Taylor展开随机有限元(TSFEM)、摄动随机有限元(PSFEM)、Neumann展开随机有限元(NSFEM)等其他随机有限元法中随机参数影响量数学展开的困难,其收敛速度和计算量与随机变量的维数无关,精度不受参数变异性大小的限制,尤其适于高度非线性问题的参数随机性分析.该法在抽取的样本数足够多时其计算结果可以认为是精确的,故常将蒙特卡罗随机有限元法作为可靠度计算的相对精确解,用以检验其他近似解法.但蒙特卡罗抽样技术完全是随机的,其精确度跟样本点的数量有关,当执行的迭代次数少的时候,会产生样本聚集问题,为获得较高精度,需要产生很大的样本空间,计算量也随之增大.利用蒙特卡罗直接抽样法与车辆轨道线下基础耦合的三维有限元仿真相结合的计算量巨大,不便于进行过渡段多参数的随机力学分析,因而必须采用更有效的抽样方法,并进一步缩减三维有限元模型的计算量.
拉丁超立方(Latin hypercube)抽样[12]是一种多维分层抽样方法,其首先对输入概率分布进行分层,从输入分布的每个区间或“层”中随机抽取样本,抽样被强制代表每个区间的值,从而避免了重复抽样,故能通过较少迭代次数的抽样,准确地重建输入分布,抽样的次数可大大减少.
运用车辆轨道耦合动力学理论,将车体简化为多刚体、钢轨等效成Euler梁、过渡段轨下基础考虑为平面应变模型,同时引入无限单元消除边界效应,并通过修正扣件弹簧的刚度矩阵实现钢轨梁与轨下基础平面模型的垂向传力耦合,建立高速铁路路桥过渡段车辆轨道线下基础系统垂向耦合振动的有限-无限元模型.进而利用该模型,应用基于拉丁超立方抽样的随机有限元法,分析了过渡段路基刚度参数变异性对过渡段车辆轨道系统动力响应的影响规律,从而为过渡段的优化设计、安全评估及施工维养提供理论依据.
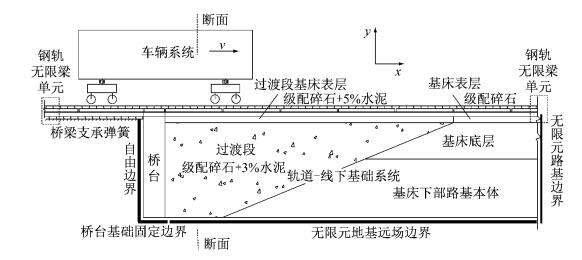
1 随机性分析模型与方法 1.1 过渡段车辆轨道线下基础耦合系统振动确定性分析模型对于《高速铁路设计规范》(TB 10621—2014)[13]中推荐的广泛应用的倒梯形路桥过渡段结构,沿线路纵向,建立车辆轨道线下基础系统垂向耦合振动模型,见图 1,图中v为速率.车辆单元取1/2车体,轨道线下基础系统建模取双线路基中单幅线路的左半结构,分析模型横断面见图 2.
|
图 1 车辆轨道线下基础系统及其边界 Fig.1 Vehicle-track-foundation system and its boundary |
|
图 2 倒梯形过渡段横断面(单位:mm) Fig.2 Obtrapezoid transition cross section(unit: mm) |
将车体简化为包括车体、转向架、轮对在内的多刚体系统,具有车体沉浮和点头运动、前后转向架沉浮和点头运动、4个轮对垂向运动等10个自由度;车体与转向架之间通过二系悬挂相连,转向架与轮对之间通过一系悬挂相连[14-15].运用Lagrange方程建立车辆系统方程,车辆系统质量、阻尼、刚度矩阵以及荷载矢量可由最小势能原理导出.单节高速车辆运动方程为
| $\begin{array}{l} {\mathit{\boldsymbol{M}}_{\rm{V}}}{{\mathit{\boldsymbol{\ddot z}}}_{\rm{V}}}\left( t \right) + {\mathit{\boldsymbol{C}}_{\rm{V}}}{{\mathit{\boldsymbol{\dot z}}}_{\rm{V}}}\left( t \right) + \\ \quad \;{\mathit{\boldsymbol{K}}_{\rm{V}}}{\mathit{\boldsymbol{z}}_{\rm{V}}}\left( t \right) = {\mathit{\boldsymbol{Q}}_{\rm{V}}}\left( t \right) \end{array}$ | (1) |
式中:MV,CV及KV分别为车辆系统的质量矩阵、阻尼矩阵和刚度矩阵;zV(t),
钢轨采用仅考虑节点竖向和转角2个自由度的二节点Euler梁单元;道床板、CA砂浆层、混凝土底座板、基床表层、桥台、台后过渡段、基床底层及基床以下路基本体等均采用平面应变四节点矩形单元[16]模拟;扣件采用弹簧阻尼单元,由弹簧单元受力平衡条件得
| $\left\{ {\begin{array}{*{20}{c}} {{f_i}}\\ {{f_j}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} k & { - k}\\ { - k} & k \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{u_i}}\\ {{u_j}} \end{array}} \right\} = {\mathit{\boldsymbol{K}}_{{\rm{fastener}}}}\mathit{\boldsymbol{u}}$ | (2) |
式中:fi,fj分别为弹簧单元节点i,j的节点力;k为扣件弹簧单元的刚度系数;ui,uj分别为i,j节点的位移;Kfastener为扣件弹簧单元的刚度矩阵;u为节点位移向量.同时忽略下部轨下基础的横向应变,将其近似简化为平面应变模型,而上部车辆系统及钢轨不便简化为平面应变模型,因而将钢轨向下传的扣件支反力沿线路横向均布于宽度为w(w为双线路基中单幅线路的左半结构宽度)的轨下基础表面,于是扣件单元中与道床板相连的节点所受的节点力应为fj/w,故将扣件单元的刚度矩阵修正为
| $\mathit{\boldsymbol{K}}_{\rm{fastener}}^{'}=\left[ \begin{matrix} k & -k \\ -k/w & k/w \\ \end{matrix} \right]$ | (3) |
通过修正扣件弹簧的刚度矩阵实现钢轨与轨下基础平面模型的垂向传力耦合,整个过渡段就可近似等效为车辆钢轨平面应变轨下基础模型.
计算模型近场采用有限元,边界采用映射无限元,从而减小人工截断边界效应.如图 1中,过渡段轨道线下基础系统主体模型采用有限单元法进行离散.对于模型边界,桥台底部采用固定边界,桥台侧立面为自由边界.钢轨左右两端各设置一个一维三节点映射无限梁单元[17],其单元位移形函数采用三节点五次Hermite插值多项式,无限梁单元的单元质量矩阵m及由支承弹性产生的单元阻尼矩阵c和刚度矩阵k1分别为
| $\left\{ \begin{align} & \mathit{\boldsymbol{m}}={{m}_{\rm{eq}}}\int_{{{x}_{1}}}^{\infty }{\mathit{\boldsymbol{N}}_{4}^{\rm{T}}{{\mathit{\boldsymbol{N}}}_{4}}\rm{d}x} \\ & \mathit{\boldsymbol{c}}={{c}_{\rm{eq}}}\int_{{{x}_{1}}}^{\infty }{\mathit{\boldsymbol{N}}_{4}^{\rm{T}}~{{\mathit{\boldsymbol{N}}}_{4}}\rm{d}x} \\ & {{\mathit{\boldsymbol{k}}}_{1}}={{k}_{\rm{eq}}}\int_{{{x}_{1}}}^{\infty }{\mathit{\boldsymbol{N}}_{4}^{\rm{T}}{{\mathit{\boldsymbol{N}}}_{4}}\rm{d}x} \\ \end{align} \right.$ | (4) |
式中:meq,ceq,keq分别为连续弹性支承轨道的等效分布质量、钢轨支承分布阻尼及分布弹性系数;N为利用三节点五次Hermite插值多项式得到的形函数.由无限长梁弯曲产生的单元刚度矩阵k2为
| $\begin{align} & {{\mathit{\boldsymbol{k}}}_{2}}=\int_{{{x}_{1}}}^{\infty }{EI{{\mathit{\boldsymbol{N}}}_{4}}\mathit{\boldsymbol{N}}_{4}^{'\rm{T}}\rm{d}x}= \\ & \ \int_{-1}^{1}{EI\mathit{\boldsymbol{N}}_{4}^{'\rm{T}}\mathit{\boldsymbol{N}}_{4}^{'}\left| \mathit{\boldsymbol{J}} \right|\rm{d}\zeta } \\ \end{align}$ | (5) |
式中:EI为梁的抗弯刚度;N′为形函数;J为雅克比矩阵.钢轨无限梁单元的单元刚度矩阵kr为
| ${{\mathit{\boldsymbol{k}}}_{\rm{r}}}={{\mathit{\boldsymbol{k}}}_{1}}+\rm{ }{{\mathit{\boldsymbol{k}}}_{2}}$ | (6) |
不同于静力问题,动力问题为防止虚假反射,需使外行波穿过有限元与无限元界面,向无限域外衰减或被无限元吸收.依据波的透射与反射理论,考虑介质的弹性恢复作用以及在人工边界处波传播的一致性,利用无限单元[17-18]并引入阻尼矩阵[18],构建等效动力无限单元使波通过有限元与无限元交界时无反射效应,波动能量被无限域吸收.模型底部边界与路基端侧面边界设置平面四节点二维映射无限单元,等效动力无限单元刚度矩阵的形成与普通等参单元类似,根据虚功原理,无限单元的刚度矩阵kifem为
| ${{\mathit{\boldsymbol{k}}}_{\rm{ifem}}}=\int_{-1}^{1}{\int_{-1}^{1}{{{\mathit{\boldsymbol{B}}}^{\rm{T}}}\mathit{\boldsymbol{DB}}\rm{det}\left| \mathit{\boldsymbol{J}} \right|\rm{d}\xi \rm{d}\eta }}$ | (7) |
式中:B,D分别为单元应变矩阵、弹性矩阵.
将轨道线下基础系统有限单元及边界无限单元相应的单元质量矩阵、刚度矩阵及阻尼矩阵依据单元局部自由度与系统整体自由度对应一致的原则,按照“对号入座”法组集成轨道线下基础系统总的质量、刚度、阻尼矩阵,并通过将假设的初始轮轨力按照等效荷载节点力分配而形成初始广义荷载向量,从而得到轨道线下基础系统振动方程:
| $\mathit{\boldsymbol{M\ddot{q}}}+\mathit{\boldsymbol{C\dot{q}}}+\mathit{\boldsymbol{Kq}}=\mathit{\boldsymbol{P}}$ | (8) |
式中:M,C,K分别为轨道线下基础系统总的质量、阻尼、刚度矩阵;P为广义载荷矢量;q为广义位移矢量;
车辆运动方程(1) 与轨道线下基础系统振动方程(8) 不是完全独立的,而是通过轮轨接触关系互相耦合的,轮轨间Hertz非线性接触轮轨力为
| ${{p}_{j}}\left( t \right)=\left\{ \begin{matrix} \frac{1}{{{G}^{3/2}}}|\Delta Z{{|}^{3/2}},&\Delta Z<0 \\ 0,&\Delta Z\ge 0 \\ \end{matrix} \right.$ | (9) |
式中:相对位移ΔZ=Zwj(x, t)-[zr(xpj, t)+zr0(xpj, t)],轮轨接触常数G=3.86R-0.115×10-8m·N-2/3(磨耗型踏面车轮);Zwj为t时刻第j位轮对的垂向位移;zr(xpj, t)为t时刻第j位轮对下钢轨的垂向位移;zr0(xpj, t)为t时刻第j位轮对下轨道的不平顺.
运用迭代法[5]对两系统分别求解,其中动力学方程的求解利用Newmark-β数值积分法,车辆轨道线下基础系统耦合方程的求解流程见图 3.求解流程主要分为车辆系统重力平衡过程及车体运动时步分析.初始时步计算通过假定轮轨力,并且在车辆初始位置做车辆系统重力平衡计算,判断车体及转向架是否满足平衡条件(可采用

|
图 3 车辆轨道线下基础系统耦合方程的求解 Fig.3 Solution of the coupled equations of the vehicle-track-foundation system |
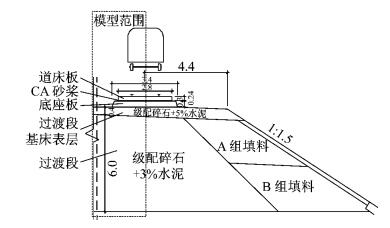
如图 4,计算中取线路总长度为120 m,其中桥梁32.7 m,桥台1.8 m,过渡段24.3 m,路基段61.2 m.采用60 kg·m-1钢轨,桥台高6.4m,道床板厚0.24 m,CA砂浆厚0.05 m,混凝土底座板厚0.3 m,基床表层厚0.4 m,基床底层厚2.3 m,基床下部路基本体厚度为3.7 m.轨道不平顺利用德国低干扰高速铁路高低不平顺模拟,波长范围为0.5~50m,并同时考虑过渡段不均匀沉降的影响,在过渡段加入1/4波长的波深a0=6 mm的余弦型不均匀沉降[15],其描述函数为

|
图 4 计算实例模型 Fig.4 Calculation model |
钢轨及轨道板的相关参数见文献[15],过渡段及路基各层材料参数参考文献[8]中试验实测选取,见表 1,车辆系统参数依据CRH3[15].模型仅考虑1节车辆自桥梁往路基方向以300 km·h-1速率通过总长为120 m的桥梁过渡段-路基组成的高铁线路,模型总自由度数为5 690,采用MATLAB软件编程实现.
| 下载CSV 表 1 过渡段及路基各层材料参数 Tab.1 Material parameters of transition zone and subgrade |
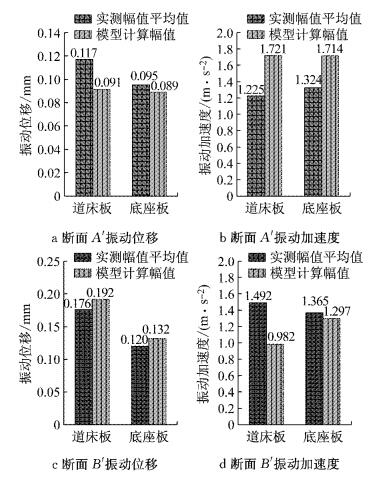
文献[19]在京沪高铁先导段安徽宿州濉河特大桥沪台端倒梯形过渡段进行了过渡段振动特性测试,过渡段桥台高7.5 m,轨道结构为CRTSⅡ型板式无砟轨道,过渡段使用级配碎石掺水泥分层压实填筑,与计算模型较为接近.试验列车为CRH380AL动力分散型电力动车组,列车轴重不大于15 t,行车速率主要集中在300~400 km·h-1,计算车体采用CRH380AL的参数.鉴于文献[19]过渡段采用了纵向锚固体系,包含摩擦板、过渡板和端刺等,相当于路基面上布置了一块刚性板,故模型验证时将台后40 m长范围内的支承层下0.4 m厚基床表层设置为0.4 m厚C30混凝土,用以考虑锚固体系.选取文献[19]过渡段的实测结果与本文模型对应位置计算结果进行对比验证,文献[19]位于台后过渡段与桥台连接处断面的测试结果与模型断面A′的计算结果进行对比;过渡段锚固体系末端过渡板与路基支承层连接处断面的实测结果与模型断面B′(台后38 m处)的计算结果进行比较,断面A′, B′的位置示意见图 4.现场道床板及底座板振动位移、加速度实测数据与本文模型断面A′、B′的确定性分析计算结果对比分别见图 5.可知,现场道床板和底座板的振动位移、振动加速度实测幅值的平均值与模型计算幅值符合较好.
对比可知,模型的假设及简化处理合理,确定性分析计算结果与实测数据具有较好的一致性,可以用于过渡段车辆轨道线下基础垂向耦合振动动力响应的随机力学分析.
1.3 过渡段动力特性的随机分析采用随机有限元分析过渡段动力特性时,首先根据过渡段路基填料特性统计特征,利用拉丁超立方抽样技术建立随机样本空间Ω(E1, E2),对每一个样本点(E1, E2)进行一次确定性分析,最后对计算结果进行统计分析.假设在n维向量空间里抽取m0个样本,拉丁超立方抽样具体步骤为:① 将每一维按等概率原则分成互不重迭的m0个等长区间;② 根据各变量的概率密度函数,在每一维里的各区间中随机抽取一个点;③ 再从每一维里随机抽出步骤② 中选取的点,将其组成样本点向量,从而得到包含m0个样本点的样本空间Ω.
过渡段路基基床表层及倒梯形部分填料动弹性模量(图、表中简写为动弹模)的分布采用截断正态分布[12, 20],其参数见表 2,确定性分析的计算为前述过渡段车辆轨道线下基础系统耦合求解过程,随机分析流程如图 6.
| 下载CSV 表 2 过渡段路基填料动弹性模量分布 Tab.2 Distribution of dynamic modulus of subgrade filling |

|
图 6 随机分析流程 Fig.6 Flow of stochastic analysis |
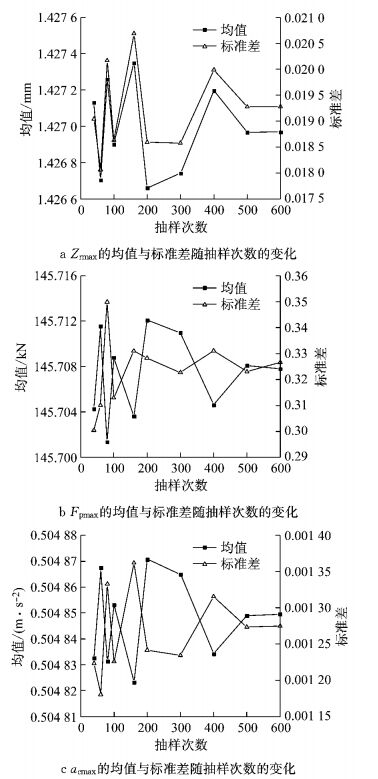
抽样次数(也即样本空间的大小)与随机性分析的精度及计算量直接相关,故需采取预先试抽样计算以确定合理的抽样次数.现选取过渡段车辆轨道系统钢轨垂向动位移最大值Zrmax、轮轨力最大值Fpmax和车体加速度最大值acmax等动力响应指标(后文均以字母符号表示),分析过渡段基床表层及倒梯形部分填料动弹性模量参数的变异性对过渡段Zrmax, Fpmax和acmax等动力响应指标的影响,通过对比不同抽样次数下各动力响应指标的统计均值、标准差及分布频率,当各指标的统计均值、标准差及分布频率趋于稳定而不随抽样次数显著改变时,可以认为抽样次数已经足够.
动力响应指标统计均值与标准差随抽样次数的变化见图 7,过渡段Zrmax, Fpmax和acmax的统计均值及标准差在抽样次数大于500次后逐趋于稳定,各动力响应指标的分布特征统计量不再随抽样次数的改变而发生显著变化.如图 8,在抽样次数为400, 500及600次时,过渡段Zrmax, Fpmax和acmax的统计频率分布规律较为一致(此处的统计频率为每个小组的频数与数据总数的比值,即频率等于频数除以总数),不随抽样次数的增加而发生显著变化.故出于精度要求及计算量的综合考虑,随机性分析的拉丁超立方抽样次数取为500次.
|
图 7 动力响应指标统计均值与标准差随抽样次数的变化 Fig.7 Statistical mean and standard deviation of the dynamic response index with the change of sampling times |

|
图 8 不同抽样次数下的频率分布对比 Fig.8 Comparison of frequency distribution under different sampling times |
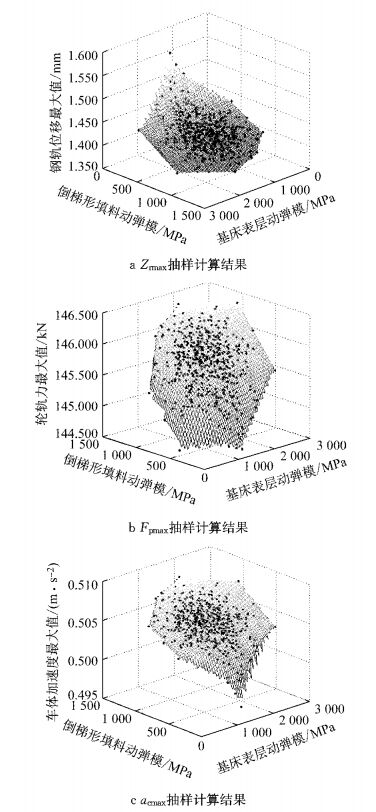
过渡段Zrmax, Fpmax和acmax等动力响应指标的500次拉丁超立方抽样计算结果分别见图 9,随着基床表层及基床表层下倒梯形部分填料动弹性模量的增大,也即过渡段路基刚度增大,钢轨垂向动位移最大值减小,轮轨力及车体加速度的最大值增大.
|
图 9 动力响应指标随机分析结果 Fig.9 Stochastic analysis results of dynamic response |
基于斯皮尔曼秩相关系数分析过渡段路基刚度对Zrmax, Fpmax和acmax等动力响应指标影响的相关性及灵敏度.设满足特定概率分布的结构设计参数x1, x2, …, xm,分析待求的k个动力响应指标y1, y2, …, yk,进行ns次随机模拟运算后得到第i(i=1, 2, …, k)个动力响应指标的ns个结构响应值yi1, yi2, …,yins,m个变量中第j(j=1, 2, …, m)个设计参数根据其概率分布函数所取得的ns个样本值为xj1, xj2, …, xjns,则由yi1, yi2, …, yins和xj1, xj2, …, xjns构成如下km个数据对:
| $\begin{align} &\left[ \begin{matrix} {{x}_{j1}} \\ {{y}_{i1}} \\ \end{matrix} \right],\left[ \begin{matrix} {{x}_{j2}} \\ {{y}_{i2}} \\ \end{matrix} \right],\ldots ,\left[ \begin{matrix} {{x}_{j{{n}_{\text{s}}}}} \\ {{y}_{i{{n}_{\text{s}}}}} \\ \end{matrix} \right] \\ &\left( i=1,2,\cdots ,k;j=1,2,\cdots ,m \right) \\ \end{align}$ | (10) |
将各数据对的斯皮尔曼秩相关系数表征为设计参数xj对动力响应yj的影响的灵敏度,分别计算过渡段基床表层及倒梯形部分填料动弹性模量对过渡段Zrmax, Fpmax和acmax等动力响应指标的灵敏度,计算结果见表 3,过渡段倒梯形部分填料动弹性模量的参数变化对过渡段动力响应的影响大于基床表层动弹性模量参数变化的影响.
| 下载CSV 表 3 相关性与灵敏度分析 Tab.3 Correlation and sensitivity analysis |
分别统计500次拉丁超立方抽样随机性计算所得过渡段Zrmax, Fpmax和acmax的最大值,并利用非参数检验方法分析其统计分布特征,随机性分析计算结果统计见表 4,数据统计分布检验见表 5,各检验均以95%置信水平.表 5中√表示通过,×表示未通过.
| 下载CSV 表 4 随机性分析结果统计 Tab.4 Statistic of stochastic analysis |
| 下载CSV 表 5 数据分布检验 Tab.5 Data distribution test |
过渡段基床表层及基床表层下倒梯形部分填料动弹性模量取值服从正态分布,但表 4与表 5中动力响应随机性分析的计算结果数据分布不对称,具有较大偏度,在95%的置信水平下,不能认为过渡段Zrmax, Fpmax和acmax服从正态分布(normal distribution)及对数正态分布(logarithmic normal distribution),而可以认为过渡段Fpmax和acmax服从韦伯分布(Weibull distribution).另外,Zrmax的变异系数大于Fpmax和acmax的变异系数,过渡段路基填料动弹性模量的变异性对钢轨垂向动位移的影响大于对轮轨力及车体加速度的影响;且各动力响应指标的变异系数已远小于过渡段路基填料动弹性模量的变异系数,轨道结构的分层设计及车辆的悬挂隔振系统大大降低了轨下基础不均匀性的影响.
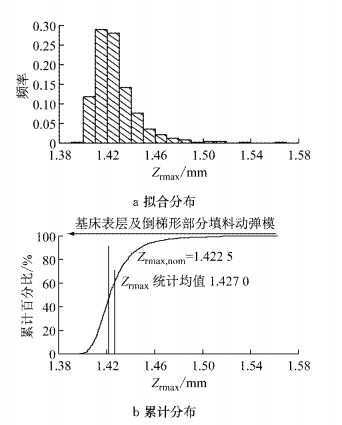
定义过渡段基床表层及基床表层下倒梯形部分填料动弹性模量参数分别取均值1 500 Mpa, 750 MPa时的确定性分析计算结果为动力响应指标名义设计值,通过计算,可得过渡段钢轨垂向动位移最大值(Zrmax)的名义设计值Zrmax, nom为1.422 5 mm,轮轨力最大值(Fpmax)的名义设计值Fpmax, nom为145.8 kN,车体加速度最大值(acmax)的名义设计值acmax, nom为0.505 0 m·s-2.如图 10所示,过渡段Zrmax, Fpmax和acmax的相应统计均值分别为1.427 0 mm,145.708 kN和0.504 8 m·s-2,由于小于基床表层及基床表层下倒梯形部分填料动弹性模量均值一侧的填料动弹性模量变化引起过渡段动力响应的变化量大于另一侧,统计均值皆偏向于小于过渡段路基填料动弹性模量均值侧.
|
图 10 Zrmax统计分布特征 Fig.10 The statistic distribution characteristics of Zrmax |
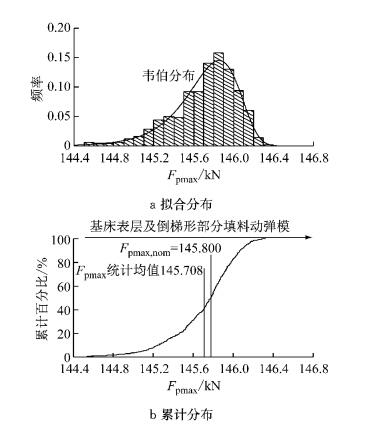
如图 10~12,在95%的置信水平下,过渡段Fpmax和acmax随机性分析计算结果近似服从韦伯分布;acmax计算结果偏度小于零,但偏斜度不大,峰度大于3,数据偏离正态性,较集中于均值上侧;Fpmax偏度稍小于零,峰度小于3,数据呈稍偏均值上侧的平顶分布.Zrmax数据变异性显著,偏度2.350 18>0,峰度9.313 98>3,严重偏离正态性,呈高峰厚尾分布,数据较集中于其均值下侧,在其均值上侧数据分布较为离散,钢轨垂向动位移易出现异常大值.图中箭头方向表示数值增大的方向.高速铁路修建过程中作为节点工程的桥梁、桥台先期施工,再进行台后路基填筑,大型路基施工机械因而应用不便而改用小型机具,结果往往造成路基填筑压实度未达标,导致过渡段路基刚度偏小,引起钢轨垂向动位移及轨面沉降偏大等险情.因为大于基床表层及基床表层下倒梯形部分填料的动弹性模量均值一侧的填料动弹性模量变化引起过渡段钢轨垂向动位移的变化量小于另一侧,所以适当提高过渡段路基填料动弹性模量既可以减小钢轨垂向动位移,又可以使数据更为集中于均值附近,使得当施工质量管控不严,尤其当填料压实度未达标、水泥掺量不合格导致过渡段路基刚度严重偏小时,过渡段钢轨动位移与设计值的偏差减小;且由于过渡段路基填料动弹性模量的变化对轮轨力及车体加速度的影响稍小,故提高过渡段路基刚度不会引起轮轨力及车体加速度的显著增大.因而,为减小钢轨垂向动位移以及便于管控施工质量,应适当提高过渡段路基刚度.
|
图 11 Fpmax统计分布特征 Fig.11 The statistic distribution characteristics of Fpmax |

|
图 12 acmax统计分布特征 Fig.12 The statistic distribution characteristics of acmax |
迄今国内外还未建立起一个权威的车辆与线路相互作用的过渡段动力学特性评价体系.对过渡段动力特性进行评价不仅面临参数随机性问题,还面临如何合理确定评价指标及其状态界定系数的问题.
由前述分析可知,钢轨垂向动位移受过渡段路基刚度参数变异性的影响较为显著,且路桥过渡段往往因压实度未达标,导致钢轨垂向动位移偏大,因而可选作过渡段动力特性的评价指标.文献[21]出于提高轨道弹性、降低轨道刚度以适应发展高速运输的需要,建议将混凝土轨枕轨道的钢轨下沉量控制为2 mm左右;王其昌等[22]、罗强[23]对车辆与轨道相互作用的动力学特性评价采用的钢轨垂向位移限值也为2 mm.故选用钢轨垂向动位移最大值Zrmax作为过渡段动力设计的安全评价指标.
评价过渡段动力设计可靠性的安全极限状态并非如“临界点”所定义的那样绝对明确,而应该是模糊的,传统可靠性理论中完全正常状态和完全失效状态的二态假设与工程实际明显不符.实际情况中交界处两侧邻近的指标并没有本质区别,例如结构的变形随着工作时间的延长,不断发展并最终被判定为“失效”,相应的极限状态的标志却常常不甚明显,只是变形程度越大,人们不可接受的程度越大.结构失效准则及其产生的失效域的边界往往是不明确的,结构的工作状态不能被简单地划分为完全安全和完全失效2个状态,结构的工作状态可以是模糊安全状态或模糊失效状态,故引入模糊状态假设以更科学合理地评价结构设计的可靠性.
以钢轨垂向动位移最大值Zrmax表征过渡段动力设计的安全状态,并将设计失效作为模糊随机事件,其状态隶属函数取作降半梯形分布[20],如下:
| $\mu \left( {{Z}_{\text{rmax}}} \right)=\left\{ \begin{matrix} 1,&{{Z}_{\text{rmax}}}\le a \\ \frac{b-{{Z}_{\text{rmax}}}}{b-a},&a<{{Z}_{\text{rmax}}}\le b \\ 0,&{{Z}_{\text{rmax}}}>b \\ \end{matrix} \right.$ | (11) |
式中:a, b为隶属度计算参数.总共进行Ns次模拟,第i次状态隶属函数为μ(Zrmaxi),动力安全设计失效概率计算公式为
| ${{p}_{\text{f}}}=\frac{\sum\limits_{i=1}^{{{N}_{\text{s}}}}{\left( 1-\mu \left( {{Z}_{\max \,i}} \right) \right)}}{{{N}_{\text{s}}}}$ | (12) |
式(11) 和(12) 中,取a=1.5 mm, b=2 mm,共进行Ns=500次拉丁超立方随机抽样,计算失效概率pf≈0.000 45,失效概率较小,动力设计较为可靠.
但需注意的是,所选用的过渡段动力设计可靠度评价指标及状态界定系数的合理性仍待进一步探讨,抽样次数不足所带来的可靠度计算误差也待进一步研究.
3 结论运用车辆轨道耦合动力学理论,并引入无限单元法消除边界效应,建立高速铁路路桥过渡段车辆轨道线下基础系统垂向耦合振动模型,进而利用该模型,应用基于拉丁超立方抽样的随机有限元法,分析了过渡段路基刚度参数变异性对过渡段车辆轨道系统动力响应的影响,并得到以下结论:
(1) 随着基床表层及倒梯形部分填料动弹性模量的增大,钢轨垂向动位移最大值减小,轮轨力及车体加速度的最大值增大,且过渡段动力响应主要对倒梯形部分填料的参数变化较为敏感.
(2) 过渡段路基刚度参数的变异性对钢轨垂向动位移的影响大于对轮轨力及车体加速度的影响,且分层设计的轨道结构及车辆的悬挂隔振系统极大降低了轨下基础不均匀性的影响,各动力响应指标的变异性降低显著.
(3) 动力响应随机性分析结果统计均值皆偏向于小于路基刚度设计值一侧,且数据分布不对称,偏离正态性;在95%的置信水平下,可以认为过渡段轮轨力、车体加速度的最大值服从韦伯分布;钢轨垂向动位移最大值的数据分布呈现明显的“高峰厚尾”,易出现异常大值,为减小钢轨垂向动位移以及便于施工质量管控,应适当提高过渡段路基刚度.
(4) 选用钢轨垂向动位移最大值作为过渡段动力设计的安全评价指标,计算显示现行设计模糊失效概率为0.000 45,失效概率较小,动力设计较为可靠;但过渡段动力设计可靠度的评价指标、状态界定系数以及抽样次数的确定有待进一步深入研究.
| [1] |
罗强, 蔡英, 翟婉明. 高速铁路路桥过渡段的动力学性能分析[J]. 工程力学, 1999, 16(5): 65 LUO Qiang, CAI Ying, ZHAI Wanming. Dynamic performance analyses on high speed railway bridge-subgrade transition[J]. Engineering Mechanics, 1999, 16(5): 65 |
| [2] |
罗强, 蔡英, 李成辉. 高速铁路路桥过渡段的动力分析与结构设计[J]. 路基工程, 1998(1): 1 LUO Qiang, CAI Ying, LI Chenghui. Dynamic analysis and structure design of subgrade-bridge transition section of high speed railway[J]. Subgrade Engineering, 1998(1): 1 |
| [3] |
刘钰, 赵国堂, 亓伟, 等. 高速铁路桥上有砟-无砟轨道过渡段动力学研究[J]. 振动与冲击, 2015(9): 76 LIU Yu, ZHAO Guotang, QI Wei, et al. Dynamic analysis of ballasted-ballastless track transition section on high speed railway bridge[J]. Journal of Vibration and Shock, 2015(9): 76 |
| [4] |
LEI X, MAO L. Dynamic response analyses of vehicle and track coupled system on track transition of conventional high speed railway[J]. Journal of Sound and Vibration, 2004, 271(3-5): 1133 DOI:10.1016/S0022-460X(03)00570-4 |
| [5] |
雷晓燕, 张斌, 刘庆杰. 轨道过渡段动力特性的有限元分析[J]. 中国铁道科学, 2009(5): 15 LEI Xiaoyan, ZHANG Bin, LIU Qingjie. Finite element analysis on the dynamic characteristics of the track transition[J]. China Railway Science, 2009(5): 15 |
| [6] |
VARANDAS J N, HÖLSCHER P, SILVA M A G. Dynamic behaviour of railway tracks on transitions zones[J]. Computers & Structures, 2011, 89(13/14): 1468 |
| [7] |
陈雪华. 高速铁路无碴轨道过渡段路基的动力特性研究[D]. 长沙: 中南大学, 2006. CHEN Xuehua. Research on dynamic characteristics of subgrade transition zone for ballastless track on high speed railway [D]. Changsha:Central South University, 2006. |
| [8] |
胡萍. 高速铁路无砟轨道密集过渡段路基动力试验与仿真分析[D]. 长沙: 中南大学, 2010. HU Ping. Dynamic experimental study and simulink analysis of closely spaced bridge-traction sections in for ballastless track on high speed railway [D]. Changsha:Central South University, 2010. |
| [9] |
许杰, 王峰, 项宝余, 等. 提速对既有线路桥过渡段路基动力响应影响分析[J]. 岩土工程学报, 2010(S2): 241 XU Jie, WANG Feng, XIANG Baoyu, et al. Impact of speed raising on dynamic response of bridge-subgrade transition of existing railway[J]. Chinese Journal of Geotechnical Engineering, 2010(S2): 241 |
| [10] |
SHAN Y, Albers B, Savidis S A. Influence of different transition zones on the dynamic response of track-subgrade systems[J]. Computers & Geotechnics, 2013, 48(48): 21 |
| [11] |
SHAHRAKI M, WARNAKULASOORIYA C, WITT K J. Numerical study of transition zone between ballasted and ballastless railway track[J]. Transportation Geotechnics, 2015, 3: 58 DOI:10.1016/j.trgeo.2015.05.001 |
| [12] |
吴振君, 王水林, 葛修润. LHS方法在边坡可靠度分析中的应用[J]. 岩土力学, 2010, 31(4): 1047 WU Zhenjun, WANG Shuilin, GE Xiurun. Application of Latin hypercube sampling technique to slope reliability analysis[J]. Rock and Soil Mechanics, 2010, 31(4): 1047 |
| [13] |
中华人民共和国铁道部. 高速铁路设计规范: TB10621—2014[S]. 北京: 中国铁道出版社, 2014. Ministry of Railways of the People's Republic of China. Code for design of high speed railway: TB10621—2014[S]. Beijing: China Railway Press, 2014. |
| [14] |
张小会, 周顺华, 宫全美, 等. 路基不均匀沉降对车辆和轨道动力响应的影响[J]. 同济大学学报(自然科学版), 2015, 43(8): 1187 ZHANG Xiaohui, ZHOU Shunhua, GONG Quanmei, et al. Effect of subgrade differential settlement on dynamic response of vehicle and slab track vertical coupled system[J]. Journal of Tongji University(Natural Science), 2015, 43(8): 1187 DOI:10.11908/j.issn.0253-374x.2015.08.010 |
| [15] |
YANG X, GU S, ZHOU S, et al. Effect of track irregularity on the dynamic response of a slab track under a high-speed train based on the composite track element method[J]. Applied Acoustics, 2015, 99: 72 DOI:10.1016/j.apacoust.2015.05.009 |
| [16] |
宫全美, 张达石. 高速铁路地基刚度的合理取值范围[J]. 同济大学学报(自然科学版), 2004, 32(10): 1390 GONG Quanmei, ZHANG Dashi. Reasonable foundation stiffness range of high speed railway[J]. Journal of Tongji University(Natural Science), 2004, 32(10): 1390 DOI:10.3321/j.issn:0253-374X.2004.10.025 |
| [17] |
蒋鸿林. 无限元方法及其应用[D]. 西安: 西安电子科技大学, 2005. JIANG Honglin. The infinite elements method and its application [D]. Xi'an: Xidian University, 2005. |
| [18] |
宿金成, 王幼清. 等效动力无限元及其在无限土体模拟中的应用[J]. 土木工程学报, 2013(2): 131 SU Jincheng, WANG Youqing. Equivalent dynamic infinite element and its application in infinite soil simulation[J]. China Civil Engineering Journal, 2013(2): 131 |
| [19] |
陈虎, 罗强, 张良, 等. 高速铁路CRTSⅡ型板式无砟轨道路桥过渡段振动特性测试分析[J]. 振动与冲击, 2014(1): 81 CHEN Hu, LUO Qiang, ZHANG Liang, et al. Test analysis of vibratio n characteristics of high-speed railway on CRTSⅡslab ballastless track bridge-subgrade transition[J]. Journal of Vibration and Shock, 2014(1): 81 |
| [20] |
王林, 徐青. 基于蒙特卡罗随机有限元法的三维随机渗流场研究[J]. 岩土力学, 2014, 35(1): 287 WANG Lin, XU Qing. Analysis of three dimensional random seepage field based on Monte Carlo stochastic finite element method[J]. Rock and Soil Mechanics, 2014, 35(1): 287 |
| [21] |
翟婉明, 蔡成标, 王其昌. 高速铁路轨道刚度与胶垫作用[J]. 铁道机车车辆, 1996, 66(4): 49 ZHAI Wanming, CAI Chengbiao, WANG Qichang. Track stiffness and rubber pad of high speed railway[J]. Railway Locomotive & Car, 1996, 66(4): 49 |
| [22] |
王其昌, 蔡成标, 罗强, 等. 高速铁路路桥过渡段轨道折角限值的分析[J]. 铁道学报, 1998, 20(3): 109 WANG Qichang, CAI Chengbiao, LUO Qiang, et al. Allowable values of track deflection angles on highspeed railway bridge-subgrade transition sections[J]. Journal of the China Railway Society, 1998, 20(3): 109 |
| [23] |
罗强. 高速铁路路桥过渡段动力学特性分析及工程试验研究[D]. 成都: 西南交通大学, 2003. LUO Qiang. Dynamic performance analyses and experiment study on bridge/approach embankment of high-speed railway[D]. Chengdu: Southwest Jiaotong University, 2003. |
 2017, Vol. 45
2017, Vol. 45