2. 同济大学(国家)磁浮交通工程技术研究中心,上海 201804
2. National Maglev Transportation Engineering R&D Center, Tongji University, Shanghai 201804, China
低速磁浮与传统轮轨交通工程相比具有转弯及爬坡能力强、噪声低、工程投资少和维护成本低等优点,已经成为一种新型的城市轨道交通方式[1-2].日本名古屋的丘陵线HSST轨道交通系统最高时速100 km·h-1,是低速磁浮列车的典型代表;而由株洲电力机车公司、湖南磁浮公司、西南交通大学、同济大学、国防科学技术大学共同参与建设的长沙磁浮快线则是我国首条低速磁浮商业运营线[3].
悬浮控制系统是低速磁悬浮交通的一项核心技术.随着电子技术、现代控制以及电磁理论等的进展,悬浮控制在近年来得到了广泛关注,并逐步发展成为当前的一个研究热点.磁浮列车常规的悬浮控制方法是将系统在平衡点处线性展开,利用线性控制理论进行控制律的设计[4-7].但悬浮系统是典型的非线性系统,当基于线性简化设计的控制系统受到较大干扰而远离平衡点时,系统有可能失去稳定.对于低速磁悬浮列车而言, 悬浮间隙约9mm,这种失稳将可能导致车辆在高速运行情况下撞击轨道, 从而出现严重安全事故.且由于上下车乘客数量对平衡点的位置有直接影响,所以悬浮列车的载客数量有限.因此,悬浮控制技术由初期仅注重稳定性的控制研究逐渐发展为注重稳定性能的同时更注重控制系统综合性能的提高,如动态响应品质、鲁棒性等.很多学者采用各种先进的控制方法来设计磁悬浮控制系统.Wai等[8]针对混合型磁悬浮系统,提出了基于状态观测器的自适应模糊神经网络控制律,该方法具有较高的控制精度,但并没有讨论收敛速度问题.王辉等[9]将轨道弹性振动作为激扰,利用增益表控制法依照系统质量自动整定反馈增益参数,从而提高车辆在轨道梁上的鲁棒性,但该方法会增大系统能耗.Tran等[10]提出一种任意有限时间跟踪控制法(AFTC)来控制存在未知动态特性的EMS(electromagnetic suspension)型磁悬浮系统. Wang等[11]采用卡尔曼滤波器的状态估计功能设计状态反馈控制器,解决了悬浮控制系统对轨道梁刚度的依赖,但控制对象采用线性近似模型,在系统远离平衡点时,控制性能会降低.Su等[12]基于非线性电磁悬浮系统的T-S (Takagi-Sugeno)模糊模型提出了模糊控制方法,仿真证明了该方法在处理有界干扰时的有效性,但这种方法增加了控制器设计的复杂度,工程应用难度大.Sun等[13]引入轨道梁的振动信息,设计一种新型的控制器,理论上确保悬浮系统稳定性和快速动态响应,但并没有进行试验验证.
国内外近年来大量的研究使磁悬浮先进智能控制方法在理论上取得了非常大的进步,但是这些方法都存在各自不同的问题,目前还难以使系统安全高效地工作.因此,迫切需要针对工程实际设计相应的非线性控制器,提高系统抗干扰和承载能力,优化控制的收敛速度,使其在存在未知动态干扰的情况下仍然能够实现稳定悬浮.针对低速磁浮列车的悬浮控制系统,本文建立非线性数学方程,搭建悬浮系统仿真平台,讨论线性控制器的性能和适用范围,并针对外界扰动、非线性、时变性设计改进的滑模控制律.
1 悬浮控制系统简介低速磁浮列车采用的是常导电磁吸引悬浮EMS方式,依靠安装在车体上的电磁铁和轨道铁轨之间的吸引力使车辆悬浮.采用“T”型导轨,车辆环抱导轨运行.在经过刚体飞行器和磁轮设计概念后, 低速磁浮列车在结构上选用较为成熟的模块控制概念, 实现了多个电磁铁之间的解耦[14-16].因此低速磁浮列车悬浮控制系统由多点控制简化为单点控制, 控制系统的性能也主要取决于单电磁铁的控制性能.
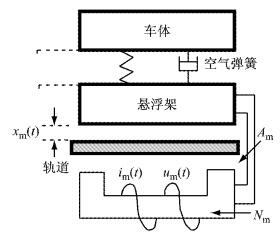
如图 1所示,目前的磁浮列车的车厢质量由多个二系空气弹簧共同支撑,并通过悬浮架将负载力传递到每个单电磁悬浮系统上.图中,xm(t)为悬浮电磁铁与轨道间的气隙;t为时间;Nm为电磁铁线圈匝数;Am为电磁铁有效磁极面积;im(t)和um(t)分别为电磁铁线圈中的电流和电压.m为车辆的负载和自身质量;fd为系统受到的干扰力;Rm为电磁铁的线圈电阻;μ0为空气磁导率.因为支撑车厢的空气弹簧刚度小于悬浮刚度,所以由车厢微振动引起的电磁铁负载变化可忽略不计.
|
图 1 磁浮列车悬浮系统结构 Fig.1 Configuration of the suspension system |
基于Euler-Lagrange法推导悬浮系统的动力学模型.Euler-Lagrang(E-L)方程的一般表达形式如下:
| $\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial \left( {T - V} \right)}}{{\partial {{\dot q}_i}}}} \right) - \frac{{\partial \left( {T - V} \right)}}{{\partial {q_i}}} = {Q_i}$ | (1) |
式中:qi,
| $\begin{array}{*{20}{c}} {\frac{{{\rm{d}}}}{{{\rm{d}}t}}\left( {\frac{{\partial L}}{{\partial {{\dot q}_i}}}} \right) - \frac{{\partial L}}{{\partial {q_i}}} = {Q_i}}&{i = 1,2, \cdots ,n} \end{array}$ | (2) |
选取系统广义坐标为q1=xm(t),
| $\left\{ \begin{array}{l} T = \frac{1}{2}{L_{\rm{M}}}\left( {{x_{\rm{m}}}\left( t \right)} \right)i_{\rm{m}}^2\left( t \right) + \frac{1}{2}m\dot x_{\rm{m}}^2\left( t \right)\\ V = - mg{x_{\rm{m}}}\left( t \right) \end{array} \right.$ | (3) |
拉格朗日算子可以表示为
| $L = \frac{1}{2}{L_{\rm{M}}}({x_{\rm{m}}}\left( t \right))i_{\rm{m}}^2\left( t \right) + \frac{1}{2}m\dot x_{\rm{m}}^2\left( t \right) + mg{x_{\rm{m}}}\left( t \right)$ | (4) |
式中:LM(xm(t))为电磁铁线圈的有效电感,是关于悬浮间隙xm(t)的非线性函数.
| ${L_{\rm{M}}}\left( {{x_{\rm{m}}}\left( t \right)} \right) = \frac{{{\mu _0}N_{\rm{m}}^2{A_{\rm{m}}}}}{{2{x_{\rm{m}}}\left( t \right)}}$ | (5) |
磁悬浮系统的广义力分别为Q1=fd和Q2=um(t)-im(t)Rm.
因此,由E-L方程的一般表达式可得
| $\left\{ \begin{array}{l} \frac{{\partial L}}{{\partial {q_1}}} = \frac{{\partial L}}{{\partial {x_{\rm{m}}}\left( t \right)}} = - \frac{{{\mu _0}{A_{\rm{m}}}N_{\rm{m}}^2i_{\rm{m}}^2}}{{4x_{\rm{m}}^2\left( t \right)}} + mg\\ \frac{{\partial L}}{{\partial {{\dot q}_1}}} = \frac{{\partial L}}{{\partial {{\dot x}_{\rm{m}}}\left( t \right)}} = m{{\dot x}_{\rm{m}}}\left( t \right)\\ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial L}}{{\partial {{\dot q}_1}}}} \right) = m{{\ddot x}_{\rm{m}}}\left( t \right)\\ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial L}}{{\partial {{\dot q}_1}}}} \right) - \frac{{\partial L}}{{\partial {q_1}}} = {f_{\rm{d}}}\\ {{\ddot x}_{\rm{m}}}\left( t \right) = \frac{{{f_{\rm{d}}}}}{m} + g - \frac{{{\mu _0}{A_{\rm{m}}}N_{\rm{m}}^2i_{\rm{m}}^2}}{{4mx_{\rm{m}}^2\left( t \right)}} \end{array} \right.$ | (6) |
和
| $\left\{ \begin{array}{l} \frac{{\partial L}}{{\partial {q_2}}} = 0\\ \frac{{\partial L}}{{\partial {{\dot q}_2}}} = \frac{{\partial L}}{{\partial {i_{\rm{m}}}\left( t \right)}} = {L_{\rm{M}}}\left( {{x_{\rm{m}}}\left( t \right)} \right){i_{\rm{m}}}\left( t \right)\\ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial L}}{{\partial {{\dot q}_2}}}} \right) = - \frac{{{\mu _0}{A_{\rm{m}}}N_{\rm{m}}^2{i_{\rm{m}}}}}{{2x_{\rm{m}}^2}}{{\dot x}_{\rm{m}}} + {L_{\rm{M}}}\frac{{{\rm{d}}{i_{\rm{m}}}}}{{{\rm{d}}t}}\\ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial L}}{{\partial {{\dot q}_2}}}} \right) - \frac{{\partial L}}{{\partial {q_2}}} = {u_{\rm{m}}} - {i_{\rm{m}}}{R_{\rm{m}}}\\ \frac{{{\rm{d}}{i_{\rm{m}}}}}{{{\rm{d}}t}} = \frac{{2{x_{\rm{m}}}\left( t \right){u_{\rm{m}}}}}{{{\mu _0}N_{\rm{m}}^2{A_{\rm{m}}}}} - \frac{{2{x_{\rm{m}}}{i_{\rm{m}}}{R_{\rm{m}}}}}{{{\mu _0}N_{\rm{m}}^2{A_{\rm{m}}}}} + \frac{{{i_{\rm{m}}}}}{{{x_{\rm{m}}}}}{{\dot x}_{\rm{m}}} \end{array} \right.$ | (7) |
此处选系统状态为y1(t)=xm(t),
| $\left\{ \begin{array}{l} {{\dot y}_1}\left( t \right) = {y_2}\left( t \right)\\ {{\dot y}_2}\left( t \right) = - \frac{{{\mu _0}{A_{\rm{m}}}N_{\rm{m}}^2}}{{4m}}{\left[ {\frac{{{y_3}\left( t \right)}}{{{y_1}\left( t \right)}}} \right]^2} + g + \frac{1}{m}{f_{\rm{d}}}\\ {{\dot y}_3}\left( t \right) = \frac{{{y_2}\left( t \right){y_3}\left( t \right)}}{{{y_1}\left( t \right)}} + \frac{{2{y_1}\left( t \right)}}{{{\mu _0}N_{\rm{m}}^2{A_{\rm{m}}}}} \cdot \\ \quad \quad \quad \left( {{u_{\rm{m}}}\left( t \right) - {y_3}\left( t \right){R_{\rm{m}}}} \right) \end{array} \right.$ | (8) |
悬浮系统通常工作在平衡的位置yle=xref,平衡位置可选为
| $z\left( t \right) = \left[ {\begin{array}{*{20}{c}} {{z_1}\left( t \right)}\\ {{z_2}\left( t \right)}\\ {{z_3}\left( t \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{y_1}\left( t \right) - {y_{1{\rm{e}}}}}\\ {{y_2}\left( t \right)}\\ {{y_3}\left( t \right) - {y_{3{\rm{e}}}}} \end{array}} \right]$ | (9) |
定义υ(t)=um(t)-ume并选取以上坐标变换,可得与式(9) 等效的系统状态空间表达式:
| $\left\{ \begin{array}{l} {{\dot z}_1}\left( t \right) = {z_2}\left( t \right)\\ {{\dot z}_2}\left( t \right) = \frac{{\left( {2{x_{{\rm{ref}}}} + {z_1}\left( t \right)} \right){z_1}\left( t \right)g}}{{{{({z_1}\left( t \right) + {x_{{\rm{ref}}}})}^2}}} - \\ \quad \quad \quad \frac{{\left( {2\sqrt \kappa {x_{{\rm{ref}}}} + {z_3}\left( t \right)} \right){z_3}\left( t \right)g}}{{\kappa {{\left( {{z_1}\left( t \right) + {x_{{\rm{ref}}}}} \right)}^2}}} + \frac{1}{m}{f_{\rm{d}}}\\ {{\dot z}_3}\left( t \right) = \frac{{{z_3}\left( t \right) + \sqrt \kappa {x_{{\rm{ref}}}}}}{{{z_1}\left( t \right) + {x_{{\rm{ref}}}}}}{z_2}\left( t \right) + \frac{{\kappa ({z_1}\left( t \right) + {x_{{\rm{ref}}}})}}{{2mg}} \cdot \\ \quad \quad \left( {\upsilon \left( t \right) - {z_3}\left( t \right){R_{\rm{m}}}} \right) \end{array} \right.$ | (10) |
相对于中继器、饱和、死区和量化等一般非线性,悬浮系统的状态空间模型式(10) 是强非线性的[8, 11, 17].如果采用常规方法将其线性化,那么系统一旦远离平衡点,强非线性系统近似后的线性模型将比一般非线性系统的近似模型更加不匹配现实物理模型,此时线性控制方法的动态表现将会恶化,甚至不再适用.
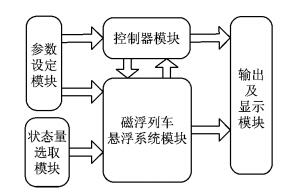
3 仿真平台设计为了便于控制策略的设计以及验证,设计仿真平台架构图如图 2所示.
|
图 2 仿真平台功能结构 Fig.2 Function structure of simulation platform |
该仿真平台由参数设定模块、磁浮列车悬浮系统模块、控制器模块、状态量选取模块以及输出显示模块组成.其中:
(1) 参数设定模块的基本功能是对磁悬浮仿真试验环境的参数进行设定,包括悬浮物体质量、电磁铁线圈匝数、电磁铁磁极面积、电磁铁内阻、漏磁率、期望悬浮间隙等以及控制器相关参数.该模块使用了MATLAB软件的GUI技术.
(2) 磁浮列车悬浮系统模块是根据磁浮系统非线性数学模型及线性化模型搭建的,可根据要求在非线性和线性模型间切换.它用来模拟磁浮系统的电气、电磁及动力学特性.
(3) 控制器模块可放置基于Simulink环境构造的各种控制器中,并且提供了各种反馈信号的接口,方便在磁悬浮仿真平台上检验和测评各种控制策略的效果.
(4) 状态量选取模块用于选取磁悬浮系统的状态变量.
(5) 输出显示模块基本功能是用于结果数据的保存与曲线的绘制以及悬浮过程的动画演示.该模块使用了MATLAB软件的VR技术.
磁浮列车悬浮系统参数如表 1所示,表中iref为平衡点电流,xref为平衡点悬浮间隙.
| 下载CSV 表 1 悬浮系统参数 Tab.1 Parameters values of the suspension system |
PD控制律是最典型的线性化控制方法.采用PD方法校正的悬浮系统控制原理如图 3所示,图中Gp(s)为PD控制律的传递函数,G0(s)为线性化后系统的传递函数[6, 7, 13].xref为平衡点间隙,xm为实际悬浮间隙,Δx为二者之差.该方法根据间隙传感器测量到的xm与xref之差,即Δx=xref-xm,对偏差进行比例和微分运算,将2种运算结果相加,就得到PD控制律的控制输出.

|
图 3 PD校正的系统控制原理框图 Fig.3 PD control system principle block diagram |
图 3中PID控制器传递函数表达式为
| ${G_{\rm{p}}}\left( s \right) = {K_{\rm{p}}}\left( {1 + \tau s} \right)$ | (11) |
式中:Kp为比例系数;τ为微分时间常数.
加入PD控制律后系统的开环传递函数为
| ${G_k}\left( s \right) = \frac{{ - {P_{\rm{i}}}{K_{\rm{p}}}\left( {\tau s + 1} \right)}}{{{L_{{\rm{ref}}}}m{s^3} + {R_{\rm{m}}}m{s^2} + (P_{\rm{i}}^2 - {L_{{\rm{ref}}}}{P_{\rm{x}}})s - {R_{\rm{m}}}{P_{\rm{x}}}}}$ | (12) |
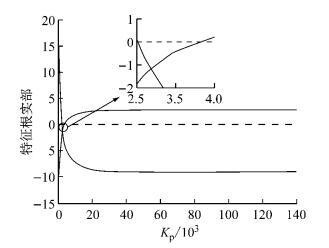
令τ=0.1,得到系统特征根实部随Kp的变化情况如图 4所示,可知系统稳定的Kp的取值范围为(2 500, 4 100).
|
图 4 τ=0.1时特征根实部随比例系数变化情况 Fig.4 Change on real component of characteristic root while τ=0.1 |
在实际的磁浮列车悬浮系统中,使用斩波器给悬浮电磁铁供电,利用电流跟随原理来调节电磁铁的电流大小.因此,在设计控制器时用电流环控制.
选取系统的状态变量为
| ${x_1} = {x_{\rm{m}}}\left( t \right)$ | (13) |
| ${x_2} = {{\dot x}_1} = {{\dot x}_{\rm{m}}}\left( t \right)$ | (14) |
系统的误差和误差变化率分别可表示为
| $e = r - {x_1}$ | (15) |
| $\dot e = \dot r - {{\dot x}_1} = \dot r - {x_2}$ | (16) |
式中:r为目标悬浮间隙.
定义系统滑模切换面S如下:
| $S = \mathit{\boldsymbol{CE}} = \mathit{\boldsymbol{C}}\left( {{\rm{ }}\mathit{\boldsymbol{R}} - \mathit{\boldsymbol{X}}} \right)$ | (17) |
式中:C=[c1, c2];
为保证系统滑动模态的稳定性,应满足Hurwitz稳定,即c1/c2>0.
为满足滑动模态的存在性及可达性,必须实现广义滑模可达性条件,即
当系统进入滑模运动时,满足
| $\dot S = {c_1}(\dot r - {{\dot x}_1}) + {c_2}(\ddot r - {P_{\rm{x}}}{x_1}/m + {P_{\rm{i}}}{u_{\rm{s}}}/m - {f_{\rm{d}}}/m)$ | (18) |
式中:fd为外加干扰,|fd|≤D,D为干扰的上界; Pi为电流系数; Px为间隙系数,其中Pi=μ0Nm2Amiref/(2xref2),Px=μ0Nm2Amiref2/(2xref3); us为控制器的输出量.
选取削弱颤振的指数趋近律设计系统控制律:
| $\dot S = - \xi {\rm{sgn}}\left( S \right) - kS$ | (19) |
根据式(15),(16) 和(19) 得系统的控制律为
| $\begin{array}{l} {u_{\rm{s}}} = \frac{m}{{{c_2}{P_{\rm{i}}}}}( - \xi {\rm{sgn}}\left( S \right) - kS - {c_1}\dot r + {c_1}{{\dot x}_1} - {c_2}\ddot r + \\ \quad \quad \quad {c_2}{P_{\rm{x}}}{x_1}/m + {c_2}D{\rm{sgn}}\left( S \right)/m) \end{array}$ | (20) |
定义Lyapunov函数为
| $V\left( x \right) = \frac{1}{2}{S^2}$ | (21) |
容易知此函数是半正定的,对其两边求导得
| $\begin{array}{l} \dot V\left( x \right) = S \cdot \dot S = - S \cdot \xi {\rm{sgn}}\left( S \right) - k \cdot {S^2} = \\ \quad \quad \quad - \xi \left| S \right| - k \cdot {S^2} \le 0 \end{array}$ | (22) |
根据Lyapunov定理,可证系统全局渐近稳定.
由于滑模控制本质的不连续开关特性会引起系统颤振,给执行器带来磨损,增加了能量消耗,制约了滑模控制在工程实际中的应用[18-19].本文将可变边界层的准滑模控制方法和指数趋近律相结合,有效避免或削弱了颤振,即采用饱和函数代替sgn(*)切换函数,在边界层以外施加指数趋近律的滑模控制,在边界层以内采用连续状态的反馈控制.其中
| ${\rm{sat}}\left( S \right) = \left\{ {\begin{array}{*{20}{c}} {\frac{S}{{{\phi _0}}},}&{\left| S \right| \le {\phi _0}}\\ {{\rm{sgn}}\left( S \right),}&{\left| S \right| > {\phi _0}} \end{array}} \right.{\rm{ }}$ | (23) |
式中:
此时控制律转化为
| $\begin{align} & u_{\text{s}}^{'}=\frac{m}{{{c}_{2}}{{P}_{\text{i}}}}\left( {{c}_{2}}{{P}_{\text{x}}}{{x}_{1}}/m-kS-{{c}_{1}}\dot{r}+{{c}_{1}}{{{\dot{x}}}_{1}}-{{c}_{2}}\ddot{r}+ \right. \\ & \left. {{c}_{2}}\text{Dsat}\left( S \right)/m-\xi \text{sat}\left( S \right) \right) \\ \end{align}$ | (24) |
引入
在仿真平台中将磁浮列车悬浮系统模块切换成线性化系统模型,设定悬浮电磁铁初始位置偏离平衡点8 mm,仿真时间为5 s,并令控制器参数τ = 0.1,Kp=4 000.得到悬浮体加速度、偏离平衡点的悬浮间隙偏差的响应和相轨迹如图 5~7所示.由图可知,悬浮系统在PD校正下能够逐渐收敛,若设定稳定域为2%,则悬浮间隙在4.7 s可达到稳定状态,最大超调量约为3.5%.

|
图 5 PD悬浮体加速度响应 Fig.5 Acceleration of magnet of PD |

|
图 6 PD悬浮间隙偏差响应 Fig.6 Response of suspension gap error of PD |

|
图 7 PD间隙偏差的相轨迹 Fig.7 Phase locus of the gap error of PD |
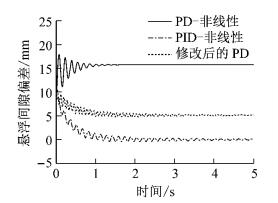
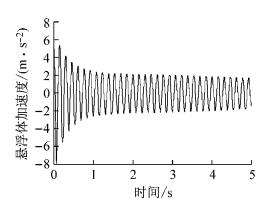
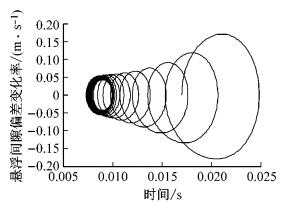
在仿真平台中将悬浮系统模块切换成非线性系统模型,将PD控制器应用于非线性模型,得到的响应如图 8中实线所示,可见偏离目标位置较大.说明从线性模型上整定的PD直接应用到非线性模型中控制效果变差.调整Kp=7 000,Kd=1 100,悬浮间隙偏差响应如图中点划线所示,随着系数的增加,静态误差变小,但比例系数的增加容易引起输入饱和、噪声等问题.所以对于非线性模型,引入积分环节来消除静态误差,此时PD控制器变为PID控制器,取Ki=900,悬浮间隙偏差响应如图 8中虚线所示,悬浮加速度和相轨迹如图 9和图 10.
|
图 8 悬浮间隙偏差响应 Fig.8 Response of suspension gap error |
|
图 9 改进后悬浮体加速度响应 Fig.9 Modified acceleration of magnet |
|
图 10 改进后悬浮间隙偏差相轨迹 Fig.10 Modified Phase locus of the gap error |
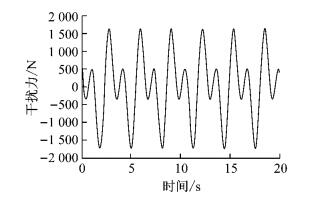
车辆在行驶中不可避免地受到扰动力作用(如:风力、台阶、电网突变产生的力等).为不失一般性,假设列车一直受到周期性的动态干扰力作用,如图 11所示[20-21].
|
图 11 动态干扰力 Fig.11 Disturbance force |
在系统仿真平台中选取非线性模型,并引入如图 11所示动态干扰,控制参数和初始条件保持不变,仿真时间设置为20 s,得到周期干扰下悬浮间隙偏差响应,如图 12,悬浮误差在±2 mm左右.由此可知PD控制律校正的方法虽然可以在一定范围干扰下保持稳定,但是鲁棒性不强,对持续的动态扰动较为敏感.

|
图 12 干扰下悬浮间隙偏差 Fig.12 Airgap error with disturbance |
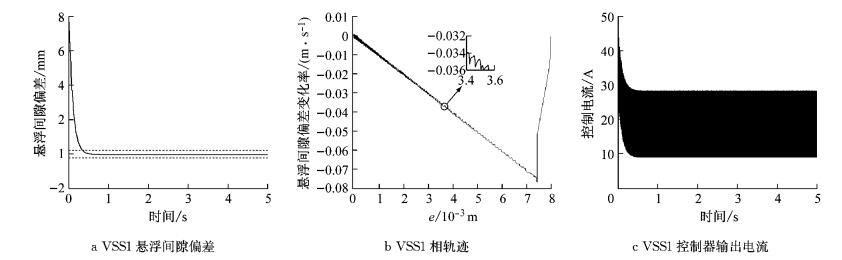
在仿真平台中选取非线性系统模型作为控制对象.根据设计的控制律式(22) 搭建非线性控制器VSS1并在仿真平台中接入相关反馈信号接口.取c1=10,c2=0,k=8,ξ=12.目标悬浮间隙为9 mm,电磁铁初始位置偏离平衡点8 mm,系统仿真结果如图 13所示.在仿真平台中引入如图 11所示的动态干扰,其他参数保持不变,系统仿真结果如图 14所示.
|
图 13 VSS1控制律仿真结果 Fig.13 Simulation results of VSS1 control law |

|
图 14 干扰下VSS1控制律仿真结果 Fig.14 Simulation results of VSS1 control law with disturbance |
由图可知,系统没有超调,在0.5 s之内基本完成调节变化,悬浮间隙响应比PD控制下响应更迅速,具有更好的动态性能和稳定性能,且对外部干扰表现出很强的鲁棒性.但是相轨迹在S=0的平面上存在锯齿形轨迹,控制器输出的控制量存在高频振荡,即系统的颤振.主要是因为理想开关的不存在的不连续性使得一维的滑动叠加了自振.
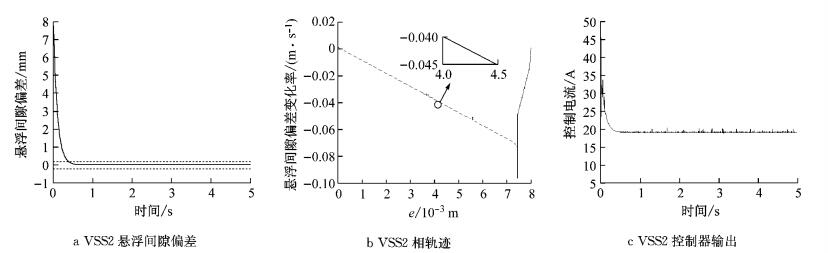
为了削弱颤振,减少能量消耗,防止控制器部件损坏,基于提出的改进型滑模控制律式(25) 搭建非线性控制器VSS2并在仿真平台中接入相关反馈信号接口.取边界层
|
图 15 改进后的滑模控制律仿真结果 Fig.15 Simulation results of modified sliding mode control law |
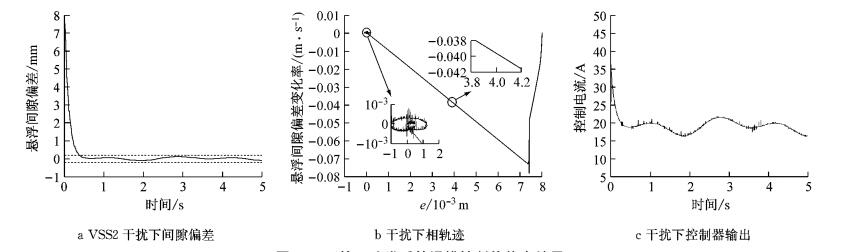
|
图 16 干扰下改进后的滑模控制律仿真结果 Fig.16 Simulation results of modified sliding mode control law with disturbance |
仿真结果表明,将可变边界层的准滑模控制方法和指数趋近律相结合是一种能够满足静态、动态调节性能并具有鲁棒性强、调节能力出色且能解决颤振问题的有效控制方法,减少系统能耗.
6 整车悬浮试验低速磁浮试验列车为五悬浮架结构, 每一个悬浮架由抗侧滚梁、直线电机、悬浮电磁铁、悬浮控制系统、迫导向机构等组成.整车动态试验在同济大学负责的国家低速磁浮示范线上进行.
悬浮控制装置包括悬浮传感器、悬浮控制电路和悬浮斩波器等.悬浮控制系统通过控制悬浮电磁铁电流的大小实现对悬浮气隙的调节和控制.悬浮传感器用于检测电磁铁与F形轨道间的间隙和间隙加速度,如图 17所示.传感器输入的信号通过变换得到相应的电信号,通过DSP(digital signal processor)进行控制算法运算,输出电磁铁需要的电流,根据实际反馈的电流输出PWM(脉冲宽度调制)脉冲信号给悬浮控制主电路,控制流程如图 18所示.

|
图 17 试验现场布置示意 Fig.17 Train experiment placement in the test |

|
图 18 悬浮控制程序框图 Fig.18 Block diagram of control program |
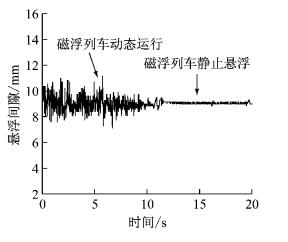
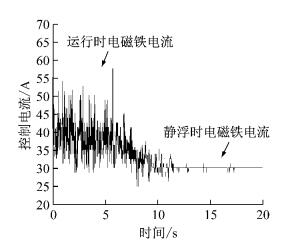
应用本文提出的VSS2控制器,悬浮目标间隙为9 mm.整车试验时悬浮间隙的响应如图 19所示,前10 s为磁浮列车以59 km·h-1运行时的间隙响应,10~20 s为减速至静止悬浮的悬浮间隙响应.由图 19可知,磁浮列车静态悬浮时,间隙保持在目标位置,控制电流平稳.动态运行时的悬浮间隙有波动,主要是由于轨缝导致.控制电流响应如图 20所示.
|
图 19 整车悬浮间隙响应 Fig.19 Suspension gap in the experiment |
|
图 20 控制电流响应 Fig.20 Control current in the experiment |
在磁浮列车运行时,台阶是不可避免的硬干扰.图 21a为磁浮列车过台阶时的悬浮间隙响应试验结果,图 21b为控制电流的响应.由图 21a可知,因为台阶的存在,14 s时悬浮间隙瞬间减小为3 mm,列车悬浮间隙的调节时间为1 s左右即恢复稳定.

|
图 21 台阶硬干扰下的响应 Fig.21 Response in the experiment across the step |
本文提出的改进后的滑模控制器更适用于工程实际.由整车试验结果分析可知,所设计的控制算法使系统稳定悬浮在目标间隙,动态性能好,鲁棒性强,有较强的抗干扰能力.
7 结论为了提高磁浮列车悬浮系统的控制性能,针对单点悬浮系统的外界扰动、非线性、时变性,提出了一种将可变边界层的准滑模控制方法和指数趋近律相结合的改进型滑模控制方法.在搭建的悬浮系统仿真平台上,通过和传统线性PD控制律进行仿真比较,结果表明,提出的改进型滑模控制律无超调、鲁棒性强、动态响应快速、系统跟踪性能好,对外界干扰具有良好的适应性,并且能消除传统滑模控制的颤振现象.在同济大学(国家)低速磁浮示范线上进行整车试验,结果表明该控制方法调节速度快,能有效抑制干扰,防止系统失稳,能更好地满足高性能磁浮列车悬浮系统对控制品质的要求.
| [1] |
SUN Yougang, LI Wanli, QIANG Haiyan, et al. An experimental study on the vibration of the low-speed maglev train moving on the guideway with sag vertical curves[J]. International Journal of Control and Automation, 2016, 9(4): 279 DOI:10.14257/ijca |
| [2] |
张佩竹. 我国中低速磁浮交通工程的自主创新技术研究[J]. 铁道工程学报, 2009, 133(10): 90 ZHANG Peizhu. Research on the technology for the self-innovation of low/medium-speed maglev traffic engineering[J]. Journal of Railway Engineering Society, 2009, 133(10): 90 DOI:10.3969/j.issn.1006-2106.2009.10.021 |
| [3] |
周晓明, 刘万明. 长沙中低速磁浮工程建设中的重要举措[J]. 城市轨道交通研究, 2016, 19(5): 1 ZHOU Xiaoming, LIU Wanming. Key technologies in the construction of medium and low speed maglev in Changsha city[J]. Urban Mass Transit, 2016, 19(5): 1 |
| [4] |
龙志强, 郝阿明, 常文森. 考虑轨道周期性不平顺的磁浮列车悬浮控制系统设计[J]. 国防科技大学学报, 2003, 25(2): 84 LONG Zhiqiang, HAO Aming, CHANG Wensen. Suspension controller design of maglev train considering the rail track periodical irregularity[J]. Journal of National University of Defense Technology, 2003, 25(2): 85 |
| [5] |
LINDLAU J D, KNOSPE C R. Feedback linearization of an active magnetic bearing with voltage control[J]. IEEE Transactions on Control Systems Technology, 2002, 10(1): 21 DOI:10.1109/87.974335 |
| [6] |
宋文荣, 于国飞, 王延风, 等. 磁悬浮微进给机构的PID控制[J]. 哈尔滨工业大学学报, 2004, 36(1): 28 SONG Wenrong, YU Guofei, WANG Yanfeng, et al. PID control of micro feed mechanism based on magnetic levitation technology[J]. Journal of Harbin Institute of Technology, 2004, 36(1): 28 |
| [7] |
戴利明, 齐斌, 周海波, 等. 磁悬浮运动平台的PID控制[J]. 现代制造工程, 2008(6): 79 DAI Liming, QI Bin, ZHOU Haibo, et al. PID control and experiment for magnetism levitation movement system[J]. Modern Manufacturing Engineering, 2008(6): 79 |
| [8] |
WAI R J, CHEN M W, YAO J X. Observer-based adaptive fuzzy-neural-network control for hybrid maglev transportation system[J]. Neurocomputing, 2016, 175: 10 DOI:10.1016/j.neucom.2015.10.006 |
| [9] |
王辉, 钟晓波, 沈钢. 一种新型磁悬浮线路设计方案及悬浮控制方法[J]. 同济大学学报(自然科学版), 2013, 41(7): 1112 WANG Hui, ZHONG Xiaobo, SHEN Gang. A new maglev line system design and control strategy[J]. Journal of Tongji University (Natural Science), 2013, 41(7): 1112 |
| [10] |
TRAN X T, KANG H J. Arbitrary finite-time tracking control for magnetic levitation systems[J]. International Journal of Advanced Robotic Systems, 2014(11): 1 |
| [11] |
WANG H, ZHONG X B, SHEN G. Analysis and experimental study on the maglev vehicle-guideway interaction based on the full-state feedback theory[J]. Journal of Vibration and Control, 2015, 12(2): 408 |
| [12] |
SU X, YANG X, SHI P, et al. Fuzzy control of nonlinear electromagnetic suspension systems[J]. Mechatronics, 2014, 24(4): 328 DOI:10.1016/j.mechatronics.2013.08.002 |
| [13] |
SUN Y G, QIANG H Y, LIN G B, et al. Dynamic modeling and control of nonlinear electromagnetic suspension systems[J]. Chemical Engineering Transactions, 2015(46): 1039 |
| [14] |
徐俊起. 基于力平衡的磁悬浮控制方法[J]. 电机与控制应用, 2010, 37(11): 20 XU Junqi. Magnetic suspension control method based on force balance[J]. Electric Machines & Control Application, 2010, 37(11): 20 DOI:10.3969/j.issn.1673-6540.2010.11.005 |
| [15] |
SUN Y G, Li W L, CHANG D F, et al. Dynamic and decoupling analysis of the bogie with single EMS modules for low-speed maglev train[J]. Advanced Science and Technology Letters, 2016, 121: 83 |
| [16] |
张思远. 磁悬浮数字控制技术[D]. 上海: 同济大学, 2009. ZHANG Siyuan. The design of digital control method for maglev[D]. Shanghai: Tongji University, 2009. |
| [17] |
QIN Y M, HUI P, RUAN W J, et al. A modeling and control approach to magnetic levitation system based on state-dependent ARX model[J]. Journal of Process Control, 2014, 24(1): 93 DOI:10.1016/j.jprocont.2013.10.016 |
| [18] |
RUDI U, ADHA I, OYAS W. Modified sliding mode control with uncertainties behavior of a magnetic levitation system [C]// 2013 International Conference on Robotics. Jogjakarta: IEEE, 2013, 823(1):194-199.
|
| [19] |
WAI R J, CHUANG K L, LEE J D. On-line supervisory control design for maglev transportation system via total sliding-mode approach and particle swarm optimization[J]. IEEE Transactions on Automatic Control, 2010, 55(7): 1544 DOI:10.1109/TAC.2010.2042228 |
| [20] |
FANG Y, FEEMSTER M, DAWSOM D. Nonlinear disturbance rejection for magnetic levitation systems[C]// Proceedings of the 2003 IEEE International Symposium on Intelligent Control. Houston: IEEE, 2003: 58-63.
|
| [21] |
MATTHEW G F, FANG Y C, DARREN M D. Disturbance rejection for a magnetic levitation system[J]. IEEE/ASME Transactions on Mechatronics, 2006, 11(6): 709 DOI:10.1109/TMECH.2006.886248 |
 2017, Vol. 45
2017, Vol. 45

