汽车的空气动力学性能与汽车的燃油经济性、操纵稳定性、安全性及舒适性密切相关.风洞试验可模拟汽车在空气中的行驶状态,是研究车辆空气动力学性能的重要手段[1].风洞来流风速的标定会影响阻力、升力、侧向力和力矩等气动力的测试精度.
传统的航空风洞通常都是闭口式风洞,多采用喷口法进行风洞来流风速的标定.汽车气动声学风洞通常采用开口式风洞,来流风速的标定多依据驻室法[2].两种标定方法均需要修正,其中基于风洞试验的来流风速修正方法耗费成本较高[3].随着计算机技术的发展,国内外研究人员利用数值仿真方法开展了一系列风洞修正研究,并将研究成果用以指导风洞试验的修正,极大地节省了研究成本[4].同时,数值仿真方法可直接计算监测点速度和压力,不需考虑支撑干扰对结果的影响[5].因此,对于研究风洞来流风速的标定方法这类问题,数值仿真技术具有极大的优势.然而,基于数值仿真技术,讨论喷口法和驻室法哪种方法更合适于汽车气动声学风洞来流速度标定的研究很少,且没有定论[6].
本文以1:15缩比模型风洞为研究对象,通过与模型风洞试验数据对比,验证了数值仿真方法的有效性.分析了空风洞中不同来流风速下,喷口法和驻室法推导的速度值与参考值之间的差值及修正系数.风洞中安装车辆,比较不同雷诺数下两种方法所得推导值的差异并给出了修正结果,最后解释了造成差异的原因.
1 模型和试验介绍 1.1 风洞模型本文研究平台为上海地面交通工具风洞中心1:15的3/4开口式汽车模型风洞.图 1为模型风洞的整体结构及三维模型,模型轴线总长度为14 227 mm,驻室试验段长度为1 000 mm,喷口出口尺寸为180 mm×434 mm×283 mm (长×宽×高),收缩段的收缩比为6:1,湍流度为0.38.模型风洞风速由变频风机控制,风机最大功率为7.5 kW,最高风速可达45 m·s-1.

|
图 1 模型风洞 Fig.1 Schematics of wind tunnel model |
试验采用皮托管测量测点处的静压与总压,热线风速仪测量测点处的速度.皮托管安装在二维移测架上进行坐标定位,头部对准来流,头部中心处小孔测来流总压P0.头部后约3~8 mm处的外套管壁上均匀地开有一排静压孔,测来流静压P.使用的热线探头是55P01型一维热线探头.试验工况为喷口速度30 m·s-1.

|
图 2 皮托管与移测架 Fig.2 Pitot tube and traversing system |
坐标原点定义为喷口截面的中轴位置在地面上的投影点O, 来流方向为x轴正方向,垂直地面方向为z轴,喷口展向为y轴.测点选在试验段对称面上距地面50 mm高度的轴向线上,以喷口出口平面上的点为起点,每隔50 mm间距设1个测点,创建20个测点,记为p1~p20,测点位置如图 3a所示.

|
图 3 计算域和网格 Fig.3 Computational domain and mesh |
计算域的设置:选取模型风洞的一部分,收缩段、试验段、扩散段建立简化的数值模型.为防止计算域出口处产生回流,增加了延长段.同时参照模型风洞,在试验段前端设置压力平衡口,平衡内外大气压.喷口出口截面尺寸为434 mm×283 mm,驻室尺寸为1 517 mm (长)×1 185 mm (宽)×818 mm (高).空风洞下,简化的数值计算域模型如图 3a所示.
汽车模型选用的是1:15的小轿车模型,如图 3b所示,模型尺寸为300 mm (长)×120 mm (宽)×90 mm (高),迎风面积约为8 081.8 mm2.由于放入汽车模型后存在一定的阻塞效应,导致风洞内有回流产生.为了充分考虑这种回流的影响,使流场的相互作用充分发挥达到稳定的状态,在收缩段的前端加设一段稳定段.
在整个计算区域创建非结构六面体网格,面网格最小为5 mm,最大为15 mm.空风洞体网格总数约为533万,有汽车模型的风洞计算域内体网格总数为707万.整个风洞壁面建立边界层网格,在试验段地面处、喷口处和收集口处分别创建五层边界层网格,使之满足非平衡壁面函数要求[7].
2.2 测点的布置首先设置收缩段入口位置的测压点,喷口法和驻室法在这个位置的测压点是重合的.沿收缩段入口长度方向取测量面,在收缩段的每个壁面和地面上均匀地选取7个测压点,共28个测压点.然后分别设置喷口法和驻室法在收缩段出口位置的测压点.喷口法将测压点设置在收缩段出口处喷口内侧,沿x方向取测量面,在收缩段出口处喷口内侧壁面和地面上均匀选取7个测压点,共28个测压点.驻室法将测压点设置在驻室内速度近乎为零的位置,沿x方向取测量面,在喷口每个外壁面上均匀选取7个测压点,共21个测压点.另外在试验中主要关心的是和汽车相关的风速的准确性,所以选择试验段对称面与喷口出口截面交线上距地面50 mm高度的点为参考点,以该点的速度值作为参考风速 (真实风速).最后,为了与试验结果对比验证计算方法的有效性,按照试验测点的位置设置了20个测点 (p1~p20).
2.3 湍流模型及边界设置采用基于雷诺时均法 (RANS) 方程框架中的可实现k-ε(其中k代表湍动能,ε代表湍流耗散率) 两方程涡黏性传输模型和非平衡壁面函数对计算域内湍流进行求解.进出口边界条件分别设为速度入口和压力出口条件,压力平衡口为入口通风口条件.根据汽车风洞实际使用情况,喷口的来流风速工况范围最大速度选择风洞最高速度45 m·s-1,最小速度选择5 m·s-1模拟汽车行驶的低速情况,具体工况设置如表 1所示.
| 下载CSV 表 1 速度工况表 Tab.1 Working conditions with different values of velocity |
计算时,先选用稳定的一阶格式,迭代1 000步后,再选用精度更高的二阶格式继续迭代大概10 000步,待残差收敛到1×10-5以下,同时计算域中观测点的速度值不再变化时,认为计算收敛.
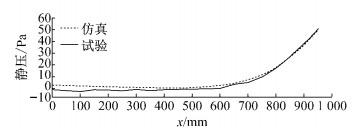
2.4 仿真结果的试验验证为保证此次数值仿真结果的真实可靠性,将空风洞下p1~p20测点的试验结果与数值仿真得到的静压值进行对比.如图 4所示,在喷口风速v=30 m·s-1的试验中,当测点与喷口的距离x大于0小于600 mm时, 静压保持不变.当x大于600 mm小于1 000 mm时,随着x的增大,静压也随之增大.数值仿真有效地模拟了试验中的变化趋势.在数值上,数值仿真与试验测得数据误差小于5%,在可接受的范围内.因此,在后续研究中均采用该数值仿真方法进行计算.
|
图 4 试验结果与数值仿真静压对比 Fig.4 Comparison of static pressure between test data and numerical results |
考虑试验成本和支撑干扰等问题,整车风洞中的试验风速测量通常是通过测量风压获取[8].具体的方法是通过测量收缩段入口静压PL和出口静压PS来得到压差,测压点位置如图 5所示.

|
图 5 喷口法与驻室法示意图 Fig.5 Schematics of nozzle method and plenum method |
通过动压的修正系数得到近似动压,再根据伯努利方程得到动压和风速之间的关系.动压和风速间的关系如下所示:
| $ {q_\infty } = \frac{1}{2}\rho U_\infty ^2 $ | (1) |
式中:ρ为空气密度;U∞为风速; q∞为动压.动压与压差测量值dP之间的关系如下所示:
| $ {q_\infty } = k{\rm{d}}P $ | (2) |
其中,dP=PL-PS,比例系数k的大小取决于风洞收缩比.联立式 (1) 和 (2) 可计算出喷口风速,如下所示:
| $ {U_\infty } = \sqrt {\frac{{2k({P_{\rm{L}}}-{P_{\rm{S}}})}}{\rho }} $ | (3) |
两种来流风速预估方法,即喷口法和驻室法的PS处理方式不同.其中,喷口法在收缩段出口处的喷口内侧分别设置一组静压孔,记作PS1; 驻室法是将收缩段出口处的测压点安置于驻室内速度近乎为零的位置,记作PS2,再根据经验公式得到风洞来流风速[9].
3.2 喷口法与驻室法结果对比分析分别将不同风速下仿真得到的PS1与PS2代入式 (3), 计算出相应喷口法风速v1和驻室法风速v2,参考风速为v,两个风速与参考点的速度分别作差比较得到喷口法与驻室法的风速误差.空风洞喷口法与驻室法下风速测量误差趋势如图 6所示.从图中可以看出, 两种测量方法的测量值与参考值存在一定误差,且误差值均是正值,也就是测量风速大于真实风速.驻室法比喷口法误差值略高,平均误差在0.2 m·s-1左右,并且随着风速的增加,误差值逐渐增大.因此,对于空风洞可以认为, 两种方法测量风速基本相同,与真实风速存在较小的误差.

|
图 6 空风洞下喷口法与驻室法风速测量误差对比 Fig.6 Comparison of velocity-measurement errors between nozzle method and plenum method in empty wind tunnel |
由于空风洞中不存在阻塞效应,来流不受反压力梯度的影响,故测量风速比较接近于真实风速,两种测量方法测得结果一致.同时由于计算压差时,喷口入口处的速度很小,将静压近似看作总压,忽略动压.随着风速的增大,PL与真实总压偏差也增大,因而测量误差值有上升趋势.
3.3 喷口法与驻室法的误差修正阻塞修正系数最早是在航空风洞中提出的[10].根据空风洞喷口法与驻室法测量结果可以看出,当k取1时,风速测量值与实际值的误差较大,平均误差为+0.2 m·s-1左右,因此需要标定k的值.通过联立式 (1) 和 (2) 可得
| $ k = {q_\infty }/{\rm{d}}P = \frac{1}{2}\rho U_\infty ^2/{\rm{d}}P $ | (4) |
运用式 (4) 对空风洞进行标定,喷口法和驻室法每种风速工况各对应一个修正系数.对所得的一系列修正系数运用Matlab拟合出空风洞下两种方法动压修正系数k关于真实风速的函数.喷口法修正系数k1如式 (5) 所示,驻室法修正系数k2如式 (6) 所示.相应曲线如图 7所示,其中v为参考风速.然后通过式 (3)、(5) 和 (6) 修正喷口法和驻室法的测量结果,修正前与修正后两种方法风速误差对比如图 8所示.图 8中,v′1为喷口法修正后速度, v′2为驻室法修正后速度.

|
图 7 修正系数曲线 Fig.7 Curves of correction coefficients |

|
图 8 空风洞下喷口法喷口与驻室法喷口与修正前后风速误差对比 Fig.8 Comparison of velocity-measurement errors between nozzle method and plenum method in empty wind tunnel before and after correction |
| $ \begin{array}{l} {k_1} =-1.434{\rm{ }}4 \times {10^{-7}}{v^4} + 1.737{\rm{ }}5 \times {10^{-5}}{v^3} - \\ \;\;\;\;\;\;\;7.634{\rm{ }}8 \times {10^{ - 4}}{v^2} + 0.014{\rm{ }}7v + 0.877{\rm{ }}9 \end{array} $ | (5) |
| $ \begin{array}{l} {k_2} =-1.431{\rm{ }}9 \times {10^{-7}}{v^4} + 1.745{\rm{ }}5 \times {10^{-5}}{v^3} - \\ \;\;\;\;\;\;\;7.746{\rm{ }}9 \times {10^{ - 4}}{v^2} + 0.015{\rm{ }}2v + 0.871{\rm{ }}1 \end{array} $ | (6) |
可以看出,k经过修正之后,喷口法和驻室法风速误差明显减小,误差平均值由原来的0.2 m·s-1下降到0.008 m·s-1左右,下降到可以接受的比较精准的范围内.同时通过方差的比较可以发现,驻室法的误差方差小于喷口法,驻室法修正结果更加稳定,对于不同工况的敏感程度较低,与风速的相关性比喷口法小.
4 有车工况下的结果分析 4.1 喷口法与驻室法结果对比分析当汽车置于风洞内进行测试时,会对上游流场产生影响,进而影响到喷口处的流场分布[11].在有小轿车的工况和第3节的空风洞一样,对最后的计算结果进行处理.图 9给出了有车工况下喷口法与驻室法风速测量误差计算结果.

|
图 9 有车工况下喷口法与驻室法风速测量误差对比 Fig.9 Comparison of velocity-measurement errors between nozzle method and plenum method with test model in wind tunnel |
可以发现,有车的情况下两种方法风速均存在较大的误差,同时随着风速的增加误差也有增大的趋势.此外, 两种方法的测量结果了有了明显的差别,驻室法风速误差值大于喷口法,喷口法的风速测量结果更接近参考风速.
分析原因主要是由于,模型前的反压力梯度会影响喷口内的流场,而参考风速测点位置取在喷口截面,放入车后受到阻塞比的影响,该处风速减小.喷口法测压点位置选在喷口内侧同样受到阻塞比的影响,而驻室法测点位置在驻室内,基本不受阻塞比影响,因此喷口法的测量结果更接近参考点风速.但喷口法与参考点风速之间仍存在一定误差,需要对测量结果进行相应的修正以保证结果的准确性.
4.2 喷口法与驻室法的误差修正根据空风洞标定结果提出的修正系数k1和k2对有车工况计算结果进行修正,修正后与未修正的风速误差对比如图 10所示.从图 10中可发现,无论是喷口法还是驻室法风速误差都有明显的降低,降低了0.21 m·s-1.喷口法经过修正后,风速计算结果与真实风速基本一致,这说明空风洞的标定对有车工况的修正是很有必要的.

|
图 10 有车工况下喷口法与驻室法修正前后风速误差对比 Fig.10 Comparison of velocity-measurement errors between nozzle method and plenum method with test model in wind tunnel before and after correction |
(1) 在空风洞中,对不同的来流风速下喷口法和驻室法风速进行计算,两种方法的结果相近,与监测值对比,都比较准确.这是由于空风洞中无障碍物的阻塞干扰,流场稳定且均匀.
(2) 通过动压修正系数对所得压差进行修正,并根据空风洞计算结果对喷口法和驻室法风速进行多项式拟合,提出了风速与修正系数之间的函数关系.空风洞风速的修正结果有明显改善,平均值从0.2 m·s-1下降到0.008 m·s-1.
(3) 在有车工况下喷口法和驻室法风速皆存在较大误差,在放入车后由于反压力梯度会影响喷口内的流场,驻室法风速误差大于喷口法.通过空风洞标定的修正系数可以使有车工况下喷口法和驻室法风速误差都下降0.21 m·s-1,说明提出的修正系数有效.
本文仅针对小轿车车型开展研究,下一步工作将针对有不同阻塞比的车型进行计算并修正.
| [1] |
谷正气. 汽车空气动力学[M]. 北京: 人民交通出版社, 2005 GU Zhengqi. Automobile aerodynamics[M]. Beijing: China Communications Press, 2005 |
| [2] |
张英朝. 基于仿真与实验的汽车风洞修正研究[D]. 长春: 吉林大学, 2010. ZHANG Yingchao. Automotive wind tunnel corrections based on numerical simulation and test[D]. Changchun: Jilin University, 2010. |
| [3] |
MERCKER E, WIEDEMANN J. On the correction of interference effects in open jet wind tunnels[R]. Detroit:SAE, 1996.
|
| [4] |
谢永慧. 合成射流对S809翼型不同攻角下流动分离控制的数值研究[C]//高等学校工程热物理第十九届全国学术会议: 热科学与技术. 郑州: 中国高等教育学会工程热物理专业委员会, 2013: 821-836. XIE Yonghui. Numerical investigation of S809 airfoil with synthetic jet actuator at different angles of attack[C]//College of Engineering Thermophysics Nineteenth National Conference:Journal of Thermal Science and Technology, Zhengzhou:China Institute of Higher Education Engineering Thermophysics Professional Committee, 2013:821-836. |
| [5] |
贾青, 杨志刚, 李启良. 汽车风洞实验段流场的试验研究[J]. 实验流体力学, 2011(6): 33 JIA Qing, YANG Zhigang, LI Qiliang. Test research of the flow field inside the test section of the automotive wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2011(6): 33 |
| [6] |
WICKERN G. Recent literature on wind tunnel test section interference related to ground vehicle testing[R]. Detroit:SAE, 2007.
|
| [7] |
LAUNDER B E, SPALDING D B. The numerical computation of turbulent flows[J]. Computational Methods in Applied Mechanics and Engineering, 1974, 3(2): 269 DOI:10.1016/0045-7825(74)90029-2 |
| [8] |
YEN J C, MARTINDALE W R, DUELL E G. The plenum method versus blockage corrected nozzle method for determining climatic wind tunnel air speed[R]. Detroit: SAE, 2004.
|
| [9] |
庞加斌, 刘晓晖, 陈力, 等. 汽车风洞试验中的雷诺数、阻塞和边界层效应问题综述[J]. 汽车工程, 2009(7): 609 PANG Jiabin, LIU Xiaohui, CHEN Li, et al. A review on Reynolds number blockage and boundary layer effects in automotive wind tunnel tests[J]. Automotive Engineering, 2009(7): 609 |
| [10] |
POPE A, HARPER J J. Low speed wind tunnel testing[M]. Hoboken: John Wiley & Sons, 1966
|
| [11] |
MERCKER E, WICKERN G, WEIDEMANN J. Contemplation of nozzle blockage in open jet wind-tunnels in view of different 'Q' determination techniques[R]. Detroit: SAE, 1997.
|
 2017, Vol. 45
2017, Vol. 45
