叶片为风电机组的主要部件，其寿命直接影响风力发电成本.疲劳测试作为风电叶片测试的重要环节，其目的在于测试叶片的疲劳寿命，同时提供试验数据给设计人员，改进风电叶片设计^[1-2].目前国内外风电叶片疲劳加载试验通常是以沿叶片展向的弯矩为试验依据，加载方法采用单点摆锤或液压加载进行疲劳性能测试^[3-4].多激振器同步加载疲劳试验风电叶片，可以解决单激振器功率有限的问题，但加载系统振动过程中存在着能量传递，构成了一个复杂的非线性机电耦合系统.多加载源振动系统耦合如何影响转子的运动状态是有待深入研究的问题，国内外研究人员在模型及数值仿真等方面展开了研究，取得了很多的成果^[5-9].风电叶片多激励疲劳加载系统中激振器之间是基于叶片柔性连接，激振器与风电叶片之间构成了一个复杂的非线性能量传递系统，振动耦合机理更复杂^[10].因此，研究其耦合振动特性，弄清基本耦合规律具有较大的现实意义.

基于以上原因，本文针对风电叶片电驱动双惯性同步激振疲劳加载系统，建立双激振器单点疲劳加载动力学模型，分析其在叶片共振条件下的稳定性条件，揭示耦合特性与机理，数值仿真得到不同加载频率下叶片的振动特性，并通过试验对理论推导结果的正确性进行验证，为更加深入研究风电叶片的疲劳加载打下基础.

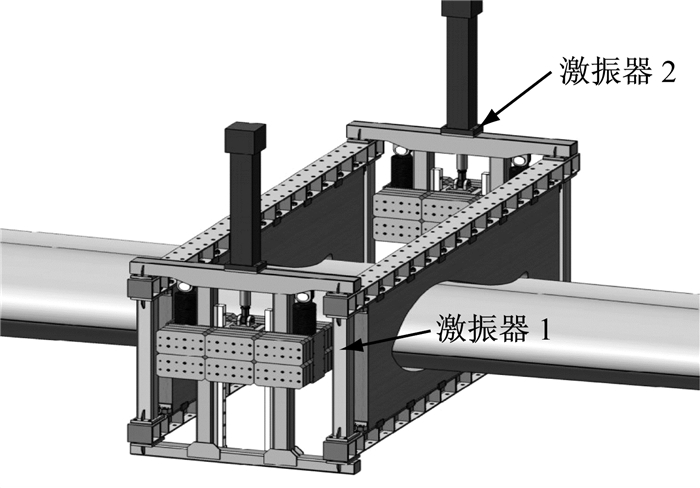
1 疲劳加载系统动力学模型

电驱动惯性叶片疲劳加载系统由疲劳加载装置、PC人机软件、就地控制柜、激光测距仪及应变仪构成，其中疲劳加载装置如图 1所示.激振器驱动质量块往复简谐运动，产生惯性力驱动叶片振动，控制调节双激振器质量块往复运动速度，使其同步运动，通过激振频率接近叶片固有频率，使叶片加载系统达到共振状态.通过改变激振器的安装方式，可实现叶片挥舞方向或摆振方向的加载.

对风电叶片疲劳加载系统建模时，假设叶片振动时，阻尼力和弹性力分别为振动速度和位移的线性函数.在上述假设条件下，建立风电叶片疲劳加载系统动力学模型如图 2所示.图中，oxyz为绝对坐标，o′x′y′z′为动坐标，o″为整个系统的质心，o₁和o₂为两质量块的运动位置；φ为坐标系间夹角，M为叶片和加载源固定部分的总质量；m_i为质量块i的质量；s_i为质量块i的运动行程；θ_mi为丝杠的相位角，θ_i(i=1, 2) 为质量块的相位角，ω_i为两质量块的角速度，ω_mi为丝杠角速度，且 $ {{\omega }_{{{m}_{i}}}}={{{\dot{\theta }}}_{{{m}_{i}}}} $，$ {{\omega }_{i}}={{{\dot{\theta }}}_{i}} $，.l_i=oo_i，l_i1为oo_i在oxy坐标平面内的投影，l_i2为oo_i在oyz坐标平面内的投影(i=1, 2)；l₀为oo′′′在oxy坐标平面内的投影；β_i1为l_i1与x轴正方向夹角，β_i2为l_i2与z轴正方向夹角，β₀为l₀与y轴负方向的夹角.

图 2中按照拉格朗日方程法，以x, y, φ, θ_mi(i=1, 2) 为广义坐标，求出系统动能、势能及能量散逸函数，建立该振动系统的动力学方程

$ \left\{ \begin{array}{l} \left( {M + \sum\limits_{i = 1}^2 {{m_i}} } \right)\ddot x + {c_x}\dot x + {k_x}x = 0\\ \left( {M + \sum\limits_{i = 1}^2 {{m_i}} } \right)\ddot y + {c_y}\dot y + {k_y}y = \sum\limits_{i = 1}^2 {{m_i}{s_i}\left( {{{\dot \theta }_i}\sin {\theta _i} - } \right.} \\ \;\;\;\;\;\;\;\left. {{{\ddot \theta }_i}\sin {\theta _i}} \right)\\ \left( {{J_z} + Ml_0^2 + \sum\limits_{i = 1}^2 {{m_i}{l^2}} } \right)\ddot \varphi + {c_\varphi }\dot \varphi + {k_\varphi }\varphi = \\ \;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^2 {{m_i}{l_{i1}}\cos {\beta _{i1}}\left( {{{\ddot \theta }_i}\cos {\theta _i} - {{\dot \theta }_i}\sin {\theta _i}} \right)} \\ {J_i}{{\ddot \theta }_{{m_i}}} = {T_i} - {m_i}\frac{{{P_h}}}{{2\pi }}\left( {\ddot y - {l_{i1}}\ddot \varphi \cos {\beta _{i1}} + {{\ddot \theta }_{{m_i}}}\frac{{{P_h}}}{{2\pi }}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {i = 1,2} \right) \end{array} \right. $

(1)

式中: k_x、k_y、k_φ分别为x、y、φ方向上叶片刚度系数；c_x、c_y、c_φ分别为x、y、φ方向上的阻尼系数；J_0i为系统绕x、z轴转动的转动惯量；J_i为电动缸i的转动惯量；T_mi为电动缸i轴上的电磁转矩(i=1, 2);P_h为丝杠导程.

系统中采用永磁同步电动(PMSM)三相星型绕组连接，基于d-q方式对PMSM进行建模，可得到永磁同步电机的方程为

$ \left\{ \begin{array}{l} {{\dot i}_d} = {p_{\rm{n}}}{\omega _{\rm{m}}}{i_{\rm{q}}} - \frac{{{R_{\rm{s}}}{i_d}}}{L} + \frac{{{u_d}}}{L}\\ {{\dot i}_q} = - {p_{\rm{n}}}{\omega _{\rm{m}}}{i_d} - \frac{{{R_{\rm{s}}}{i_q}}}{L} - \frac{{{p_{\rm{n}}}{\omega _{\rm{m}}}{\psi _{\rm{f}}}}}{L} - \frac{{{u_q}}}{L}\\ {{\dot \omega }_{\rm{m}}} = \frac{{{T_{{\rm{em}}}}}}{{{J_{\rm{m}}}}} - \frac{{{c_{\rm{m}}}{\omega _{\rm{m}}}}}{{{J_{\rm{m}}}}} - \frac{{{T_L}}}{{{J_{\rm{m}}}}}\\ {{\dot \theta }_{\rm{m}}} = {\omega _{\rm{m}}} \end{array} \right. $

(2)

式中：u_d、u_q为d、q轴定子电压分量；i_d、i_q为d、q轴定子电流分量；ψ_d、ψ_q为d、q轴定子磁链；R_s为定子电阻；p_n为磁极对数; T_em为电机电磁转距; T_L为负载转矩；J_m为转子和负载的总转动惯量；ω_m为电机转子机械角速度; c_m为摩擦系数；L_d、L_q为定子绕组d、q轴等效电感，L_d=L_q=L.

式(1) 和式(2) 联合构成了风电叶片双激振器单点疲劳加载振动系统的数学模型，该模型表现振动系统内部各参数之间关系中的变量彼此耦合，影响整个振动系统耦合特性的因素主要是初始相位差、加载力矩、激振频率、叶片各个方向的刚度和阻尼以及电机的机械特性等.

2 疲劳加载系统的耦合近似解析

为了分析激振器在理想状态下的电机转矩变化情况，即m_i=m₀，s_i=s₀，l_i1=l₀，β_i1=β₀ (i=1, 2)，采用小参数周期平均法对方程组进行近似求解.设加载系统稳态运行时两激振器(质量块)平均相位为θ，相位差为α，平均角速度为ω₀，则激振器的相位分别为θ₁和θ₂，振动系统运行时激振器平均角速度的波动系数为ε₁，瞬时相位差相对于平均角速度的波动系数为ε₂，可得

$ \left\{ \begin{array}{l} {\theta _1} = \theta + \alpha /2\\ {\theta _2} = \theta - \alpha /2\\ \dot \theta = {\omega _0}\left( {1 + {\varepsilon _1}} \right)\\ \dot \alpha = {\omega _0}{\varepsilon _2} \end{array} \right. $

(3)

可得两激振器的瞬时速度和加速度分别为$ \dot{\theta } $、$ {{\ddot{\theta }}_{i}} $ (i=1, 2)

$ \left\{ \begin{array}{l} {{\dot \theta }_1} = {\omega _0}\left( {1 + {\varepsilon _1} + {\varepsilon _2}} \right)\\ {{\dot \theta }_2} = {\omega _0}\left( {1 + {\varepsilon _1} - {\varepsilon _2}} \right)\\ {{\ddot \theta }_1} = {\omega _0}\left( {{{\dot \varepsilon }_1} + {{\dot \varepsilon }_2}} \right)\\ {{\ddot \theta }_2} = {\omega _0}\left( {{{\dot \varepsilon }_1} - {{\dot \varepsilon }_2}} \right) \end{array} \right. $

(6)

若当时间t→∞时，系统在单周期T=2π/ω内$ \dot{\theta } $和$ \dot{\alpha } $波动系数的均值为0，即$ {{{\bar{\varepsilon }}}_{1}}=0 $，$ {{{\bar{\varepsilon }}}_{2}}=0 $则系统实现频率俘获，振动系统实现同步激振状态，且两激振器在单周期内的平均角速度均为ω₀.

系统稳态运行时，由于$ {{{\dot{\varepsilon }}}_{1}}\ll 1 $, $ {{{\dot{\varepsilon }}}_{2}}\ll 1 $，在计算中可以忽略$ {{{\ddot{\theta }}}_{i}} $的影响，取φ的平衡点为0点.因此，将式(4) 代入式(1) 前2个方程并忽略二阶项可得

$ \left\{ \begin{array}{l} \ddot y + \frac{{{c_y}}}{m}\dot y + \omega _y^2y = \omega _0^2p\left[ {{{\left( {1 + {\varepsilon _1} + {\varepsilon _2}} \right)}^2}\sin \left( {\theta + \alpha /2} \right) + } \right.\\ \;\;\;\;\;\;\;\left. {{{\left( {1 + {\varepsilon _1} - {\varepsilon _2}} \right)}^2}\sin \left( {\theta - \alpha /2} \right)} \right]\\ \ddot \varphi + \frac{{{c_\varphi }}}{{{J_\varphi }}}\dot \varphi + \omega _\varphi ^2\varphi = \omega _0^2q\cos {\beta _0}\left[ {{{\left( {1 + {\varepsilon _1} - {\varepsilon _2}} \right)}^2}\sin \left( {\theta - } \right.} \right.\\ \;\;\;\;\;\;\left. {\left. {\alpha /2} \right) + {{\left( {1 + {\varepsilon _1} + {\varepsilon _2}} \right)}^2}\sin \left( {\theta + \alpha /2} \right)} \right] \end{array} \right. $

(5)

式中：$ p={{m}_{0}}{{s}_{0}}/m $；$ q={{m}_{0}}{{l}_{0}}{{s}_{0}}/{{J}_{\varphi }} $；$ {{\omega }_{y}}=\sqrt{{{k}_{y}}/m} $；$ {{\omega }_{\varphi }}=\sqrt{{{k}_{\varphi }}/{{J}_{0}}} $.

与θ关于t变化相比，α、ε₁、ε₂较小且相对于平均角速度ω₀是慢变的，系统位移响应可以用平均速度下的位移响应来近似替代.根据线性方程的叠加原理，可以得到振动系统y和φ方向的稳态响应为

$ \left\{ \begin{array}{l} y = {A_y}\left[ {\sin \left( {\theta + \alpha /2 + {\gamma _y}} \right) + \sin \left( {\theta - \alpha /2 + {\gamma _y}} \right)} \right]\\ \varphi = {A_\varphi }\left[ {\sin \left( {\theta + \alpha /2 + {\gamma _\varphi }} \right) + \sin \left( {\theta - \alpha /2 + {\gamma _\varphi }} \right)} \right] \end{array} \right. $

(6)

式中：$ {{A}_{y}}=p/\sqrt{{{\left[{{\left( {{\omega }_{y}}/{{\omega }_{0}} \right)}^{2}}-1 \right]}^{2}}+{{\left( {{c}_{y}}/m \right)}^{2}}} $；

$ \begin{array}{l} {A_\varphi } = - q/\sqrt {{{\left[ {{{\left( {{\omega _\varphi }/{\omega _0}} \right)}^2} - 1} \right]}^2} + {{\left( {{c_\varphi }/m} \right)}^2}} ;\\ {\gamma _y} = \arctan \left[ {{c_y}{\omega _0}/\left( {{k_y} - m\omega _0^2} \right)} \right];\\ {\gamma _\varphi } = \arctan \left[ {{c_\varphi }{\omega _0}/\left( {{k_\varphi } - m\omega _0^2} \right)} \right]. \end{array} $

由式(1) 可知电动机的负载转矩由振动阻矩与惯性转矩构成，将式(5) 对时间求二阶全微分，并略去ε₁, ε₂的二阶高次项，得

$ \left\{ \begin{array}{l} \ddot y \approx \frac{{{\partial ^2}y}}{{\partial {\theta ^2}}}\omega _0^2 + 2\frac{{{\partial ^2}y}}{{\partial {\theta ^2}}}\omega _0^2{\varepsilon _1} + 2\frac{{{\partial ^2}y}}{{\partial \theta \partial \alpha }}\omega _0^2{\varepsilon _2} + \\ \;\;\;\;\;\;\frac{{\partial y}}{{\partial \theta }}{\omega _0}{{\dot \varepsilon }_1} + \frac{{\partial y}}{{\partial \alpha }}{\omega _0}{{\dot \varepsilon }_2}\\ \ddot \varphi \approx \frac{{{\partial ^2}\varphi }}{{\partial {\theta ^2}}}\omega _0^2 + 2\frac{{{\partial ^2}\varphi }}{{\partial {\theta ^2}}}\omega _0^2{\varepsilon _1} + 2\frac{{{\partial ^2}\varphi }}{{\partial \theta \partial \alpha }}\omega _0^2{\varepsilon _2} + \\ \;\;\;\;\;\;\frac{{\partial \varphi }}{{\partial \theta }}{\omega _0}{{\dot \varepsilon }_1} + \frac{{\partial \varphi }}{{\partial \alpha }}{\omega _0}{{\dot \varepsilon }_2} \end{array} \right. $

(7)

将式(7) 与式(3)、(4) 一起代入式(1) 的第4式，并在0~2π内积分，求取一个周期内负载转矩的平均值.由于ε₁≪1，ε₂≪1，且相对于ω₀是慢变的，所以在一个运转周期内可将α、ε₁、ε₂、$ {{{\dot{\varepsilon }}}_{1}} $、$ {{{\dot{\varepsilon }}}_{2}} $取其各自的均值$ {\bar{\alpha }} $、$ {{\bar{\varepsilon }}_{1}} $、$ {{\bar{\varepsilon }}_{2}} $、$ {{\bar{\dot{\varepsilon }}}_{1}} $、$ {{\bar{\dot{\varepsilon }}}_{2}} $，得到负载转矩均值微分方程：

$ \left\{ \begin{array}{*{35}{l}} {{J}_{0}}\omega _{0}^{2}{{\left( {{{\bar{\dot{\varepsilon }}}}_{1}}-{{{\bar{\dot{\varepsilon }}}}_{2}} \right)}^{2}}+{{c}_{1}}\omega _{0}^{2}\left( 1+{{{\bar{\varepsilon }}}_{1}}+{{{\bar{\varepsilon }}}_{2}} \right)\left( {{{\bar{\dot{\varepsilon }}}}_{1}}+{{{\bar{\dot{\varepsilon }}}}_{2}} \right)= \\ \ \ \ \ \ \ {{T}_{1}}{{\omega }_{0}}\left( {{{\bar{\dot{\varepsilon }}}}_{1}}+{{{\bar{\dot{\varepsilon }}}}_{2}} \right)-{{{\bar{W}}}_{\text{TL1}}} \\ {{J}_{0}}\omega _{0}^{2}{{\left( {{{\bar{\dot{\varepsilon }}}}_{1}}-{{{\bar{\dot{\varepsilon }}}}_{2}} \right)}^{2}}+{{c}_{1}}\omega _{0}^{2}\left( 1+{{{\bar{\varepsilon }}}_{1}}-{{{\bar{\varepsilon }}}_{2}} \right)\left( {{{\bar{\dot{\varepsilon }}}}_{1}}+{{{\bar{\dot{\varepsilon }}}}_{2}} \right)= \\ \ \ \ \ \ \ {{T}_{1}}{{\omega }_{0}}\left( {{{\bar{\dot{\varepsilon }}}}_{1}}-{{{\bar{\dot{\varepsilon }}}}_{2}} \right)-{{{\bar{W}}}_{\text{TL2}}} \\ \end{array} \right. $

(8)

$ \left\{ \begin{array}{l} {{\bar W}_{{\rm{TL1}}}} = {m_0}{s_0}\omega _0^2\cos {\theta _1}\left( {\ddot y - {l_{i1}}\ddot \varphi \cos {\beta _{i1}}} \right)\\ {{\bar W}_{{\rm{TL2}}}} = {m_0}{s_0}\omega _0^2\cos {\theta _2}\left( {\ddot y - {l_{i1}}\ddot \varphi \cos {\beta _{i1}}} \right) \end{array} \right. $

(9)

式中：$ {{J}_{0}}={{J}_{i}}+{{m}_{i}}{{\left( {{P}_{\text{h}}}/2\text{ }\!\!\pi\!\!\text{ } \right)}^{2}} $.

实现频率俘获的前两个条件为这两项同时为$ {{{\bar{\varepsilon }}}_{1}}=0 $和$ {{{\bar{\varepsilon }}}_{2}}=0 $，将式(9) 两式分别相减，并考虑$ \dot{\alpha }={{\omega }_{0}}{{\varepsilon }_{2}} $，把式(7) 代入式(8) 整理可得

$ \Delta {{\bar W}_{{\rm{TL}}}} = {{\bar W}_{{\rm{TL1}}}} - {{\bar W}_{{\rm{TL2}}}} = m_0^2s_0^2{\omega ^4}W\sin \alpha $

(10)

式中：$ W=\frac{l_{0}^{2}{{\cos }^{2}}{{\beta }_{0}}\ \cos \ {{\gamma }_{\varphi }}}{{{J}_{\varphi }}-{{k}_{\varphi }}/\omega _{0}^{2}}-\frac{\cos \ {{\gamma }_{y}}}{N-{{k}_{y}}/\omega _{0}^{2}} $

由式(9)、(10) 可以看出，振动系统对相位超前的激振器施加阻力矩，对相位滞后的激振器施加了驱动力矩，而这个力矩大小与sin α成正比.从数学表达式上看振动系统与动力系统通过负载转矩相互影响，当激振器相位差α=±π/2时两电机的负载转矩差最大，两电机速度变化趋势最大，说明此时相位差为最不稳定点，系统通过调节两激振器的相位差，调节两电动机负载转矩来实现系统同步.

在同步运转状态的邻近区域，若设J₁≈J₂=J₀，$ {{{\ddot{\theta }}}_{2}}-{{{\ddot{\theta }}}_{1}}\approx \ddot{\alpha } $，$ {{{\dot{\theta }}}_{2}}-{{{\dot{\theta }}}_{1}}\approx \dot{\alpha } $($ {\ddot{\alpha }} $和$ {\dot{\alpha }} $均为微小的量)，这时两个激振器相位角差对时间的运动微分方程式可表示为

$ {J_0}\ddot \alpha + {c_{{\rm{eq}}}}\dot \alpha + m_0^2s_0^2{\omega ^4}W\sin \alpha = \Delta {T_{\rm{g}}} - \Delta {T_{\rm{f}}} $

(11)

式中：c_eq为当量阻力矩系数；$ {\dot{\alpha }} $为角速度之差；$ {\ddot{\alpha }} $为角加速度之差.

假设系统相位差角α的常值α₀是系统的同步点，Δα为相位差小变量，常值α₀可由下式求出：

$ \sin {\alpha _0} = \frac{{\Delta {T_{\rm{g}}} - \Delta {T_{\rm{f}}}}}{{m_0^2s_0^2{\omega ^4}W}} $

(12)

代入式(11) 消去α₀，可求出判别同步运转状态稳定性的扰动方程式

$ {J_0}\Delta \ddot \alpha + {c_{{\rm{eq}}}}\dot \alpha + m_0^2s_0^2{\omega ^4}\left( {W\cos {\alpha _0}} \right) \cdot \Delta \alpha = 0 $

(13)

运动状态是否稳定要由W cos α₀的正负来决定，式(13) 的特征方程可表示为

$ {J_0}{\lambda ^2} + {c_{{\rm{eq}}}}\lambda + m_0^2s_0^2{\omega ^4}\left( {W\cos {\alpha _0}} \right) = 0 $

(14)

如要式(13) 的解收敛于零，需满足的条件为

$ c_{{\rm{eq}}}^2 - 4{J_0}m_0^2s_0^2{\omega ^4}\left( {W\cos {\alpha _0}} \right) < 0 $

(15)

由式(15) 知，相位差同步稳定点Δα与耦合系数W、阻尼系数c_eq、转动惯量等参数密切相关.耦合系数与各方向的刚度比、阻尼比及响应状态密切相关，同时与达到稳定点的速度与旋转轴的阻尼系数密切相关.从稳定性条件可得，较大惯量和驱动矩对系统稳定是有益的.

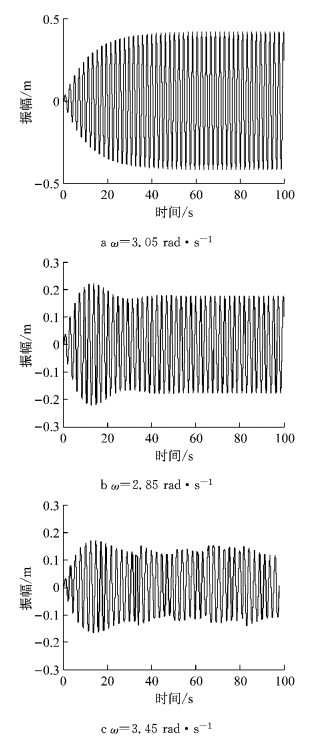
3 疲劳加载过程数值仿真分析

采用Matlab软件对加载过程的振动特性进行数值仿真，部分参数定义如下：叶片质量M=14 743 kg，质量块m₁=m₂=1 000 kg，加载点刚度值k=230 kN·m^-1，阻尼比ξ=0.025.激振频率分别取ω=3.05 rad·s^-1、ω=2.85 rad·s^-1和ω=3.45 rad·s^-1，仿真结果如图 3所示.从仿真曲线可以看出，当质量块角速度ω=3.05 rad·s^-1时，激振频率接近于叶片的低阶固有频率，曲线见图 3a，叶片振幅逐渐增大，最后趋于稳定；当激振频率小于叶片的固有频率，且偏差较大时，曲线见图 3b，叶片振幅规则波动后稳定.当激振频率大于叶片固有频率，且偏差较大时，曲线见图 3c，叶片振幅也产生波动，但振幅趋势逐渐变小，最终基本趋于稳定.

采用相图法来表示非线性二阶系统的动态特性，针对该系统忽略重力影响，仅考虑垂直方向的运动，将式(1) 运动微分方程数学模型简化成自治系统^[11].定义z′、z″为参数T的一阶、二阶微分；T=ωt, i=p_h/2π, $ \omega =\sqrt{{{k}_{y}}/m} $, $ z=y\sqrt{m/\left( {{J}_{\text{m}}}+{{i}^{2}} \right)} $，μ=c_y/(J_m+i²)ω，λ=c_y/mω, $ \sigma ={{m}_{1}}i/\sqrt{m\left( {{J}_{\text{m}}}+{{i}^{2}} \right)} $，τ=T_m/[(J_m+i²)ω²].对四维相空间定义共振超平面：ω=dθ/dt=1，ω是系统固有频率.初始参数取，z′(0)=z(0)=0，θ′(0)=θ(0)=0.

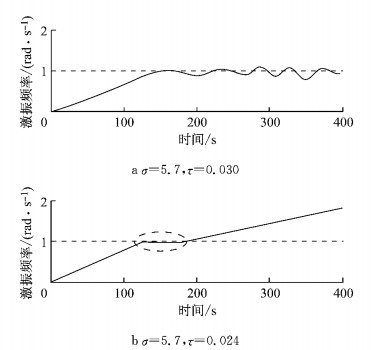
改变参数σ数值仿真，频率曲线如图 4所示.从图 4a可看出，z方向位移随着激振频率增大而增大，当达到130 s时，在共振点ω=1附近振荡，激振器与叶片频率逐渐同步，位移逐渐增大.从图 4b中可看出，随着激振频率递增，当达到130 s时，激振频率曲线出现一段水平，z方向振幅最大，但立刻又发生频率超越，激振继续增大，z方向振幅却逐渐变小，并最终趋于稳定.

4 试验及分析

将某型2.0 MW叶片根部固定在筒型加载支座上，在叶片的25 m处夹具上固定加载装置，沿叶片展向35 m处添加400 kg及47 m处添加700 kg的配重块.试验环境温度为20 ℃、湿度为30%，测试过程中对频率、应变、位移等进行监控，应变片位置确定为监控关键截面，应变仪精度为0.3%，激光测距仪分辨率取0.1 mm，测距30 m.试验现场如图 5所示.

试验时采用虚拟主令控制策略，图 6为控制同步下的相位差实测曲线.在控制作用下相位差能维持在0°附近，能消除自同步带来的相位差.加载试验装置中电机与质量块之间通过丝杠传动，相位差的波动较小，其值约±2°左右，控制同步减小了耦合作用对电动机的影响.在满足电动机功率的条件下对双激振器加载的同步控制是可行的.

频率扫描搜索测试叶片振幅变化，扫频下叶片振幅与时间的关系曲线如图 7所示.频率接近于叶片低阶固有频率进行疲劳试验，叶片振幅逐渐增大，加载装置能很好地捕捉叶片共振点.

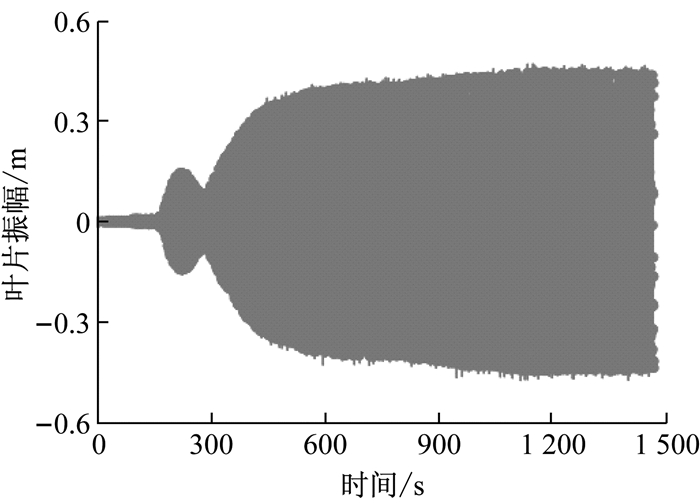
采用激光测距仪对叶片振动位移进行测量，数据采样时间30 ms，振幅与时间的关系曲线如图 8所示.振幅逐步达到共振峰值并趋于稳定，叶片加载点稳定幅值约为0.41 m，加载点振幅只有微小变化，峰值变化率误差为5%.叶片疲劳测试中，动态应变仪实时记录叶片各点载荷应变值，在加载点附近区域的应力超过叶片材料的条件疲劳极限，该区域的主梁帽承受了较大载荷.

5 结论

(1) 针对风电叶片电驱惯性同步激振疲劳加载系统，建立了叶片双激振器单点疲劳加载的机电耦合数学模型，得到影响整个振动系统耦合特性的因素主要是相位差、加载力矩、激振频率、叶片各个方向的刚度和阻尼、电机的机械特性等.

(2) 机械振动系统与动力系统通过负载转矩相互影响，而负载转矩会影响电动机速度，激振器相位差π/2时相位差为最不稳定点，调节两电动机负载转矩来实现系统激振器同步，耦合系数与稳定点速度等参数密切相关，较大惯量和驱动矩对系统的稳定是有益的.

(3) 运用数值仿真和试验方法对不同加载频率下叶片振动曲线进行了验证，若两者频率相近时，叶片稳定振幅达到最大，两激振器之间相位也逐渐增大，共振时达到最大，控制同步方式可消除相位差，叶片应变不会发生突变波动，使叶片振幅及应变误差减小，试验过程获取叶片振动参数方法正确可靠.