2. 同济大学 道路与交通工程教育部重点实验室,上海 201804
2. Key Laboratory of Road and Traffic Engineering of the Ministry of Education, Tongji University, Shanghai 201804, China
目前,故障诊断工作主要集中在针对具体系统或者特定故障选择合适的检测、诊断推理或者计算策略,但对于一个系统而言,系统故障可分离性是客观存在的,仅与系统的测量信息有关,或者说与系统的结构有关.若一个系统故障不可分离,采用传统的故障诊断思路则只是徒劳,若一个系统故障可分离,但诊断推理的结果却是空白,则只能说明采用的推理算法或过程错误.故对系统故障可分离性的分析是实现故障诊断的有效前提,而本文就是对一般系统的故障可分离性进行探讨,并且付诸列车轮对装置的诊断实践.
目前,故障诊断工作主要集中在针对具体系统或者特定故障选择合适的检测、诊断推理或者计算策略,但对于一个系统而言,系统故障可分离性是客观存在的,仅与系统的测量信息有关,或者说与系统的结构有关.若一个系统故障不可分离,采用传统的故障诊断思路则只是徒劳,若一个系统故障可分离,但诊断推理的结果却是空白,则只能说明采用的推理算法或过程错误.故对系统故障可分离性的分析是实现故障诊断的有效前提,而本文就是对一般系统的故障可分离性进行探讨,并且付诸列车轮对装置的诊断实践.
故障诊断是依靠测量信息中包含的状态特征或故障特征实现的[1-4],是指诊断推理算法能够识别出系统的状态特征[5],而故障分离是指进一步确认系统的状态并分离出实际故障,定位故障发生的部位及机理分析等.可见,可诊断性是第一位的,可分离性是第二位的,即诊断的任务首先是识别、确认或预报故障的发生,而进一步才是故障的分离与定位,分离定位是建立在可诊断的基础上的[6].
但有时仅凭借系统表现出来的现象和测量信息,获得的系统状态特征往往是不完善和不确定的;或存在特定的几类故障,它们几乎都可能发生,它们的故障测量特征也几乎相同,那么,所设计的诊断推理策略是否有足够的能力或者是在什么样的条件下能将这几种故障分离开来,即测量特征的分辨能力问题;或者由于系统存在大量的过程噪声(包括扰动和通道噪声等),系统特征被淹没在噪声之中,而诊断推理策略是否有足够的能力提取状态特征以识别和确认系统故障,这些都需要先对故障分离问题进行探讨.
从数学上来看,如式(1) 所示离散线性系统:
| $\left\{ \begin{array}{l} \left[ \begin{array}{l} {x_1}\left( {k + 1} \right)\\ {x_2}\left( {k + 1} \right) \end{array} \right] = \left[ \begin{array}{l} 1,1\\ 1,1 \end{array} \right]\left[ \begin{array}{l} {x_1}\left( k \right)\\ {x_2}\left( k \right) \end{array} \right] + \left[ \begin{array}{l} {b_1}\\ {b_2} \end{array} \right]u\left( k \right)\\ y\left( k \right) = \left[ {1,1} \right]\left[ \begin{array}{l} {x_1}\left( k \right)\\ {x_2}\left( k \right) \end{array} \right] \end{array} \right.$ | (1) |
尽管系统是不完全能观,但是显然任何一个状态对系统输出都是有影响的(除去这样的x1(0)=x2(0)=0特殊情况),通过连续的监视性测量可以确认故障的发生,然而其故障却是不可分离的,因为通过系统输出所观测到的是两个状态之和x1(t)+x2(t).
设系统Σ1的数学模型为
| ${\Sigma _1}:\mathit{\boldsymbol{y}}\left( t \right) = p\left( {\mathit{\boldsymbol{x}}\left( t \right),\mathit{\boldsymbol{u}}\left( t \right)} \right)$ | (2) |
式中:u(t)∈Rl是外部激励;x(t)∈Rn是系统的行为;y(t)∈Rm是行为所导致的输出; p是泛函算子.
所谓的不可分离问题就是:对可诊断的x1∈ Rn和x2∈Rn,x1≠x2,以及任意的激励u(t)∈Rl,相应的输出是y1(t)∈Rm,y2(t)∈Rm,在诊断推理机的映射δ1的作用下有式(3) 成立:
| $\begin{array}{l} {\delta _1}\left( {{\mathit{\boldsymbol{y}}_1}\left( t \right),\mathit{\boldsymbol{u}}\left( t \right)} \right) = \left( {{\rm{or}} \approx } \right)\\ {\delta _1}\left( {{\mathit{\boldsymbol{y}}_2}\left( t \right),\mathit{\boldsymbol{u}}\left( t \right)} \right) \in R\left( {特征集合} \right) \end{array}$ | (3) |
实际上,所谓的状态故障的可分离性问题,通常也包括故障诊断的深度或程度问题,或者也可以说是故障诊断的准确度与可信度问题,当然也涉及到诊断的误报问题(漏报问题应该属于状态故障的可诊断性问题).也就是如何通过测量信息,准确地识别出故障的状态、类型、发生故障的部位(故障定位问题)甚至包括故障发生的机理.但是,诊断的深度或程度与人们对对象的认识深度与程度是完全不同的概念,诊断中的可分离性即可实现的诊断深度是一个客观问题,而对事物的认识程度是一个主观问题[1].
本文中记:
定义1 如果对式(2) 所给出的系统,在任意给定的激励u(t) ∈Rl的作用下,以x1和x2 ∈Rn为初始值的系统,其相应的输出都有:y1(t)=y2(t),则称x1和x2是不可分辨的.所有的与x1不可分辨的集合记为:I(x1).
状态故障的可分离性是故障诊断实现的前提,要确定故障可分离的条件,首先就必须清楚何为可分离问题.而故障的可分离性却是一个很强的条件,有时对于有限的诊断,或者对某些特定的状态诊断来说,并不一定需要如此强的条件;另一方面,就非线性系统来说,可分离与弱可分离也并不等价;因此这里就有故障可分离与弱可分离问题.
定义2 状态故障的可分离与弱可分离性定义:
(1) 如式(2) 所描述的系统,如果对于给定的状态x0是可分辨的,并且通过相应的输出测量可以确认状态x0,则称状态x0是状态可分离的;如果对任意的x1和x2 ∈Rn,x1≠x2,t∈T,其输出不相同,即:y1(t)≠y2(t),并且可以通过相应的测量信息y1(t)与y2(t)确认x1和x2,则称式(2) 所代表的系统是故障状态可分离的系统,即通过测量信息(y(t), u(t))能够明确系统是哪一个状态引起系统输出异常.
(2) 如式(2) 所示的系统,对初始状态x0∈Rn ,若存在x0的任意一个开邻域U ∈Rn,对任意的x∈U,都存在一个特定的输入控制u(t) ∈Rl,其输出可分辩,并可通过测量y(t)确认x0,则称系统在x0是弱可分离的.
由于故障分离的重要性,本文就连续线性系统和连续非线性系统存在过程扰动时,状态故障的可分离条件进行了探讨.此外,本文还提出了一个新的诊断系统,它可以运用故障分离技术确认在何处发生故障以及故障发生的原因.给出了形式上一致的可分离条件,并且付诸列车轮对装置的诊断实践.
2 存在扰动时的状态故障可分离的基本前提在实际的故障诊断系统中,如何在严重噪声信号中提取系统故障的有效信息,是一个非常关键的步骤.因此来讨论系统存在过程扰动时,状态故障可分离的条件.
线性定常系统的结构如下所示:
| $\left\{ \begin{align} & {{\mathit{\boldsymbol{x}}}^{'}}\left( t \right)=\mathit{\boldsymbol{Ax}}\left( t \right)+\mathit{\boldsymbol{Bu}}\left( t \right)+\mathit{\boldsymbol{E }}\!\!\omega\!\!\rm{ }\left( t \right) \\ & \mathit{\boldsymbol{y}}\left( t \right)=\mathit{\boldsymbol{Cx}}\left( t \right) \\ \end{align} \right.$ | (4) |
式中:A为n×n矩阵; B为n×l矩阵; C为m×n矩阵; u(t)为l×1控制输入; ω(t) ∈Rr是随机过程干扰(但不一定满足零均值条件,也不一定是均匀功率谱密度的白噪声,其模值‖ω‖可能较大),干扰转移矩阵E是m×r矩阵.若给系统建造一个状态观测器:
| ${{{\mathit{\boldsymbol{\hat{x}}}}}^{'}}\left( t \right)=\mathit{\boldsymbol{Ax}}\left( t \right)+\mathit{\boldsymbol{Bu}}\left( t \right)\mathit{\boldsymbol{+GC}}\left( \mathit{\boldsymbol{x}}\left( t \right)-\mathit{\boldsymbol{\hat{x}}}\left( t \right) \right)$ |
则系统的状态方程的解为:
| $\mathit{\boldsymbol{x}}\left( t \right)={{\rm{e}}^{\left( \mathit{\boldsymbol{A}}-\mathit{\boldsymbol{GC}} \right)\left( t-{{t}_{0}} \right)}}x\left( {{t}_{0}} \right)+\int_{{{t}_{0}}}^{t}{{{\mathit{\boldsymbol{e}}}^{\left( \mathit{\boldsymbol{A}}-\mathit{\boldsymbol{GC}} \right)\tau }}}E\mathit{\boldsymbol{\omega}}\left( \tau \right)\rm{d}\tau $ | (5) |
不违反一般性原则,假定系统初始状态x(t0)=0和t0=0,这并不影响以后的讨论,则系统的测量输出差为
| $\mathit{\boldsymbol{y}}\left( t \right)=\mathit{\boldsymbol{\hat{y}}}\left( t \right)=C\int_{{{t}_{0}}}^{t}{{{\rm{e}}^{\left( \mathit{\boldsymbol{A}}-\mathit{\boldsymbol{GC}} \right)\tau }}}E\mathit{\boldsymbol{\omega}}\left( \tau \right)\rm{d}\tau $ | (6) |
而由定义2可以看出,所谓系统状态是故障可分离的,就是在存在扰动ω(t)时,能够唯一确定系统的状态x(t).也就是说,若系统是状态能观测的,而ω(t)对系统的输出y(t)没有影响,则通过状态观测器就可以获得唯一的状态估计.因此,若系统状态能观测,并且有E=0或者ω(t)=0,则系统必定状态故障能分离.
定义3 线性映射的扩张空间、张成子空间、核、值域和不变映射[2-3]:
(1) 如果设e1, e2, …, ek∈ Rj为一组向量,它的线性组合的全体组成的集合称为e1, e2, …, ek的扩张,记为:
| $\begin{array}{l} {\rm{span}}\left\{ {{\mathit{\boldsymbol{e}}_1},{\mathit{\boldsymbol{e}}_2}, \cdots ,{\mathit{\boldsymbol{e}}_k}} \right\},{\rm{或span}}\left\{ {{\mathit{\boldsymbol{e}}_i},i \in k} \right\}\\ {\rm{或span}}\left\{ {{\mathit{\boldsymbol{e}}_i},i \in k} \right\} = \left\{ {\mathit{\boldsymbol{e}} \in {{\bf{R}}^j},\mathit{\boldsymbol{e}} = \sum\limits_{i = 1}^k {{c_i}{\mathit{\boldsymbol{e}}_i}} } \right\} \end{array}$ | (7) |
显然,若e1, e2, …, ek线性无关,则:span{ e1, e2, …, ek}= Rk即构成k维线性子空间.
(2) 设矩阵C的列向量为:c1, c2, …, ck,则记矩阵A和C张成的子空间为<A|C>:<|A|C>是以c1, c2, …, ck, c1 A, c2 A, …, ck A, …, c1 An-1, c2 An-1, …, ckAn-1为基扩张成的线性子空间.
(3) 如果令:C:X→Y是一个线性映射,定义KerC是C的核,lmC是C的值域,即:
KerC={x:x∈X, 并且有Cx=0}; lmC={Cx, 对于任意的x∈X}
若称线性映射C是可逆的,如果有:lmC=Y,并且:Ker C=ϕ.
(4) 设A:X→X是线性映射,S⊂X是商空间.如果有:Aφ⊂S,则称是A-不变的.
由式(6) 可以看出,所谓系统状态ω(t)是故障可分离的,则其首先必须满足的条件是:若x(t0)=0,则必有
| $\mathit{\boldsymbol{C}}\int_{{{t}_{0}}}^{t}{{{\rm{e}}^{\left( \mathit{\boldsymbol{A}}-\mathit{\boldsymbol{GC}} \right)\tau }}E\mathit{\boldsymbol{\omega}}\left( \tau \right)\rm{d}\tau =0}$ | (8) |
对任意的矩阵E和任意的向量ω(t)∈ Rr.
即:
| $\mathit{\boldsymbol{C}}<\mathit{\boldsymbol{A}}-\mathit{\boldsymbol{GC}}\left| \rm{lm}\mathit{\boldsymbol{E}}>=0 \right.$ | (9) |
因此有:
定理1 所谓系统状态ω(t)是故障可分离的,则其必须满足的条件是:
① 系统(4) 是状态可观测的,即(A, C)是状态能观测;
② 并且存在矩阵G,使得有C < A-GC|lmE > =0
由于lmE⊂C < A-GC|lmE > =0,且C < A-GC|lmE > 是(A-GC)-不变的,则式(9) 的几何意义是:存在G,使包含lmE的最小(A-GC)-不变子空间,也就是在Eω作用下,x(0)=0可观测的状态全体包含在KerC中.
如果子空间R0是(A-GC)-不变的,即:
| $\left( \mathit{\boldsymbol{A}}-\mathit{\boldsymbol{GC}} \right){{\bf{R}}_{0}}\subset {{\bf{R}}_{0}}$ |
就有:AR0⊂R0+lmB
则称R0为(A, C)-不变子空间.
定理2 R0是(A, C)不变子空间,当且仅当存在G,使得R0是(A-GC)-不变的.
若记所有属于R0的(A, C)-不变子空间的全体的集合记为V(A, C, R0), 该集合的最大元记为V*(A, C, R0).因此满足式(9) 的条件是存在G,使得有:
| $\mathit{\boldsymbol{C}}<\mathit{\boldsymbol{A}}-\mathit{\boldsymbol{GC}}\left| \rm{lm}\mathit{\boldsymbol{E}}> \right.\in V\left( \mathit{\boldsymbol{A}},\mathit{\boldsymbol{C}},\rm{Ker}\ C \right)$ | (10) |
定理3 式(4) 所表达的系统,在存在过程干扰的前提下,若通过状态观测器法是可以实现故障状态可分离的条件是:
① 系统(4) 是状态可观测的,即(A, C)是状态能观测;
② lmE⊂V*(A, C, Ker C).
由不变空间的定义,显然系统的不可观测子空间
| $\text{rank}\left[ {{c}_{1}},{{c}_{2}},\cdots ,{{c}_{k}},{{c}_{1}}A,{{c}_{2}}A,\cdots ,{{c}_{k}}A,\cdots ,{{c}_{1}}{{A}^{n-1}},{{c}_{\text{2}}}{{A}^{n-1}},\cdots ,{{c}_{k}}{{A}^{n-1}} \right]=n,$ |
此时系统的不可观测子空间
定理4 式(4) 所表达的系统,在存在过程干扰的前提下,若满足以下的条件,则通过状态观测器法是可以实现故障状态可分离的:
| $\left( 1 \right)\mathop {\mathop \cap \limits^n }\limits_{i = 1} \,\rm{Ker}\left( \mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{A}}}^{i-1}} \right)=\varnothing $ |
| $\left( 2 \right){\rm{lm}}\mathit{\boldsymbol{E}}\subset {{V}^{*}}\left( \mathit{\boldsymbol{A}},\mathit{\boldsymbol{C}},{\rm{Ker}}\;C \right).$ |
同线性系统(4),下面考虑式(11) 所示存在过程干扰的非线性系统:
| $\left\{ \begin{align} & {{\mathit{\boldsymbol{x}}}^{'}}\left( t \right)=\mathit{\boldsymbol{f}}\left( x \right)+\mathit{\boldsymbol{g}}\left( x \right)\mathit{\boldsymbol{u}}\left( t \right)+\mathit{\boldsymbol{e}}\left( x \right)\mathit{\boldsymbol{\omega}}\left( t \right) \\ & \mathit{\boldsymbol{y}}\left( t \right)=\mathit{\boldsymbol{h}}\left( x \right) \\ \end{align} \right.$ | (11) |
其中:x(t)∈M(n维连通微分流形),f为可微向量场,u(t)为l×1控制输入,g(x)=[g1(x), g2(x), …, gl(x)],e(x)=[e1(x), e2(x), …, ek(x)],ω(t)∈Mk是过程扰动,h和g为可微映射,h(x)=[h1(x), h2(x), …, hm(x)]T[7-8].
定义4 所谓系统(11) 是故障状态可分离的,是指在定义2的基础上,而且对任意的过程扰动ω1(t)∈Rr、ω2(t)∈Rr和对任意的x0=x(t0) ∈Rn,均有:
| $\mathit{\boldsymbol{y}}\left( {t,{x_0},\mathit{\boldsymbol{\omega }}{_1}\left( t \right)} \right) = \mathit{\boldsymbol{y}}\left( {t,{x_0},\mathit{\boldsymbol{\omega }}{_2}\left( t \right)} \right)$ | (12) |
条件(12) 称为是过程扰动输出无关的.
因此,如果希望系统是状态故障可以分离的,在系统(11) 是状态可观测的基础上,只要系统的扰动无关的.以下就主要讨论过程扰动输出无关的条件[4].
设M是n维微分流形,以C∞(M)表示M上的所有可微函数的集合,C∞(x)表示在x∈M点的所有可微函数组成的集合.则有如下的定义:
(1) 映射L:C∞(x)→R(实数域),称为点x的切向量,如果:
(a) L(αf+βh)=αL(f)+βL(h), 任意的α, β∈ R,和任意的f, h∈C∞(x);
(b) L(f, h)=fL(h)+gL(f), 任意的f, h∈C∞(x).
用TxM记M上的点x的全体切向量的集合,在其上以通常的方式定义加法、数乘后构成(上的线性空间,则称之为x点的切空间.
(2) 微分流形M上的分布Δ是一种法则,它将M上的每一点对应于该点切空间TxM的一个子空间Δ(x).若对任意的x∈M存在x的邻域Ux和其上线性无关的k个向量场X1, X2, …, Xk,使X1(x), X2(x), …, X(x)k构成Δ(x)的基底,则称Δ为可微分布,X1, X2, …, Xk称为分布Δ的局部基底.
(3) 若f, h∈V(M)(M上的不变子空间全体),Δ为可微分布,若对任意的x∈M,h(x)∈Δ(x), 记为:h∈Δ;并且记:[f, Δ]=span{[f, h]:h∈Δ},显然[f, Δ]仍然是M上的可微分布.分布Δ称为f的不变分布,若满足:[f, Δ]⊂Δ.
(4) 微分流形M上的分布Δ称为(f, h)不变的,如果存在α(x),β(x),使:
| $\left[ \mathit{\boldsymbol{f}}+\mathit{\boldsymbol{h}}\ \mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ }\left( x \right),\mathit{\Delta } \right]\subset \mathit{\Delta };\left[ \mathit{\boldsymbol{f}}\ \mathit{\boldsymbol{ }}\!\!\beta\!\!{\rm{ }}\ _{i}^{\rm{T}}\left( x \right),\mathit{\Delta } \right]\subset \mathit{\Delta },i\in r$ |
(f, h)不变分布是(A, C)-不变子空间的推广,就象f不变分布是A-不变子空间的推广一样.
(5) 如果对任意的向量X∈Δ,有X=Xhi=0, i∈m,则称分布Δ与h相容.分布Δ与h相容等价于Δ∈(span{dhj, j∈m})⊥.
定理5 若系统输入u(t)=0,输出的第i个分量yi(t)不受扰动信号ωi(t)影响,当且仅当存在一个分布Δ,满足:
(1) Δ是f, e1, …, ei-1, ei+1, …, er的不变分布;
(2) ei∈Δ∈(span{dhj, j∈m})⊥.其中:dhj是hj的微分.
建造式(11) 所描述系统的状态观测器如式(13) 所示:
| ${{\mathit{\boldsymbol{\hat{x}}}}^{'}}=\mathit{\boldsymbol{f}}\left( {\mathit{\hat{x}}} \right)+\mathit{\boldsymbol{g}}\left( t \right)\mathit{\boldsymbol{u}}\left( t \right)+\left[ \mathit{\boldsymbol{q}}\left( x \right)\mathit{\boldsymbol{h}}\left( x \right)-\mathit{\boldsymbol{q}}\left( {\mathit{\hat{x}}} \right)\mathit{\boldsymbol{h}}\left( {\mathit{\hat{x}}} \right) \right]$ | (13) |
式(13) 的状态观测器可以是一个非线性自适应观测器、扩展卡尔曼滤波器或者是一个神经网络构成的观测器等.于是有:
| ${{\left( \mathit{\boldsymbol{x}}-\mathit{\boldsymbol{\hat{x}}} \right)}^{'}}=\mathit{\boldsymbol{f}}\left( x \right)-\mathit{\boldsymbol{f}}\left( {\mathit{\hat{x}}} \right)+\mathit{\boldsymbol{q}}\left( x \right)\mathit{\boldsymbol{h}}\left( x \right)-\mathit{\boldsymbol{q}}\left( {\mathit{\hat{x}}} \right)\mathit{\boldsymbol{h}}\left( {\mathit{\hat{x}}} \right)+\mathit{\boldsymbol{g}}\left( x \right)\mathit{\boldsymbol{\omega}}\left( t \right)$ | (14) |
或者改写为
| $\begin{array}{l} \left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{\hat x}}} \right)' = \left[ {1 - \mathit{\boldsymbol{q}}\left( x \right)} \right]\left[ \begin{array}{l} \mathit{\boldsymbol{f}}\left( x \right)\\ \mathit{\boldsymbol{h}}\left( x \right) \end{array} \right] + \left[ {1, - \mathit{\boldsymbol{q}}\left( {\mathit{\hat x}} \right)} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ \begin{array}{l} \mathit{\boldsymbol{f}}\left( {\mathit{\hat x}} \right)\\ \mathit{\boldsymbol{h}}\left( {\mathit{\hat x}} \right) \end{array} \right] + \mathit{\boldsymbol{g}}\left( x \right)\mathit{\boldsymbol{\omega }}\left( t \right) \end{array}$ | (15) |
其中q(x)满足
定理6 式(11) 系统基于式(13) 的状态观测器,则输出是过程扰动无关的条件是:存在一个分布Δ,满足以下的条件:
(1) 分布Δ是f(x), h(x)不变的;
(2) e(x)∈Δ⊂(span{dhi, i∈m})⊥
于是,类似于定理2,对于非线性系统(11),有:
定理7 Δ是在开集U上(f, h)不变分布的充分必要条件为:在U上有:
| $\left[ {\mathit{\boldsymbol{f}},\Delta } \right] \subset \Delta+ {\rm{span}}\left\{ {{h_1},{h_2}, \cdots ,{\mathit{h}_m}} \right\}$ |
| $\left[ {{\mathit{\boldsymbol{h}}_i},\Delta } \right] \subset \Delta +{\rm{span}}\left\{ {{h_1},{h_2}, \cdots ,{\mathit{h}_m}} \right\}$ |
注意,这里的(f, h)不变分布是一个局部的概念.
由定理7可知,两个(f, h)不变分布之和是(f, h)不变分布.由此有如下的定理:
定理8 在与h相容的局部(f, h)不变分布中,有最大者存在,此最大者记为Δmax(这与线性系统中的最大不变子空间(定理4))相比较).
定理9 设Δmax是r维的,则至少有r个输出,不妨记为:y1, y2, …yr,是过程干扰输出无关的.
对每一个给定的控制u(t)就确定了一个向量场{f(x), g(x),u(t)},所有这些向量场的集合记为:F0;记H0={h1, h2, …, hm};G为C∞(M)中包含G0且对F0中元的导数是闭合的最小子空间.G中的元是如下的形式:
| ${L_{{f_1}}}\left( { \cdots \left( {{L_{{f_j}}}\left( {{h_i}} \right)} \right) \cdots } \right),$ |
而记:dG≡{dφ:φ∈G},
其中dG(x)是dG在x点张成的向量空间.由非线性系统的可观测性定义,系统局部弱可观测的条件是:dim{dG(x)}=n,由此讨论并结合定理9可得:
定理10 对式(11) 所描述的系统,若Δmax是常维数的,并且满足:
| ${\rm{dim}}\left\{ {d\mathit{\boldsymbol{G}}\left( x \right)} \right\} = n$ |
| $\mathit{\boldsymbol{g}}\left( x \right) \in {\mathit{\Delta }_{\max }};$ |
则系统必定是状态故障可分离的.
4 轮对滚动轴承故障分离实践 4.1 轮对滚动轴承装置故障可分离性分析轮对轴承故障是列车走行部系统故障主要故障之一,而轮对轴承的故障检测和分离问题是一种典型的存在扰动的非线性状态分离问题,其干扰信号的能级远远大于有效信号的能级.首先,对轴承系统故障的相关原理进行分析,以滚动轴承运动部件的单一局部故障为例进行分析,列车轮对轴承在运转时可以看作一个振动系统,通过动力学方程(16) 分析其振动特征[7].
| $R\ddot x + Q\dot x + Kx = {F_0}\left( t \right) + {F_a}\left( t \right)$ | (16) |
R为轴承装置的当量质量;x为接触点径向相对位移;Q为轮对轴承阻尼;K为轮对轴承接触刚度;F0(t)为系统初始激振力,包含列车轮轨接触系统通过转向架给轴承施加的作用力;Fa(t)为局部故障激振力,它包含故障缺陷所产生的激励,受接触刚度和故障函数的影响.由式(16) 可知,轴承系统是一个典型的非线性系统,该系统以车轴转速作为输入,振动信号作为系统的输出.下面对系统发生故障时,系统的振动输出与故障状态特征的关系进行分析.
以轴承外圈故障为例,其外圈故障特征频率fk与转频fn间的关系如式(17) 所示:
| ${f_{\rm{k}}}{\rm{ = }}{f_{\rm{n}}}\frac{1}{2}z\left( {1 - \frac{d}{D}\cos \beta } \right)$ | (17) |
式中:Z为滚动体个数;d为滚动体直径;D为轴承节径;β为接触角.
当列车车轴的转频fn发生变化时,故障特征频率fk也会随之波动,但是局部缺陷所激发出的振动冲击与列车车轴每转动关系是固定不变的,该关系不受负载变化、转速波动等外部因素影响,其只由轴承的类型和结构参数决定.故引入定义故障特征参数K为故障部件每周的振动冲击个数(本文所涉及的频率,其单位均为Hz).
| $K = \frac{1}{2}z\left( {1 - \frac{d}{D}\cos \beta } \right)$ | (18) |
得到相应的旋转部件的故障特征频率计算公式可以简化为
| ${f_{\rm{k}}}{\rm{ = }}{f_{\rm{n}}}K$ | (19) |
即在给定转频fn的情况下,轴承的故障特征频率是确定的,故障频率特征只由故障部件的类型、结构和尺寸参数决定,与存在的负载变化和过程扰动无关,因而满足定理9和定理10.同样的,对于轴承的其他部件的故障,如内圈故障、滚子故障等,由于部件不同,结构参数不同,从而对应着相应的故障特征频率,如式(20) 所示.
例如,轴承型号为552732QT,根据轴承相关参数可得其故障特征频率分别为
| $\left\{ \begin{array}{l} {f_{\rm{w}}}{\rm{ = }}{K_{\rm{w}}} \cdot {f_{\rm{n}}}{\rm{ = }}7.195\;2{f_{\rm{n}}},外圈故障\\ {f_{\rm{n}}}{\rm{ = }}{K_{\rm{n}}} \cdot {f_{\rm{n}}}{\rm{ = }}9.804\;8{f_{\rm{n}}},内圈故障\\ {f_{\rm{a}}}{\rm{ = }}{K_{\rm{a}}} \cdot {f_{\rm{n}}}{\rm{ = 2}}{\rm{.929}}\;{\rm{3}}{f_{\rm{n}}},滚子故障 \end{array} \right.$ | (20) |
式中:fw为外圈的故障特征频率; fa为滚子故障特征频率.
由式(18)~(20) 可知,振动信号作为可观测的输出信号,能够计算出不同故障状态下的故障特征参数K,并能唯一确认故障的状态特征频率fk.故障状态特征fk和振动输出之前是一一对应的关系,即不同的故障状态就有不同的故障信号输出,满足定义2系统故障可分离的条件.
另外,由于故障频率特征只由故障部件的类型、结构和尺寸参数决定,与存在的负载变化和过程扰动无关.对任意的过程扰动,各个部件的故障特征频率是由故障特征参数K和转频fn确定的,即输出与扰动无关,满足系统故障可分离定义4,由定理10可知,列车轮对故障状态是可观测和分离的,从而可根据故障状态特征频率来诊断相应的故障.
4.2 轴承系统故障诊断方法既然轴承系统是故障可分离的,则一定存在相应的推理算法及过程来实现系统的故障诊断和定位.由于在实际中轮对轴承早期故障信号非常微弱,通常淹没在车轴振动信号(比如过道岔)扰动中,故可以利用号称“数字显微器”的小波变换对微弱信号进行适当分析,分离出相应的故障特征频率.首先通过对振动信号的整周期等角度采样,再借助第二代小波变换进行分解,保留所需频带的轴承信号,然后再用Hilbert变换进行信号的包络解调,最后对所得的信号进行分离.分离结果能够有效地显示滚动轴承的各个故障频率特征,找出所包含的故障特征谱,并与理论值进行比较分析进而诊断出各类故障,以实现无偏差的精确诊断.这种综合分析方法示意图如图 1所示[7].

|
图 1 基于第二代小波变换的故障分离示意图 Fig.1 Schematic diagram of fault separation based on second generation wavelet transform |
该综合分析法中的关键部分是小波变换,其通过构造与损伤引起的冲击振荡波形相匹配的基函数,将信号分解到不同的频带,提取隐藏在高频振荡衰减振动中的低频故障信息,从而获取信噪比较低的轴承故障特征频率.
4.3 滚动轴承故障分离案例分析案例1 552732QT型电力机车轮对轴承早期外圈轻微擦痕(无手感)故障识别.振动信号的采样频率为25.6 kHz,轴承外圈故障特征频率的计算值为60.851 2 Hz.图 2为原始振动信号解调频谱,图 3为第二代小波解调谱.在原始信号的解调谱中未发现对应的轴承外圈故障特征频率60.851 2 Hz成分,而在第二代小波解调谱中发现了与外圈故障损伤特征频率相对应的频率成分60.585 9 Hz(与外圈故障特征频率计算值60.851 2 Hz接近),诊断为轴承外圈故障.

|
图 2 原始信号解调谱 Fig.2 Original signal demodulation spectrum |

|
图 3 第二代小波包分解信号解调谱 Fig.3 Signal demodulation spectrum of the wavelet transform |
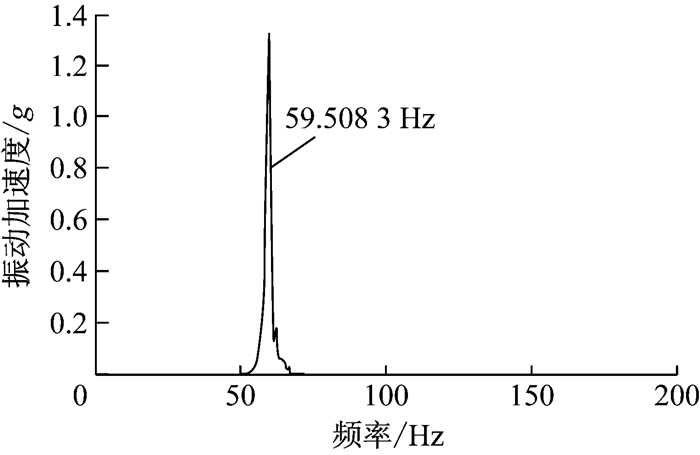
案例2 韶8电力机车轮对轴承外圈严重剥离故障(面积为53 mm×30 mm)识别.振动采样频率为25.6 kHz,轴承外圈故障特征频率为59.768 9 Hz.图 4为第二代小波包分解信号外圈特征谱.在第二代小波包分解信号外圈特征谱中发现了与外圈故障损伤特征频率相对应的频率成分59.508 3 Hz(与外圈故障特征频率计算值59.768 9 Hz接近),诊断为轴承外圈故障,在真实故障中也可以明显看出是轴承外圈严重剥离.
|
图 4 第二代小波包分解信号解调谱 Fig.4 Signal demodulation spectrum of the second generation of wavelet transform |
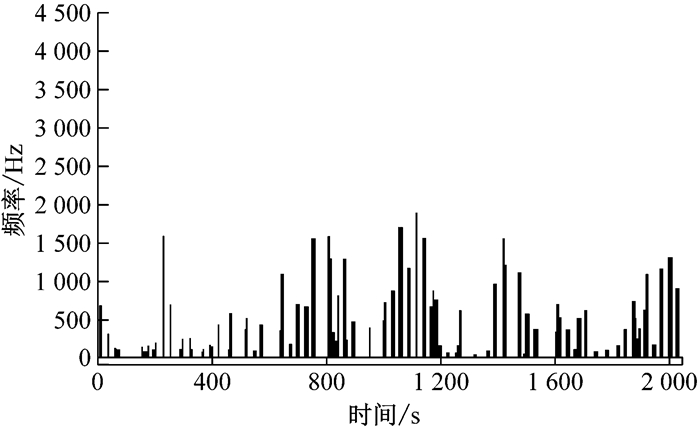
案例3 湖东机务段SS4G-0446机车轴承外环严重剥离故障识别.该机车上安装的机车走行部故障监测诊断系统,产生外环报警系统软件分析界面如图 5、图 6,由图可见所示信号强度约65 dB,振动信号的频谱曲线的峰值与外环的各阶理论故障频率吻合,具有很明显的外环故障特征,故障诊断为外环故障,通过轴承解体图 7c可以明确看到外环严重剥离.
|
图 5 原始信号时域波形 Fig.5 Time domain waveform of original signal |

|
图 6 小波变换后信号频域波形 Fig.6 Frequency domain waveform of wavelet transform |
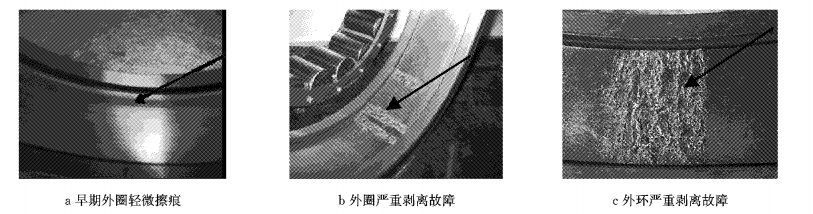
|
图 7 滚动轴承故障解体图 Fig.7 Fault separation diagram of rolling bearings |
对滚动轴承进行解体,从解体图中可以确定基于第二代小波变换的故障分离方法的可行性,能准确识别滚动轴承的故障.
5 结论通过详细推导,论证了故障可分离是客观存在的,并根据对存在过程扰动的连续非线性系统的数学分析,得到了与连续线性系统形式上一致的故障可分离条件.经过案例分析,进一步验证了结论正确性,说明得到的故障可分离条件可用于轨道系统并对机电一体化的故障诊断起到了重要的指导作用.
| [1] |
贾庆贤, 张迎春, 管宇, 等. 基于解析模型的非线性系统故障诊断方法综述[J]. 信息与控制, 2012(3): 356 JIA Qingxian, ZHANG Yingchun, GUAN Yu, et al. Fault diagnosis of nonlinear systems based on analytical models: a survey[J]. Information and control, 2012(3): 356 |
| [2] |
刘朝辉. 一类非线性系统的自适应故障诊断方法研究[D]. 沈阳: 东北大学, 2014. LIU Chaohui. Research on adaptive fault diagnosis method of a class of nonlinear system[D]. Shenyang: Northeastern University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10145-1016020673.htm |
| [3] |
林立雄, 刘成瑞, 仲训昱, 等. 基于微分几何的非线性系统故障诊断[J]. 华中科技大学学报(自然科学版), 2015, 43(9): 24 LIN Lixiong, LIU Chengrui, ZHONG Xunyu, et al. Fault diagnosis for nonlinear systems based on differential geometry approach[J]. Journal of Huazhong University(Science and Technology), 2015, 43(9): 24 |
| [4] |
吴昊. 滚动轴承动特性及轴承一转子系统动力学模型研究[D]. 上海: 华东理工大学, 2010. WU Hao. Research on the dynamic characteristics of rolling element bearings and the dynamic model of bearing rotor system[D]. Shanghai: East China University of science and technology, 2010. http://d.wanfangdata.com.cn/Thesis/Y1859243 |
| [5] |
李娟, 吕新丽. 含两类时滞的线性系统的故障诊断及故障可诊断性[J]. 计算机应用研究, 2009, 27(10): 3727 LI Juan, LV Lixin. Fault diagnosis and diagnosability for linear systems with two kinds of time-delays[J]. Application Research of Computers, 2009, 27(10): 3727 DOI:10.3969/j.issn.1001-3695.2009.10.037 |
| [6] |
郭其一, 冯江华, 刘可安, 等. 可靠性工程与故障诊断技术[M]. 北京: 科学出版社, 2016 GUO Qiyi, FENG Jianghua, LIU Ke'an, et al. Reliability engineering and fault diagnosis technology[M]. Beijing: Science Press, 2016 |
| [7] |
陈省身, 陈维恒. 微分几何讲义[M]. 北京: 北京大学出版社, 2001 CHEN Shengshen, CHEN Weiheng. Lectures on differential geometry[M]. Beijing: Peking University Press, 2001 |
| [8] |
周振荣, 杨文茂, 郑高峰, 等. 微分几何[M]. 武汉: 武汉大学出版社, 2008 ZHOU Zhenrong, YANG Wenmao, ZHENG Gaofeng, et al. Differential geometry[M]. Wuhan: Wuhan University Press, 2008 |
 2017, Vol. 45
2017, Vol. 45

