2. 同济大学 上海市地面交通工具空气动力与热环境模拟重点实验室,上海 201804
2. 2 Shanghai Key Laboratory of Vehicle Aerodynamics and Vehicle Thermal Management Systems, Tongji University, Shanghai 201804, China
车辆外流为三维、非定常、近地面钝体流动[1].应用定常或脉冲射流、等离子和合成射流等主动流动控制技术可有效控制气动阻力[2-6].
合成射流激励器(射流器)不需气源,可实现输入质量为0,而输入动量不为0,故也称其为零质量射流技术.该技术具有响应的频带较宽、结构紧凑、容易装配等优点,在国外成为了车辆流动控制的研究热点.然而,相关研究[7-10]处于起步阶段,多为射流器对二维车辆的流动控制.文献[5-6]通过试验给出了合成射流对三维车辆阻力和压力的控制结果,但未将激励参数和流动分析相结合,给出减阻机理.
激励频率是进行经典钝体流动控制的关键影响参数[11],三维车辆的相关研究开展较少.本文与风洞试验结果对比,首先验证大涡模拟(large-eddy simulation, LES)仿真有效.然后,通过流动分析和频谱方法,研究合成射流激励频率(40~1 500 Hz)对车辆流场和气动力的影响,给出不同频率下的流动控制和减阻机理.
1 风洞试验 1.1 合成射流激励器如图 1所示,单只射流器由腔体、出口喉部和激励源组成.多只射流器的组合构成合成射流阵列.根据文献[5-6]输入正弦波信号,激励电压为10~80 V,激励频率为40~1 500 Hz.通过热线风速仪测量得到射流器出口速度,出口瞬态速度的最大值可达50 m·s-1.

|
图 1 合成射流激励器 Fig.1 Synthetic jet actuator |
Ahmed body模型[1]可有效模拟车辆尾部流场.以0.3倍缩比的Ahmed body模型作为研究对象,如图 2a所示,模型尾部倾角为25°,长、宽、高分别为L=0.322 m, W=0.120 m, H=0.089 m.面y=0,速度和压力测点分布见图 2b.
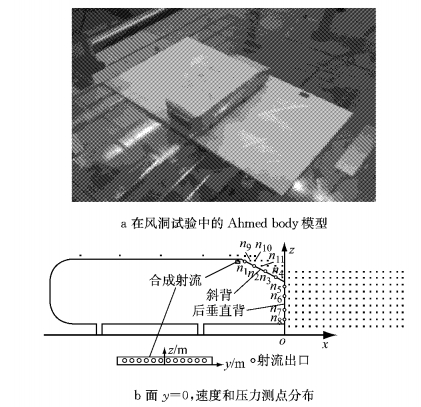
|
图 2 Ahmed body模型风洞试验 Fig.2 Wind tunnel experiment of Ahmed body |
为了验证数值仿真的有效性,将仿真结果与文献[5-6]的试验结果进行对比.文献[5-6]将合成射流阵列安装在Ahmed body模型顶部和斜背交界处,测量了有无控制下的阻力和压力(图 2b).图中,n1~n11为11个点的位置.合成射流出口数量为12个,出口直径d=2 mm,出口中心间距为10 mm.
由于文献[5-6]未给出流场和频谱信息,为了进一步分析流场机理,本文进行了无控制下的流场试验.试验在上海地面交通工具风洞中心的整车缩比模型风洞进行,喷口面积0.123 m2,试验段湍流强度为0.38%,最大风速为48 m·s-1.坐标原点定义为Ahmed body模型后垂直背中心轴在地面上的投影点O,气流方向为x轴,垂直地面方向为z轴,车体展向为y轴.如图 2b所示,利用热线风速仪对车辆尾迹内多个测点速度进行了测量.
2 数值仿真方法与结果验证 2.1 计算域与网格划分无控制下的数值仿真、试验与文献[5-6]保持同一雷诺数,皆为ReL=4.29×105.计算域长、宽、高分别设置为2.58, 0.84, 0.36 m.流场的计算空间采用六面体网格划分.按照大涡模拟对网格的要求,保证第一层网格尺寸y+小于1.如图 3a所示,对车体近壁面、射流器与外流掺混区、斜背和近尾迹区进行加密.表面网格尺寸0.25~2 mm,无控制下网格数为1 800万,增加网格数对计算结果影响很小.如图 3b所示,对每个射流器内部结构划分了网格,与无控制下相比,有控制的网格数增加了2%.
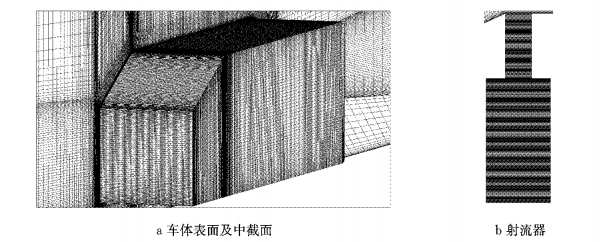
|
图 3 车辆及射流器网格加密区 Fig.3 Refined mesh around Ahmed body and jets |
文献[12]指出雷诺平均方法无法有效模拟类车体的斜背分离及其再附着流动,而大涡模拟可获得较好结果.因此,本文使用商业软件Fluent 12.1进行大涡模拟的计算.采用WALE亚格子模型,迭代方法为SIMPLEC算法,计算时间步长0.000 1 s.地面和车身采用无滑移边界条件,所有监测的流场参数皆满足相应的收敛条件.
根据合成射流仿真控制模型[13],如图 3b中网格外边界所示,得到内腔和出口喉部简化几何.将初始激励作为速度入口条件引入射流器,进行流场计算.定义初始激励速度:
| $ {V_{{\rm{sja}}}} = {V_0}d/D \cdot {\rm{sin}}\left( {2\pi {f_{\rm{a}}} \cdot t} \right) $ | (1) |
式中: D为腔体直径;d为射流出口直径;fa为激励频率;定义空间和时间上的平均速度V0为
| $ {V_0} = \frac{{\rm{\pi }}}{{Td}}\int_0^{\frac{T}{2}} {\int_0^d {v\left( {y, t} \right){\rm{d}}y{\rm{d}}t} } $ | (2) |
式中:v(y, t)为射流出口瞬态速度;T=1/fa,研究的激励频率fa包括:40, 65, 90, 120, 150, 180, 210, 360, 500, 1 000, 1 500 Hz,通过速度边界条件引入流场.定义动量系数Cμ为
| $ {C_{\rm{ \mathsf{ μ} }}} = N \cdot \left( {{d^2}/W \cdot H} \right){\left( {{V_{{\rm{sja}}}}{\rm{/}}U} \right)^2} $ | (3) |
式中:N为射流出口数量; d为射流出口直径; U为来流风速; W和H分别为车辆模型的宽度和高度,研究不同射流速度下对应的动量系数分别为Cμ1=2.8×10-3和Cμ2=2.1×10-2.
2.3 仿真结果验证定义减阻幅度ΔCD/CD, 0,其中ΔCD=CD, 0-CD, fa,CD, 0和CD, fa分别为无控制和施加合成射流的车辆阻力系数.在参考试验[5-6]中的合成射流开启后,动量系数达到Cμ1时,不同激励频率试验对应的减阻幅度区间为0<ΔCD/CD, 0<5%,随着动量系数的增大,减阻幅度增大;在数值仿真中,如图 4所示,动量系数为Cμ1时,不同激励频率下对应的减阻幅度区间为1.5%<ΔCD/CD, 0<5.5%,当动量系数从Cμ1增大到Cμ2时,在相同激励频率下,减阻幅度增大.数值仿真有效地预测了不同激励参数下减阻幅度的变化趋势.
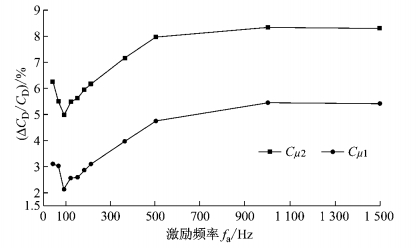
|
图 4 不同激励下减阻效果 Fig.4 Drag reduction with different driving frequency |
在面y=0上,如图 5所示,对于车身后垂直背(0<z<0.075 m)和斜背(0.075<z<0.1 m),在合成射流控制的前后,试验测量得到的平均压力系数Cp与仿真计算结果皆较为吻合.

|
图 5 后垂直背和斜背平均压力系数,面y=0上 Fig.5 Mean pressure coefficient on the slant and rear vertical base, plane y=0 |
无控制下,风洞试验结果表明尾迹各测点峰值皆对应自然涡脱落频率f0,数值仿真与试验得到的斜背回流区测点频率范围为35~45 Hz,尾迹测点频率处于75~90 Hz范围内.因此,数值仿真可有效预测流场各点频谱.
3 结果分析 3.1 气动力比较在不同激励频率和动量系数作用下,如图 4所示,车辆都实现了减阻.当激励频率在40≤fa≤90 Hz范围内,随着fa的增大,阻力增大,减阻幅度降低;当90≤fa≤1 000 Hz,增加fa使得阻力减小,减阻幅度增大;当激励频率fa=1 500 Hz,阻力不再减小.将动量系数从Cμ1提高到Cμ2,减阻幅度增大.
不同激励频率对车头压力无影响,控制前后车尾和车头的前后压差的变化,导致压差阻力产生了差异,进一步使得减阻幅度不同.与无控制下相比,如图 6的车身表面压力云图所示,施加不同激励频率的合成射流皆使得斜背和后垂直背上部分区域的压力升高;射流器布置于斜背和顶部交界处,此处气流在合成射流作用下动量增大,压力减小,在其他激励频率下,得到的结果类似.对于后垂直背和斜背,在激励频率fa=210 Hz与fa=40 Hz作用下的压力近似,皆高于fa=90 Hz和fa=120 Hz的压力,低于fa=1 000 Hz的压力.因此,如图 4所示,fa=210 Hz与fa=40 Hz作用下的减阻幅度差异不大,都大于fa=90 Hz和fa=120 Hz对应值,低于fa=1 000 Hz对应值.
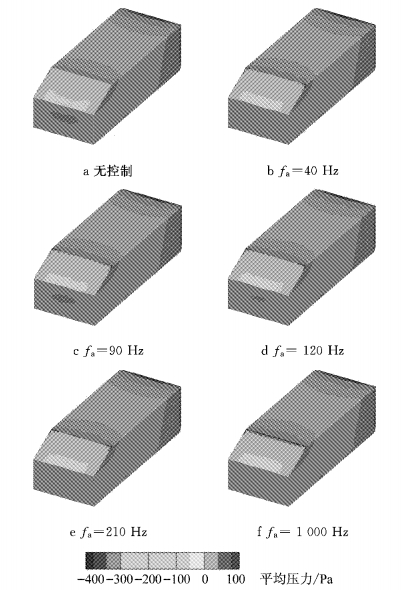
|
图 6 不同激励频率下平均压力分布 Fig.6 Mean pressure distribution with different driving frequency |
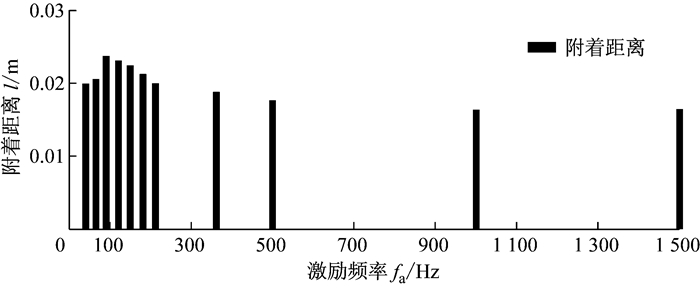
下面以施加动量系数为Cμ1,fa=90 Hz的合成射流为例,与无控制下流动对比,说明激励频率对流场和阻力的影响.在斜背上,如图 7所示,无控制下附着线与顶部分离线夹角较大.流向上布置的合成射流使得出口附近速度增大,增强了边界层抵抗逆压梯度的能力,减弱了流动分离作用,附着线更靠近并平行于顶部分离线.如图 7和图 8所示,斜背回流区被压缩,涡量减小,压力系数Cp升高,阻力系数降低.为了解释不同激励频率作用下阻力产生差异的原因,定义附着距离l为面y=0上的车顶分离点到斜背附着点间的距离,表征回流区大小.无控制下l=0.047 m,如图 9所示,在不同激励频率下,附着距离皆小于l=0.03 m.随着激励频率增大,附着距离先增大后减小再增大,与阻力随激励频率变化趋势一致.

|
图 7 有无控制下的流场对比 Fig.7 Comparison of natural and controlled flow |

|
图 8 背部等值面涡量 Fig.8 Isosurface of vortices near the slant |
|
图 9 不同激励频率下的附着距离 Fig.9 Flow reattachment distance on the slant with different driving frequencies |
在附着流的下游,由于斜背气流分离减弱,附着位置提前.如图 7c和7d所示,回流区外的气流速度升高,减弱了气流从后垂直背上端的分离,如图 6所示,使得后垂直背上半部分的压力皆高于无控制下的压力,而下半部分变化不大.
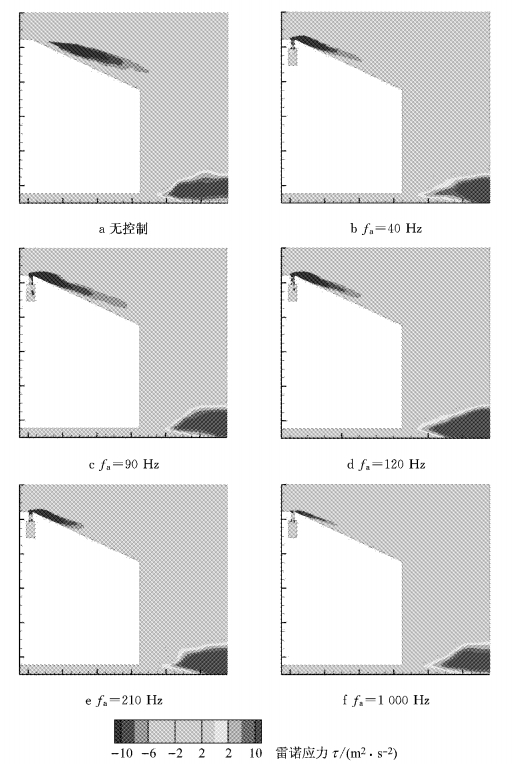
不同的激励频率导致合成射流内流与车辆外流的掺混程度产生差异,雷诺应力τ反映了不同流层间的掺混程度, 雷诺应力τ≠0分布区域Sτ与回流区大小成正比[10].如图 10所示,有激励控制下的雷诺应力τ≠0分布区域Sτ皆小于无控制下对应范围,fa=1 000 Hz对应的Sτ最大.fa=40 Hz与fa=210 Hz的分布近似,小于fa=120 Hz对应的Sτ,小于fa=1 000 Hz对应的Sτ.在壁面压力和雷诺应力的共同作用下,斜背回流区分离泡达到平衡[10].各个激励频率下的雷诺应力分布对回流区分离泡结构的影响不同,气流的附着位置及其附着距离随之变化.对斜背上方Sτ的雷诺应力绝对值|τ|进行积分,用此积分值表征雷诺应力对回流区分离泡的作用,在各个激励频率下的积分值
|
图 10 不同激励频率下, 面y=0上雷诺应力分布 Fig.10 Distribution of Renold stress in plane y=0 with different driving frequencies |
无控制下,斜背回流区内的点n1、n2、n3、n4压力和空间点n9、n10和n11速度信号的频谱峰值对应频率皆为f0=40 Hz,该频率对应斜背动态附着现象.施加动量系数为Cμ1,fa=90 Hz的合成射流后,合成射流涡对的周期性诱导作用对距离射流器出口较近的斜背外流影响较大.如图 11所示,点n9、n10、n11的速度和点n1、n2、n3、n4的压力皆按fa=90 Hz变化,动态附着现象仍然存在,对应频率为激励频率.图中,Ek为功率谱密度的能量值.

|
图 11 涡脱落频率分布 Fig.11 Power spectral density of velocity |
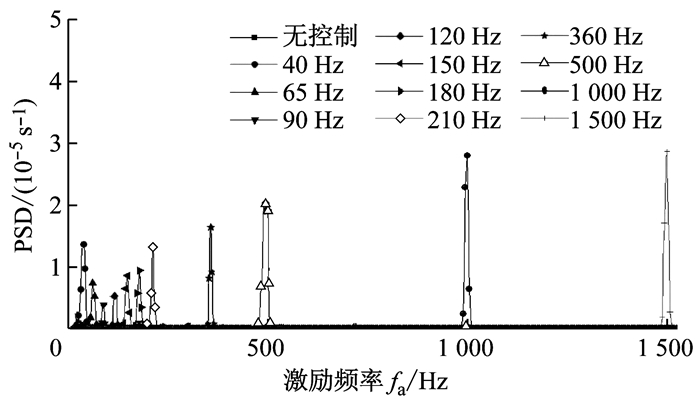
在其他激励频率作用下,合成射流控制了斜背回流区的动态附着现象,速度和压力信号的频谱峰值皆对应激励频率.压力的周期性变化导致压差阻力随之周期性变化,如图 12所示,阻力系数频谱中呈现激励频率对应的主峰值.图中,PSD表示功率谱密度值.
|
图 12 阻力系数功率谱密度 Fig.12 Power spectral density of drag coefficient signal |
不同激励频率下的频谱峰值高度表征了合成射流对流场控制的强弱程度.对于40 Hz≤fa≤90 Hz,激励频率增大,合成射流对流场的控制减弱,阻力系数频谱峰值降低,阻力增大.对于90 Hz≤fa≤1 000 Hz,激励频率增大,对流场的控制增强,阻力系数频谱峰值升高,阻力减小.
4 结论通过与试验结果对比,验证了数值仿真方法可有效模拟激励频率对车辆流动控制的影响,进一步分析得到以下结论:
合成射流阵列安装在车辆顶部和斜背交界处,施加不同激励频率皆可降低气动阻力.随着激励频率的增加,表面压力先减小后增大,阻力变化规律反之.不同激励频率下流动分离导致的附着距离和雷诺应力的分布差异解释了气动力变化的原因.
在不同激励频率作用下,合成射流控制了斜背回流区的动态附着现象,动态附着现象对应的频率为激励频率.流场的改变使得压力系数周期性变化,导致了压差阻力的变化.因此,阻力系数按激励频率震荡.
合成射流影响流场的参数较多,未来将对射流方向和其他射流位置等参数进行相关研究.
| [1] |
CHOI H, LEE J, PARK H. Aerodynamics of heavy vehicles[J]. Annual Review of Fluid Mechanics, 2014, 46(1): 441 DOI:10.1146/annurev-fluid-011212-140616 |
| [2] |
AUBRUN S, MCNALLY J, ALVI F, et al. Separation?ow control on a generic ground vehicle using steady microjet arrays[J]. Experiments in Fluids, 2011, 51(5): 1177 DOI:10.1007/s00348-011-1132-0 |
| [3] |
BOUCINHA V, WEBER R, KOURTA A. Drag reduction of a 3D bluff body using plasma actuators[J]. International Jounal of Aerodynamics, 2011, 1(3-4): 262 |
| [4] |
PATRICK G, KOURTA A. Aerodynamic drag control by pulsed jets on simpli?ed car geometry[J]. Experiments in Fluids, 2013, 54(2): 1 |
| [5] |
PARK H, CHO J, LEE J, et al. Aerodynamic drag reduction of ahmed model using synthetic jet array[R]. Washington D C: SAE, 2013. http://papers.sae.org/2013-01-0095/
|
| [6] |
CHO J, PARK H, LEE J. Experimental study on synthetic jet array for aerodynamic drag reduction of a simplified car[J]. Journal of Mechanical Science and Technology, 2013, 27(12): 3721 DOI:10.1007/s12206-013-0917-x |
| [7] |
HAN Xingsi, Krajnovic S, Basara B. Study of active?ow control for a simpli?ed vehicle model using the PANS method[J]. International Journal of Heat and Fluid Flow, 2013, 42(4): 139 |
| [8] |
AGARWAL R. Computational study of drag reduction of models of truck-shaped bodies in ground effect by active flow control[R]. Washington D C: SAE, 2013. http://papers.sae.org/2013-01-0954/
|
| [9] |
KRAJNOVIC S, FERNANDES J. Numerical simulation of the flow around a simplified vehicle model with active flow control[J]. International Journal of Heat and Fluid Flow, 2011, 32(2): 192 |
| [10] |
PARKIN D, THOMPOSON M, Sheridan J. Numerical analysis of bluff body wakes under periodic open-loop control[J]. Journal of Fluid Mechanics, 2014, 739(1): 94 |
| [11] |
MA Liqun, FENG Lihao. Experimental investigation on control of vortex shedding mode of a circular cylinder using synthetic jets placed at stagnation points[J]. Science China Technological Sciences, 2013, 56(1): 158 DOI:10.1007/s11431-012-5074-4 |
| [12] |
MINGUEZ M, PASQUETTI R, SERRE E. High-order large-eddy simulation of flow over the "Ahmed body" car model[J]. Physics of Fluids, 2008, 20(9): 1 |
| [13] |
KOTAPATI R B, MITTAL R, CATTAFESTA L. Numerical study of a transitional synthetic jet in quiescent external flow[J]. Journal of Fluid Mechanics, 2007, 581(7): 287 |
| [14] |
RANDEMANGE G, GOHLKE M, ADOT O. Turbulent wake past a three-dimensional blunt body. part 1: global modes and bi-stability[J]. Journal of Fluid Mechanics, 2013, 722(5): 51 |
 2017, Vol. 45
2017, Vol. 45

