2. 同济大学 智能型新能源汽车协同创新中心,上海 201804
2. State Intelligent Car of New Energy Resources Collaborative Innovation Center, Tongji University, Shanghai 201804, China
运动规划是与机器人、人工智能和控制理论等学科息息相关的一个研究领域,其任务是规划出驱使机器人从当前位置运动到目标位置的一系列指令[1].随着智能汽车的兴起,以无人车为研究对象的运动规划问题越来越受到重视.
传统机器人领域的运动规划算法包括概率路图法[2]、可视图法[3]、细胞分解法[4]等基于几何模型的搜索算法,以及基于虚拟势场和导航函数的人工势场方法[5]等.
近年来新的运动规划算法不断出现和发展,在无人车运动规划领域具有代表性的是基于随机采样的快速随机扩展树法[6]和各种基于搜索的状态格子算法[7].这些算法已经被成功用于2007年DARPA挑战赛各个参赛队伍的无人车辆上.例如麻省理工学院(MIT)参赛车辆使用基于随机采样的算法获得了比赛第四名[8].此外,国内也对运动规划算法进行了大量的研究.例如北京理工大学的IN2BOT车辆利用搜索算法[9]在中国智能车挑战赛中取得佳绩.
本文总结了目前文献中经常出现的各种适用于无人车运动规划的算法,分别从理论、算法实时性等方面分析比较了它们在理论上的优势和缺点,为今后的深入研究提供参考.
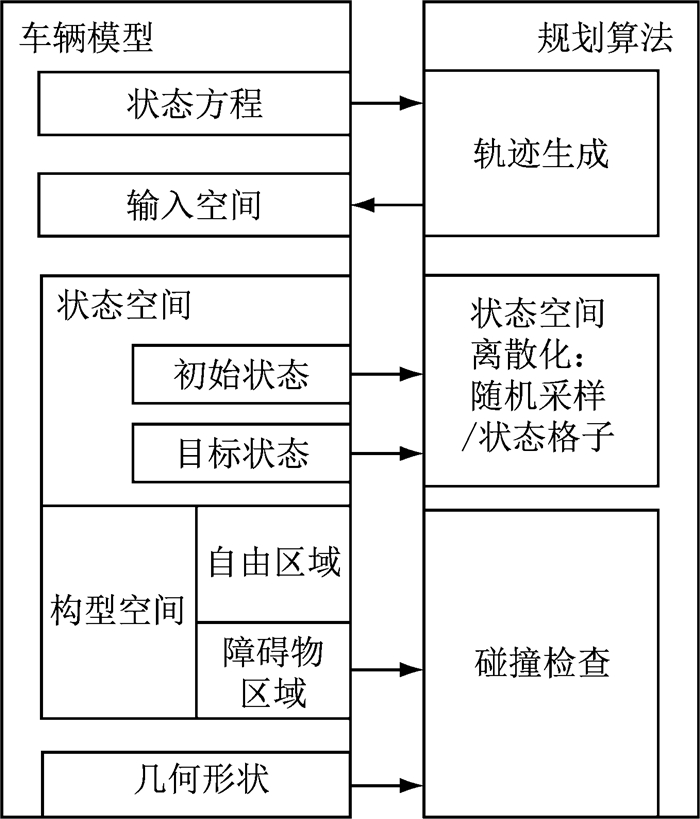
1 问题定义当给定车辆的几何形状和动力学模型、所处环境障碍物的分布情况、以及一个初始状态和一个目标状态集之后,运动规划的任务就是找出一系列控制输入,驱动车辆从初始状态运动到目标状态,并且在运动过程中避免和障碍物发生碰撞.
为了更好地描述运动规划问题以及规划算法,必须选择正确描述车辆模型.车辆模型与规划算法的关系如图 1所示.
|
图 1 车辆模型和规划算法的关系 Fig.1 Relationship between the vehicle model and planning algorithm |
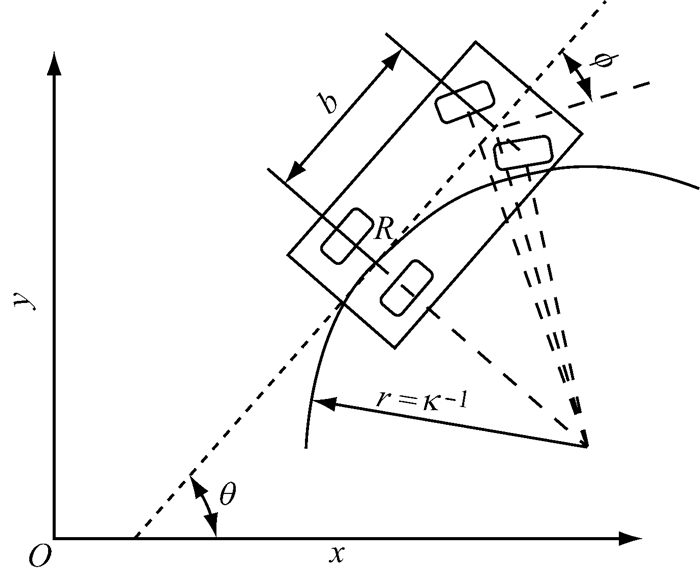
目前最常用的是具有阿克曼转向性质的车辆模型.该模型将车辆视为平面刚体,具有3个自由度,构形空间C为二维特殊欧式群SE(2),选取后轴中心R作为参考点.如图 2中,车辆(轴距为b)在大地坐标系下的坐标为(x, y),航向角为θ,那么车辆位置唯一确定.另外,在转向时,在方向盘转角为ϕ的情况下,车辆转向路径的半径r和曲率κ分别如图 2所示.车辆的状态方程见式(1).
| $ \begin{array}{l} \dot x = v{\rm{cos}}\;\theta \\ \dot y = v{\rm{sin}}\;\theta \\ \dot \theta = v \kappa\\ \dot v = a\\ \dot \kappa = \frac{{\dot \phi }}{{b{\rm{co}}{{\rm{s}}^2}\varphi }} \end{array} $ | (1) |
|
图 2 车辆模型 Fig.2 Vehicle model |
式中:v为速度;a为加速度;κ为曲率;
车辆可以看作是构形空间中的一点,构形空间中与障碍物发生干涉的点的集合为构形空间障碍Cobstacle,构形空间自由区域为Cfree=C-Cobstacle,连续映射τ: [0, 1]→Cfree称为构形空间中的一条可行路径.可行路径并不能反映车辆所受到的非完整约束,在构形空间上再加上速度、曲率的维度,则得到状态空间.类似于构形空间,可以定义状态空间的起始构型Xinit和终止构型Xgoal,障碍区域Xobstacle和自由区域Xfree,可行轨迹在构形空间中的投影就是可行路径.
因此,运动规划问题可用三元组(Xfree, Xinit, Xgoal)来描述,规划算法就是要找出状态方程(1) 的一系列输入,其对应的轨迹是状态空间中的可行轨迹,起始于初始状态,最终到达目标状态集中.
对于像无人车这样具有连续状态空间的运动规划问题,计算复杂度都是非常高的.为了提高算法效率和实用性,必须降低算法对完备性的要求.基于随机采样和基于网格搜索的算法是目前常用的规划算法,它们分别具有概率完备性和解析度完备性,从而降低算法的计算复杂度.
2 轨迹生成 2.1 轨迹生成与非线性控制轨迹生成是各类无人车运动规划算法的一个基本程序,其目的是构造状态空间中的一条轨迹(不考虑障碍物)连接任意给定的两个状态.这一问题的解决方法一般有幂零法[10]、数值计算法[11]、Chained Form[12]以及微分平坦法[13].其中幂零法可以求得一系列分段常数的控制输入,其对应轨迹可连接任意给定的初始状态和目标状态,但是运动规划采用的无人车模型是不满足幂零的条件的;数值计算方法往往用来求解最优轨迹,但是求解效率较低;对于可转化为Chained Form的系统,可以使用三角函数或多项式函数精确求解控制输入,但是多数情况下其轨迹过于复杂;微分平坦是某些非线性系统具有的一种良好性质,对于这类系统可以通过构建系统平坦输出来解决轨迹生成问题,是目前常用的方法.
运动规划所采用的车辆模型具有微分平坦性质,其平坦输出为后轴中心R的坐标,因此轨迹生成就是要构造R的一条足够光滑且满足各种有界性的轨迹来连接两个给定状态.
2.2 轨迹生成方法常见的轨迹生成方法有两大类,直接构造法和路径-速度分解法:
(1) 直接构造法是指直接构造车辆后轴中心R坐标关于时间的函数。文献[14]针对非结构化环境使用5次多项式来构造满足初始和终止位置、速度和加速度的轨迹,而且5次多项式使得加速度变化率最小,有利于车辆的平稳行驶.但是这一方法需要多次调整轨迹的时间区间,来保证整条轨迹上速度、加速度、曲率和曲率变化率的有界性.文献[15]在[14]的基础上针对结构化环境中的轨迹生成方法作出了改进,计算道路中线的Frenet标架下轨迹的坐标,可以适应各种道路环境下的轨迹生成问题.
(2) 路径-速度分解法[16]最初是为了解决有移动障碍物的环境下运动规划的问题而提出的,先构造一条避开静态障碍物的路径,再在路径上规划速度,避开移动障碍物.对于轨迹生成而言无需考虑障碍物,只需要考虑无人车的运动学和动力学约束.直接轨迹生成法要一次性满足速度、加速度、曲率和曲率导数的有界性,难度较大;而路径-速度分解法先生成一条曲率连续有界的路径,然后在路径上生成连续有界的速度,同时保证有界的加速度和有界的曲率导数,降低了轨迹生成的难度.
(a)路径生成
Dubins曲线[17]和Reeds and Shepp (RS)曲线[18]是连接构形空间中任意两点的最短路径,分别对应无倒车和有倒车的情况.它们都是由最大曲率圆弧和直线组成的,在圆弧和直线连接处存在曲率不连续,实际车辆按照这样曲线行驶时必须在曲率不连续处停车调整方向轮才能继续行驶.
回旋线[19]的曲率与曲线长度成正比关系,可以用作直线到圆弧之间的过渡曲线,从而改造Dubins曲线和RS曲线,实现曲率连续性,比较有代表性的是CC-Steer[20],适用于低速下的运动规划.
多项式螺旋线[21]的曲率是曲线长度的多项式函数,回旋线是一种特殊的多项式螺旋线.根据微分几何理论,给定函数κ(s),则整个曲线的形状就完全确定了.但是为了求解曲线形状,在给定边界条件后必须使用数值手段求解多项式中的待定系数,求解效率较低.
样条曲线具有封闭的表达式,容易保证曲率连续性.B样条曲线[22]可以实现曲率连续性,三次Bézier曲线[23]可以保证曲率的连续性和有界性.η3曲线[24]是一种七次样条曲线,它有着很好的性质:曲率连续性和曲率导数的连续性,这对于高速行驶车辆是很有意义的.
(b)速度生成
文献[25]通过对路径指定线加速度来生成速度.线加速度可以是某一常数,或是由比例-微分控制器来生成.文献[26]研究了在给定时间内通过一段给定路径的速度生成问题,其解决方案是将时间域划分为若干区间,使用速度关于时间的三次样条函数来插值,但这一方法容易产生加速度变化率较大的问题.文献[27]直接用速度关于路径长度的三次多项式来生成速度,这种方法较为简单.
3 基于采样的算法基于随机采样的运动规划算法的基本思路是通过对状态空间均匀随机采样来构建一个连通图,当初始、目标状态都在图中或是都可以连接到图中时,则问题得以解决.基于随机采样的算法不需要对状态空间自由区域显式建模,轨迹的可行性由碰撞检测来验证.典型的基于随机采样的算法有概率路图法[28](probabilistic roadmap, PRM)和快速随机扩展树法[6](rapidly random tree, RRT).
3.1 基本算法PRM/RRT 3.1.1 PRM的构建(1) 预处理阶段:对状态空间内的安全区域均匀随机采样n个点,每个采样点分别与一定距离内的邻近采样点连接,并丢弃掉与障碍物发生碰撞的轨迹,最终得到一个连通图.
(2) 查询阶段:对于给定的一对初始和目标状态,分别将其连接到已经构建的图中,再使用搜索算法寻找满足要求的轨迹.
容易看出,一旦构建一个PRM之后,可以用于解决不同初始、目标状态的运动规划问题,但是这个特性对于无人车运动规划而言是不必要的.另外PRM要求对状态之间作精确连接,这对于存在复杂微分约束的运动规划问题是十分困难的.
3.1.2 RRT的构建(1) 树的初始化:初始化树的结点集和边集,结点集只包含初始状态,边集为空.
(2) 树的生长:对状态空间随机采样,当采样点落在状态空间安全区域时,选择当前树中离采样点最近的结点,将其向采样点扩展(或连接).若生成的轨迹不与障碍物发生碰撞,则将该轨迹加入树的边集,该轨迹的终点加入到树的结点集.
(3) 重复步骤(2),直至扩展到目标状态集中.
相比PRM的无向图而言,RRT构建的是初始状态作为根结点、目标状态作为叶结点的树结构,对于不同的初始和目标状态,需要构建不同的树.另外,RRT不要求状态之间的精确连接,更适合解决像无人车运动规划这样的运动动力学问题.
3.2 提高算法效率和求解质量的措施基于随机采样的规划算法具有概率完备性.以RRT为例,随着采样点数目的增加,树最终会稠密地充满整个状态空间自由区域,找到可行解的概率是收敛到1的.然而,除了概率完备性,人们更希望算法有更高的效率,且能求得更高质量的解.为此,标准RRT在以下几方面作了改进.
(1) 均匀采样:标准RRT算法对状态空间均匀随机采样,当前树中结点获得扩展的概率与其Voronoi区域面积成正比,所以树会向着状态空间的空旷区域生长,均匀充满状态空间的自由区域.盲目的扩展伴随着大量的碰撞检查,严重影响程序效率.
文献[29]提出RRT-Connect算法,同时构建两棵分别起始于初始状态和目标状态的树,当两棵树生长到一起时则找到可行解.Goal-biasing[30]是指在随机采样序列中以一定比例插入目标状态,引导树向目标状态扩展,加快求解速度,提高求解质量.
文献[31]提出启发式RRT算法(heuristic RRT, hRRT),使用启发式函数增加扩展代价低的结点被采样的概率,这个函数要求计算树中每个结点的代价,但是在复杂环境中,代价函数的定义往往是很困难的.
文献[32]提出f-biased采样方法,先将状态空间离散化为网格,再使用Dijkstra算法计算每个网格上的代价,这个网格所在区域的点的代价值都等于该值.利用这样的代价函数可以构建更好的启发式函数来引导树的扩展.
文献[33]中结合驾驶员视觉注意力模型进行偏向性采样中,利用视觉特征信息引导运动规划,使规划出的轨迹更符合人类驾驶行为.
(2) 距离度量:距离用来度量构形空间(状态空间)中两个构形(状态)之间路径(轨迹)的代价,这个代价可以理解为路径的长度、消耗的能量或是花费的时间.不同于欧氏空间,车辆的构形空间或状态空间中距离没有闭形表达式,其计算难度等价于轨迹生成的难度;如果考虑障碍物的话,距离的计算难度是等价于整个运动规划的难度的.因此,运动规划中距离的定义是采用类似欧氏距离的表达式.文献[34]给出构形空间SE(3) 中加权距离表达式:
| $ \rho \left( {{q_0}, {q_1}} \right) = {\omega _{\rm{t}}}\left\| {{\mathit{\boldsymbol{X}}_0}-{\mathit{\boldsymbol{X}}_1}} \right\| + {\omega _{\rm{r}}}f\left( {{R_0}, {R_1}} \right) $ | (2) |
其中q=(X, R), f(R0, R1)表示从姿态R0旋转到R1的距离.ωt和ωr表示权重.文献[6]给出了状态空间中加权距离表达式:
| $ \begin{array}{l} \rho \left( {{x_1}, {x_2}} \right) = {\omega _p}{\left\| {{p_1}-{p_2}} \right\|^2}{\rm{ + }}{\omega _q}{\left( {1-\left| {{q_1} \cdot {q_2}} \right|} \right)^2}{\rm{ + }}\\ \;\;\;\;\;\;\;\;\;{\omega _v}{\left\| {{V_1}-{V_2}} \right\|^2} + {\omega _w}{\left\| {{w_1} - {w_2}} \right\|^2} \end{array} $ | (3) |
式中:p为刚体质心坐标;q为表示刚体姿态的四元数;V、w分别为线速度、角速度;ωp、ωq、ωr和ωw表示各个部分的权重.
类似这些距离的表达式并不能真实反映构形或状态之间的远近.然而,标准RRT根据采样点选择树中临近点进行扩展时,要使用这样的距离表达式来比较远近,难免会带来误差,影响RRT探索整个状态空间的能力.RG-RRT [35](reachability guided RRT)可以消除不准确的距离对RRT探索能力的影响.RG-RRT计算树中结点的能达集,当采样点到结点的距离大于采样点到该结点能达集的距离时,该节点才有可能被选中进行扩展.
(3) 障碍物:碰撞检查是基于采样的算法的效率瓶颈之一,通常的做法是对路径等距离离散化,再对每个点处的构形作碰撞检查.文献[36]提出RC-RRT(resolution complete RRT)来降低靠近障碍物的结点获得扩展的概率,具体做法是对输入空间离散化,对于某个结点,其某个输入只能使用一次;若某个输入对应的轨迹与障碍物碰撞,则对该节点加上一个惩罚值,该惩罚值越高,该节点获得扩展的概率越小.文献[37]结合RG-RRT和RC-RRT的优点,提出了EG-RRT(environment guided RRT)使算法更适合处理有狭窄通道的障碍物环境.文献[38]与文献[39]分别提出DD-RRT(dynamic domain RRT)与ADD-RRT(adaptive dynamic domain RRT),限制采样区域在当前树所在的局部空间,以防止靠近障碍物的结点反复扩展失败,提高算法效率.文献[40]中提出了T-RRT算法,它作用于代价地图上,在进行搜索和扩展时,引入了过渡测试(transition test),利用Metropolis准则来判断新结点的代价是否能够满足扩展的要求,同时控制无效扩展,从而提高算法效率并提高路径的质量.
(4) 实时性:anytime RRT[41]是一种实时性较高的算法,它先快速构建一个RRT,获得一个可行解并记录其代价.之后算法会继续采样,但仅将有利于降低可行解代价的结点插入树中,从而逐渐获得较优的可行解.Replanning[42]是另一种实时规划算法,它将整个规划任务分解为若干等时间的子任务序列,在执行当前任务的同时规划下一个任务.
3.3 最优性尽管各种改进措施可以大幅度提高求解质量,但是仍难以保证获得最优解.近年来最优化规划算法发展较快,出现了许多能求渐进最优解的算法.
文献[43-45]根据随机几何图理论对标准PRM和RRT做出改进,得到了具有渐近最优性质的PRM*、RRG和RRT*算法.在状态空间中随机采样n个点,并将距离小于r(n)的点连起来,就构成了随机几何图(random geometric graph, RGG).渐近最优性要求r(n)满足:
| $ r\left( n \right) = \gamma {\left( {\frac{{\log \left( n \right)}}{n}} \right)^{1/d}} $ | (4) |
式中:γ与具体环境有关;d为状态空间维数.按照这一理念对标准PRM和RRT改造即得到PRM*和RRG算法.在RRG基础上引入“重新连接”步骤,即检查新插入结点作为其临近点的父结点是否会使其临近点的代价降低,若降低,则去掉临近点原来的父子关系,将当前插入点作为其父结点,这就是RRT*算法.大量的结点连接和局部调整使得PRM*和RRT*的效率十分低下.文献[46]中提出了LBT-RRT算法,将RRG和RRT*算法结合起来,引入一个估计参数1+ε,当ε=0时,LBT-RRT算法就是RRG算法,而当ε=∞时,则就是RRT*算法.算法构造RRG所用的图和RRT*所用的树,第一张图保证最终路径的最低代价,第二个树则保证路径代价在1+ε倍的最低代价中,通过1+ε提高算法的效率并保证路径的渐进最优性.文献[47]在PRM*的基础上做出改进,大大减少了结点连接的数量,并且可以获得弱渐近最优性,在实际应用中可以获得比PRM*和RRT*更高的效率.
尽管RRT*及其变种Anytime-RRT*已被用于解决带有微分约束的运动规划问题,但是效率很低.文献[48]提出了不需要求解两点边值问题的渐进最优算法SST*(stable sparse RRT*),通过对输入空间采样来扩展树,并且引入“修剪”树的操作来维持稀疏的数据结构,提高了算法效率.
RRT*与标准RRT一样具有盲目探索整个状态空间的特点,其计算效率还有很大的提升空间.文献[49]提出了Informed RRT*算法,来避免RRT*对整个状态空间的不必要的探索,其思路是先用RRT*找到一个解,然后把采样区域限制到一个以初始、目标状态为焦点并包含当前解的椭球内,继续优化当前解.文献[50]提出了BIT*(batch informed trees)算法,其思路是先构建一个满足渐进最优条件的RGG,然后利用启发式搜索构建一个从初始状态到目标状态的树,之后反复构造更稠密的RGG,并在已有的树结构基础上作优化.经试验验证,BIT*可以获得比RRT*、FMT*和Informed RRT*更高的效率.
另外还有一类算法将RRT*和其他的算法融合,可以大大提高算法的效率,例如文献[51]提出TG-RRT*算法,在生成随机点后,利用起始点、终止点、随机点组成三角形的内心或形心来代替随机点,通过三角几何学缩小搜索范围,从而大大减小算法所用的搜索时间和生成的结点数;文献[52]中将RRT*和T-RRT结合,在RRT*中引入过渡测试,使RRT*具备渐近最优的性质,同时提高算法效率.
4 基于搜索的算法解决运动规划问题的另一大类算法是启发性搜索算法,其基本思想是将状态空间通过确定的方式离散成一个图,然后利用各种启发式搜索算法搜索可行解甚至是最优解.这类算法具有解析完备性,甚至是解析最优性.尽管对于高维状态空间,搜索算法需要处理大量网格,效率低下,但是对于无人车运动规划问题而言,这类算法已经有了比较成熟的应用.
4.1 状态格子状态格子[53]是一种对状态空间离散化的手段.状态格子由结点(表示状态)和从该结点出发到达相邻结点的运动基元组成,一个状态结点可以通过其运动基元变换到另一个状态结点.这样,状态格子就将原来连续的状态空间转化为一个搜索图,运动规划问题就变成了在图中搜索出一系列将初始状态变换到目标状态的运动基元.
规则状态格子可以对状态空间进行离散化,不依赖于具体的环境结构,构造方便,每个格子都可以由一个格子通过平移变换得到,运动基元不必在线计算.但是在结构化环境中,车辆在大地坐标系上的航向角取值范围大,按照固定的离散方式无法反映环境的特点.文献[54]针对道路上车辆的运动规划问题构造了符合道路形状的状态格子,格子在工作空间上按道路中线分布,方向角与道路中线的切线方向一致,曲率中心与道路中心曲率中心一致.这样规划出的路径更加符合道路的形状,缺点是格点的运动基元需要根据道路形状在线计算.文献[54]将时间考虑为状态格子的维度,方便处理移动障碍物.文献[25]把速度、时间和加速度加入到状态格子的维度,使车辆具备了在高速公路上实现保持车距、变换车道等基本功能.
4.2 搜索算法构建起状态格子后往往要使用图搜索算法来搜索最优轨迹.
Dijkstra[55]算法是经典的最短路径搜索算法,然而对于给定的一组初始、目标状态,其广度优先的性质将会导致太多无关节点的搜索,效率很低.A*[56]是一种启发式最优搜索算法,其框架与Dijkstra基本一致,不同点在于引入了对当前结点到目标结点最低代价的估计函数.A*算法维护两个集合:OPEN和CLOSED,OPEN是存储待扩展节点的优先队列,根据通过当前结点的路径总代价来排序,CLOSED存储已经扩展过的节点.算法每次从OPEN中取出最优先的节点,进行扩展,并将该节点插入到CLOSED中,该节点所扩展到的节点如果不在CLOSED中,就插入到OPEN中,这样循环下去,直到扩展到目标结点.可见A*算法通过启发式函数引导靠近目标结点的节点获得优先扩展的机会;但在格子数量很多时,A*处理的节点数目过多.
Weighted A*[57]通过增加启发式函数的权重进一步引导搜索方向向这目标节点进行,搜索速度很快,但是容易陷入局部极小值,无法保证全局最优解.ARA*[58]是在Weighted A*基础上发展出的具有Anytime性质的搜索算法,它通过多次调用Weighted A*算法且每次调用就缩小启发式函数的权重,这样算法可以快速求出可行解,通过引入集合INCONS使得每次循环可以继续使用上一次循环的信息,对路径做出优化,逐渐逼近最优解.
由于一个启发式函数很难同时兼顾效率和最优性,那么考虑到启发式函数对搜索结果和结点数目的影响,Sandip Aine等提出了MHA*算法[59],引入多个启发式函数,保证其中有一个启发式函数在单独使用时可以找到最优解,从而通过协调不同启发式函数生成的路径代价,可以兼顾算法的效率和最优性.DMHA*[60]在MHA*的基础上在线实时生成合适的启发式函数,从而避免局部最小值问题.A*-Connect[61]是将RRT-Connect的思想运用到MHA*上,分别从起点和终点进行搜搜,直到两个树重合为止.
A*及其变种算法Weighted A*、ARA*可以有效解决确定性环境中的搜索问题,但对于环境复杂多变的情况,环境中的代价分布会发生变化,简单地重复使用A*虽然可以重新搜索出最优路径,但是计算效率较低.LPA*[62]可以处理状态格子的运动基元的代价是时变的情况,当环境发生变化时可以通过对较少数目节点的重新搜索规划出新的最优路径;D*[63]适合处理复杂多变的环境,能够根据所获取环境信息快速重新规划从当前状态到目标状态的最优轨迹,适合机器人在行进过程中探测出新的障碍物时重新选择路径;D*-Lite[64]是对LPA*的发展,可以获得与D*同样的结果,但是效率比D*高.
另外,A*还有其他一些变种.M*[65]是专门进行多个机器人运动规划的搜索算法;R*[66]是由A*结合随机采样发展而来的搜索算法,它避免了对启发式函数的过度依赖,同时通过随机采样来避开局部极小值,获得全局最优解;Field-D*[67]和Theta*[68]都是对传统工作空间网格法的发展.
5 算法实现上述基于随机采样的算法和基于搜索的算法在很多无人车上都得到应用.例如2007年DARPA挑战赛第一名车辆“Boss”[69]中,运动规划模块采用三次螺旋线作为轨迹曲线,利用A*算法作为规划算法,将障碍物、车道、曲线曲率、曲率导数以及车辆速度、加速度等因素纳入轨迹代价中,在状态空间中不断搜索得到最终路径.再如在2016年中国智能车未来挑战赛中取得佳绩的西安交通大学的“夸父一号”[70]中,利用Bézier曲线作为轨迹曲线,根据城市环境常见工况,例如换道,转弯,U型转弯等,预先生成模板路径曲线库,在规划之前先在曲线库中根据边界条件选择模板曲线,再根据实际环境利用RRT算法对曲线进行修改,从而大大提高了算法效率.
除了可以通过自己编写代码实现算法外,各个研究机构分别推出开放源代码的程序库,供世界各地学者使用交流.其中,以基于采样的算法程序库OMPL[71]和基于搜索的算法程序库SBPL[72]最具代表性.
开源运动规划库(open motion planning library,OMPL)是用C ++编写的程序库,包含两个部分:核心算法库OMPL,包含各种基于采样的运动规划算法的实现;界面OMPL.app,是核心算法库的的可视化前端,使用Python+PyQt实现.OMPL并不提供碰撞检查程序库,可以结合FCL[73]等开源程序库来使用.
SBPL(search-based planning library)是专门针对基于搜索的运动规划算法而开发的程序库,几乎涵盖了第4.2节所列举的所有搜索算法,使用C ++实现.
6 发展趋势随着无人车技术的发展,运动规划算法与其他方法结合,从而优化规划过程.
(1) 与车辆动力学结合
将动力学参数评价指标和最优规划等结合,利用直接构造法进行规划是近年采用较多的方法,在这个过程中可以充分考虑车辆动力学因素,规划出的轨迹更加合理.Benz S500 Intelligent Drive采用直接构造法[74],将车辆在车道中的相对位置、加速度、横摆角速度以及曲率等作为优化指标,利用序列二次规划方法进行轨迹计算.沈峘等[75]基于单轨模型,结合车辆无滑移条件,利用魔术公式来描述轮胎与路面的动力学模型,构造车辆动力学约束公式,同时将车辆动力性、操纵性和稳定性评价指标作为优化指标,将整个运动规划问题转化为非线性规划问题,从而获得可行轨迹.国防科技大学[76]将模型预测控制融入轨迹规划中,预先选择边界条件范围离线计算可行路径集,在行为决策系统做出全局路径后,将阿克曼转角模型作为预测模型,在需要规划轨迹的全局路径段从可行路径集中选择部分路径并结合速度计算生成备选轨迹集,之后将动力学因素和障碍物等作为评价指标,利用最优规划从备选轨迹集中选出最终轨迹.该方法由于使用离线计算的可行路径集,因此大大提高算法效率.
运动规划也在自主泊车领域得到应用,自主泊车的工况相对单一,并且车辆行驶速度较低,因此采用的方法更加灵活.陈荣华等[77]利用基于互补约束的数学规划方法(MPCC)和R函数法将泊车过程中的避障条件约束转化为避障模型,同时结合车辆动力学模型建立行车模型,对泊车过程进行联立动态规划,提高了规划算法的普适性和鲁棒性.李红等[78]考虑下层路径跟踪的限制,在障碍物约束的基础上,加入车辆转向角度和角速度约束,对泊车轨迹进行优化,从而提高规划结果的实用性.
(2) 与状态参数估计结合
状态参数估计可以更加准确获得车辆参数,因此可以将状态估计器加入规划模块中,通过在线估计车辆状态并将其反馈给规划器,提高轨迹质量.不同地面类型会引起车辆滑移特性的变化,进而影响车辆状态,文献[79]针对这种现象设计滑移估计器,结合CC-RRT*算法,不断结合估计参数重新规划轨迹,通过闭环规划提高轨迹安全性.
(3) 与机器学习结合
机器学习作为人工智能的重大分支,其与运动规划的结合可以改善规划结果.例如文献[80]针对RRT算法,训练了一个具有恒定积分时间的非线性参数模型,该模型取代了距离度量模块用于计算节点间代价,从原理上讲,该模型建立在POSQ扩展函数——用于解决两点边值(boundary value problem, BVP)问题的转向模型函数的基础上,模型的训练输入为该扩展函数对应的距离度量结果,积分时间的大小决定了距离度量的计算复杂度,同时该文献对比了其他训练模型,如神经网络模型、支持向量机模型等,发现这种模型在度量精确度和计算时间上都有很大的优势.文献[81]则利用局部加权学习的方法取代距离度量,同时根据估计结果计算树中结点对应的代价较小的区域,除此之外,每个搜索过的结点都被标记了“安全”和“危险”两个标签,利用贝叶斯分类器估计整个状态空间中的安全区域,从而每次都只在安全区域中采样,随着采样的不断进行,估计的安全区域就更加准确,这两个措施使搜索更加趋向于代价低的安全区域,加快搜索速度.文献[82]则将机器学习融入速度生成中,预先模拟多个试验场景,生成每个场景对应安全轨迹的速度文件,用卷积神经网络训练之,从而加快安全速度的生成.国内也有这些方面的研究.例如国防科技大学在A*算法中加入学习模型[83],将整个搜索过程分为利用A*算法搜索路径离散点作为子目标点以及利用离线训练好的模型生成最终路径两个阶段,其中训练集合的输入为初始状态和车辆模型的控制输入,输出为对应的终止状态和轨迹对应的代价,训练方法为最小二乘迭代法,由此可以看出,训练得到的模型会综合考虑车辆动力学特性和路径安全性,经过验证,这种方法在计算效率和普适性方面都有极大的提高.
6 总结(1) 采用具有阿克曼转向性质的车辆模型,可以利用其微分平坦性质简化轨迹生成问题.
(2) 直接轨迹生成法相对路径-速度分解法而言还不够成熟,使用多项式螺旋线生成路径对速度生成和碰撞检查都有利,应用比较成熟.
(3) 缺少准确的距离度量是基于采样的运动规划算法的主要缺陷,相关改进算法的效率有待验证;各种最优化算法虽然不断提高效率,但离实际应用还有距离;Anytime-RRT/RRT*是实用性比较高的算法.
(4) 基于搜索的运动规划算法在非结构化环境和结构化环境中无人车运动规划问题上都有成功的应用,是一类具有很大实用意义的方法.
| [1] |
LAVALLE S M. Planning algorithms[M]. New Yrok: Cambridge University Press, 2006
|
| [2] |
KAVRAKI L E, SVESTKA P, LATOMBE J C, et al. Probabilistic roadmaps for path planning in high-dimensional configuration spaces[J]. IEEE transactions on Robotics and Automation, 1996, 12(4): 566 DOI:10.1109/70.508439 |
| [3] |
SIMÉON T, LAUMOND J P, NISSOUX C. Visibility-based probabilistic roadmaps for motion planning[J]. Advanced Robotics, 2000, 14(6): 477 DOI:10.1163/156855300741960 |
| [4] |
BROOKS R A, LOZANO-PEREZ T. A subdivision algorithm in configuration space for findpath with rotation[R]. Cambridge: Massachusetts Institute of Technology Cambridge Artificial Intelligence Lab, 1982. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6313352
|
| [5] |
KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots[J]. The International Journal of Robotics Research, 1986, 5(1): 90 DOI:10.1177/027836498600500106 |
| [6] |
LAVALLE S M, KUFFNER J J. Randomized kinodynamic planning[J]. The International Journal of Robotics Research, 2001, 20(5): 378 DOI:10.1177/02783640122067453 |
| [7] |
PIVTORAIKO M, KELLY A. Efficient constrained path planning via search in state lattices[C]//International Symposium on Artificial Intelligence, Robotics, and Automation in Space. Munich: I-SAIRAS, 2005: 1-7. http://adsabs.harvard.edu/abs/2005ESASP.603E..33P
|
| [8] |
LEONARD J, HOW J, TELLER S, et al. A perception-driven autonomous urban vehicle[J]. Journal of Field Robotics, 2008, 25(10): 727 DOI:10.1002/rob.v25:10 |
| [9] |
FU M, SONG W, YI Y, et al. Path planning and decision making for autonomous vehicle in urban environment[C]//Intelligent Transportation Systems (ITSC), 2015 IEEE 18th International Conference.[S.l.]: IEEE, 2015: 686-692. http://trid.trb.org/view.aspx?id=1406036
|
| [10] |
SASTRY S S. Nonlinear systems: analysis, stability, and control[M]. [S.l.]: Springer Science & Business Media, 2013
|
| [11] |
BETTS J T. Survey of numerical methods for trajectory optimization[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(2): 193 DOI:10.2514/2.4231 |
| [12] |
MURRAY R M, SASTRY S S. Nonholonomic motion planning: Steering using sinusoids[J]. Automatic Control, IEEE Transactions on, 1993, 38(5): 700 DOI:10.1109/9.277235 |
| [13] |
ROUCHON P, MARTIN P, MURRAY R M. Flat systems, equivalence and trajectory generation[R]. Pasadena: California Institute of Technology, 2003.
|
| [14] |
TAKAHASHI A, HONGO T, NINOMIYA Y, et al. Local path planning and motion control for AGV in positioning[C]//Intelligent Robots and Systems' 89. The Autonomous Mobile Robots and Its Applications. IROS'89. Proceedings., IEEE/RSJ International Workshop. Tsukuba: IEEE, 1989: 392-397. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=637936
|
| [15] |
WERLING M, ZIEGLER J, KAMMEL S, et al. Optimal trajectory generation for dynamic street scenarios in a frenet frame[C]//Robotics and Automation (ICRA), 2010 IEEE International Conference.[S.l.]: IEEE, 2010: 987-993. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5509799
|
| [16] |
PHAM Q C, CARON S, LERTKULTANON P, et al. Admissible velocity propagation: beyond quasi-static path planning for high-dimensional robots[J]. The International Journal of Robotics Research, 2017, 36(1): 44 DOI:10.1177/0278364916675419 |
| [17] |
DUBINS L E. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents[J]. American Journal of Mathematics, 1957, 79(3): 497 DOI:10.2307/2372560 |
| [18] |
REEDS J, SHEPP L. Optimal paths for a car that goes both forwards and backwards[J]. Pacific Journal of Mathematics, 1990, 145(2): 367 DOI:10.2140/pjm |
| [19] |
WILDE D K. Computing clothoid segments for trajectory generation[C]//Intelligent Robots and Systems, IROS 2009. IEEE/RSJ International Conference.[S.l.]: IEEE, 2009: 2440-2445. http://dl.acm.org/citation.cfm?id=1733140
|
| [20] |
FRAICHARD T, SCHEUER A. From reeds and shepp's to continuous-curvature paths[J]. Robotics, IEEE Transactions on, 2004, 20(6): 1025 DOI:10.1109/TRO.2004.833789 |
| [21] |
KELLY A. Reactive nonholonomic trajectory generation via parametric optimal control[J]. The International Journal of Robotics Research, 2003, 22(7-8): 583 DOI:10.1177/02783649030227008 |
| [22] |
KOMORIYA K, TANIE K. Trajectory design and control of a wheel-type mobile robot using B-spline curve[C]//Proceedings of the '89 IEEE/RSJ International Workshop on Intelligent Robots and Systems.[S.l.]: IEEE, 1989:398-405.
|
| [23] |
YANG K, SUKKARIEH S. 3D smooth path planning for a UAV in cluttered natural environments[C]//Intelligent Robots and Systems, Iros, IEEE/RSJ International Conference.[S.l.]: IEEE, 2008:794-800. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=4650637
|
| [24] |
PIAZZI A, BIANCO C G L, ROMANO M. Smooth path generation for wheeled mobile robots using η3-splines[M]. Rijeka: InTech, 2010
|
| [25] |
MCNAUGHTON M, URMSON C, DOLAN J M, et al. Motion planning for autonomous driving with a conformal spatiotemporal lattice[C]//Robotics and Automation (ICRA), 2011 IEEE International Conference on. Shanghai: IEEE, 2011, 19(6):4889-4895. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5980223
|
| [26] |
GUARINO Lo Bianco C. Minimum-jerk velocity planning for mobile robot applications[J]. Robo Ranaon on, 2013, 29(5): 1317 |
| [27] |
XU W, WEI J, DOLAN J M, et al. A real-time motion planner with trajectory optimization for autonomous vehicles[C]//In IEEE ICRA-International Conference on Robotics and Automation. Saint Paul: IEEE, 2012, 162(4):2061-2067. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6225063
|
| [28] |
KAVRAKI L, KOLOUNTZAKIS M N, LATOMBE J. Analysis of probabilistic roadmaps for path planning[C]//Robotics and Automation, IEEE International Conference on. Minneapolis: IEEE, 1996, 4(1):3020-3025. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=660866
|
| [29] |
KUFFNER J J, LAVALLE S M. RRT-connect: an efficient approach to single-query path planning[C]//Robotics and Automation, Proceedings of ICRA '00. IEEE International Conference. San Francisco: IEEE, 2000:995-1001. http://ci.nii.ac.jp/naid/80011973097/ja/
|
| [30] |
LAVALLE S M. Motion planning[J]. IEEE Robotics & Automation Magazine, 2011, 18(1): 79 |
| [31] |
URMSON C, SIMMONS R. Approaches for heuristically biasing RRT growth[C]//Intelligent Robots and Systems, Proceedings of 2003 IEEE/RSJ International Conference. Las Vegas: IEEE, 2003:1178-1183. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1248805
|
| [32] |
KIESEL S, BURNS E, RUML W. Abstraction-guided sampling for motion planning[C]//The Fifth Annual Symposiumon Combinatiorial Search. Buffalo: SOCS, 2012: 162-163.
|
| [33] |
杜明博. 基于人类驾驶行为的无人驾驶车辆行为决策与运动规划方法研究[D]. 合肥: 中国科学技术大学, 2016. DU Mingbo. Research on behavioral decision making and motion planning methods of autonomous vehicle based on human driving behavior[D]. Hefei: University of Science and Technology of China, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10358-1016103089.htm |
| [34] |
KUFFNER J J. Effective sampling and distance metrics for 3D rigid body path planning[C]//In IEEE International Conference on Robotics and Automation. New orleans: IEEE, 2004:3993-3998. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1308895
|
| [35] |
SHKOLNIK A, WALTER M, TEDRAKE R. Reachability-guided sampling for planning under differential constraints[C]//Robotics and Automation, ICRA'09. IEEE International Conference. Kobe: IEEE, 2009: 2859-2865. http://dl.acm.org/citation.cfm?id=1704153
|
| [36] |
CHENG P, LAVALLE S M. Reducing metric sensitivity in randomized trajectory design[C]//Intelligent Robots and Systems, Proceedings of 2001 IEEE/RSJ International Conference.[S.l.]: IEEE, 2001: 43-48. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=973334
|
| [37] |
JAILLET L, HOFFMAN J, BERG J V D, et al. EG-RRT: Environment-guided random trees for kinodynamic motion planning with uncertainty and obstacles[C]//Intelligent Robots and Systems (IROS), 2011 IEEE/RSJ International Conference. San Francisco: IEEE, 2011: 2646-2652. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6094802
|
| [38] |
YERSHOVA A, JAILLET L, SIMÉON T, et al. Dynamic-domain RRTs: efficient exploration by controlling the sampling domain[C]//Robotics and Automation, ICRA 2005. Proceedings of the 2005 IEEE International Conference. Barcelona: IEEE, 2005:3856-3861. http://ieeexplore.ieee.org/document/1570709/
|
| [39] |
JAILLET L, YERSHOVA A, LAVALLE S M, et al. Adaptive tuning of the sampling domain for dynamic-domain RRTs[C]//Intelligent Robots and Systems, IEEE/RSJ International Conference, Edmonton: IEEE, 2005:2851-2856. http://ieeexplore.ieee.org/document/1545607/
|
| [40] |
JAILLET L, CORTÉS J, SIMÉON T. Sampling-based path planning on configuration-space costmaps[J]. IEEE Transactions on Robotics, 2010, 26(4): 635 DOI:10.1109/TRO.2010.2049527 |
| [41] |
FERGUSON D, STENTZ A. Anytime RRTs[C]//Intelligent Robots and Systems, IEEE/RSJ International Conference. Beijing: IEEE, 2006:5369-5375. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=4059281
|
| [42] |
TSIANOS K I, KAVRAKI L E. Replanning: a powerful planning strategy for hard kinodynamic problems[C]//Intelligent Robots and Systems, IROS 2008. IEEE/RSJ International Conference. Nice: IEEE, 2008:1667-1672. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4650965
|
| [43] |
KARAMAN S, FRAZZOLI E. Incremental sampling-based algorithms for optimal motion planning[J]. International Journal of Robotics Research, 2010, 30(7): 5326 |
| [44] |
KARAMAN S, FRAZZOLI E. Sampling-based algorithms for optimal motion planning[J]. The International Journal of Robotics Research, 2011, 30(7): 846 DOI:10.1177/0278364911406761 |
| [45] |
KARAMAN S. Sampling-based algorithms for optimal path planning problems[D]. Cambridge: Massachusetts Institute of Technology, 2012. http://dl.acm.org/citation.cfm?id=2518457
|
| [46] |
SALZMAN O, HALPERIN D. Asymptotically near-optimal RRT for fast, high-quality, motion planning[C]//2014 IEEE International Conference on Robotics and Automation (ICRA). Stockholm: IEEE, 2014: 4680-4685. http://ieeexplore.ieee.org/document/7452671/
|
| [47] |
JANSON L, SCHMERLING E, CLARK A, et al. Fast marching tree: A fast marching sampling-based method for optimal motion planning in many dimensions[J]. The International Journal of Robotics Research, 2015, 34(7): 883. http://www.ncbi.nlm.nih.gov/pubmed/27003958
|
| [48] |
LI Y, LITTLEFIELD Z, BEKRIS K E. Asymptotically optimal sampling-based kinodynamic planning[J]. The International Journal of Robotics Research, 2016, 35(5): 528 DOI:10.1177/0278364915614386 |
| [49] |
GAMMELL J D, SRINIVASA S S, BARFOOT T D. Informed RRT*: optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic[C]//Intelligent Robots and Systems(IROS 2014), 2014 IEEE/RSJ International Conference on. Chicago: IEEE, 2014: 2997-3004. http://arxiv.org/abs/1404.2334
|
| [50] |
GAMMELL J D, SRINIVASA S S, BARFOOT T D. Batch informed trees (BIT*): sampling-based optimal planning via the heuristically guided search of implicit random geometric graphs[C]//Robotics and Automation (ICRA), 2015 IEEE International Conference on. Seattle: IEEE, 2015: 3067-3074. http://ieeexplore.ieee.org/xpl/abstractAuthors.jsp?reload=true&arnumber=7139620
|
| [51] |
QURESHI A H, MUMTAZ S, IQBAL K F, et al. Triangular geometry based optimal motion planning using RRT*-motion planner[C]//Advanced Motion Control (AMC), 2014 IEEE 13th International Workshop. Yokohama: IEEE, 2014: 380-385. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6823312
|
| [52] |
DEVAURS D, SIMÉON T, CORTÉS J. Optimal path planning in complex cost spaces with sampling-based algorithms[J]. IEEE Transactions on Automation Science and Engineering, 2016, 13(2): 415 DOI:10.1109/TASE.2015.2487881 |
| [53] |
PIVTORAIKO M, KELLY A. Differentially constrained mobile robot motion planning in state lattices[J]. Journal of Field Robotics, 2008, 26(3): 308 |
| [54] |
KUSHLEYEV A, LIKHACHEV M. Time-bounded lattice for efficient planning in dynamic environments[C]//Robotics and Automation, 2009. ICRA '09. IEEE International Conference. Kobe: IEEE, 2009:1662-1668. http://dl.acm.org/citation.cfm?id=1704139
|
| [55] |
DIJKSTRA E W. A note on two problems in connexion with graphs[J]. Numerische Mathematik, 1959, 1(1): 269 DOI:10.1007/BF01386390 |
| [56] |
HART P E, NILSSON N J, RAPHAEL B. A formal basis for the heuristic determination of minimum cost paths[J]. IEEE Transactions on Systems Science and Cybernetics, 1968, 4(2): 100 DOI:10.1109/TSSC.1968.300136 |
| [57] |
FURCY D A. Speeding up the convergence of online heuristic search and scaling up offline heuristic search[D]. [S.l.]: Georgia Institute of Technology, 2004. https://smartech.gatech.edu/handle/1853/4855?show=full
|
| [58] |
LIKHACHEV M, GORDON G J, THRUN S. ARA*: Anytime A* with provable bounds on sub-optimality[C]//Advances in Neural Information Processing Systems.[S.l.]: NIPS, 2004: 767-774. http://www.seas.upenn.edu/~maximl/files/ara_nips03_abs.html
|
| [59] |
AINE S, SWAMINATHAN S, NARAYANAN V, et al. Multi-heuristic A*[J]. The International Journal of Robotics Research, 2016, 35(1-3): 224 DOI:10.1177/0278364915594029 |
| [60] |
ISLAM F, NARAYANAN V, LIKHACHEV M. Dynamic multi-heuristic A*[C]//Robotics and Automation (ICRA), 2015 IEEE International Conference. Seattle: IEEE, 2015: 2376-2382. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7139515
|
| [61] |
ISLAM F, NARAYANAN V, LIKHACHEV M. A*-connect: bounded suboptimal bidirectional heuristic search[C]// IEEE International Conference on Robotics and Automation. Stockholm: IEEE, 2016: 2752-2758. http://ieeexplore.ieee.org/document/7487437/
|
| [62] |
KOENIG S, LIKHACHEV M, Furcy D. Lifelong planning A*[J]. Artificial Intelligence, 2004, 155(1): 93 |
| [63] |
STENTZ A. Optimal and efficient path planning for partially-known environments[C]//Robotics and Automation, Proceedings of 1994 IEEE International Conference. San Diego: IEEE, 1994:3310 -3317. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=351061
|
| [64] |
KOENIG S, MEMBER S, LIKHACHEV M. Fast replanning for navigation in unknown terrain[J]. IEEE Transactions on Robotics, 2005, 21(3): 354 DOI:10.1109/TRO.2004.838026 |
| [65] |
WAGNER G, CHOSET H. M*: a complete multirobot path planning algorithm with performance bounds.[J]. Intelligent Robots and Systems (IROS), 2011, 10(1):3260. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6095022
|
| [66] |
LIKHACHEV M, STENTZ A. R* search[C]//Natronal Conference on Artificial Intelligence.[S.l.]: AAAI Press, 2008:344-350. http://dl.acm.org/citation.cfm?id=1619995.1620051
|
| [67] |
FERGUSON D, STENTZ A. FIELD D*: an interpolation-based path planner and replanner[C]//Proceedings of the International Symposium on Robotics Research (ISRR). San Francisco: ISRR, 2005:1926-1931. http://link.springer.com/10.1007/978-3-540-48113-3_22
|
| [68] |
NASH A, DANIEL K, KOENIG S, et al. Theta*: any-angle path planning on grids[C]//AAAI. Vancouver: AAAI, 2007: 1177-1183. http://dl.acm.org/citation.cfm?id=1619835
|
| [69] |
MCNAUGHTON M. Parallel algorithms for real-time motion planning[M]. Pittsburgh: Carnegie Mellon University, 2011
|
| [70] |
MA L, XUE J, KAWABATA K, et al. Efficient sampling-based motion planning for on-road autonomous driving[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(4): 1961 DOI:10.1109/TITS.2015.2389215 |
| [71] |
SUCAN I A, MOLL M, KAVRAKI E E. The open motion planning library[J]. Robotics & Automation Magazine, IEEE, 2012, 19(4): 72 |
| [72] |
LIKHACHEY M, DORNBUSH A, MACALLISTER B, Search-based planning laboratory[DB/OL]. [2013-04-23]. http://www.sbpl.net/, 2013.
|
| [73] |
PAN J, CHITTA S, MANOCHA D. FCL: a general purpose library for collision and proximity queries[C]//Robotics and Automation (ICRA), 2012 IEEE International Conference. Saint Paul: IEEE, 2012:3859-3866. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6225337
|
| [74] |
ZIEGLER J, BENDER P, SCHREIBER M, et al. Making bertha drive—an autonomous journey on a historic route[J]. Intelligent Transportation Systems Magazine, IEEE, 2014, 6(2): 8 DOI:10.1109/MITS.2014.2306552 |
| [75] |
沈峘, 凌锐, 李舜酩. 考虑轮胎无滑移的智能车辆连续曲率轨迹规划方法[J]. 中国机械工程, 2012, 23(18): 2263 SHEN Huan, LING Rui, LI Shunming. Continuous curvature trajectory planning method for intelligent vehicle considering no slip constraints[J]. China Mechanical Engineering, 2012, 23(18): 2263 DOI:10.3969/j.issn.1004-132X.2012.18.025 |
| [76] |
LI X, SUN Z, CAO D, et al. Development of a new integrated local trajectory planning and tracking control framework for autonomous ground vehicles[J]. Mechanical Systems and Signal Processing, 2017, 87(B): 118 |
| [77] |
陈荣华, 王可心, 邵之江. 自主泊车的全联立动态优化方法[J]. 控制理论与应用, 2016, 33(5): 561 CHEN Ronghua, WANG Kexin, SHAO Zhijiang. Simultaneous dynamic optimization for autonomous parking[J]. Control Theory and Application, 2016, 33(5): 561 |
| [78] |
李红, 王文军, 李克强. 基于B样条理论的平行泊车路径规划[J]. 中国公路学报, 2016, 29(9): 143 LI Hong, WANG Wenjun, LI Keqiang. Path planning for parallel parking based on B spline theory[J]. China Journal of Highway and Transport, 2016, 29(9): 143 |
| [79] |
LEE S U, IAGNEMMA K. Robust motion planning methodology for autonomous tracked vehicles in rough environment using online slip estimation[C]//Intelligent Robots and Systems (IROS), 2016 IEEE/RSJ International Conference. Daejeon: IEEE, 2016: 3589-3594. https://www.deepdyve.com/lp/institute-of-electrical-and-electronics-engineers/robust-motion-planning-methodology-for-autonomous-tracked-vehicles-in-QrmhqHXkAm
|
| [80] |
PALMIERI L, ARRAS K O. Distance metric learning for RRT-based motion planning with constant-time inference[C]//Robotics and Automation (ICRA), 2015 IEEE International Conference. Seattle: IEEE, 2015: 637-643. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7139246
|
| [81] |
ARSLAN O. Machine learning and dynamic programming algorithms for motion planning and control[D]. Atlanta: Georgia Institute of Technology, 2015. https://smartech.gatech.edu/handle/1853/54317
|
| [82] |
CHAULWAR A, BOTSCH M, UTSCHICK W. A hybrid machine learning approach for planning safe trajectories in complex traffic-scenarios[C]//Machine Learning and Applications (ICMLA), 2016 15th IEEE International Conference. Anaheim: IEEE, 2016: 540-546.
|
| [83] |
ZUO L, GUO Q, XU X, et al. A hierarchical path planning approach based on A? and least-squares policy iteration for mobile robots[J]. Neurocomputing, 2015, 170(C): 257 |
 2017, Vol. 45
2017, Vol. 45

