2. 安徽工程大学 计算机与信息学院,安徽 芜湖 241000;
3. 同济大学 软件学院, 上海 201804;
4. 上海电力学院 计算机科学与技术学院, 上海 200090
2. College of Computer and Information Science, Anhui Polytechnic University, Wuhu, Anhui 241000, China;
3. School of Software Engineering, Tongji University, Shanghai 201804, China;
4. School of Computer Science and Technology, Shanghai University of Electric Power, Shanghai 200090, China
粗粒度可重构体系结构(coarse-grained reconfi-gurable architecture,CGRA)可以获得高的计算性能和低的功耗消费[1].针对不同互连结构运算阵列,已有多种映射方法被提出[2-8],但是存在以下缺陷:一是对数据流图(data flow graph,DFG)进行流水时域映射时,没有对可重构单元阵列(reconfigurable cell array,RCA)量化评估指标进行细化;二是没有给出或者说明RCA块流水执行流程.
针对已有研究的缺陷,本文进行了探索,其主要贡献如下所述:
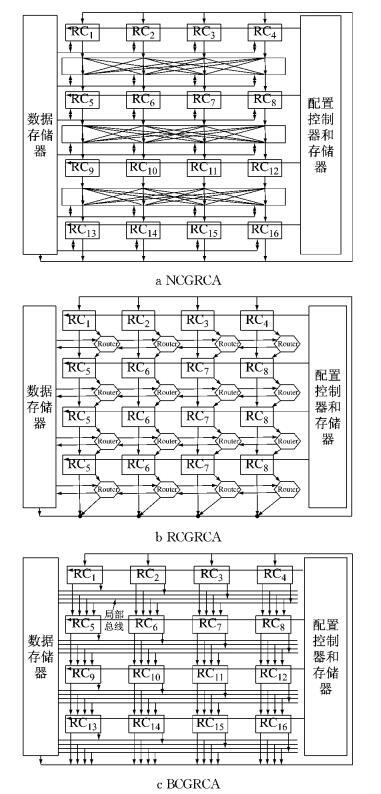
(1) 设计了三种行流水结构及映射算法,可重构多媒体系统(reconfigurable multimedia system,REMUS[7])具有近邻型粗粒度可重构单元阵列(neighbor coarse grained reconfigurable cell array,NCGRCA)的特征,在此基础上,设计了NCGRCA架构,同时设计了路由型粗粒度可重构单元阵列(router coarse grained reconfigurable cell array,RCGRCA)架构、总线型粗粒度可重构单元阵列(bus coarse grained reconfigurable cell array,BCGRCA)架构(图 1);同时设计了一种面向上述架构流水映射(pipeline mapping,PM)算法,该算法综合考虑了流水线架构下的混合多层迭代启动间距、块间流水通信成本等多个要素.
|
图 1 三种RCA流水线结构 Fig.1 Three RCA pipeline structures |
(2) 将两个循环体的启动间距(initiation interval,Ⅱ)推广到运算节点层面,考虑了循环DFG多个运算节点并行执行启动间距,同时给出了流水映射的形式化定义及流水执行成本的计算公式.
1 相关工作相关典型研究阐述如下:文献[2]提出了一种满射映射(epimorphism mapping,EPIMap)算法,该算法通过加旁节点过渡块间数据和重复计算来获得启动间距的较小化,但是没有给出启动间距的说明.文献[3]从操作级层面对不跨层RCA互连时延评估进行了研究.文献[4]基于统一CGRA行并行架构,设计实现了RCA块内跨行旁节点添加算法,并给出了其临界条件.文献[5]考虑行并行粗粒度RCA执行的多个硬件资源约束,提出了一种粗粒度可重构体系结构多目标优化映射算法.文献[6]设计了CGRA多线程编译框架,并对多线程CGRA的性能和功耗进行了分析.但是上述文献对行并行和配置流水RCA执行定量分析考虑不足,没有给出RCA块执行的流水分段,对流水块间通信成本考虑不足.
本文研究的两个条件:① 面向行流水RCA,提出将一条完整指令拆分6个流水段.乘法运算设为2时钟周期(cycle),其他算术逻辑运算时延设为1 cycle,另外5个流水段执行时间均为1 cycle.② 一块RCA块内和块间数据传输和执行按行流水进行,配置成本包括RCA全局互连控制、重复单元(reconfi-gurable cell, RC)逻辑算术运算和路由控制等.
2 映射流水架构和RCA流水执行分析 2.1 映射流水架构图 1给出了行并行NCGRCA、RCGRCA、BCGRCA流水架构.传统经典的CGRA架构主要有有Morphosys[8]、REMARC[9](reconfigurable multimedia array coprocessor)、LEAP[10](loop engine on array processors).相比现有架构,NCGRCA、BCGRCA、RCGRCA三种结构具有的特点是:① RCA块内和块间映射成功节点可按行流水执行和配置;② 上下行的可重构单元点点互连流水传递数据消除了RCA块内运算节点跨层数据传输的互连时延;③ 三种流水架构可以实现RCA块间流水.图 1中,Router表示路由器.
2.2 RCA流水执行分析定义1 RCA重复使用数M:一个循环DFG可以表示为G=(V,E,W,D)[11],基于CGRA,V表示运算节点的集合,E表示运算节点对之间边的集合,W表示运算节点占用的可重构单元(reconfigurable cell, RC)个数,D表示运算节点执行时延的集合.本文研究的对象为定点数,一个节点占用一个RC.若DFG规模大于一块RCA面积,该DFG按硬件约束被划分映射到RCA上, 并按时间域重复使用,这个重复使用数被记为M.
定义2 RCA非原始输入(出)N1和N2的细分:G=(V,E,W,D),设RCAk和其紧邻RCAk+1分别表示第k和k+1块RCA,R{k}-n表示RCAk的最后一行,R{k+1}-1表示RCAk+1的第一行,若运算节点va,vb∈V已经被映射RCAk的R{k}-n行,若va,vb的直接不跨层后继vc,vd被映射到紧邻的RCAk+1的R{k+1}-1,由于RCA为行流水结构,这样RCAk+1块的运算节点vc,vd的非原始输入可以通过块间流水数据线直接从RCAk块R{k}-n行获得,这样的非原始输入不需要存储到数据存储器,则称为非原始输入N11,否则需要存储到数据存储器的非原始输入称为N12.同理,va,vb的非原始输出可以通过块间流水数据线直接传递到RCAk+1块,这样的非原始输出不需要存储到数据存储器,则称为非原始输出N21,否则需要存储到数据存储器的非原始输出称为N22.N11和N12称为RCA非原始输入N1的细分;N21和N22称为RCA非原始输出N2的细分.N1和N12的关系是N12=N1-N11,N2和N22的关系是N22=N2-N21,N11和N21不需要存储,可作为行流水执行的一个段.
定义3 RCA配置时间CCON的细分:非流水或流水RCA架构,完成一个任务DFG的配置时间CCON大致包括两个部分:一个是完成RCA每次重复执行的全局运行控制字等配置成本,记为CCON1;一个是完成RC逻辑算术运算、路由等的动态配置时间记为CCON2.CCON1和CCON2称为流水RCA配置时间CCON的细分.
定义4 行指令级并行和行操作级并行:循环DFG中的任务节点按约束被映射到一块RCA上后,若运算节点按行进行指令级分段并发执行,称为运算节点的行指令级并行.若按运算操作节点的类型并发执行,称为运算节点的行操作级并行.
分析1 RCA流水执行分析:RCA按行操作并行执行,可以获得好的计算性能,基于流水RCA定量评估仍然是个难题,原因如下:① RCA块内已映射节点的数据通路和RCA整体运行控制方式等均有所不同,RCA每次运行均要消耗CCON1;② 行流水RCA结构,相邻行的节点可以点点流水快速执行,但是不相邻行的节点或位于不同RCA块的节点的存储成本也需要考虑.
由分析1可以得出:DFG经过时域划分与映射后,RCA流水执行步骤:
(1) 固定配置:即CCON1,其值为一个常数θ,不同的CGRA有所不同,REMUS的θ=17cycle;
(2) 预取数据:即不相邻块的数据提前预取非原始输入N12或原始输入Norg1的成本,其表示一块RCA流水执行前从数据存储器预取数据并存入待执行RC的自身寄存器堆文件,目的是防止流水执行RC的读数据冲突;
(3) 流水计算:即Spipeline,其表示一个RCA块内操作按行流水并行执行的成本;
(4) 数据存储:即非原始数据不相邻块输出N22或计算结果原始输出Norg2的成本.
基于流水执行步骤,给出如下定义:
定义5 RCA六段流水:流水线RCA一条完整的指令执行可划分为取指令(instruction fetch,IF)、指令译码(instruction decode,ID)、取数据(data fetch,DF)、硬件配置(hardware configuration,HC)、执行(execute,EX)、写回(write back,WB)6段流水.各段流水完成的功能为:IF的功能是从指令存储器取出一条指令;ID的功能是确定运算类型;DF的功能是从RC寄存器堆或从RCA块紧邻上一行RC输入数据(即N11);HC的功能是通过配置寄存器来实现RC计算、路由等功能;EX的功能是完成算术逻辑或复杂混合运算;WB把RC计算结果写入紧邻下一行RC寄存器堆作为直接数据来源(即N21)或写入数据存储器中.通过流水获得一个DFG执行计算延迟可表示为Spipeline.Spipeline包含了N11、N21等计算成本.表 1给出重复使用一块RCA的不跨RCA行操作级并行和指令级并行执行评估指标说明.
| 下载CSV 表 1 CGRA操作级和指令级执行评估指标 Tab.1 CGRA Operational level and instruction level execution evaluation indicators |
一块RCA流水执行流程如图 2所示,循环DFG在一块RCA上流水执行总时延TTOTAL=α·(固定配置成本)+β·(通信成本) +γ·(流水执行成本)=α· T固定配置+β·(T预取+ T存储)+ γ·T流水=α·CCON1+β·[(N12+Norg1)+(N22+Norg2)]+γ·Spipeline,其中,α、β、γ为流水线RCA成本修正系数,其值由具体可重构计算体系结构决定,本文设定评估系数的值为α=β=γ=1.

|
图 2 一块RCA流水执行流程 Fig.2 A RCA pipeline execution process |
定义6 RCA混合多层迭代启动间距(multi-level iteration initiation interval,MIII):传统的循环流水线启动间距是指相邻两个循环体的启动时间间隔,本文将其推广到计算任务节点启动时间间隔,有依赖的运算任务节点DFG被划分映射到RCA后,由于RCA的互连方式、面积等多个约束,会导致RCA块间或块内有的运算节点进行有依赖流水运行,有的运算节点进行无依赖流水运行,RCA按段流水执行,每个节点的启动间距为一个固定值,将其称为RCA混合多层迭代启动间距MIII.MIII按映射到RCA块内后,运算节点有无依赖可分为图 3a~3c三种情形.无依赖流水MIII=0;6段RCA流水相邻行点之间存在依赖或混合依赖,下一行节点取数据段必须在上一行相关节点写回段后执行,故MIII=3,RCA按行流水执行三种情况如图 3d~3f所示.由图 3可以得出流水段数为m(本文m=6),每段流水线时间Δt(本文Δt=1cycle),可以得出运算节点执行时间相等时,运算节点无依赖Spipeline=(m-1)Δt,运算节点有或混合依赖时Spipeline=2mΔt-2Δt.将其推广,得到定理1:

|
图 3 三种依赖RCA时空图 Fig.3 Three dependence RCA space-time diagrams |
定理1 一块行可流水执行RCAk×b,有m段,n个计算任务,Δt为每段流水线的执行时间,Spipeline为一块RCAk×b流水线所消费的时间,level_max为一块RCA已经成功映射的最长依赖子图长度,EX1,EX2,…,EXm为最长依赖子图m个节点的执行时延,EXmax-nodei为一块RCA无依赖节点的最大执行时延,且执行时间不等或相等.则按块流水执行Spipeline为:
(1) 无依赖执行:
| $ {S_{{\rm{pipeline}}}} = m\cdot\Delta t + \theta {\rm{ ,}}\theta = {\rm{E}}{{\rm{X}}_{{\rm{max - node}}}}_i\Delta t $ |
(2) 有依赖或混合依赖:
| $ \begin{array}{l} {S_{{\rm{pipeline}}}} = {\rm{level\_max}} \cdot m\cdot\Delta t-2\cdot\left( {{\rm{level\_max}}-1} \right)\cdot\\ {\rm{ }}\Delta t = \sum\limits_{{\rm{level}}\_i = 1}^k {\{ {\rm{max}}\{ {\rm{E}}{{\rm{X}}_1}, {\rm{E}}{{\rm{X}}_2}, \ldots, {\rm{E}}{{\rm{X}}_m}\}- \Delta t\} } \end{array} $ |
证明:(1) 无依赖:设有n个节点被同时映射到一块RCA,节点间无块内数据输入输出依赖.流水线段数为m,且时间为Δt,则累加和为m·Δt,节点执行时间EXi(i∈[1,n])属于流水线中的一段,且EXi≥Δt.(a)若一块RCA中n个无依赖节点EXi均相等,且EXi=EXmax-nodei=Δt,则θ=0;EXi=EXmax-nodei≠Δt,则θ=EXi-Δt;(b)若一块RCA中n个无依赖节点EXi不相等,由于某个节点的EXi决定了m段流水线执行段的延迟,所以θ=EXmax-nodei-Δt.
(2) 有依赖或者混合依赖:设RCA具有k行,并且行与行之间的数据存在依赖,设有若干个子图被成功映射到一块RCA,则最长子图的执行时延决定了该块RCA的Spipeline,由于每行节点执行DF段依赖于上一行的WB段,故当前行的ID和上一行的EX和WB可以并发执行.则按硬件约束,RCA第1行成功映射的节点数为e个,第1行RCA的基本执行时间T1=m·Δt+max{EX1,…,EXe};第2行流水执行时间依赖于第1行的数据写回,第2行成功映射的节点数为f个,则第2行可并发节点的取指和译码段可与上一行的执行和写回段重叠,第2行节点数据获取段须在第1行的运算数据写回段后进行,故实际流水段少了2Δt,又因为第2行节点的执行时间段不等,需单独计算,第2行的执行时间为T2=m·Δt-2·Δt+max{EXe+1,…,EXe+f };依次递推,若第i行映射的节点集合为{vk,…,vn },则Ti=m·Δt-2·Δt+max{EXk,…,EXn }.
综上所述:
| $ \begin{array}{l} {S_{{\rm{pipeline}}}} = {T_1} + {T_2} + \ldots {T_k} = m\cdot\Delta t + {\rm{max\{ E}}{{\rm{X}}_{\rm{1}}}{\rm{, E}}{{\rm{X}}_{\rm{2}}}{\rm{, }}\\ {\rm{ \ldots, E}}{{\rm{X}}_e}\} + {\rm{ }}m\cdot\Delta t2\cdot\Delta t + {\rm{max\{ E}}{{\rm{X}}_{e + 1}}, \\ {\rm{E}}{{\rm{X}}_{e + 2}}, \ldots, {\rm{E}}{{\rm{X}}_{e + f}}\} + \ldots + {\rm{ }}m\cdot\Delta t-2\cdot\Delta t + \\ {\rm{max}}\left\{ {{\rm{E}}{{\rm{X}}_k} \ldots, {\rm{E}}{{\rm{X}}_n}} \right\} = {\rm{level\_max}}\cdot m\cdot\Delta t\\ 2\cdot\left( {{\rm{level\_max}}{\rm{1}}} \right)\Delta t + {\rm{max\{ E}}{{\rm{X}}_{e + 1}}, \\ {\rm{E}}{{\rm{X}}_{e + 2}}, \ldots, {\rm{E}}{{\rm{X}}_{e + f}}\} + \ldots = {\rm{level\_max}}\cdot m\cdot\\ {\rm{E}}{{\rm{X}}_{e + 2}}, \ldots, {\rm{E}}{{\rm{X}}_{e + f}}\} + \ldots = {\rm{level\_max}}\cdot m\cdot\\ \Delta t-2\cdot\left( {{\rm{level\_max}}{\rm{1}}} \right)\cdot\Delta t + \\ \sum\limits_{{\rm{level}}\_i = 1}^k {\{ {\rm{max}}\left\{ {{\rm{E}}{{\rm{X}}_1}, {\rm{E}}{{\rm{X}}_2}, \ldots, {\rm{E}}{{\rm{X}}_m}} \right\}\Delta t\} } \end{array} $ |
证毕.
3 实验动机和流水映射算法设计 3.1 实验动机本文实验动机包括以下两点:① 针对已有算法块间通信成本等指标仍较大的缺陷,设计一个考虑RCA块间按行流水线并行执行的流水映射(pipeline mapping, PM)算法.② 考虑流水线背景下的Spipeline、N12、N22、CCON1等指标的统计.
3.2 PM算法设计多目标优化映射(multi-objective optimization map,MOM)算法在行可并行操作级CGRA获得了较好计算性能[5],但是通过深入的研究,在RCA流水线执行的背景下,发现MOM仍然存在N12、N22等均较大的缺陷.为了克服这些不足,本文设计了流水映射PM算法,该算法考虑RCA块内和块间流水成本N12、N22等的优化,采用的方法说明如下:
方法1 最小化RCA块内和块间流水数据输入和输出成本.
由2.2节可知,数据输入和输出成本是TTOTAL的重要组成部分,所以对此优化具有一定意义.方法1具体包括两个方面:一方面是RCA块内流水数据输入和输出次数,由于本文是针对行并行流水RCA,且是点点行流水执行,对于跨层循环DFG通过加过多旁节点来带来配置成本的大量增加[4],通过对并行CGRA编译器的实际测试,每条DFG路径加旁节点(bypass node, BN)的个数约为小于等于2时,在不增加配置成本的前提下,可以减少RCA块内流水数据输入和输出次数;另一方面是充分考虑相邻块行流水的断流,策略是将当前RCA最后一行的节点直接后继映射到紧邻RCA的第一行,这样可减少RCA块间行流水执行的数据输入和输出次数.综上所述,方法1目的是优化N12、N22.
方法2 尽可能减少行流水RCA混合多层迭代启动间距MIII.
采用按行左右运算节点无依赖映射、紧邻行上下有依赖点点映射方法.循环有依赖DFG被映射到6段流水RCA后,当前行节点的IF和ID可以与上一行节点的EX和WB段重叠执行,一方面保证了当前行节点的取数据DF(即在上一行节点的写回WB后执行)得以顺利执行;另一方面减少了MIII.同时进行节点贪婪映射,对一块RCA上的RC进行最大化利用,从而减少了RCA块使用次数的配置成本.方法2目的是优化Spipeline、CCON1和M.
由上述方法构造调度函数D(vi)=depth(vi)+delay(vi),函数值越大优先级越高,其中,depth(vi)表示DFG中点vi的层号,其目的使层号大的节点具有高的优先级,体现N12、N22的优化;delay(vi)表示DFG中点vi的执行时延,其目的尽可能把执行时延相同的点放在同一行,体现Spipeline的优化;并且采用节点贪婪映射,尽可能塞满每块RCA,体现CCON1和M优化.根据上述方法设计的PM算法流程见图 4.设Max-level和n分别表示一个DFG最大层次号和节点总数,由PM算法流程图可知,按DFG层次和节点号扫描DFG消耗的时间复杂度为O(Max-level·n),每次扫描DFG计算就绪节点vi的调度函数D(vi)的值消耗的时间复杂度为O(n),综上所述,PM算法平均复杂度为O(Max-level·n2).

|
图 4 PM算法流程图 Fig.4 PM algorithm flow chart |
例1 为了说明PM算法的映射效果,给出如下例子,一段循环代码及DFG(其包括24个原始输入和4个原始输出)如图 5a~5b所示,相关的映射结果如图 5c~5d所示.图 5中,i1~i4为4个输入变量,BN1~BN8表示添加8个旁节点,v1~v32为32个顶点.表 2给出了PM和MOM算法比较,结果显示PM具有较好的优化结果.

|
图 5 MOM和PM映射结果比较 Fig.5 Comparison of MOM and PM mapping result |
| 下载CSV 表 2 MOM和PM映射比较 Tab.2 Comparison of MOM and PM mapping |
为了便于比较,本文采用了IDCT、BTREE32、FDCT2、DCT8、FFT16等基准程序(表 3),随机选定RCA面积(可表示为ARPU)为16RC(RCA4×4)、64RC(RCA8×8),对于不同的ARPU值,采用一组基准程序集对PM、MOM、EPIMap等三种时域映射算法进行了测试.
| 下载CSV 表 3 基准程序集 Tab.3 Benchmark program sets |
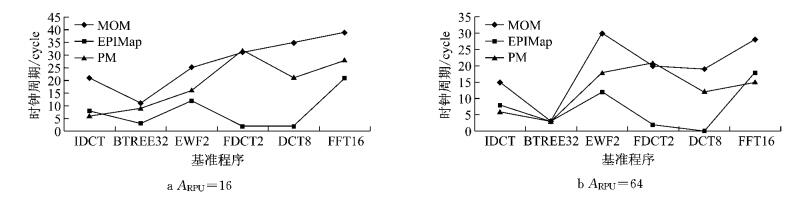
由图 6可以看出,当ARPU=16和ARPU=64时,相比较MOM,随着ARPU的增大,除了FDCT2,PM算法均获得了较少的M值;相比较EPIMap,PM算法获得了M全部优化.

|
图 6 MOM、PM、EPIMap映射M比较 Fig.6 Comparison of M for MOM, PM, EPIMap mapping |
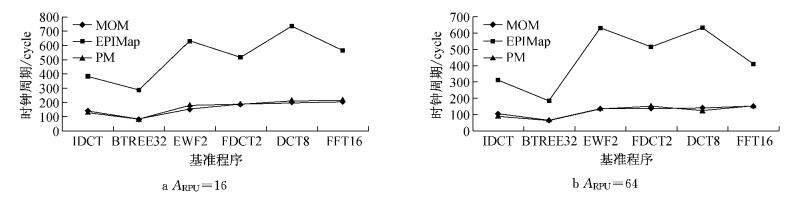
由图 7和图 8可以看出,当ARPU=16和ARPU= 64时,由于MOM对块间通信成本考虑不够,所以PM算法在指标N12方面获得了全面的优化;在指标N22方面, 除了基准FDCT2相当外,PM算法也是获得了较好的优化.因为EPIMap以增大M作为代价来减少N11和N22,所以EPIMap获得的N12和N22值要优于PM算法.

|
图 7 MOM、PM、EPIMap映射N12比较 Fig.7 Comparison for N12 of MOM, PM, EPIMap mapping |
|
图 8 MOM、PM、EPIMap映射N22比较 Fig.8 Comparison of N22 for MOM, PM, EPIMap mapping |
由图 9可以看出,当ARPU=16和ARPU=64时,由于EPIMap的M大,导致Spipeline较大,相比较EPIMap,PM算法在指标Spipeline方面获得了全面优化.MOM在优化Spipeline方面取得了较好的效果,PM在Spipeline优化方面不及MOM.

|
图 9 MOM、PM、EPIMap映射Spipeline比较 Fig.9 Comparison of Spipeline for MOM, PM, EPIMap mapping |
由图 10可以看出,当ARPU=16和ARPU=64时,由于EPIMap的M大,导致RCA固定配置成本的增大,所以相比较EPIMap,PM算法在指标CCON方面获得了全面优化.随着ARPU的增大,除了FDCT2,PM获得了较少的M值,所以相比MOM,PM在指标CCON也获得了一定的优化.
|
图 10 MOM、PM、EPIMap映射CCON比较 Fig.10 Comparison of CCON for MOM, PM, EPIMap mapping |
由表 4可以看出,当ARPU=16和ARPU=64时,相比MOM算法,由于MOM的通信成本N12和N22考虑不够,导致TTOTAL较大,PM分别获得了TTOTAL平均4.0%和4.3%的总体优化.相比EPIMap算法,由于EPIMap算法的M、Spipeline、CCON等均较大,虽然通信成本N12和N22较小,但是不足以平衡TTOTAL,导致PM的总体性能优于EPIMap,PM获得了TTOTAL改进百分比分别为52.1%(ARPU=16) 和56.2%(ARPU=64).
| 下载CSV 表 4 ARPU=16和ARPU=64 MOM、PM、EPIMap映射TTOTAL比较 Tab.4 Comparison of TTOTALfor MOM, PM, EPIMap mapping Based on ARPU=16 and ARPU=64 |
从4.1节的实验结果可知,相比于MOM和EPIMap算法,随着硬件面积的增大,PM算法在M、CCON、TTOTAL等较具优势.但是PM算法的Spipeline不如MOM算法,N12和N22不如EPIMap算法.PM算法适用场合:行流水RCA且要求较少TTOTAL.
5 结语本文基于REMUS设计了NCGRCA架构,同时设计了RCGRCA、BCGRCA行流水并行执行架构,并分析了三种行流水结构阵列执行步骤,给出了流水线RCA性能评估新的细化指标Spipeline、N12、N22等,提出了一种流水映射PM算法,基于一组映射基准程序集,与MOM、EPIMap两种算法进行了比较,结果表明,PM算法在减少M、TTOTAL等方面具有可行性.
| [1] |
Kim C, Chung M, Cho Y, et al. ULP-SRP: Ultra low-power Samsung reconfigurable processor for biomedical applications[J]. ACM Transactions on Reconfigurable Technology and Systems, 2014, 7(3): 1 |
| [2] |
Hamzeh M, Shrivastava A, Vrudhula S. EPIMap:using epimorphism to map applications on CGRAs[C]// Proceedings of International Conference on 49th Design Automation Conference. Austin; IEEE Computer Society Press, 2012:1284-1291.
|
| [3] |
陈乃金, 冯志勇. 不跨层行操作并行RCA互连时延性能评估[J]. 天津大学学报(自然科学与工程技术版), 2017, 50(4): 429 CHEN Naijin, FENG Zhiyong. Interconnect delay perfor-mance evaluation for non-crossing level and row operands parallel RCA[J]. Journal of Tianjin University(Science and Technology), 2017, 50(4): 429 |
| [4] |
陈乃金, 冯志勇, 江建慧. 用于二维RCA跨层数据传输的旁节点无冗余添加算法[J]. 通信学报, 2015, 36(4): 1 CHEN Naijin, FENG Zhiyong, JIANG Jianhui. Bypass node non-redundant adding algorithm for crossing-level data transmission in two-dimension reconfigurable cell array[J]. Journal on Communications, 2015, 36(4): 1 DOI:10.11959/j.issn.1000-436x.2015094 |
| [5] |
陈乃金, 江建慧. 一种粗粒度可重构体系结构多目标优化映射算法[J]. 电子学报, 2015, 43(11): 2151 CHEN Naijin, JIANG Jianhui. A Multi-objective Optimization Mapping Algorithm for Coarse Grained Reconfigurable Architectures[J]. Acta Electronica Sinica, 2015, 43(11): 2151 DOI:10.3969/j.issn.0372-2112.2015.11.003 |
| [6] |
PAGER J, Jhrieyapaul R, Shrivastava A. A software scheme for multithreading on CGRAs[J]. ACM Transactions on Embedded Computing Systems, 2015, 14(1): 1 |
| [7] |
魏少军, 刘雷波, 尹首一. 可重构计算处理器技术[J]. 中国科学:信息科学, 2012, 42(12): 1559 WEI Shaojun, LIU Leibo, YIN Shouyi. Key techniques of reconfigurable computing processor[J]. Science China Information Sciences, 2012, 42(12): 1559 |
| [8] |
SINGH H, LEE M H, LU G M, et al. MorphoSys: An integrated reconfigureable system for data parallel and computation intensive applications[J]. IEEE Transactions on Computers, 2000, 49(5): 465 DOI:10.1109/12.859540 |
| [9] |
Miyamori T, Olukotun K, Budiu M, et al. REMARC: reconfigurable multimedia array coprocessor[J]. IEICE Transactions on Information and Systems, 1999, E82-D(2): 389 |
| [10] |
窦勇, 邬贵明, 徐进辉, 等. 支持循环自动流水线的粗粒度可重构阵列体系结构[J]. 中国科学:信息科学, 2008, 38(4): 579 DOU Yong, WU Guiming, XU Jinhui, et al. A coarse-grained reconfigurable computing architecture with loop self-pipelining[J]. Science China Information Sciences, 2008, 38(4): 579 |
| [11] |
陈乃金, 江建慧, 陈昕, 等. 一种考虑执行延迟最小化和资源约束的改进层划分算法[J]. 电子学报, 2012, 40(5): 1055 CHEN Naijin, JIANG Jianhui, Chen Xin, et al. An Improved Level Partitioning Algorithm Considering Minimum Execution Delay and Resource Restraints[J]. Acta Electronica Sinica, 2012, 40(5): 1055 |
 2017, Vol. 45
2017, Vol. 45
