2. 上海师范大学 信息与机电工程学院,上海 200234
2. College of Information, Mechanical and Electronic Engineering, Shanghai Normal University, Shanghai 200234, China
双足机器人技术是推动未来科技发展的重要技术之一,其在近些年来受到广泛专注.2016年初,美国Boston Dynamics公司发布的最新版双足机器人Atlas实现了在不平整路面环境中的稳定行走,展示了优秀的行走能力[1];双足机器人Hubo在2015年6月美国举办的DARPA机器人挑战赛中获得冠军,成功完成了包含斜面和楼梯等环境中的复杂行走任务[2];日本Honda公司2011年发布了最新版的双足机器人ASIMO[3],该机器人采用零力矩点(ZMP)控制技术实现了稳定的跑步、行走及上下楼梯运动;西班牙PAL Robotics公司研制的REEM C是一款以研究为目的双足机器人平台,具有比ASIMO更优的硬件配置及更长的续航时间[4];然而,这类机器人的行走需要对全身关节进行实时控制,行走步态仍不够灵活,且行走过程中的单位能量消耗大.
针对主动控制双足机器人存在的问题,研究双足行走的一个新的思路是从考虑机器人本体的行走自然动力学特性出发,在此基础上研究稳定的行走步态.McGeer[5]首次提出了仅依靠重力和自身结构特性就能沿斜面向下稳定行走的“被动动态行走”,该类行走方式具有内在的稳定性,并且行走能耗非常低.Goswami[6]和Garcia[7]分别提出了经典的圆规行走模型和最简行走模型,阐述了被动动态行走的步态特征及其内在的固有稳定性.在此基础上,一些机构分析了行走的运动机制和能耗问题并研究设计了多款双足机器人.Srinivasan等[8]采用能量优化轨迹控制方法在低速行走步态和高速跑步步态之间发现一种中速摆动跑步态;Collins等[9]通过在被动动态行走机器人上增加少量关节驱动,实现了其平地上的行走;Ruina等设计的行走机器人Ranger采用了一种低带宽的基于事件反射的控制方法,该机器人在无人触碰的情况下独自完成了60 km的行走,行走能量效率与人类相当[10];Grizzle等采用虚拟约束和混合零动力学的方法设计一种时间不变反馈控制器,并将其应用在双足机器人MABEL上,该机器人实现了快速跑步运动[11].国内重庆邮电大学研制的双足机器人“行者一号”完成了134 km的行走且仅消耗0.8度电[12],该机器人在机构设计上避免了摆动脚擦地现象,节省了行走的能量消耗.这类双足机器人在设计中利用生物的行走动力学运动机制,仅需要很少的控制就完成了步态自然、稳定的双足行走,行走的单位能量消耗也非常低.
被动动态行走模型性能和机理是设计该类行走机器人的基础研究问题.近些年来,学者们进行了不断探索.Ransing等[13]研究了“脚跟到脚趾”的滚动接触对被动双足模型的动力学影响作用;Safa等[14]提出一种“地面吸引子”的方法使被动动态行走模型在更陡的坡面上实现了稳定行走;Gritli等[15]通过混合庞加莱界面的OGY(Ott-Grebogi-Yorke)控制方法计算被动动态行走模型的Lyapunov指数谱;国内北京大学设计具有分段足的双足行走模型在不平整斜面上完成了稳定行走[16],清华大学提出双足机器人虚拟斜坡行走步态生成算法[17],吉林大学对无动力双足机器人的控制策略和算法进行研究[18].
本文对一种简单被动动态行走模型及其稳定性进行了详细研究.在两杆三质点类圆规双足被动行走模型上增加支撑脚横向和纵向两个自由度,以该模型为研究对象,求解被动动态行走步态,并分析其局部和全局稳定性.该模型能够调整机器人的质量分布和长度比例,在逼近真实行走模型的同时尽量简单,所揭示的机器人动态行走机理更具有代表性和普遍性;支撑脚自由度的增加,一方面能够通过瞬间等效冲量来描述摆动脚触地过程和支撑脚的蹬地过程,简化了对这些过程的描述,另一方面能够计算支撑脚与地面间的摩擦力和支持力,从而能够分析行走过程中支撑脚是否打滑和离地.
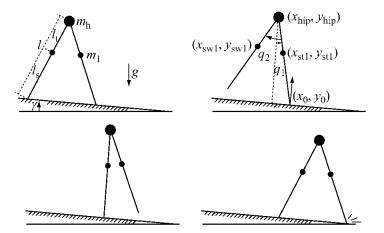
1 双足机器人模型 1.1 模型分析本文采用两杆三质点类圆规双足机器人模型,其结构如图 1所示.该模型由两条完全相同的刚性杆铰接组成,足部简化为点状足,三个质点分别在髋关节和两条腿上,其中髋关节的质点mh表示机器人的上身质量,两条腿被认为质量集中在质点ml上,且腿长为l,lt、ls分别表示mh到ml及ml到腿的末端的距离.行走斜面的夹角为γ,重力加速度为g.q1为支撑腿与斜面法线的夹角,q2为摆动腿与支撑腿间的夹角,且逆时针为正. (xstl, ystl)表示支撑腿上质点的坐标,(xhip, yhip)表示髋关节处质点的坐标,(xswl, yswl)表示摆动腿上质点的坐标. (x0, y0)表示支撑足的笛卡尔直角坐标系坐标,其中模型行走方向和向上方向为正,并设定支撑足的初始坐标为(0, 0),因此行走模型共包含4个自由度q=(q1, q2, x0, y0)T.
|
图 1 类圆规双足机器人模型的被动动态行走步态流程 Fig.1 A typical step of the compass-like passive dynamic walking model |
本文提出的类圆规模型不仅包含描述行走过程中模型各个部件状态的广义坐标q1、q2,还提出包括描述支撑足状态的广义坐标x0、y0.对支撑足状态的描述,具有如下的几个优点:在行走过程中单腿支撑的连续摆动阶段,支撑足是唯一与地面接触的部位,通过对支撑足的状态进行约束,即可求得地面与支撑足之间的约束力,包括沿斜面方向的摩擦力及沿斜面法线方向的地面支撑力,从而能够检验支撑足是否满足约束的摩擦系数及是否离开地面;在行走过程中,模型在摆动腿触地时将发生足地碰撞,在支撑足设计瞬间等效冲量代替角动量守恒求解足地碰撞过程,简化行走模型设计的复杂度.由于在支撑足增加了自由度,为了使支撑足相对斜面的位置在行走过程中始终保持不变,需要对支撑足进行位置约束.
机器人的被动动态周期行走步态从摆动足触地后转换为新的支撑足的瞬间开始,此时两足同时在坡面上,随后摆动腿离开地面向前自由摆动,直到摆动足与地面发生碰撞,一个周期的的行走过程完成并进入下一个行走周期,模型此时的初始状态与上一步的初始状态完全相同.模型在行走过程中仅靠重力提供能量输入,而在足地碰撞过程中进行能量输出,从而保证行走过程中的能量平衡状态.在研究被动动态行走问题时,通常做出如下假设:碰撞和双足转换过程瞬间完成,碰撞足无弹起;坡面的摩擦系数足够大从而保证支撑足无相对地面的滑动;由于两杆模型的结构特征,当支撑腿与摆动腿接近重合时,允许摆动足低于斜面的情况发生,该问题在实际的机器人原型设计中能够通过设计膝关节、三维模型、踝关节翻转或摆动腿收缩等方法解决[19].
1.2 摆动阶段的动力学分析摆动阶段的动力学方程通过如下形式的拉格朗日方程进行推导:
| $\left\{ \begin{array}{l} \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial L}}{{\partial \dot q}}} \right) - \frac{{\partial L}}{{\partial q}} = 0\\ L = T - V \end{array} \right.$ | (1) |
式中:L为拉格朗日量;T为系统动能,V为系统势能.
定义X=(xstl, ystl, xhip, yhip, xswl, yswl)T为行走模型中各质点在笛卡尔直角坐标系中的坐标,则X与q之间的关系如下:
| $\mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{x_{{\rm{st}}1}}}\\ {{y_{{\rm{st1}}}}}\\ {{x_{{\rm{hip}}}}}\\ {{y_{{\rm{hip}}}}}\\ {{x_{{\rm{sw1}}}}}\\ {{y_{{\rm{sw1}}}}} \end{array}} \right]{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{x_0} - {l_{\rm{s}}}\sin \left( {{q_1}} \right)}\\ {{y_0} + {l_{\rm{s}}}\cos \left( {{q_1}} \right)}\\ {{x_0} - \left( {{l_{\rm{s}}} + {l_{\rm{t}}}} \right)\sin \left( {{q_1}} \right)}\\ {{y_0} + \left( {{l_{\rm{s}}} + {l_{\rm{t}}}} \right)\cos \left( {{q_1}} \right)}\\ {{x_0} - \left( {{l_{\rm{s}}} + {l_{\rm{t}}}} \right)\sin \left( {{q_1}} \right) + {l_{\rm{t}}}\sin \left( {{q_1} + {q_2}} \right)}\\ {{y_0} + \left( {{l_{\rm{s}}} + {l_{\rm{t}}}} \right)\cos \left( {{q_1}} \right) + {l_{\rm{t}}}\cos \left( {{q_1} + {q_2}} \right)} \end{array}} \right]$ | (2) |
因此得到如下形式的行走模型摆动阶段的动力学方程:
| $\mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{\ddot q}} + \mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{\dot q}} + \mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\gamma }}} \right) = \mathit{\boldsymbol{J}}_r^{\rm{T}}\mathit{\boldsymbol{u}}$ | (3) |
式中:q=(q1, q2, x0, y0)T; M(q)为
在一个行走周期中,双足机器人的支撑足位置应当保持不变.由于本模型设计支撑足具有沿斜面和斜面法线的两个自由度,为了使支撑足始终保持静止状态,需要对支撑足进行两个方向的约束,即支撑足与地面的摩擦力防止支撑足沿斜面的滑动,地面对支撑足的支持力保证行走过程中支撑足始终在斜面之上.因此,行走模型需要满足如下条件:
| ${\mathit{\boldsymbol{J}}_{\rm{r}}}\left[ {\mathit{\boldsymbol{q}}\;\;\;\mathit{\boldsymbol{\dot q}}\;\;\;\mathit{\boldsymbol{\ddot q}}} \right] = 0$ | (4) |
| ${\mathit{\boldsymbol{J}}_\mathit{r}} = \left[ {\begin{array}{*{20}{c}} 0&0&1&0\\ 0&0&0&1 \end{array}} \right]$ | (5) |
由式(3)~(5) 得到式(6):
| ${\mathit{\boldsymbol{J}}_\mathit{r}}\mathit{\boldsymbol{\ddot q}} = - {\mathit{\boldsymbol{J}}_\mathit{r}}\mathit{\boldsymbol{M}}{\left( \mathit{\boldsymbol{q}} \right)^{ - 1}}\left( {\mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{\dot q}} + \mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\gamma }}} \right) - \mathit{\boldsymbol{J}}_r^{\rm{T}}\mathit{\boldsymbol{u}}} \right)$ | (6) |
从而得到地面对支撑足的约束力u=[uF uN]T:
| $\mathit{\boldsymbol{u}} = {\left( {{\mathit{\boldsymbol{J}}_\mathit{r}}\mathit{\boldsymbol{M}}{{\left( \mathit{\boldsymbol{q}} \right)}^{ - 1}}\mathit{\boldsymbol{J}}_r^{\rm{T}}} \right)^{ - 1}}{\mathit{\boldsymbol{J}}_\mathit{r}}\mathit{\boldsymbol{M}}{\left( \mathit{\boldsymbol{q}} \right)^{ - 1}}\left( {\mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{\dot q}} + \mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\gamma }}} \right)} \right)$ | (7) |
通过将式(4)、(5) 和(7) 代入式(3) 求解机器人模型的状态,就能够保证支撑足的位置在行走周期过程中始终不变.
1.4 足地碰撞过程在行走周期结束时,摆动足与地面发生碰撞,根据第1.1节提到的足地碰撞瞬间完成且支撑足无弹起的假设,机器人模型各关节的空间位置在碰撞前后不变,仅双腿的角速度发生不连续变化,碰撞前后摆动腿与支撑腿互换.足地碰撞发生时,模型各关节位置满足:
| ${y_0}/l + \cos \left( {{q_1}} \right) - \cos \left( {{q_1} + {q_2}} \right) = 0$ |
机器人模型碰撞前两腿的状态将转换为碰撞后下一步的初始状态,满足如下关系:
| $\left[ {\begin{array}{*{20}{c}} {q_1^ + }\\ {q_2^ + }\\ {x_0^ + }\\ {y_0^ + } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {q_1^ - + q_2^ - }\\ { - q_2^ - }\\ {x_0^ - + l\left( {\sin \left( {q_1^ - + q_2^ - } \right) - \sin \left( {q_1^ - } \right)} \right)}\\ 0 \end{array}} \right]$ | (8) |
式中:上标“-”表示碰撞前瞬间模型状态;上标“+”表示碰撞后瞬间模型状态.
足地碰撞后双腿的角速度将产生跳变,本文采用等效冲量法对碰后双腿角速度进行求解.
足地碰撞瞬间前,摆动足具有一定的线速度,而在碰撞后瞬间,摆动足切换为支撑足,由于碰撞过程瞬间完成且摆动足无弹起,新的支撑足在碰撞后将静止在地面上,即新的支撑足速度为0.因此采用如下等效冲量方法对足地碰撞过程进行求解:在足地碰撞瞬间前,摆动腿与支撑腿先互换角色,因此原摆动足被视为新的支撑足,且新的支撑足具有与原摆动足相同的线速度;原支撑足成为新的摆动足并即将脱离地面.新支撑足与地面的碰撞相当于地面对支撑足进行冲击,使得支撑足所具有的线速度在瞬间变为0,从而完成足地碰撞,开始下一步的行走.在足地碰撞前后机器人动力学模型并未发生改变.计算得到碰撞前瞬间支撑腿与摆动腿互换角色后模型的速度与互换前模型速度的关系如下,模型在两条腿互换后的状态用“*”表示:
| $\left[ {\begin{array}{*{20}{c}} {\dot q_1^*}\\ {\dot q_2^*}\\ {\dot x_0^*}\\ {\dot y_0^*} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\dot q_1^ - + \dot q_2^ - }\\ { - \dot q_2^ - }\\ {\dot x_0^ - + l\left( {\dot q_1^ - + \dot q_2^ - } \right)\cos \left( {q_1^ - + q_2^ - } \right) - l\dot q_1^ - \cos q_1^ - }\\ {\dot y_0^ - + l\left( {\dot q_1^ - + \dot q_2^ - } \right)\sin \left( {q_1^ - + q_2^ - } \right) - l\dot q_1^ - \sin q_1^ - } \end{array}} \right]$ | (9) |
机器人模型足地碰撞过程中地面对新支撑足的冲量等于在碰撞前后机器人模型动量的增量,从而得到如下关系:
| $\mathit{\boldsymbol{M}}\left( {{\mathit{\boldsymbol{q}}^ + }} \right){{\mathit{\boldsymbol{\dot q}}}^ + } - \mathit{\boldsymbol{M}}\left( {{\mathit{\boldsymbol{q}}^*}} \right){{\mathit{\boldsymbol{\dot q}}}^*} = \mathit{\boldsymbol{J}}_i^{\rm{T}}\mathit{\boldsymbol{P}}$ | (10) |
式中:
足地碰撞后,支撑足处于静止状态,即支撑足在x和y方向的速度均为0,得到如下表达式:
| ${\mathit{\boldsymbol{J}}_i}{{\mathit{\boldsymbol{\dot q}}}^ + } = 0$ | (11) |
由于碰撞前摆动腿已与支撑腿互换,因此得到q+= q*.由式(10)、(11) 推出:
| ${\mathit{\boldsymbol{J}}_i}{{\mathit{\boldsymbol{\dot q}}}^*} + {\mathit{\boldsymbol{J}}_i}\mathit{\boldsymbol{M}}{\left( {{\mathit{\boldsymbol{q}}^*}} \right)^{ - 1}}\mathit{\boldsymbol{J}}_i^{\rm{T}}\mathit{\boldsymbol{P}} = 0$ | (12) |
从而得到地面对支撑足的瞬间冲量为
| $\mathit{\boldsymbol{P}} = - {\left( {{\mathit{\boldsymbol{J}}_i}\mathit{\boldsymbol{M}}{{\left( {{\mathit{\boldsymbol{q}}^*}} \right)}^{ - 1}}\mathit{\boldsymbol{J}}_i^{\rm{T}}} \right)^{ - 1}}{\mathit{\boldsymbol{J}}_i}{{\mathit{\boldsymbol{\dot q}}}^*}$ | (13) |
因此,将式(13) 代入式(10) 能够得到碰撞后模型的速度状态,其中I为4×4的单位矩阵:
| ${{\mathit{\boldsymbol{\dot q}}}^ + } = \left( {I - \mathit{\boldsymbol{M}}{{\left( {{\mathit{\boldsymbol{q}}^*}} \right)}^{ - 1}}\mathit{\boldsymbol{J}}_i^{\rm{T}}{{\left( {{\mathit{\boldsymbol{J}}_i}\mathit{\boldsymbol{M}}{{\left( {{\mathit{\boldsymbol{q}}^*}} \right)}^{ - 1}}\mathit{\boldsymbol{J}}_i^{\rm{T}}} \right)}^{ - 1}}{\mathit{\boldsymbol{J}}_i}} \right){{\mathit{\boldsymbol{\dot q}}}^*}$ | (14) |
本文提出的行走模型包含描述支撑足状态的自由度,因此在支撑足与地面发生交互时,动力学模型中包含了机器人系统状态的变化信息.足地碰撞过程可以被认为是地面对新的支撑足产生冲量,使其速度瞬间变为0.通过该约束条件与机器人动力学系统进行联合求解,即可表述足地碰撞的整个过程.
等效冲量方法依靠动力学模型中包含的机器人系统的状态信息完成对足地碰撞过程的描述,从而避免了传统角动量守恒方法对足地碰撞过程表达式的重新推导,简化了该离散相的求解过程.
2 周期的被动动态行走步态被动动态行走机器人能够利用自身的动力学特性仅依靠重力完成斜面上的行走.由于双足行走具有明显的周期特征,取足地碰撞后瞬间为庞加莱截面,则可以构造一个庞加莱映射,将足地碰撞后瞬间机器人的状态映射到下一步足地碰撞后瞬间:
| ${\mathit{\boldsymbol{q}}_{n + 1}} = f\left( {{\mathit{\boldsymbol{q}}_n}} \right)$ | (15) |
具有满足式(16) 的庞加莱映射不动点的行走步态称为周期行走步态.双足被动动态行走的一步为一个行走周期,包含摆动过程和足地碰撞过程.
| ${\mathit{\boldsymbol{q}}_{n + 1}} = {\mathit{\boldsymbol{q}}_n}$ | (16) |
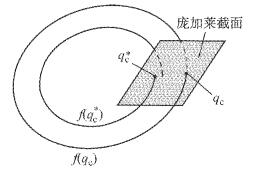
通过式(15)、(16) 可以得到周期行走步态的初始状态qc映射到自身的关系,行走步态从与庞加莱截面相交的初始状态qc出发,经过一个周期后,与庞加莱截面仍交于qc(图 2):
| ${\mathit{\boldsymbol{q}}_{\rm{c}}}{\rm{ = }}f\left( {{\mathit{\boldsymbol{q}}_{\rm{c}}}} \right)$ | (17) |
|
图 2 机器人行走步态的庞加莱截面示意图 Fig.2 Poincare section of the walking gait |
而对于不同于qc的初始状态qc*,在行走过程中将沿着与qc不同的轨迹变化,在一个行走周期后,与庞加莱截面相交于不同于初始状态qc*的点.
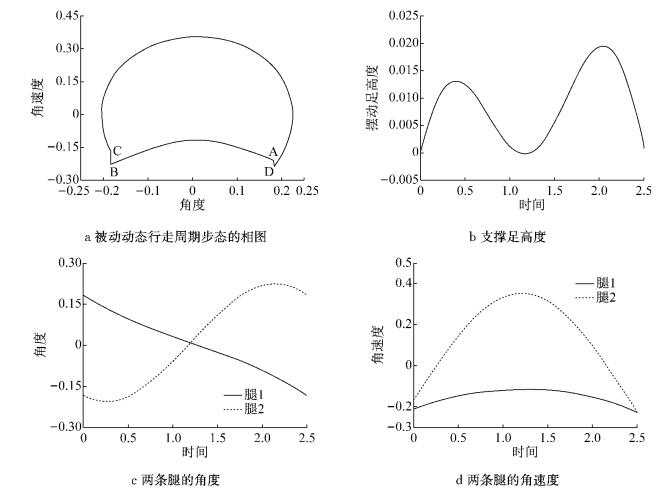
图 3a所示典型双足被动动态行走周期步态的相图,该算例采用的参数如表 1所示,其中模型的总质量为1.该双足行走相图描述了机器人一条腿的运动过程,整个闭环曲线对应于机器人连续两步的行走.足地碰撞后瞬间,支撑腿相对于地面的角度和角速度状态如图中A时刻所示,支撑腿开始向前以支撑腿为支点类似于倒立摆的摆动,当摆动到垂直于地面位置时,支撑腿的角速度最小,在图中支撑腿的状态为顺时针发展方向;随后当支撑腿摆动到B时刻时,摆动足触地发生瞬间的足地碰撞过程,支撑腿与摆动腿切换相互角色;碰撞后原支撑腿成为新的摆动腿,其相对于地面的角度和角速度如C时刻所示,摆动腿离开地面,并开始以髋关节为圆点类似于单摆的运动,可以看到摆动腿的角度先增大再开始减小;在摆动腿触地切换为支撑腿前(D时刻),摆动腿先向前摆动,然后再向回摆动,直到与地面碰撞;碰撞后摆动腿又切换为支撑腿(A时刻),完成周期的行走过程.
|
图 3 机器人被动动态行走周期步态过程 Fig.3 Process of the periodic passive dynamic walking gait |
| 下载CSV 表 1 双足被动动态行走模型参数值 Tab.1 Parameters of the passive dynamic walking model |
在周期行走过程中,摆动足距地面的高度如图 3b所示,可以看到摆动足距地面的高度先增大再减小,当时间t为1.1时,该高度几乎为0,发生了支撑足的擦地情况,这主要是由于机器人模型是由两条长度相同的直腿构成的,在支撑腿与摆动腿重合的瞬间,支撑腿与斜面并不完全垂直,造成摆动腿在与支撑腿重合的前后发生擦地现象.该问题可以通过设计膝关节、三维模型或可翻转的踝关节等方法得以解决.
本文计算所得到的结果都是量纲一化后的结果,采用量纲一化的结果使得计算结果与所选择的模型参数大小无关,更具有普遍性,便于使用和参考.如图 3c、3d所示周期步态中两条腿的状态,其中的时间、速度分别通过时间除以
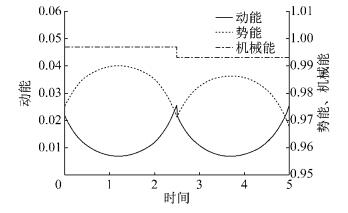
被动动态行走机器人的模型没有设计任何驱动装置,机器人仅依靠重力完成斜面上的下坡行走,整个机器人系统的能量输入为重力,能量输出为足地碰撞过程所消耗的动能,在每个行走周期过程中机械能守恒,系统能量在动能和势能之间相互转移.如图 4为机器人两步行走过程中机械能、势能和动能的变化情况(图中所有量的单位量纲一化,下同),可以看到在每步中机械能保持不变,势能先增大再减小,动能的变化趋势则与势能相反.在一个周期行走结束发生足地碰撞瞬间,机器人各关节的速度由于碰撞而减小,导致系统的动能瞬间减小;由于机器人各关节的空间位置在碰撞过程中不变,系统的势能不变,因此,足地碰撞瞬间动能的损失导致了机器人机械能的减少.当足地碰撞发生后,此时系统的机械能和势能相比上一步周期步态的初始时刻都减少了0.003 7,这主要是由于机器人沿斜面行走,重心位置的降低造成机器人势能的减少,而动能在足地碰撞后与上一步周期步态的初始时刻状态相同.从能量的角度来看,每步行走中重力势能所转化成的动能与足地碰撞时系统减少的动能达到了平衡状态,使得每步行走的初始状态完全相同,从而实现了周期的行走过程.在每步行走中减少的重力势能ΔV可以通过如下式(18) 计算得到:
| $\Delta V = mg{l_{{\rm{step}}}}\sin \gamma $ | (18) |
|
图 4 机器人周期步态行走过程中的能量变化情况 Fig.4 Energy variation during the periodic walking motion |
式中:m为机器人的总质量;lstep为机器人行走步态的步长.
3 被动动态行走步态的稳定性被动动态行走模型是一个复杂的非线性系统,行走过程包括连续的摆动过程和离散的碰撞切换过程.通过求解庞加莱截面的不动点,得到周期的被动动态行走步态.该周期步态满足新一步的初始状态与上一步完全相同,然而对于行走过程中其他时刻机器人模型的状态并没有严格要求.因此,被动动态行走又称为“极限环行走”的运动方式.极限环行走是指一个周期性的行走脚步序列,该序列从整体来看它是稳定的,但是局部并不是在任何时刻都稳定[20].周期性的脚步序列是指行走运动是一系列状态空间内精确闭环轨迹的循环,该循环由机器人两条腿的交替行走来完成.这条轨迹不需要在任何局部都稳定,即不需要轨迹上所有点都能吸引状态空间中相邻的点.然而该闭环轨迹又是稳定的,状态空间中相邻的轨迹被闭环轨迹吸引,在多步的行走之后,最终被吸引到该闭环轨迹.从极限环行走的描述来看,研究被动动态行走的稳定性需要从两个方面来考虑:局部稳定性和全局稳定性[21].局部稳定性是研究庞加莱截面的不动点对状态空间相邻的点的吸引情况;而全局稳定性则是研究周期行走的闭环轨迹对状态空间中相邻轨迹的吸引状况.
3.1 局部稳定性没有任何扰动的被动动态行走步态能够呈现出精确的周期特性,构成闭环轨迹.上一步庞加莱截面的不动点qc能够精确映射到下一步的不动点,如式(19).不动点对状态空间相邻的点的吸引情况能够说明行走过程的局部稳定能力[22].假设机器人从不动点周围相邻的点开始行走,即行走步态的初始状态与不动点之间有较小的误差,通过几步的行走,如果该误差能够消除,行走步态轨迹在庞加莱截面上变为不动点,则行走步态是稳定的,反之,则行走步态不稳定.对机器人行走的初始状态施加微小的扰动Δqn,则推导得到如下关系:
| $\begin{array}{l} {\mathit{\boldsymbol{q}}_{\rm{c}}} + \Delta {\mathit{\boldsymbol{q}}_{n + 1}} = {\mathit{\boldsymbol{q}}_{n + 1}} = f\left( {{\mathit{\boldsymbol{q}}_n}} \right) = f\left( {{\mathit{\boldsymbol{q}}_{\mathit{c + }}}\Delta {\mathit{\boldsymbol{q}}_n}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; \approx f\left( {{\mathit{\boldsymbol{q}}_{\rm{c}}}} \right) + \mathit{\boldsymbol{J}}\Delta {\mathit{\boldsymbol{q}}_n}{\rm{ = }}\mathit{\boldsymbol{qJ}}\Delta {\mathit{\boldsymbol{q}}_n} \end{array}$ | (19) |
其中:
机器人从初始状态qc+Δ qn开始行走,在一步的行走完成后映射到下一步庞加莱截面不动点的相邻点qc+ JΔ qn,机器人不动点的误差从Δ qn变为JΔ qn,即:
| $\Delta {\mathit{\boldsymbol{q}}_{n + 1}}{\rm{ = }}\mathit{\boldsymbol{J}}\Delta {\mathit{\boldsymbol{q}}_n}$ | (20) |
因此,行走的稳定性可以由雅克比矩阵J决定,行走中的误差通过乘数J向下一步传递,如果雅克比矩阵的最大特征值(λmax)小于1或者所有特征值均在复平面单位圆内,行走中的误差在后续步中将越来越小,周期行走是稳定的,反之,行走中的误差会被放大,周期行走不稳定.雅克比矩阵的特征值也被称为Floquet乘数.
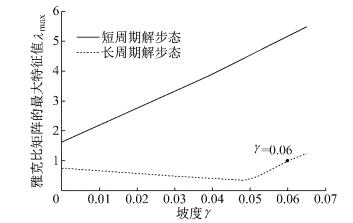
图 5所示不同坡面上的行走步态的雅克比矩阵最大特征值λmax,可以看出长周期步态在坡面角度γ < 0.06时,雅克比矩阵的最大特征值小于1,周期步态稳定,模型能够持续行走下去;当坡面角度γ > 0.06时,长周期步态不稳定;短周期步态的雅克比矩阵始终大于1,并且随着坡面角度的增大而增大,因此短周期步态不稳定,模型以周期解作为初始状态开始行走,经过几步的行走之后,微小的扰动将被放大,模型最终翻倒.
|
图 5 雅克比矩阵最大特征值与坡面角度的关系 Fig.5 Maximal absolute eigenvalue of the Jacobian as a function of the slope angle |
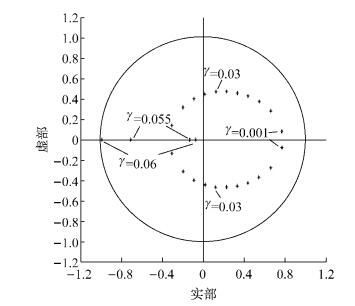
图 6所示长周期步态在坡面角度小于0.06时雅克比矩阵的特征值在复平面的空间分布图,可以看到所有的特征值都在单位圆内,因此,行走步态稳定.不同坡面角度γ对应于4个特征值,其中两个在坐标原点.当坡面角度γ=0.001时,另外两个特征值在实轴的正半轴上;随着坡面角度的增大,两个特征值离开实轴,并沿着圆形的轨迹向单位圆的左半侧移动,且两个特征值关于实轴对称;当γ=0.055时,两个特征值在实轴的负半轴上;随着坡面角度的继续增大,两个特征值向实轴的两侧运行,当γ > 0.06时,其中一个特征值将移动到单位圆外,行走步态将不稳定.
|
图 6 雅克比矩阵的特征值在复平面的空间分布图(坡面角度γ < 0.06) Fig.6 Eigenvalues of the Jacobian in the complex plane (slope angle γ < 0.06) |
以γ=0.009为例,长周期步态的周期解及雅克比矩阵的特征值分别为
| $\mathit{\boldsymbol{q}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{q_1}}\\ {{{\dot q}_1}}\\ {{q_2}}\\ {{{\dot q}_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0.183\;3}\\ { - 0.210\;8}\\ { - 0.366\;5}\\ {0.043\;35} \end{array}} \right]$ | (21) |
| $\mathit{\boldsymbol{\lambda }} = \left[ {\begin{array}{*{20}{c}} {0.56 + 0.35{\rm{i}}}\\ {0.56 - 0.35{\rm{i}}}\\ 0\\ 0 \end{array}} \right]$ | (22) |
短周期步态的周期解及雅克比矩阵的特征值为
| $\mathit{q}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{q_1}}\\ {{{\dot q}_1}}\\ {{q_2}}\\ {{{\dot q}_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0.175\;4}\\ { - 0.215\;6}\\ { - 0.350\;9}\\ {0.040\;10} \end{array}} \right]$ | (23) |
| $\mathit{\lambda } = \left[ {\begin{array}{*{20}{c}} {2.15}\\ {0.69}\\ 0\\ 0 \end{array}} \right]$ | (24) |
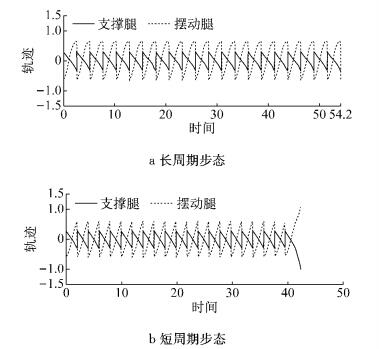
因此计算得到长周期步态雅克比矩阵的最大特征值为0.67,而短周期步态的为2.15.长周期步态和短周期步态在γ=0.009的坡面上的行走过程中模型的角度轨迹如图 7所示,可以看到长周期步态能够始终保持稳定的行走;而短周期步态模型行走不稳定,最终翻倒.
|
图 7 长周期步态和短周期步态的行走过程中模型的角度轨迹(γ=0.009) Fig.7 Motion trajectories of the long period solution and short period solution (γ=0.009) |
利用3.1节局部稳定性分析方法能够判断不动点的渐进稳定性,然而研究行走过程中如果遇到干扰,机器人在状态空间的运动轨迹是否能够收敛到闭环轨迹上的问题,需要考虑机器人行走步态的全局稳定性.被动动态行走在状态空间中形成闭环轨迹,在闭环轨迹的邻域中,所有在有限步行走后能够最终收敛到闭环轨迹上的初始状态点的集合被称为吸引域[23].吸引域的面积表明行走步态在干扰下的稳定能力,吸引域面积越大,表明步态的抗干扰能力越强,因此,通过分析行走步态的吸引域就能得到机器人步态在状态空间的闭环轨迹对相邻轨迹的吸引情况.
吸引域的性质在双足行走机器人的理论和设计中都具有重要的意义:由于被动动态行走的吸引域面积非常小,从如何增大吸引域面积的角度研究双足行走问题,对提高双足机器人的行走能力提供了很好的思路;在实际的动态行走机器人设计中,双足行走机器人初始状态范围与吸引域面积有关,吸引域面积越大,机器人能够完成稳定行走的初始状态范围越大.
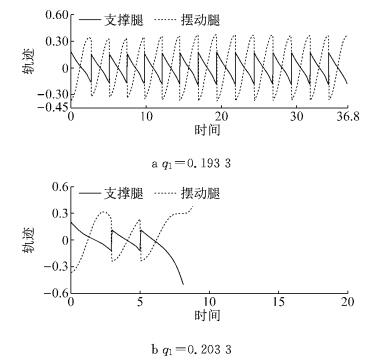
由式(21)、(22) 得到行走模型中摆动腿变量对行走的影响作用非常小,因此仅采用支撑腿变量描述行走步态的吸引域.通过对式(21)、(22) 中周期解q1=0.183 3,
| 下载CSV 表 2 吸引域中初始状态在后续步中的发展情况 Tab.2 Path from the initial conditions in the basin of attraction |
|
图 8 不同初始状态的行走过程中模型的角度轨迹 Fig.8 Motion trajectories of the walking with different initial conditions |
本文在两杆三质点类圆规双足被动行走模型上增加支撑脚横向和纵向两个自由度,以该模型为研究对象,求解被动动态行走步态,并分析其局部和全局稳定性.当斜面角度小于0.06时,模型的长周期步态稳定.随着斜面角度的增大,稳定步态的雅克比矩阵特征值沿着圆形轨迹向单位圆的左半侧移动,当斜面角度大于0.06时,其中一个特征值将移动到单位圆外,行走步态将不稳定.对于吸引域内的初始状态,经过有限步,行走步态最终收敛到长周期解;而对于吸引域外部的点,行走步态最终翻到.本文为理解双足行走的运动机理提供指导,同时也为设计稳定、高效的双足机器人提供分析思路.
| [1] |
KUINDERSMA S, DEITS R, FALLON M, et al. Optimization-based locomotion planning, estimation, and control design for the Atlas humanoid robot[J]. Autonomous Robots, 2016, 40(3): 429 DOI:10.1007/s10514-015-9479-3 |
| [2] |
DRC-HUBO. Home of DRC-HUBO[EB/OL].[2017-07-31]. http://www.drc-hubo.com/, 2015.
|
| [3] |
Honda. The Honda worldwide ASIMO site[EB/OL]. [2016-01-26]. http://world.honda.com/ASIMO/, 2011.
|
| [4] |
PAL robotics. REEM-C humanoid robotics research platform[EB/OL]. [2017-07-31]. http://reemc.pal-robotics.com/en-us/, 2013.
|
| [5] |
MCGEER T. Passive dynamic walking[J]. The International Journal of Robotics Research, 1990, 9(9): 68 |
| [6] |
GOSWAMI A, THUILOT B, ESPIAU B. A study of the passive gait of a compass-like biped robot: symmetry and chaos[J]. The International Journal of Robotics Research, 1998, 17(12): 1282 DOI:10.1177/027836499801701202 |
| [7] |
GARCIA M, CHATTERJEE A, RUINA A. Simplest walking model: stability, complexity, and scaling[J]. Journal of Biomechanical Engineering, Transactions of the ASME, 1998, 120(2): 281 DOI:10.1115/1.2798313 |
| [8] |
SRINIVASAN M, RUINA A. Computer optimization of a minimal biped model discovers walking and running[J]. Nature, 2006, 439(7072): 72 DOI:10.1038/nature04113 |
| [9] |
COLLINS S, RUINA A, TEDRAKE R, et al. Efficient bipedal robots based on passive dynamic walkers[J]. Science Magazine, 2005, 157(2): 1082 |
| [10] |
BHOUNSULE PA, CORTELL J, GREWAL A, et al. Low-bandwidth reflex-based control for lower power walking: 65 km on a single battery charge[J]. The International Journal of Robotics Research, 2014, 33(10): 1305 DOI:10.1177/0278364914527485 |
| [11] |
Sreenath K, Park H W, Poulakakis L, et al. Embedding active force control within the compliant Hybrid zero dynamics to achieve stable, fast running on MABEL[J]. The International Journal of Robotics Research, 2013, 32(3): 324 DOI:10.1177/0278364912473344 |
| [12] |
李清都. 中国机器人打破持续行走里程吉尼斯世界纪录[EB/OL]. [2015-11-01]. http://news.xinhuanet.com/world/2015-11/01/c_1117003511.htm, 2015. LI Q D. Chinese robot breals the continuing walking mileage Guinness world record [EB/OL].[2015-11-01]. http://news.xinhuanet.com/world/2015-11/01/c_1117003511.htm, 2015. |
| [13] |
MAHMOODI P, RANSING R S, FRISWELL M I. Modelling the effect of 'heel to toe' roll-over contact on the walking dynamics of passive biped robots[J]. Applied Mathematical Modelling, 2013, 37(12-13): 7352 DOI:10.1016/j.apm.2013.02.048 |
| [14] |
SAFA A T, NARAGHI M. The role of walking surface in enhancing the stability of the simplest passive dynamic biped[J]. Robotica, 2014, 33(1): 195 |
| [15] |
Gritli H, Belghith S. Computation of the lyapunov exponents in the compass-gait model under OGY control via a hybrid Poincaré map[J]. Chaos Solitons & Fractals, 2015, 81(S6-7): 172 |
| [16] |
HUANG Y, WANG Q, GAO Y, et al. Modeling and analysis of passive dynamic bipedal walking with segmented feet and compliant joints[J]. Acta Mechanica Sinica, 2012, 28(5): 1457 DOI:10.1007/s10409-012-0079-6 |
| [17] |
李立国, 赵明国, 张乃尧. 平面双足机器人虚拟斜坡行走步态生成算法研究[J]. 机器人, 2009, 31(1): 77 LI L G, ZHAO M G, ZHANG N Y. Research on virtual slope walking gait generation algorithm for plannar biped robot[J]. Robot, 2009, 31(1): 77 |
| [18] |
刘振泽, 田彦涛, 张佩杰, 等. 无动力双足步行机器人控制策略与算法[J]. 控制理论与应用, 2009, 26(2): 113 LIU Z Z, TIAN Y T, ZHANG P J, et al. Control strategies and algorithms for passive compass-like biped robot[J]. Control Theory and Applications, 2009, 26(2): 113 |
| [19] |
MCGEER T. Passive walking with knees[C]//Proc. of the IEEE International Conference on Robotics and Automation. Cincinnati: IEEE, 1990: 1640-1645.
|
| [20] |
HOBBELEN Daan G E, WISSE M. Limit cycle walking, chapter 14 of humanoid robots human-like machines[M]. [S.l.]: Advanced Robotic Systems International and I-Tech Education and Publishing, 2007.
|
| [21] |
SCHWAB A L, WISSE M. Basin of attraction of the simplest walking model[C]//Proc. of DETC'01. Pittsburgh; ASME, 2001: 531-539.
|
| [22] |
WISSE M, SCHWAB A L, VAN der Helm F C T. Passive dynamic walking model with upper body[J]. Robotica, 2004, 22(6): 681 DOI:10.1017/S0263574704000475 |
| [23] |
HSU C S. Cell-to-cell mapping: a method of global analysis for nonlinear system[M]. New York: Springer-Verlag, 1987
|
 2017, Vol. 45
2017, Vol. 45

