在Web2.0的大环境下,社交网络服务已成为当前最具发展前景的互联网应用服务之一.它的出现使得人们的网络生活与现实生活联系得越来越密切,俨然已成为人们在互联网上传播信息、进行社会交流活动的重要平台.随着越来越多的用户通过社交网络进行信息交流与传播,安全性问题日益凸现出来,用户的隐私暴露风险不断增加.因此,社交网络中的隐私安全问题成为一个亟待解决的问题.
从现有的研究来看,k-anonymity及其扩展模型的基本思想是将数据集中与攻击者背景知识相关的属性定义为准标识符,通过对记录的准标识符值进行泛化、压缩处理,使得所有记录被划分到若干个等价类,每个等价类中的记录具有相同的准标识符值,从而实现将一个记录隐藏在一组记录中.但这些模型存在主要缺陷,如不能提供足够的安全保障,其安全性与攻击者所掌握的背景知识相关,尽管因新型攻击的出现l-diversity,t-closeness等模型相继被提出并在隐私保护领域广泛应用,但这些模型无法提供一种有效且严格的方法来证明其隐私保护水平,因此当模型参数改变时,无法对隐私保护水平进行定量分析,削弱了隐私保护处理结果的可靠性.而差分隐私保护模型定义了严格的攻击模型,同时能够抵御基于背景知识的攻击,对隐私泄露风险给出了严谨、定量化的表示和证明,极大地保证了数据的可用性,被广泛应用到各个领域[1-2].Dwork等[3]提出对一般查询函数提供差分隐私保护的方法通过计算出真实的查询结果,然后加入一些噪声后再把结果返回给用户.Hay等[4]提出一种后处理技术,在不牺牲差分隐私保护力度的情况下提高查询结果的精确度.算法的核心思想是对加噪后的查询结果予以一致性约束,找出“最接近”且满足查询序列约束条件的结果.
目前将差分隐私保护方法应用到社交网络图结构有两种常用的标准:节点差分隐私和边差分隐私.节点差分隐私是指从原图中删除或添加任意一个节点和连接该节点的所有边,此时攻击者不能确定是否个体节点出现在图中,能够完全保护了所有个体.而边差分隐私是指从原图中删除或添加一条边,能以较高的概率确定个体节点间是否有关系,其保护力度比节点差分隐私较弱.
在图挖掘方面,Nissim等[5]提出了局部敏感度的概念,用局部敏感度的平滑上界和局部敏感度一起确定噪声量的大小,即将局部敏感度代入β-平滑上界的函数中则可得到平滑敏感度,进而用于计算噪声大小.Karwa等[6]将此方法扩展应用到k-星计数查询,并提出算法用来查询k-三角形个数.Wang等[7]提出一种“拆分与结合”的方法来实现差分隐私保护的查询.在图发布方面,Chen等[8]针对数据集相关程度为k时,提出基于密度的方法(density exploration and reconstruction, DER)将原图的邻接矩阵进行分区从而重构出加入差分隐私保护后的待发布图.
在上述研究工作基础上,本文重点围绕社交网络发布图和原图的结构一致性,并以提高发布图的精确度为目标,从社交网络图结构的特点出发,设计一个满足差分隐私保护的发布图模型(classification based graph-publishing model, CGM),通过使用图结构中的节点和边来进行建模社会关系.节点表示社交网络中的用户个体,边用来记录个体间的关系或活动.
为此,本文主要工作如下:
(1) 针对社交网络发布图生成中的隐私保护问题,在分析社交网络的特性基础上,将社交网络原图根据节点标签分类为多个子图,保证子图内边的分布比较集中,子图间边的连接较弱.
(2) 针对分类后的每个子图,利用四叉树进行区域划分,并在树的叶子节点添加满足差分隐私保护的噪声,然后根据四叉树叶子节点构建待发布子图,再重组成待发布图.
(3) 利用度发布、最短路径、聚类系数等统计分析方法,通过实验结果验证分析待发布图与原图的结构一致性和有用性。
1 社交网络图发布问题描述 1.1 差分隐私保护模型差分隐私是Dwork在2006年针对数据库的隐私泄露问题提出的一种新的隐私定义[3],它能够解决传统隐私保护模型的缺陷.首先,假设攻击者能够获得除目标记录外所有其他记录的信息,这些信息的总和可以理解为攻击者所能掌握的最大背景知识.在这一最大背景知识假设下,差分隐私保护能够抵御关于背景知识的攻击.其次,它建立在坚实的数学基础之上,对隐私保护进行了严格的定义并提供了量化的、可证明的评估方法,使得不同参数处理下的数据集所提供的隐私保护水平具有可比较性[9].
差分隐私保护模型的思想来源于一个朴素的观察:当数据集D中包含个体Alice时,设对D进行任意查询操作f(例如计数、求和、平均值等)所得到的结果为f(D),如果将Alice的信息从D中删除后进行查询得到的结果仍然为f(D),则可以认为,Alice的信息并没有因为被包含在数据集D中而产生额外的风险.
差分隐私保护是基于数据失真的隐私保护技术,采用添加噪声机制使敏感数据失真但同时保证数据的有用性.它可以实现在数据集中添加或删除一条数据不会影响到查询输出结果,因此可以保证这一条记录被识别或敏感属性被泄露[8].
ε-差分隐私保护是基于“邻近数据集”概念进行定义的.设两个数据集D和D′,具有相同的属性结构,两者的对称差记作DΔD′,|DΔ D′|表示DΔD′中记录的数量.若|DΔ D′|=1,则称D和D′为邻近数据集.
定义1[10](ε-差分隐私保护).设有随机算法M.对于任意两个邻近数据集D和D′,以及算法M所有可能的输出构成集合的任何子集SM,若算法M满足Pr[M(D)∈SM]≤exp(ε)·Pr[M(D′)∈SM],则算法M提供ε-差分隐私保护,其中参数ε称为隐私保护预算,exp为自然对数函数,Pr为概率.算法M通过对输出结果的随机化来提供隐私保护,同时通过参数ε来保证在数据集中删除任一记录时,算法输出同一结果的概率不发生显著变化.
(1) 隐私保护预算
隐私保护预算ε体现了算法所能够提供的隐私保护水平.ε值越小,表示隐私保护水平越高.在实际应用中,ε通常取很小的值,例如0.01、0.1等.
(2) 敏感度
差分隐私保护是通过在查询函数的返回值中加入适量的噪声来实现的.加入噪声过多会影响结果的可用性,过少则无法提供所需的安全保证.差分隐私用敏感度来决定加入噪声量的大小.它指删除数据集中任意一条记录对查询结果造成的最大改变.在差分隐私保护模型中定义了两种常用的敏感度,全局敏感度和局部敏感度[11].通常,局部敏感度要比全局敏感度小.但是,由于它在一定程度上体现了数据集的数据分布特征,如果直接用来计算噪声大小则会泄露数据集中的敏感信息.
1.2 社交网络隐私保护问题描述在社交网络中,组成社交网络的各个元素均可能涉及到隐私信息,包括节点、边、图性质等.本文主要针对的是待发布图与原图的结构一致性及可用性,通过分别求解原图和待发布图的度分布、最短路径和聚类系数三种图特征来度量.
度分布指图的度频率分布,当给定原图和发布图的频率分布,本文利用Kullback-Leiber距离(KL-距离)测量两者之间的差距;最短路径两节点间所有的路径中长度值最小的路径.若两节点之间是不可达的,则其路径长度为∞.给定原图和发布图的最短路径,本文将利用相对误差来评估待发布图的精确度;给定原图和发布图的聚类系数,利用相对误差来测量待发布图的失真率.
2 面向社交网络图发布隐私保护算法针对社交网络发布图隐私保护问题,社交网络中的数据大多数都是相关的,网络结构可以通过节点之间的邻接矩阵表示,矩阵中元素为0表示两节点之间没有关联,元素为1表示两节点之间有关联.对于一个相关度为k的数据集D(即D中任意一条记录至多与其余k-1条记录相关联),将至多k条记录分为一组,通过以“组”为单位添加来消除数据相关的影响,能够实现ε/k-隐私保护.
本文提出的CGM算法主要包含三个步骤,见表 1.在算法中隐私预算总值为ε/k,分成三个部分εC,εE,εR,分别为每个步骤中的隐私预算.算法的3个步骤分别为:
| 下载CSV 表 1 CGM算法 Tab.1 CGM Algorithm |
(1) 图分类(ClassfiedGraph):旨在使得分类后的子图具有更高的关联度,即邻接矩阵中的1值集中分布在某个区域,对于社交网络而言,拥有某种特性的两个节点相关联的可能性更高,因此可根据该特性将原图进行分类,分类后的每个子图Ci将以较高概率满足密集分布.本文利用桥的概念,通过计算原图中的桥从而将原图分解成多个不连通的子图,以保证每个子图内具有较高的关联度.
(2) 划分密集区域(ExporeDenseRegion):通过利用标准四叉树,以满足差分隐私保护的方式,将子图的邻接矩阵Ai进行分区.该过程会产生加噪后的四叉树,树的节点代表邻接矩阵的区域大小以及该区域内加噪后1值的个数.
(3) 重构邻接矩阵(ArrangeEdge):在该过程中,根据上个步骤构建完成四叉树Qi,编排叶子节点中区域内1值的分布,从而重构出发布图的邻接矩阵Ai.
2.1 图分类对于一个图来说,图中顶点的标号不同会导致1值分布不同的邻接矩阵,要计算1值密集分布的邻接矩阵,需要根据社交网络的特征,如拥有共同爱好的用户节点之间存在边的可能性更大,采用分类的思想,求解原图的所有不连通子图,使得子图内邻接矩阵较为密集.连接两个子图之间的边叫做桥,即给定图G,V是顶点集合,E是边的集合,若存在E的子集E′,使得B(G-E′) > B(G),且对于任意的E′的子集E″,均有B(G-E″)=B(G),其中B(G)表示图G的连通分支数,则称E′是G的边割(简称割集).若E′={e},则称e为割边或桥.加噪后桥的个数将被记录,以便在最后阶段进行重组时加以应用.本文采用Kosaraju算法求解图的强连通分量,它能够在O(|V|+|E|)时间复杂度范围内找到强连通分量.该算法首先对图G进行深度优先搜索(depth-first search, DFS),计算出各顶点完成搜索的时间T;然后计算图的逆图,对其也进行DFS搜索,搜索时顶点的访问顺序不是按照顶点标号的大小,而是按照各顶点T值由大到小的顺序;逆图DFS所得到的森林即对应的连通区域.同时,值得注意的是在求解原图的桥时,为满足差分隐私保护需添加拉普拉斯噪声.
2.2 划分密集区域本文中使用四叉树作为划分邻接矩阵的基本数据结构.四叉树的每一个节点代表一个矩形区域,每一个矩形区域又可划分为四个小矩形区域,作为子节点所代表的区域.在执行过程中,根据叶子节点的条件求解树的高度,再根据最大密度差函数判断并且利用指数机制选出最好的分割点,划分每个子图的邻接矩阵,直到满足成为叶子节点的条件,以形成1值密集或稀疏的区域,并利用四叉树的叶子节点进行表示.
一个标准的四叉树的分割点是独立于输入的数据,它总是选择每一维空间的中间点进行分割,树中的每个节点代表邻接矩阵的一个区域.而在本文中,要在满足差分隐私的条件下来构建四叉树.其中,每个节点不仅表示区域大小,同时包含该区域加噪后的1个数(用count来表示).
(1) 截止条件
在划分空间的过程中,其中一个关键的问题是决定树的高度,在自适应隐私预算分配的情况下计算出一个数据相关的四叉树的高度是很困难的.因此可以利用标准四叉树和几何隐私预算方案[12]来推导一个合理地较为准确的估计值.几何隐私预算方案的原理是:在树的同一层高度j的所有节点拥有相同的隐私预算值εj,并且以21/3倍的速度随着节点深度的增加而增加.
除了树的高度这一截止条件,为了提高算法的有用性和效率,还将应用两个启发式条件:① 如果一个区域是足够密集的(计算该区域的加噪后1值个数),则可以以很高的准确度重构出加噪后的版本,无需将其进一步划分;② 如果一个区域是过于稀疏的,会导致过多的噪声,也无需将其进一步划分.
(2) 分区
对于非叶子区域R,以最大密度差的方法利用指数机制选出最好的分割点,将R划分成4个子区域,这样的分割点能最好区分出密集子区域和稀疏子区域.分割点由邻接矩阵的行、列两个坐标组成.若R的大小为m×l,则至多有(m-1)×(l-1) 中可能的分割点.将所有的分割点数据集记为P,则选择其中一个分割点p∈P的有用性函数定义为q(R, p)=
(3) 隐私预算分配
本文将总的隐私预算值ε/k分成三个部分εC,εE,εR,分别用在算法的三个过程中.εE又被分成两个部分:εcnt用来计算区域内的加噪后1值个数;εPar用来选择分割点.在决定预算值的分配上面,一般来说,将较多的预算值分配给εcnt和εR,因为只有获得相对准确的加噪后1值个数,才能更精确地重构出待发布的邻接矩阵.因为很难理论上量化这些值,将在实验过程中选择合适的分配.
2.3 重构邻接矩阵根据叶子节点,编排节点中区域R的1值的分布,从而重构出发布子图的邻接矩阵.将原始邻接矩阵A中的一个区域记为R,在重构后的邻接矩阵A中对应区域记为R.
重构R的简单方法是使得R中的1值随机分布,但这会让误差很大.所以给定区域R,大小为m×l,加噪后的1值计数
在图分类过程中,采用全局敏感度来计算桥的个数以满足差分隐私保护,划分密集区域和构建邻接矩阵的过程同样也是满足差分隐私保护的.根据差分隐私保护的序列组合性,将重构后的每个子图相加构建发布图,同时将初始分类时记录的桥的个数随机添加到组合后的发布图中,此时完成该发布图模型的整个过程,且整个过程满足差分隐私保护的定义.
3 算法实现与性能分析在构建满足差分隐私保护的发布图模型的基础上,利用度分布、最短路径、聚类系数等图统计分析方法作为度量指标,通过实验验证经过CGM模型处理后的发布图与原图的结构一致性.
实验中的数据集是ego-Gplus、ego-Facebook、Wiki-vote和soc-Epinions1,来源于斯坦福大学的Stanford Network Analysis Project数据平台.ego-Gplus的数据来自Google+收集的使用“共享圈”的用户.ego-Facebook的数据来自使用Facebook应用程序的用户.Wiki-vote的数据包括自维基百科成立后几年间的用户投票数据,节点表示用户,若用户i和j之间有边则代表i曾投票给j.soc-Epinions1数据来源是一个广大用户通过Epinions.com网址确定“谁信任谁”的网站.网址的成员可以决定是否要“信任”对方.所有的信任关系相互作用形成“信任网络”,该网络会结合评估评级以确定哪些评论显示给用户.
实验过程应用到数据集得到满足差分隐私保护的发布图,其中相关度系数k=15,隐私预算值分别为0.6, 0.7, 0.8, 0.9, 1.0,并多次对0.2|V|、0.4|V|、0.6|V|、0.8|V|、|V|节点数进行实验(V为实验数据集中节点的集合,|V|表示节点数量),实验数据集情况见表 2.
| 下载CSV 表 2 实验数据集 Tab.2 Experiment Dataset |
(1) 实验一:利用平均相对误差从聚类系数的角度测试,比较了CGM和DER方法得到的发布图的可用性.图 1给出在ego-Gplus、ego-Facebook、Wiki-vote和soc-Epinions1数据集上的结果.随着隐私预算的增加,平均相对误差均在减小.其中ego-Facebook的差值呈平稳下降的趋势,表明在CGM和DER方法在该数据集中能更好地应用.数据集Wiki-vote中误差值偏大,适用性均较差,在预算值较大的时候,CGM模型产生的查询结果准确性更高.

|
图 1 聚类系数的平均相对误差 Fig.1 Average relative error of clustering coefficient |
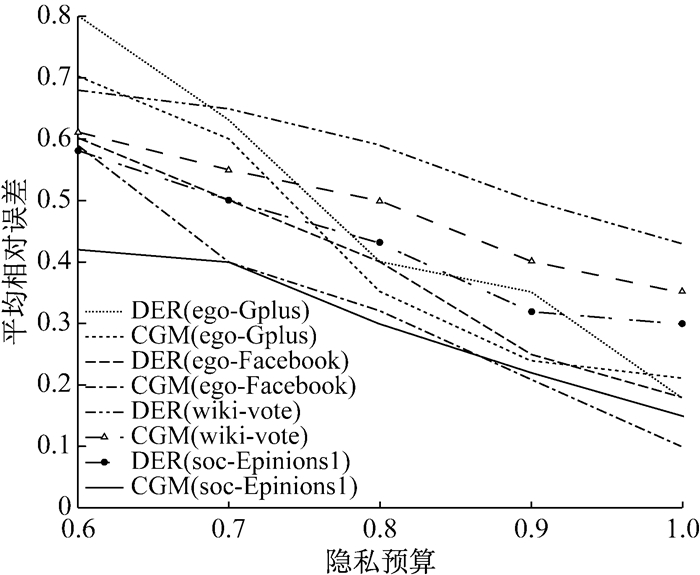
(2) 实验二:利用发布图与原图最短路径的相对误差验证发布图的有用性,从图 2中可以看到CGM模型的产生的相对误差均呈现下降的趋势,相比DER方法,CGM模型在Wiki-vote和soc-Epinions1数据集上的误差值较小,有用性更强.
|
图 2 最短路径的平均相对误差 Fig.2 Average relative error of shortest path |
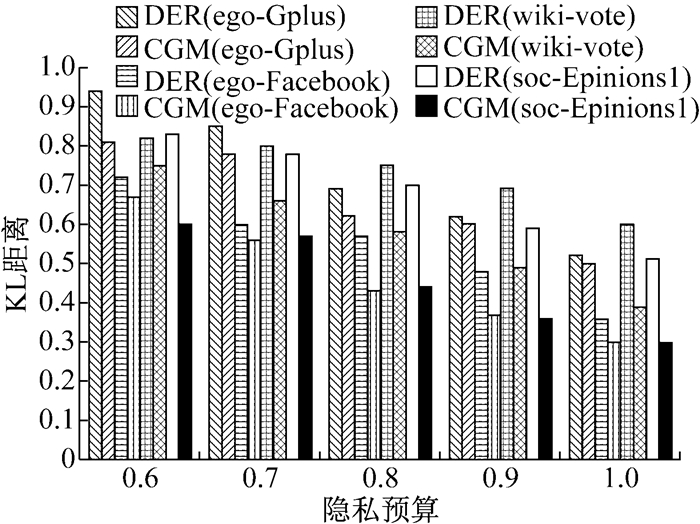
(3) 实验三:通过发布图和原图度分布的KL距离的分析比较,可以观察到CGM方法产生的KL距离在所有的参数设置中均小于DER方法,从图 3可以看出,其KL距离随着隐私预算的增加普遍偏小,因此更适用于求解度分布.
|
图 3 度分布的KL距离 Fig.3 KL distance of degree distribution |
从上述实验结果中,可以看出,在社交网络图发布方面,CER方法在求解度分布、最短路径、聚类系数时待发布图与原图的误差值保持在一个相对平衡的值范围内0.32~0.53,从而得出实施CER方法后得出的待发布图模型与原图保有结构一致性.且从图中可以看出,与DER方法相比,最短路径和聚类系数的相对误差值平均小了0.1,度分布的KL-距离值最小接近了0.2,因此发布图的数据有用性更高.但从差值的分布情况来看,查询结果的准确度仍有待提高.后续研究旨在得出更好的构建四叉树划分空间的方法和隐私预算分配算法等.
4 总结本文从社交网络发布数据的隐私保护角度出发,为解决社交网络数据发布的隐私保护问题,同时保证保护后的发布图的有用性,设计了一个满足差分隐私保护的社交网络图发布生成模型,包括三个主要过程:根据原图的节点特性进行分类,划分成多个子图,记录加噪后的桥的个数;针对每个子图,划分邻接矩阵的密集区域,形成四叉树,树的节点由区域大小和加噪后的个数组成;根据每个子图的树的叶子节点重构出对应的邻接矩阵,再把每棵树相应的邻接矩阵组合成发布图的邻接矩阵,并将记录的桥添加到该矩阵中.最后,利用度分布、最短路径、聚类系数等统计分析方法,验证了该发布图的有用性,以及与其他方法对比分析得出在扩展性等方面具有一定优势.
| [1] |
WANG Jun, LIU Shubo, LI Yongkai. A review of differential privacy in individual data release[J]. International Journal of Distributed Sensor Networks, 2015(9): 1 |
| [2] |
熊平, 朱天清, 王晓峰. 差分隐私保护及其应用[J]. 计算机学报, 2014, 37(1): 101 XIONG Ping, ZHU Tianqing, WANG Xiaofeng. A survey on differential privacy and applications[J]. Chinese Journal of Computers, 2014, 37(1): 101 |
| [3] |
DWORK C, MCSHERRY F, NISSIM K, et al. Calibrating noise to sensitivity in private data analysis[C]//Proceedings of the 3rd Conference on Theory of Cryptography. New York: Springer-Verlag, 2006: 265-284.
|
| [4] |
HAY M, RASTOGI V, MIKLAU G. Boosting the accuracy of differentially private histograms through consistency[C]//Proceedings of the 36th International Conference on Very Large Data Bases. Singapore: VLDB Endowment, 2010: 1021-1032.
|
| [5] |
NISSIM K, RASKHODNIKOVA S, SMITH A. Smooth sensitivity and sampling in private data analysis[C]//Proceedings of the 39th Annual ACM Symposium on Theory of Computing. San Diego: ACM Symposium on Theory of Computing, 2007: 75-84.
|
| [6] |
KARWA V, RASKHODNIKOVA S, SMITH A, et al. Private analysis of graph structure[C]//Proceedings of the 37th International Conference on Very Large Data Bases. Washington: VLDB Endowment, 2011: 1146-1157.
|
| [7] |
WANG Yue, WU Xintao, ZHU Jun, et al. On learning cluster coefficient of private networks[J]. Social Network Analysis and Mining, 2013, 3(4): 925 DOI:10.1007/s13278-013-0127-7 |
| [8] |
CHEN R, FUNG B C M, PHILIP S Y, et al. Correlated network data publication via differential privacy[J]. The VLDB Journal, 2014, 23(4): 653 DOI:10.1007/s00778-013-0344-8 |
| [9] |
DWORK C. The promise of differential privacy: a tutorial on algorithmic techniques[J]. IEEE Symposium on Foundations of Computer Science, 2011, 47(10): 1 |
| [10] |
DWORK C. A firm foundation for private data analysis[J]. Communications of the ACM, 2011, 54(1): 86 DOI:10.1145/1866739 |
| [11] |
DWORK C. Differential privacy[C]//Proceedings of the 33rd International Colloquium on Automata, Languages and Programming. Venice: Springer-Verlag Berlin and Heidelberg, 2006: 1-12.
|
| [12] |
SALA A, ZHAO X, WILSON C, et al. Sharing graphs using differentially private graph models[C]//Proceedings of the 2011 ACM SIGCOMM conference on Internet measurement conference. New York: ACM, 2011: 81-98.
|
 2017, Vol. 45
2017, Vol. 45

