2. 中车长春轨道客车股份有限公司 国家轨道客车工程研究中心, 吉林 长春 130062
2. CRRC Changchun Railway Vehicle Co., Ltd. National Engineering Research Center of Railway Vehicles, Changchun 130062, China
车体地板作为铁道车辆的关键部件,对列车乘坐舒适性的影响很大.地板结构一般由地板支撑件、地板和地板布三部分构成,其与列车的不同部位有着接口关系,在轨道车辆中有承上启下的作用.特别是,高速动车组因速度较高,对减振降噪和舒适度指标的要求更高.目前,对铁道车辆地板振动问题的研究较少.文献[1]研究了不同地板材料对振动传递和辐射效率的影响,发现铝地板结构的振动传递小于不锈钢地板结构,尤其是在高频域.文献[2]针对CRH2B型动车客室地板异常振动进行故障原因分析,发现电机机械振动特性改变,振动的激励频率和地板局部结构的固有特征发生重叠,从而造成共振现象.文献[3]认为,选择适当的地板支撑件中的木骨和泡沫的硬度和弹性模量参数,可以使地板达到最优的舒适度,反之,会直接影响地板上下浮动的大小以及乘客感官舒适度.
在国内某型动车组线路运行时,发现地板振动脚感发麻问题,严重影响乘坐舒适度.为了解决该问题,本文首先通过振动传递分析与运行舒适度计算分析探究地板振动原因;随后,通过模态计算分析与随机振动分析,进一步分析地板振动机理,并对地板进行减振优化研究,最后对相关的优化方案进行了试验验证.
1 车辆线路运行试验针对地板振动脚感发麻问题,对车辆地板进行振动传递试验分析,从传递路径上探究地板振动的原因.试验主要测试车内木地板、弹性支撑(减振元件,实测动刚度参数为450 N·mm-1)、车体底架钢结构的垂向加速度,并对试验数据进行处理分析.加速度传感器分别布置在车体两侧转向架中心上方位置,如图 1所示.其中,A为车体钢结构表面,B为弹性支撑座中部(弹性支撑铝合金板),C为弹性支撑上表面(橡胶表面),D为弹性支撑上方地板处,E为距D点纵向100 mm地板处,F为距D点纵向200 mm地板处(且F点位于转向架中心正上方,是国际铁路联盟(Union Internationale des Chemins de Fer, UIC)舒适性指标测点,同时用以考察运行舒适度指标情况).地板测点现场图如图 2所示.试验时,车辆以特定速度在一段坡度平缓、平直的运营线路上运行,且保证车上无人员走动,记录稳态振动试验结果不小于5 min.

|
图 1 弹性支撑测点分布图 Fig.1 Acceleration distribution of the test |

|
图 2 弹性支撑处地板测点现场图 Fig.2 Spot map of the measuring point of the floor |
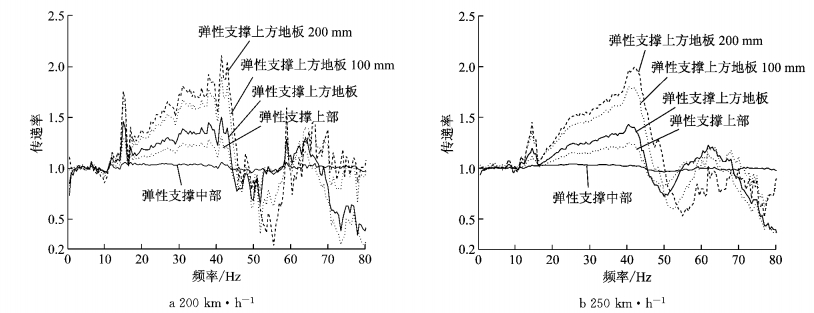
振动传递率可以评价减振系统的性能,本文选取地板垂向振动加速度传递率进行分析.以线路运行时,车体钢结构的振动(测点A)作为输入,其他测点的振动作为输出响应,分别获得200 km·h-1与250 km·h-1速度级下各层结构之间的振动传递关系,结果如图 3所示.从结果中不难看到,当车辆在200 km·h-1与250 km·h-1速度级运行时,车体钢结构至地板弹性支撑上方、车体钢结构至地板面的振动传递率在20~50 Hz频率范围内均大于1,呈明显放大趋势;车体钢结构到弹性支撑上方地板测点D、测点E(一侧100 mm)、测点F(一侧200 mm)的振动传递率随纵向距离的增加而增大,且传递率数值最大超过2.上述结果表明,该车辆地板在20~50 Hz频带范围内存在振动放大现象.
|
图 3 地板振动加速度传递率 Fig.3 Acceleration transmission of the floor structure |
为进一步研究地板振动问题,本节对车辆进行了运行舒适度分析.舒适度,即车辆在线路上行进时所产生的三向加速度振动(包括纵向、横向及垂向)对舒适度的影响.本文选用UIC513《铁路车辆内旅客振动舒适性评价标准》来评价地板振动舒适度,其量化计算公式的简化方法为[4]
| $ {N_{{\rm{MV}}}} = 6\sqrt {{{\left( {a_{x{P^{\rm{d}}}95}^W} \right)}^2} + {{\left( {a_{y{P^{\rm{d}}}95}^W} \right)}^2} + {{\left( {a_{z{P^{\rm{d}}}95}^W} \right)}^2}} $ | (1) |
式中:NMV为地板振动的舒适度指标;a为加速度,下标x、y、z表示三个维度方向; P为地板测点; 下标“95”表示95%的置信度;b、d是垂直、水平权重(W)曲线下标.图 4所示为垂直与水平方向权重曲线(纵向与水平方向权重曲线相同).图中, UIC表示国际铁路联盟(International Union of Rail ways).从图中可以看出,舒适度对垂直和水平方向的频率权重曲线Wa-Wd和Wa-Wb存在明显不同(Wa为加速度的权重).水平方向0.6~2.0 Hz频率范围的加权值较高,超过0.8;垂直方向在4~20 Hz频率范围的加权值较高,超过0.8;此外,垂直方向在20~40 Hz频率范围的加权值超过了0.4.

|
图 4 UIC指标权重曲线 Fig.4 Weight curve of UIC index |
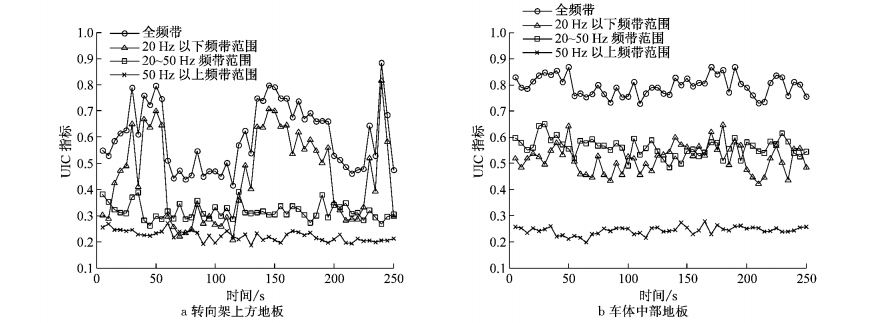
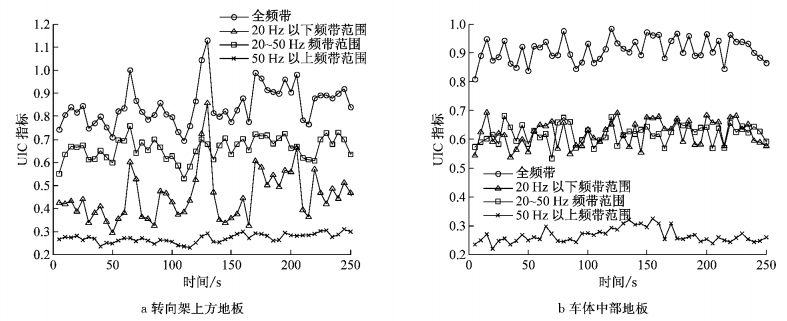
图 5、图 6分别为不同运行速度时,转向架上方地板和车体中部地板的运行舒适度指标试验结果.为了便于深入分析,每5 s进行一次舒适度指标计算,并做相应处理,分别研究20 Hz以下、20~50 Hz以及50 Hz以上频带范围的振动对舒适度的影响.从图 5中结果可以看到,当运行速度为200 km·h-1时,全频带的舒适度指标结果最大值为0.9(舒适性佳);对于转向架上方车体而言,20 Hz以下频带范围的舒适度指标要略高于20~50 Hz频带范围的指标,50 Hz以上频带范围的指标最小,表明此时20 Hz以下频带范围的振动对舒适度指标的贡献量最大,其次为20~50 Hz频带范围,50 Hz以上频带范围最小;对于车体中部而言,20 Hz以下频带与20~50 Hz频带范围的结果相差不大,二者对舒适度指标贡献量基本相当.图 6结果显示,当运行速度达到250 km·h-1时,全频带舒适度指标最大值为1.15(舒适性良好);对于转向架上方车体而言,20~50 Hz频带范围的舒适度指标要明显高于20 Hz以下频带范围的指标;而对于车体中部而言,结果与200 km·h-1接近.
|
图 5 车辆运行速度200 km·h-1时,舒适度试验结果 Fig.5 UIC indices of 200 km·h-1 |
|
图 6 车辆运行速度250 km·h-1时,舒适度试验结果 Fig.6 UIC indices of 250 km·h-1 |
总结上述试验结果,得到以下结论:
(1) 虽然20~50 Hz频带范围的舒适度指标权重较小(图 4),但该频带范围的振动强(图 3),导致其对舒适度指标的贡献仍然很大;
(2) 该车舒适度指标虽然较低,但是,地板存在20~50 Hz频带范围的振动放大现象,该频率范围覆盖了人体腿部敏感频率[5],导致乘客乘坐时仍会脚感发麻;
(3) 随着运行速度的提高,该车地板20~50 Hz频带的振动对舒适度指标贡献量逐渐增大,因此,为改善舒适度,抑制地板的中、高频振动也十分重要.
2 车辆有限元模型建模为了对地板进行振动及减振优化研究,本文采用虚拟样机技术,运用有限元软件建立包含地板的车体精细化有限元模型.
2.1 地板和木骨材料性能参数试验为获得实际的地板及地板支撑件木骨材料属性,首先对样件进行材料性能试验.采取无约束支撑,通过三点弯曲方式,测试样件材料的抗弯刚度[6-7],并根据公式计算材料的弹性模量参数,如下:
| $ f = \frac{{F{l^3}}}{{48EI}} $ | (2) |
式中:l为试验跨距; F为试验中点处挠度f对应的载荷值; I为惯性矩; E为等效弹性模量.地板木板和木骨的截面均为矩形,宽为b,高为h,故惯性矩I为
| $ I = \frac{1}{{12}} \cdot b{h^3} $ | (3) |
根据式(2) 与式(3) 可得材料的弹性模量为
| $ E = \frac{{{l^3}}}{{4b{h^3}}} \cdot \frac{E}{f} $ | (4) |
试验分别对5件木板和木骨样件进行抗弯刚度试验,图 7是5件木板和木骨的抗弯刚度试验结果.可以看出,在载荷相同的情况下,各试验样件中心的挠度有微小的差别.此外,当载荷在一定范围内时,位移与载荷呈准线性关系.一般地,车体地板在真实振动环境下的结构变形很小,属于该线性范围内.对多组抗弯刚度曲线进行平均,并求出平均后线性区域的斜率,即F/f.随后,根据式(4) 计算获得木板和木骨的弹性模量.本文中木地板与木骨的弹性模量分别为6.3 GPa与8.5 GPa.

|
图 7 材料抗弯刚度曲线 Fig.7 Bending rigidity curve of the test material |
根据地板三维模型,运用有限元软件对其进行网格划分,建立地板精细化有限元模型.图 8为地板三维实体模型,其中,地板减振方式采用木骨泡沫垫减振和弹性支撑(橡胶减振件).木骨泡沫垫是12 mm厚的海绵状聚氨酯混合体,能够起到减振的效果;弹性支撑件由上下两块铝型材及中间的橡胶材料组成,地板结构中弹性支撑共213个.

|
图 8 地板三维实体模型 Fig.8 3D solid model of the floor |
建模过程中,由于弹性支撑橡胶具有一定非线性特性,且数量众多,为降低计算成本,考虑到橡胶小变形时具有线性弹性特性[8],本文对弹性支撑模型进行了等效处理.在模型上表面施加均布载荷,通过调整硫化橡胶模型材料弹性模量,使其变形量与弹性支撑实际刚度的变量相匹配时,即得到硫化橡胶的等效弹性模量.图 9、图 10分别为弹性支撑有限元模型约束与载荷示意图和弹性支撑刚度为450 N·mm-1时的应力图,此时得到材料的等效弹性模量为1.8 MPa.

|
图 9 弹性支撑模型载荷与约束示意图 Fig.9 Load and constraint diagram of the elastic support model |

|
图 10 弹性支撑应力图 Fig.10 Stress of the elastic support |
最后,运用有限元软件,对车体几何模型进行网格划分,将建立好的地板模型与车体模型进行连接.此外,车体底架边梁相应位置还联接了牵引变流器、通风机、电源箱、污物箱等车下设备,车顶联接了空调设备.建立的包含地板的车体精细化有限元离散模型如图 11所示,整车承载结构的质量为10.7 t,整备状态质量为34 t,车体材料参数如表 1所示.整备状态车体共划分762 704个节点,628 541个单元.

|
图 11 包含地板的车体精细化有限元模型 Fig.11 Finite element (FE) model of the car body that includes the floor |
| 下载CSV 表 1 车体材料参数表 Tab.1 Material parameter of the car body |
模型建立完毕后,需要对其进行校验.本文分别通过模态分析、振动响应分析及传递率对所建模型的合理性进行验证.首先,运用Block Lanczos方法对整车进行自由模态分析,并将计算结果与试验模态结果进行对比,如表 2所示.从表 2结果可以看出,模态参数计算结果与试验结果吻合良好,车体主要低阶模态误差相差不大,最大误差仅为5.1%.
| 下载CSV 表 2 车体主要低阶模态参数对比 Tab.2 Comparison of main low-order modal parameters of the car body |
随后,对该模型进行振动响应验证.振动响应计算需求解式(5) 所示的系统微分方程[9],
| $ \mathit{\boldsymbol{M\ddot u}} + \mathit{\boldsymbol{C\dot u}} + \mathit{\boldsymbol{Ku}} = \mathit{\boldsymbol{P}}\left( t \right) $ | (5) |
式中:M, C, K分别是全局质量、阻尼、刚度矩阵; P(t)为广义力矩阵; u、
式(5) 可通过模态法求解[10],利用模态分析计算出式(5) 的n个互异特征值ω0i(i=1, 2, …n)以及对应的特征向量φi,则物理坐标系下的响应u可写为
| $ \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} q}} $ | (6) |
式中:Φ=[φ1φ2…φn],为系统的特征向量矩阵;q为模态坐标向量.通过坐标变换,式(5) 可写为
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\mathit{\boldsymbol{M \boldsymbol{\varPhi} \ddot q}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\mathit{\boldsymbol{C \boldsymbol{\varPhi} \dot q}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\mathit{\boldsymbol{K \boldsymbol{\varPhi} q}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\mathit{\boldsymbol{P}} $ | (7) |
当系统为实模态时,依据特征向量的正交性对式(7) 进行解耦,便可以求出模态坐标系下的响应,再通过式(6) 即可求出物理坐标系的响应.选取空气弹簧上方的车体实测振动加速度作为计算输入(车辆运行速度250 km·h-1),采用模态法计算分析车体响应,以转向架中心上方地板处为参考点,将计算结果与试验结果进行对比,如表 2所示.从表 2结果可以看出,仿真和实测结果吻合,最大误差为7%.
| 下载CSV 表 2 车体振动加速度对比(车辆运行速度250 km·h-1) Tab.2 Comparison of vehicle vibration acceleration (250 km·h-1) |
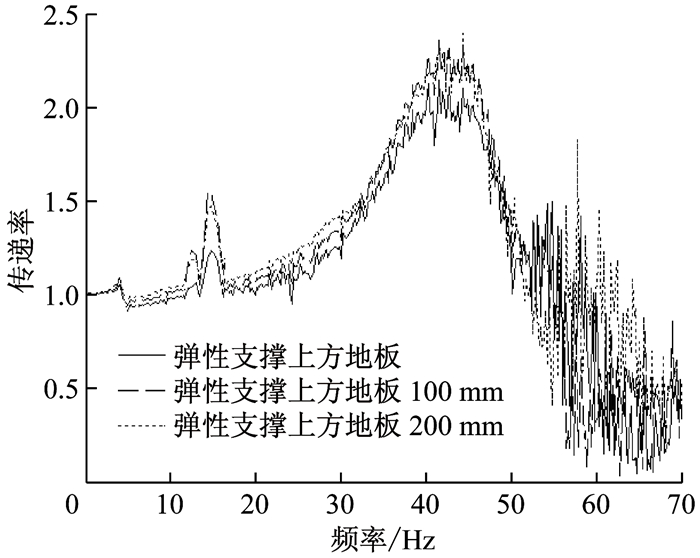
最后,运用有限元模型,以地板D、E、F测点为参考点,计算得到车体钢结构至地板的振动传递率,结果如图 12所示.不难看到,有限元计算结果中,车体钢结构至地板弹性支撑上方、车体钢结构至地板面的振动传递率在频域20~50 Hz范围内亦呈放大趋势;车体钢结构到弹性支撑上方地板测点D、测点E(一侧100 mm)、测点F(一侧200 mm)的振动传递率随纵向距离增加而增大,这与试验结果趋势接近.综合上述结果表明,所建立的有限元模型是合理的.
|
图 12 有限元模型振动传递率计算结果 Fig.12 Transmission calculation results of the FE model |
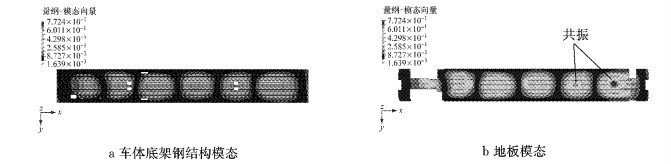
运用该模型,进一步研究地板在20~50 Hz频域内振动放大的根本原因.为清晰地显示地板振动,截取了该频段范围内底架和地板的三个同阶模态振动云图,如图 13~图 15所示.观察振动云图不难发现,底架与地板在该频段范围内均存在大量局部模态,且对比底架钢结构振动而言,地板振动能量显著放大;究其原因,是因为由弹性支撑连接的底架结构与地板结构的局部模态频率接近,进而导致地板与车体底架发生局部共振现象,地板振动能量放大.
|
图 13 第29阶模态(25.572 Hz) Fig.13 The 29th order eigenmode(25.572 Hz) |

|
图 14 第39阶模态(32.114 Hz) Fig.14 The 39th order eigenmode(32.114 Hz) |

|
图 15 第55阶模态(38.563 Hz) Fig.15 The 55th order eigenmode(38.563 Hz) |
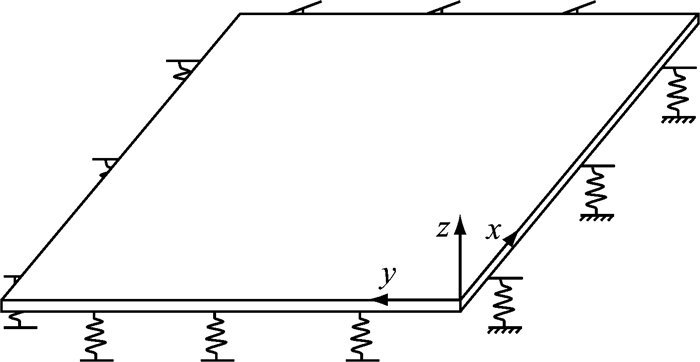
由于底架与地板结构不易改动,因而需要对弹性支撑的刚度进行优化.弹性支撑上方的地板可以视作具有弹性支撑边界条件的平板,如图 16所示.
|
图 16 弹性支撑边界条件下的地板 Fig.16 Floor under the elastic support boundary condition |
图 16所示板件的振动微分方程为
| $ D{\nabla ^4}w\left( {x, y} \right)-\rho h{\omega ^2}\left( {x, y} \right) = 0 $ | (8) |
式中:
| $ \left\{ \begin{array}{l} {k_{x0}}w = {Q_x}\\ {k_{xl}}w =-{Q_x}\\ {k_{y0}}w = {Q_y}\\ {k_{yl}}w =-{Q_y}\\ {M_x} = {M_y} = 0 \end{array} \right. $ | (9) |
式中:kx0、kxl、ky0、kyl分别是x=0、x=l、y=0、y=l边上的弹性支撑刚度函数; Qx、Qy为剪力; Mx、My为弯矩.
运用Rayleigh-Ritz法对系统的振动微分方程进行求解[11],并最终得到系统矩阵方程,
| $ \left( {\pmb{K}-{\omega ^2}\pmb{M}} \right)\pmb{A} = {\bf{0}} $ | (10) |
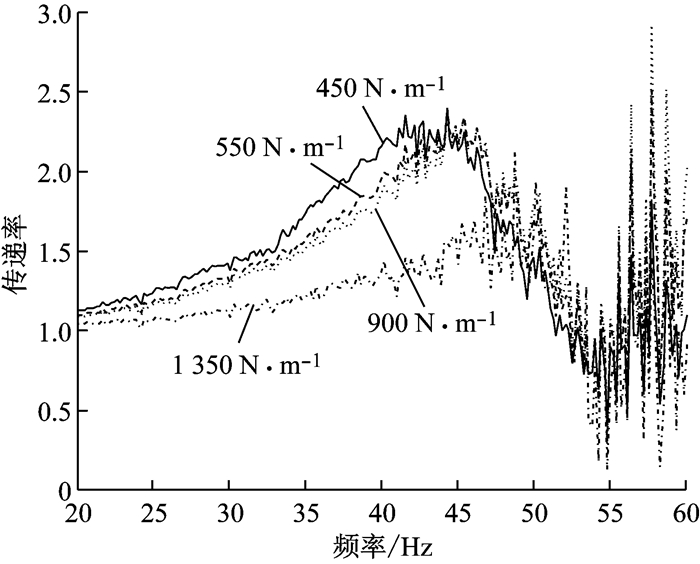
式中:A为级数展开系数; K、M分别为刚度矩阵和质量矩阵.求解地板系统的模态参数(模态频率和特征向量)即变为求式(10) 的特征值问题[12].上述求解地板系统的模态参数表明,地板的模态频率会受到弹性支撑刚度的影响.因此,优化弹性支撑刚度,便可以优化地板的模态频率,使地板振动传递主频移动,从而尽量避开原始共振频带.图 17为不同弹性支撑刚度下,车体钢结构到地板测点F的振动传递率计算结果,其中,弹性支撑刚度的考察范围依据现有的实际刚度给出.可以看到,随着弹性支撑刚度的增加,地板振动传递主频右移,且当弹性支撑刚度达到1 350 N·mm-1时,20~50 Hz频带范围内的地板振动传递率得到了有效降低.
|
图 17 测点F振动传递率计算结果 Fig.17 Result of transmission of the measuring point F |
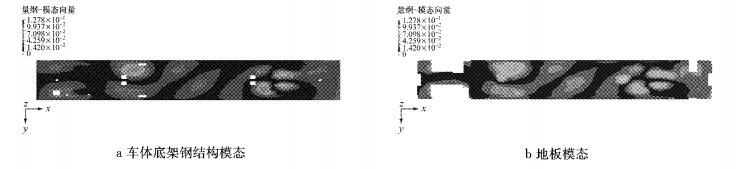
图 18~图 20所示为弹性支撑刚度1 350 N·mm-1时,底架和地板的三个同阶模态振动云图计算结果.不难发现,此时相对底架钢结构振动而言,地板振动能量没有明显放大,地板与车体底架未发生共振现象.

|
图 18 第20阶模态(22.509 Hz) Fig.18 The 20th order eigenmode(22.509 Hz) |
|
图 19 第38阶模态(32.132 Hz) Fig.19 The 38th order eigenmode(32.132 Hz) |

|
图 20 第58阶模态(39.909 Hz) Fig.20 The 58th order eigenmode(39.909 Hz) |
对弹性支撑优化方案进行线路运行试验验证.图 21所示为地板弹性支撑刚度分别为原始方案和优化方案时,车体底架钢结构至地板测点E(一侧100 mm)、测点F(一侧200 mm)的振动传递率.可以看到,与原始方案相比(450 N·mm-1),当弹性支撑刚度为1 350 N·mm-1时,在20~50 Hz频率范围的地板振动传递率得到明显下降,最大不超过1.3,且地板振动脚感发麻问题得到明显改善.

|
图 21 弹性支撑优化方案试验验证 Fig.21 Test verification of the elastic support optimization |
(1) 针对国内某型动车组运行时,地板振动脚感发麻问题,进行了线路运行试验,通过振动传递分析与运行舒适度计算分析发现,该车运行舒适度指标虽然较低,但是,地板存在20~50 Hz频带范围的振动放大现象,该频率范围覆盖了人体腿部敏感频率,导致乘客乘坐时仍会脚感发麻;
(2) 建立了精细化整车有限元模型,并通过模态分析、振动响应及振动传递率分析验证了模型的合理性;运用该模型研究了地板振动放大机理,发现由于弹性支撑参数不当,导致底架结构与地板结构的局部模态频率接近,进而导致地板与车体底架发生局部共振现象,地板振动能量放大;
(3) 对弹性支撑的刚度进行优化,并进行了试验验证,结果表明,当弹性支撑刚度为1 350 N·mm-1时,可有效降低地板在20~50 Hz频率范围的振动传递率,且地板振动脚感发麻问题得到明显改善.
| [1] |
SHIN B S. 铁道车辆地板结构的声-振传递特性[J]. 国外铁道车辆, 2015, 52(5): 41 SHIN B S. Sound and vibration characteristics of floor structures in rolling stock[J]. Foreign Rolling Stock, 2015, 52(5): 41 |
| [2] |
吕雄伟. CRH2B型动车组客室地板异常振动分析[J]. 上海铁道科技, 2012(1): 70 LV Xiongwei. Analysis of the abnormal vibration of the floor of EMU CRH2B[J]. Shanghai Railway Science and Technology, 2012(1): 70 |
| [3] |
贾焕英, 蔡彦强. 高速动车组地板系统的分析研究[J]. 铁道机车车辆, 2013, 33(5): 26 JIA Huanying, CAI Yangqiang. Research on the floor structure of high-speed EMU[J]. Railway Locomotive and Car, 2013, 33(5): 26 |
| [4] |
International Union of Railways & European Committee for Standard. UIC Code 513 Guideline for evaluation passenger comfort relation to vibration in railway vehicles[S]. Paris: International Union of Railways (UIC) & European Committee for Standard (CEN), 1994.
|
| [5] |
董霜, 朱元清. 环境振动对人体的影响[J]. 噪声与振动控制, 2004, 24(3): 22 DONG Shuang, ZHU Yuanqing. Effects of environment vibration on man[J]. Noise and Vibration Control, 2004, 24(3): 22 |
| [6] |
中国标准出版社. 纤维增强塑料弯曲性能试验方法: GB/T 14492005[S]. 北京: 中国标准出版社, 2005. China Standard Press. Fiber-reinforced plastic composites-Determination of flexural properties: GB/T 14492005[S]. Beijing: China Standard Press, 2005. |
| [7] |
中国标准出版社. 纤维增强塑料性能试验方法总则: GB/T 14462005[S]. 北京: 中国标准出版社, 2005. China Standard Press. Fiber-reinforced plastic composites-Fiber-reinforced plastic composites—The generals for determination of properties: GB/T 14462005[S]. Beijing: China Standard Press, 2005. |
| [8] |
IBRAHIM R A. Recent advances in nonlinear passive vibration isolators[J]. Journal of Sound and Vibration, 2008, 314(3-5): 371 DOI:10.1016/j.jsv.2008.01.014 |
| [9] |
周劲松. 铁道车辆振动与控制[M]. 北京: 中国铁道出版社, 2012 ZHOU Jinsong. Railway vehicle vibration and control[M]. Beijing: China Railway Publication House, 2012 |
| [10] |
宫岛, 周劲松, 孙文静, 等. 基于格林函数法的铁道车辆弹性车体垂向振动分析[J]. 机械工程学报, 2013, 49(12): 116 GONG Dao, ZHOU Jinsong, SUN Wenjing, et al. Vertical vibration analysis of flexible car body for railway vehicle based on Green function[J]. Journal of Mechanical Engineering, 2013, 49(12): 116 |
| [11] |
LI W L. Vibration analysis of rectangular plates with general elastic boundary supports[J]. Journal of Sound and Vibration, 2004, 273(3): 619 DOI:10.1016/S0022-460X(03)00562-5 |
| [12] |
GONG Dao, ZHOU Jinsong, SUN Wenjing. Influence of under-chassis-suspended equipment on high-speed EMU trains and the design of suspension parameters[J]. Journal of Rail and Rapid Transit, 2016, 230(8): 1790 DOI:10.1177/0954409715614601 |
 2017, Vol. 45
2017, Vol. 45

