骨盆是人体骨骼的重要部分,骨盆周围分布着重要的器官及血管神经,是一个复杂且关键的结构.骨盆骨折是严重的创伤性骨折,常合并有其他重要器官及系统的损伤.早期诊断、院前急救和骨折复位固定是控制出血、降低死亡率的关键.早期诊断中,骨盆骨折的分型至关重要,分型结果是后续治疗的基础,直接决定了治疗方案和手术方法.基于骨盆的稳定性,Tile将骨盆骨折分成A、B、C三种类型.其中A型为稳定的骨盆环损伤,B型为部分稳定骨折,C型为不稳定骨折[1].A型骨折一般采取保守治疗,B型骨折采用固定前环的措施,对C型骨折进行骨盆环前后联合固定.
目前,对骨盆骨折的分型诊断主要集中在患者到达医院之后,医生采用X光、CT(computed tomography slices)片及其他辅助设备,如图 1所示.电子设备的使用能快速准确地定位骨盆损伤,帮助医生划分骨折类型.然而,对设备的依赖也导致时间的浪费:运送患者从事故现场到医院的时间得不到充分利用,患者到达医院后需要等待空闲的设备和医生,等待时间的累积可能导致患者错过救援的“黄金时间”.为充分利用等待时间,本文收集患者的体表特征,设计图 1的新诊疗路径.基于统计和贝叶斯网络方法,分析体表特征间关系、体表特征与骨盆骨折类型间关系,初步判断骨盆损伤患者的骨折类型,采取相应的急救措施.同时将患者的情况及时告知医院,方便医生提前准备相关的诊断仪器,制定可能的治疗方案,为后续治疗节约时间.

|
图 1 两种诊疗路径对比 Fig.1 Comparison of two paths of diagnosis and treatment |
朴素贝叶斯分类方法的准确率和分类效率较高,然而其特征属性需要满足条件独立或完全独立的条件.实际案例中的特征属性往往具有较强的相关性,限制了朴素贝叶斯分类的能力.贝叶斯网络(Bayesian network, BN)将有向无环图与概率理论有机结合,可简洁有效地表示变量间的相互关系,为不确定性推理提供强有力的工具.贝叶斯网络理论中,结构学习的问题可以表述为给定节点变量集X的一个观测数据集D,通过学习找出一个最匹配数据集D的网络结构G,评分函数表示网络结构与真实网络的匹配程度.
1 文献综述在不确定决策领域中,机器学习和决策制定首要采用概率图模型,贝叶斯网络是其中应用最广泛的一类.贝叶斯网络中的推断和学习涉及到复杂的优化问题,其学习包括结构学习和参数学习两部分,结构学习是最为重要的内容.Larraaga等[2]回顾了通用随机搜索算法在贝叶斯网络推理和学习中求解非确定性多项式(non-deterministic polynomial, NP)难题的应用.基于局部结构的推导,Minn等[3]采用基于约束的学习类算法(accelerated PC)获得BN,该方法继承了PC(peter & Clark)算法的高数据效率特性,节省了计算量.Cooper等[4]采用K2算法构造BN,通过局部贪婪搜索选择最优的网络结构,并将此方法应用于数据缺失和含有隐藏变量的例子.Gasse等[5]提出新的H2PC(hybrid PC)混合算法:重构贝叶斯网络框架,基于贪婪爬山搜索方法确定边的方向.Gheisari等[6]使用基于粒子群算法的贝叶斯网络构造算法(BNC-PSO),在算法中增加插入边和删除边的功能,使得粒子能够达到最优解.循环删除程序的增加防止了无效解的迭代,马尔可夫链的引入证明了该算法的全局收敛性.Yang等[7]提出细菌觅食优化方法(bacterial foraging optimization, BFO-B),算法中的每个细菌对应一个贝叶斯网络结构候选解,BFO在网络空间中搜索最优网络结构,K2准则引导搜索进程.Kreimer等[8]采用条件熵方法学习最优结构,该方法在计算时间和计算性能上较之其他方法有显著优势.
网络结构学习包含评分和搜索两部分,评分准则衡量贝叶斯网络对于给定数据集的质量,搜索程序在可能的空间中智能移动搜索,建立合理的网络结构.K2算法是贝叶斯网络中最有效的结构学习方法之一,然而其性能很大程度上依赖节点的排列顺序.基于当子节点被分配给正确的父节点时,其条件概率更高的已知,Ko等[9]设计了新的评分函数和节点排序方法.给定两个变量时,利用评分函数推断出更好的父节点;考虑所有变量时,推断出父节点候选节点,由此确定K2算法中节点的输入顺序.基于隐式推理框架,Bouchaala等[10]提出隐式评分法,采用K2和最大生成树(maximum weight spanning tree,MWST)算法实现网络结构学习.Hruschka等[11]提出特征排序算法,采用信息增益和卡方检验两种方法得到有效的变量顺序,大幅降低了K2算法的计算复杂度.以信息理论方法和评分函数方法为基础,Chen等[12]采用条件独立测试方法获得节点排序信息.针对贝叶斯评分准则中难以估计的自由参数,Cano等[13]采用局部边际化元参数的方法,接受更广泛的参数假设,并基于简单局部平均的方法来评估自由参数.Wang等[14]使用带平滑参数的高斯核函数估计属性密度,基于分类精度准则,贪婪搜索父节点,构建扩展朴素贝叶斯分类器.
目前,BN已在多个领域的决策和诊断中获得成功应用.范建平等[15]基于聚类的贝叶斯网络模型约简医疗指标,通过分类及提取主特征和类特征,研究中医症候分型及动态演变,为类风湿关节炎病因的研究、诊断提供了重要依据.针对贪婪贝叶斯模式搜索(greedy Bayesian pattern search algorithm, GBPS)算法易陷入局部最优的不足,王学伟等[16]在GBPS算法的邻域生成过程中引入有向边的变向操作,并用该算法研究中医临床诊断数据中症状与辨证要素间的复杂关系.为研究精神分裂症疾病中基因型对外表型的影响,Ouali等[17]使用贝叶斯网络方法确定连续变量的最佳分界点.采用贝叶斯狄利克雷等效,Akaik信息准则和最小描述长度三种评分标准,使用三种搜索算法:K2算法,爬山算法和模拟退火算法实现.
为充分利用救援时间,快速准确地诊断骨盆骨折类型,本文选取了患者的18个体表特征,采用基于K2算法的贝叶斯网络方法挖掘特征间、特征与骨折类型间的关系.为弥补K2算法在输入顺序上的不足,设计4种节点输入策略,分析不同策略对结果的影响.最后,基于患者体表特征描述和与骨折类型相关的主特征分析,对骨盆骨折患者进行初步诊断分型.
2 贝叶斯网络及构造 2.1 贝叶斯网络定义贝叶斯网络又称为贝叶斯信念网络,由网络结构BS和条件概率表BP组成,即BN为BS, BP.贝叶斯网络结构是一个有向无环图(directed acyclic graph, DAG),其中节点集合为X,xi∈X表示随机变量;节点间的有向边集合为A,aij∈A表示随机变量间的直接依赖关系.aij为xi与xj间的有向连接,xi→xj,xi被称为xj的父节点.使用π(xi)表示变量xi的父节点集合,条件概率分布P(xi|π(xi))可定量表示xi与π(xi)之间的依赖关系.条件概率表中的元素对应图中的节点,存储该节点与其父节点的联合条件概率.在确定节点及其父节点集后,假设该节点独立于它的所有非父节点,即贝叶斯网络中的条件独立性假设.因此,贝叶斯网络中所有节点的联合概率可以表示为各节点条件概率的乘积,如式(1).
| $ \begin{align} &P\left( {{x}_{1}}, {{x}_{2}}, \ldots, {{x}_{n}} \right)=\underset{i=1}{\overset{n}{\mathop{\prod }}}\, P\left( {{x}_{i}}|{{x}_{1}}, {{x}_{2}}, \ldots, {{x}_{i-1}} \right)= \\ &\underset{i=1}{\overset{n}{\mathop{\prod }}}\, P\left( {{x}_{i}}|\pi \left( {{x}_{i}} \right) \right) \\ \end{align} $ | (1) |
给定测试数据集D,构造贝叶斯网络的任务即找到最佳匹配数据集D的网络结构.网络结构的学习包含结构学习和参数学习,结构学习确定网络的拓扑结构,参数学习定义网络拓扑结构的条件概率.结构学习分为完备数据和不完备数据两种情况,完备数据下结构学习算法有3类:基于约束的学习算法(constraint based, CB)、基于评分搜索的学习算法(scoring and searching, SS)和混合学习算法.本文采用基于评分搜索的算法,K2算法.
2.2 评分函数贝叶斯网络学习中使用的评分函数主要分为两大类:基于贝叶斯的评分函数和基于信息论的评分函数.Cooper等[3]于1992年提出了用于计算贝叶斯网络评分的K2算法,计算公式如式(2):
| $ \begin{align} &P\left( {{B}_{\text{S}}}, D \right)= \\ &P\left( {{B}_{S}} \right)\underset{i=1}{\overset{n}{\mathop{\prod }}}\, \underset{j=1}{\overset{{{q}_{i}}}{\mathop{\prod }}}\, \frac{\left( {{r}_{i}}-1 \right)!}{\left( {{N}_{ij}}+{{r}_{i}}-1 \right)!}\underset{k=1}{\overset{{{r}_{i}}}{\mathop{\prod }}}\, {{N}_{ijk}}! \\ \end{align} $ | (2) |
式中:D为包含m个样本的数据集;ri表示随机变量xi所有可能取值的数量;qi为π(xi)中包含实例的数量;wij为π(xi)中第j个实例的取值情况,1≤j≤qi;Nijk表示数据库D中变量xi取其第k个值xik,且其父代π(xi)取其第j个值wij的样本数量,则
可分解是评分函数一个非常重要的特性,利用该特性,网络结构的评分可以转化为各点局部结构的评分之和.当贝叶斯网络中一个点的局部结构发生变化时,只需重新计算该点的局部结构评分,可分解的评分函数能大大降低重复计算的次数.因此,使用式(2) 的代数形式,式(3).其中,f(xi, π(xi))表示每个节点的K2评分,其具体的计算见式(4),常数log P(BS)可省去不计.通过取对数的方法,将相乘的评分函数形式转化为各节点结构评分相加的形式,降低了计算的复杂度,减少了计算时间.
| $ \begin{align} &f\left( {{B}_{\text{S}}}, D \right)= \\ &\text{log}\left( P\left( {{B}_{\text{S}}}, D \right) \right)\approx \sum\limits_{i-1}^{n}{f\left( {{x}_{i}}, \pi \left( {{x}_{i}} \right) \right)} \\ \end{align} $ | (3) |
| $ \begin{align} &f\left( {{x}_{i}}, \pi \left( {{x}_{i}} \right) \right)=\sum\limits_{j=1}^{{{q}_{i}}}{\left( \text{log}\left( \frac{\left( {{r}_{i}}-1 \right)!}{\left( {{N}_{ij}}+{{r}_{i}}-1 \right)!} \right) \right.}+ \\ &\left. \sum\limits_{k=1}^{{{r}_{i}}}{\text{log}\left( {{N}_{ijk}}! \right)} \right) \\ \end{align} $ | (4) |
每个节点与其父节点的联合概率均小于1,分解后每个节点的K2评分值都是负数.要构造最优的贝叶斯网络结构,就是要寻找最大的K2评分值.
2.3 搜索方法K2搜索算法在给定输入节点顺序的情况下,依次计算各点的评分值.给定最大父节点数量,选择评分值最高的节点或节点组合作为该点的父节点.K2算法的算法性能很大程度上取决于输入节点的顺序,输入顺序中排在前面的节点被默认是后续节点的父节点.随机设置的节点顺序或由数据集给定的节点顺序往往导致较差的结果,由领域专家确定节点顺序的方法因专家的难以获得而无法实施.本文中18个体表特征间的关系及先后输入顺序未知,因此采用4种策略确定节点的输入顺序:① 数据集给定的节点顺序,即样本中各特征的编号顺序;② 采用信息增益方法计算三种骨盆骨折类型下各特征的值,十折交叉验证后按从大到小的顺序排列各特征值,其对应编号作为输入顺序;③ 采用卡方检验方法计算三种骨盆骨折类型下各特征的值,十折交叉验证后按从大到小的顺序排列各特征值,其对应编号作为输入顺序;④ 对每一个节点,遍历除其之外的所有节点,选择最大值代表的节点或节点组合作为该节点的父节点,该策略下节点的输入顺序对算法结果没有影响.为挖掘骨盆骨折类型与体表特征间的关联,分析不同骨盆骨折的主特征,4种策略下骨折类型均作为最后一个变量输入.每个节点的最大父节点数量一般设定为n-1,本文取18.
信息增益和卡方检验是有效的特征选择方法,可以度量三种骨盆骨折类型下各特征的重要程度.卡方检验通过一定的测量方法赋予每个特征权重,量化特征与类别间的相关度,关联性越强分值越高;信息增益衡量特征为分类系统带来的信息多少,越重要的特征带来的信息越多.三种骨盆骨折类型下,各特征的信息增益值和卡方检验值在软件Weka3.6.4中计算得到.
K2算法的伪代码描述如下:
| 下载CSV 表 Tab. |
收集2012年上海市第一人民医院骨盆骨折患者的电子病历和纸质病历,病历详细记录了患者的基本资料、体检报告数据、入院诊断、手术资料和出院信息等.由于病历中包含的数据过多、过杂,首先筛选出标记骨盆骨折类型的病历,其次提取与本研究相关的患者的体格检查描述.标记骨盆骨折类型的样本共有172例,筛选出的18个体表特征并依次编号为:① 腰部压痛、② 臀部压痛、③ 髋部压痛、④ 骨盆分离试验阳性、⑤ 下肢疼痛、⑥ 纵向叩击痛、⑦ 腹部压痛、⑧ 耻骨联合处压痛、⑨ 皮肤擦伤、⑩ 肩部压痛、B11髂区压痛、B12骨盆压痛、B13上肢肿胀、B14骶骨压痛、B15胸廓挤压试验阳性、B16头部受伤、B17 4字征实验阳性和B18对光反射.设计如表 1的数据结构表,记录每个患者的骨折类型及存在的体表特征,并将文字描述转化成可以处理的0-1数字.所有患者的统计情况表中不予列出.
| 下载CSV 表 1 病例样本整理后的数据结构 Tab.1 Data structure after case arrangement |
完成病历的逐条筛选后,计算三种骨盆骨折类型的患者数量,统计每种骨盆骨折下各体表特征出现的次数,绘制如表 2所示的体表特征频数分布表.
| 下载CSV 表 2 骨盆骨折类型及体表特征频数分布 Tab.2 Classification of pelvic fracture and frequencies of surface characteristics |
基于第4节的资料收集和特征选取,得到实验需要的数据集.根据4种节点输入顺序策略,首先计算三种骨折类型下每个特征的信息增益值和卡方检验值;按照特征值从大到小的顺序进行排列,返回特征值在数据集中的编号,如表 3所示;依次排列编号作为节点的输入顺序,进行实验计算.比较不同输入策略下,实验结果和算法性能的差异,构造骨盆骨折类型与体表特征的关系网络图.
| 下载CSV 表 3 策略2和3下各体表特征排序 Tab.3 Sorting of each surface characteristic under strategy 2 and 3 |
针对三种骨盆骨折类型,采用4种节点输入策略进行计算,计算结果比较见表 4和表 5:
| 下载CSV 表 4 4种节点输入策略的算法性能比较 Tab.4 Performance comparison of 4 node input strategies |
| 下载CSV 表 5 4种节点输入策略的结果比较 Tab.5 Result comparison of 4 nod input strategies |
通过比较可以发现:
(1) 策略1的计算时间最短,策略4的计算时间最长,策略2和3的计算时间与策略1的差距较小.A型骨折下,策略2和3分别比策略1的计算时间多了7.13%和6.69%;B型骨折下,策略2和3分别比策略1的计算时间多了0.78%和2.62%;C型骨折下,策略2和3分别比策略1的计算时间多了42.22%和7.29%.
(2) 对比策略1,策略2~4对节点的K2评分值有不同程度的优化.策略4优化的节点数量最多,三种骨折类型中的优化数量分别占所有节点的61%、61%和39%;策略2和3优化的节点数量基本一致.
(3) 策略1下连接的边数最少,即发现的节点间关系的数量最少,而采用策略4的遍历方法能找到节点间的尽可能多的关系.
综上,由于K2算法中先输入节点被默认是后输入节点的父节点,在给定节点顺序下(前3种策略),算法的计算时间相差不大.策略2和3采用特征选择方法,根据特征重要性制定节点顺序.随机产生的节点顺序或数据集中给定的输入顺序一般只能发现相邻节点间的关系;采用相关特征选择方法,根据特征重要性制定节点顺序时,易于挖掘与骨盆骨折类型高度相关的特征间关系.对节点进行遍历计算,通过计算选择评分函数值较高的节点作为其父节点,虽然导致计算时间增加,但可以发现所有特征间的关系及特征与骨折类型间的关系.
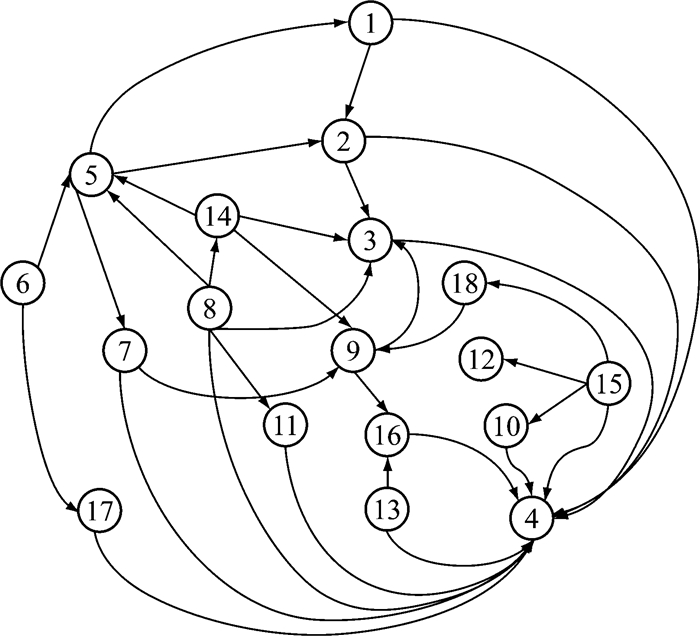
4.3 体表特征间关联分析运行K2算法,采用遍历节点的输入策略,分析体表特征间的相互关系,如图 2所示.图中节点分别表示:① 腰部压痛、② 臀部压痛、③ 髋部压痛、④ 骨盆分离试验阳性、⑤ 下肢疼痛、⑥ 纵向叩击痛、⑦ 腹部压痛、⑧ 耻骨联合处压痛、⑨ 皮肤擦伤、⑩ 肩部压痛、B11髂区压痛、B12骨盆压痛、B13上肢肿胀、B14骶骨压痛、B15胸廓挤压试验阳性、B16头部受伤、B17 4字征实验阳性和B18对光反射.由图可知:节点4是众多节点的子节点,即存在由一些部位的压痛可以推断出骨盆分离试验阳性的结论.
|
图 2 体表特征间网络关联图 Fig.2 Network diagram of surface characteristics |
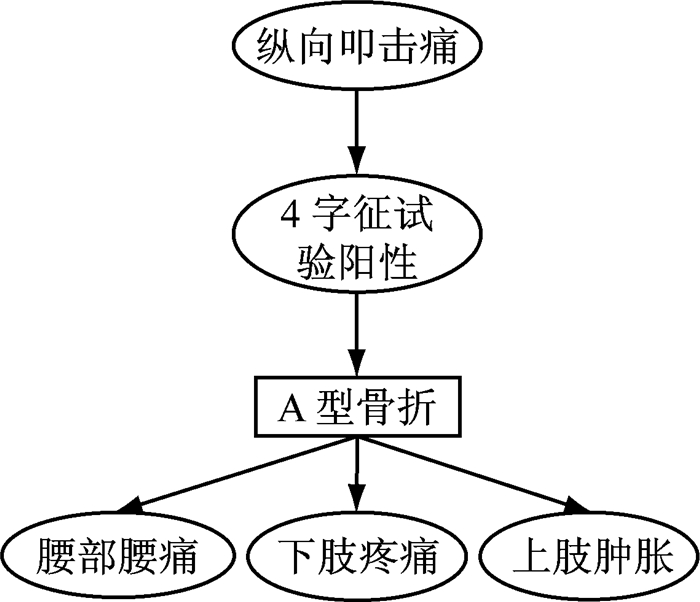
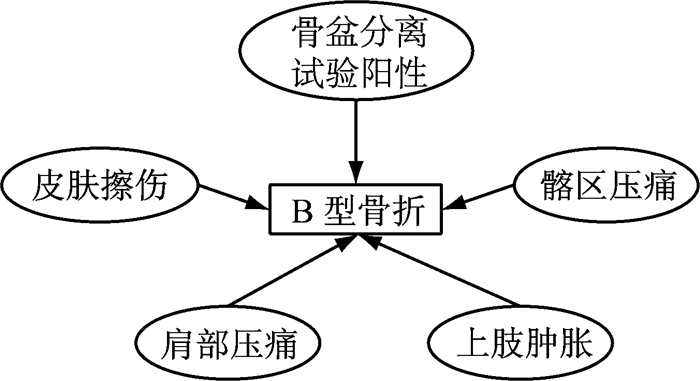
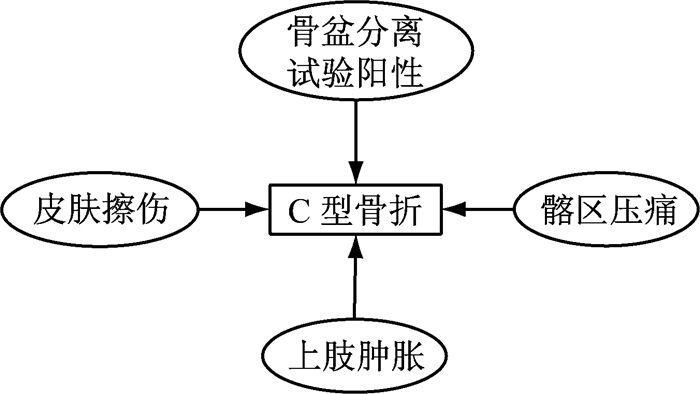
通过分析骨盆骨折类型与体表特征间关系,分别得到与三种骨折类型相关的体表特征,如图 3~图 5所示.从图中可以发现:4字征试验阳性是A型骨折的父节点,而A型骨折容易导致腰部压痛、下肢疼痛及上肢肿胀这些体表特征的出现;当存在骨盆分离试验阳性、皮肤擦伤、髂区压痛、肩部压痛和上肢肿胀这些体表特征时,极有可能是B型骨盆骨折;骨盆分离试验阳性、皮肤擦伤、髂区压痛和上肢肿胀这些体表特征是发生C型骨盆骨折时存在的主要特征.
|
图 3 A型骨盆骨折相关特征 Fig.3 Features related to type A pelvic fracture |
|
图 4 B型骨盆骨折相关特征 Fig.4 Features related to type B pelvic fracture |
|
图 5 C型骨盆骨折相关特征 Fig.5 Features related to type C pelvic fracture |
本文对收集到的172例骨盆骨折患者的病历进行整理,从原始病历的体表特征中提取18个指标.根据Tile分型方法将患者分成3类,其中A型骨折9例,B型骨折118例,C型骨折45例,统计不同骨折类型下各体表特征的频数.采用基于K2算法的贝叶斯网络结构学习算法学习体表特征间关系;设计不同的节点输入策略,分析不同节点输入顺序对算法性能的影响;分别提取与三种骨盆骨折类型直接相关的特征.特征间关联分析及特征与骨盆骨折类型的分析可以为骨盆骨折类型的初步判断提供依据,并采取有针对性的急救措施,为后续治疗节约时间.由于收集到的病历数量有限,特别是A型骨盆骨折病历的严重不足,导致对A型骨盆骨折的研究不充分,相关特征的挖掘不全面;同时,三种骨盆骨折类型的病历数量相差较大,文章没有考虑样本数据量对计算结果准确性的影响.
进一步的研究包括:收集更多骨盆骨折患者的资料,降低样本量对结果的影响;提取更全面有效的指标,删减冗余、无效的指标,更好挖掘各骨盆骨折类型的主特征;改进结构学习算法或采用更有效的方法,使之更好地适用于医学统计与分析.
| [1] |
PIZANIS A, POHLEMANN T, BURKHARDT M, et al. Emergency stabilization of the pelvic ring:clinical comparison between three different techniques[J]. Injury, 2013, 44(12): 1760 DOI:10.1016/j.injury.2013.07.009 |
| [2] |
LARRAÑAGA P, KARSHENAS H., BIELZA C., et al. A review on evolutionary algorithms in Bayesian network learning and inference tasks[J]. Information Sciences, 2013, 233: 109 DOI:10.1016/j.ins.2012.12.051 |
| [3] |
MINN S, 傅顺开. 贝叶斯网络结构加速学习算法[J]. 计算机科学, 2016, 43(3): 263 MINN S, FU Shunkai. Bayesian network structure accelerated learning algorithm[J]. Computer Science, 2016, 43(2): 263 DOI:10.11896/j.issn.1002-137X.2016.02.055 |
| [4] |
COOPER G F, HERSKOVITS E. A Bayesian method for the induction of probabilistic networks from data[J]. Machine Learning, 1992, 9(4): 309 |
| [5] |
GASSE M, AUSSEM A, ELGHAZEL H. A hybrid algorithm for Bayesian network structure learning with application to multi-label learning[J]. Expert Systems with Applications, 2014, 41(15): 6755 DOI:10.1016/j.eswa.2014.04.032 |
| [6] |
GHEISARI S, MEYBODI M R. BNC-PSO: structure learning of Bayesian networks by Particle Swarm Optimization[J]. Information Sciences, 2016, 348(2016): 272 |
| [7] |
YANG C C, JI J Z, LIU J, et al. Structural learning of Bayesian networks by bacterial foraging optimization[J]. International Journal of Approximate Reasoning, 2016, 69: 147 DOI:10.1016/j.ijar.2015.11.003 |
| [8] |
KREIMER A, Herman M. A novel structure learning algorithm for optimal Bayesian network: best parents[J]. Procedia Computer Science, 2016, 96: 43 DOI:10.1016/j.procs.2016.08.092 |
| [9] |
KO S, Kim D W. An efficient node ordering method using the conditional frequency for the K2 algorithm[J]. Pattern Recognition Letters, 2014, 40: 80 DOI:10.1016/j.patrec.2013.12.021 |
| [10] |
BOUCHAALA L, Masmoudi A, Gargouri F, et al. Improving algorithms for structure learning in Bayesian Networks using a new implicit score[J]. Expert Systems with Applications, 2010, 37(7): 5470 DOI:10.1016/j.eswa.2010.02.065 |
| [11] |
HRUSCHKA Jr E R, Ebecken N F F. Towards efficient variables ordering for Bayesian networks classifier[J]. Data & Knowledge Engineering, 2007, 63(2): 258 |
| [12] |
CHEN X W, Anantha G, Lin X. Improving Bayesian network structure learning with mutual information-based node ordering in the K2 algorithm[J]. IEEE Transactions on Knowledge and Data Engineering, 2008, 20(5): 1 DOI:10.1109/TKDE.2008.59 |
| [13] |
CANO A, GMEZ-OLMEDO M, MASEGOSA A R, et al. Locally averaged Bayesian Dirichlet metrics for learning the structure and the parameters of Bayesian networks[J]. International Journal of Approximate Reasoning, 2013, 54(4): 526 DOI:10.1016/j.ijar.2012.09.003 |
| [14] |
WANG S C, GAO R, WANG L M. Bayesian network classifiers based on Gaussian kernel density[J]. Expert Systems with Applications, 2016, 51(C): 207 |
| [15] |
范建平, 李常洪, 吴美琴, 等. 贝叶斯网络在中医诊断中的应用研究[J]. 管理科学学报, 2008, 11(6): 143 FAN Jianping, LI Changhong, WU Meiqin, et al. Study on application of Bayesian network in Chinese medicine diagnose[J]. Journal of Management Sciences in China, 2008, 11(6): 143 |
| [16] |
王学伟, 瞿海斌, 刘雪松, 等. 贝叶斯网络杂交学习算法及其在中医中的应用[J]. 浙江大学学报(工学版), 2005, 39(7): 948 WANG Xuewei, ZHAI Haibin, LIU Xuesong, et al. Bayesian network approach to knowledge discovery in traditional Chinese medicine[J]. Journal of Zhejiang University (Engineering Science), 2005, 39(7): 948 |
| [17] |
OUALI A, CHERIF A R, KREBS M O. Data mining based Bayesian networks for best classification[J]. Computational Statistics & Data Analysis, 2006, 51(2): 1278 |
 2017, Vol. 45
2017, Vol. 45

