近年来,恐怖主义者开始使用高致命性、非常规生化武器来攻击建筑类民用设施,通过蓄意施放化学战剂(chemical warfare agent, CWA)或生物战剂(biological warfare agent, BWA)毒剂对建筑人居环境健康、安全提出了挑战.[1-3].2011年,维基解密一份关塔那摩监狱关押者审讯记录的文件披露,基地组织曾计划在美国向公共建筑的空调系统投放剧毒氰化物[4].由于建筑内部存在不同的房间组合及空调风系统配置,搭配形成了复杂的空气流通通道,突发污染可以通过建筑与风系统耦合的复杂通道在建筑内迅速扩散,污染物传播速度快、情况复杂[5-7].而通过直接向风系统投放污染物的袭击模式更为隐蔽,波及范围更广,造成的危害更为严重[8].当突发污染事件发生时,如何在有限时间内迅速反演得到污染源的位置、强度及投放初始时刻信息,对于如何采取相应的应急通风措施并根据源位置确定室内人员的最优逃生线路意义重大.
目前建筑环境污染传播溯源研究尚处于起步阶段,但国内外部分开创性研究成果已见诸报道.Zhang和Chen[9-10]首次提出了利用准可逆法辨识单室内的气态污染源的方法与过程.Liu和Zhai[11-12]建立了基于建筑物多区网络模型的联合概率快速反演方法.UC Berkeley(USA)[13-14]在建筑网络空间传感器优化布置方法上做了大量开创性的研究.但前人的研究均没有涉及可能发生于空调风系统的突发污染溯源方法,在实践上尚需针对风系统反演数学模型及非稳态源定位、源强解析与投放时间分析等方面开展系统研究,需要取得相关理论、方法与模型的突破及创新[15].
本文建立了以风系统突发污染节点解析模型为优化对象的适应度函数,以一个全空气系统中的突发污染为例,建立了不同污染场景下的风系统传感器模拟浓度数据库,当风系统中的传感器监测到污染物浓度时应用遗传算法进行溯源,该方法成功地反演出了风系统中瞬时投放的点源信息(包括源位置、强度及投放初始时刻);讨论了采用不同传感器数目对反演结果准确性的影响,分析了传感器的布置位置与时间对反演结果总平均相对误差的影响,得到了传感器性能(监测误差及传回数据时间间隔)对反演源位置参数x0的影响.
1 基于遗传算法的污染溯源模型 1.1 模型的建立在风系统内,可认为某一段风管道的风速保持不变,则在系统内某位置处瞬时投放污染物的对流扩散控制方程为
| $ \frac{{\partial C}}{{\partial t}}{\rm{ = }}\varepsilon_x\frac{{{\partial ^2}C}}{{\partial {x^2}}}-{u_x}\frac{{\partial C}}{{\partial x}}-KC $ | (1) |
式中:C为污染物浓度;t为系统时间;x为污染物所处的空间位置;εx为湍流扩散系数;ux为风管断面平均风速;K为污染物衰减系数.
方程(1) 的解析解如下,推导过程详见文献[16]:
| $ C = \frac{{{M_0}}}{{A\sqrt {4\pi {\varepsilon _x}t} }}\exp \left[{-\frac{{{{\left( {x-{u_x}t} \right)}^2}}}{{4{\varepsilon _x}t}}} \right]\exp \left[{-Kt} \right] $ | (2) |
| $ {\mathit{\boldsymbol{C}}_{\rm{d}}} = {\mathit{\boldsymbol{M}}^{-1}}\mathit{\boldsymbol{f}} $ | (3) |
式(2)、(3) 中:M0为污染物投放总量,mg;A为风管道横截面积,m2;Cd为瞬时投放点源主管道上每个断面向下游输出的污染物浓度;M-1为节点向支管输出的污染物系数矩阵;f为初始浓度向量.
其中,式(2) 描述瞬时投放点源条件下风系统直管段内的污染物浓度分布;式(3) 是考虑了系统三通和四通节点位置处的风量及污染物量的平衡后得到的风系统各断面污染物浓度分布的矩阵方程式.式(2)、(3) 描述的模型的准确性已在文献[17]中通过实验验证.
风系统突发污染溯源分析是在风机稳定运行前提下,假设恐怖分子在风管道内某位置处投放了一定量的污染物,通过事先布置在风系统内的传感器实时监测,获得这些监测点的浓度数据,根据浓度数据辨识出污染源信息,而不同污染物投放场景下的传感器理论浓度分布均可通过公式(2) 和(3) 计算得到,反演模型的数学表达式为
| $ g\left( I \right) = {\sum\limits_{j = 1}^{{N_{\rm{t}}}} {\sum\limits_{i = 1}^{{N_{\rm{r}}}} {\left[{\frac{{C_{{\rm{cal}}}^i\left( j \right)-C_{{\rm{mes}}}^i\left( j \right)}}{{C_{{\rm{mes}}}^i\left( j \right)}}} \right]} } ^2} $ | (4) |
式中,Nt为传感器监测次数; Nr为传感器个数; Ccali(j)和Cmesi(j)分别为污染源在i监测点,j时刻的理论计算浓度和实际监测浓度.
风系统污染物浓度在线监测系统可在突发污染发生时及时地从系统中提取大量流量及浓度数据,风系统突发污染溯源就是在系统污染物浓度分布模拟分析的基础上通过传感器实测浓度值与模型理论计算浓度值的对比分析来辨识污染源信息的.
1.2 优化变量与约束条件在风系统突发污染溯源过程中,首先需将风系统划分为若干节点,节点划分依据主要是参考前人在水污染领域及室内空气品质领域的研究.首先在水污染领域,为了反演得到输配水系统中的污染源,设置节点进行分析是常用方法[18-19];其次在室内空气品质领域,污染物多区反演模型建立的实质即为节点分析法,将各房间当作节点考虑并添加适当的边界条件,在反演过程中得到污染源位于模型中的某个节点是目前的常用方法[11-12].由此可知节点的设置是对所求反演问题的适当简化.同理,污染物投放量M及投放初始时刻T也需分别假设一个适当范围,其中污染物投放量M的取值范围主要参考了文献[5]、[15]和[20]中关于生化毒气投放剂量与流行病学关系的论述.
本文假设风系统内的每个节点均是一个可能的污染物投放位置,以污染源信息(X, M, T)为具体优化参数,分别给出X、M和T的约束范围:
| $ \mathit{\boldsymbol{X}} \in \left( {{\mathit{\boldsymbol{X}}_{{\rm{node }}\;1}},{\mathit{\boldsymbol{X}}_{{\rm{node }}\;2}},{\bf{\cdots}} ,{\mathit{\boldsymbol{X}}_{{\rm{node }}\;n}}} \right) $ | (5) |
| $ \mathit{\boldsymbol{M}} \in \left( {{\mathit{\boldsymbol{M}}_1},{\mathit{\boldsymbol{M}}_2},\cdots ,{\mathit{\boldsymbol{M}}_n}} \right) $ | (6) |
| $ \mathit{\boldsymbol{T}} \in \left( {{\mathit{\boldsymbol{T}}_1},{\mathit{\boldsymbol{T}}_2}, \cdot \cdot \cdot ,{\mathit{\boldsymbol{T}}_n}} \right) $ | (7) |
式(5)~(7) 中:(Xnode 1, Xnode 2, …, Xnode n)分别为风系统中各节点所在位置;(M1, M2, …, Mn)分别为可能被投放至风系统的污染物量;(T1, T2, …, Tn)分别对应可能的污染物投放时刻.上述污染源信息参数均预先存储在遗传算法所需调用的数据库中,详见表 1.表中,tF为初始时刻,tL为最终时刻.
| 下载CSV 表 1 风系统内各传感器在不同污染投放场景下的浓度模拟数据 Tab.1 Calculated concentration of sensors considering different releasing scenarios in ventilation system |
遗传算法是基于自然选择和基因遗传学原理的随机优化搜索算法,适合于处理传统算法无法解决的高度非线性问题[21-22],且可直接用于离散变量的计算.由于本文所建立的模型变量包含离散变量(节点流量及浓度),属于复杂非线性问题,因此本文采用遗传算法进行溯源,具体实现流程见图 1.

|
图 1 风系统突发污染溯源算法实现流程 Fig.1 Procedure of sudden contaminant source identification method in ventilation system |
由于遗传算法的种群选择具有一定的随机性,故不同场景下的反演值均是算法多次运行结果的平均值.遗传算法基本参数设置详见表 2,其确定主要参照了文献[20]和[21]中推荐的数据.
| 下载CSV 表 2 遗传算法基本参数设置表 Tab.2 Parameters of genetic algorithm method |
本文用反演结果总平均相对误差来评价遗传算法溯源结果与真实源参数之间的偏差,其定义如下:
| $ \xi = \sum\limits_{i = 1}^n {\frac{{\left| {{\pmb{p}_i}-{\pmb{p}_0}} \right|}}{{\left| {{\pmb{p}_0}} \right|}}} /n $ | (8) |
式中:ξ为反演结果总平均相对误差;pi为反演得到的源参数向量;p0为实际源参数向量;i为向量的第i个参数;n为参数个数.
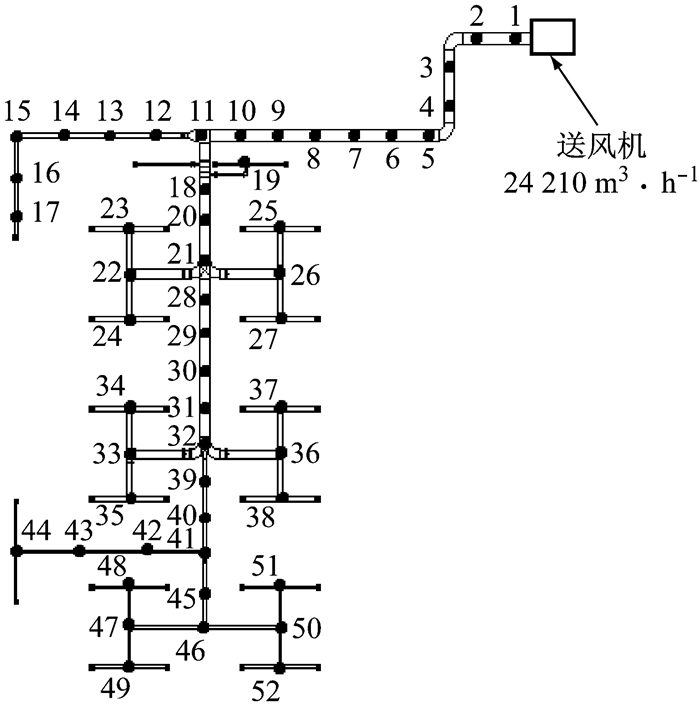
2 溯源结果及分析 2.1 传感器数目对溯源结果的影响分析针对图 2所示的风系统,通过前期计算已知该系统风量分布,完成了风系统网络动力学模型构建.
|
图 2 设置节点后的风系统示意 Fig.2 Air duct system |
图中,(圆点表示所设节点,数字代表节点编号)
当风系统内部的传感器数目过少时,算法无法根据少量的监测数据分析出污染源信息,因此,需首先考察传感器数目对反演结果平均误差(ξ)的影响,进而确定该风系统内安装几个传感器,最后再深入分析传感器性能参数变化对ξ的影响.考虑基于风系统最小污染物输出量的风系统传感器优化布置方案如图 3所示,传感器优化布置实现过程详见参考文献[16].

|
图 3 不同传感器数目对应的传感器优化布置方案 Fig.3 Optimal sensor layouts based on different number of sensors |
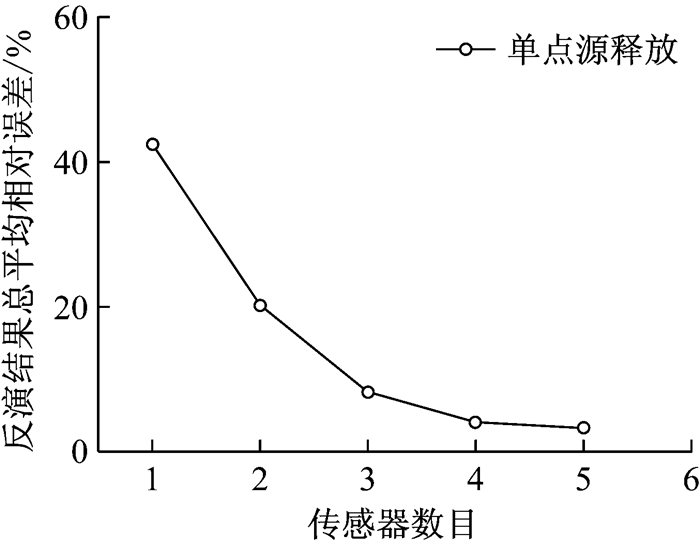
由图 4可知,风系统内传感器数目的多少显著影响ξ的大小(假设采用理想传感器,传感器监测值即为该位置处的真实浓度),当风系统内采用单个传感器时,ξ接近50%,这在工程上是不能接受的,表明单个传感器反馈的数据太少,无法解决遗传算法因反问题的病态性而产生的误差;当采用双传感器系统时,该误差显著下降,此时的ξ接近20%,但是由于风系统可能发生的污染源数目是不确定的,从理论角度来说,对于需要同时反演多个污染源的场景,双传感器系统仍然是不安全的;而当风系统内安装有三个以上传感器时,传感器数目的多少对ξ的影响较小,采用三传感器系统的ξ低于10%,考虑到单个传感器的成本较高,对于本算例的风系统而言,在其中优化布置三个传感器在应对突发污染时是较为安全且经济的.
|
图 4 传感器数目对反演结果总平均误差的影响 Fig.4 Impact of sensor quantity on the overall average relative error of inversion results |
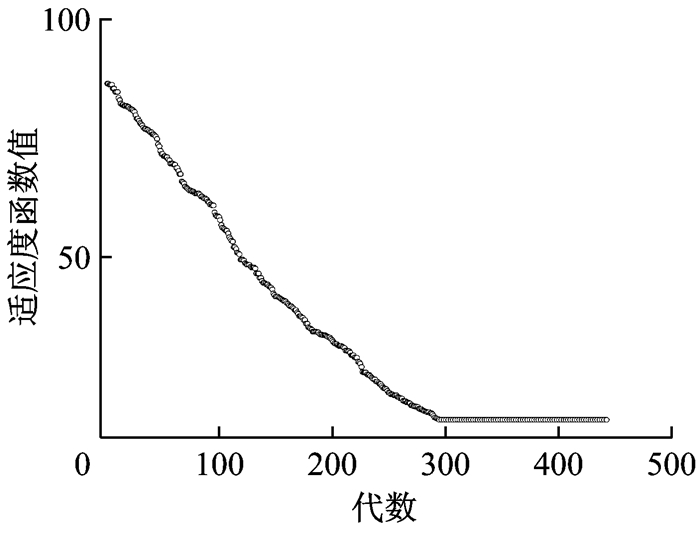
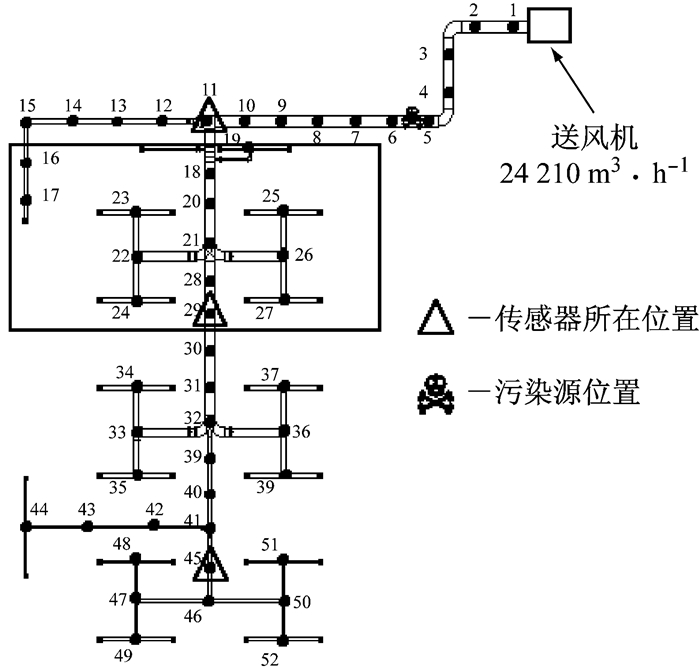
在图 2所示的风系统中设置三个传感器时,运用第1节方法对突发污染源(Xnode 5, T=10 s, M=50 mg)进行反演,图 5为瞬时投放点源反演对应的适应度函数收敛性,从图中可以看出反演计算收敛子代数少,收敛时间短(约5 s).在最不利情况下,即污染源不位于算例中假设的任一节点时,如污染源位于节点5和6之间的任意位置,此时优化后的三传感器系统仍能监测到污染物,但由于计算机事先并未储存污染源位置在节点5和6之间的传感器模拟浓度数据,故反演源位置需在节点5和6之间进行判断,该判断过程增加了反演所需总时间,对于本算例,反演总时间约为9 s,收敛子代数为700,较污染源位置位于节点5时,反演所需总时间增加约4 s,收敛子代数增加约400代.根据式(3) 计算可知,在风系统采取相应的应急动作前,污染物浓度已到达节点30前的所有风口,如图 6所示,节点30后的风口还未出现污染物,此时通过系统控制风阀切断污染源或是关闭风机都有利于为室内人员的疏散逃生争取时间.需要指出的是该区域仅是模型计算的定性影响范围,实际影响范围还需根据风系统与建筑的耦合形式及室内人员分布进行确定,这部分内容将在作者之后的研究中予以充分考虑,最终目的是得到不同的应急通风方式在应对突发污染时的有效性,获得室内人员按以反演源位置为约束条件确定的最优逃生路线上的动态污染物暴露量.
|
图 5 溯源适应度函数收敛情况 Fig.5 Convergence property of inversion calculation |
|
图 6 反演所需时间内,模型计算的污染物定性影响区域示意 Fig.6 Affect zone of contaminant under model simulation within the required time of inversion |
第2.1节分析中的传感器布置方案是基于风系统最小污染物输出量这一目标函数优化后得到的,为了全面评价传感器布置位置及监测时间对ξ的影响,以实际污染源位置为原点,传感器位置及首次监测到污染物时间为x和y轴,ξ为z轴,得到图 7.由图可知,在反演过程中,传感器监测位置与时间是一对耦合的参数,首个监测到污染物的传感器离污染源越远,ξ越大,同时该误差是随传感器首次监测到污染物的时间增长而增大的.故在二维时空坐标中存在一个点使ξ最小.
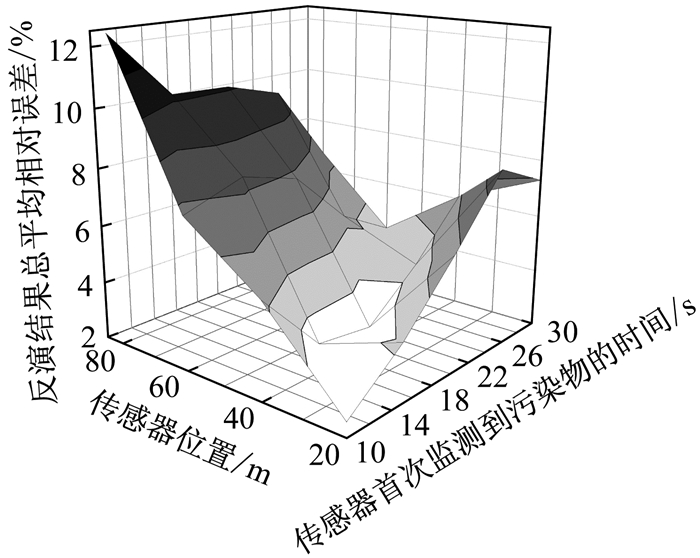
|
图 7 传感器监测位置及首次监测到污染物的时间对反演结果总平均相对误差的影响 Fig.7 Impact of the location and measurement time of sensors on the overall average relative error of inversion results |
由于2.1节的分析均假设风系统内采用的传感器监测误差为0,但实际工程中采用的传感器均存在一定的误差,同时传感器向控制中心传回的数据也有一定的时间间隔,接下来的分析中将主要考虑这两个因素对反演源位置x0的影响.
当风系统内发生突发污染时,通过反演确定污染源的位置最为关键,源位置的确定可以保证后续一系列应急措施的迅速开展.从图 8可以看出传感器监测误差及传回数据时间间隔在反演源位置参数x0上是独立的,源位置参数x0的反演相对误差与传感器监测误差无关,而随传回数据时间间隔的增大而增大,这是因为针对源位置x0的反演仅与污染物传播时间项有关,亦即只要知道污染物传播到传感器监测点所需要的时间,由于对流项中的风速是已知的,源位置x0也就确定了,而监测误差则属于传感器自身特性,并不影响源位置x0的反演结果.传回数据时间间隔越大,表明相同时间内传回的数据量越小,可供算法用于修正反演误差的数据也越少,故反演相对误差也越大.
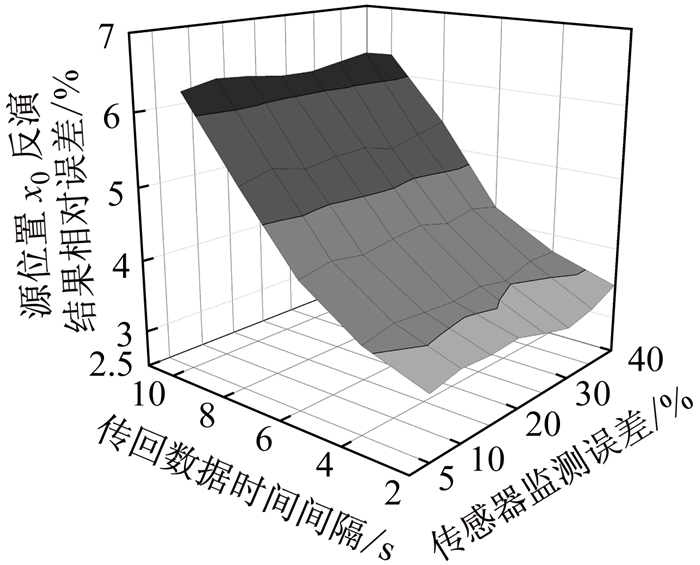
|
图 8 传感器误差及传回数据间隔时间对反演源位置x0影响 Fig.8 Impact of detecting error of sensors and time interval of feedback data on the identification of source location x0 |
风系统内节点划分主要参考地下水及输配水系统中的节点划分原则[18-19],首先系统流量发生变化的位置需要设置节点,包括系统中的三通/四通等;其次,由于生化袭击具有随机性,理论上风系统中的每个位置都可能成为污染物的投放位置,因此对于长直管段,也需要将其划分为若干节点.在三通/四通位置处的节点已设置的条件下,当长直管段节点间距在一定范围内增大时,系统所包含的节点总数降低,也就意味着可能发生突发污染的节点数减少,对应数据库中储存的突发污染事件减少,若在这些节点投放污染物,通过遗传算法能在存储的较少的污染场景中更快地匹配到污染源信息,但节点间距过大则会使节点无法有效覆盖整个风系统,从而导致算法由全局寻优转变为局部寻优,无法应对真实的随机突发污染事件.故节点间距存在一个适当的范围,在此范围内既能在一定程度上减少遗传算法存储数据量,降低运算负荷,又能兼顾在整个风系统内溯源的目的,根据上述原则确定的本算例风系统的节点数取值范围为[35, 88],当节点总数为35时,由于长直管段上的节点间距较大,故当随机的突发污染事件发生在这些节点之间时,通过遗传算法反演得到的源位置与真实源位置之间的总平均相对误差约为25%,略大于工程允许的误差范围,但由于节点数减少使反演过程所需总时间降低至3 s以下,为风系统采取应急动作保障室内人员安全争取了时间,故将节点数的下限设置为35, 而节点上限则将反演源位置与真实源位置之间的总平均相对误差降低至5%,但相应的反演所需总时间增加至18 s以上,此时再缩短节点间距还原更多的真实投放场景无法显著降低反演误差并会较大幅度地增加反演所需时间,故节点数的上限取为88.
3 结论为了在空调风系统内突发污染发生的短时间内辨识到污染源,进而采取相应的应急措施保障室内人员安全,建立了不同污染场景下的风系统传感器模拟浓度数据库,以传感器模拟计算浓度与实测浓度差的平方为适应度函数,基于遗传算法优化了该适应度函数,实现了风系统突发污染快速溯源,主要有以下三点结论:
(1) 针对某一特定风系统,经位置优化后的传感器数目越多,ξ越小,但当风系统中的传感器数目超过3个时,每增加一个传感器,ξ仅降低约3.5%,考虑到单个传感器成本较高,故该风系统内宜设置3个传感器.
(2) 在反演过程中,传感器监测位置与时间是一对耦合的参数,首个监测到污染物的传感器离污染源越远,ξ越大,同时该误差是随传感器首次监测到污染物的时间增长而增大的.而源位置参数x0的反演相对误差与传感器监测误差无关,却随传感器传回数据时间间隔增大而增大.
(3) 当风系统节点总数在适当范围内时,既能在一定程度上减少遗传算法存储数据量,降低运算负荷,又能兼顾在整个风系统内溯源的目的.
| [1] |
PRICE P N, SOHN M D, GADGIL A J, et al. Protecting buildings from a biological or chemical attack: actions to take before or during a release[R]. Berkely:[s.n.], 2003. http://digital.library.unt.edu/ark:/67531/metadc738959/
|
| [2] |
KOWALSKI W J, BAHNFLETH W P. Immune-building technology and bioterrorism defense, a review of the effectiveness of dilution ventilation, filtration, and ultraviolet germicidal irradiation in mitigating five biological-weapon agents[J]. HPAC Engineering, 2003, 75(1): 57 |
| [3] |
SETTLES G S. Fluid mechanics and homeland security[J]. Annual Review of Fluid Mechanics, 2006, 38: 87 DOI:10.1146/annurev.fluid.38.050304.092111 |
| [4] |
THOMPSON B P, BANK L C. Survey of bioterrorism risk in buildings[J]. Journal of Architectural Engineering, 2008, 14(1): 17 |
| [5] |
蔡浩, 龙惟定, 谭洪卫, 等. 空气传播的生化袭击与建筑环境安全(2):典型生化袭击场景的分析与评价[J]. 暖通空调, 2005, 35(2): 52 CAI Hao, LONG Weiding, TAN Hongwei, et al. Airborne biochemical attacks and building environment security (2): analysis and evaluation of typical scenes of chemical and biological attacks[J]. Journal Heating Ventilating and Airconditioning, 2005, 35(2): 52 |
| [6] |
YANG J R, LI X T. Prediction of transient contaminant dispersion and ventilation performance using the concept of accessibility[J]. Energy and Buildings, 2003, 36(3): 293 |
| [7] |
WANG L Z, DOLS W S. Using CFD capabilities of CONTAM 3.0 for simulating airflow and contaminant transport in and around buildings[J]. Heating Ventilation and Air Conditioning & Refrigerater Research, 2010, 16(6): 749 |
| [8] |
GLOVER N J. Countering chemical and biological terrorism[J]. Civil Engineering, 2002, 72(5): 62 |
| [9] |
ZHANG T, CHEN Q Y. Identification of contaminant sources in enclosed environments by inverse CFD modeling[J]. Indoor Air, 2007, 17(3): 167 DOI:10.1111/ina.2007.17.issue-3 |
| [10] |
ZHANG T, YIN S, WANG S G. An inverse method based on CFD to quantify the temporal release rate of a continuously released pollutant source[J]. Atmospheric Environment, 2013, 77: 62 DOI:10.1016/j.atmosenv.2013.04.057 |
| [11] |
LIU X, ZHAI Z. Prompt tracking of indoor airborne contaminant source location with probability-based inverse multi-zone modeling[J]. Building and Environment, 2009, 44(6): 1135 DOI:10.1016/j.buildenv.2008.08.004 |
| [12] |
LIU X, ZHAI Z. Inverse modeling methods for indoor airborne pollutant tracking: literature review and fundamentals[J]. Indoor Air, 2007, 17(6): 419 DOI:10.1111/ina.2007.17.issue-6 |
| [13] |
SREEDHARAN P, SOHN M D, NAZAROFF W W, et al. Influence of indoor transport and mixing time scales on the performance of sensor systems for characterizing contaminant releases[J]. Atmospheric Environment, 2007, 41: 9530 DOI:10.1016/j.atmosenv.2007.08.039 |
| [14] |
SREEDHARAN P, SOHN M D, NAZAROFF W W, et al. Towards improved characterization of high-risk releases using heterogeneous indoor sensor systems[J]. Building and Environment, 2011, 46: 438 DOI:10.1016/j.buildenv.2010.08.006 |
| [15] |
彭小勇. 大空间建筑突发事件毒气扩散和控制方法的研究[D]. 长沙: 国防科学技术大学, 2007. PENG Xiaoyong. Research of the poison gas diffusion and controlling methods on emergent events in large space buildings[D]. Changsha:National University of Defense Technology, 2007.s http://cdmd.cnki.com.cn/article/cdmd-90002-2008098737.htm |
| [16] |
曾令杰.公共建筑风系统突发污染一维反问题研究[D].上海:同济大学,2016. ZENG Lingjie. Research on one-dimensional inverse problem of sudden contamination through ventilation system in public buildings[D]. Shanghai:Tongji university, 2016. |
| [17] |
GAO Jun, ZENG Lingjie, WU Li, et al. Solution for sudden contamination transport through air duct system: under a puff release[J]. Building and Environment, 2016, 100: 19 DOI:10.1016/j.buildenv.2016.01.024 |
| [18] |
NEUPAUER R M, WILSON J L. Adjoint sensitivity analysis of contaminant concentrations in water distribution systems[J]. Journal of Engineering Mechanics, 2011, 137: 31 DOI:10.1061/(ASCE)EM.1943-7889.0000197 |
| [19] |
PREIS A, Ostfeld A. Contamination source identification in water Systems: a hybrid model trees-linear programming scheme[J]. Journal of Water Resources Planning and Management, 2006, 132(4): 263 DOI:10.1061/(ASCE)0733-9496(2006)132:4(263) |
| [20] |
KOWALSKI W J. Immune building systems technology[M]. New York: The McGraw-Hill Companies Inc, 2003
|
| [21] |
董深, 吕谋, 盛泽斌, 等. 基于遗传算法的供水管网反问题漏失定位[J]. 哈尔滨工业大学学报, 2013, 45(2): 106 DONG Shen, LV Mou, SHENG Zebin, et al. Inverse transient leakage location of water supply network based on genetic algorithm[J]. Journal of Harbin Institute of Technology, 2013, 45(2): 106 DOI:10.11918/j.issn.0367-6234.2013.02.019 |
| [22] |
PRASAD T D, PARK N S. Multiobjective genetic algorithms for design of water distribution networks[J]. Journal of Water Resources Planning and Management, 2004, 130(1): 73 DOI:10.1061/(ASCE)0733-9496(2004)130:1(73) |
 2017, Vol. 45
2017, Vol. 45

