2. 同济大学 道路与交通工程教育部重点实验室, 上海 201804
2. Key Laboratory of Road and Traffic Engineering of the Ministry of Education, Tongji University, Shanghai 201804, China
城市的快速发展给城市道路交通运行带来巨大压力;建设城市快速路系统已成为我国大城市缓解城市中长距离交通压力的重要方式.我国城市快速路系统设计标准缺乏应急车道和紧急停车带设计[1],使得发生在快速路上的交通事件往往容易造成较为严重的交通拥堵;频发的突发交通事件给城市快速路的运行带来了巨大影响.据相关研究表明,2013年上半年上海市中心城快速路系统日均发生92.8起交通事件,半年合计16 869起[2].国外有关数据也表明,突发性事件所造成的拥堵占城市快速路总拥堵的60%以上[3].有效对交通事件引起的偶发性拥堵进行管理是提升城市快速路交通运行效率的重要手段之一.
交通事件持续时间作为定量指标,客观上反映出交通事件对交通运行的影响程度.实时、可靠的交通事件持续时间预测可为交通控制系统、交通诱导系统、出行者服务系统提供有效的指导信息,以便有关管理部门采取必要的交通管理控制措施,诱导驾驶员选择行驶路径,从而提高道路运行效率,并减少交通拥堵所引发的环境污染(汽车尾声和噪声)[4].因此,迫切需要开展基于实时交通数据,结合道路几何特征、事件特征等数据的交通事件持续时间预测模型研究.
目前交通事件持续时间预测模型主要采用生存分析统计模型和数据挖掘模型两大类分析方法.NAM[5]等采用参数风险模型对高速公路交通事件持续时间进行分析;HOJATI[6]等提出参数加速失效模型;杨文臣[7]等将比例风险模型应用于城市快速路交通事件持续时间分析.这类生存分析方法采用参数风险模型、参数加速失效模型或比例风险模型定量分析解释变量对持续时间概率的影响.但该类传统生存分析方法相较于其他分析方法,往往需要依赖于限制性假设(如比例风险假设),并且需要对协变量间的交互作用进行识别[8].另一类交通事件持续时间模型则采用数据挖掘分析方法,主要包括贝叶斯网络模型[9]、贝叶斯网络和非参数回归相结合的模型[10]、神经网络模型[11]和决策树模型[12-13]等.这类模型的优势在于可直接利用数据进行学习,而不需要去了解事件的详细信息.但这类模型同样存在自身的缺陷,如神经网络模型需要大量参数且学习时间较长,决策树模型容易过拟合.随机森林[14]是由BREIMAN提出的一种集成学习算法.随机森林是BAGGING的一个扩展变体,它以决策树为基学习器构建BAGGING集成的基础上,进一步在决策树的训练过程中引入了随机属性选择.随机森林具有很好的抗噪声能力,可以同时应用于回归和分类问题,且无需对变量进行选择.杨超等采用随机森林回归模型对上海市城市快速路交通事件持续时间进行分析[15],结果表明,平均预测误差为6 min,在持续时间7~30 min内的估计精度较高,但是在6 min以内和30 min以上的估计精度较差.
相关研究表明,交通事件持续时间分布不呈正态分布,且往往含有截尾数据,因此适合正态分布的传统多元回归分析方法并不适用[16].ISHWARAN提出的随机生存森林[8],是随机森林在生存分析上的延伸和拓展,主要应用于右删失型的生存数据.随机生存森林既发挥了随机森林和生存分析的优势,同时也克服了传统生存分析需要依赖于强制性假设的缺陷.随机生存森林目前主要应用在医学[17]、经济学[18],本文首次尝试在交通事件持续时间预测领域应用随机生存森林.
本文基于2014年4月上海快速路的交通事件数据,结合道路几何线形数据、交通运行、天气状况等内容组成的原始样本数据,将其中80%的数据作为训练数据集,20%的数据作为测试数据集.基于训练数据集分别运用随机森林的方法和随机生存森林的方法对事件持续时间进行建模,分析显著影响因素.最后基于测试数据集进行模型精度检验,并以平均绝对误差(mean absolute error,MAE)、均方误差(mean squared error,MSE)、标准化平均绝对方差(normalized mean square error,NMSE)这三个典型的评价指标对两个模型预测精度进行校验和对比.
1 数据描述研究数据包括2014年4月上海市城市快速路事件数据、道路几何线形数据、线圈检测交通数据(事件发生前10 min车道流量总和、平均车速)、天气状况.基于研究数据,将事件发生路段检测线圈的编号,与道路几何线形数据属性中的路段编号及线圈检测交通数据的编号相对应,并剔除重复、缺失和异常的数据,生成1 931组完整交通事件数据集.每组数据包含交通事件持续时间和可能影响事件持续时间的事件特征、环境特征、交通状况特征及道路特征4类影响因素.为了提高交通事件持续时间预测的精度,首先对记录信息中的分类数据事件类型、事件发生地点、事件发生时间、是否通行高峰、匝道类型、有无瓶颈、是否弯道、是否隧道、是否限速标志等变量进行离散化处理,将其转化为因子变量,统计信息见表 1.
| 下载CSV 表 1 交通事件持续时间影响因素描述统计 Tab.1 Descriptive variables of traffic incident duration |
通过随机抽样的方法,将1 545组数据(占样本总量约为80%)用于标定持续时间预测模型,386组数据(占样本总量20%)用于检验模型的预测结果,两组数据的数据特征基本一致,见表 2.
| 下载CSV 表 2 交通事件持续时间的数据描述统计 Tab.2 Descriptive statistics of traffic incident duration |
本文分别运用随机森林和随机生存森林的方法对交通事件持续时间进行建模.
2.1 随机森林随机森林[14, 19]是由BREIMAN于2001年提出的一种机器学习算法.首先,随机森林是利用Bootstrap重抽样方法从原始训练集样本中抽取多个样本.其次,对每个Bootstrap样本进行决策树建模,然后组合多棵决策树的预测,通过投票得出最终的预测结果.其中Bootstrap重抽样方法中每个样本未被抽取的概率为
| $ P = {\left( {1 - \frac{1}{N}} \right)^N} $ | (1) |
当N→∞时,有
| $ \mathop {\lim }\limits_{N \to \infty } P = \mathop {\lim }\limits_{N \to \infty } {\text{ }}{\left( {1 - {\text{ }}\frac{1}{N}} \right)^N} = {{\text{e}}^{ - 1}} \approx 0.368 $ | (2) |
式中:P为样本未被抽取的概率;N为原始训练集中样本的个数.
因此在原始训练集中约有37%的样本不会出现在Bootstrap样本中,这些数据称为袋外数据(out-of-bag,OOB).随机森林以袋外数据来估计模型的性能,称为OOB估计.对于随机森林中的每一棵决策树,都可以得到一个OOB误差估计,将森林中所有决策树的OOB误差估计取平均,即可得到随机森林的泛化误差.
大量理论和实证研究都证明了随机森林具有很高的预测准确率,对异常值和噪声具有很好的容忍度,且不容易出现过拟合和局部收敛问题.
2.2 随机生存森林随机生存森林[8]由ISHWARAN提出,是随机森林的衍生.随机生存森林与经典随机森林相似,通过Bootstrap重抽样方法从原始训练集中抽取多个样本,并对每个样本建立生存树,最后综合这些生存树的预测结果.
(1) 从训练集中抽取出Bootstrap样本集,并对每个样本集都建立一个二元递归生存树.
(2) 在每棵生存树生长时,每个结点随机选择P个候选变量进行分裂,同时根据生存分裂规则,选择使子结点生存值差异最大的分裂变量.
(3) 让生存树尽可能的生长,直到每个终结点的样本数不小于最小的默认值.
(4) 计算每棵树的生存函数,森林的组合值就是平均生存函数.计算生存函数时采用KM(Kaplan-Meier)估计法.
随机生存森林每棵树的生存函数是通过终结点KM风险估计获得的.对任意一个终结点h,定义ti, h为第i个个体在结点h的死亡时间,记di, h和Yi, h分别为在时间ti, h结束的个体数量和期望数量.终结点h的累积生存函数
| $ {{\hat H}_h}\left( t \right) = \sum\limits_{{t_{i,h}}} {} \leqslant t\frac{{{d_{i,h}}}}{{{Y_{i,h}}}} $ | (3) |
若树中有多个终结点,那么该树就有多个KM风险估计.终结点h在协变量xi的作用下,对应的单棵树的生存函数为
| $ \hat H(t|{x_i}) = {{\hat H}_h}\left( t \right),{\text{if}}\;{x_i} \in h $ | (4) |
为得到随机生存森林的生存函数He*(t|xi),需对Ntree棵树进行平均,即
| $ H_{\text{e}}^*(t|{x_i}) = \frac{1}{{{N_{{\text{tree}}}}}}\sum\limits_{b = 1}^{{N_{{\text{tree}}}}} {{{\hat H}_b}\left( {t|{x_i}} \right)} $ | (5) |
式中:
构建随机森林模型的关键问题是如何通过OOB估计来选择每棵决策树分裂结点所需的最优特征变量的数目和决策树数目.随机生存森林作为随机森林的衍生模型,同样需要通过OOB估计来选择每棵生存树分裂结点所需的特征变量的数目、生存树数目以及结点的分裂规则.
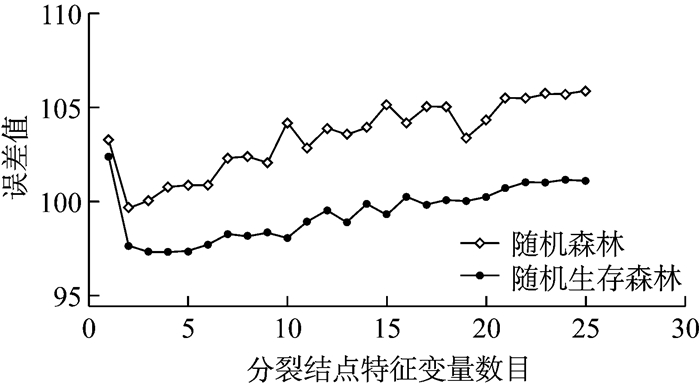
首先对随机森林中的决策树和随机生存森林中的生存树的分裂结点的特征变量数目进行选择,如图 1所示,通过计算可以得到当随机森林中决策树分裂结点的特征变量数目为2时,模型误差变化达到最小,确定随机森林中每棵决策树分裂结点特征变量数目为2.同理,可以确定随机生存森林中每棵生存树分裂结点的数目为4.
|
图 1 分裂结点特征变量数目分析 Fig.1 Analysis of attributes number about the split node |
其次,对随机森林中决策树和随机生存森林中生存树的数目进行选择,如图 2所示,随着随机森林中决策树数目的递增,OOB误差逐渐降低,并于950后趋于稳定.因此,可以确定随机森林中决策树数目为950.同理,可以确定随机生存森林中生存数数目为900.

|
图 2 决策树/生存树数目分析 Fig.2 Number analysis of decision tree/survival tree |
对1 545组交通事件数据进行分析,建立随机森林和随机生存森林模型,并分析其显著影响因素,最后以386组交通事件数据对两个模型预测精度进行检验并对比结果.
3.1 模型分析结果 3.1.1 随机森林模型分析结果随机森林自身提供了两种特征选择的方法:平均精确度减少(mean decrease accuracy)和平均节点不纯度减少(mean decrease in node impurity).由于基于平均精确度减少的方法比基于节点不纯度减少的方法具有更好的非偏倚性能,因此多采用基于平均精确度减少的方法进行变量筛选[20-22].采用基于OOB误差的平均精确度减少方法,具体描述如下:首先对于森林中每棵决策树用袋外数据进行预测,并记录每棵树t的OOB误差;然后随机打乱袋外样本数据中变量Xj的值,重新测试每棵树t的OOB误差;最后计算两次测试的OOB误差的差值的平均值;并对两次测试OOB误差的差值的标准差进行规范化.该方法所得到的值越大,则表示其特征变量重要性越高.
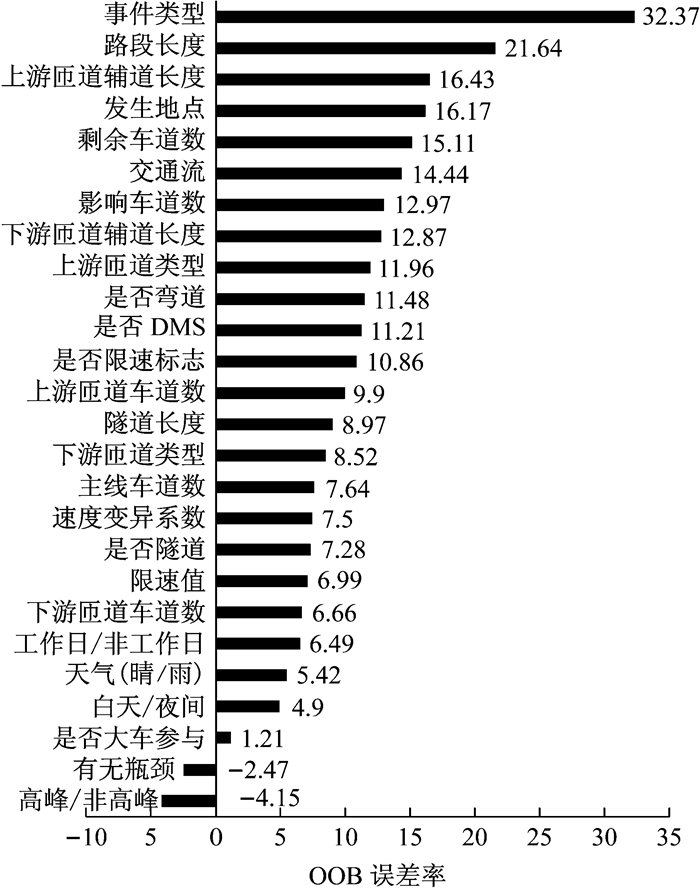
快速路交通事件持续时间随机森林模型变量重要性结果如图 3所示.从图中可以看到,事件类型、路段长度、事件发生地点、影响车道数、剩余车道数、交通流总量及上下游匝道辅道长度对模型的预测结果起到关键作用.是否高峰以及有无瓶颈对模型的预测结果的影响较小.
|
图 3 随机森林特征变量重要性排序(平均精确度减少) Fig.3 Variable importance of random forests by mean decrease accuracy |
随机生存森林提供两种变量筛选方法[23],第一种是通过计算OOB误差率对变量的重要性(VIMP)进行筛选.VIMP值越大表明其预测能力越强.第二种通过树的最小深度变量筛选方法,即计算从树根节点到最近变量的最大子树根节点的距离,称为变量的最小深度.变量的最小深度越小,预测性越强.
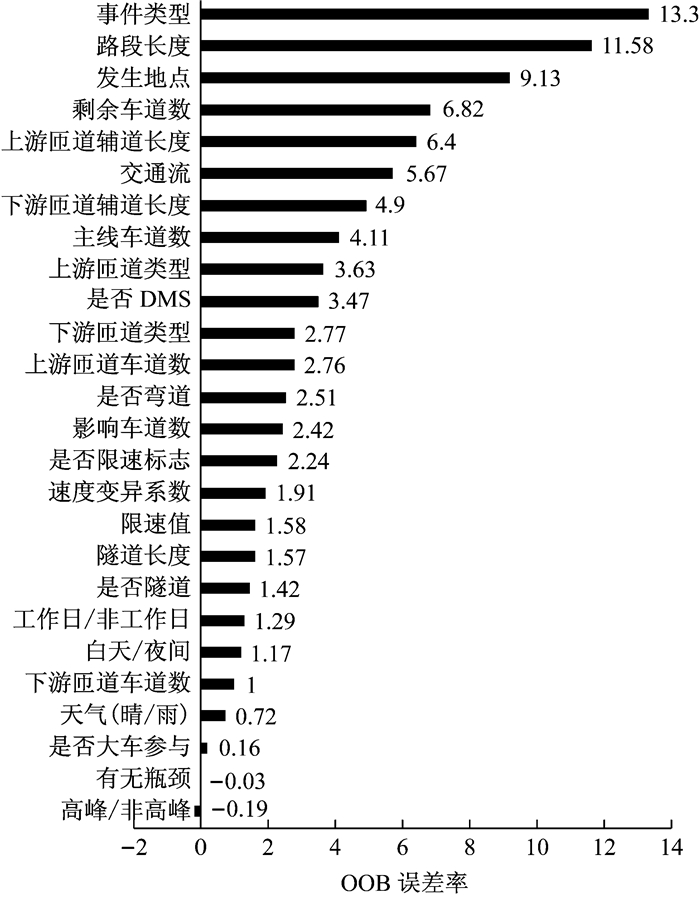
本文选择VIMP的方法进行变量筛选,如图 4所示.事件类型、路段长度、发生地点、剩余车道数、路段长度、交通流量总和以及上下游匝道辅道长度对模型的预测结果具有显著影响.
|
图 4 随机生存森林特征变量重要性排序(VIMP) Fig.4 Variables importance of random survival forests by VIMP |
随机森林变量筛选方法平均精确度减少与随机生存森林变量筛选方法VIMP均依据OOB误差率对变量的重要性进行排序,排序结果如图 3和图 4所示.通过Wilcoxon秩和检验的方法检验随机森林和随机生存森林变量重要性排序是否存在显著差异,得到其P值为0.503,大于显著水平0.05,因此可以认为两个模型变量重要性排序无显著差异.
从图 3和图 4可得出,随机森林和随机生存森林前6个显著变量均为事件类型、路段长度、发生地点、剩余车道数、交通流以及上游匝道辅道长度.其中,事件类型对持续时间的影响最为显著.该结论与HAJATI[6]、杨超[10, 15]及姬杨蓓蓓[13]等对显著变量分析的结论基本一致.其中,HAJATI[6]采用参数加速失效模型对高速路交通事件持续时间进行分析,得出事件类型、事件严重程度、发生地点、发生时间等对持续时间有显著影响.杨超[10, 15]分别采用贝叶斯网络和随机森林的方法对上海市快速路交通事件数据进行分析,得出对持续时间显著影响的3个因素分别为事件类型、影响车道数和交通状态,其中事件类型是影响交通事件持续时间的首要因素.姬杨蓓蓓[13]采用贝叶斯决策树的方法对上海市快速路交通事件持续时间进行分析,得出事件类型为决策树中的第一层测试属性.
3.3 模型预测结果分析模型预测结果分别以平均绝对误差(MAE)、均方误差(MSE)、标准化平均绝对方差(NMSE)作为主要评价指标,其指标计算公式如下:
| $ {\delta _{{\text{MAE}}}} = \frac{1}{n}\sum\limits_{i = 1}^n {|{p_i} - {y_i}|} $ | (6) |
| $ {\delta _{{\text{MSE}}}} = \frac{1}{n}\sum\limits_{i = 1}^n {|{p_i} - {y_i}{|^2}} $ | (7) |
| $ {\delta _{{\text{NMSE}}}} = \frac{{\frac{1}{n}\sum\limits_{i = 1}^n {|{p_i} - {y_i}{|^2}} }}{{\frac{1}{n}\sum\limits_{i = 1}^n {{{\left| {\frac{1}{n}\sum\limits_{i = 1}^n {{y_i}} - {y_i}} \right|}^2}} }} $ | (8) |
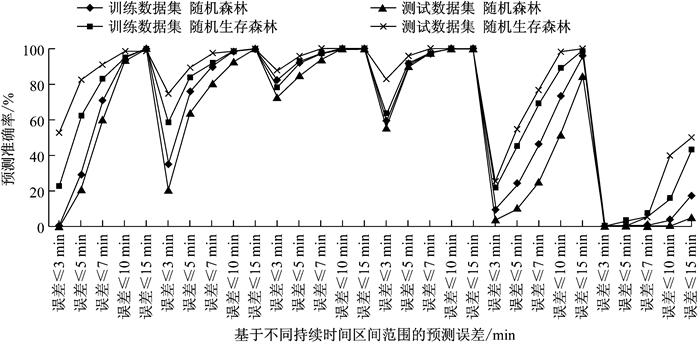
式中:pi为预测值;yi为真实值.两个模型的检验结果,见表 3.同时在交通事件持续时间的不同区间范围内分别以预测误差小于3 min、5 min、7 min、10 min和15 min为评价标准,见图 5.
| 下载CSV 表 3 预测模型检验结果 Tab.3 Test results of the forecast model |
|
图 5 基于不同持续时间区间范围的模型预测结果分析 Fig.5 Test result of forest model based on different ranges of duration |
结果表明,随机生存森林模型的泛化能力比随机森林模型更强.从图 5可以看出,相对于随机森林,随机生存森林的预测准确率明显提高.基于测试数据集,随机生存森林模型对于事件持续时间为3~15 min的事件预测准确率较高.对于事件持续时间在3 min以内的交通事件来说,随机生存森林模型预测结果误差小于3 min的准确率占测试样本容量的52.75%,误差结果小于5 min的准确率占测试样本容量的82.42%,虽然模型在该范围的准确率较低,但由于持续时间较短,对交通所造成的影响也很小,因此几乎可以忽略不计.对于持续时间在15~30 min的交通事件,随机生存森林模型预测准确率较低,预测结果误差小于5 min的准确率占测试样本容量的55.00%,但预测结果误差小于10 min的准确率占测试样本容量的98.33%.对于持续时间在30 min以上的交通事件,由于其总样本量仅为5.7%,未来在获取更多样本数据的条件下可以进一步优化模型.
同时,从表 3可以看出,随机生存森林模型的3个评价指标平均绝对误差、均方误差、标准化平均绝对方差分别较随机森林模型提升了47.70%,72.24%和72.09%.
4 结论本文利用上海快速路交通事件数据进行分析,采用随机生存森林模型构建快速路交通事件持续时间预测模型.随机生存森林模型作为随机森林模型的衍生模型,同时结合随机森林和生存分析的优点,具有较强的泛化能力,是首次应用于交通事件持续时间预测问题.
通过对交通事件持续时间的研究,影响快速路交通事件持续时间的显著变量主要有:事件类型、路段长度、发生地点、剩余车道数、交通流量总和、以及上下匝道长度等,其中,事件类型对持续时间的影响最为显著.该结论与HAJATI[6]、杨超[10, 15]及姬杨蓓蓓[13]等对显著变量分析的结论基本一致.同时,通过研究发现,实时的交通流量总和对持续时间的影响较大,因此交通管理部门可通过实时观测交通运行状况,及时诱导驾驶员行为,缩短交通事件持续时间.
基于验证数据的预测结果表明,随机生存森林模型平均绝对误差为3.53,均方误差为27.15,标准化平均绝对方差为0.24,3个评价指标均显著优于随机森林模型.采用随机生存森林模型可提高快速路交通事件持续时间预测精度,为交通管理者的管理决策提供重要的指导,降低交通事件引发的拥堵时间,提高快速路运行效率与安全性.
由于随机生存森林是个很难解释的黑盒子[17],因此下一步将基于本文研究,对显著变量的影响方向及作用力度进行深度分析,以求对交通运行管理提供可靠的决策指导.
| [1] |
北京市市政工程设计研究总院. 城市快速路设计规程[M]. 北京: 中华人民共和国住房和城乡建设部, 2009 Beijing General Municipal Engineering Design and Research Institute. Specification for design of urban expressway[M]. Beijing: Ministry of Housing and Urban-Rural Development of the People's Republic of China, 2009 |
| [2] |
孙为珊. 上海市快速路常发性拥堵原因及改善建议[J]. 中国市政工程, 2014(3): 9 SUN Weishan. Cause and suggestion of frequency congestion in shanghai expressway[J]. China Municipal Engineering, 2014(3): 9 |
| [3] |
US Department of Transportation. Traffic incident management handbook[M]. Washington D C: Federal Highway Administration, 2010
|
| [4] |
姬杨蓓蓓, 张小宁, 孙立军. 交通事件持续时间预测方法综述[J]. 公路工程, 2008, 33(3): 72 JIYANG Beibei, ZHANG Xiaoning, SUN Lijun. A review of the traffic incident duration prediction methods[J]. Highway Engineering, 2008, 33(3): 72 |
| [5] |
NAM D, MANNERING F. An exploratory hazard-based analysis of highway incident duration[J]. Transportation Research Part A, 2008, 34(2): 85 |
| [6] |
HOJATI A T, FERREIR L, WASHINGTON S, et al. Hazard based models for freeway traffic incident duration[J]. Accident Analysis and Prevention, 2013, 52(12): 171 |
| [7] |
杨文臣, 张轮, 施奕骋, 等. 城市快速路交事件持续时间生存分析[J]. 交通运输系统工程与信息, 2014, 14(5): 168 YANG Wencheng, ZHANG Lun, SHI Yicheng, et al. Survival analysis of traffic incident duration for urban expressways[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14(5): 168 |
| [8] |
ISHWARAN H, KOGALUR U B, BLACKSTONE E H, et al. Random survival forests[J]. The Annals of Applied Statistics, 2008, 2(3): 841 DOI:10.1214/08-AOAS169 |
| [9] |
OZBAY K, NOYAN N. Estimation of incident clearance times using bayesian networks approach[J]. Accident Analysis and Prevention, 2006, 38(3): 542 DOI:10.1016/j.aap.2005.11.012 |
| [10] |
杨超, 汪超. 快速路交通事件持续时间预测模型[J]. 同济大学学报(自然科学版), 2013, 41(7): 1015 YANG Chao, WANG Chao. Traffic incident duration forecast model of expressway[J]. Journal of Tongji University (Natural Science), 2013, 41(7): 1015 |
| [11] |
VLAHOGINANI E I, KARLAFTIS M G. Fuzzy-entropy neural network freeway incident duration modeling with single and competing uncertainties[J]. Computer-Aided Civil and Infrastructure Engineering, 2013, 28(6): 420 DOI:10.1111/mice.2013.28.issue-6 |
| [12] |
GARIB A, RADIAN A E, AI-DEEK H. Estimating magnitude and duration of incident delays[J]. Journal of Transportation Engineering, 1997, 123(6): 459 DOI:10.1061/(ASCE)0733-947X(1997)123:6(459) |
| [13] |
姬杨蓓蓓, 张小宁, 孙立军. 基于贝叶斯决策树的交通事件持续时间预测[J]. 同济大学学报(自然科学版), 2008, 36(3): 319 JIYANG Beibei, ZHANG Xiaoning, SUN Lijun. Trafic incident duration prediction grounded on bayesian decision method-based tree algorithm[J]. Journal of Tongji University (Natural Science), 2008, 36(3): 319 |
| [14] |
SCHAPIRE R E. Random forests[J]. Machine Learning, 2001, 45(1): 5 DOI:10.1023/A:1010933404324 |
| [15] |
杨超, 李海霞. 基于随机森林的城市快速路交通事件持续时间估计[J]. 交通信息与安全, 2015, 33(6): 72 YANG Chao, LI Haixia. Estimation of the duration of the incidents at urban expressways using random forest[J]. Journal of Transport Information and Safety, 2015, 33(6): 72 |
| [16] |
康国祥, 方守恩. COX Regression模型在交通事件持续时间研究中的应用[J]. 交通信息与安全, 2011, 29(2): 104 KANG Guoxiang, FANG Shouen. Application of cox regression model in traffic incident duration[J]. Journal of Transport Information and Safety, 2011, 29(2): 104 |
| [17] |
HSICH E, GORODESKI E Z, BLACKSTONE E H. Dentifying important risk factors for survival in patient With systolic heart failure using random survival forests[J]. Circulation: Cardiovascular Quality and Outcomes, 2011, 4(1): 39 DOI:10.1161/CIRCOUTCOMES.110.939371 |
| [18] |
SILVIA F D F. Random survival forest models for SME credit risk measurement[J]. Methodology and Computing in Applied Probability, 2009, 11(1): 29 DOI:10.1007/s11009-008-9078-2 |
| [19] |
方匡南, 吴见彬, 朱建平, 等. 随机森林方法研究综述[J]. 统计与信息论坛, 2011, 26(3): 32 FANG Kuangnan, WU Janbin, ZHU Jianping, et al. Research on random forest[J]. Statistics and Information Forum, 2011, 26(3): 32 |
| [20] |
CALLE M L, URREA V. Letter to the editor: stability of random forest importance measures[J]. Briefings in Bioinformatics, 2011, 12(1): 86 DOI:10.1093/bib/bbq011 |
| [21] |
STROBL C, BOULESTEIX A L, ZEILEIS A, et al. Bias in random forest variable importance measures: illustrations, sources and a solution[J]. BMC Bioinformatics, 2007, 8(1): 25 DOI:10.1186/1471-2105-8-25 |
| [22] |
NICODEMUS K K. Letter to the editor: on the stability and ranking of predictors from random forest variable importance measures[J]. Briefings in Bioinformatics, 2011, 12(4): 369 DOI:10.1093/bib/bbr016 |
| [23] |
ISHWARAN H, KOGALUR U B, GORODESKI E Z, et al. High-dimensional variable selection for survival data[J]. American Statistical Association, 2010, 105(489): 205 DOI:10.1198/jasa.2009.tm08622 |
 2017, Vol. 45
2017, Vol. 45

