2. 重庆交通职业学院, 重庆 402247;
3. 山东省潍坊市人民医院, 山东 潍坊 261599;
4. 山东省建筑科学研究院, 山东 济南 250031
2. Chongqing Vocational College of Transportation, Chongqing 402247, China;
3. Weifang People's Hospital of Shandong Province, Weifang 261599, China;
4. Shandong Provincial Academy of Building Research, Ji'nan 250031, China
根据欧洲钢结构设计规范Eurocode3[1-2],高强度结构钢(简称高强钢)是指名义屈服强度大于等于420 MPa的结构用钢.同普通结构钢相比,采用高强钢可有效提高铁矿石资源利用率,减轻构件自重,创造更多净使用空间,因此近10年来,高强钢已逐渐应用于世界各地的重要结构、标志性建筑以及大跨度体育场馆中,如我国的国家体育场、凤凰国际传媒中心以及国外的纽约自由塔、索尼中心等.目前,学术界针对高强钢结构在常温下的力学性能已取得一些初步研究成果,包括高强钢材料以及高强钢构件和节点的力学性能等[3].
美国9.11恐怖事件后,人们对WTC1、WTC2以及WTC7的倒塌分析结果说明[4],正是由于火灾作用下该结构的梁柱节点失效,导致柱失去侧向支撑而发生屈曲破坏,最终引起该结构的连续坍塌.因此,火灾对建筑钢结构节点的影响早已成为钢结构领域的研究热点.2008年,SHI等[5]通过火灾试验,研究了节点尺寸以及螺栓数量对带加劲肋端板连接节点力学性能的影响,并采用ANSYS对试验结果进行验证.2011年,YU等[6]对平齐式端板连接节点进行了一系列火灾试验,探究节点在弯矩和轴力共同作用下的抗火性能,并采用ABAQUS进行数值模拟,发现试验中端板小裂缝对节点承载力没有影响.2014年,王宇等[7]采用足尺试验对端板连接节点的关键部位和失效荷载进行研究,并利用ANSYS对此类节点不同工况下受力性能进行有限元分析.同年,高义奇等[8]对平齐端板式节点和腹板双角钢节点进行恒载升温试验,并分析两类节点在高温以及拉剪共同作用下的变形发展和破坏规律.随后,高义奇等[9]采用通用有限元软件ABAQUS建立平齐端板节点的三维实体分析模型,并考虑材料非线性和节点大变形等影响,较准确地模拟出此类节点的受力过程.可以看出,对节点火灾下力学性能采用试验研究并结合有限元模拟分析的方法越来越受到各国学者的青睐.
目前,国内外对高强钢的研究主要集中于常温下材料性能以及梁、柱等构件的受力性能,对于高强钢结构节点力学性能的研究非常有限.COELHO和BIJLAARD[10]的研究表明,常温下S690高强钢端板连接节点具有一定的转动能力,且满足Eurocode3对节点承载力的要求.孙飞飞等[11]对Q690高强钢端板连接节点的试验结果表明,Eurocode3对节点承载力的预测公式适用于高强钢节点,但转动刚度与破坏模式的预测方法不适用于高强钢节点.然而,国内外关于高强钢端板连接节点在火灾作用下的力学性能研究尚未有文献报道.
为研究高强钢端板连接节点在火灾下的力学性能,对7个平齐式端板连接节点在550℃的火灾高温下进行足尺试验研究.为对比分析,同时对上述7个节点试件在常温下的相应受力性能进行试验研究.基于试验研究结果,本文采用通用有限元软件ABAQUS建立端板连接节点火灾下和常温下的有限元模型,并详细介绍建模和分析过程.通过有限元模拟揭示了火灾下以及常温下高强钢端板连接节点的力学性能,如节点的弯矩转角关系曲线、破坏模式以及端板屈服线模式等,并将有限元结果同试验结果进行对比分析,以验证有限元模型的准确性.
1 试验概况 1.1 节点试件节点试件依据Eurocode3:Part1-8[2]设计,如图 1所示.高强钢端板材料为S690和S960,普通钢端板材料为Q235和Q345,其中相同材质端板又分两种厚度,梁和柱等构件采用Q345,具体详见表 1.

|
图 1 端板连接节点试件尺寸(单位:mm) Fig.1 Dimension of endplate connection specimen(Unit:mm) |
| 下载CSV 表 1 试件概括 Tab.1 Test specimens and fire test conditions |
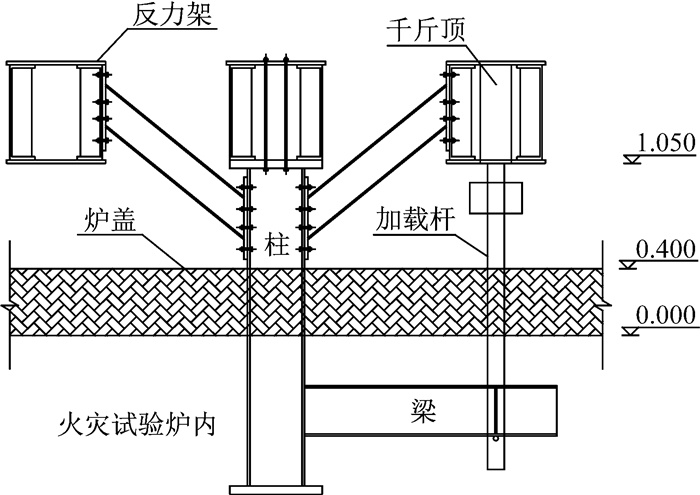
试验研究分为常温试验和火灾试验两部分,均在同济大学土木工程防灾国家重点实验室进行.其中,火灾试验在图 2所示的火灾试验炉中进行.结合已有试验设备,考虑到火灾条件下对梁施加拉力远比施加压力稳定,故将梁柱节点试件整体倒转,以方便从炉外施加荷载.火灾试验过程中,试件在炉盖以下部分受火,而炉盖之上部分则处于常温环境,如图 3所示.

|
图 2 火灾试验炉 Fig.2 Fire test furnace |
|
图 3 火灾试验装置(单位:m) Fig.3 Fire test set-up(Unit:m) |
试件安装完毕后,加载设备和数据采集仪器经调试校准后,在常温下对节点试件进行预加载,预加载没有问题后,进行火灾试验.本试验采用恒温加载的试验方法,即试件以恒定速率升至目标火灾温度550 ℃,然后在该温度下对梁端施加荷载直到试件破坏.升温速率取10 ℃·min-1,该值同未保护的建筑结构在真实火灾作用下的升温速度相当.加载期间采用位移控制,速率为10 mm·min-1.
试验得到高强钢端板连接节点在火灾下的受力性能以及失效机理,并将试验结果同现行欧洲钢结构设计规范Eurocode3中相应条文进行对比分析,具体详见文献[12].
2 有限元模拟 2.1 有限元模型端板连接节点有限元模型的几何特性与节点试件相同.由于节点几何尺寸、荷载、温度分布以及边界条件等均对称,因此对节点试件的一半进行建模分析以缩短计算时间.有限元模型部件及装配件如图 4所示.

|
图 4 有限元模型 Fig.4 FE model |
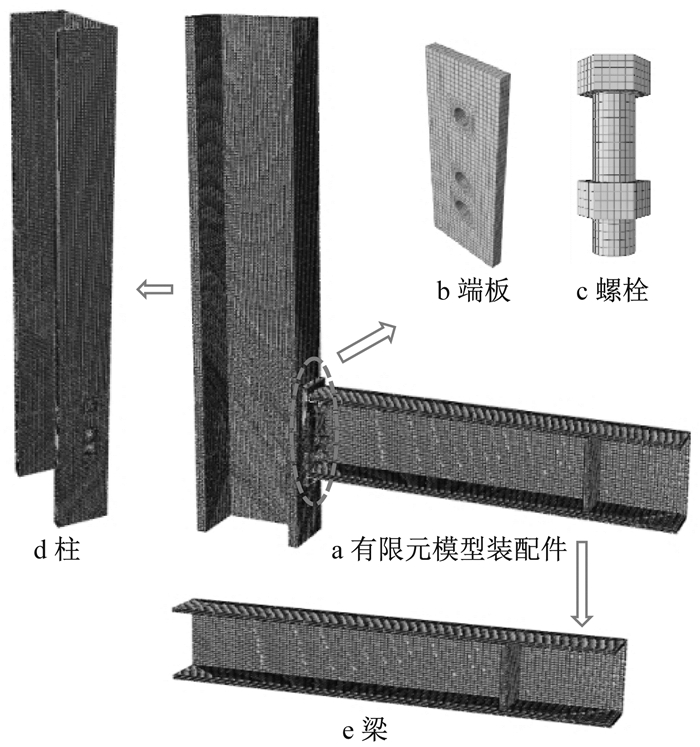
节点有限元模型包括7组面面接触关系和7组绑定约束并考虑材料非线性效应,因此,网格划分应足够精细,如图 5所示.端板螺栓孔附近往往是材料屈服最先发生的地方,故在此区域细化网格以得到准确的应力分布情况,如图 5c所示.
|
图 5 有限元模型网格划分 Fig.5 Mesh generation of FE model |
ABAQUS具有丰富的单元库,如6面体单元、壳单元、接触单元以及梁单元等,在三维有限元模型中,通常选择六面体单元.Bursi和Jaspart[13-14]比较了3种8节点6面体单元.
(1) C3D8(8节点6面体线性完全积分单元):具有8个高斯积分点,连续积分结果较为准确,但当结构受力由弯矩控制时,采用线性完全积分单元可能会出现剪切自锁问题.
(2) C3D8R(8节点6面体线性缩减积分单元):具有1个高斯积分点,虽然在弯矩作用下可避免剪切自锁效应,但应力刚度矩阵的阶数缺乏会造成假性奇异(沙漏)模型,使计算结果不精确.
(3) C3D8I(8节点6面体线性非协调模式单元):具有8个高斯积分点以及13个额外的自由度,在分析由弯矩主导的问题时,额外自由度可减少常规位移单元引起的附属剪切应力[15],此外,这些额外自由度可消除弯矩作用下泊松效应引起的假性硬化.在常规位移单元中,弯曲产生的沿各应力主向的应力通常按线性规律变化,过大估计刚度会使应力失真,而非协调模式可避免上述情况发生.
通过对比上述3种6面体单元可知,当结构受力由弯矩控制时,无论针对线性分析还是非线性分析,采用C3D8I单元所得计算结果均很精确[13],因此本文有限元模型采用此种单元.
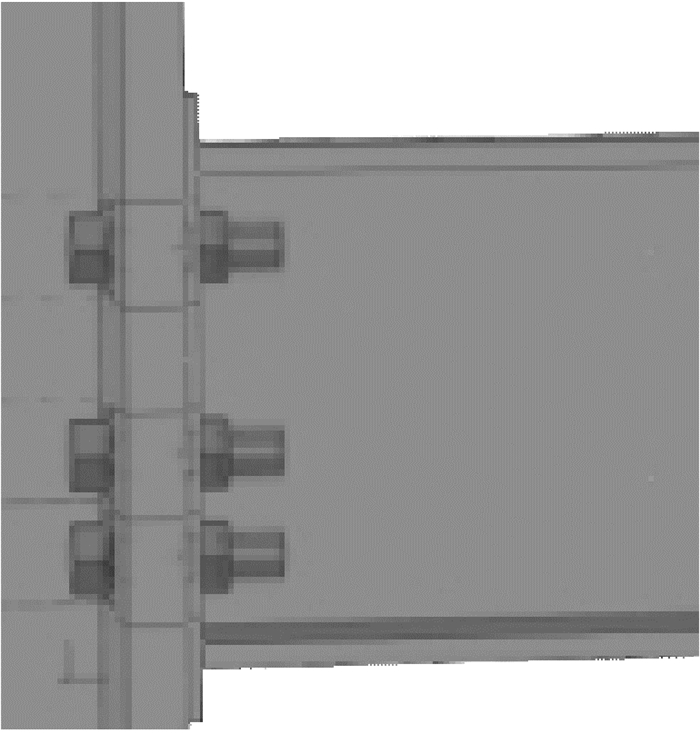
2.3 接触定义和分析步设置有限元模型中的接触关系包括螺栓柱翼缘、柱翼缘端板、端板螺母以及螺栓杆螺栓孔,如图 6所示,其中,刚度较大的接触面为接触主面,刚度较小的接触面为接触从面.螺栓杆与螺母之间采用绑定约束,如图 7所示.所有接触关系的接触属性均为小滑移以准确传递荷载,摩擦系数取0.44.

|
图 6 有限元模型接触关系 Fig.6 Contact pairs in FE model |
|
图 7 螺栓与螺母的绑定约束 Fig.7 Tie constraints of bolts and nuts |
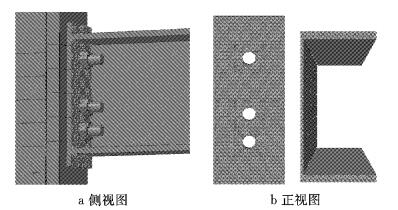
为解决接触分析中的收敛问题,整个计算过程分为5个分析步.第1步,临时约束螺栓以及端板的所有自由度,然后对螺栓施加10N的预紧力,模型温度场设置为20 ℃;第2步,释放螺栓和端板的所有自由度;第3步,固定螺栓长度;第4步,将温度场设定为550 ℃(常温有限元分析过程温度场保持不变);第5步,在梁端布有加劲肋的加载点处施加等效竖向荷载.其中,前3个分析步可保证接触关系平稳建立,从而有效减少计算损耗并避免分析误差.此外,有限元模型中梁和端板之间的焊缝通过约束绑定模拟,而未对焊缝实体建模以简化有限元模型,如图 8所示.
|
图 8 端板与梁间的绑定约束 Fig.8 Tie constraint between endplate and beam |
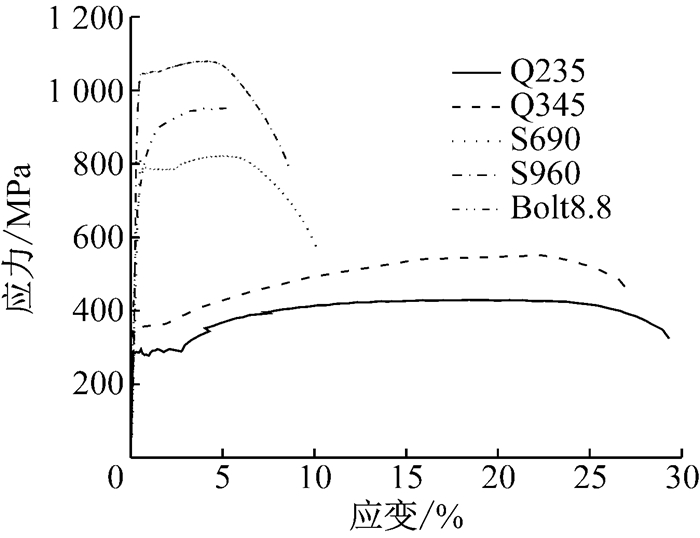
普通钢(Q235和Q345) 的常温力学性能通过拉伸试验得到,火灾下力学性能依据Eurocode3:Part1-2[1]中钢材高温模型;8.8级螺栓在常温下以及高温下的力学性能采用Sheffield大学的试验研究成果[16-19];高强钢S690和S960在常温下以及火灾下力学性能采用文献[20-21]的试验研究成果.常温下高强钢强度指标及其在火灾高温550℃下的降低系数如表 2所示,常温下螺栓以及不同试验用钢的应力应变关系曲线如图 9所示.
| 下载CSV 表 2 高强钢S690和S960的屈服强度和极限强度及其火灾高温550 ℃下的降低系数 Tab.2 Yield and ultimate strengths of S690 and S960 at ambient temperature and their reduction factors at 550 ℃ |
|
图 9 常温下各种材料应力应变关系曲线 Fig.9 Stress-strain curves of various materials at ambient temperature |
ABAQUS中有限元模型材料属性通过材料的真实应力σtrue以及真实塑性应变εpl确定,计算公式如下:
| $ {\sigma _{{\text{true}}}} = {\sigma _{{\text{eng}}}}(1 + {\varepsilon _{{\text{eng}}}}) $ | (1) |
| $ {\varepsilon _{{\text{pl}}}} = {\varepsilon _{{\text{true}}}} - \frac{{{\sigma _{{\text{true}}}}}}{E} $ | (2) |
式中:σtrue是材料的真实应力;σeng是材料的工程应力;εeng是材料的工程应变;εpl是材料的真实塑性应变;εtrue是材料的真实应变;E是材料的弹性模量.
2.5 基于变形的失效准则有限元模型中T-stub的变形能力由材料极限应变εu控制,当节点任一组件受力达到材料极限应变εu,即可认为节点发生破坏.
在端板连接节点中,螺栓受力分承受拉力和受拉弯作用两种情况,螺栓危险截面应变分布如图 10所示.受拉螺栓的破坏准则为ε11, av, b=εu, b,其中ε11, av, b是螺栓平均主应变;εu, b是螺栓的极限应变.而在T-stub中,螺栓往往受到轴力和弯矩的共同作用,因此螺栓危险截面应变分布由对称变为不对称,且螺栓杆轴向不再是应力主向.COELHO等[22-23]提出一种拉弯螺栓的破坏准则:类似于受拉螺栓的破坏准则,当拉弯螺栓平均主应变ε11, av, b达到螺栓极限应变εu, b即认为螺栓破坏.本文有限元模型采用上述拉弯螺栓破坏准则.
3 有限元模型验证 3.1 常温下节点变形将常温下所有节点试件的最终变形状态同有限元模型进行对比,图 11和图 12分别示出节点2-3A(S690 15mm)节点域和组件的对比情况,可以看出,试验结果和有限元模型吻合程度很好.图 12c揭示出螺栓破坏发生的位置.其余节点可得到类似的结果,详见文献[24].

|
图 11 常温下节点2-3 A (S690 15 mm)变形终态对比 Fig.11 Comparison on final deformation state of connection 2-3 A (S690 15 mm) at ambient temperature |

|
图 12 常温下节点2-3 A (S690 15 mm)组件变形终态对比 Fig.12 Comparison on components of 2-3 A (S690 15 mm) after failure at ambient temperature |
通过有限元模拟的等效塑性应变(PEEQ)云图可确定材料是否屈服.以节点2-4A(S960 12 mm)为例,图 13显示有限元模拟所得的等效塑性应变(PEEQ)与试验结果吻合度很高.类似地,常温下其余节点可得到相同结论.

|
图 13 常温下节点2-4 A (S960 12 mm)的试验变形与数值模拟的等效塑性应变对比 Fig.13 Experimental final deformation and numerically predicted PEEQ of 2-4 A (S960 12 mm) at ambient temperature |
将火灾高温550 ℃下所有节点试件的最终变形状态同有限元模型进行对比,图 14和图 15分别示出节点2-3E(S690 15 mm)节点域和组件的对比情况,可以看出,试验结果同有限元模型吻合度很好,其余节点可得到类似的结果,详见文献[22].同样地,图 15c显示出螺栓破坏发生的位置.在试验研究中,首排受拉螺栓破坏后,第二排受拉螺栓可经历较大弯曲变形直至发生破坏;在有限元模型中,第一个节点组件(首排受拉螺栓)发生破坏时有限元分析随即停止,因此,有限元模型不能模拟首排受拉螺栓破坏后至第二排受拉螺栓破坏的过程以及其余组件相应的变形.

|
图 14 火灾高温550 ℃下节点2-3 E (S690 15 mm)变形终态对比 Fig.14 Comparison on final deformation state of connection 2-3 E (S690 15 mm) at elevated temperature 550 ℃ |

|
图 15 火灾高温550 ℃下节点2-3 E (S690 15 mm)组件变形终态对比 Fig.15 Comparison on components of 2-3 E (S690 15 mm) after failure at elevated temperature 550 ℃ |
以节点2-4E(S960 12 mm)为例,将火灾高温550 ℃下有限元模拟的等效塑性应变(PEEQ)同试验结果进行对比,如图 16所示,可以看出,有限元模拟同试验结果基本一致.类似地,高温下其余节点可得到相同结论.

|
图 16 火灾高温550 ℃下节点2-4 E (S960 12 mm)的试验变形与数值模拟的等效塑性应变对比 Fig.16 Test final deformation and numerical PEEQ of 2-4 E (S960 12 mm) at 550 ℃ |
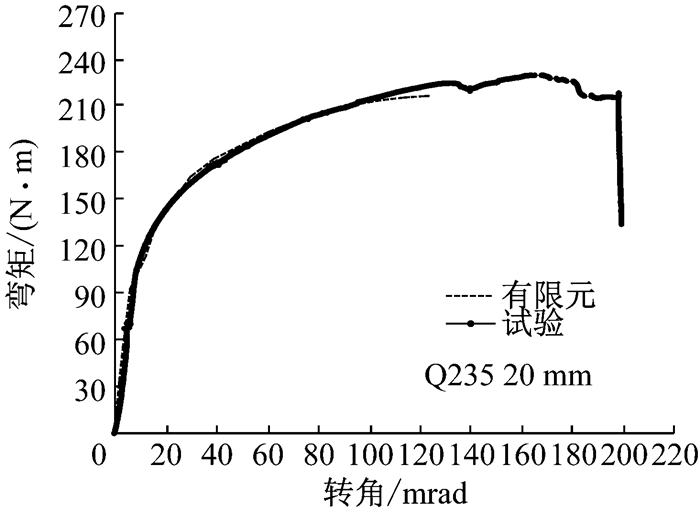
常温下所有节点有限元模拟所得的弯矩转角关系曲线同试验结果对比如图 17~图 23所示.
|
图 17 常温下节点1-1 A的弯矩转角关系 Fig.17 Moment-rotation comparison of 1-1 A at ambient temperature |

|
图 18 常温下节点1-2 A的弯矩转角关系 Fig.18 Moment-rotation comparison of 1-2 A at ambient temperature |
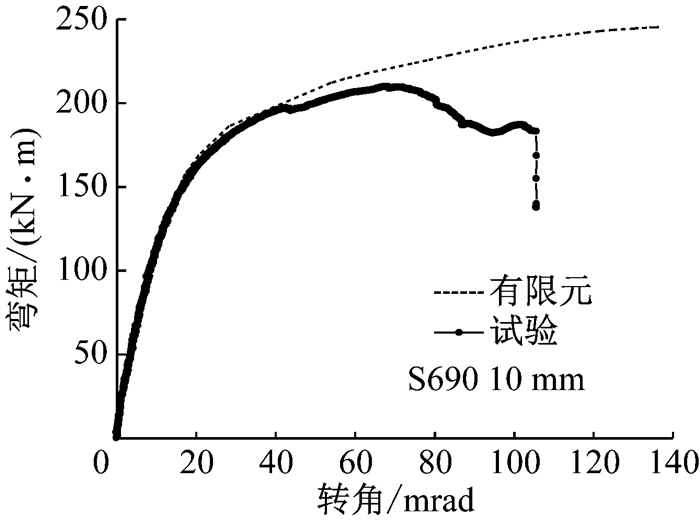
|
图 19 常温下节点1-3 A的弯矩转角关系 Fig.19 Moment-rotation comparison of 1-3 A at ambient temperature |
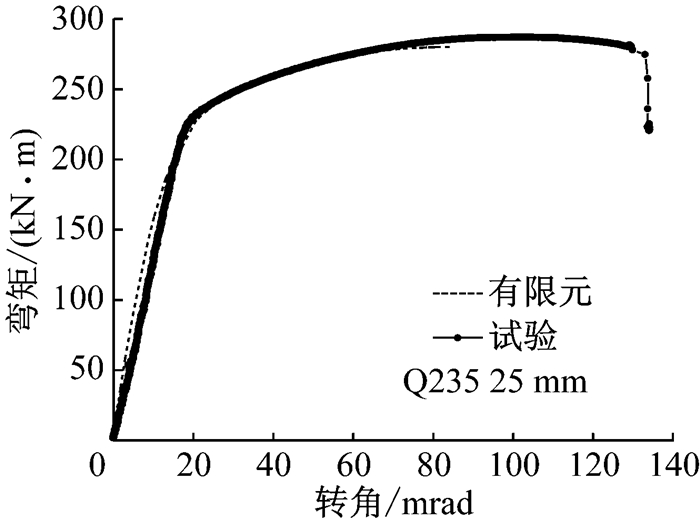
|
图 20 常温下节点2-1 A的弯矩转角关系 Fig.20 Moment rotation comparison of 2-1 A at ambient temperature |
|
图 21 常温下节点2-2 A的弯矩转角关系 Fig.21 Momentrotation comparison of 2-2 A at ambient temperature |

|
图 22 常温下节点2-3 A的弯矩转角关系 Fig.22 Momentrotation comparison of 2-3 A at ambient temperature |

|
图 23 常温下节点2-4 A的弯矩转角关系 Fig.23 Momentrotation comparison of 2-4 A at ambient temperature |
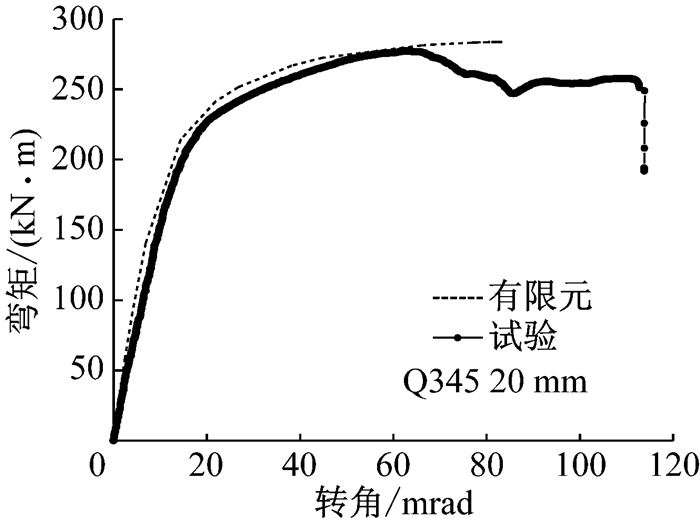
由节点弯矩转角关系对比可看出,所有节点有限元模拟的弯矩转角关系同试验结果均吻合较好.以节点2-4A(S960 12 mm)为例,如图 23所示,有限元分析得到的弯矩转角关系曲线在节点初始刚度、节点抗弯承载力和弯矩极值所对应的转角ϕMmax等方面均与试验结果吻合较好.然而,有限元分析在某一组件的平均主应变极值达到材料的极限应变时便停止,不能模拟出试验中节点弯矩转角曲线的下降段,也就无法确定节点极限转角ϕC.值得一提的是,节点1-3A(S960 10 mm)转角小于40 mard时,有限元模型和试验所得节点弯矩转角关系曲线几乎重合,如图 19所示,当节点转角超过40mard后两曲线出现差异.这是因为节点1-3A的端板很薄(所有节点中端板最薄的),施焊过程对端板热影响区的不利影响最大,造成端板热影响区在产生一定塑性变形后较早地出现破坏,如图 24所示.然而,在有限元模型中,未考虑焊接热影响区对端板的影响,因此有限元分析所得的1-3 A (S960 10 mm)的节点抗弯承载力和节点转动能力均高于试验结果.

|
图 24 常温下节点1-3 A (S960 10 mm)在焊缝热影响区较早破坏 Fig.24 Early cracking on the endplate at the heat affected zone of welds for connection 1-3 A (S960 10 mm) at ambient temperature |
表 3列出常温下所有节点有限元模拟和试验结果的抗弯承载力,可以看出,有限元模型同试验结果吻合很好,最大偏差仅为5.69%.由于节点1-3A较早出现破坏因此不在对比范围之内.
| 下载CSV 表 3 常温下有限元模型抗弯承载力与试验结果对比 Tab.3 Validation of numerical study against experimental study at ambient temperature |
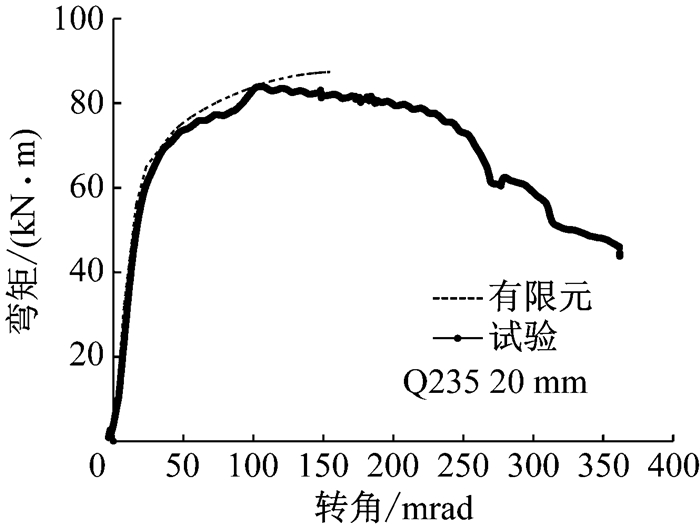
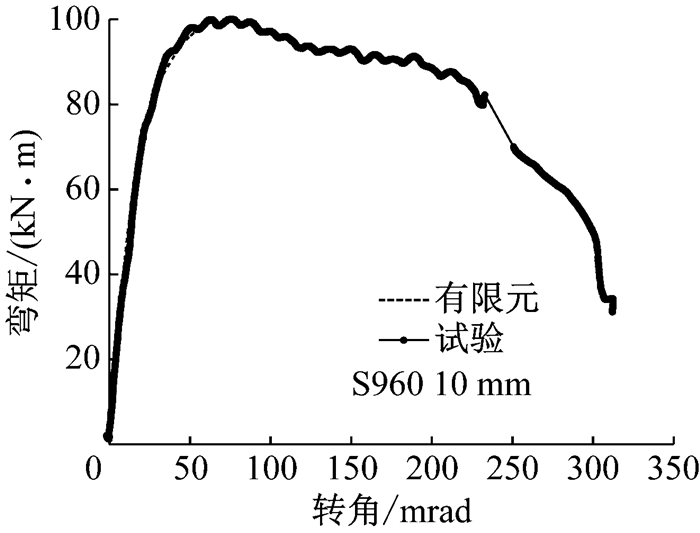
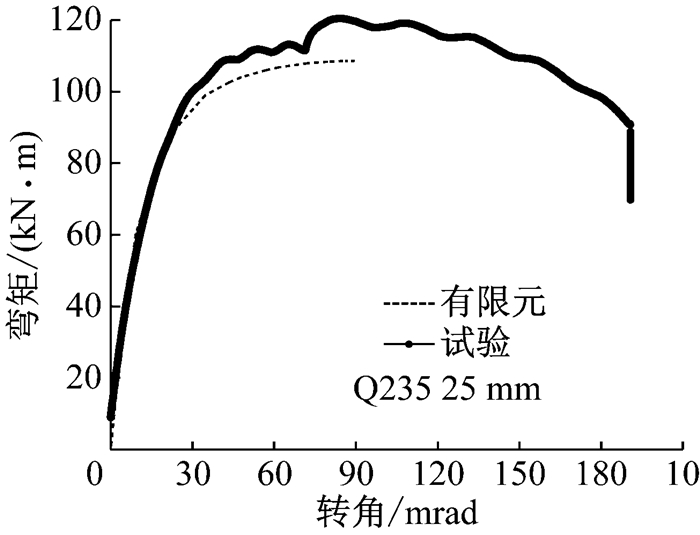
火灾高温550 ℃下所有节点有限元模拟的弯矩转角关系曲线同试验结果对比如图 25~图 31所示.
|
图 25 火灾下节点1-1 E的弯矩转角关系 Fig.25 Moment-rotation comparison of 1-1 E at elevated temperature 550 ℃ |

|
图 26 火灾下节点1-2 E的弯矩转角关系 Fig.26 Moment-rotation comparison of 1-2 E at elevated temperature 550 ℃ |
|
图 27 火灾下节点1-3 E的弯矩转角关系 Fig.27 Moment-rotation comparison of 1-3 E at elevated temperature 550 ℃ |
|
图 28 火灾下节点2-1 E的弯矩转角关系 Fig.28 Moment-rotation comparison of 2-1 E at elevated temperature 550 ℃ |

|
图 29 火灾下节点2-2 E的弯矩转角关系 Fig.29 Moment-rotation comparison of 2-2 E at elevated temperature 550 ℃ |
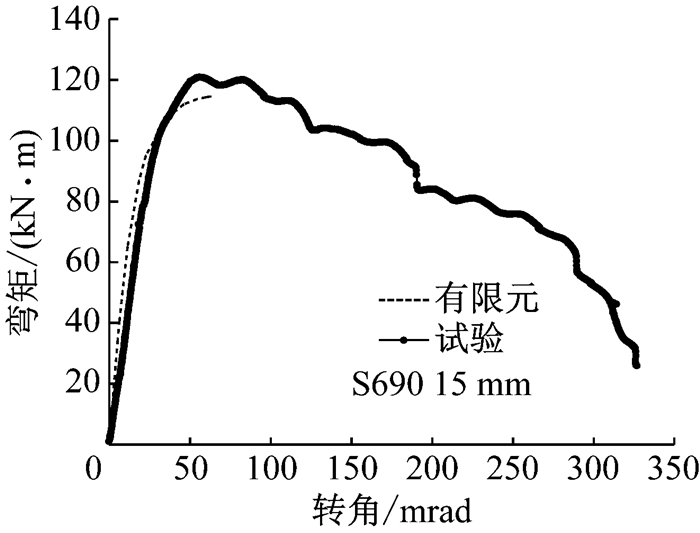
|
图 30 火灾下节点2-3 E的弯矩转角关系 Fig.30 Moment-rotation comparison of 2-3 E at elevated temperature 550 ℃ |

|
图 31 火灾下节点2-4 E的弯矩转角关系曲线 Fig.31 Moment-rotation comparison of 2-4 E at elevated temperature 550 ℃ |
由以上对比可看出,有限元模型的节点弯矩转角关系曲线在初始刚度、抗弯承载力和荷载极值所对应的转角ϕMmax等方面均与试验结果吻合较好.表 4列出火灾下所有节点有限元模拟和试验所得的抗弯承载力,二者最大偏差为9.80%.由此可得出结论,无论在常温下还是火灾下,本文对高强钢端板连接节点力学性能的有限元分析具有可靠的准确度.
| 下载CSV 表 4 火灾下有限元模型抗弯承载力与试验结果对比 Tab.4 Validation of numerical study against experimental study at elevated temperature |
试验时节点试件在加载过程中任意时刻的应力分布可通过有限元模型得到.以节点1-2A(S690 12 mm)为例,如图 32所示,可以看出常温下端板的应力云图清晰地显示出节点屈服线模式和试验结束时的应力状态,并且同试验结果吻合很好.火灾高温下所有节点亦可以得出类似结论,以节点1-2E(S690 12 mm)为例,如图 33所示.由于火灾下节点的应力分布难以通过试验获得,本文的有限元模型可用于准确预测高强钢端板连接节点在常温下以及火灾下的应力分布.

|
图 32 常温下节点1-2 A (S690 12 mm)的屈服线模式和试验结束时的应力状态 Fig.32 Stress state at the end of test and yield line pattern of 1-2 A (S690 12 mm) at ambient temperature |

|
图 33 火灾高温550 ℃下节点1-2 E (S690 12 mm)的屈服线模式和试验结束时的应力状态 Fig.33 Stress state at the end of test and yield line pattern of 1-2 E (S690 12 mm) at elevated temperature 550 ℃ |
通过建立高强钢端板连接节点的三维有限元模型,研究此类节点在火灾550℃下和常温下的力学性能.有限元分析结果与试验结果对比表明,无论在火灾下还是常温下,本文有限元模型在节点弯矩转角关系、节点变形以及端板屈服线模式等方面同试验结果均具有很好的吻合度.因此,该有限元模型可准确模拟出高强钢端板连接节点的受力性能.此外,只需将不同种类高强钢材料的高温力学性能赋予该有限元模型,即可进行参数分析,以探究相应高强钢端板连接节点在不同火灾作用下的力学性能.
该有限元模拟可确定高强钢端板连接节点第一个破坏组件,但其余组件破坏的发生以及发展过程尚不能被模拟.为改善这种情况,在后续有限元模型的建立过程中,可对焊缝进行实体建模、考虑热影响区的影响以及考虑不同组件的断裂特性等.
| [1] |
European Committee for Standardization. Design of steel structures, part 1-2: general rules-structural fire design: EN1993-1-2, Eurocode3[S]. Brussels: European Committee for Standardization, 2005.
|
| [2] |
European Committee for Standardization. Design of steel structures, part 1-8: design of joints: EN1993-1-2, Eurocode3[S]. Brussels: European Committee for Standardization, 2005.
|
| [3] |
施刚, 班慧勇, 石永久, 等. 高强度钢材钢结构研究进展综述[J]. 工程力学, 2013, 30(1): 1 SHI Gang, BAN Huiyong, SHI Yongjiu, et al. Overview of research for high strength steel structures[J]. Engineering Mechanics, 2013, 30(1): 1 |
| [4] |
余红霞. 火灾下钢节点牢固性的研究与展望[J]. 工程力学, 2011, 28(4): 116 YU Hongxia. Discussions on the robustness of steel connections in fire[J]. Engineering Mechanics, 2011, 28(4): 116 |
| [5] |
SHI Gang, SHI Yongjiu, WANG Yuanqing, et al. Numerical simulation of steel pretensioned bolted end-plate connections of different types and details[J]. Engineering Structures, 2008, 30: 2677 DOI:10.1016/j.engstruct.2008.02.013 |
| [6] |
YU H X, BURGESS I W, DAVISON J B, et al. Experimental and numerical investigations of the behaviour of flush endplate connections at elevated temperatures[J]. Journal of Structural Engineering, ASCE, 2011, 137(1): 80 DOI:10.1061/(ASCE)ST.1943-541X.0000277 |
| [7] |
王宇, 于保阳, 齐琳. 钢结构端板连接梁柱结点抗火性能试验和有限元分析[J]. 沈阳建筑大学学报(自然科学版), 2014(6): 1044 WANG yu, YU Baoyang, QI Lin. Experimental research and finite element analysis on the fire-resistance performance of joints of end-plate connection in steel structure[J]. Journal of Shenyang Jianzhu University(Natural Science), 2014(6): 1044 DOI:10.11717/j.issn:2095-1922.2014.06.11 |
| [8] |
高义奇, 余红霞, 施刚. 火灾下拉剪组合作用对高强螺栓节点性能影响的试验研究[J]. 工程力学, 2014, 31(9): 97 GAO Yiqi, YU Hongxia, SHI Gang. Experimental research on the behavior of high-strength bolted connections under combined tension and shear in fire[J]. Engineering Mechanics, 2014, 31(9): 97 |
| [9] |
高义奇, 施刚, 余红霞. 拉剪组合作用下平齐端板节点火灾行为的有限元分析[J]. 工程力学, 2015, 32(11): 100 GAO Yiqi, SHI Gang, YU Hongxia. Fem analysis of flush endplate connections under the combined effect of tension and shear in fire[J]. Engineering Mechanics, 2015, 32(11): 100 DOI:10.6052/j.issn.1000-4750.2014.04.0342 |
| [10] |
COELHO A M G, BIJLAARD F S K. Experimental behaviour of high strength steel end-plate connections[J]. Journal of Constructional Steel Research, 2007, 63(9): 1228 DOI:10.1016/j.jcsr.2006.11.010 |
| [11] |
孙飞飞, 孙密, 李国强, 等. Q690高强钢端板连接梁柱节点抗震性能试验研究[J]. 建筑结构学报, 2014, 35(4): 116 SUN Feifei, SUN Mi, LI Guoqiang, et al. Experimental study on seismic behavior of high-strength steel beam-to-column end-plate connections[J]. Journal of Building Structures, 2014, 35(4): 116 |
| [12] |
强旭红, 任楚超, 姜旭, 等. 高强平齐式端板连接火灾下性能试验[J]. 同济大学学报(自然科学版), 2017, 45(5): 673 QIANG Xuhong, REN Chuchao, JIANG Xu, et al. Experimental and theoretical study on behavior of high strength steel endplate connections under fire conditions[J]. Journal of Tongji University(Natural Science), 2017, 45(5): 673 |
| [13] |
BURSI O S, JASPART J P. Benchmarks for finite element modelling of bolted steel connections[J]. Journal of Constructional Steel Research, 1997, 43(1-3): 17 DOI:10.1016/S0143-974X(97)00031-X |
| [14] |
BURSI O S, JASPART J P. Basic issues in the finite element simulation of extended end plate connections[J]. Computers & Structures, 1998, 69(3): 61 |
| [15] |
Dassault Systèmes Simulia Corp. ABAQUS analysis user's manual 6.10 version[M]. Rhode Island: Dassault Systèmes Corp, 2010
|
| [16] |
HU Y, DAVISON J B, BURGESS I W, et al. Experimental study on flexible end plate connections in fire [C]//5th European Conference on Steel Structures. Graz:[s.n.], 2012: 1007-1012. https://envbldg.shef.ac.uk/publications/experimental-study-flexible-end-plate-connections-fire
|
| [17] |
HU Y, DAVISON J B, BURGESS I W, et al. Comparative study of the behaviour of BS 4190 and BS EN ISO 4014 bolts in fire[C]//Proceedings of ICSCS, 2007. Manchester: ICSCS, 2007: 1-8.
|
| [18] |
HU Y. Robustness of flexible endplate connections under fire conditions [D]. Sheffield: University of Sheffield, 2009. http://etheses.whiterose.ac.uk/14969/
|
| [19] |
THEODOROU Y. Mechanical properties of grade 8.8 bolts at elevated temperatures [D]. Sheffield: University of Sheffield, 2003.
|
| [20] |
QIANG X, BIJLAARD F, KOLSTEIN H. Dependence of mechanical properties of high strength steel S690 on elevated temperatures[J]. Construction & Building Materials, 2012, 30(30): 73 |
| [21] |
QIANG X, JIANG X, BIJLAARD F S K, et al. Mechanical properties and design recommendations of very high strength steel S960 in fire[J]. Engineering Structures, 2016, 112: 60 DOI:10.1016/j.engstruct.2016.01.008 |
| [22] |
COELHO A M G, BIJLAARD F S K, SILVA L Sd. On the deformation capacity of beam-to column bolted connections[C]//European Convention for Constructional Steelwork—Technical Committee 10: Structural Connections (ECCS-TC10). Coimbra: [s.n.], 2002: 1-8.
|
| [23] |
COELHO A M G. Characterization of the ductility of bolted end plate beam to column steel connections [D]. Coimbra: University of Coimbra, 2004. https://estudogeral.sib.uc.pt/jspui/handle/10316/1980
|
| [24] |
QIANG X. Behaviour of high strength steel endplate connections in fire and after fire [D]. Delft: Delft University of Technology, 2013. https://repository.tudelft.nl/islandora/object/uuid:9bcf2c58-e5c3-4fac-a920-38622212f8fe?collection=research
|
 2017, Vol. 45
2017, Vol. 45


