2. 浙江理工大学 建筑工程学院, 浙江 杭州 310018;
3. 同济大学 土木工程防灾国家重点实验室, 上海 200092
2. School of Civil Engineering and Architecture, Zhejiang Sci-Tech University, Hangzhou 310018, China;
3. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China
为了科学地描述混凝土材料性质的随机性并反映混凝土材料的随机损伤机制[1],研究者将确定性损伤力学扩展,通过随机的损伤演化法则描述混凝土随机的损伤演化过程,基于微弹簧模型发展了早期的混凝土随机损伤本构模型[2-3].为了反映混凝土在拉、压应力状态下不同的损伤机制,李杰等对KANDARPA[3]的微弹簧模型做了改进和发展,逐渐形成了一系列细观随机断裂损伤本构模型[4-7].细观随机断裂损伤本构模型,将材料细观损伤的产生与发展凝炼、抽象为简单的力学模型,并由此给出损伤演化法则.对混凝土细观结构的合理抽象,是研究者智慧的体现.然而,在这样的抽象过程中,一方面简化了模型,另一方面也使得损伤发展过程中材料内部应力的复杂演化关系被简单化处理,从而使模型对复杂物理过程的反映能力受到了削弱.
随着计算力学、多尺度方法的发展,一些学者试图直接从材料微缺陷入手、给出裂纹发展与损伤演化之间的定量关系,发展了多尺度损伤模型.早期的多尺度损伤模型,将不均匀材料考虑为两相介质复合材料用以研究纤维增强材料[8-9].近年来,由细观尺度微裂缝演化得到宏观尺度损伤演化的多尺度损伤模型[10-12],获得了研究者越来越多的关注,逐渐成为固体力学的研究热点.FENG和YU[13]详述了包括混凝土在内的拟脆性材料细观损伤模型中最基本的三个问题,即:损伤变量的选取、裂纹扩展区方向和基于微裂纹开展的多尺度损伤本构模型.对混凝土材料而言,通过对其细观结构进行客观描述,从细观微缺陷的发展导致应力重分布的角度研究损伤演化,同时考虑细观组分与微缺陷分布的随机性对损伤演化的影响,从而给出具有明确物理机制的损伤表示,是对细观随机断裂损伤本构模型的合理发展.
文本依据多尺度分析的基本思想,利用多尺度能量积分以及能量损伤表达建立宏-细观尺度之间的联系.基于基本单元体数值分析结果,根据多尺度能量传递定理式,积分得到单元体能量的演化,分别计算受拉与受剪损伤的演化曲线.建议了一类实用的损伤演化公式,并分别给出了受拉、受剪损伤发展参数的均值、标准差与概率密度分布.通过对混凝土宏观试验的模拟,验证了本文给出的多尺度损伤本构模型的正确性.为将多尺度理论应用于混凝土结构分析,提供了一定的理论基础.
1 多尺度随机损伤演化 1.1 多尺度损伤表示如图 1所示,混凝土宏观结构体是由非均匀的细观结构(各相组分、微裂缝等)组成的.将宏观结构所在的坐标系定为x=(x1, x2),细观结构所在的坐标系定为y=(y1, y2).同时,给出宏观坐标和细观坐标之间的转换关系如下:

|
图 1 宏观与细观结构 Fig.1 Macro-structure and micro structure of concrete |
| $ \mathit{\boldsymbol{y}} = \frac{\mathit{\boldsymbol{x}}}{\lambda } $ | (1) |
式中:λ为尺度参数,表示细观结构尺寸与宏观结构之间的关系,λ一般为一个较小的值.对于规则的宏观和细观结构,λ可以表示为λ=Lmicro/Lmacro,其中Lmicro为细观单元的尺寸;Lmacro为宏观单元的尺寸.
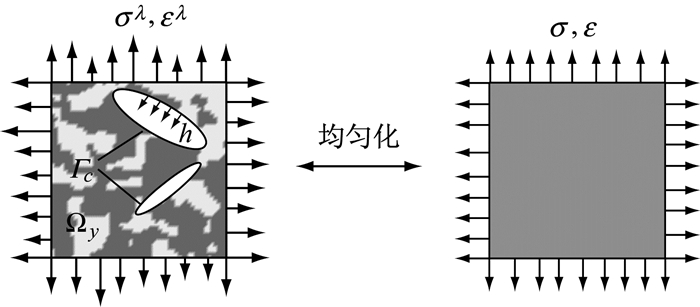
图 1所示的两尺度问题,宏观尺度上固体材料所占据的区域为Ω,其边界为Γ.边界面力t作用于宏观结构体边界Γt上;边界位移u作用于宏观结构体边界Γu上,且Γt∩Γu∈Γ.宏观结构由大量细观单元构成,细观单元所占据的区域为Ωy,其内部含有的微缺陷(微孔洞、微裂缝)边界为Γc,在裂纹表面上作用面力为h.
对于不考虑体力的情况,可给出宏观单元的平衡方程以及边界条件如下:
| $ \nabla {\mathit{\boldsymbol{\sigma }}^\lambda } = 0\;在\;\mathit{\Omega }\;中 $ | (2) |
| $ {\mathit{\boldsymbol{\sigma }}^\lambda }\mathit{\boldsymbol{n}} = \mathit{\boldsymbol{t}}\;在\;{\mathit{\Gamma }_{\rm{t}}}\;上 $ | (3) |
| $ \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{\bar u}}\;在\;{\mathit{\Gamma }_{\rm{u}}}\;上 $ | (4) |
| $ {\mathit{\boldsymbol{\sigma }}^\lambda }\mathit{\boldsymbol{n}} = \mathit{\boldsymbol{h}}\;在\;{\mathit{\Gamma }_{\rm{c}}}\;上 $ | (5) |
式中:σλ为同时考虑宏观坐标和细观坐标的宏观应力.换言之,求解式(5) 所得的σλ为宏观坐标系的函数且包含了细观结构的影响.然而,直接对式(2)~式(5) 求解需采用并行多尺度方法[14],计算量难以承受.因此,研究者往往采用均匀化方法[15]对该问题进行求解.
如图 2所示,均匀化应力、应变可以分别表示为单元体边界上总的外力形成的张力和单元体边界上的总位移在单元体内部的平均,二者均为细观单元体的外部表现.对于式(2)~式(5) 给出的无体力问题,有均匀化应力、应变表示为
|
图 2 含缺陷材料的均匀化 Fig.2 Homogenization of micro-cracked material |
| $ \mathit{\boldsymbol{\bar \sigma }} = \frac{1}{{{V_y}}}\oint_{\partial {\mathit{\Omega }_y}} {\left( {{\mathit{\boldsymbol{t}}^\lambda } \otimes \mathit{\boldsymbol{x}}} \right){\rm{d}}\mathit{\Omega }} $ | (6) |
| $ \mathit{\boldsymbol{\bar \varepsilon = }}\frac{1}{{2{V_y}}}\oint_{\partial {\mathit{\Omega }_y}} {\left( {{\mathit{\boldsymbol{u}}^\lambda } \otimes \mathit{\boldsymbol{n}} + \mathit{\boldsymbol{n}} \otimes {\mathit{\boldsymbol{u}}^\lambda }} \right){\rm{d}}\mathit{\Gamma }} $ | (7) |
同时,引入细观单元内的平均化应力、应变的表达式为
| $ \left\langle {{\mathit{\boldsymbol{\sigma }}^\lambda }} \right\rangle = \frac{1}{{{V_y}}}\int_{{\mathit{\Omega }_y}} {{\mathit{\boldsymbol{\sigma }}^\lambda }{\rm{d}}\mathit{\Omega }} $ | (8) |
| $ \left\langle {{\mathit{\boldsymbol{\varepsilon }}^\lambda }} \right\rangle = \frac{1}{{{V_y}}}\int_{{\mathit{\Omega }_y}} {{\mathit{\boldsymbol{\varepsilon }}^\lambda }{\rm{d}}\mathit{\Omega }} $ | (9) |
考虑到内部微裂缝表面作用的应力(内聚应力)为自平衡力系,即裂纹开展方向两侧的内聚应力大小相同方向相反.因此,可以给出均匀化应力与平均化应力之间的关系如下:
| $ \mathit{\boldsymbol{\bar \sigma = }}\left\langle {{\mathit{\boldsymbol{\sigma }}^\lambda }} \right\rangle $ | (10) |
式(10) 表示对于含有微裂缝的材料,均匀化应力与平均化应力相等.
同理,给出均匀化应变与平均化应变之间的关系,即
| $ \left\langle {{\varepsilon^\lambda }} \right\rangle = \bar \varepsilon -\frac{1}{{2{V_y}}}\oint_{{\mathit{\Gamma }_{\rm{c}}}} {\left( {{\mathit{\boldsymbol{n}} } \otimes \mathit{\boldsymbol{u}}^\lambda + {\mathit{\boldsymbol{u}}^\lambda } \otimes \mathit{\boldsymbol{n}}} \right){\rm{d}}\mathit{\Gamma }} $ | (11) |
式(11) 表明对于含有微裂缝的材料,均匀化应变等于平均化应变与裂纹张开位移沿着裂纹表面积分之和.
进一步考虑平均化弹性Helmholtz自由能势与均匀化弹性Helmholtz自由能势之间的关系,即多尺度能量积分[12],有
| $ {{\bar \psi }^e} = \frac{1}{{{V_y}}}\left( {\int_{{\mathit{\Omega }_y}} {{\psi ^\lambda }{\rm{d}}\mathit{\Omega }} + \frac{1}{2}\oint_{{\mathit{\Gamma }_{\rm{c}}}} {{\mathit{\boldsymbol{u}}^\lambda }\mathit{\boldsymbol{h}}{\rm{d}}\mathit{\Gamma }} } \right) $ | (12) |
根据弹塑性损伤理论框架[16],混凝土的基本损伤机制为受拉损伤和受剪损伤,可以给出受拉、受剪损伤变量的表达式, 即
| $ {d^ \pm } = 1 - \frac{{{{\bar \psi }^{e \pm }}}}{{\bar \psi _0^{e \pm }}} $ | (13) |
式中:上标“±”分别代表受拉、受剪应力状态;ψ0±为弹性Helmholtz自由能势,表示为
| $ \bar \psi _0^{e \pm } = \frac{1}{2}{\varepsilon ^{e \pm }}{E_0}{\varepsilon ^{e \pm }} $ | (14) |
由式(13) 可知,通过建立典型意义上的基本分析单元、并在单元上施加不同的边界条件(单轴受拉、纯剪),通过数值方法获得损伤演化的能量变化过程.
1.2 受拉损伤演化根据试验观测[17],在拉应力为主的应力状态下,混凝土宏观力学性能的劣化应用受拉损伤变量来描述.混凝土对于受拉损伤单元,存在σ=σ+,σ-=0.在受力过程中,有ψ0e-=0,d-=0.
根据式(13),受拉损伤变量可以表示为
| $ {d^ + } = 1 - \frac{{{{\bar \psi }^{e + }}}}{{\bar \psi _0^{e + }}} $ | (15) |
在受拉应力状态下,脆性材料发生受拉损伤,产生垂直于最大主拉应力方向的裂缝,由此导致单元内部应力—应变重分布过程.可以通过细观单元分析给出细观度上的应力、应变演化过程,利用上述多尺度能量积分,可以计算出ψe+(εe, d+),并由式(15) 给出受拉基本单元的损伤演化过程.
1.3 受剪损伤演化在压应力为主的应力状态下,在偏量空间内不存在拉应力,混凝土宏观力学性能的劣化用受剪损伤变量来描述[16].
对细观单元施加纯剪边界条件,有σ+=0,ψ0e+=0,d+=0.纯剪情况下的受剪损伤变量ds可以表示为
| $ {d_{\rm{s}}} = 1 - \frac{{{{\bar \psi }^{{e_{\rm{s}}}}}}}{{\psi _0^{{e_{\rm{s}}}}}} $ | (16) |
式中:ψ0es表示为受剪状态下的初始Helmholtz自由能势,而ψe(τ, ds)则可以按多尺度分析方式给出.
值得注意的是,还需要建立式(16) 给出的受剪损伤和受压应力状态的关系[16].图 3给出了在单向受压状态下,混凝土细观单元内的损伤产生和演化.

|
图 3 单向受压损伤表示 Fig.3 Shear damage under compression |
在图 3中,细观单元在压应力下,其中裂缝产生和开展的方向与压应力方向夹角为α.首先,将应力投影到与裂缝正交的坐标系x′y′内,即
| $ \left\{ \begin{array}{l} {{\sigma '}_x} = \sigma {\cos ^2}\alpha \\ {{\sigma '}_y} = \sigma {\sin ^2}\alpha \\ \tau ' = \left( {\sigma \sin 2\alpha } \right)/2 \end{array} \right. $ | (17) |
可见,在与裂缝正交的坐标系内,不仅有正应力,也有剪应力.由于两个方向的正应力σ′x与σ′y均为压应力,它们不会在裂缝端部产生应力集中,也不会引起对应方向上受压刚度的退化[16].根据虎克定律,计算对应方向上的应变,有
| $ \left\{ \begin{array}{l} {{\varepsilon '}_x} = \frac{1}{E}\left[ {\sigma {{\cos }^2}\alpha - \nu \sigma {{\sin }^2}\alpha } \right]\\ {{\varepsilon '}_y} = \frac{1}{E}\left[ {\sigma {{\sin }^2}\alpha - \nu \sigma {{\cos }^2}\alpha } \right] \end{array} \right. $ | (18) |
式中,ν为泊松比.
应力投影得到的剪应力τ′,会引起微裂缝的产生和开展、并导致细观单元的损伤演化.
利用应力等效原理,考虑细观受剪单元的静力平衡(图 3)不难给出
| $ \tau = \left( {1 - {d_{\rm{s}}}} \right)G\gamma $ | (19) |
利用应变转轴公式,可以得到在原坐标系x,y中与加载方向对应的应变为
| $ \begin{array}{l} \varepsilon = \left( {1 - \frac{{1 + v}}{2}{{\sin }^2}2\alpha } \right)\frac{\sigma }{E} + \left[ {\frac{{1 + v}}{{2\left( {1 - {d^ - }} \right)}}{{\sin }^2}2\alpha } \right]\frac{\sigma }{E} = \\ \;\;\;\;\;\left[ {1 + \left( {\frac{{{d^ - }}}{{1 - {d^ - }}}} \right)\frac{{1 + v}}{2}{{\sin }^2}2\alpha } \right]\frac{\sigma }{E} \end{array} $ | (20) |
简化式(20),可以将受压状态下损伤应力—应变关系可以表示为
| $ \sigma = \left( {1 - {d^ - }} \right)E\varepsilon $ | (21) |
式中,d-为受压状态下的受剪损伤变量,可以写为
| $ {d^ - } = \frac{{\left( {1 - \beta } \right){d_{\rm{s}}}}}{{1 - \beta {d_{\rm{s}}}}} $ | (22) |
| $ \beta = 1 - \frac{{1 + v}}{2}{\sin ^2}2\alpha $ | (23) |
在细观单元模拟中,夹角α可以通过模型主裂纹开展方向与压应力加载方向之间的夹角确定.
将d-定义为与受压应力状态对应的受剪损伤变量.由式(22) 可知:ds=0时,d-=0且ds=1时,d-=1,说明d-满足作为损伤变量的基本条件.
因此,通过基本单元受剪的模拟,可以获得受剪损伤演化曲线并通过式(22) 将其转换至压应力空间.
2 细观单元分析在建立了多尺度损伤表示后,最为重要的工作即为细观单元的分析,以合理地描述混凝土细观结构,给出均匀化应力应变关系与损伤演化曲线.
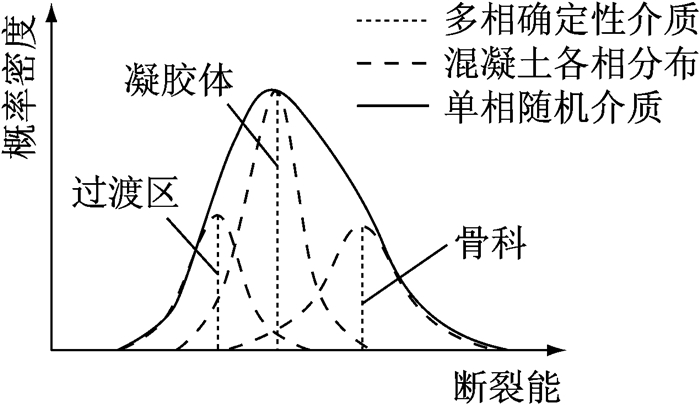
2.1 混凝土细观建模根据各组分材料的本构相似性和概率可加原则,可以将混凝土视为单一随机介质[16],如图 4所示.
|
图 4 混凝土材料的三种描述方式 Fig.4 Three reconstruction models of concrete |
在空间上,单相随机介质可以采用随机场来进行描述,并采用随机谐和函方法给出材料物理性质的随机场描述[18].对混凝土而言,Hillerborg等[19]、Bazant[20]认为断裂能决定了应力应变曲线下降段的形式,因而对材料的破坏起到了非常重要的作用.因此,本文取细观断裂能分布作为基本随机场.通常可取这一随机场的一维概率密度分布为正态分布.
众多学者对固体随机材料的相关函数进行了研究,其中应用最为广泛的为指数形式[21-22].本文取断裂能随机场的相关函数形式为
| $ R\left( {{\tau _1},{\tau _2}} \right) = \exp \left( { - {{\left( {\frac{{{\xi _1}}}{{{b_1}}}} \right)}^2} - {{\left( {\frac{{{\xi _2}}}{{{b_2}}}} \right)}^2}} \right) $ | (24) |
式中:定义距离ξ1=x2-x1,ξ2=y2-y1;b1和b2分别为x和y方向的相关长度.
BAZANT和PIJAUDIER-CABOT[23]的研究指出,混凝土材料性质的相关长度可以视为其骨料对材料非局部化的影响区域,并将其定义为混凝土3倍最大骨料粒径dm.根据REN等[24]的混凝土试验级配,最大骨料粒径为dm=8 mm.据此,本文采用的相关长度[25]为b1=b2=24 mm.
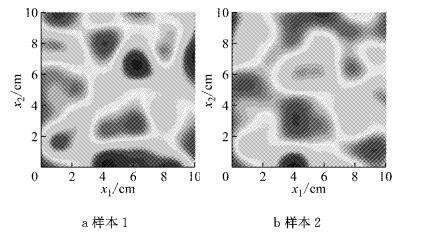
依据上述条件,给出混凝土断裂能随机场的模拟结果.图 5给出了目标功率谱函,其中k1和k2为波数.图 6给出了采用随机谐和分量N1×N2=8×8的功率谱密度函数.通过功率谱密度函数,可以在数值特征即集合的角度验证本文给出的随机场建模方法的精确性.图 7给出了采用随机谐和函数生成的2个混凝土断裂能样本.

|
图 5 目标功率谱密度 Fig.5 Target power spectral density function |

|
图 6 随机谐和函数建模功率谱密度 Fig.6 Reconstructed power spectral density function |
|
图 7 混凝土断裂能样本 Fig.7 Samples of fracture energy of concrete |
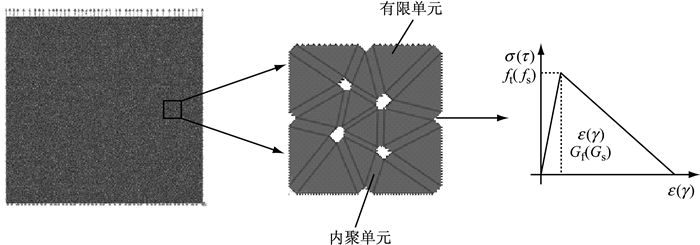
采用内聚单元方法模拟了混凝土细观单元单轴受拉试验的裂缝开展过程和应力—应变关系,并根据多尺度损伤表达,给出受拉损伤演化曲线.所采用的试件几何尺寸为b=100 mm,h=100 mm.根据REN等[24]的实验结果,混凝土确定性弹性参数为E=37 559 MPa,ν=0.2.混凝土内聚单元模型采用如图 8给出的应力裂纹张开位移关系,其中,内聚应力强度ft=3.28 MPa,混凝土断裂能随机场均值μGf=100 N·m-1,断裂能标准差为σGf=10 N·m-1,相关函数形式由式(24) 给出,数值模拟采用的断裂能分布样本如图 8所示.采用有限元软件ABAQUS Explicit进行建模,混凝土试块以及其边界如图 8所示.划分有限单元平均尺寸为1 mm,内聚单元平均宽度为0.01 mm.模型单元总数为5万个,其中有限单元数量为2万个,内聚单元3万个.图 8给出的数值模型中,三角形单元代表有限单元;四边形单元代表内聚单元,其表示裂纹可能开展的路径.
|
图 8 单轴受拉基本单元数值模型 Fig.8 Numerical model of uniaxial tension |
根据图 8所示的数值模型,模拟了混凝土单轴受拉试验.模拟中,采用随机谐和函数所生成的样本数为300.图 9给出了混凝土材料的破坏模拟过程.分析整个非线性发展过程可见:在加载初期,混凝土试块应力分布较为均匀,应变随着应力的增长而呈现线性增加,如图 9a所示;随着应力的继续增大,混凝土试块内部开始出现随机的微小裂缝,此时应力分布显示出细微地非均匀性,在微小裂纹附近形成应力集中,如图 9b所示;在非线性发展后期,出现典型的应变局部化现象,试件在端部或者中部出现一条垂直于受拉方向的主裂缝,而其他裂缝并没有明显的产生和发展,见图 9c.图 9d也给出了混凝土典型试块单轴受拉状态下的破坏结果与试验结果的对比.这说明采用本文方法,可以较为完整地反映混凝土裂纹开展与破坏模式.

|
图 9 试件破坏模拟与试验结果 Fig.9 Tensile failure simulation and test failure mode of concrete |
图 10给出了所有样本的均匀化应力应变曲线,其中黑色的曲线代表均值曲线.根据式(15) 给出的多尺度损伤表达,图 11给出所有样本的受拉损伤演化曲线以及均值受拉损伤演化曲线.

|
图 10 单轴受拉应力应变曲线及样本均值 Fig.10 Uniaxial tensile stress-strain relationship |

|
图 11 样本受拉应力损伤曲线 Fig.11 Tensile damage curves |
基本单元的纯剪模拟采用了与基本单元单轴受拉模拟相同的材料参数.剪切模量为E/2(1+ν)=15 208 MPa.受拉、受剪内聚应力强度分别为fs=ft=3.28 MPa.断裂能取值为Gf=Gs,即剪切断裂能与断裂能相同.
图 12给出了纯剪条件下基本单元的裂纹发展与破坏全过程:在加载初期,应力呈现均匀分布,无裂缝产生,见图 12a;在加载的中后期(ε=0.7εu),出现较多斜向微裂缝,见图 12 b;加载的后期(ε=εu),形成贯通的45°斜裂缝,材料破坏,见图 12 c.事实上,混凝土在受压试验过程中,微裂纹首先汇集形成与加载方向形成较小角度的多条不连续剪切裂缝带,随着加载的增加,这些剪切带相互联结,最终成为一条大致呈现45°的贯通斜裂缝,与剪切破坏具有相似性.

|
图 12 受剪破坏模拟与试验结果 Fig.12 Shear failure simulation |
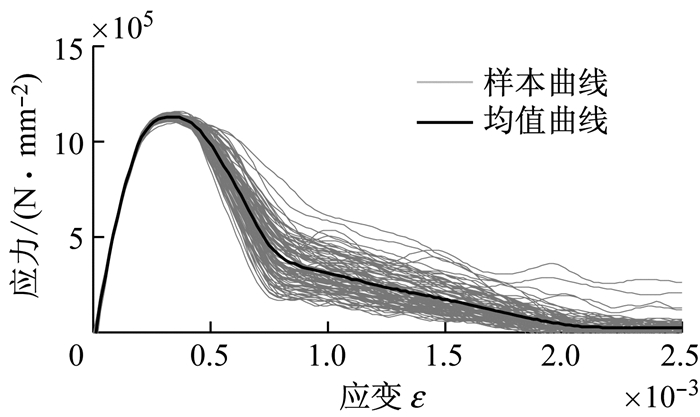
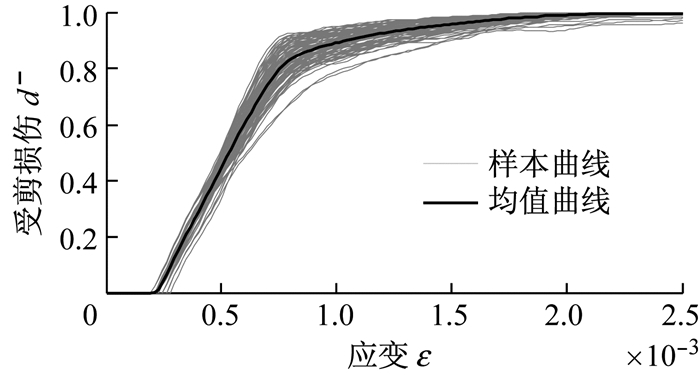
图 13给出了所有样本的受剪均匀化应力应变曲线,其中黑色的曲线代表均值曲线.同时考虑式(16) 给出的纯剪应力作用下的多尺度损伤演化表达.根据细观分析可知:受剪主裂纹开展方向与压应力方向大约为α=45°.采用式(22) 将其转化到受压应力空间,可以给出混凝土受剪损伤演化曲线,如图 14所示.
|
图 13 受剪应力应变曲线及样本均值 Fig.13 Uniaxial tensile stress-strain relationship |
|
图 14 样本受剪应力损伤曲线 Fig.14 Tensile damage curves |
上述细观单元分析给出的应力损伤关系曲线仅给出了弹性应变与损伤之间的一一映射关系,并未给出损伤演化的具体表达式,较难直接应用于工程结构有限元分析中.因此,本节提出了对工程简化的混凝土损伤演化公式,并通过上述多尺度分析结果标定其中参数.
本文建议的统一受拉、受剪损伤公式表示为
| $ {d^ \pm } = 1 - \frac{{{\rho _{{\rm{t}}/{\rm{c}}}}}}{{{\alpha _{{\rm{t}}/{\rm{c}}}}x_{{\rm{t}}/{\rm{c}}}^{1.1{n_{\rm{t}}}/{n_{\rm{c}}}} + {\rho _{{\rm{t}}/{\rm{c}}}}}} $ | (25) |
| $ {\rho _{{\rm{t}}/{\rm{c}}}} = \frac{{{f_{{\rm{t}}/{\rm{c}}}}}}{{E{\varepsilon _{{\rm{t}}/{\rm{c}}}}}} $ | (26) |
| $ {n_{{\rm{t}}/{\rm{c}}}} = \frac{{E{\varepsilon _{{\rm{t}}/{\rm{c}}}}}}{{E{\varepsilon _{{\rm{t}}/{\rm{c}}}} - {f_{{\rm{t}}/{\rm{c}}}}}} $ | (27) |
| $ {x_{{\rm{t}}/{\rm{c}}}} = \frac{\varepsilon }{{{\varepsilon _{{\rm{t}}/{\rm{c}}}}}} $ | (28) |
式中:αt/c为混凝土受拉、受剪损伤发展参数,用以控制应力应变曲线下降段形式;ft/c为混凝土抗拉、抗剪强度.可以根据实际分析取抗拉强度标准值、实测值或设计值,根据REN等[24]试验结果,本例中取抗拉强度ft=3.28 MPa、fc=56 MPa;εt为与单轴抗拉强度ft以及单轴抗压强度fc相应的混凝土峰值拉应变,本例取εt=180×10-6、εc=2 200×10-6;E为混凝土弹性模量,E=37 559 MPa;xt/c为规则化拉、压应变.
根据热力学基本原理,损伤演化方程并不是任意的,需满足某些基本条件[16],即
| $ \left\{ \begin{array}{l} d\left( 0 \right) = 0\;\;\;初始状态下,混凝土无损伤\\ d\left( \infty \right) = 1\;\;\;完全损伤材料的损伤为1\\ \dot d > 0\;\;\;\;\;\;\;\;损伤不可恢复 \end{array} \right. $ | (29) |
根据式(29) 考察给出的实用受拉损伤演化公式为
| $ {d^ \pm }\left( 0 \right) = 1 - \frac{{{\rho _{{\rm{t}}/{\rm{c}}}}}}{{{\rho _{{\rm{t}}/{\rm{c}}}}}} = 0 $ | (30) |
| $ {d^ \pm }\left( \infty \right) = 1 - \frac{{{\rho _{{\rm{t}}/{\rm{c}}}}}}{\infty } = 1 $ | (31) |
| $ \begin{array}{*{20}{c}} {\dot d^ \pm } = \frac{{{\alpha _{{\rm{t}}/{\rm{c}}}}\left( {1.1{n_{{\rm{t/c}}}} - 1} \right){\rho _{{\rm{t}}/{\rm{c}}}}x_{{\rm{t}}/{\rm{c}}}^{\left( {1.1{n_{{\rm{t/c}}}} - 1} \right)}}}{{{{\left( {{\alpha _{{\rm{t}}/{\rm{c}}}}x_{{\rm{t}}/{\rm{c}}}^{1.1{n_{\rm{t/c}}}} + {\rho _{{\rm{t}}/{\rm{c}}}}} \right)}^2}}} > 0\\ {若\;{\alpha _{{\rm{t}}/{\rm{c}}}} \ge 0} \end{array} $ | (32) |
分析表明本文给出的实用损伤演化关系满足损伤演化的基本原则.
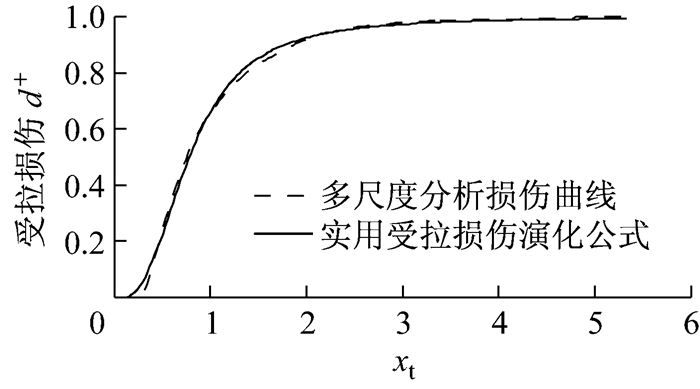
式(25) 中,在确定了ρt/c和xt/c之后,损伤演化过程仅由参数αt/c确定.结合细观随机介质单元多尺度模拟结果,见图 11和图 14,对混凝土损伤发展参数αt/c进行最小二乘识别.采用随机介质模拟所获得的受拉损伤演化曲线作为目标函数,可以获得αt的均值为αt=1.103 0,标准差为σαt=0.352 8.采用随机介质模拟所获得的受剪损伤演化曲线作为目标函数,可以获得均值αc=0.665 4,标准差为σαc=0.147 4.图 15给出了本文提出的实用受拉损伤演化公式与基于随机介质分析所获得的损伤演化均值的对比.图 16给出了本文提出的实用受剪损伤演化公式与基于随机介质分析所获得的受剪损伤演化均值的对比.
|
图 15 实用受拉损伤演化曲线 Fig.15 Pragmatic tensile damage law of concrete |

|
图 16 实用受剪损伤演化曲线 Fig.16 Pragmatic shear damage law of concrete |
可以进一步对受拉、受剪损伤发展参数的概率密度分布进行统计.不妨采用对数正态分布进行描述为
| $ f\left( x \right) = \left\{ \begin{array}{l} \frac{1}{{\sqrt {2{\rm{\pi }}} {\sigma _{{\alpha _{{\rm{t}}/{\rm{c}}}}}}x}}{{\rm{e}}^{ - \frac{{\left( {{\rm{In}}x - {\mu _{{\alpha _{{\rm{t}}/{\rm{c}}}}}}} \right)}}{{2\sigma _{{\alpha _{{\rm{t}}/{\rm{c}}}}}^2}}}},\;\;\;\;x > 0\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (33) |
式中:μαt/c为损伤发展参数αt/c的均值;σαt/c为损伤发展参数αt/c的标准差.
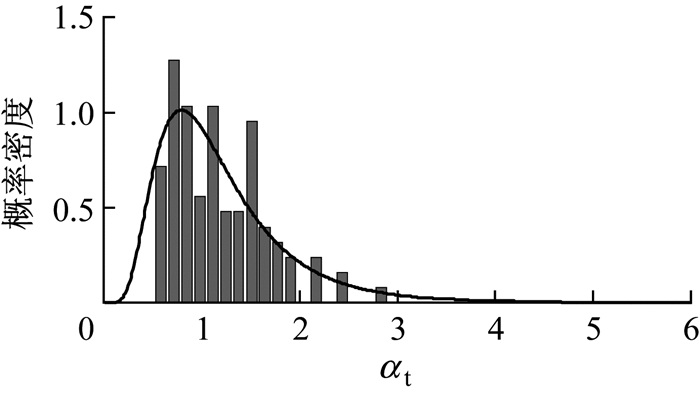
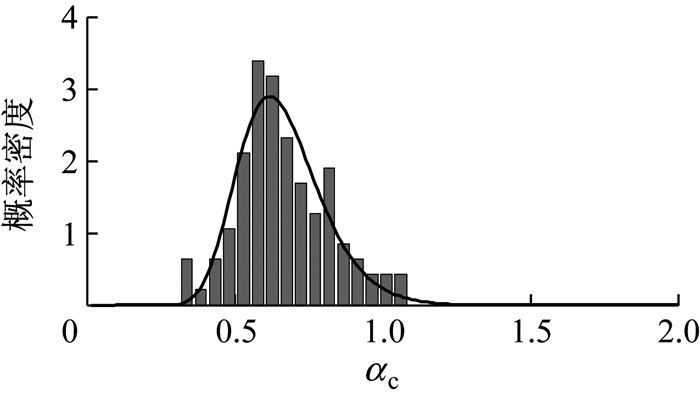
图 17和图 18分别给出了受拉和受剪损伤发展参数的概率密度分布.其中直方图代表细观单元分析所获得的损伤发展参数统计结果,曲线代表本文采用的对数正态分布表示的损伤发展参数的概率分布.
|
图 17 受拉损伤发展参数概率密度分布 Fig.17 Probability distribution of αt |
|
图 18 受剪损伤发展参数概率密度分布 Fig.18 Probability distribution of αc |
在实际分析中,可以将损伤发展参数视为随机变量并采用图 17和图 18给出损伤发展参数的概率密度分布.此时,不仅给出了损伤演化均值变化过程,而且给出了这一变化过程的概率密度描述, 这正是研究随机损伤本构关系的目的之一.同时,采用实用的损伤演化公式并给定其参数分布能够较大程度地简化多尺度损伤本构关系.
最后,给出塑性应变的演化,即可建立完整的实用损伤本构模型, 有
| $ \sigma = \left( {1 - {d^ \pm }} \right)E\left( {\varepsilon - {\varepsilon ^p}} \right) $ | (34) |
式中,εp为塑性应变,表达式为[7]
| $ \left\{ \begin{array}{l} {\varepsilon ^{p + }} = 0\\ {\varepsilon ^{p - }} = {\xi _p}{\varepsilon ^{e - }} \end{array} \right. $ | (35) |
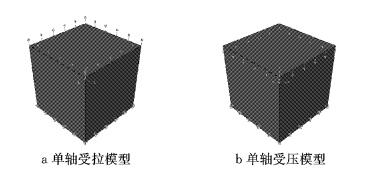
通过混凝土宏观试验结果,验证了给出的多尺度损伤本构模型的正确性.数值模型中,混凝土弹性参数、损伤演化公式(式(25))中参数选取与第3节选取参数相同.塑性变形通过式(35) 给出的实用公式计算,ξp=0.2.在数值算例中,将损伤演化规律公式采用式(25) 与弹塑性损伤本构[26]结合,编制相应的UMAT并采用ABAQUS进行数值计算.利用ABAQUS计算了单个实体单元的单轴受拉试验结果.单元尺寸与试验一致,为100 mm×100 mm×100 mm.ABAQUS模拟中采用位移加载.图 19给出了ABAQUS数值模型与边界条件.
|
图 19 单轴拉压数值模型与边界条件 Fig.19 Numerical models and boundary conditions |
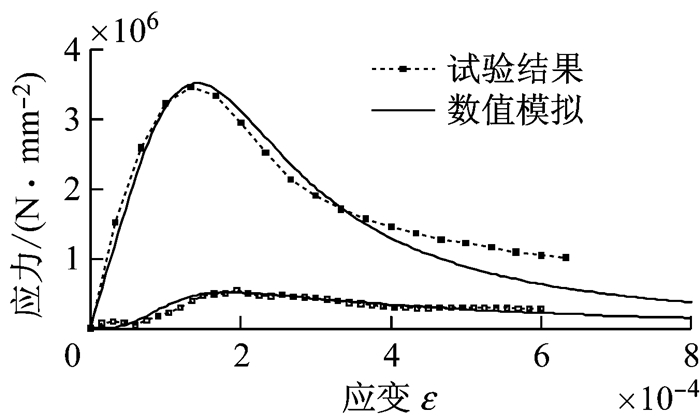
图 20与图 21给出了混凝土单轴受拉和单轴受压情况下的模拟分析结果.数值模拟结果在均值和标准差意义上均与试验结果具有较好的一致性,充分说明了模型可以反映混凝土力学性能存在的离散性,为多尺度随机本构关系在工程实际中的应用奠定了基础.同时,宏观数值模拟中采用的损伤参数来自于细观结构的多尺度模拟,这说明多尺度损伤本构能够较好地预测混凝土的非线性行为.
|
图 20 单轴受拉模拟结果 Fig.20 Simulation results of uniaxial tensile test |

|
图 21 单轴受压模拟结果 Fig.21 Simulation results of uniaxial compressive test |
给出了基于多尺度分析的混凝土随机损伤本构模型.首先,应用了多尺度能量积分与多尺度损伤表达.通过单相介质随机场建立了混凝土细观单元,分别给出了混凝土受拉、受剪两类细观单元的数值模拟并给出了均匀化的应力应变关系与损伤演化曲线.建议了一类实用的损伤演化公式,并确定了随机损伤演化参数的均值、标准差以及概率密度分布.通过对混凝土宏观试验的模拟,验证了给出的多尺度损伤本构模型的正确性.为将多尺度理论应用于混凝土结构分析,提供了一定的理论基础.以期适用于混凝土结构的非线性分析,便于工程应用.
| [1] |
李杰. 混凝土随机损伤力学的初步研究[J]. 同济大学学报(自然科学版), 2004, 32(10): 1270 LI Jie. Research on the stochastic damage mechanics for concrete materials and structures[J]. Journal of Tongji University (Natural Science), 2004, 32(10): 1270 DOI:10.3321/j.issn:0253-374X.2004.10.002 |
| [2] |
BREYSSE D. Probabilistic formulation of damage-evolution law of cementitious composites[J]. Journal of Engineering Mechanics, 1990, 116(7): 1489 DOI:10.1061/(ASCE)0733-9399(1990)116:7(1489) |
| [3] |
KANDARPA S, KIRKNER D J, SPENCER B F, et al. Stochastic damage model for brittle materials subjected to monotonic loading[J]. Journal of Engineering Mechanics, 1996, 122(8): 788 DOI:10.1061/(ASCE)0733-9399(1996)122:8(788) |
| [4] |
李杰, 张其云. 混凝土随机损伤本构关系[J]. 同济大学学报(自然科学版), 2001, 29(10): 1135 LI Jie, ZHANG Qiyun. Study of stochastic damage constitutive relationship for concrete material[J]. Journal of Tongji University (Natural Science), 2001, 29(10): 1135 DOI:10.3321/j.issn:0253-374X.2001.10.001 |
| [5] |
李杰, 卢朝辉, 张其云. 混凝土随机损伤本构关系——单轴受压分析[J]. 同济大学学报(自然科学版), 2003, 31(5): 505 LI Jie, LU Zhaohui, ZHANG Qiyun. Study on stochastic damage constitutive law for concrete material subjected to uniaxial compressive stress[J]. Journal of Tongji University (Natural Science), 2003, 31(5): 505 |
| [6] |
李杰, 杨卫忠. 混凝土弹塑性随机损伤本构关系研究[J]. 土木工程学报, 2009, 42(2): 31 LI Jie, YANG Weizhong. Elastoplastic stochastic damage constitutive law for concrete[J]. China Civil Engineering Journal, 2009, 42(2): 31 |
| [7] |
LI J, REN X. Stochastic damage model for concrete based on energy equivalent strain[J]. International Journal of Solids and Structures, 2009, 46(11): 2407 |
| [8] |
ALLEN D H, JONES R H, BOYD J G. Micromechanical analysis of a continuous fiber metal matrix composite including the effects of matrix viscoplasticity and evolving damage[J]. Journal of the Mechanics and Physics of Solids, 1994, 42(3): 505 DOI:10.1016/0022-5096(94)90029-9 |
| [9] |
VOYIADJIS G Z, PARK T. Elasto-plastic stress and strain concentration tensors for damaged fibrous composites[J]. Studies in Applied Mechanics, 1996, 44: 81 DOI:10.1016/S0922-5382(96)80006-7 |
| [10] |
FISH J, WAGIMAN A. Multiscale finite element method for a periodic and non-periodic heterogeneous medium[J]. ASME Applied Mechanics Division Publication, 1993, 157(6): 95 |
| [11] |
DASCALU C, BILBIE G. A multiscale approach to damage configurational forces[J]. International Journal of Fracture, 2007, 147(1-4): 285 DOI:10.1007/s10704-008-9189-3 |
| [12] |
REN X, CHEN J, LI J, et al. Micro-cracks informed damage models for brittle solids[J]. International Journal of Solids and Structures, 2011, 48(10): 1560 DOI:10.1016/j.ijsolstr.2011.02.001 |
| [13] |
FENG X Q, YU S W. Damage micromechanics for constitutive relations and failure of microcracked quasi-brittle materials[J]. International Journal of Damage Mechanics, 2010, 19(8): 911 DOI:10.1177/1056789509359662 |
| [14] |
范镜泓. 材料变形与破坏的多尺度分析[M]. 北京: 科学出版社, 2008 FAN Jinghong. Multiscale analysis for deformation and failure of material[M]. Beijing: Science Press, 2008 |
| [15] |
LI J, REN X D. Homogenization-based multi-scale damage theory[J]. Science China Physics, Mechanics and Astronomy, 2010, 53(4): 690 DOI:10.1007/s11433-010-0160-8 |
| [16] |
李杰, 陈建兵, 吴建营. 混凝土随机损伤力学[M]. 北京: 科学出版社, 2014 LI Jie, CHEN Jianbing, WU Jianying. Stochastic damage mechanics of concrete structures[M]. Beijing: Science Press, 2014 |
| [17] |
RESENDE L. A damage mechanics constitutive theory for the inelastic behaviour of concrete[J]. Computer Methods in Applied Mechanics and Engineering, 1987, 60(1): 57 DOI:10.1016/0045-7825(87)90130-7 |
| [18] |
梁诗雪, 孙伟玲, 李杰. 随机场的随机谐和函数表达[J]. 同济大学学报(自然科学版), 2012, 40(7): 965 LIANG Shixue, SUN Weiling, LI Jie. Simulation of multi-dimensional random fields by stochastic harmonic functions[J]. Journal of Tongji University (Natural Science), 2012, 40(7): 965 |
| [19] |
HILLERBORG A, MODÉER M, PETERSSON P. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J]. Cement and Concrete Research, 1976, 6(6): 773 DOI:10.1016/0008-8846(76)90007-7 |
| [20] |
BAZANT Z P. Size effect in blunt fracture: concrete, rock, metal[J]. Journal of Engineering Mechanics, 1984, 110(4): 518 DOI:10.1061/(ASCE)0733-9399(1984)110:4(518) |
| [21] |
SHINOZUKA M, DEODATIS G. Simulation of multi-dimensional Gaussian stochastic fields by spectral representation[J]. Applied Mechanics Reviews, 1996, 49(1): 29 DOI:10.1115/1.3101883 |
| [22] |
YANG Z J, SU X T, CHEN J F, et al. Monte-Carlo simulation of complex cohesive fracture in random heterogeneous quasi-brittle materials[J]. International Journal of Solids and Structures, 2009, 46(17): 3222 DOI:10.1016/j.ijsolstr.2009.04.013 |
| [23] |
BAZANT Z P, PLANAS J. Fracture and size effect in concrete and other quasibrittle materials[M]. Boca Raton: CRC Press, 1997
|
| [24] |
REN X D, YANG W Z, ZHOU Y, et al. Behavior of high-performance concrete under uniaxial and biaxial loading[J]. ACI Materials Journal, 2008, 105(6): 548 |
| [25] |
LIANG S X, REN X D, LI J. A random medium model for simulation of concrete failure[J]. Science China Technological Sciences, 2013, 56(5): 1273 DOI:10.1007/s11431-013-5200-y |
| [26] |
李杰, 吴建营. 混凝土弹塑性损伤本构模型研究Ⅰ:基本公式[J]. 土木工程学报, 2006, 38(9): 14 LI Jie, WU Jianying. Elastoplastic damage constitutive model for concrete based on damage energy release rates, Part Ⅰ: Basic formulations[J]. China Civil Engineering Journal, 2006, 38(9): 14 |
 2017, Vol. 45
2017, Vol. 45

