2. 同济大学 岩土工程与地下结构教育部重点实验室, 上海 200092
2. Key Laboratory of Geotechnical and Underground Engineering of the Ministry of Education, Tongji University, Shanghai 200092, China
加筋垫层法作为一种浅层天然地基处理方法,常用于路堤工程中改善软土地基的受力状况,提高路堤的稳定性[1],而在加筋垫层路堤设计中,稳定性分析是其中一项重要内容.对于加筋路堤,研究人员通常采用足尺试验[2-3]、离心机模型试验[4]、有限元数值模拟[5-6]以及模型试验与有限单元法相结合[7-8]的方法进行稳定性分析.该类方法虽然比较符合工程实际,计算结果较为准确,但不利于工程运用及推广,因此,需要对考虑较为全面的稳定性分析简化计算方法进行探讨,以满足工程人员对计算准确度及应用推广的要求.
路堤施工过程中天然地基土体在外荷载作用下会进行再固结.林孔锱[9]、沈珠江等[10]认为软土地基潜在滑动面上的有效固结应力是影响其土体抗剪强度的关键因素;TANCHAISAWAT等[3]和ROWE等[8]也分别通过足尺试验和现场监测并结合有限元数值模拟的方法证实了软基在路堤施工过程中超孔隙水压力和固结程度的变化会对加筋路堤稳定性产生影响.除了地基土固结因素以外,在稳定性分析中如何考虑筋材加筋作用对稳定性的贡献也是一个影响软基加筋路堤稳定性评价差异程度的关键因素.ROWE[11]提出“允许相容应变”概念,认为在稳定性分析中应考虑到土体与筋材之间的应变协调作用;随后JURAN[12]在此理论基础上又综合考虑了土的剪胀及筋材的变形,提出了改进的“位移法”稳定性计算理论;朱湘等[13]结合直剪试验和力学分析,认为筋材拉力对局部地基土体的抗剪强度有促进作用.可见,分析加筋垫层对软基路堤稳定性的影响时,不能仅按照传统的加筋路堤稳定性分析理论简单地将加筋垫层作用简化为作用在滑动面上的水平拉力,而不考虑筋材与土体间的相互作用,忽略筋材拉力对土体抗剪强度的影响.
基于以上分析,软基加筋垫层路堤稳定性分析应考虑地基土在附加荷载作用下固结的影响,同时应全面考虑加筋垫层对路堤稳定性的贡献.目前国内路基工程相关规范[14-15]中的加筋路堤稳定性验算公式主要是针对加筋土边坡和加筋土挡墙结构形式的加筋路堤,但软基加筋垫层路堤的工作机理和破坏模式却不同于加筋土边坡和加筋土挡墙.一些国内标准[16-17]及英国规范BS8006[18]虽给出了加筋垫层路堤的稳定性计算公式,但这些公式或者是未考虑软基固结对土体抗剪强度的影响,或者是对加筋垫层作用考虑的不够全面,因此,本文全面考虑加筋垫层作用,对现有的有效固结应力法稳定性验算公式[16]进行改进,利用编写的软基路堤稳定性计算程序对工程案例进行不同工况条件下的稳定性计算.最后,通过对计算结果进行对比分析讨论了本文提出的改进公式与现有公式的差异及其适用性.
1 软基加筋垫层路堤的有效固结应力法分析原理 1.1 软基路堤稳定性分析的有效固结应力原理天然状态下,软土地基在其自重作用下已经固结.路堤进行分期填筑的施工过程中,软基又将在填土荷载、施工荷载等附加应力的作用下进行再固结,这一过程中路堤的整体稳定性取决于潜在滑动面上有效固结应力的大小.有效固结应力法既能够考虑在施工过程中路堤填土对地基土体有效应力增长的有利因素,又能兼顾地基土体在不排水破坏过程中剪切引起的孔压对其稳定性产生的不利影响[9],所以,相较总应力法和有效应力法,该方法更加适合进行软基加筋垫层路堤的稳定性分析.
根据有效固结应力理论[9-10],地基土在破坏之前固结状态下的有效应力直接影响土体的抗剪强度,且土体从固结状态发展到破坏状态的过程迅速,土体的含水量来不及变化.因此,软基加筋垫层路堤稳定性分析的有效固结应力法宜采用土体的不排水抗剪强度指标进行计算.
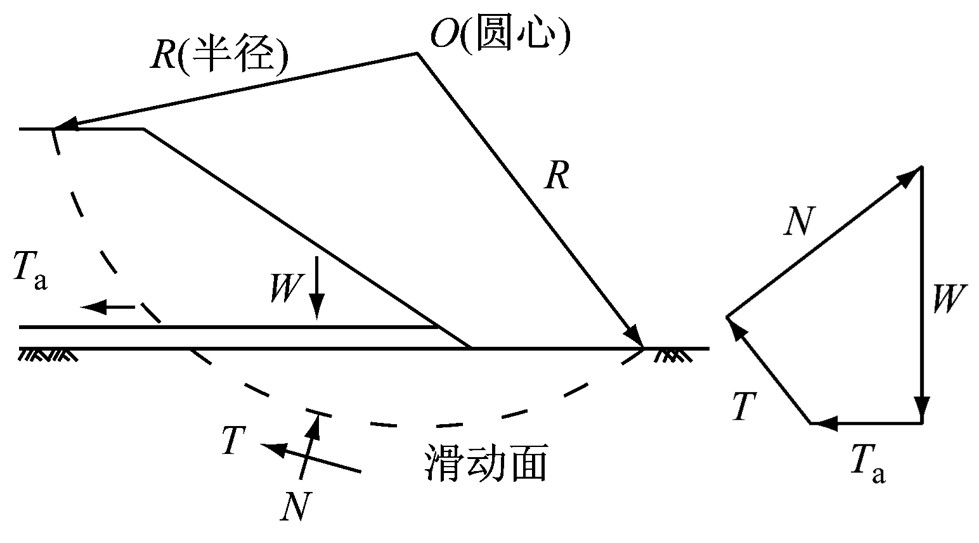
1.2 加筋垫层作用的力学原理如图 1所示,极限平衡状态下,加筋垫层路堤在重力W、支持力N、抗剪力T以及筋材拉力Ta的共同作用下保持平衡.
|
图 1 加筋垫层路堤稳定性分析受力简图 Fig.1 Stress analysis of reinforced embankment over soft foundation soils in stability calculation |
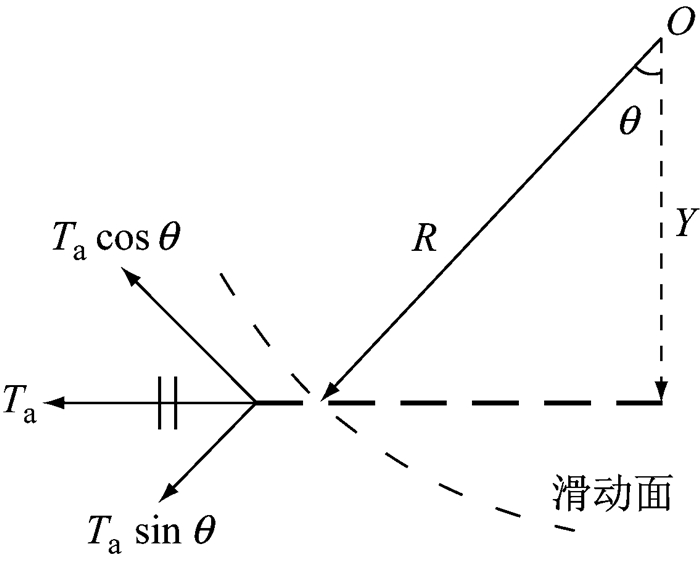
软基路堤底部加筋垫层中的筋材受力情况如图 2所示,筋材主要承受拉力作用,其受拉时在土体潜在滑动面上同时产生一个抵抗土体滑动的切向抗滑力Tacosθ和一个增强土体抗剪强度的法向附加正应力Tasinθ.
|
图 2 筋材受力分析 Fig.2 Stress analysis of reinforcement |
根据圆弧滑动面法,当考虑加筋垫层作用对软基路堤稳定性的影响时,与未进行加筋处理的软基路堤相比,潜在滑动面上的总滑动力矩不变,总抗滑力矩增加,且其增量由以下两部分组成.
筋材拉力的切向抗滑力作用MR1为
| $ \Delta {M_{{\rm{R1}}}} = {T_{\rm{a}}}\cos \theta R = {T_{\rm{a}}}Y $ | (1) |
筋材拉力的法向附加正应力作用ΔMR2为
| $ \Delta {M_{{\rm{R2}}}} = {T_{\rm{a}}}\sin \theta \tan \varphi R $ | (2) |
式中:Ta为极限状态下加筋垫层中筋材提供的张拉力;θ为筋材拉力法向分量与竖直方向的夹角;Y为筋材到滑弧圆心的垂直距离;R为最危险滑动面半径;φ为土体的内摩擦角.
因此,加筋垫层中筋材的加筋作用对路堤整体稳定性的贡献有两部分:一部分是筋材张拉力的切向分量提供的抗滑力矩TaY,是由于当滑裂面通过加筋垫层时,筋材受到剪切作用产生拉应变,其切向分量的方向与土体的剪切方向一致,能直接提供抵抗土体剪切应力的拉应力;另一部分是筋材张拉力的法向分量提供的抗滑力矩TaRsinθtanφ,是由于加筋垫层受剪时,筋材张拉力会在在潜在滑动面上产生一个法向附加正应力,附加正应力会提高剪切面上的摩擦反力增加土体的抗剪强度.
传统的加筋路堤稳定性计算公式[14-16, 18]将筋材作用均简化为作用在滑动土体上的水平拉力,只单独考虑筋材拉力对稳定性的影响,认为筋材对路堤稳定性的贡献仅仅就是筋材张拉力提供的抗滑力矩TaY,未将筋材作用纳入整个加筋垫层体系去考虑其对路堤稳定性的影响,忽略了筋材拉力使土体抗剪强度增加对路堤稳定性的贡献.所以,加筋垫层路堤稳定性分析应全面考虑加筋垫层中筋材的力学作用.
2 有效固结应力法公式改进基于公路标准[16]中软基路堤稳定性分析的有效固结应力法,考虑路堤底部加筋垫层的加筋作用,软基上加筋垫层路堤稳定性分析的有效固结应力法的力学计算如图 3所示,WⅠi、WⅡi分别为土条i地基部分、路堤部分的重力.

|
图 3 加筋垫层路堤有效固结应力法力学计算简图 Fig.3 Mechanical calculation diagram of reinforced embankment over soft foundation soils with effective consolidation stress method |
(1) 引用瑞典条分法的计算假设:假设滑动面为圆柱面,滑动体为刚体,不考虑土条两侧土体的法向和切向作用力.
(2) 根据相关文献研究[7, 19]可假设筋材拉力为线性分布,土条两侧筋材拉力差值为ΔTai,若滑动体内筋材穿过的土条数为m,则ΔTai=Ta/m.
2.2 力学计算分析参考公路标准[16]中无筋路堤的有效固结应力法,当考虑加筋垫层作用时,筋材拉力只是增加了滑动面上的总抗滑力矩,并不影响总滑动力矩及土体自身抗剪强度产生的抗滑力矩,所以,基于现有的有效固结应力法公式[16],只需对考虑筋材作用下的总抗滑力矩进行分析计算,即可得出加筋垫层路堤稳定性分析的有效固结应力法公式.
公路标准[16]中潜在滑动面上滑动土体的总滑动力矩Ms与土体自身抗剪强度产生的抗滑力矩MRS分别如式(3)、式(4) 所示.
| $ {M_{\rm{S}}} = \sum\nolimits_A^B {{{\left( {{W_{\rm{I}}} + {W_{{\rm{II}}}}} \right)}_i}R\sin {\partial _i}} + \sum\nolimits_B^C {{W_{{\rm{II}}i}}R\sin {\partial _i}} $ | (3) |
| $ \begin{array}{l} {M_{{\rm{RS}}}} = \sum\nolimits_A^B {\left[ {\left( {{W_{{\rm{I}}i}}\cos {\partial _i}\tan {\varphi _{{\rm{qi}}}} + {W_{{\rm{II}}i}}{U_i}\cos {\partial _i} \cdot } \right.} \right.} \\ \;\;\;\;\;\;\;\;\;\left. {\left. {\tan {\varphi _{{\rm{cqi}}}}} \right) + {c_{{\rm{qi}}}}{l_i}} \right]R + \sum\nolimits_B^C {\left( {{W_{{\rm{II}}i}}\cos {\partial _i} \cdot } \right.} \\ \;\;\;\;\;\;\;\;\;\left. {\tan {\varphi _{{\rm{qi}}}} + {c_{{\rm{qi}}}}{l_i}} \right)R \end{array} $ | (4) |
式中:∂i为土条底面中点oi到滑动面圆心O连线与竖直方向的夹角; Ui为地基土平均固结度;li为土条i底面弧长;cqi、φqi为地基土或路堤填土快剪强度指标;φcqi为地基土固结快剪强度指标.
如图 3a所示,由于各土层土体的力学特性不同,将滑动面圆弧按照穿过的土层分为地基土部分和路堤填土部分即AB弧段和BC弧段分别计算.取滑动体中的第i个土条进行受力分析,如图 3b所示,将土条所受的作用力汇交至第i个滑弧li的中点oi进行静力平衡分析;其中土条重力Wi、支持力Ni、抗滑力Ti的作用点均在oi,仅需对土条两侧筋材的拉力增量ΔTai=Tai-Ta(i-1)进行静力等效处理;然后求出筋材作用产生的抗滑力矩增量,根据极限平衡法推导出稳定性安全系数的计算公式.
2.3 计算筋材拉力作用产生的抗滑力矩增量土条i的受力分析如图 3b所示,考虑加筋垫层作用时土条两侧筋材的拉力增量ΔTai所产生的抗滑力矩增量可由其切向分量ΔTaicos∂i及法向分量ΔTaisin ∂i分别来计算;此外,ΔTai对滑弧li的中点oi进行静力等效变换时产生的一个附加力矩-ΔTai(Rcos∂i-Y)也应考虑到其中.
(1) AB弧段内ΔTai产生的抗滑力矩
由式(1) 可得ΔTai切向分量抗滑力矩MRT1为
| $ {M_{{\rm{RT}}1}} = \sum\nolimits_A^B {\Delta {T_{{\rm{a}}i}}R\cos {\partial _i}} $ | (5) |
由式(2) 可得ΔTai法向分量抗滑力矩MRT2为
| $ {M_{{\rm{RT}}2}} = \sum\nolimits_A^B {\Delta {T_{{\rm{a}}i}}R\sin {\partial _i}\tan {\varphi _{qi}}} $ | (6) |
静力等效变换产生的附加力矩MRT3为
| $ {M_{{\rm{RT}}3}} = - \sum\nolimits_A^B {\Delta {T_{{\rm{a}}i}}\left( {R\cos {\partial _i} - Y} \right)} $ | (7) |
则由式(5)~(7) 可得,AB弧段内ΔTai产生的抗滑力矩MRR1为
| $ \begin{array}{l} {M_{{\rm{RR}}1}} = {M_{{\rm{RT}}1}} + {M_{{\rm{RT}}2}} + {M_{{\rm{RT}}3}} = \\ \;\;\;\;\;\;\;\;\;\;\;\sum\nolimits_A^B {\Delta {T_{{\rm{a}}i}}R\sin {\partial _i}\tan {\varphi _{qi}}} + \sum\nolimits_A^B {\Delta {T_{{\rm{a}}i}}Y} \end{array} $ | (8) |
(2) BC弧段内ΔTai产生的抗滑力矩
参考AB弧段内相关公式的推导过程,则BC弧段内ΔTai产生的抗滑力矩MRR2为
| $ {M_{{\rm{RR}}2}} = \sum\nolimits_B^C {\Delta {T_{{\rm{a}}i}}R\sin {\partial _i}\tan {\varphi _{{\rm {q}}i}}} + \sum\nolimits_B^C {\Delta {T_{{\rm{a}}i}}Y\left( 9 \right)} $ | (9) |
(3) 滑动面上筋材拉力Ta产生的抗滑力矩
相对于整个滑动土体而言, 土条i两侧的ΔTai属于内力,则在整个滑动面上有
| $ \sum\nolimits_A^B {\Delta {T_{{\rm{a}}i}}Y} + \sum\nolimits_B^C {\Delta {T_{{\rm{a}}i}}} = {T_{\rm{a}}} $ | (10) |
所以,由式(8)~(10) 可得,圆弧滑动面上筋材拉力Ta产生的总抗滑力矩增量MRR为
| $ \begin{array}{l} {M_{{\rm{RR}}}} = {M_{{\rm{RR}}1}} + {M_{{\rm{RR}}2}}\\ \;\;\;\;\;\;\;\;\;\;\;\sum\nolimits_A^C {\Delta {T_{{\rm{a}}i}}R\sin {\partial _i}\tan {\varphi _{{\rm q}i}}} + {T_{\rm{a}}}Y \end{array} $ | (11) |
根据圆弧滑动面法,软基上加筋垫层路堤整体稳定性安全系数为滑动土体总抗滑力矩与总滑动力矩的比值,则由式(3)、式(4) 及式(11) 可得
| $ {F_{\rm{S}}} = \frac{{{M_{{\rm{RS}}}} + {M_{{\rm{RR}}}}}}{{{M_{\rm{S}}}}} = \frac{\begin{array}{l} \sum\nolimits_A^B {\left[ {\left( {{W_{{\rm{I}}i}}\cos {\partial _i}\tan {\varphi _{{{\rm q}i}}} + {W_{{\rm{II}}i}}{U_i}\cos {\partial _i}\tan {\varphi _{cqi}}} \right) + {c_{{{\rm q}i}}}{l_i}} \right] + } \\ \sum\nolimits_B^C {\left( {{W_{{\rm{II}}i}}\cos {\partial _i}\tan {\varphi _{{{\rm q}i}}} + {c_{{{\rm q}i}}}{l_i}} \right)} + \sum\nolimits_A^C {\Delta {T_{{\rm{a}}i}}R\sin {\partial _i}\tan {\varphi _{{\rm q}i}}} + {T_a}\cos \theta \end{array}}{{\sum\nolimits_A^B {{{\left( {{W_{\rm{I}}} + {W_{{\rm{II}}}}} \right)}_i}\sin {\partial _i}} + \sum\nolimits_B^C {{W_{{\rm{II}}i}}\sin {\partial _i}} }} $ | (12) |
式(12) 即为改进后的有效固结应力法公式.该公式与传统的加筋路堤稳定性验算公式[14-16]相比,采用了有效固结应力理论考虑了地基在路堤施工过程中固结对土体抗剪强度的影响,并全面考虑了加筋垫层作用.与BS8006法[18]相比,该公式考虑了加筋垫层中筋材法向作用力对土体抗剪强度的影响.与相关标准中的改进的稳定性计算方法[17]相比,该公式应用有效固结应力替代总应力来计算地基土体的抗剪强度,更加符合工程实际情况.
3 工程算例对比分析规范[14]给出了一般结构形式的加筋路堤稳定性验算公式,即
| $ {F_{\rm{S}}} = {F_{{\rm{S0}}}} + \frac{{\sum {{T_{{\rm{a}}j}}{Y_j}} }}{{{M_{\rm{S}}}}} $ | (13) |
式中:FS0为未加筋时的稳定性安全系数;Taj为第j层筋材提供的拉力;Yj为第j层筋材到滑动面圆心的垂直距离.
该规范中规定未加筋时路堤的稳定性安全系数FS0采用公路标准[16]规定的方法计算;若采用该规范中的有效固结应力法计算FS0,并将加筋垫层视为路堤底部铺设的单层筋材;则加筋垫层路堤的稳定性验算公式可写为
| $ {F_{\rm{S}}} = \frac{{{M_{\rm{R}}}}}{{{M_{\rm{S}}}}} = \frac{{{M_{{\rm{RS}}}} + {T_{\rm{a}}}Y}}{{{M_{\rm{S}}}}} $ | (14) |
与改进式(12) 相比,式(14) 的分子少了一项
若令ΔFS=
下面将利用编写的计算机程序进行工程算例分析,讨论改进公式与公路土工合成材料应用标准中的公式相比对路堤稳定性安全系数的影响程度.
3.1 工程实例计算某软土地基上修建的加筋垫层路堤,其设计填筑高度为H=6.0 m,顶部宽度B=32.0 m,路堤边坡坡度为1:1.5,采用土工格栅加筋垫层进行路基处理, 其计算如图 4所示.

|
图 4 工程实例计算简图 Fig.4 Calculation diagram of engineering project |
由分项
| 下载CSV 表 1 不同土层参数条件下的路堤稳定性计算结果(地基土重度γ1=17 kN·m-3,填土重度γ2=20 kN·m-3,筋材拉力Ta=50 kN·m-1) Tab.1 Safety factor of embankment stability using different soil parameters (gravity of foundation soil γ1=17 kN·m-3, gravity of fill γ2=20 kN·m-3, tensile force of reinforcement Ta=50 kN·m-1) |
| 下载CSV 表 2 不同筋材拉力条件下的路堤稳定性计算结果 Tab.2 Safety factor of embankment stability using different tension of reinforcement(γ1=17 kN·m-3, γ2=20 kN·m-3, cq1=5 kPa, φq1=10°, U=60%, cq2=20 kPa, φq2=30°) |
各工况条件下FS均大于FS1,说明改进公式能更加全面地体现加筋垫层对路堤稳定性提高的促进作用.由表 1可以看出,随着地基软土及路堤填土内摩擦角的增大,ΔFS、S均有不同程度地增加,表明改进公式与规范公式[14]计算出的安全系数差值随着滑动面上土体内摩擦角的增大而增大,其占加筋作用对路堤稳定性贡献的比例也随之增加.当地基软土及路堤填土的内摩擦角较小时,如工况①,改进公式与规范公式的安全系数计算值相差0.008 5,其占加筋作用对路堤稳定性贡献的比例只有7.2%,此时可不考虑筋材拉力法向分量对路堤稳定性贡献.当地基软土及路堤填土的内摩擦角较大时,如工况⑤,改进公式与规范公式的安全系数计算值相差0.020 6,其占加筋垫层对路堤稳定性贡献的比例达到了17.6%,此时若忽略筋材拉力法向分量对路堤稳定性贡献显然是不合理的.
由表 2的计算结果可以看出,在土层参数相同的条件下,随着加筋垫层中筋材提供的拉力值的增加,虽然S不变,但ΔFS却持续增加.当Ta较小时,如工况⑥,ΔFS只有0.006 2,可忽略筋材拉力法向分量对稳定性提高的促进作用;但当Ta较大时,如工况⑩,ΔFS可达0.031,此时则应全面考虑加筋垫层作用对路堤稳定性贡献.
4 结论加筋垫层路堤分期填筑施工过程中,潜在滑动面上固结状态下的有效应力是影响其整体稳定性的关键因素.此外,加筋垫层对路堤稳定性的提高不仅仅是由于筋材拉力直接提供了一个抗滑力矩,其加筋作用对土体抗剪强度的增加也是另一个影响稳定性的重要因素.因此,软基加筋垫层路堤的稳定性分析应综合考虑以上两个因素.
全面考虑加筋垫层对路堤稳定性提高的促进作用,对现有的有效固结应力法公式进行了改进;通过工程案例的编程计算分析得出:当地基土及路堤填土的内摩擦角较小、加筋垫层中筋材提供的拉力值较小时,可忽略加筋作用使土体抗剪强度增加对路堤整体稳定性的影响.反之,当滑动面上土体的内摩擦角较大,且加筋垫层设计中筋材可提供的拉力值较大时,则应同时考虑加筋垫层对路堤稳定性提高两方面的促进作用,宜采用改进有效固结应力法公式计算路堤的整体稳定性安全系数.
| [1] |
HIRD C C, RUSSELL D, JEWELL R A. The stability of single-stage constructed reinforced embankments on soft clay[J]. Geotechnical Engineering, 1997, 125(4): 191 |
| [2] |
CHEN Jianfeng, LIU Junxiu, XUE Jianfeng, et al. Failure analyses of a reinforced embankment by strength reduction and limit equilibrium methods considering hardening of soft clay[J]. KSCE Journal of Civil Engineering, 2014, 18(7): 2043 DOI:10.1007/s12205-014-0288-6 |
| [3] |
TANCHAISAWAT T, BERGADO D T, VOOTTIPRUEX P. 2D and 3D simulation of geogrid-reinforced geocomposite material embankment on soft Bangkok clay[J]. Geosynthetics International, 2009, 16(6): 420 DOI:10.1680/gein.2009.16.6.420 |
| [4] |
CHEN Jianfeng, YU Songbo. Centrifugal and numerical modeling of a reinforced lime-stabilized soil embankment on soft clay with wick drains[J]. International Journal of Geomechanics, 2011, 11(3): 167 DOI:10.1061/(ASCE)GM.1943-5622.0000045 |
| [5] |
BORGES J L, CARDSOSO A S. Overall stability of geosynthetic-reinforced embankments on soft soils[J]. Geotextiles and Geomembranes, 2002, 20(6): 395 DOI:10.1016/S0266-1144(02)00014-6 |
| [6] |
WULANDARI P S, TJANDRA D. Analysis of geotextile reinforced road embankment using PLAXIS 2D [C] // 5th Euro Asia Civil Engineering Forum. Surabaya: Pevita Harapan University & Atma Jaya Yogyakarta University, 2015: 358-362. http://www.sciencedirect.com/science/article/pii/S1877705815033925?via%3Dihub
|
| [7] |
EI-NAGGAR M E, KENNEDY J B. New design method for reinforced sloped embankments[J]. Engineering Structures, 1997, 19(1): 28 DOI:10.1016/S0141-0296(96)00048-X |
| [8] |
ROWE R K, LI A. Geosynthetic-reinforced embankments over soft foundations[J]. Geosynthetics International, 2005, 12(1): 50 DOI:10.1680/gein.2005.12.1.50 |
| [9] |
林孔锱. 预压地基的强度增长与稳定计算问题[J]. 岩土工程学报, 1998, 20(1): 93 LIN Kongzi. Strength increase and stability analysis of preloading foundation[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(1): 93 |
| [10] |
沈珠江. 软土工程特性和软土地基设计[J]. 岩土工程学报, 1998, 20(1): 100 SHEN Zhujiang. Engineering properties of soft soils and design of soft ground[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(1): 100 |
| [11] |
ROWE R K. An approximate method for estimating the stability of geotextile-reinforced embankments[J]. Canadian Geotechnical Journal, 1985, 22(3): 392 DOI:10.1139/t85-050 |
| [12] |
JURAN I, IDER H M, FARRAG K. Strain compatibility analysis for geosynthetics reinforced soil walls[J]. Journal of Geotechnical Engineering-ASCE, 1990, 116(2): 312 DOI:10.1061/(ASCE)0733-9410(1990)116:2(312) |
| [13] |
朱湘, 黄晓明, 邓学钧. 加筋路堤圆弧滑动稳定性验算公式的改进[J]. 东南大学学报, 1999, 29(5): 109 ZHU Xiang, HUANG Xiaoming, DENG Xuejun. An improved formula of conventional slip circle analysis in reinforced embankments[J]. Journal of Southeast University, 1999, 29(5): 109 DOI:10.3969/j.issn.1001-0505.1999.05.023 |
| [14] |
中华人民共和国交通运输部. 公路土工合成材料应用技术规范: JTG/T D32—2012 [S]. 北京: 人民交通出版社, 2012. Ministry of Transport of the People's Republic of China. Technical specifications for application of geosynthetics in highway: JTG/T D32—2012 [S]. Beijing: China Communications Press, 2012. |
| [15] |
中华人民共和国铁道部. 铁路路基土工合成材料应用技术规范: TB 10118—2006 [S]. 北京: 中国铁道出版社, 2006. Ministry of Railways of the People's Republic of China. Code for design for applications of geosynthetics on subgrade of railway: TB 10118—2006 [S]. Beijing: Chinese Railway Press, 2006. |
| [16] |
中华人民共和国交通运输部. 公路软土地基路堤设计与施工技术细则: JTG/T D31-02—2013 [S]. 北京: 人民交通出版社, 2013. Ministry of Transport of the People's Republic of China. Technical guidelines for design and construction of highway embankment on soft ground: JTG/T D31-02—2013 [S]. Beijing: China Communications Press, 2013. |
| [17] |
浙江省质量技术监督局. 公路软土地基路堤设计规范: DB33 T 904—2013 [S]. 北京: 人民交通出版社, 2014. Technology Supervision Bureau of Zhejiang Province. Code for design of highway embankment on soft ground: DB 33 T 904—2013 [S]. Beijing: China Communications Press, 2014. |
| [18] |
British Standard Institute. Code of practice for strengthened/ reinforced soils and other fills: B S 8006-1—2010 [S]. London: British Standard Institute, 2010.
|
| [19] |
TANDJIRIA V, LOW B K, TEH C I. Effect of reinforcement force distribution on stability of embankments[J]. Geotextiles and Geomembranes, 2002, 20(6): 423 DOI:10.1016/S0266-1144(02)00015-8 |
 2017, Vol. 45
2017, Vol. 45

