2. 加州大学河滨分校 环境技术研究中心,河滨 92507
2. Center for Environmental Research & Technology, University of California, Riverside, Riverside 92507, USA
现阶段,城市机动车污染排放已成为影响城市空气质量的重要原因.近20年来,研究发现车辆能耗排放特征与车辆瞬时的运行工况密切相关,美国研究人员先后开发了微观车辆排放模型并得到了广泛的应用,如CMEM (comprehensive modal emissions model)[1]及MOVES (motor vehicle emissions simulator)[2]模型.由于无线传输技术的发展,高精度移动传感器可以采集逐秒的车辆运行数据作为微观车辆排放模型的核心输入,从而准确地估计车辆能耗排放特征.然而,由于高精度数据存储的空间需求,移动传感器多以一定的时间间隔传输数据,称之为稀疏移动传感器数据.例如,上海市装载全球定位系统(global positioning system, GPS)的出租车及公交车以10~30 s不等的时间间隔传输当前车辆的经纬度及速度信息.因此,有必要提出一种扩展稀疏移动传感器数据应用范围的方法,以便准确地估计车辆实际运行工况的能耗排放特征.
研究发现移动传感器数据的采集精度一定程度上抑制了此类数据的交通应用分析.QUIROGA及BULLOCK建议车辆轨迹数据采集间隔为1 s左右,以减小高速公路运行时间估计的误差[3].HERRING使用浮动车数据,提出一种概率模型,从而估计主干路出行时间分布[4].WANG等人提出一种隐马尔科夫模型以克服浮动车数据的稀疏特征[5].LIU等人采用线性插值的方式重建了浮动车行驶轨迹并利用MOVES2010b模型测算了上海车辆排放特征[6].HAO等人近期提出一种随机概率模型,利用稀疏移动传感器数据估计了路段出行时间分布特征[7],后基于同样的方法计算了车辆排放特征[8].SHAN等人提出了快速路车辆轨迹重建的随机概率模型[9].
然而,车辆能耗排放特征与车辆运行模式密切相关.LIN及NIEMEIER在行驶工况构建中指出了传统行驶工况构建的弊端,提出了考虑车辆运行模式的行驶工况合成方法[10].SUN等人重构了交叉口自由流及拥堵流的轨迹特征,考虑了车流匀速段的波动特征,但车辆匀速模式下生成的数据并非为正态分布[11].本文首次提出了基于运行模式的车辆能耗排放估计方法,兼顾了匀速模式下的波动特征且符合正态分布特性.本文所提出的方法真实再现了符合实际车辆运动学特征的车辆轨迹,准确地估计了车辆能耗排放特征,从而拓展了稀疏移动传感器数据的应用范围.
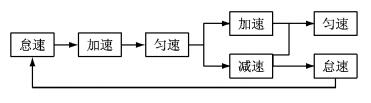
1 基于运行模式的车辆轨迹重建 1.1 模型假设车辆运行模式可分为怠速(1)、加速(2)、匀速(3) 及减速(4),用数字1、2、3、4分别代表这4种车辆运行模式.车辆实际的运动状态即在这4种状态来回切换,如图 1所示.车辆当前时刻可以处于匀速状态之后减速/加速到一个特定的速度,之后又处于匀速状态.其中,怠速指的是车辆速度为0,研究中可以认为是一种特殊的匀速状态.
|
图 1 车辆运行模式转换 Fig.1 Vehicle driving mode transition |
对于一组稀疏移动传感器数据,如一定时间间隔的GPS数据点,只要确定车辆运行模式的时间及距离,即可重建车辆在该时间间隔范围内的运行轨迹.车辆轨迹重建可转化为两个问题:① 识别车辆运行过程中的极值点速度;② 分配运行模式的时间和距离.
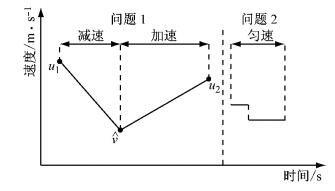
由图 2可知,对于一组特定的稀疏数据点对,已知车辆的起点速度(u1)、终点速度(u2)、时间间隔(Δt)以及行驶距离(Δd),车辆轨迹重建的重点即是车辆运行模式序列识别及运行模式的时间/距离分配,同时需要满足车辆实际的运行时间及距离的约束条件.研究中假设一定时间间隔内车辆速度除了起始点,至多存在一个极值点速度(
|
图 2 车辆轨迹重建问题描述 Fig.2 Problem formulation of vehicle trajectory reconstruction |
在实际车辆行驶过程中,车辆运行状态可以从加速到匀速再到加速,亦可以是减速到匀速再到减速.而在短时间间隔内,车辆的加速过程或减速过程通常一次完成.根据NGSIM (next generation simulation)[12]数据集中快速路US101特定路段15 min车辆轨迹数据,统计表明10 s时间间隔内加速过程中存在匀速状态的比例仅为2.7%,而减速过程中存在匀速状态的比例仅为0.6%.因此,本文假设车辆匀速段运行模式均发生在起终点及极值点处,如图 3所示.

|
图 3 车辆运行模式转变假设 Fig.3 Vehicle driving mode transition assumption |
根据模型的假设可知,为重建车辆轨迹,首先需要确定车辆运行模式的变化特征,称之为运行模式序列(M);紧接着确定每个运行模式的速度起终点,即运行模式速度转化矩阵(V);同时可以确定车辆运行模式的时间矩阵(T)及距离矩阵(X),从而识别该时间范围内的运行状态,即{ m, v, t, x}.如图 3可知,M=[3, 4, 3, 2, 3]T, V=[u1, u1,
车辆运行模式序列(M)与起终点速度及平均速度(
| 下载CSV 表 1 不同运行模式序列的概率特征 Tab.1 Probability of different modal activity sequences |
显然,确定车辆运行状态(m)后,矩阵v, t, x的长度即可确定.矩阵V的概率如式(1) 所示,等于极值点速度
| $ P\left( {\mathit{\boldsymbol{V = v}}\left| {\mathit{\boldsymbol{M}} = \mathit{\boldsymbol{m}}} \right.} \right) = \left\{ \begin{array}{l} P\left( {\hat v} \right),\;\;\;\;K = 5\\ 1,\;\;\;\;\;\;\;\;\;\;K = 3 \end{array} \right. $ | (1) |
式中:K指的是矩阵M的长度.
此外,对于一个特定的车辆运行模式,车辆在该模式下运行的时间和距离是独立于其他车辆运行模式的.对于某一运行模式的时间及距离联合概率如下:
| $ \begin{array}{l} P\left( {{T_i} = {t_i}\left| {\mathit{\boldsymbol{V = v}},\mathit{\boldsymbol{M}} = \mathit{\boldsymbol{m}}} \right.} \right) = {f_T}\left( {{t_i};{v_i},{v_{i + 1}},{m_i}} \right)\\ P\left( {{X_i} = {x_i}\left| {{T_i} = {t_i},\mathit{\boldsymbol{V}} = \mathit{\boldsymbol{v}},\mathit{\boldsymbol{M}} = \mathit{\boldsymbol{m}}} \right.} \right) = \\ \;\;\;\;\;\;\;\;{f_X}\left( {{x_i};{t_i},{v_i},{v_{i + 1}},{m_i}} \right) \end{array} $ | (2) |
式中:i指的是第i个运行模式,即mi;ti指该车辆运行模式的时间消耗;xi指的是行驶距离;vi指的是mi的起点速度;vi+1指的是mi的终点速度.
因此,对于某一组运行状态{ m, v, t, x},由于相关事件是相互独立的,事件的联合概率即是该车辆运行状态的概率,有
| $ \begin{array}{l} P\left( {\mathit{\boldsymbol{M}} = \mathit{\boldsymbol{m}},\mathit{\boldsymbol{V = }}v,\mathit{\boldsymbol{T}} = \mathit{\boldsymbol{t}},\mathit{\boldsymbol{X}} = \mathit{\boldsymbol{x}}} \right) = \\ \;\;\;\;\;\;\;\;\prod\limits_i {P\left( {{X_i} = {x_i}\left| {{T_i} = {t_i},\mathit{\boldsymbol{V}} = v,\mathit{\boldsymbol{M}} = m} \right.} \right)} \cdot \\ \;\;\;\;\;\;\;\;\prod\limits_i {P\left( {{T_i} = {t_i}\left| {\mathit{\boldsymbol{V}} = v,\mathit{\boldsymbol{M}} = m} \right.} \right)} \cdot \\ \;\;\;\;\;\;\;\;P\left( {\mathit{\boldsymbol{V}} = v\left| {\mathit{\boldsymbol{M}} = m} \right.} \right)P\left( {\mathit{\boldsymbol{M}} = m} \right) \end{array} $ | (3) |
针对一组有效的车辆运行状态{ m, v, t, x},受到车辆运行时间及距离的约束,即该运行状态需要满足时间及空间的约束条件,同时矩阵v, t, x的元素值均不小于0.相关约束条件如下:
| $ \begin{array}{l} {\mathit{\Omega }_V} = \left\{ {\mathit{\boldsymbol{v}}\left| {{v_1} = {v_2} = {u_1},{v_k} = {v_{k + 1}} = {u_2},{v_i} \ge 0,k = 3\;或\;5} \right.} \right\}\\ {\mathit{\Omega }_T} = \left\{ {\mathit{\boldsymbol{t}}\left| {{t_1} \ge 0, \cdots ,{t_k} \ge 0,k = 3\;或\;5} \right.} \right\}\\ {\mathit{\Omega }_X} = \left\{ {\mathit{\boldsymbol{x}}\left| {{x_1} \ge 0, \cdots ,{x_k} \ge 0,k = 3\;或\;5} \right.} \right\} \end{array} $ | (4) |
| $ \sum {{t_i}} = \Delta t,\sum {{x_i}} = \Delta d $ | (5) |
因此,对于一个有效的车辆运行状态{ m, v, t, x},其概率计算如下:
| $ P\left( \begin{array}{l} \mathit{\boldsymbol{M}} = \mathit{\boldsymbol{m}},\mathit{\boldsymbol{V}} = \mathit{\boldsymbol{v}},\mathit{\boldsymbol{T}} = \mathit{\boldsymbol{t}},\mathit{\boldsymbol{X}} = \mathit{\boldsymbol{x}}\\ \left| {\sum\limits_{i = 1}^{{K_{\max }}} {{T_i} = \Delta t} ,\sum\limits_{i = 1}^{{K_{\max }}} {{X_i} = \Delta x} } \right. \end{array} \right) $ | (6) |
对某一特定的车辆运行模式,如其模式为加速模式或减速模式,已知车辆加减速过程中开始速度vi、结束速度vi+1、运行时间ti及行驶距离xi.为重建车辆加减速过程轨迹,AKÇELIK及BIGGS等人指出多项式加速度模型在数学结构上符合车辆加速特征,然而参数标定复杂.线性加速度模型较好地反映了车辆实际的加减速特征,且计算过程简易[13].本文假设车辆的加速度为线性变化,即
| $ {a_i}\left( t \right) = {a_{i,1}} + {r_i}t $ | (7) |
式中:ai(t)指第i个运行模式下第t时刻的加速度,ai, 1及ri为待计算的参数,t=0, 1, …,ti.
根据相关的速度、时间及距离约束条件,可有
| $ \begin{array}{l} {v_{i + 1}} = {v_i} + {a_{i,1}}{t_i} + \frac{1}{2}{r_i}t_i^2\\ {x_i} = {v_i}{t_i} + \frac{1}{2}{a_{i,1}}t_i^2 + \frac{1}{6}{r_i}t_i^3 \end{array} $ | (8) |
从而,可以计算得
| $ \begin{array}{l} {r_i} = \frac{{6\left( {{v_i} + {v_{i + 1}}} \right){t_i} - 12{x_i}}}{{t_i^3}}\\ {a_{i,1}} = \frac{{{v_{i + 1}} - {v_i}}}{{{t_i}}} - \frac{1}{2}{r_i}{t_i} \end{array} $ | (9) |
由此,计算得到车辆加减速过程的逐秒加速度及速度特征,从而重建车辆加速及减速过程中的逐秒轨迹.
1.4 车辆匀速模式波动特征实际驾驶过程中,驾驶员无法保持某一速度不变,存在车辆匀速模式波动特征.因此,模型中融合车辆匀速状态下的速度上下波动特征.对于某一车辆匀速模式的时间为τ s(τ是一个正整数且τ≥2),假设对于每一秒运动特征,其加速度为aj是一个正态随机数,其中j=1, 2, …, τ,符合高斯正态分布为N(0, σc).
首先, 生成(τ-1) 个随机数,符合正态分布N(0, σc),为βj,则有矩阵B=[β1, β2, …, βτ-1]T.随后借鉴Hao等人提出的速度波动方法[8],通过式(10) 可生成矩阵A=[α1, α2, …, ατ-1]T,该矩阵内元素符合正态分布N(0, σc),且满足
| $ \begin{array}{l} \mathit{\boldsymbol{A = }}\sigma \sqrt {\frac{\tau }{{\tau - 1}}} \mathit{\boldsymbol{QB}}\\ {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{Q}} = 0;{\mathit{\boldsymbol{Q}}^{\rm{T}}}\mathit{\boldsymbol{Q = }}I \end{array} $ | (10) |
式中:e是一个1×τ的单位矩阵; Q为τ(τ-1) 正交基.验证过程可详见文献[8].
2 车辆能耗排放估计方法 2.1 车辆能耗排放模型MOVES模型是美国最新开发并使用最为广泛的微观车辆能耗排放模型.该模型的核心输入是车辆比功率分布特征.车辆比功率(vehicle specific power, VSP)计算公式如下:
| $ U = \frac{{{w_1}v}}{W} + \frac{{{w_2}{v^2}}}{W} + \frac{{{w_3}{v^3}}}{W} + \left( {a + g\sin \theta } \right)v $ | (11) |
式中:U为车辆比功率;v为车辆当前瞬时速度;a为车辆当前瞬时加速度;g为重力加速度;sin θ反应了道路坡度特征(平地时为0);W为固定的质量参数(不同车辆类型数值不同);w1、w2和w3为道路行驶荷载系数(不同车辆类型系数存在差异性).由于NGSIM数据集中注明了车辆类型,研究中仅考虑轻型车,且道路坡度为0,则w1=0.156 461,w2=0.002 002,w3=0.000 493,W=1.866 86.
对于已知的车辆轨迹数据,可以计算得到车辆比功率分布特征,使用MOVES2014a软件,输入其他参数,如车龄分布、气象参数等,从而估计车辆能耗排放特征,如排放因子及排放总量.本文使用的是稀疏移动传感器数据,限于篇幅,研究中仅关注车辆HC (hydrocarbon compounds)、NOx及能耗的排放因子特征.
2.2 基于运行模式的车辆能耗排放估计方法基于运行模式的车辆能耗排放估计方法关键在于选择哪一组有效的车辆运行状态{ m, v, t, x}.由于车辆匀速模式分配的假设条件,研究中定义一组有效的运行状态{ m, v, t, x},满足时间需求的情况下,其运行距离误差ε小于1.5 m,即
| $ \varepsilon = \left| {\sum {{x_i} - \Delta d} } \right| \le 1.5 $ | (12) |
对于无效的运行状态{ m, v, t, x},其概率为0,通过式(6) 可以计算得到某一有效的车辆运行状态概率数值.研究中选择概率最大的有效的车辆运行状态{ m*, v*, t*, x*}作为车辆轨迹重建的基础,即
| $ \max P\left( \begin{array}{l} \mathit{\boldsymbol{M}} = {\mathit{\boldsymbol{m}}^ * },\mathit{\boldsymbol{V}} = {\mathit{\boldsymbol{v}}^ * },\mathit{\boldsymbol{T}} = {\mathit{\boldsymbol{t}}^ * },\mathit{\boldsymbol{X}} = {\mathit{\boldsymbol{x}}^ * }\\ \left| {\sum\limits_{i = 1}^{{K_{\max }}} {{T_i} = \Delta t} ,\sum\limits_{i = 1}^{{K_{\max }}} {{X_i} = \Delta x} } \right. \end{array} \right) $ | (13) |
车辆轨迹重建后,通过MOVES2014a模型,即可计算得到车辆不同速度下的HC、NOx及能耗的排放因子特征.
3 模型标定 3.1 实际车辆轨迹运行模式分割研究旨在构建基于运行模式的车辆能耗排放估计方法.需要根据实际的车辆运行轨迹甄别车辆怠速、加速、匀速及减速运行特征,如加减速时间及距离分布特征.研究中使用NGSIM快速路US101及地面道路Lankershim Blvd真实的车辆逐秒轨迹数据集进行模型标定,时间范围为15 min.
直观地说,当车辆的加速度不为0时,认为车辆处于加减速状态;当车辆加速度为0时,若其速度不为0,车辆处于匀速状态,否则车辆处于怠速状态.显然,车辆实际运动过程中,对于匀速状态,车辆加速度存在不为0的情况,即车速具有波动特征.因此,以加速度数值为唯一判别指标,判断车辆运行模式是不准确的.
本次研究中,车辆加速模式定义为车辆的瞬时加速度大于s1m·s-2,持续3 s及以上,导致累计的速度增加大于s2m·s-1.同样地,车辆减速模式定义为车辆瞬时减速度(绝对值)大于s3m·s-2,持续3 s及以上,导致累计的速度减小大于s4m·s-1.剩余部分即为匀速或怠速模式,而当速度大于s5m·s-1时,车辆处于匀速状态,否则为怠速状态.研究中采用遗传算法标定相关5个参数数值(s1, s2, s3, s4, s5).遗传算法的重点是确定适应度函数.研究发现,对于理想的匀速模式,车辆加速度标准差(θ1)趋于0,平均加速度(θ2)应该也趋于0.研究中设置的适应度函数为
| $ F = k\sum {{\theta _1}} + \left( {1 - k} \right)\sum {{\theta _2}} $ | (14) |
式中:F是指适应度函数;k是指θ1的权重,设定为0.5.此外,研究中设定个体中染色体长度为20,种群规模为100,交叉及变异概率分别为0.8及0.005.考虑到车辆匀速模式下的波动特征,5个标定参数的取值范围分别是:[0.25 0.5]m·s-2, [0.75 1.5]m·s-1, [0.25 0.5]m·s-2, [0.75 1.5]m·s-1, [0.25 0.5]m·s-1.
标定结果表明,对于快速路,参数组合为0.33 m·s-2、1.01 m·s-1、0.49 m·s-2、1.49 m·s-1和0.39 m·s-1,误差最小为2 225.6 m·s-2;对于地面道路,参数组合为0.29 m·s-2、1.03 m·s-1、0.29 m·s-2、0.88 m·s-1和0.44 m·s-1,误差最小为1 080.1 m·s-2.由于受到交叉口等因素的影响,对简断车流而言,车辆加减速模式启动阈值判断低于快速路.本文提出的车辆轨迹运行模式分割方法有效地真实再现车辆实际运行轨迹特征,同时识别了车辆匀速模式的加速度波动特征.不同道路特征典型车辆轨迹运行模式划分如图 4所示.车辆当前时刻的加速度为下一时刻及上一时刻速度差的一半.且在实际车辆行驶过程中,驾驶员存在急刹的行为,从而导致了图 4中少部分的标定结果与视觉判断的差异性.以后的研究中,需要进一步考虑车辆急刹及急加行为.

|
图 4 典型车辆轨迹运行模式划分 Fig.4 Typical partitioning results on different types of road |
为计算车辆某一运行状态的联合概率,需要估计极值点的概率分布特征.研究中认为不同时间间隔Δt下,极值点速度
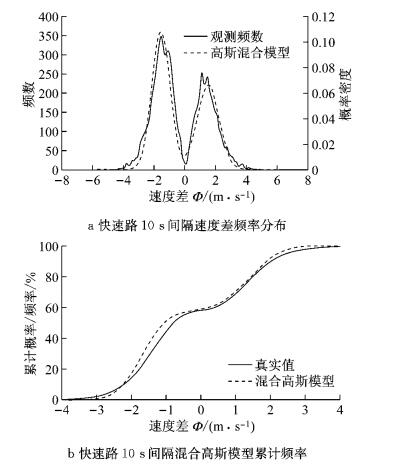
|
图 5 极值点概率分布特征估计 Fig.5 Probability distribution estimation of inflection speed |
由图 5a可知,实际的10 s间隔速度差,存在两个峰值,分别为-1.54 m·s-1及1.11 m·s-1,且最大值及最小值在±5 m·s-1左右,表现为双峰分布.研究中采用混合高斯模型估计φ的概率分布特征,有
| $ P\left( \varphi \right) = \sum\limits_{g = 1}^G {{\pi _g}P\left( {\varphi \left| g \right.} \right)} $ | (15) |
| $ P\left( {\hat v} \right) = P\left( {\bar v - \varphi } \right) = P\left( \varphi \right) = \sum\limits_{g = 1}^G {{\pi _g}P\left( {\varphi \left| g \right.} \right)} $ | (16) |
式中:g是指第g个高斯分布N(qg, σg);πg是第g个高斯分布的权重,
| $ \max \sum\limits_i {\log \left( {\sum\limits_{g = 1}^G {{\pi _g}N\left( {{\varphi _i}\left| {{q_g},{\sigma _g}} \right.} \right)} } \right)} $ | (17) |
本文采用最大期望算法求解混合高斯模型,不同道路类型不同时间间隔的混合高斯模型参数如表 2及表 3所示.图 5b绘制了10 s时间间隔的混合高斯模型速度差累计频率分布图.研究表明,混合高斯模式能够准确地反映了车辆真实的运动特征.
| 下载CSV 表 2 快速路不同时间间隔下极值点分布特征 Tab.2 Parameters for Gaussian mixture model at Δ intervals on freeways |
| 下载CSV 表 3 地面道路不同时间间隔下极值点分布特征 Tab.3 Parameters for Gaussian mixture model at Δ intervals on arterial roads |
对比表 2及表 3可知,由于快速路无交叉口、开道口等因素干扰,车流表现为连续流特征,同一时间间隔下q1及q2绝对值小于地面道路参数数值.
3.3 加减速运行模式分布特征研究中假设车辆加减速运行模式的平均加速度倒数满足高斯分布,即车辆加减速过程中时间消耗t除以速度差Δv满足高斯分布,有
| $ \varphi = \frac{t}{{\Delta v}} \sim N\left( {{\mu _t},{\sigma _t}} \right) $ | (18) |
此外,当已知车辆加减速过程中的运行时间时,若车辆处于匀加速或匀减速状态,则行驶距离
| $ \begin{array}{*{20}{c}} {d = t\left( {{v_{\rm{s}}} + {v_{\rm{e}}}} \right)\mathit{\Phi }}\\ {\mathit{\Phi } = \frac{d}{{t\left( {{v_{\rm{s}}} + {v_{\rm{e}}}} \right)}} \sim \left( {{\mu _d},{\sigma _d}} \right)} \end{array} $ | (19) |
根据NGSIM数据集,利用文中提出的车辆运行模式分割方法,记录车辆加减速过程中运行时间、行驶距离及速度差,从而通过最大似然估计方法可以标定出车辆加减速过程中运行时间及行驶距离概率分布特征,如表 4所示.
| 下载CSV 表 4 不同道路类型下车辆加减速概率分布特征 Tab.4 Parameters calibration of acceleration and deceleration modals on different road types |
由表 4不难发现,车辆加减速过程中,快速路的平均加速度或减速度要小于地面道路平均加速度或减速度.车辆加减速过程不为匀加速或匀减速过程,Φ数值在0.45左右.
3.4 匀速模式车速波动特征假设车辆匀速模式下的时间距离分配服从均匀分布.1.4节中论述并提出了车辆匀速模式车速波动特征.根据实际车辆运行轨迹数据,通过车辆模式分割,可估计得到快速路车辆匀速模式车辆加速度波动服从正态分布N(0, 0.4),地面道路匀速模式车辆加速度波动服从正态分布N(0, 0.2).
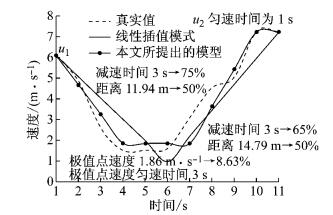
4 车辆能耗排放因子估计 4.1 车辆运行轨迹重建对于稀疏移动传感器数据,车辆能耗排放估计的基础是车辆轨迹重建.本文使用NGSIM数据集中快速路US101及地面道路Lankershim Blvd另一15min的真实车辆轨迹数据集生成稀疏移动传感器数据,利用所提出的模型估计车辆能耗排放因子.图 6给出了一组10 s间隔的快速路数据的车辆轨迹重建过程.已知车辆的起点及终点速度为6.09 m·s-1及7.23 m·s-1,时间间隔为10 s,行驶距离为38.23 m.针对该数据对,通过式(13),可估计得到最大概率的运行状态组合,存在一个极值点,速度为1.86 m·s-1,概率为8.63%;加速及减速模式的时间均为3 s,行驶距离分别为11.94 m及10.88 m;匀速模式分布在极值点及终点处,时间分别为3 s及1 s.运行状态的联合概率为
| $ \begin{array}{l} P = 1 \times 0.0863 \times 0.75 \times 0.5 \times 0.65 \times 0.5 = \\ \;\;\;\;\;\;\;0.0105 \end{array} $ |
|
图 6 快速路10 s间隔车辆轨迹重建 Fig.6 A case study of a sparse data pair with 10 s time interval on freeway |
针对同一组数据对,本文还利用了线性插值的方法重建了车辆轨迹.线性插值的速度平均绝对误差为0.71 m·s-1,本文提出的模型仅为0.40 m·s-1.这是由于线性插值的模型不足所引起的,主要包括有4个方面的不足:① 线性插值模型中不存在匀速或怠速车辆运行模式;② 线性模型假设车辆以匀加速或匀减速运行,且可以处于任何一个加速度值,不符合实际特征;③ 当存在极值点时,线性插值模型假设车辆加速时间和减速时间相同;④ 当存在极小值速度时,可能会估计出小于0的速度.本文所提出的基于车辆运行模式的轨迹重建方法更为遵循实际的车辆运动学特征,从而更好地估计车辆能耗排放特征.
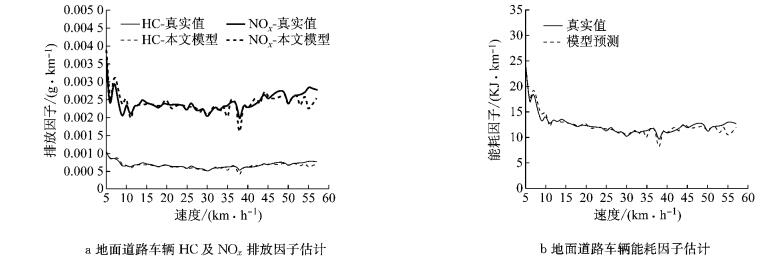
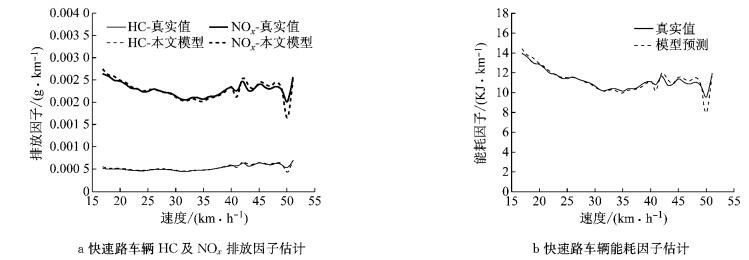
4.2 车辆能耗排放因子估计通过4.1节的描述,类似地,可以估计出车辆整个运行轨迹,从而计算得到车辆比功率分布,利用MOVES2014a模型测算得到不同道路特征下的车辆能耗排放因子,分别如图 7及图 8所示.其中,排放真实值指的是用真实的车辆轨迹数据输入MOVES2014a模型中所计算得到的排放因子.此外,显然同一平均速度下,单车的排放因子是存在差异性的,为了衡量不同速度下的模型估计效果,采用同一速度下平均化的处理方式计算得到排放因子—速度关系图.
|
图 7 地面道路10 s间隔车辆能耗排放因子估计 Fig.7 Vehicle fuel/emission factors estimation with 10 s time interval on arterial roads |
|
图 8 快速路10 s间隔车辆能耗排放因子估计 Fig.8 Vehicle fuel/emission factors estimation with 10 s time interval on freeways |
由图 7及图 8可知,针对10 s间隔的稀疏移动传感器数据,本文提出的基于运行模式的车辆能耗排放估计方法很好地再现了真实环境下车辆运行特征,从而准确地估计了车辆能耗因子及排放因子.研究中使用平均绝对百分比误差作为衡量指标,计算公式如下:
| $ R = \frac{{\sum {\left| {\frac{{{e_t} - {{\hat e}_t}}}{{{e_t}}}} \right|} }}{n} $ | (20) |
式中:R为车辆能耗或排放的平均绝对百分比误差;et为某一速度下真实的能耗/排放因子;
对地面道路来说,车辆能耗因子平均绝对百分比误差仅为3.6%,HC平均绝对误差百分比为3.9%,NOx为4.2%.同样地,快速路上,车辆能耗因子平均绝对百分比误差为2.4%,HC为2.8%,NOx为2.7%.此外,由图 8可知,由于快速路上车流表现为连续流特征,极端拥堵情况下的数据是缺失的,如速度小于15 km·h-1.对比快速路及地面道路车辆能耗排放因子特征,同一速度下,快速路上车辆速度波动特征小于地面道路速度波动,快速路车辆能耗排放因子略小于地面道路车辆能耗排放因子.
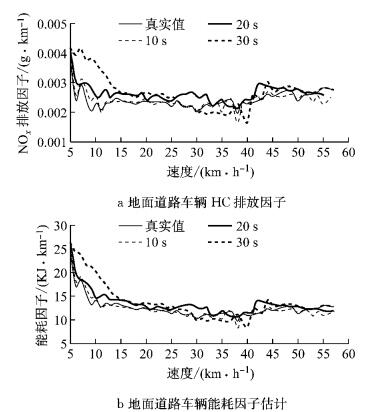
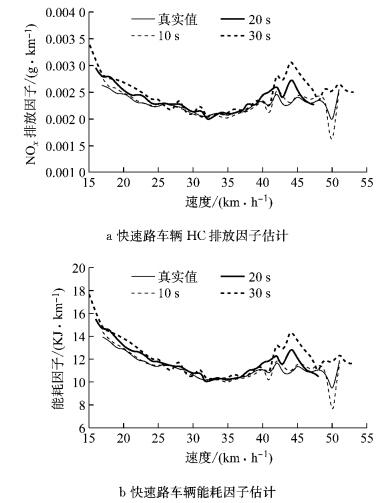
4.3 时间间隔敏感性分析4.2小节中分析了10 s时间间隔的车辆能耗排放估计的准确度,本节对时间间隔的敏感性进行分析,包括20 s时间间隔及30 s时间间隔,如图 9及图 10所示:
|
图 9 地面道路不同时间间隔车辆能耗排放因子估计 Fig.9 Vehicle fuel/emission factors estimation at different time intervals on arterials |
|
图 10 快速路不同时间间隔下车辆能耗排放因子估计 Fig.10 Vehicle fuel/emission factors estimation at different time intervals on freeways |
由图 9及图 10可知,针对20 s时间间隔的稀疏移动传感器数据,本文所提出的方法能够准确地估计车辆能耗排放特征;当时间间隔为30 s时,估计的车辆能耗排放因子对比真实值呈现较大的波动状态,尤其是当快速路车辆速度在40~50 km·h-1之间,地面道路速度小于15 km·h-1时.不同时间间隔不同道路特征下的车辆能耗排放因子平均绝对误差及评价绝对百分比误差如表 5及表 6所示。
| 下载CSV 表 5 车辆能耗排放因子平均绝对误差 Tab.5 Mean absolute error of vehicle fuel/ emissions factors |
由表 6可知,时间间隔为20 s,车辆能耗排放因子平均绝对百分比误差均小于8%,这说明了本文提出的基于运行模式的车辆能耗排放模型能够很好的估计车辆能耗排放特征.而当时间间隔为30 s时,由于假设的车辆运动特征,如只存在一个极值点及一次完成加速或减速过程,并不能很好地反映车辆实际的行驶工况,导致误差偏大.
| 下载CSV 表 6 车辆能耗排放因子平均绝对百分比误差 Tab.6 Mean absolute percentage error of vehicle fuel/emissions factors |
在4.1节中指出了线性插值模型的不足,以20 s时间间隔为例,说明了本文所提出的模型比线性插值模型的优越性,如表 7所示。
| 下载CSV 表 7 20 s间隔下车辆能耗排放因子平均绝对百分比误差 Tab.7 Mean absolute percentage error of vehicle fuel/emissions factors with 20 s time interval |
由表 7可知,线性插值模型本身一定程度上也较好地反映了车辆逐秒速度波动特征,其车辆能耗排放因子平均百分比误差均小于10%;然而对比发现,基于运行模式的车辆能耗排放估计方法的平均绝对百分比误差更小,更能够准确地描述了车辆在一定时间间隔内的波动特征.
5 总结现有的微观车辆能耗排放计算软件的核心输入是车辆的逐秒行驶轨迹.本文使用稀疏移动传感器数据,提出了一种基于运行模式的车辆能耗排放估计方法.论文首先识别了一定时间间隔内车辆的运行模式序列,其次估计每一个运行模式下的行驶时间及行驶距离,计算不同有效车辆运行状态的概率特征,重建车辆运行轨迹,后基于MOVES模型,从而估计车辆能耗排放特征.论文利用NGSIM实际的车辆轨迹数据对模型进行了标定,提出了一种改进的车辆运行模式分割算法.此外,论文利用NGSIM另一时段数据对模型进行了验证,分析了不同时间间隔下模型的敏感性特征,同时与线性插值模型进行了对比分析.研究发现,本文所提出的模型在20 s时间间隔内能够很好地估计车辆的实际能耗排放特征.相较于线性插值模型,由于其模型本身能够反应车辆速度的波动特征,本文所提出的模型其误差依然小于线性插值模型,说明了模型的优越性及准确性.本文的研究成果拓展了稀疏移动传感器应用范围,能够有效地估计不同城市不同道路属性下车辆的能耗排放因子,为定量化地分析城市交通能耗排放特征提供了理论基础和实际应用价值.
| [1] |
SCORA G, BARTH M. Comprehensive modal emissions model (CMEM): version 3.01. user guide[R]. Riverside: Centre for Environmental Research and Technology of University of California, Riverside, 2006.
|
| [2] |
Transportation and Air Quality U S Environmental Protection Agency. MOVES2014 a user guide[R]. Washington D C: United States Environmental Protection Agency, 2015.
|
| [3] |
QUIROGA C, BULLOCK D. Travel time studies with global positioning and geographic information systems: an integrated methodology[J]. Transportation Research Part C, 1998, 6(1-2): 101 DOI:10.1016/S0968-090X(98)00010-2 |
| [4] |
HERRING R, HOFLEITNER A, ABBEEL P, et al. Estimating arterial traffic conditions using sparse probe data[C]//Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems. Madeira Island: IEEE, 2010: 929-936.
|
| [5] |
WANG X, PENG L, CHI T, et al. A hidden Markov model for urban-scale traffic estimation using floating car data[J]. PLos ONE, 2015, 10(12): e0145348 DOI:10.1371/journal.pone.0145348 |
| [6] |
LIU H, CHEN X, WANG Y, et al. Vehicle emission and near-road air quality modeling for Shanghai, China based on global positioning system data from taxis and revised MOVES emission inventory[J]. Transportation Research Record: Journal of the Transportation Board, 2013(2340): 38 |
| [7] |
Hao P, Boriboonsomsin K, Wu G, et al. Probabilistic model for estimating vehicle trajectories using sparse mobile sensor data[C]//Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems. Qingdao: IEEE, 2014: 1363-1368.
|
| [8] |
HAO P, WU G, BORIBOONSOMSIN K, et al. Modal activity-based vehicle energy/emissions estimation using sparse mobile sensor data[C]//Proceedings of the Transportation Research Board 95th Annual Meeting. Washington D C: TRB, 2016: 1-16.
|
| [9] |
SHAN X, HAO P, CHEN X, et al. Probabilistic model for vehicle trajectories reconstruction using sparse mobile sensor data on Freeways[C]//Proceedings of the 19th International IEEE Conference on Intelligent Transportation Systems. Rio de Janeiro: IEEE, 2016: 689-694.
|
| [10] |
LIN J, NIEMEIER D. Estimating regional air quality vehicle emission inventories: constructing robust driving cycles[J]. Transportation Science, 2003, 37(3): 330 DOI:10.1287/trsc.37.3.330.16045 |
| [11] |
SUN Z, HAO P, BAN X, et al. Trajectory-based vehicle energy/emissions estimation for signalized arterials using mobile sensing data[J]. Transportation Research Part D, 2015, 34: 27 DOI:10.1016/j.trd.2014.10.005 |
| [12] |
Federal Highway Administration. NGSIM overview[R]. U S Department of Transportation Federal Highway Administration, 2017.
|
| [13] |
AKÇELIK R, BIGGS D C. Acceleration profile models for vehicles in road traffic[J]. Transportation Science, 1987, 21(1): 36 DOI:10.1287/trsc.21.1.36 |
 2017, Vol. 45
2017, Vol. 45

