2. 长安大学 理学院, 陕西 西安 710064;
3. 陕西延长石油延安能源化工有限责任公司, 陕西 延安 727500
2. College of Science, Chang'an University, Xi'an 710064, China;
3. Shaanxi Yanchang Petroleum Yan'an Energer & Chemical Industry Co. Ltd., Yan'an 727500, China
桥面铺装的平整度是影响车桥铺装层耦合振动体系动力响应的关键,桥面的不平顺会致使桥面线形偏离绝对基准平面,从而导致车辆在行驶过程中不断受到外界产生的激励.与此同时,车辆由于受到变化的外界激励作用,其自身振动状态也随之改变,反过来会影响铺装层及桥梁体的动力响应,从而使结构实际内力及位移值不同于绝对平整的桥面体系[1].桥面铺装的平整度沿用了路面平整度的概念.路面平整度是评价路面平顺程度的一个重要指标,它不仅影响了行车的舒适程度,还与车辆振动、行驶速度、沥青混凝土面层性质等有关,是一个影响了人、车、路面三方面的指标.路面不平激起的车辆振动会在缩短汽车寿命的同时加剧路面的破坏[2].铺装层不平整所引起的车辆随机振动是致使桥面铺装层破坏和使用寿命减少的重要因素之一.现有文献多数只针对钢桥面铺装做了动力学分析[3-4],但混凝土桥梁铺装层的相关研究较少.而装配式梁桥、连续梁桥以及刚构桥在城市立交和高速公路上依然被广泛采用,研究混凝土桥梁铺装层在车辆随机振动作用下的动力响应依然有工程价值和意义.由于现有设计规范中并未针对桥面铺装的平整度做出评定或规定,且现有车桥耦合的研究重心大多集中在桥的梁体上,并不关注铺装层的受力情况,研究中仅将铺装层作为二期恒载来考虑[5-7].这直接导致了实际工程中,由于铺装层自身的退化和破坏以及造成的桥梁体损伤,已经导致了不可忽视的经济损失.因此有必要在车桥耦合振动模型中考虑铺装层的作用效应,对铺装层在随机动载作用下的控制应力响应进行研究.
本文建立了车桥铺装结构的耦合振动体系,运用MATLAB软件仿真得到基于功率谱密度的铺装层不平整度激励,通过求解振动系统的动力微分方程,将不平度激励转换为车辆随机动载并将其施加在由ANSYS建立的桥梁实体模型上,得出随机动载作用下应力响应的时程曲线,通过与移动恒载的响应进行比较,进一步研究铺装层不平整度对铺装层应力响应的影响规律,以期能够更好地应用于工程实践.
1 车辆振动动力学模型选取在车辆振动模型中,常见的动力学模型有单轮双自由度模型(1/4车辆模型),见图 1,它最为简单常用,在模拟车辆动载时强而有力[8],因为单轮双自由度车辆模型真实反映了车辆悬架系统.该模型包括了荷载变化、悬架系统受力等大部分基本特征信息,不失一般性,且在振动系统计算求解时相对容易,计算量小,控制方便,对低频激励效果更好[9].本文采用双自由度车辆模型,车辆后轴单侧参数采用桥梁规范的标准车结构参数,见表 1[10].

|
图 1 单轮双自由度车辆模型 Fig.1 Single-wheel double-DOF vehicle model |
| 下载CSV 表 1 车辆系统参数 Tab.1 Vehicle system parameters |
针对图 1所示的双自由度单轮振动模型,建立其动力学微分方程如下:
| $ \begin{gathered} {m_{\text{s}}}{{\ddot x}_{\text{s}}} = - {k_{\text{s}}}({x_{\text{s}}} - {x_{\text{t}}}) - {c_{\text{s}}}({{\dot x}_{\text{s}}} - {{\dot x}_{\text{t}}}) \hfill \\ {m_{\text{t}}}{{\ddot x}_{\text{t}}} = {k_{\text{s}}}({x_{\text{s}}} - {x_{\text{t}}}) + {c_{\text{s}}}({{\dot x}_{\text{s}}} - {{\dot x}_{\text{t}}}) - {k_{\text{t}}}({x_{\text{t}}} - \hfill \\ \;\;\;\;\;\;{x_{\text{g}}}) - {c_{\text{t}}}({{\dot x}_{\text{s}}} - {{\dot x}_{\text{g}}}) \hfill \\ \end{gathered} $ | (1) |
式中:xs,xt分别为悬架质量垂直振动位移和轮胎垂直振动位移;xg为铺装层不平整度激励位移;ẋs, ẋt, ẋg表示三者对时间的一阶导数;
| $ {F_{\text{t}}} = {F_{\text{d}}} + G $ | (2) |
| $ {F_{\text{d}}} = {k_{\text{t}}}({x_{\text{t}}} - {x_{\text{g}}}) + {c_{\text{t}}}({{\dot x}_{\text{t}}} - {{\dot x}_{\text{g}}})\\ G = \left( {{m_{\text{s}}} + {m_{\text{t}}}} \right)g $ | (3) |
式中:Fd为轮胎附加动载;G为车辆静载;g为重力加速度.
2 铺装层不平整度指标IRI的生成IRI是当前国际上广泛采用的平整度指标,根据Paterson的研究,绝对平整的铺装层面的IRI为0,中等平整度的铺面约为6 m·km-1,非常不平整路面的IRI约为12 m·km-1.IRI其实是一个量纲为一的数,习惯上用m·km-1表示.国内评价桥面铺装层平整度常用颠簸累加值BI或方差,这两个指标都与IRI存在良好的线形相关性[11].
| $ {I_{{\text{RI}}}} = \frac{1}{L}\int_0^L {\left| {{x_{\text{t}}} - {x_{\text{s}}}} \right|} {\text{d}}x $ | (4) |
式中:L为选取的路面长度,工业界习惯采用功率谱密度来描述路面的平整度,铺装层功率谱可表示如下:
| $ {G_{\text{d}}}\left( n \right) = {G_{\text{d}}}({n_0}){(n/{n_0})^{ - w}} $ | (5) |
式中:n为空间频率(m-1), 是波长的倒数;n0为参考空间频率,通常取0.1 m-1;Gd(n0)为n0下的路面谱值,称为路面平整度系数(m3);w为频率指数.
不平度IRI的时域模型仿真方法主要有4种:滤波白噪声法、谐波叠加法(或称三角级数合成法)、基于离散时序的AR(自回归)和AMAR法、PSD离散采样法[12].在计算过程中,通常已知不平整度IRI,反算功率谱密度PSD,进而求得路面随机高程.相关研究表明1/4车辆模型下二者关系为
| $ {G_{\text{d}}}\left( n \right) = 1.63{K_0}{(n/{n_0})^{ - w}}I_{{\text{RI}}}^2 $ | (6) |
式中:K0=10-6 m3.若Gd(ω)为以角频率表示的铺装层表面功率谱密度,则铺装层表面不平度的随机响应d(t)可表示为
| $ d\left( t \right) = \sum\limits_{k = 1}^M {{A_k}\cos({\omega _k}t + {\phi _k})} $ | (7) |
式中:M为正整数;ϕk为区间[0,2π]上分布的随机变量;ωk为角频率.转换到空间频域,并利用ω=2πvn,可得
| $ d\left( t \right) = \sum\limits_{k = 1}^M {\sqrt {3.26{K_0}\Delta n} \frac{{{n_0}}}{{{n_k}}}\cos \left( {2\pi v{n_k}t + {\phi _k}} \right)} $ | (8) |
式中:Δn=(nm-n1)/M,一般路面构造波长取0.1~2 m作为计算簧载频响函数的积分区间,v为车辆行驶速度.
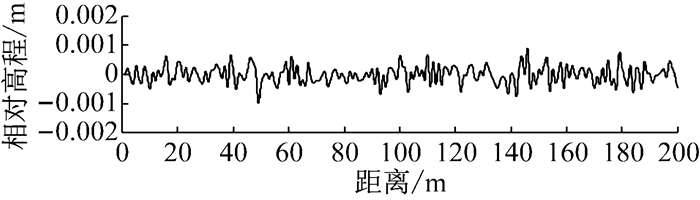
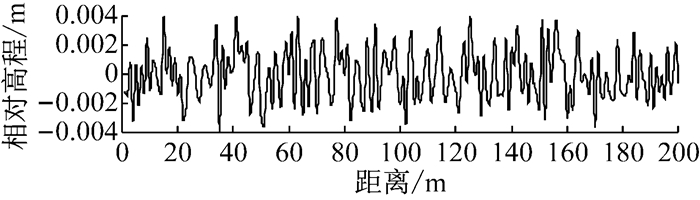
利用式(8) 通过IRI求出基于铺装层不平度的车辆随机动载[13-14].取M=400,n=1,v=20 m·s-1,铺装层表面长度为200 m, 当IRI=2,IRI=10时铺装层表面不平度激励分别见图 2和图 3.
|
图 2 IRI=2时铺装层表面不平度模拟 Fig.2 Simulation of pavement roughness when IRI=2 |
|
图 3 IRI=10时铺装层表面不平度模拟 Fig.3 Simulation of pavement roughness when IRI=10 |
选取跨径为20 m的简支箱梁桥作为典型模型,截面为单箱单室箱型截面,桥面宽20.8 m,双向四车道,梁高2.1 m,顶板厚0.3 m,混凝土垫层厚度为0.03 m,防水层厚3 mm,沥青混凝土层厚度为0.08 m,腹板厚0.4 m,荷载采用1/4车辆模型,作用形式为偏载,车轮横向作用位置按公路桥涵设计通用规范(JTG D60—2015) 布置在翼缘板最外侧(见图 4)[15].运用有限元程序Ansys实体建模分析[16-17],其中梁体、混凝土垫层以及沥青铺装层用实体单元Solid45模拟,防水层采用三维膜单元shell41单元模拟.桥梁体及铺装层有关模型参数见表 2.

|
图 4 有限元模型及轮载横向布载位置 Fig.4 Finite element analysis model and load position |
| 下载CSV 表 2 建模材料参数 Tab.2 Parameters of the model |
模型采取简支边界条件,桥梁一端约束X、Y和Z三个方向的自由度,另一端释放纵桥向Z方向的自由度.依据规范,车轮接地采用双轮接地形式,重轮接地面积为0.6 m×0.2 m,沥青层与防水层、三角垫层及桥面板之间的采取结点耦合处理,层间始终保持连续接触状态.
假设:① 桥面板和铺装层都处于线弹性工作状态;② 桥面板、铺装层和防水层共同承受车辆荷载,且材料并未出现破坏;③ 工作时接触面未出现滑移脱空,层间处于连续接触状态.
相关文献表明铺装层的破坏多为沥青铺装层拉应力失效及黏结层剪切滑移和脱层[18].故本文以铺装层横桥向及纵桥向拉应力、黏结层间的法向拉力和切应力作为铺装层典型控制应力.本文约定如下:σ1为沥青面层内的第一主应力(拉);σz为沥青面层的纵桥向拉应力;σx为面层横桥向拉应力;τxy为黏结层横桥向剪应力;τyz为层间顺桥向剪应力;σy为接触层间法向拉应力.
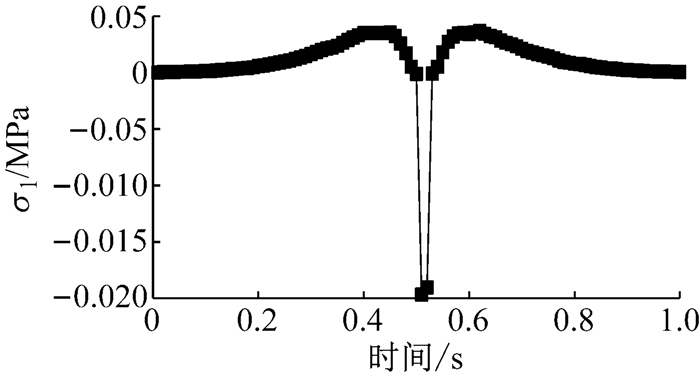
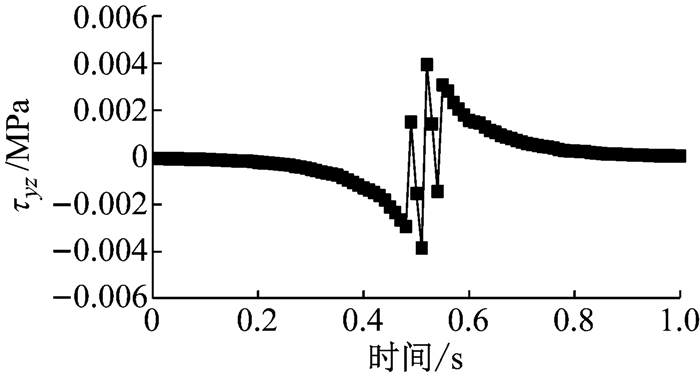
4 铺装层应力响应分析为了研究随机动载作用下铺装层的应力分布情况,本文先选择跨中固定位置的沥青面层节点及防水黏结层的节点为研究对象,作出该处节点的应力时程曲线,其次作出铺装层各控制应力极值的时程曲线(动载作用下,每个荷载步里铺装层全部节点中的最大应力响应值).结果表明:随机动载作用下跨中固定节点的各项应力时程曲线与移动活载作用下相似:荷载作用在跨中位置处时,应力响应达到峰值,桥两端的响应值最小,分别见图 5~图 10.可见,铺装结构固定位置节点的应力时程变化无法反映动荷载的随机特征,亦无法反映整个铺装结构体系随荷载变化的应力分布情况.而铺装层控制应力极值响应作为研究随机动载响应分析的动力学指标具,不仅可以反映车辆荷载的随机性,还能够抓住结构最不利响应,故而下文中采用该指标进行研究分析.

|
图 5 跨中固定位置节点τxy时间历程曲线 Fig.5 Time curves of τxy at the fixed point |
|
图 6 跨中固定位置节点σ1时间历程曲线 Fig.6 Time curves of σ1 at the fixed point |

|
图 7 跨中固定位置节点σz时间历程曲线 Fig.7 Time curves of σz at the fixed point |
|
图 8 跨中固定位置节点τyz时间历程曲线 Fig.8 Time curves of τyz at the fixed point |

|
图 9 跨中固定位置节点σx时间历程曲线 Fig.9 Time curves of σx at the fixed point |
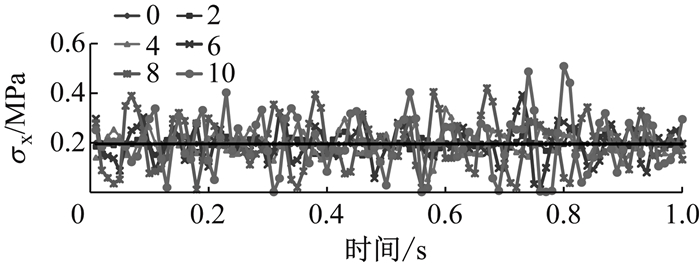
|
图 10 不同桥面不平度下沥青面层横桥向拉应力极值曲线 Fig.10 Extreme value curves of σx at top surface of asphalt layer with different pavement surface roughness |
汽车行驶在平顺性差异较大的不同桥面上时,车轮附加动载存在着较大的差异.为了分析桥面不平整度对铺装层动力响应的影响规律,本文从绝对平整即IRI=0,轻度不平整IRI=2,一般不平整IRI=4, 6以及严重不平整IRI=8,10共6个等级,分别仿真得到不同不平度下的车辆的动荷载,并对车桥桥面铺装耦合振动体系进行了有限元分析,得出不同桥面不平度下,沥青面层以及防水黏结层控制应力极值的变化的时程曲线,即车辆行驶到不同位置时,铺装层应力极值的变化情况,见图 10~图 15.

|
图 11 不同桥面不平度下沥青面层纵桥向拉应力极值曲线 Fig.11 Extreme value curves of σz at top surface of asphalt layer with different pavement surface roughness |

|
图 12 不同桥面不平度下沥青面层拉应力极值曲线 Fig.12 Extreme value curves of σ1 at top surface of asphalt layer with different pavement surface roughness |

|
图 13 不同桥面不平度下黏结层法向拉应力极值曲线 Fig.13 Extreme value curves of σy at interface layer with different pavement surface roughness |
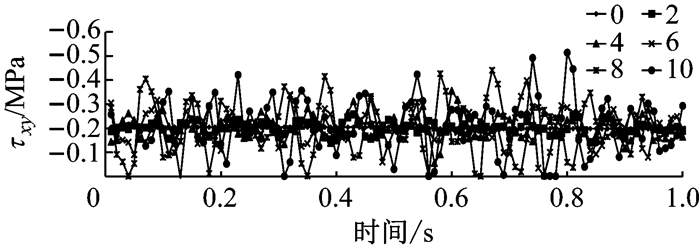
|
图 14 不同桥面不平度下黏结层横桥向应力极值曲线 Fig.14 Extreme value curves of τxy at interface layer with different pavement surface roughness |

|
图 15 不同桥面不平度下黏结层纵桥向剪应力极值曲线 Fig.15 Extreme value curves of τyz at interface layer with different pavement surface roughness |
当IRI=0时车轮的附加动载为0,此时即为移动恒载工况.表 3列出了在移动活载及IRI=2工况下,铺装层各项控制应力的极值响应,可以看出,当铺装层平整度良好时,各项控制应力的极值较为接近,即当铺装层平顺性良好时,可以近似用移动活载来计算铺装层的应力响应.
| 下载CSV 表 3 移动活载与随机荷载应力响应极大值的比较 Tab.3 Comparison of maximum stress value between random load and moving constant load |
由图 10~图 15可以看出:① 车辆在不同不平度下的桥面上行驶,各条铺装层控制应力极值响应曲线的最大值均大于移动活载,且随着IRI增大,铺装层内各应力极值响应的振荡幅度和应力最大值也越大;② 在桥面平顺性良好时(IRI=2),应力最大值波动较小,随机荷载应力响应同移动活载情况下较为接近,但在IRI≥4时,各应力极值响应曲线的波动效应明显增大,曲线峰值甚至达到移动活载的2倍甚至更多;③ 不平度对黏结层层间剪应力影响显著.在IRI=10时,顺桥向剪应力τyz最大值已经达到0.53 MPa,明显大于IRI=2时的剪应力水平.可见当桥面平顺性不断恶化时,防水黏结层在随机荷载作用下极容易发生剪切破坏,进而导致接触层推移、脱空等病害发生.
表 4为考虑不平整度的车辆随机动载作用下,铺装层各控制应力极值响应曲线的最大值较移动活载作用下的放大系数(动载放大系数).可以看出,虽然施加的是随机动载,但是在同一不平度下,铺装层各项应力峰值的放大系数十分接近;且当桥面情况良好时(IRI=2),各应力响应峰值的放大系数为0.3左右;当桥面状况一般(IRI=4) 时,动载放大系数约为0.6;而当平顺性较差(IRI=6,8) 时,动载放大系数分别接近0.9和1.3;在桥面情况很差(IRI=10),各项应力响应峰值的动载放大系数甚至达到1.6.由此可见,如果桥面铺装层的平整度较差,车辆随机动载将引起铺装层的严重破坏.
| 下载CSV 表 4 不同平整度下铺装层应力极值放大系数 Tab.4 magnification coefficient of maximum pavement stress value among different IRI |
图 16作出了不同速度下,动载放大系数和IRI的关系,从中可以发现:当固定车速而不平度变化时,在不同速度下,动载放大系数均随着IRI的增大而增大,且当IRI≤4时,各曲线的增长趋势非常接近,而IRI>4时,不同速度下动载放大系数曲线的差异较大,受IRI影响最大和最小的曲线分别的是v=10和v=15.与此同时,由于桥面不平度增大,车辆附加动载迅速增大,当IRI >6时,动载放大系数将超过1,此时的冲击作用不仅会使乘客舒适度下降,影响车辆使用寿命,还将使桥面铺装层平顺性继续恶化,严重的还会导致沥青铺装层发生破坏.

|
图 16 不同速度下IRI与动载放大系数关系曲线 Fig.16 The relation between dynamic amplification coefficient and IRI for different velocities |
鉴于在同一不平整度下,铺装层内各项控制应力极值响应峰值的放大系数非常接近,若能找到一套完整、准确的关于铺装层不平整度的测量和评估标准,则可在宏观上把握铺装各项控制应力的变化情况,进而可以更直观和方便地实现对桥面铺装的健康监测和损伤评估.
5 结论(1) 铺装层控制应力的极值响应曲线随着时间的增加而不断改变,其波动频率与随机动载变化的频率相似.在随机动载和移动活载分别作用下,随机动载的破坏效应要大于移动活载,因此在对铺装结构进行分析时,不仅要考虑荷载的动态响应,还应该考虑到荷载的随机振动效应.
(2) 桥面状况良好时,随机动载作用下铺装层应力响应接近于移动恒载,随着不平度增大,各应力最大值和响应曲线的波动效应均增大,当桥面平顺性较差时,铺装层的各项控制应力的极值相比于绝对平顺时增大了1.
(3) 不同车速下,动载放大系数均随着IRI的增大而增大,且当IRI≤4时,各曲线的增长趋势非常接近,而IRI>4时,不同速度下动载放大系数曲线的差异较大.
(4) 在同一不平整度下,各项控制应力极值响应的峰值放大系数非常接近,若能找到一套完整、准确的关于铺装层不平整度的测量和评估标准,则可在宏观上把握铺装各项控制应力的变化情况,进而可以更直观和方便的实现对桥面铺装的健康监测和损伤评估.
| [1] |
王达, 韩万水, 黄平明, 等. 桥面平整度对大跨度悬索桥车桥耦合振动的影响[J]. 长安大学学报(自然科学版), 2009, 29(4): 53 WANG Da, HAN Wanshui, HUANG Pingming, et al. Influence of bridge surface roughness on vehicle-bridge coupled vibration of long-span suspension bridge[J]. Journal of Chang'an University(Natural Science Edition), 2009, 29(4): 53 |
| [2] |
段虎明, 石峰, 谢飞, 等. 路面不平度研究综述[J]. 振动与冲击, 2009, 28(9): 95 DUAN Minghu, SHI Feng, XIE Fei, et al. A survey of road roughness study[J]. Journal of Vibration and Shock, 2009, 28(9): 95 |
| [3] |
钱振东, 刘云, 黄卫. 考虑不平度的桥面铺装动响应分析[J]. 土木工程学报, 2007, 40(4): 49 QIAN Zhendong, LIU Yun, HUANG Wei. Analysis of the dynamic response of steel-deck pavement with roughness[J]. China Civil Engineering Journal, 2007, 40(4): 49 |
| [4] |
张磊, 伍石生, 黄卫, 等. 面向桥面铺装动力响应分析的多尺度桥梁模型[J]. 中国公路学报, 2012, 25(3): 87 ZHANG Lei, WU Shisheng, HUANG Wei, et al. Multi-scale model for the bridge deck pavement dynamic analysis[J]. China Civil Engineering Journal, 2012, 25(3): 87 |
| [5] |
LAWSS, ZHU X Q. Bridge dynamic response due to road surface roughness and braking of vehicle[J]. Journal of Sound and Vibration, 2005, 282(3-5): 805 DOI:10.1016/j.jsv.2004.03.032 |
| [6] |
DAS A, DUTTA A, TALUKDAR S. Efficient dynamic analysis of cable-stayed bridges under vehicular movement using space and time adaptivity[J]. Finite Elements in Analysis and Design, 2004, 40(4): 407 DOI:10.1016/S0168-874X(03)00070-2 |
| [7] |
LIU C, HUANG D, WANG T L. Analytical Dynamic Impact Study Based on Correlated Road Roughness[J]. Computers & Structures, 2002, 80(20-21): 1639 |
| [8] |
孙璐, 邓学钧. 移动的车辆随机荷载作用下桥梁的瞬态响应[J]. 振动与冲击, 1997, 16(1): 142 SUN Lu, DENG Xuejun. Transient response of bridge to traveling random vehicle loads[J]. Journal of Vibration and Shock, 1997, 16(1): 142 |
| [9] |
SUN L, KENNEDY T. Spectral analysis and parametric study of stochastic pavement load[J]. Journal of Engineering Mechanics, 2002, 128(3): 318 DOI:10.1061/(ASCE)0733-9399(2002)128:3(318) |
| [10] |
李金辉, 何杰, 李旭宏. 车辆随机及移动荷载作用下路面动态响应[J]. 长安大学学报(自然科学版), 2015, 35(2): 38 LI Jinhui, HE Jie, LI Xuhong. Dynamic response of pavement under vehicle random load and moving constant load[J]. Journal of Chang'an University Nature Science Edition, 2015, 35(2): 38 |
| [11] |
彭家, 何杰, 李旭宏, 等. 路面不平度随机激励时域模型的仿真比较与评价[J]. 解放军理工大学学报(自然科学版), 2009, 10(1): 77 PENG Jia, HE Jie, LI Xuhong, et al. Simulation comparison and evaluation of common time domain models under road irregularity excitation[J]. Journal of PLA University of Science and Technology(Natural Science Edition), 2009, 10(1): 77 |
| [12] |
张永林, 钟毅芳. 车辆路面不平度输入的随机激励时域模型[J]. 农业机械学报, 2004, 35(2): 9 ZHANG Yonglin, ZHONG Yifang. Time domain model of road undulation excitation to vehicles[J]. Transaction of the Chinese Society of Agricultural Machinery, 2004, 35(2): 9 |
| [13] |
CHENG Y, CHEUNG Y K. Effects of random road surface roughness and long-term deflection of prestressed concrete girder and cable-stayed bridges on impact due to moving vehicles[J]. Computers and Mechanics, 2001, 79: 853 |
| [14] |
SCHIEHLEN W, HU B. Spectral simulation and shock absorber identification[J]. International Journal of Non-linear Mechanics, 2003, 38: 161 DOI:10.1016/S0020-7462(01)00053-1 |
| [15] |
中交公路规划设计院有限公司. 公路桥涵设计通用规范: JTG D60—2015[S]. 北京: 人民交通出版社, 2015. CCCC Highway Consultants Co.Ltd. General Specifications for Design of Highway Bridges and Culverts: JTG D60—2015[S]. Beijing: China Communications Press. 2015. |
| [16] |
张立明. ALGOR, ANSYS在桥梁工程中的应用方法与实例[M]. 北京: 人民交通出版社, 2003 ZHANG Liming. ALGOR, ANSYS applied to bridge engineering[M]. Beijing: China Communications Press, 2003 |
| [17] |
李围. ANSYS土木工程应用实例[M]. 北京: 中国水利水电出版社, 2007 LI Wei. The example of civil engineering by ANSYS[M]. Beijing: China Waterpower Press, 2007 |
| [18] |
徐勤武, 胡长顺, 王虎. 混凝土桥面复合式铺装层受力分析和设计[J]. 长安大学学报(自然科学版), 2007, 27(4): 28 XU Qinwu, HU Changshun, WANG Hu. Mechanic analysis and design of composite type overlay on concrete bridge pavement[J]. Journal of Chang' an University (Natural Science Edition), 2007, 27(4): 28 |
 2017, Vol. 45
2017, Vol. 45

