2. 同济大学建筑设计研究院(集团)有限公司,上海 200082
2. Tongji Architectural Design (Group) Co., Ltd., Shanghai 200082, China
交通需求管理措施可以主动引导居民出行,达到出行在时间和空间上的分散以及出行结构的优化,进而解决交通拥堵问题[1].弹性工作制是需求管理的措施之一,是指员工在完成规定工作任务或固定工作时长下,可以灵活、自主地选择工作的具体时间或地点,以代替统一、固定的上下班时间的制度[2].当员工开始工作时间的选择自由度变大后,其在安排工作和其他活动时就能更加灵活自主,并可根据交通拥堵状况调整出发时间,避开高峰出行,达到自身效益的最大化,对整个交通系统来说,出行较分散,拥堵时间减少,系统效率得到提高.非弹性的员工有严格固定的上下班时间,无法避开高峰时段出行,需忍受较长的出行时间.文献[3]表明当减少通勤活动的时空制约时,居民会明显地选择避让“高峰”.还有一些国家通过实施弹性工作制来缓解交通拥堵,并取得了较好的效果.目前德国约1/4的员工、美国近43%的全职员工可以弹性地选择上班时间[2].韩国自2014年起开始广泛实施“5小时弹性工作制”.我国目前实施弹性工作制的企业较少,较多城市实施错峰上下班制度来缓解高峰拥堵.错峰出行本质上不同于弹性工作制,以单位为个体进行上下班时间的错开,单位员工仍不具备灵活选择上班时间的自由,对高峰拥堵的缓解效果十分有限;而弹性工作制以出行个体为单位,自由安排上下班时间.
弹性系数[4-5]可描述某项活动在时间安排上的灵活性,通常用于单次出行或早晚出行链构建的出行效用方程,分析弹性工作制对通勤者出行时间选择的影响和缓解交通拥堵的效果.弹性系数法最早见于文献[5],弹性系数ξ∈[0, 1]表示活动的弹性程度.当弹性系数为1时,表示上班的时间完全弹性;反之,当弹性系数为0时,上班时间完全固定.这种方法后续被很多研究采用[6-8].弹性系数法可以使得出发时间选择函数连续化,能简化模型的建立和求解,但无法描述特定的弹性工作制度,其含义与实际应用较难对应.
文献[6-7, 9]将弹性工作制对缓解通勤拥堵的作用拓展至早晚出行链.通勤者不仅需要考虑早上单次出行的效用,还将同时考虑早上出发时间的选择对晚上下班时间的影响.Ettema等[10]拓展了基于活动效用模型的应用,提出了同时考虑出发时间和活动持续时间的多维出行选择模型.Li等[7]将早到(迟到)的惩罚费用加入出行效用方程中,构建基于活动的出行模型,结果表明出行者早晚出发率的解析解存在的条件为上班活动的边际效用是常值.Jenelius[8]进一步对弹性活动下的平均行程时间价值和行程时间可靠度价值进行了研究.通过建立模型对弹性工作制的治堵效果进行了分析,但仍缺乏对混合弹性和非弹性员工共同出行的考虑.员工是否可以采用弹性工作制或其弹性时间很大程度取决于其岗位性质,不同企业中可采用弹性工作制的员工比例也不相同.因此,研究弹性和非弹性多用户出行更符合实际应用的要求.
除了建模分析法,后评估法也用于评价弹性工作制的效果.该方法通过调查收集弹性工作制实施后的交通数据,分析弹性工作制对通勤者出行行为和交通拥堵的影响.Tacken等[11]对400名阿姆斯特丹的工人进行调查,在考虑很多出发时间约束的情况下(如预约医生、道路拥挤情况等),实行弹性工作制后,员工仍会通过改变出发时刻降低个人的出行时长,通勤的整体交通量在时间维度上得以分散.不少研究分析了弹性工作制实施前后整体出行时长和出行分布等的变化.He[12]对美国加利福尼亚州2个较拥堵的区进行统计,发现弹性工作制员工比非弹性工作制员工在高峰时段前出发率低3.3%,在高峰期间出发率低4.11%,在高峰后出发率高7.41%,表明了弹性工作制员工会延后其出行来避开拥堵.
国内对弹性工作制的交通出行影响分析较少[9],更多集中在错峰上下班制度对交通出行和交通延误的影响[13].错峰上下班对改善交通状况的效果有限[14-15],同时对实施的条件要求较高,应用不当反而有不利的影响[16-17].不同的错峰上下班政策对交通状况也有不同的影响[18].石骞[19]指明,错时上下班策略的制定是一个系统的、区域的概念.
目前研究表明,弹性工作制缓解交通拥堵的作用是显而易见的,但其不足之处主要体现在以下几个方面:①未考虑弹性工作制的实施规模对交通出行的影响.在现实情况中,不同类型企业或者同一企业不同类型的岗位适合不同的工作制度,并非所有员工都适用弹性工作制度[20].例如,流水线作业的员工不适合弹性工作制,而对从事创造性工作的员工实施弹性工作制能增加其工作效率.对于不同地区,其产业模式、产业比例不同,可采取弹性工作制的员工比例也不同,因此不能一概而论.分析不同弹性工作制员工比例下的出行情况和路网拥堵情况是十分必要的.②目前研究主要基于弹性系数的行为建模进行弹性工作制的影响分析.弹性系数的概念不容易解释现实中具体的弹性工作制度.例如,当一家公司允许员工上班迟到2 h,通过延迟2 h下班来弥补迟到,弹性系数法无法模拟这种上班形式.针对以上不足,本文建立了基于活动效用的出发时间选择模型,提出了针对核心和弹性工作时段所形成的弹性工作制下的出发时间选择行为模型,对不同弹性员工比例下的出行规律以及拥堵情况进行分析,为制定弹性工作制度提供决策支持和理论依据.
1 弹性工作制对出行的影响分析 1.1 弹性工作制形式本文研究的弹性工作制由弹性工作时段和核心工作时段组成.弹性员工可以选择在弹性时间段内根据自身需求抵达或离开单位,核心时间段是必须保证的工作时间.该制度与传统的使用弹性系数的工作制度相比,更具体更具有针对性.在弹性系数方法中设置弹性系数为1,并添加弹性区间约束,是一种明确的弹性工作制度形式,如图 1所示.

|
图 1 核心工作时段和弹性时段结合的上班制度 Fig.1 Working arrangement with core working time and flexible working time |
图 1中,TSO表示公司开始营业时间,TPA表示公司规定的必须在岗的开始时间,TPD表示必须在岗时间段的结束时间,TEO表示公司停止营业时间.通常情况下,员工每天期望工作的时段(或者说工作效率较高的时段)是比较固定的,这里用TSW表示这个时段的起始时间.
为了达到较高的效益,公司开始营业的时间应满足TSO<TSW,规定必须在岗的开始时间满足TPA>TSW.同理,必须在岗的结束时间应满足TPD<TEO.本文中用Tw表示员工的工作时间,对于所有员工假设Tw固定且相等,另外还需满足TSO+Tw<TEO, TPA+Tw≤TEO.
1.2 弹性员工的出行行为建模常见的行为选择模型分为基于出行效用和基于活动效用的模型.基于出行效用的模型通常仅考虑出行成本对出行选择的影响,但出行选择依赖于一天内完成活动的相互关系以及活动的效用.因此,本文采用基于活动效用的方法构建行为模型.根据Doherty等[21]的调查研究,大约有90%的员工都符合“家-公司-家”这类典型的活动链.影响出行的主要活动有3个:早上居家、上班、晚上居家.活动之间分别由从家到工作地点的早通勤出行和从工作地点到家的晚通勤出行连接.
为了更方便地建立、求解模型,考虑了以下3个假设来简化模型:
(1) 不考虑寻找车位时间,假设到达公司时刻立即投入工作.
(2) 员工的活动边际效用假设为时间变量的任意连续可导函数.
(3) 弹性工作制员工晚上的出发时间根据早上的到达时间和工作时间长度确定.当工作时间(工作效用)相同时,第1个结束工作的员工会因为没有拥堵而最早出发,因此也会最早到达,相比于后出发的员工有较高的居家效用.当达到用户均衡时所有员工的效用相同,因此较晚下班的员工同样会较晚上班来满足居家效用相同.
通勤者的效用由以下几部分组成:早(晚)居家效用、上班效用、早(晚)通勤出行损失、早到(或晚到)惩罚、下班早退(或较晚离开)惩罚.该方法与Ettema等[10]提出的效用模型构成相同,都是包含了早晚居家和工作3个活动的效用以及早晚2次出行的效用.区别在于本文针对具体的弹性工作制度,定义了相应的效用模型.对于弹性员工,其早到或晚到延误惩罚在弹性工作时段为零.另外,除了构建弹性工作制下的行为模型,还分析了基于此效用模型的出行规律以及不同弹性员工比例对交通出行的影响.弹性员工在TSO之前到达会产生早到费用,迟于TPA到达需要接受公司的惩罚而产生晚到费用,对于下班离开时间,亦同.弹性员工的效用与早上出发时间td1和晚上出发时间td2有关,表示如下:
| $ \begin{array}{l} U\left( {{t_{{\rm{d}}1}},{t_{{\rm{d}}2}}} \right) = \theta \int_{{t_{{\rm{s2}}}}}^{{t_{{\rm{d2}}}}} {\left( {{u_2}\left( {t - \left( {\left\langle {\max \left( {{t_{{\rm{s2}}}},{T_{{\rm{SO}}}}} \right),{T_{{\rm{PA}}}}} \right\rangle - } \right.} \right.} \right.} \\ \;\;\;\;\;\;\;\left. {\left. {\left. {{T_{{\rm{SW}}}}} \right)} \right)} \right){\rm{d}}t + \theta \int_0^{{t_{{\rm{d}}1}}} {{u_1}\left( t \right){\rm{d}}t - \upsilon {T_1}\left( {{t_{{\rm{d}}1}}} \right) + } \\ \;\;\;\;\;\;\;\theta \int_{{t_{{\rm{s3}}}}}^{24} {{u_3}\left( t \right){\rm{d}}t - \upsilon {T_2}\left( {{t_{{\rm{d}}2}}} \right) - {\gamma _1}\max \left\{ {0,{t_{{\rm{s2}}}} - {T_{{\rm{PA}}}}} \right\}} - \\ \;\;\;\;\;\;\;{\gamma _2}\max \left\{ {0,{T_{{\rm{PD}}}} - {t_{{\rm{d}}2}}} \right\} - {\eta _1}\max \left\{ {0,{T_{{\rm{SO}}}} - {t_{{\rm{s2}}}}} \right\} - \\ \;\;\;\;\;\;\;{\eta _2}\max \left\{ {0,{t_{{\rm{s2}}}} - {T_{{\rm{EO}}}}} \right\} \end{array} $ | (1) |
式中:ui(t)表示活动i在t时刻的边际效用,下标1表示早上居家活动,下标2表示工作活动,下标3表示晚上居家活动;tsi表示活动i的开始时间;tdi表示出行i的出发时间;η1和γ1分别为早上早到和晚到的单位时间的效用损失;γ2和η2分别为晚上早离开和晚离开公司的单位时间的效用损失;T1(td1)和T2(td2)分别为早晚出行的行程时间;υ为早晚出行的单位时间效用损失;θ为系数.
式(1)表明,在早上td1时刻出发,晚上td2时刻离开公司的弹性员工,其一天的效用等于早上居家、上班工作和晚上居家的活动效用总和与早上上班早到或迟到、晚上下班早退或晚退的惩罚以及早晚出行成本的差值.
该行为模型与传统的基于出行的模型相比,优势在于:①更符合实际出行的行为选择;②考虑了完整的早晚出行链;③与传统的基于弹性系数的建模方法相比,本文的行为模型针对具体的弹性工作制度,与实际应用更相符.
1.3 完全弹性工作制对出行的影响分析Vickrey[22]瓶颈模型被广泛应用于出发时间选择以及出行动态演化过程的解析研究中[23].本文也应用了该模型,分析100%的员工都可以实施弹性工作制(完全弹性工作制度)下出行在时间维度上的演化情况.Vickrey的瓶颈模型假设居民从家到工作地点只有一条道路连接,在道路的某处存在瓶颈,其通行能力为S.基于瓶颈模型的早晚出行链模型如图 2所示.

|
图 2 基于瓶颈模型的早晚出行链模型 Fig.2 Integrated morning-evening commute chain based on the bottleneck model |
由于在通勤路段上存在瓶颈,因此当交通量超过其通行能力时就会产生拥堵.此时,行程时间为自由流行程时间(固定值)和排队拥堵时间之和,如下所示:
| $ {T_1} = {T_{\rm{f}}} + \frac{{{D_1}\left( {{t_{{\rm{d1}}}}} \right)}}{S} - \left( {{t_{{\rm{d1}}}} - {t_{{\rm{d1,be}}}}} \right) $ | (2) |
| $ {T_2} = {T_{\rm{f}}} + \frac{{{D_2}\left( {{t_{{\rm{d2}}}}} \right)}}{S} - \left( {{t_{{\rm{d2}}}} - {t_{{\rm{d2,be}}}}} \right) $ | (3) |
| $ {t_{{\rm{s2}}}} = {t_{{\rm{d1}}}} + {T_1} = {T_{\rm{f}}} + \frac{{{D_1}\left( {{t_{{\rm{d1}}}}} \right)}}{S} + {t_{{\rm{d1,be}}}} $ | (4) |
| $ {t_{{\rm{s3}}}} = {t_{{\rm{d2}}}} + {T_2} = {T_{\rm{f}}} + \frac{{{D_2}\left( {{t_{{\rm{d2}}}}} \right)}}{S} + {t_{{\rm{d2,be}}}} $ | (5) |
式(2)~(5)中:Tf为上下班途中自由流行程时间;td1, be表示早上第一个出行者的出发时刻;td2, be表示晚上第一个出行者的下班时刻;D1(t)、D2(t)分别表示t时刻早上、晚上累计出发流量.
当路网达到用户均衡状态时,每个用户不能通过改变早(晚)出发时间(td1, td2)来提高自己的效用.根据假设(3),将早晚出发时间的关系(ts2=td1+T1,ts3=ts2+Tw+T2)代入式(1),效用方程只与td1有关,如下所示:
| $ \begin{array}{l} U\left( {{t_{{\rm{d1}}}}} \right) = \theta \int_{{t_{{\rm{s2}}}}}^{{t_{{\rm{s2}}}} + {T_{\rm{w}}}} {\left( {{u_2}\left( {t - \left( {\left\langle {\max \left( {{t_{{\rm{s2}}}},{T_{{\rm{SO}}}}} \right),{T_{{\rm{PA}}}}} \right\rangle - } \right.} \right.} \right.} \\ \left. {\left. {\left. {{T_{{\rm{SW}}}}} \right)} \right)} \right){\rm{d}}t + \theta \int_0^{{t_{{\rm{d}}1}}} {{u_1}\left( t \right){\rm{d}}t - \upsilon {T_1}\left( {{t_{{\rm{d}}1}}} \right) + } \\ \theta \int_{{t_{{\rm{s3}}}}}^{24} {{u_3}\left( t \right){\rm{d}}t - \upsilon {T_2}\left( {{t_{{\rm{d}}2}}} \right) - {\gamma _1}\max \left\{ {0,{t_{{\rm{s2}}}} - {T_{{\rm{PA}}}}} \right\} - } \\ {\gamma _2}\max \left\{ {0,{T_{{\rm{PD}}}} - {t_{{\rm{d}}2}} - {T_{\rm{w}}}} \right\} - \\ {\eta _1}\max \left\{ {0,{T_{{\rm{SO}}}} - {t_{{\rm{s2}}}}} \right\} - {\eta _2}\max \left\{ {0,{t_{{\rm{s2}}}} + {T_{\rm{w}}} - {T_{{\rm{EO}}}}} \right\} \end{array} $ | (6) |
根据上述分析,弹性工作者的出发时间选择行为模型如下所示:
| $ \begin{array}{l} \mathop {\max }\limits_{{t_{{\rm{d1}}}}} U\left( {{t_{{\rm{d1}}}}} \right)\\ {\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.0}} \le {t_{{\rm{dl}}}} < 24\\ \;\;\;\;\;{t_{{\rm{s2}}}} + {T_{\rm{w}}} \le {t_{{\rm{s3}}}}\\ \;\;\;\;\;0 < {t_{{\rm{s3}}}} \le 24\\ \;\;\;\;\;0 < {T_{\rm{w}}} \le 24 \end{array} $ | (7) |
假设活动的边际效用服从如下函数:
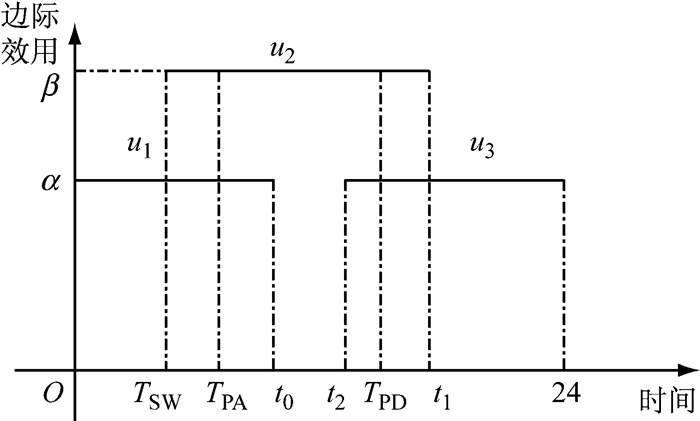
| $ {u_1} = \left\{ \begin{array}{l} \alpha ,\;\;\;\;0 < t < {t_0}\\ 0,\;\;\;\;\;t \in 其他 \end{array} \right. $ | (8) |
| $ {u_2} = \left\{ \begin{array}{l} \beta ,\;\;\;\;{T_{{\rm{SW}}}} \le t \le {t_1}\\ 0,\;\;\;\;\;t \in 其他 \end{array} \right. $ | (9) |
| $ {u_3} = \left\{ \begin{array}{l} \alpha ,\;\;\;\;{t_2} < t < 24\\ 0,\;\;\;\;\;t \in 其他 \end{array} \right. $ | (10) |
式中:t0为在家效用的截止时间,晚于TPA;t2为晚上居家效用开始时间,不妨设其为小于TPD的某个值;α、β分别为居家边际效用和工作边际效用,且α<β;t1=TSW+Tw.效用函数如图 3所示.
|
图 3 常数下的边际效用函数 Fig.3 Constant marginal utility functions |
对于瓶颈模型来说,早上流量到达率不会超过瓶颈的通行能力,加之固定的工作时长Tw, 则有T2=Tf,
| $ U\left( {{t_{{\rm{dl}}}}} \right) = \varphi \left( {{t_{{\rm{dl}}}}} \right) + \psi \left( {{t_{{\rm{s}}2}}} \right) $ | (11) |
| $ \varphi \left( {{t_{{\rm{dl}}}}} \right) = \theta \alpha {t_{{\rm{dl}}}} + \upsilon {t_{{\rm{dl}}}} - \upsilon {T_{\rm{f}}} $ | (12) |
| $ \psi \left( {{t_{{\rm{s}}2}}} \right) = \mathit{\Xi + \Theta } - \upsilon {t_{{\rm{s2}}}} - \theta \alpha \left( {{t_{{\rm{s2}}}} + {T_{\rm{w}}} - 24} \right) $ | (13) |
| $ \mathit{\Xi } = \theta \int_{{t_{{\rm{s2}}}}}^{{t_{{\rm{s2}}}} + {T_{\rm{w}}}} {{u_2}\left( {t - \left( {\left\langle {\max \left( {{t_{{\rm{s2}}}},{T_{{\rm{SO}}}}} \right),{T_{{\rm{PA}}}}} \right\rangle - {T_{{\rm{SW}}}}} \right)} \right){\rm{d}}t} $ | (14) |
| $ \begin{array}{l} \mathit{\Theta } = - {\gamma _1}\max \left\{ {0,{t_{{\rm{s}}2}} - {T_{{\rm{PA}}}}} \right\} - {\gamma _2}\max \left\{ {0,{T_{{\rm{PD}}}} - {t_{{\rm{s2}}}} - } \right.\\ \;\;\;\;\;\;\left. {{T_{\rm{w}}}} \right\} - {\eta _1}\max \left\{ {0,{T_{{\rm{SO}}}} - {t_{{\rm{s2}}}}} \right\} - \\ \;\;\;\;\;\;{\eta _2}\max \left\{ {0,{t_{{\rm{s2}}}} + {T_{\rm{w}}} - {T_{{\rm{EO}}}}} \right\} \end{array} $ | (15) |
Han等[24]和Heydecker等[25]分别使用不同方法对包含出发时间选择的动态用户均衡状态进行分析.Han等[24]指出,当φ′(td1)≥0并且ψ′(ts2)≤0时,方程存在解.对式(12)和式(13)进行求导,得
| $ \varphi '\left( {{t_{{\rm{d1}}}}} \right) = \theta \alpha + \upsilon $ | (16) |
| $ \psi '\left( {{t_{{\rm{s}}2}}} \right) = - \upsilon - \theta \alpha + \frac{{\partial \mathit{\Xi }}}{{\partial {t_{{\rm{s2}}}}}} + \frac{{\partial \mathit{\Theta }}}{{\partial {t_{{\rm{s2}}}}}} $ | (17) |
其中
| $ \frac{{\partial \mathit{\Xi }}}{{\partial {t_{{\rm{s2}}}}}} = \left\{ \begin{array}{l} \theta \beta ,\;\;\;\;\;\;\;{t_{{\rm{s2}}}} \le {T_{{\rm{SO}}}}\\ - \theta \beta ,\;\;\;\;\;{T_{{\rm{PA}}}} \le {t_{{\rm{s2}}}}\\ 0,\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (18) |
| $ \frac{{\partial \mathit{\Theta }}}{{\partial {t_{{\rm{s2}}}}}}{\rm{ = }}\left\{ \begin{array}{l} - \left( {{\gamma _2} + {\eta _1}} \right),\;\;\;{t_{{\rm{s2}}}} \le {T_{{\rm{SO}}}},\forall {t_{{\rm{d2}}}} \le {T_{{\rm{PD}}}}\\ - \left( {{\eta _2} + {\eta _1}} \right),\;\;\;{t_{{\rm{s2}}}} \le {T_{{\rm{SO}}}},\forall {T_{{\rm{EO}}}} < {t_{{\rm{d2}}}}\\ - \left( {{\gamma _2} + {\gamma _1}} \right),\;\;\;{T_{{\rm{PA}}}} < {t_{{\rm{s2}}}},\forall {t_{{\rm{d2}}}} \le {T_{{\rm{PD}}}}\\ - \left( {{\gamma _1} + {\eta _2}} \right),\;\;\;{T_{{\rm{PA}}}} < {t_{{\rm{s2}}}},\forall {T_{{\rm{EO}}}} \le {t_{{\rm{d2}}}}\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (19) |
对于式(16), φ′(td1)=θα+υ>0恒成立,因此边际效用为常数时模型存在解析解只需要满足-υ-θ(α-β)-η1-min{γ2, η2}≤0即可,整理得
| $ \upsilon + {\eta _1} = \min \left\{ {{\gamma _2},{\eta _2}} \right\} \ge \theta \left( {\beta - \alpha } \right) $ | (20) |
在求解析解时,需要将时间看作连续变量,将假设参数代入式(1)中,可得
| $ \begin{array}{l} U\left( {{t_{{\rm{d1}}}},{t_{{\rm{d2}}}}} \right) = \theta \alpha {t_{{\rm{d1}}}} + \theta \beta {T_{\rm{w}}} + \theta \alpha \left( {24 - {t_{{\rm{s3}}}}} \right) - \upsilon \left( {{T_1} + {T_2}} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} \left( {{\eta _1} + \theta \beta } \right)\left( {{T_{{\rm{SO}}}} - {t_{{\rm{s2}}}}} \right) + {\gamma _2}\left( {{T_{{\rm{PD}}}} - {t_{{\rm{d2}}}}} \right),\;\;\;\;{t_{{\rm{s2}}}} \le {T_{{\rm{SO}}}},\forall {t_{{\rm{d2}}}} \le {T_{{\rm{PD}}}}\\ \left( {{\eta _1} + \theta \beta } \right)\left( {{T_{{\rm{SO}}}} - {t_{{\rm{s2}}}}} \right) + {\eta _2}\left( {{t_{{\rm{d2}}}} - {T_{{\rm{EO}}}}} \right),\;\;\;\;{t_{{\rm{s2}}}} \le {T_{{\rm{SO}}}},\forall {T_{{\rm{EO}}}} < {t_{{\rm{d2}}}}\\ \left( {\theta \beta + {\gamma _1}} \right)\left( {{t_{{\rm{s2}}}} - {T_{{\rm{PA}}}}} \right) + {\gamma _2}\left( {{T_{{\rm{PD}}}} - {t_{{\rm{d2}}}}} \right),\;\;\;\;{T_{{\rm{PA}}}} < {t_{{\rm{s2}}}},\forall {t_{{\rm{d2}}}} \le {T_{{\rm{PD}}}}\\ \left( {\theta \beta + {\gamma _1}} \right)\left( {{t_{{\rm{s2}}}} - {T_{{\rm{PA}}}}} \right) + {\eta _2}\left( {{t_{{\rm{d2}}}} - {T_{{\rm{EO}}}}} \right),\;\;\;\;{T_{{\rm{PA}}}} < {t_{{\rm{s2}}}},\forall {T_{{\rm{EO}}}} < {t_{{\rm{d2}}}}\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. \end{array} $ | (21) |
将瓶颈模型行程时间代入式(21),得到
| $ \begin{array}{l} U = \theta \alpha {t_{{\rm{d1}}}} + \theta \beta {T_{\rm{w}}} + \theta \alpha \left( {24 - {t_{{\rm{s2}}}} - {T_{\rm{w}}} - {T_{\rm{f}}}} \right) - \upsilon \left( {{T_{\rm{f}}} + \frac{{{D_1}\left( {{t_{{\rm{d1}}}}} \right)}}{S} - {t_{{\rm{d1}}}} + {t_{{\rm{d1,be}}}} + {T_{\rm{f}}}} \right) - \\ \;\;\;\;\;\;\left\{ \begin{array}{l} \left( {{\eta _1} + \theta \beta } \right)\left( {{T_{{\rm{SO}}}} - {t_{{\rm{s2}}}}} \right) + {\gamma _2}\left( {{T_{{\rm{PD}}}} - {t_{{\rm{s2}}}} - {T_{\rm{w}}}} \right),\;\;\;\;{t_{{\rm{s2}}}} \le {T_{{\rm{SO}}}},\forall {t_{{\rm{d2}}}} \le {T_{{\rm{PD}}}}\\ \left( {{\eta _1} + \theta \beta } \right)\left( {{T_{{\rm{SO}}}} - {t_{{\rm{s2}}}}} \right) + {\eta _2}\left( {{t_{{\rm{s2}}}} + {T_{\rm{w}}} - {T_{{\rm{EO}}}}} \right),\;\;\;\;{t_{{\rm{s2}}}} \le {T_{{\rm{SO}}}},\forall {T_{{\rm{EO}}}} < {t_{{\rm{d2}}}}\\ \left( {\theta \beta + {\gamma _1}} \right)\left( {{t_{{\rm{s2}}}} - {T_{{\rm{PA}}}}} \right) + {\gamma _2}\left( {{T_{{\rm{PD}}}} - {t_{{\rm{d2}}}} - {T_{\rm{w}}}} \right),\;\;\;\;{T_{{\rm{PA}}}} < {t_{{\rm{s2}}}},\forall {t_{{\rm{d2}}}} \le {T_{{\rm{PD}}}}\\ \left( {\theta \beta + {\gamma _1}} \right)\left( {{t_{{\rm{s2}}}} - {T_{{\rm{PA}}}}} \right) + {\eta _2}\left( {{t_{{\rm{s2}}}} + {T_{\rm{w}}} - {T_{{\rm{EO}}}}} \right),\;\;\;\;{T_{{\rm{PA}}}} < {t_{{\rm{s2}}}},\forall {T_{{\rm{EO}}}} < {t_{{\rm{d2}}}}\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. \end{array} $ | (22) |
式(22)是U关于td1的函数,当满足用户均衡时,
| $ \begin{array}{l} {f_1}\left( {{t_{{\rm{dl}}}}} \right) = \frac{{{\rm{d}}{D_1}}}{{{\rm{d}}{t_{{\rm{dl}}}}}} = \\ \;\;\;\;\left\{ \begin{array}{l} \frac{{\theta \alpha + \upsilon }}{{\theta \alpha + \upsilon - {\eta _1} - \theta \beta - {\gamma _2}}}S,\;\;\;\;\;{t_{{\rm{s2}}}} \le {T_{{\rm{SO}}}},\forall {t_{{\rm{d2}}}} \le {T_{{\rm{PD}}}}\\ \frac{{\theta \alpha + \upsilon }}{{\theta \alpha + \upsilon + {\eta _2} - \theta \beta - {\eta _1}}}S,\;\;\;\;\;{t_{{\rm{s2}}}} \le {T_{{\rm{SO}}}},\forall {T_{{\rm{EO}}}} < {t_{{\rm{d2}}}}\\ \frac{{\theta \alpha + \upsilon }}{{\theta \alpha + \upsilon + {\gamma _1} + \theta \beta - {\gamma _2}}}S,\;\;\;\;\;{T_{{\rm{PA}}}} < {t_{{\rm{s2}}}},\forall {t_{{\rm{d2}}}} \le {T_{{\rm{PD}}}}\\ \frac{{\theta \alpha + \upsilon }}{{\theta \alpha + \upsilon + {\gamma _1} + \theta \beta + {\eta _2}}}S,\;\;\;\;\;{T_{{\rm{PA}}}} < {t_{{\rm{s2}}}},\forall {T_{{\rm{EO}}}} < {t_{{\rm{d2}}}}\\ S,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. \end{array} $ | (23) |
晚上出发时间受到瓶颈限制,td2时刻的出发率f2(td2)为瓶颈的通行能力,如下所示:
| $ {f_2}\left( {{t_{{\rm{d2}}}}} \right) = \frac{{{\rm{d}}{D_2}}}{{{\rm{d}}{t_{{\rm{d2}}}}}} = S $ | (24) |
通过设定案例来清晰直观地展示完全弹性工作制下员工早、晚出行特征.假设瓶颈模型的基本参数如表 1所示,这些参数可任意设定.
| 下载CSV 表 1 瓶颈模型参数 Tab.1 Parameters of the bottleneck model |
Tseng等[26]利用荷兰采集的大量数据对Ettema等[10]提出的基于活动的效用模型参数进行了标定和显著性评估,评估结果显示数据质量良好.因此,本文借鉴该论文的参数标定结果(见表 2).
| 下载CSV 表 2 居民出行特征参数 Tab.2 Parameters of trip characteristics |
根据式(20),(υ+η1+min{γ2, η2})/θ+α=55.98≥25,显然表 2的参数满足解存在的要求.当达到用户均衡时,每个出行者的效用相同,目标方程的一阶偏导为零,可以得到居民出发时间分布的解析解,其早晚出发率(f1, f2)的时间分布如图 4所示.

|
图 4 活动边际效用为常数的累计出发和到达流量分布(完全弹性工作制) Fig.4 Cumulative departures and arrivals with constant marginal utility (flexible working arrangement) |
出行平均行程时间如下所示:
| $ \bar \tau = \left\{ \begin{array}{l} {T_{\rm{f}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;N \le \left( {{T_{{\rm{PA}}}} - {T_{{\rm{SO}}}}} \right)S\\ 13.40 + {T_{\rm{f}}},\;\;\;\;\;N = 2500,S = 1000 \end{array} \right. $ | (25) |
实际生活中活动的边际效用函数通常不是常数.根据Tseng等[26]的调查,上班出行阶段活动效用的影子价格随时间变化很大.例如,在工作的开始阶段,员工逐渐进入工作状态,这时的边际活动效用逐渐增加;随后进入一个相对稳定的阶段,员工的边际活动效用趋于一个比较稳定的较高值;最后,由于员工疲劳等因素,员工的边际活动效用逐渐下降,直至下班.Jenelius等[6]曾使用指数边际效用的形式研究弹性工作制,本文同样选取活动边际效用函数为指数的情况,通过仿真的方法得到出行规律.
假设活动边际效用函数
| $ \begin{array}{l} {u_1}\left( t \right) = {u_{1,\max }} - \frac{{{u_{1,\max }} - {u_{1,\min }}}}{{1 + \exp \left( { - {\varphi _1}\left( {t - {\omega _1}} \right)} \right)}},\;\;\;\;\;0 < t < 24\\ {u_2}\left( t \right) = \\ \left\{ \begin{array}{l} {u_{2,\min }} + \frac{{{u_{2,\max }} - {u_{2,\min }}}}{{1 + \exp \left( { - {\varphi _{2,{\rm{a}}}}\left( {t - {\omega _{2,{\rm{a}}}}} \right)} \right)}},\;\;\;\;\;2 \le t \le {t_{2,{\rm{sh}}}}\\ {u_{2,\max }} - \frac{{{u_{2,\max }} - {u_{2,\min }}}}{{1 + \exp \left( { - {\varphi _{2,{\rm{b}}}}\left( {t - {\omega _{2,{\rm{b}}}}} \right)} \right)}},\;\;\;\;\;{t_{2,{\rm{sh}}}} < t \le 24 \end{array} \right.\\ {u_3}\left( t \right) = {u_{3,\min }} + \frac{{{u_{3,\max }} - {u_{3,\min }}}}{{1 + \exp \left( { - {\varphi _3}\left( {t - {\omega _3}} \right)} \right)}},\;\;\;\;\;0 < t < 24 \end{array} $ | (26) |
式中:t2, sh为工作边际效用开始转换的点,
如表 3所示,本文借鉴了Jenelius等[6]的边际效用参数,其标定数据来源于Tseng等[26]的问卷调查.居民的边际活动效用如图 5所示,每个活动的开始阶段都有一段“预热”时间,结束阶段都有一段“降温”时间.
| 下载CSV 表 3 活动边际效用参数 Tab.3 Parameters of marginal utility functions |

|
图 5 指数函数下的边际效用函数 Fig.5 Exponential marginal utility functions |
当活动的边际效用函数不是常数值时,根据Li等[7]和Jenelius等[6]的分析,在非常严格而苛刻的条件下(Jenelius等假设了行程时间为固定值),才可以得到解析解.即便如此,仍得不到早晚出发时间组合解.解析解需要满足如下条件:
| $ \varphi \left( {{t_{{\rm{d1}}}}} \right) = \theta \int_0^{{t_{{\rm{d1}}}}} {{u_1}\left( t \right){\rm{d}}t + \upsilon {t_{{\rm{d1}}}} - \upsilon {T_{\rm{f}}}} $ | (27) |
| $ \psi \left( {{t_{{\rm{s2}}}}} \right) = - \upsilon {t_{{\rm{s2}}}} - \theta \int_{{t_{{\rm{s3}}}}}^{24} {{u_3}\left( t \right){\rm{d}}t + \mathit{\Xi } + \mathit{\Theta }} $ | (28) |
显然,若满足
| $ \frac{{\upsilon + {\eta _1} + \min \left\{ {{\gamma _2},{\eta _2}} \right\}}}{\theta } + {u_{3,\min }} \ge {u_{2,\max }} $ | (29) |
将表 2和表 3的数据代入式(29),可得到(2.842+0.378+0.378)/0.1+0=35.98>25.因此,当瓶颈模型中只存在弹性工作制员工时,边际效用为指数函数且采用表 2和表 3参数的情况下存在解.
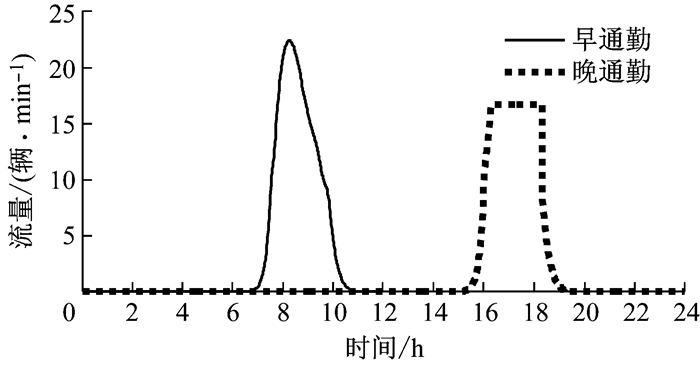
根据以往的研究,当活动的边际效用函数采用如图 5所示的模型时,难以得到解析解.因此,本文通过仿真的方法得到完全弹性工作制下的早晚出发流量,如图 6所示.
|
图 6 指数边际效用下的出发流量(完全弹性工作制) Fig.6 Departure rates with exponential marginal utility (flexible working arrangement) |
从图 6可以得到以下结果:
(1) 早高峰流量较大,最大出行流量超过瓶颈通行能力(17辆·min-1)35%左右,持续时间约1 h.
(2) 由于边际效用连续平缓变化,早高峰的出行流量图为尖峰状,即存在明显的高峰;在边际效用为常数的状况下(见图 3),[TSO, TPA]时段内的出行流量始终相同.
(3) 仿真在经过100次左右的循环后收敛指标趋于稳定,维持在0.02左右.从一天总效用随出发时间变化图可以看出,所有居民在有出发流量的时间段内总效用基本相同,说明仿真结果几乎达到了用户均衡状态(见图 7).

|
图 7 完全弹性下的总效用变化 Fig.7 Time dependent total utility with flexible working arrangement |
本节对非弹性工作制下的出行规律进行研究,并与弹性工作制下的出行规律进行了对比分析.
2.1 非弹性员工出行行为建模与弹性工作制的出行效用方程类似,非弹性工作制总效用方程如下所示:
| $ \begin{array}{l} U\left( {{t_{{\rm{d1}}}},{t_{{\rm{d2}}}}} \right) = \theta \int_0^{{t_{{\rm{d1}}}}} {{u_1}\left( t \right){\rm{d}}t} + \theta \int_{{t_{{\rm{s2}}}}}^{{t_{{\rm{d2}}}}} {{u_2}\left( t \right){\rm{d}}t - \upsilon {T_1}\left( {{t_{{\rm{d1}}}}} \right) + } \\ \;\;\;\;\;\;\;\theta \int_{{t_{{\rm{s3}}}}}^{24} {{u_3}\left( t \right){\rm{d}}t - \upsilon {T_2}\left( {{t_{{\rm{d2}}}}} \right) - {\gamma _1}\max \left\{ {0,{t_{{\rm{s2}}}} - {T_{{\rm{PA}}}}} \right\}} - \\ \;\;\;\;\;\;\;{\eta _1}\max \left\{ {0,{T_{{\rm{PA}}}} - {t_{{\rm{s2}}}}} \right\} - {\gamma _2}\max \left\{ {0,{T_{{\rm{PD}}}} - {t_{{\rm{d2}}}}} \right\} - \\ \;\;\;\;\;\;\;{\eta _2}\max \left\{ {0,{t_{{\rm{d2}}}} - {T_{{\rm{PD}}}}} \right\} \end{array} $ | (30) |
式(30)表明,非弹性员工在早上td1时刻出发、晚上td2时刻离开公司的一天效用,包括早上居家、上班工作和晚上居家的活动效用与早上上班早到或迟到、晚上下班早离开或晚离开的惩罚及出行成本的差值.本文假设非弹性员工的效用方程参数与弹性员工相同.
由于单位或者公司规定了具体的上下班时间,员工不能自主决定上下班时间,因此可以认为非弹性员工的早晚出发时间互不相关.因此,出行者早晚的效用可以单独求解,早上与晚上出行的效用函数如下所示:
| $ \begin{array}{*{20}{c}} {U\left( {{t_{{\rm{d1}}}}} \right) = \theta \int_0^{{t_{{\rm{d1}}}}} {{u_1}\left( t \right){\rm{d}}t} + \theta \int_{{t_{{\rm{s2}}}}}^{\rm{e}} {{u_2}\left( t \right){\rm{d}}t - \upsilon {T_1}\left( {{t_{{\rm{d1}}}}} \right) - } }\\ {{\gamma _1}\max \left\{ {0,{t_{{\rm{s2}}}} - {T_{{\rm{PA}}}}} \right\} - {\eta _1}\max \left\{ {0,{T_{{\rm{PA}}}} - {t_{{\rm{s2}}}}} \right\}} \end{array} $ | (31) |
| $ \begin{array}{*{20}{c}} {U\left( {{t_{{\rm{d2}}}}} \right) = \theta \int_{{t_{\rm{e}}}}^{{t_{{\rm{d2}}}}} {{u_2}\left( t \right){\rm{d}}t} + \theta \int_{{t_{{\rm{s3}}}}}^{{\rm{24}}} {{u_3}\left( t \right){\rm{d}}t - \upsilon {T_2}\left( {{t_{{\rm{d2}}}}} \right) - } }\\ {{\gamma _2}\max \left\{ {0,{T_{{\rm{PD}}}} - {t_{{\rm{d2}}}}} \right\} - {\eta _2}\max \left\{ {0,{t_{{\rm{d2}}}} - {T_{{\rm{PD}}}}} \right\}} \end{array} $ | (32) |
式中:te表示早上所有通勤者全部到达公司的时刻.
非弹性员工在达到用户均衡时,每个出行者都不能通过改变其出发时间来增加其出行效用.根据用户均衡特点,对式(31)和式(32)求偏导得
| $ \begin{array}{l} \frac{{\partial U}}{{\partial {t_{{\rm{d1}}}}}} = \theta {u_1}\left( {{t_{{\rm{d1}}}}} \right) - \upsilon \frac{{\partial {T_1}}}{{\partial {t_{{\rm{d1}}}}}} - \theta {u_2}\left( {{t_{{\rm{s2}}}}} \right) - \upsilon \frac{{\partial {t_{{\rm{s2}}}}}}{{\partial {t_{{\rm{d1}}}}}} + \\ \;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} - {\gamma _1}\frac{{\partial {t_{{\rm{s2}}}}}}{{\partial {t_{{\rm{d1}}}}}},\;\;\;\;\;\;{t_{{\rm{s2}}}} > {T_{{\rm{PA}}}}\\ {\eta _1}\frac{{\partial {t_{{\rm{s2}}}}}}{{\partial {t_{{\rm{d1}}}}}},\;\;\;\;\;\;\;\;{t_{{\rm{s2}}}} \le {T_{{\rm{PA}}}} \end{array} \right. \end{array} $ | (33) |
| $ \begin{array}{l} \frac{{\partial U}}{{\partial {t_{{\rm{d2}}}}}} = \theta {u_2}\left( {{t_{{\rm{d2}}}}} \right) - \upsilon \frac{{\partial {T_2}}}{{\partial {t_{{\rm{d2}}}}}} - \theta {u_3}\left( {{t_{{\rm{s3}}}}} \right)\frac{{\partial {t_{{\rm{s3}}}}}}{{\partial {t_{{\rm{d2}}}}}} + \\ \;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} {\gamma _2},\;\;\;\;\;\;{t_{{\rm{d2}}}} < {T_{{\rm{PD}}}}\\ - {\eta _2},\;\;\;\;{t_{{\rm{d2}}}} \ge {T_{{\rm{PD}}}} \end{array} \right. \end{array} $ | (34) |
为保证对比分析的有效性,假设非弹性员工和弹性员工具有相同的边际效用函数和参数.非弹性工作制假定参数TPA=9 h,TPD=17 h.
2.2.1 边际效用为常数的模型求解令式(33)和(34)为零可得
| $ {f_1}\left( {{t_{{\rm{d1}}}}} \right) = \frac{{{\rm{d}}{D_1}}}{{{\rm{d}}{t_{{\rm{d1}}}}}} = \left\{ \begin{array}{l} \frac{{\theta \alpha + \upsilon }}{{\theta \beta + \upsilon + {\gamma _1}}}S,\;\;\;\;{t_{{\rm{s2}}}} > {T_{{\rm{PA}}}}\\ \frac{{\theta \alpha + \upsilon }}{{\upsilon - {\eta _1}}}S,\;\;\;\;\;\;\;\;\;\;{t_{{\rm{s2}}}} \le {T_{{\rm{PA}}}} \end{array} \right. $ | (35) |
| $ {f_2}\left( {{t_{{\rm{d2}}}}} \right) = \frac{{{\rm{d}}{D_2}}}{{{\rm{d}}{t_{{\rm{d2}}}}}} = \left\{ \begin{array}{l} \frac{{\theta \beta + \upsilon + {\gamma _2}}}{{\theta \alpha + \upsilon }}S,\;\;\;\;{t_{{\rm{d2}}}} < {T_{{\rm{PD}}}}\\ \frac{{\upsilon - {\eta _2}}}{{\theta \alpha + \upsilon }}S,\;\;\;\;\;\;\;\;\;\;{t_{{\rm{s2}}}} \ge {T_{{\rm{PD}}}} \end{array} \right. $ | (36) |
最早和最晚出发用户行程时间为自由流时间,总需求为N,由式(35)和(36)可以得到居民早晚出发时间分布的解析解,如图 8所示.

|
图 8 活动边际效用为常数的累计出发流量和到达流量分布(非弹性工作制) Fig.8 Cumulative departures and arrivals with constant marginal utility (fixed working arrangement) |
依照弹性工作制案例设定的参数,通过计算得到,早上居民平均行程时间τ=48.62 min,晚上出行平均行程时间τ=48.62 min.对比图 8(非弹性工作制)和图 4(完全弹性工作制)发现,弹性工作制起到了“削峰”和节省平均行程时间的作用.
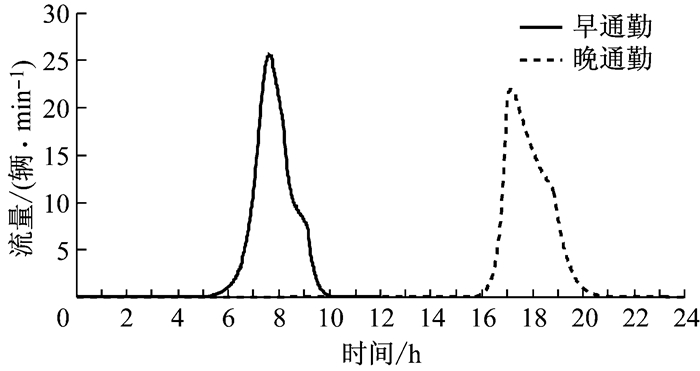
2.2.2 边际效用为指数函数的模型求解采用与求解弹性工作制模型同样的方法,通过仿真求解边际效用为指数函数时,非弹性工作制下的出发率分布.由于早晚出行独立,假设te为正常上班的中间时间点,本文取中午12点.仿真得到的出发流量如图 9所示.从图中可以看出,早高峰时段十分拥挤,出行流量超过瓶颈通行能力(17辆·min-1)53%左右;晚高峰拥挤持续时间较长,拥堵状况比早高峰严重.图 10为仿真收敛指标.
|
图 9 指数边际效用下的出发流量(非弹性工作制) Fig.9 Departure rates with exponential marginal utility (fixed working arrangement) |

|
图 10 仿真收敛指标(非弹性工作制) Fig.10 Convergence index (fixed working arrangement) |
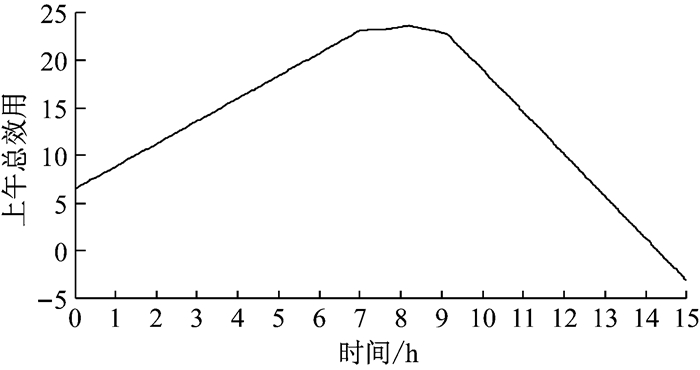
图 11和图 12别给出了上午和下午总效用随时间的动态变化.可以看出,所有员工在有出发流量的时间段内(上午出行时间段为7: 00—9: 00,下午出行时间段为17: 00—19: 00)总效用基本相同,说明仿真近似达到了用户均衡状态.
|
图 11 出行者上午总效用随出发时间的动态变化(非弹性工作制) Fig.11 Time dependent utility of morning commuters (fixed working arrangement) |

|
图 12 出行者下午总效用随下班时间的动态变化(非弹性工作制) Fig.12 Time dependent utility of evening commuters (fixed working arrangement) |
表 4对比了2种工作制度下的路网平均行程时间,得到以下结果:
| 下载CSV 表 4 基于瓶颈模型的平均行程时间 Tab.4 Mean travel times based on the bottleneck model |
(1) 在瓶颈模型下,边际效用函数采用常数值形式和指数函数形式,表明弹性工作制下的交通状态都优于非弹性工作制下的交通状态.
(2) 边际效用函数为非常数值时(例如指数函数形式),边际效用随时间连续平缓变化,弹性工作员工也出现了明显的集中出行(如图 6早高峰出行),而采用常数值时没有明显的集中出行现象(见图 4),说明采用常数边际效用会在一定程度上夸大弹性工作制的效果.仿真采用了随机用户均衡分配方法,而解析结果采用的是确定性用户均衡方法,不能直接对仿真结果和解析结果进行对比.
(3) 由式(25)可以看出,在瓶颈模型下,当弹性工作时段长度大于全部需求与瓶颈通行能力的比值时,可以完全消除延误.
3 弹性与非弹性混合工作制度对出行的影响分析由于不同的工作岗位适合不同的工作制度,现实中普遍存在同一公司2种制度混合实施的情况.因此,本节分析不同弹性员工比例下的混合多用户均衡,研究混合工作制度对交通出行的影响.由于动态交通仿真需要大量的运行时间,边际效用函数为常数时运算速度快,因此本文应用了边际效用为常数的行为模型进行分析.
弹性工作者早晚出发时间相互关联,非弹性工作者早晚出发时间相互独立.2类用户的早晚出发时间分布相互影响,2类用户通过调整各自的出发时间,最终达到各自在出发时间上的均衡.以弹性员工早上出发率作为输入基准,并将弹性员工早上出发流量的相对变化值作为收敛指标,仿真流程如图 13所示.

|
图 13 2类用户均衡仿真流程图 Fig.13 Flow chart of the bi-user equilibrium simulations |
本文采用用户的平均行程时间作为评判不同工作制度效果的指标.表 5给出了仿真不同弹性比例下2类员工的平均行程时间.图 14和图 15展示了全体员工的人均行程时间和早晚人均行程时间随弹性比例的变化情况.可以看出:
| 下载CSV 表 5 不同弹性比例下的平均行程时间 Tab.5 Mean travel times in relation to percentages of flexible workers |
|
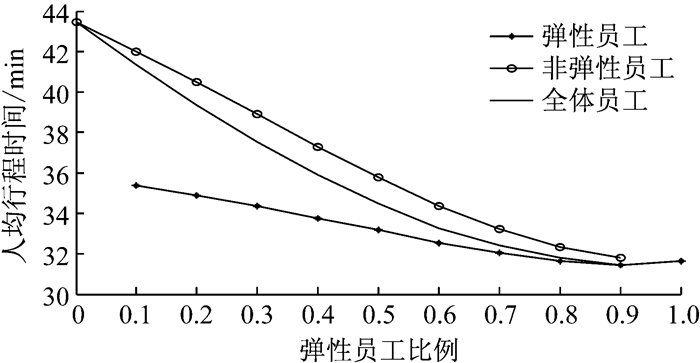
图 14 不同用户全天人均行程时间与弹性员工比例的关系 Fig.14 Mean travel times of both flexi-and non-flexi commuters in relation to percentages of flexible workers |
|
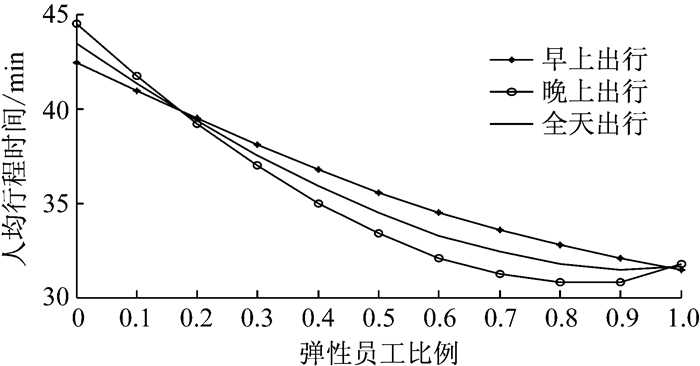
图 15 早晚路网人均行程时间与弹性员工比例的关系 Fig.15 Mean travel times of morning and evening commuters in relation to percentages of flexible workers |
(1) 在瓶颈模型下,随着弹性员工比例的增加,全体出行者的平均行程时间逐渐降低,弹性工作制度可以缓解早晚交通拥堵.
(2) 随着弹性员工比例增加,弹性员工的平均行程时间基本不变,非弹性员工的平均行程时间下降明显.当弹性比例达到60%左右时,2类员工的平均行程时间相同且不再变化(见图 14).
(3) 随着弹性员工比例的增加,弹性工作制缓解交通拥堵的作用会随之减弱.图 15表明,当弹性员工比例增加到60%~70%时,无论是早上出行还是晚上出行的平均行程时间都不再有明显下降,说明弹性员工的比例增加到一定程度时,其缓解交通拥堵的作用逐渐消失.
4 结论与展望考虑早晚通勤出行链,基于活动效用最大化理论,建立了针对核心工作时段弹性工作制下的弹性和非弹性用户出行行为模型,通过解析方法和仿真方法分别分析了弹性工作制对交通拥堵的缓解效果.
首先,基于Vickrey瓶颈模型,分析了活动边际效用为常数和指数函数2种情况下完全弹性工作制和固定上班时间制下的出行流量分布情况.案例分析表明,弹性工作制下,交通拥堵得到明显缓解,平均行程时间减少了27%.
其次,通过仿真方法,模拟了弹性和非弹性多用户均衡状态下的交通出行情况.分析了弹性员工比例从0%到100%情况下的出行规律.结果表明,弹性工作制度可以明显缓解早晚高峰的交通拥堵,出行者的平均行程时间减少了15%~25%.随着弹性员工比例的增加,人均行程时间逐渐降低.当弹性员工比例达到60%~70%,人均延误不再随弹性员工比例的增加而降低.
本文假设了弹性工作员工的工作时长是固定的,并证明了解的存在性.针对现实中存在弹性工作员工的工作时长可变现象,后续研究可以考虑采用其他方法对这种可变工作时长进行建模和分析.
| [1] |
KUZMYAK J R. Evaluation of travel demand management measures to relieve congestion: final report[R]. Silver Spring: Federal Highway Administration, 1990.
|
| [2] |
张瑞玲. 弹性工作制及其在中国的应用现状[J]. 东方企业文化, 2013(4): 59 ZHANG Ruiling. The study of flexible work arrangement and the application status in China[J]. Company and Industry, 2013(4): 59 |
| [3] |
陈梓烽, 柴彦威. 通勤时空弹性对居民通勤出发时间决策的影响:以北京上地清河地区为例[J]. 城市发展研究, 2014(12): 65 CHEN Zifeng, CHAI Yanwei. Modelling the choice of departure time for commuting trip chains incorporating space-time flexibility variables: evidence from the Shangdi-Qinghe area of Beijing[J]. Urban Development Studies, 2014(12): 65 DOI:10.3969/j.issn.1006-3862.2014.12.011 |
| [4] |
YOSHIMURA M, OKUMURA M. Optimal commuting and work start time distribution under flexible work hours system on motor commuting[C]// Proceedings of the Eastern Asia Society for Transportation Studies. Hanoi:[s.n.], 2001:455-469.
|
| [5] |
ETTEMA D, TIMMERMANS H. Modeling departure time choice in the context of activity scheduling behavior[J]. Transportation Research Record Journal of the Transportation Research Board, 2003, 1831(1): 39 |
| [6] |
JENELIUS E, MATTSSON L G, LEVINSON D. Traveler delay costs and value of time with trip chains, flexible activity scheduling and information[J]. Transportion Research, Part B: Methodological, 2011, 45(5): 789 DOI:10.1016/j.trb.2011.02.003 |
| [7] |
LI Z C, LAM W H K, WONG S C. Bottleneck model revisited: an activity-based perspective[J]. Transportation Research, Part B: Methodological, 2014, 68: 262 DOI:10.1016/j.trb.2014.06.013 |
| [8] |
JENELIUS E. The value of travel time variability with trip chains, flexible scheduling and correlated travel times[J]. Transportation Research, Part B: Methodological, 2012, 46(6): 762 DOI:10.1016/j.trb.2012.02.003 |
| [9] |
黎晴, 张小宁. 模拟早晚高峰交通出行率的方法研究[J]. 城市交通, 2006, 4(1): 64 LI Qing, ZHANG Xiaoning. Modeling departure rates of moring and evening rush hours[J]. Urban Transport of China, 2006, 4(1): 64 |
| [10] |
ETTEMA D, BASTIN F, POLAK J, et al. Modelling the joint choice of activity timing and duration[J]. Transportation Research, Part A: Policy and Practice, 2007, 41(9): 827 DOI:10.1016/j.tra.2007.03.001 |
| [11] |
TACKEN M, DE BOER E. Flexitime and the spread of traffic peak hour: an analysis of conditions and behavior[R]. Delft: Delft University of Technology, 1990.
|
| [12] |
HE S Y. Does flexitime affect choice of departure time for morning home-based commuting trips? Evidence from two regions in California[J]. Transport Policy, 2013, 25(1): 210 |
| [13] |
杨晓光, 褚浩然. 错峰出行对城市交通的影响分析[J]. 同济大学学报(自然科学版), 2006, 34(7): 899 YANG Xiaoguang, CHU Haoran. Study on macro-travel impact analysis of staggered shifts[J]. Journal of Tongji University (Natuarl Science), 2006, 34(7): 899 |
| [14] |
杜华兵, 陈金川, 郭继孚. 北京市实施错时上下班的可行性分析[J]. 城市交通, 2004, 2(4): 64 DU Huabing, CHEN Jinchuan, GUO Jifu. Feasibility analysis on implementing different working hour of Beijing[J]. Urban Transport of China, 2004, 2(4): 64 |
| [15] |
关仕罡, 闫攀宇. 广州市错时上下班政策研究[J]. 交通与运输(学术版), 2010(增刊2): 42 GUAN Shigang, YAN Panyu. Research on the policy of Guangzhou staggered working hours[J]. Traffic & Transportation (Academic Edition), 2010(S2): 42 |
| [16] |
刘天顺, 谷江河, 徐瑞华. 国内外错时上下班经验之所鉴[J]. 交通与运输(学术版), 2005(2): 29 LIU Tianshun, GU Jianghe, XU Ruihua. Domestic and overseas experiences about alternative work schedues[J]. Traffic & Transportation (Academic Edition), 2005(2): 29 |
| [17] |
谢留宏, 路峰, 张俊辉, 等. 北京实行错峰上下班解决交通拥堵问题的分析探讨[J]. 交通标准化, 2011(增刊1): 53 XIE Liuhong, LU Feng, ZHANG Junhui, et al. Analysis and investigation on implementation of peak shifting to slove traffic congestion problem in Beijing[J]. Transportation Standardization, 2011(S1): 53 |
| [18] |
ZONG F, JUAN Z C, JIA H F. Examination of staggered shifts impacts on travel behavior: a case study of Beijing, China[J]. Transport, 2013, 28(2): 175 DOI:10.3846/16484142.2013.803263 |
| [19] |
石骞. "错时上下班"实施方法与效果评价研究[D]. 长春: 吉林大学, 2012. SHI Qian. Study on the implement way and evaluation of staggered rush hour plan[D]. Changchun: Jilin University, 2012. |
| [20] |
刘春波. M公司弹性工作制方案设计研究[D]. 大连: 大连理工大学, 2014. LIU Chunbo. Study on flexible working in M company[D]. Dalian: Dalian University of Technology, 2014. |
| [21] |
DOHERTY S T, AXHAUSEN K W. The development of a unified modeling framework for the household activity-travel scheduling process[M]. Berlin Heidelberg: Springer, 1999: 35-56
|
| [22] |
VICKREY W S. Congestion theory and transport investment[J]. The American Economic Review, 1969, 59(2): 251 |
| [23] |
LI H, TU H, ZHANG X. Travel time variations over time and routes: endogenous congestion with degradable capacities[J]. Transportmetrica B: Transport Dynamics, 2017, 5(1): 60 |
| [24] |
HAN K, FRIESZ T L, YAO T. Existence of simultaneous route and departure choice dynamic user equilibrium[J]. Transportation Research, Part B: Methodological, 2013, 53: 17 DOI:10.1016/j.trb.2013.01.009 |
| [25] |
HEYDECKER B G, ADDISON J D. Analysis of dynamic traffic equilibrium with departure time choice[J]. Transportation Science, 2005, 39(1): 39 DOI:10.1287/trsc.1030.0075 |
| [26] |
TSENG Y Y, VERHOEF E T. Value of time by time of day: a stated-preference study[J]. Transportation Research, Part B: Methodological, 2008, 42(7): 607 |
 2017, Vol. 45
2017, Vol. 45
