2. 同济大学 土木工程防灾国家重点实验室,上海 200092
2. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China
复合泊松过程在保险、金融、医学和工程等领域都有广泛应用[1-4].根据复合泊松过程的基本性质实现复合泊松过程的数值模拟,对于解决实际问题具有十分重要的意义.通常,复合泊松过程的模拟多采用蒙特卡罗方法[5-6].这一方法在模拟过程中需要引入大量基本随机变量,因此对后续的分析造成诸多不必要的困难.鉴于此,本文提出了利用随机谐和函数[7-8]生成复合泊松过程的方法,该方法可通过数量有限的随机变量反映目标随机过程的概率分布特性.本文以复合泊松过程在车辆荷载模型中的应用为例,分别采用蒙特卡罗方法与随机谐和函数方法生成车辆荷载复合泊松过程.通过2种方法的对比,验证了本文建议方法的正确性与有效性.
1 复合泊松过程 1.1 泊松过程泊松过程是一类应用广泛的计数过程.若计数过程{N(t), t≥0}满足以下条件[9]:①N(0)=0;②过程具有独立增量; ③在时间长度为t的任意区间中的事件数服从以λt为均值的泊松分布,即对于一切s, t≥0有
| $ \begin{array}{*{20}{c}} {P\left\{ {N\left( {t + s} \right) - N\left( s \right) = n} \right\} = }\\ {{{\rm{e}}^{ - \lambda t}}\frac{{{{\left( {\lambda t} \right)}^n}}}{{n!}}, \;\;\;\;n = 0, 1, 2, \cdots } \end{array} $ | (1) |
则称之为具有速率λ(λ>0)的泊松过程.其中,λ表示事件在单位时间内发生的平均次数.
在泊松过程中,令Tn表示第n次与第(n-1)次事件发生的时间间隔,Wn表示第n次事件发生的时刻,则Wn与Tn之间的关系为
| $ {W_n} = {T_1} + {T_2} + \cdots + {T_n}, \;\;\;\;n = 1, 2, \cdots $ | (2) |
可以证明[1, 5],Tn服从参数为λ的指数分布,且T1, T2, T3, …相互独立,Tn的密度函数
| $ {f_{{T_n}}}\left( x \right) = \left\{ \begin{array}{l} \lambda {{\rm{e}}^{ - \lambda x}}, \;\;\;x > 0\\ 0, \;\;\;\;\;\;\;\;\;x \le 0 \end{array} \right. $ | (3) |
然而,Wn服从参数为λ和n的Erlang分布,即Wn的密度函数
| $ {f_{{W_n}}}\left( x \right) = \left\{ \begin{array}{l} \frac{{{\lambda ^n}}}{{\left( {n - 1} \right)!}}{x^{n - 1}}{{\rm{e}}^{ - \lambda x}}, \;\;\;x > 0\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x \le 0 \end{array} \right. $ | (4) |
复合泊松过程是在泊松过程的基础上,通过对泊松过程的每一点赋予一独立同分布的随机变量得到的.它的具体定义为[9]:若{N(t), t≥0}是一个泊松过程,则{Xn, n=1, 2, …}是一族独立同分布的随机变量,并且与过程{N(t), t≥0}独立.对于任意t≥0,X(t)可以表示为
| $ X\left( t \right) = \sum\limits_{n = 1}^{N\left( t \right)} {{X_n}} $ | (5) |
则称随机过程X(t)为复合泊松过程.
针对复合泊松过程在不同实际问题中的应用,{Xn, n=1, 2, …}可以服从不同的概率分布.例如,对于复合泊松过程在车辆荷载模型中的应用,Xn服从对数正态分布.
1.3 复合泊松过程模拟的蒙特卡罗方法复合泊松过程的数值模拟主要在于相邻2次事件发生的时间间隔{Tn, n=1, 2, …, N}以及每次事件发生时幅值{Xn, n=1, 2, …, N}的随机生成.模拟复合泊松过程最常采用的方法是蒙特卡罗方法.在这一方法中,直接生成事件发生的时间间隔随机变量序列{Tn, n=1, 2, …, N}与事件所对应的幅值随机变量序列{Xn, n=1, 2, …, N},并通过对时间的判断将两者复合起来以得到复合泊松过程.图 1为利用蒙特卡罗方法模拟复合泊松过程的具体步骤.
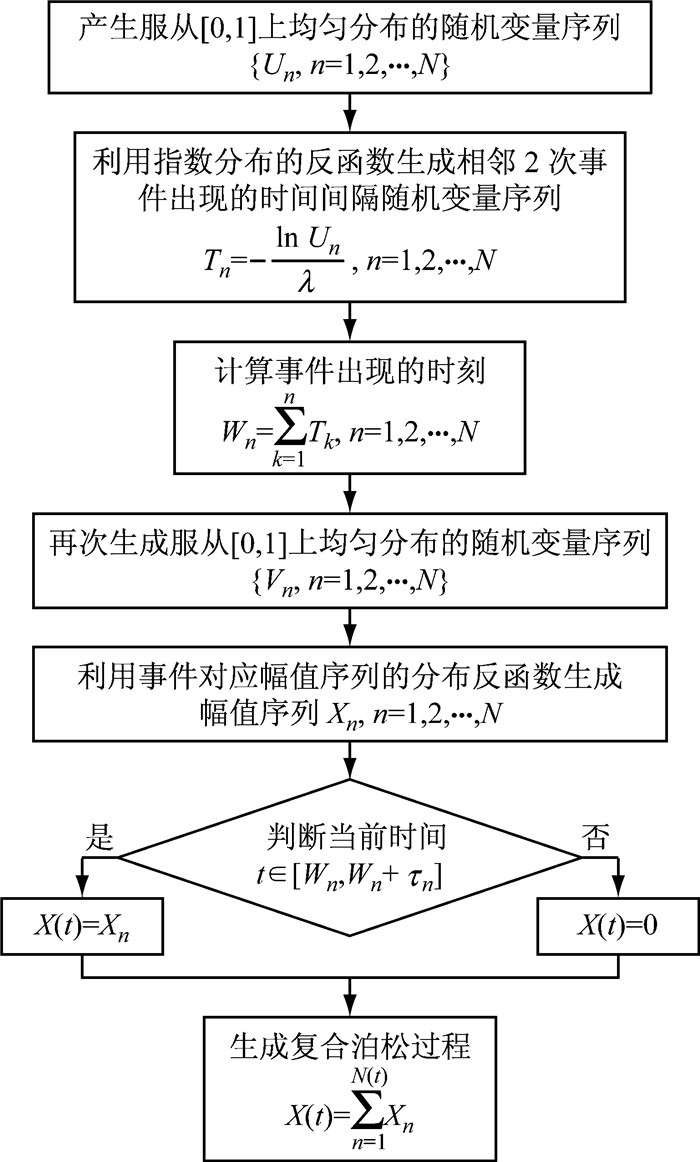
|
图 1 蒙特卡罗方法模拟复合泊松过程的流程图 Fig.1 Flow chart of Monte Carlo method for compound Poisson process simulation |
从图 1中可看出,在蒙特卡罗方法中,若要模拟有N个事件发生的复合泊松过程,就需要N个时间间隔随机变量与N个事件对应的幅值随机变量,共需2N个基本随机变量.
2 复合泊松过程模拟的随机谐和函数法 2.1 随机谐和函数文献[7]提出了平稳随机过程的随机谐和函数表达,根据这一表达,随机过程Y(t)可表示为[7-8]
| $ Y\left( t \right) = \sum\limits_{i = 1}^{{N_\omega }} {A\left( {{\omega _i}} \right)\cos \left( {{\omega _i}t + {\varphi _i}} \right)} $ | (6) |
式中:A(ωi)、ωi、φi分别为第i个谐和分量的幅值、圆频率和相位角.通常,设ωi, p(1≤i≤Nω-1)为[0, ωu]的内点,且满足0 < ω1, p < ω2, p < … < ωN-1, p < ωu,记ω0, p=0,ωN, p=ωu,这里ωu < ∞为上限截止频率.
设随机过程Y(t)的功率谱密度函数为SY(ω),-ωu≤ω < ωu,且其单边功率谱为GY(ω),满足GY(ω)=2SY(ω),0≤ω < ωu,则式(6)随机谐和函数Y(t)中的ωi、φi和A(ωi)应分别满足以下条件[7]:
(1) φi(i=1, 2, …, Nω)为相互独立的随机变量,服从[0, 2π]的均匀分布.
(2) ωi(i=1, 2, …, Nω)为相互独立的随机变量,服从(ωi-1, p, ωi, p]区间的均匀分布[8],概率密度函数
| $ {p_{{\omega _i}}}\left( \omega \right) = \left\{ \begin{array}{l} \frac{1}{{\Delta {\omega _i}}}, \;\;\;\;\omega \in \left( {{\omega _{i - 1, p}} - {\omega _{i, p}}} \right)\\ 0, \;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (7) |
式中:Δωi=ωi, p-ωi-1, p.
(3) A(ωi)(i=1, 2, …, Nω)为随机变量ωi的函数,有
| $ A\left( {{\omega _i}} \right) = \sqrt {\frac{{{G_Y}\left( {{\omega _i}} \right)\Delta {\omega _i}}}{{\rm{ \mathsf{ π} }}}} = \sqrt {\frac{{2{S_Y}\left( {{\omega _i}} \right)\Delta {\omega _i}}}{{\rm{ \mathsf{ π} }}}} $ | (8) |
如前所述,蒙特卡罗方法需要引入大量基本的随机变量,为了减少基本随机变量的个数,本文建议引入随机谐和函数模拟复合泊松过程.
在复合泊松过程中,相邻2个事件发生的时间间隔Tn本身构成一个随机序列{Tn, n=1, 2, …, N},此序列是独立同分布于指数分布的,其典型样本见图 2.同样地,事件对应的幅值随机序列{Xn, n=1, 2, …, N}也是独立同分布的,其分布满足给定的具体形式,图 3为该随机序列的一个典型样本.
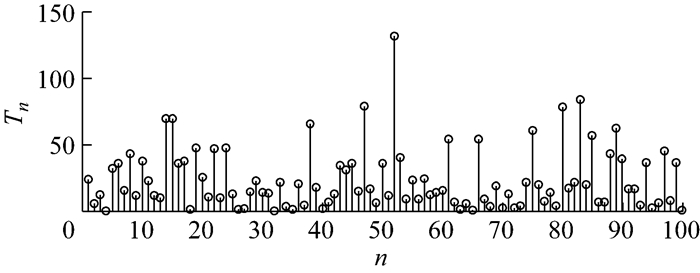
|
图 2 事件发生时间间隔的随机过程 Fig.2 Stochastic process of time intervals between events |
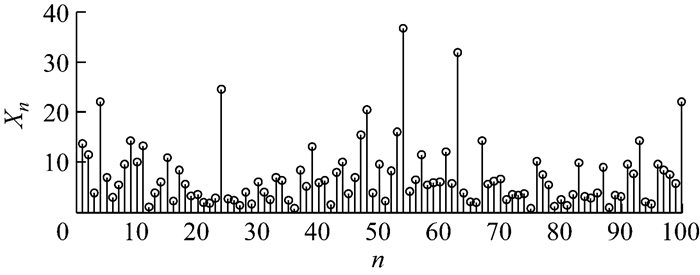
|
图 3 事件对应幅值的随机过程 Fig.3 Stochastic process of amplitudes of events |
由于随机序列{Tn, n=1, 2, …, N}与{Xn, n=1, 2, …,N}均是独立同分布的,因此可利用离散化的随机谐和函数{YT(tn), n=1, 2, …, N}、{YX(tn), n=1, 2, …, N}分别生成时间间隔序列{Tn, n=1, 2, …,N}与幅值序列{Xn, n=1, 2, …,N},并认为{YT(tn), n=1, 2, …, N}、{YX(tn), n=1, 2, …, N}均为高斯白噪声序列,且可表示为
| $ \begin{array}{*{20}{c}} {{Y_T}\left( {{t_n}} \right) = \sum\limits_{i = 1}^{{N_T}} {{A_T}\left( {{\omega _{T, i}}} \right)\cos \left( {{\omega _{T, i}}{t_n} + {\varphi _{T, i}}} \right)}, }\\ {n = 1, 2, \cdots, N} \end{array} $ | (9) |
| $ \begin{array}{*{20}{c}} {{Y_X}\left( {{t_n}} \right) = \sum\limits_{i = 1}^{{N_X}} {{A_X}\left( {{\omega _{X, i}}} \right)\cos \left( {{\omega _{X, i}}{t_n} + {\varphi _{X, i}}} \right)}, }\\ {n = 1, 2, \cdots, N} \end{array} $ | (10) |
考虑到实际工程中的应用,{YT(tn), n=1, 2, …, N}、{YX(tn), n=1, 2, …, N}为有限带宽白噪声序列,其功率谱密度函数
| $ {S_{{Y_T}}}\left( \omega \right) = \left\{ \begin{array}{l} {S_T}, \;\;\;\;\;\left| \omega \right| \le {\omega _{{\rm{u}}T}}\\ 0, \;\;\;\;\;\;\;其他 \end{array} \right. $ | (11) |
| $ {S_{{Y_X}}}\left( \omega \right) = \left\{ \begin{array}{l} {S_X}, \;\;\;\;\;\left| \omega \right| \le {\omega _{{\rm{u}}X}}\\ 0, \;\;\;\;\;\;\;其他 \end{array} \right. $ | (12) |
式中:ST、SX为常数;ωuT、ωuX分别为{YT(tn), n=1, 2, …, N}、{YX(tn), n=1, 2, …, N}的上限截止频率.
白噪声序列{YT(tn), n=1, 2, …, N}、{YX(tn), n=1, 2, …, N}的方差σYT2、σYX2分别为
| $ \sigma _{{Y_T}}^2 = {R_{{Y_T}}}\left( 0 \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - {\omega _{{\rm{u}}T}}}^{{\omega _{{\rm{u}}T}}} {{S_{{Y_T}}}\left( \omega \right){\rm{d}}\omega } = \frac{{{S_T}{\omega _{{\rm{u}}T}}}}{{\rm{ \mathsf{ π} }}} $ | (13) |
| $ \sigma _{{Y_X}}^2 = {R_{{Y_X}}}\left( 0 \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - {\omega _{{\rm{u}}X}}}^{{\omega _{{\rm{u}}X}}} {{S_{{Y_X}}}\left( \omega \right){\rm{d}}\omega } = \frac{{{S_X}{\omega _{{\rm{u}}X}}}}{{\rm{ \mathsf{ π} }}} $ | (14) |
根据式(13)、(14),可确定ST、SX的取值为
| $ {S_T} = \frac{{{\rm{ \mathsf{ π} }}\sigma _{{Y_T}}^2}}{{{\omega _{{\rm{u}}T}}}} $ | (15) |
| $ {S_X} = \frac{{{\rm{ \mathsf{ π} }}\sigma _{{Y_X}}^2}}{{{\omega _{{\rm{u}}X}}}} $ | (16) |
依据式(9)和(10),可以分别生成复合泊松过程的时间间隔序列与幅值序列,分述如下:
(1) 生成时间间隔序列{Tn, n=1, 2, …, N}
由于离散化的随机谐和函数{YT(tn), n=1, 2, …, N}各时点符合正态分布[10],而{Tn, n=1, 2, …, N}为指数分布,故要引入反函数变换法获取{Tn, n=1, 2, …, N},具体步骤如下所示:
步骤1 利用正态分布的分布函数F(x)求得随机谐和函数{YT(tn), n=1, 2, …, N}各时点的分布值F(YT(tn)),如下所示:
| $ \begin{array}{*{20}{c}} {F\left( {{Y_T}\left( {{t_n}} \right)} \right) = \int_{ - \infty }^{{Y_T}\left( {{t_n}} \right)} {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} {\sigma _{{Y_T}}}}}{{\rm{e}}^{ - \frac{{{{\left( {x - {\mu _{{Y_T}}}} \right)}^2}}}{{2\sigma _{{Y_T}}^2}}}}{\rm{d}}x}, }\\ {n = 1, 2, \cdots, N} \end{array} $ | (17) |
式中:μYT表示各时点所服从正态分布的均值.
步骤2 令{Tn, n=1, 2, …, N}各元素的分布函数值G(Tn)与{YT(tn), n=1, 2, …, N}各时点的分布值F(YT(tn))相等,如下所示:
| $ G\left( {{T_n}} \right) = F\left( {{Y_T}\left( {{t_n}} \right)} \right), \;\;\;n = 1, 2, \cdots, N $ | (18) |
式中:G(x)为指数分布的分布函数.
步骤3 由指数分布反函数G-1G(x)获得{Tn, n=1, 2, …, N},如下所示:
| $ \begin{array}{*{20}{c}} {{T_n} = {G^{ - 1}}\left( {G\left( {{T_n}} \right)} \right) = - \frac{1}{\lambda }\ln \left( {1 - G\left( {{T_n}} \right)} \right), }\\ {n = 1, 2, \cdots, N} \end{array} $ | (19) |
图 4给出了由随机谐和函数生成时间间隔序列的具体过程.
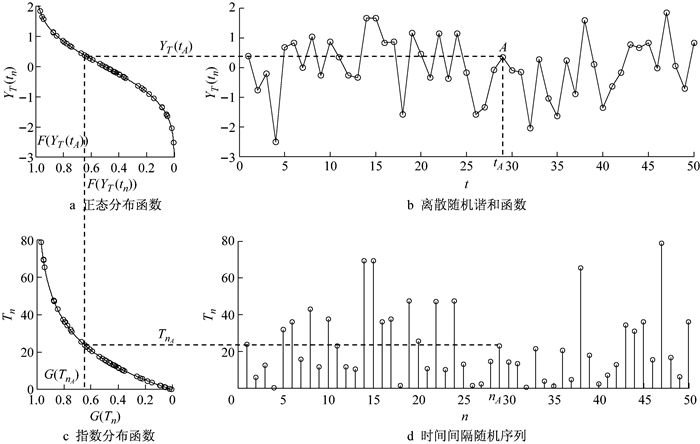
|
图 4 时间间隔序列Tn的随机生成 Fig.4 Random generation of time interval sequence Tn |
(2) 生成事件对应的幅值序列{Xn, n=1, 2, …, N}
同样地,可应用反函数变换法生成事件所对应的幅值序列{Xn, n=1, 2, …, N},具体步骤如下所示:
步骤1 由正态分布的分布函数F(x)得到随机谐和函数{YX(tn), n=1, 2, …, N}各时点的分布值,如下所示:
| $ \begin{array}{*{20}{c}} {F\left( {{Y_X}\left( {{t_n}} \right)} \right) = \int_{ - \infty }^{{Y_X}\left( {{t_n}} \right)} {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} {\sigma _{{Y_X}}}}}{{\rm{e}}^{ - \frac{{{{\left( {x - {\mu _{{Y_X}}}} \right)}^2}}}{{2\sigma _{{Y_X}}^2}}}}{\rm{d}}x}, }\\ {n = 1, 2, \cdots, N} \end{array} $ | (20) |
步骤2 令{Xn, n=1, 2, …, N}各元素的分布值N(Xn)与{YX(tn), n=1, 2, …, N}各时点的分布值F(YX(tn))相等,如下所示:
| $ N\left( {{X_n}} \right) = F\left( {{Y_X}\left( {{t_n}} \right)} \right), \;\;\;n = 1, 2, \cdots, N $ | (21) |
式中:N(x)为事件对应幅值所服从的分布函数.
步骤3 由Xn的分布反函数N-1(N(Xn))获得{Xn, n=1, 2, …, N},如下所示:
| $ {X_n} = {N^{ - 1}}\left( {N\left( {{X_n}} \right)} \right), \;\;\;n = 1, 2, \cdots, N $ | (22) |
以复合泊松过程在车辆荷载模型中的应用为例,此时{Xn, n=1, 2, …, N}为各车辆荷载出现时的荷载幅值,且独立同分布于对数正态分布.图 5为车辆荷载幅值序列随机生成的示意图.
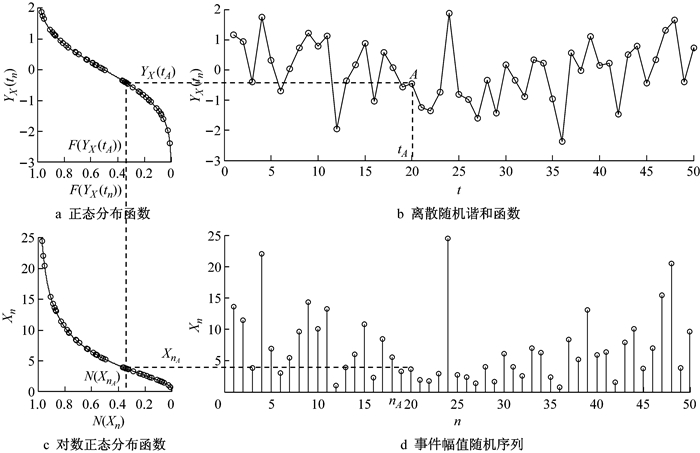
|
图 5 对应幅值序列Xn的随机生成 Fig.5 Random generation of amplitude sequence Xn |
图 6给出了采用随机谐和函数方法来模拟复合泊松过程的具体步骤.
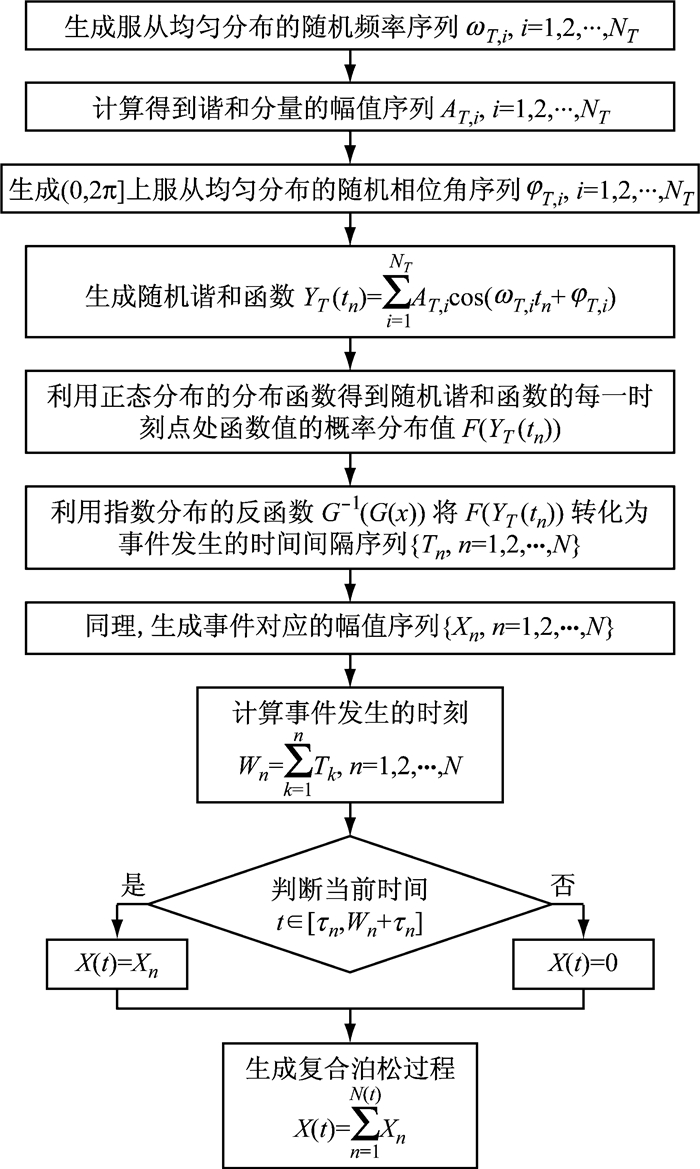
|
图 6 随机谐和函数方法模拟复合泊松过程流程图 Fig.6 Flow chart of stochastic harmonic function method for compound Poisson process simulation |
可见,在随机谐和函数方法中,随机谐和函数的圆频率随机变量序列{ωi, i=1, 2, …, N}和相位角随机变量序列{φi, i=1, 2, …, N}是生成复合泊松过程的基本随机变量.随机谐和函数过程往往只需较少的基本随机变量即可生成,这也就意味着生成复合泊松过程的基本随机变量数目将大大减少.
3 对公路车辆随机荷载的应用 3.1 公路桥梁车辆荷载过程公路桥梁的车辆荷载是典型的复合泊松过程,本文以此为背景来说明前文方法的应用.在本文中,车辆荷载模型是基于“公路桥梁车辆荷载研究”课题组[11]所采集和整理的数据经统计分析得到的.该课题共测录了6万多辆机动车的各项数据,包括整车质量、轴质量、车速和车辆通过测点的时刻等.在统计分析时,采用K-S检验法对采集的车辆荷载的各类数据集分别按正态、对数正态、极值Ⅰ型、威布尔和伽玛共5种分布类型依次进行检验,且各类分布参数通过极大似然估计法得到.一般运行状态下,车辆荷载截口概率分布的拟合检验结果及其相应的参数估计值见表 1.
| 下载CSV 表 1 车辆荷载截口概率分布及其参数 Tab.1 Probability distributions and parameters of vehicle load |
从表 1中可看出,一般运行状态下,车辆出现的时间间隔服从指数分布,且车辆荷载持续时间非常短,因此车辆荷载随机过程L(t)通常采用滤过复合泊松过程[11-12]来描述,可表示为
| $ \begin{array}{*{20}{c}} {L\left( t \right) = \sum\limits_{n = 1}^{N\left( t \right)} {{\xi _n}I\left( {t;{\tau _n}} \right)} }\\ {I\left( {t;{\tau _n}} \right) = \left\{ \begin{array}{l} 1, \;\;\;t \in {\tau _n}\\ 0, \;\;t \notin {\tau _n} \end{array} \right.} \end{array} $ | (23) |
{N(t), t≥0}为描述车辆荷载到达次数的泊松过程,表示为
| $ P\left[{N\left( t \right) = k} \right] = {{\rm{e}}^{ - \hat \lambda t}}\frac{{{{\left( {\hat \lambda t} \right)}^k}}}{{k!}}, \;\;\;k = 1, 2, \cdots $ | (24) |
式中:
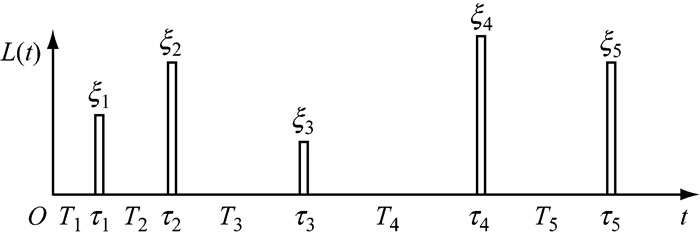
|
图 7 滤过复合泊松过程示意图 Fig.7 Diagram of filtered compound Poisson process |
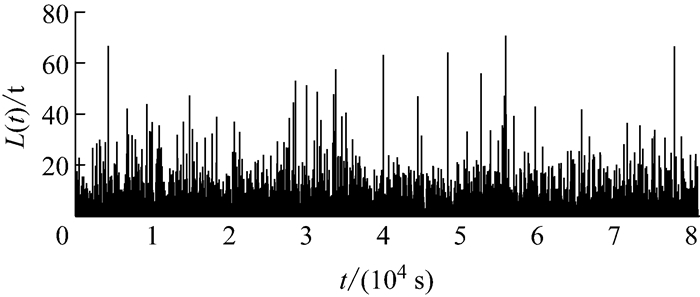
根据蒙特卡罗方法的原理,模拟生成车辆荷载过程的时间间隔序列{Tn, n=1, 2, …, NT}和荷载幅值序列{ξn, n=1, 2, …, Nξ},如图 8、9所示.模拟中取NT=Nξ=3 501对两者分别进行概率统计,可得到拟合的概率分布,如图 10a、11a所示.为了验证模拟生成的车辆荷载时间间隔序列与幅值序列的正确性,将两者的拟合分布分别与其所对应的真实分布进行对比(见图 10b、11b),可见两者吻合良好.
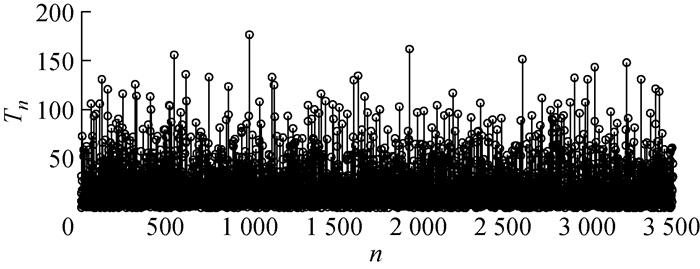
|
图 8 蒙特卡罗方法生成的车辆荷载过程时间间隔序列 Fig.8 Time interval sequences of vehicle load process generated by Monte Carlo method |
|
图 9 蒙特卡罗方法生成的车辆荷载过程荷载幅值序列 Fig.9 Load amplitude sequences of vehicle load process generated by Monte Carlo method |

|
图 10 蒙特卡罗方法生成的车辆荷载时间间隔序列的验证 Fig.10 Verification of time interval sequences of vehicle load process generated by Monte Carlo method |

|
图 11 蒙特卡罗方法生成的车辆荷载幅值序列的验证 Fig.11 Verification of load amplitude sequences of vehicle load process generated by Monte Carlo method |
通过引入相对熵来判断拟合的优劣程度.相对熵D定义为[13]
| $ D\left( {P\left\| Q \right.} \right) = \sum\limits_x {P\left( x \right)\ln \frac{{P\left( x \right)}}{{Q\left( x \right)}}} $ | (25) |
式中:P(x)为真实分布;Q(x)为拟合分布.
对上例分析可知,车辆荷载时间间隔序列的相对熵仅为8.090×10-4,荷载幅值序列的相对熵仅为2.253×10-4,从而说明采用蒙特卡罗方法生成的时间间隔序列和荷载幅值序列能很好地反映真实的分布.
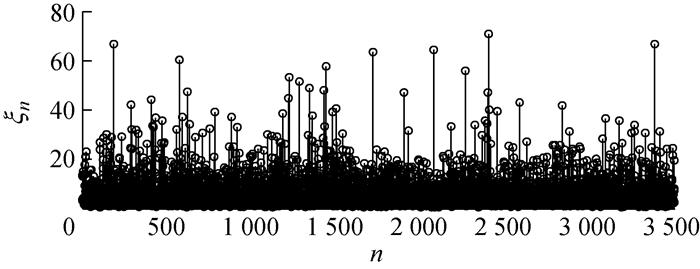
图 12为利用蒙特卡罗方法生成的车辆荷载过程的样本.模拟中,共有7 002个基本随机变量,如此巨大的随机变量个数必然为后续的结构系统分析带来困难.
|
图 12 蒙特卡罗方法模拟车辆荷载过程 Fig.12 Vehicle load process simulated by Monte Carlo method |
利用上述基于随机谐和函数生成复合泊松过程的原理和步骤模拟车辆荷载随机过程.对于生成车辆荷载出现的时间间隔序列,离散随机谐和函数{YT(tn), n=1, 2, …, N}的圆频率序列ω和相位角序列φ各采用5个随机变量即可,即
| $ \omega = \left\{ {{\omega _1}, {\omega _2}, {\omega _3}, {\omega _4}, {\omega _5}} \right\} $ | (26) |
| $ \varphi = \left\{ {{\varphi _1}, {\varphi _2}, {\varphi _3}, {\varphi _4}, {\varphi _5}} \right\} $ | (27) |
式中:ω为[0, π]的内点,即ωuT=π.
随机谐和函数{YT(tn), n=1, 2, …, N}各时点服从标准正态分布,其功率谱密度函数
| $ {S_{{Y_T}}}\left( \omega \right) = \left\{ \begin{array}{l} {S_T} = \frac{{{\rm{ \mathsf{ π} }}\sigma _{{Y_T}}^2}}{{{\omega _{{\rm{u}}T}}}} = 1, \;\;\;\;\left| \omega \right| = {\omega _{{\rm{u}}T}}\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (28) |
进一步可得到{YT(tn), n=1, 2, …, N}的幅值序列{A(ωi), i=1, 2, …, 5},有
| $ A\left( {{\omega _i}} \right) = \sqrt {\frac{{2{S_Y}\left( {{\omega _i}} \right)\Delta {\omega _i}}}{{\rm{ \mathsf{ π} }}}} = \sqrt {\frac{{2\Delta {\omega _i}}}{{\rm{ \mathsf{ π} }}}} $ | (29) |
同样地,用于生成车辆荷载幅值序列的随机谐和函数{Yξ(tn), n=1, 2, …, N}的圆频率序列ω′与相位角序列φ′也各采用5个随机变量,其功率谱密度函数同式(28),幅值序列同式(29).
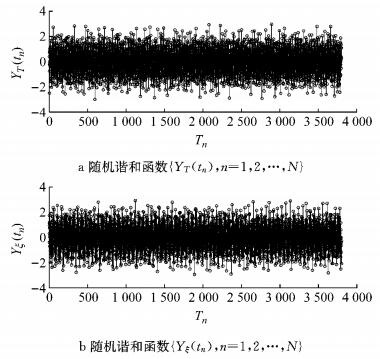
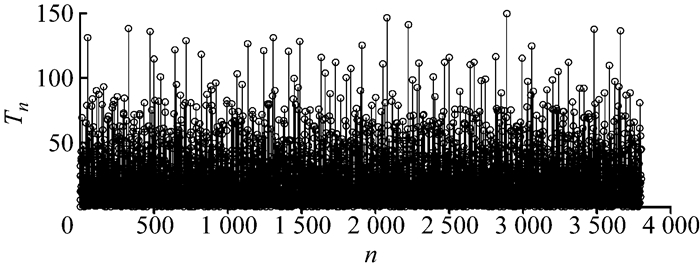
图 13为模拟车辆荷载过程的随机谐和函数{YT(tn), n=1, 2, …, N}和{Yξ(tn), n=1, 2, …, N}的样本图.基于随机谐和函数{YT(tn), n=1, 2, …, N}和{Yξ(tn), n=1, 2, …, N}分别生成车辆荷载过程的时间间隔序列{Tn, n=1, 2, …, N}和荷载幅值序列{ξn, n=1, 2, …, N},如图 14、15所示.
|
图 13 模拟车辆荷载过程的随机谐和函数 Fig.13 Stochastic harmonic function used to simulate vehicle load process |
|
图 14 随机谐和函数方法生成的车辆荷载过程时间间隔序列 Fig.14 Time interval sequences of vehicle load process generated by stochastic harmonic function |

|
图 15 随机谐和函数方法生成的车辆荷载过程荷载幅值序列 Fig.15 Load amplitude sequences of vehicle load process generated by stochastic harmonic function |
为了验证模拟生成的车辆荷载时间间隔序列与幅值序列的正确性,图 16和图 17分别给出了模拟序列的拟合分布及其与所对应的真实分布的对比,可见两者符合良好.根据式(25)分别计算时间间隔序列与荷载幅值序列的相对熵,发现时间间隔序列的相对熵为3.052 0×10-6,荷载幅值序列的相对熵为1.036 8×10-17.与蒙特卡罗方法的相对熵进行对比,采用随机谐和函数方法生成的时间间隔序列与荷载幅值序列更接近真实的概率分布.
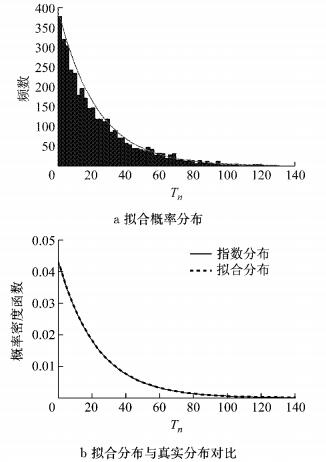
|
图 16 随机谐和函数生成的车辆荷载时间间隔序列的验证 Fig.16 Verification of time interval sequences of vehicle load process generated by stochastic harmonic function |
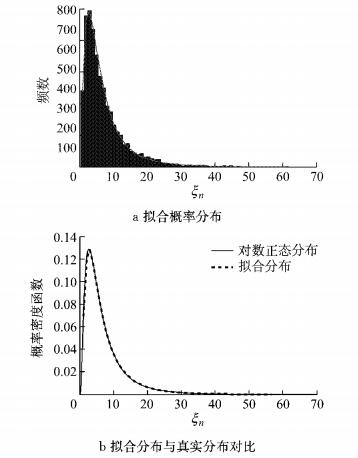
|
图 17 随机谐和函数生成的车辆荷载幅值序列的验证 Fig.17 Verification of load amplitude sequences of vehicle load process generated by stochastic harmonic function |
最终,将车辆荷载出现的时间间隔序列{Tn, n=1, 2, …}和车辆荷载幅值序列{ξn, n=1, 2, …}复合起来,即可得到车辆荷载过程.图 18为利用随机谐和函数方法模拟生成的车辆荷载过程的样本.
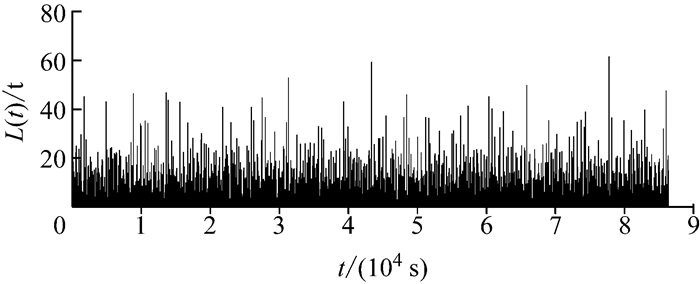
|
图 18 随机谐和函数方法模拟车辆荷载过程 Fig.18 Vehicle load process simulated by stochastic harmonic function method |
随机谐和函数方法在模拟过程中只采用了20个基本随机变量,与蒙特卡罗方法相比极大地减少了基本随机变量的个数,不仅证实了随机谐和函数方法的优越性,也为后续结构随机响应分析提供了极大便利.
4 结语本文提出了采用随机谐和函数来模拟复合泊松过程的方法,并证实了此方法的有效性与优越性.相比于传统的蒙特卡罗方法,本文方法可极大地减少基本随机变量的个数,为工程结构的随机非线性响应分析及结构可靠度分析提供了便利.
| [1] |
ROLSKI T, SCHMIDLI H, SCHMIDT V, et al. Stochastic processes for insurance and finance[M]. New York: John Wiley & Sons, 2009
|
| [2] |
KEGLER S R. Applying the compound Poisson process model to the reporting of injury-related mortality rates[J]. Epidemiologic Perspectives & Innovations, 2007, 4(1): 1 |
| [3] |
张雅清, 王艳玲, 李晓虹. 复合泊松过程在系统可靠性中的应用[J]. 河南师范大学学报(自然科学版), 2007, 35(1): 38 ZHANG Yaqing, WANG Yanling, LI Xiaohong. Application of compound Poisson process in system reliability[J]. Journal of Henan Normal University (Natural Science), 2007, 35(1): 38 |
| [4] |
ÖZEL G, INAL C. The probability function of the compound Poisson process and an application to aftershock sequence in Turkey[J]. Environmetrics, 2008, 19(1): 79 DOI:10.1002/(ISSN)1099-095X |
| [5] |
钱伟民, 梁汉营, 杨国庆. 应用随机过程[M]. 北京: 高等教育出版社, 2014 QIAN Weimin, LIANG Hanying, YANG Guoqing. Applied stochatic process[M]. Beijing: Higher Education Press, 2014 |
| [6] |
夏冬晴, 补爱军, 蒋耀龙. 基于泊松过程的模拟方法研究[J]. 邵阳学院学报(自然科学版), 2007, 4(1): 7 XIA Dongqing, BU Aijun, JIANG Yaolong. Study of simulation method based on Poisson process[J]. Journal of Shaoyang University (Natural Science Edition), 2007, 4(1): 7 |
| [7] |
陈建兵, 李杰. 随机过程的随机谐和函数表达[J]. 力学学报, 2011, 43(3): 505 CHEN Jianbing, LI Jie. Stochastic harmonic function and spectral representations[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(3): 505 DOI:10.6052/0459-1879-2011-3-lxxb2010-375 |
| [8] |
孙伟玲, 陈建兵, 李杰. 随机过程的第二类随机谐和函数表达[J]. 同济大学学报(自然科学版), 2011, 39(10): 1413 SUN Weiling, CHEN Jianbing, LI Jie. Stochastic harmonic functions of second kind for spectral representations[J]. Journal of Tongji University (Natural Science), 2011, 39(10): 1413 DOI:10.3969/j.issn.0253-374x.2011.10.001 |
| [9] |
ROSS S M. Stochastic Processes[M]. 2nd ed. New York: John Wiley, 1996
|
| [10] |
CHEN J, SUN W, LI J, et al. Stochastic harmonic function representation of stochastic processes[J]. Journal of Applied Mechanics, 2013, 80(1): 011001 |
| [11] |
"公路桥梁车辆荷载研究"课题组. 公路桥梁车辆荷载研究[J]. 公路, 1997(3): 8 The Research of Vehicle Load of Highway and Bridge" Research Team. The research of vehicle load of highway and bridge[J]. Highway, 1997(3): 8 |
| [12] |
郭彤, 李爱群, 赵大亮. 用于公路桥梁可靠性评估的车辆荷载多峰分布概率模型[J]. 东南大学学报(自然科学版), 2008, 38(5): 763 GUO Tong, LI Aiqun, ZHAO Daliang. Multiple-peaked probabilistic vehicle load model for highway bridge reliability assessment[J]. Journal of Southeast University (Natural Science), 2008, 38(5): 763 DOI:10.3969/j.issn.1001-0505.2008.05.005 |
| [13] |
HIAI F, PETZ D. The proper formula for relative entropy and its asymptotics in quantum probability[J]. Communications in Mathematical Physics, 1991, 143(1): 99 DOI:10.1007/BF02100287 |
 2017, Vol. 45
2017, Vol. 45
