由于大运量、高可靠性等特点,城市轨道交通成为公共交通的重要组成部分.然而,运营实践中,一些突发事件(设施设备故障、大客流、天气影响等)将直接干扰正常运营,使列车发生延误.较长时间的延误会导致系统能力损失、沿线客流积压、服务质量下降,严重时还会带来安全风险.对此,调度人员需要高效的列车运行调整方法,以保障延误期间的安全运营和服务水平,并尽快恢复正常秩序.目前运营现场主要依据预案和调度员经验来制定调整方案,在动态性、全局性和优化决策等方面还存在诸多不足.因此,延误下的列车运行调整优化亟需进一步研究.
轨道交通系统的列车运行调整一直是研究的热点,长期以来研究的重点多是以列车恢复正点、按图行车为目标,如路飞等[1]、柏赟等[2]主要以列车延误时间最小为目标,Schachtebeck等[3]考虑延误下衔接列车调整问题,使调整运行图尽量贴近计划运行图.近年来,从乘客角度出发的列车运行调整问题引起越来越多的关注.如Niu等[4]以铁路客运专线为背景,以最小化乘客候车等待时间为目标,构建旅客列车运行图优化模型.Sato等[5]以减小乘客后续出行不便为目标,综合改变列车性质、次序和车底周转、股道分配等措施,建立重调度模型和算法.Kliewer等[6]通过实例发现简单的乘客等待时间调整规则更有利于线路间的列车接续.由于城市轨道交通客流量大,行车间隔小,加上乘客出行的弱计划性等特征,使得列车运行调整的原则、目标和方法较传统铁路都有较大的差异性,其中最大的区别在于城市轨道交通需要以尽快输送客流为目的,但针对该方面的研究成果较少.乔珂等[7]以全部乘客等待时间最小为目标,提出了首站控制和多站协调控制的列车运行调整策略,主要考虑行车间隔均衡性,但有些车停站时间过长,容易造成车内大量乘客出行时间延长.Yin等[8]针对较小干扰下后续列车运行调整问题,建立综合考虑减小乘客延误时间、出行时间和能源消耗的随机规划模型,设计的近似动态规划算法可以快速得到解,但主要用于轻微的干扰情况.江志彬等[9]得出在初始延误时间较长,造成行车间隔过长时,扣车是最常见且最有效的策略,但缺少针对性的量化分析.
因此本文根据调度实际环境,以列车能力与客流需求的交互为基础,考虑运行过程的安全约束和能力限制,研究延误下列车协同(扣车)调整优化问题,构建相应模型和算法,以期尽快疏散客流.
1 问题描述城市轨道交通列车运行调整是一类大规模的组合优化问题,属于典型的NP难问题[10],涉及乘客、列车、设施条件、调整策略等诸多因素,具有时间和空间上的动态性,且需要兼顾:①客流分布的不均衡性,不同时空位置的调整程度应当不同;②以计划运行图为主要依据,制定的调整方案必须符合列车开行规则、安全与资源约束等条件.
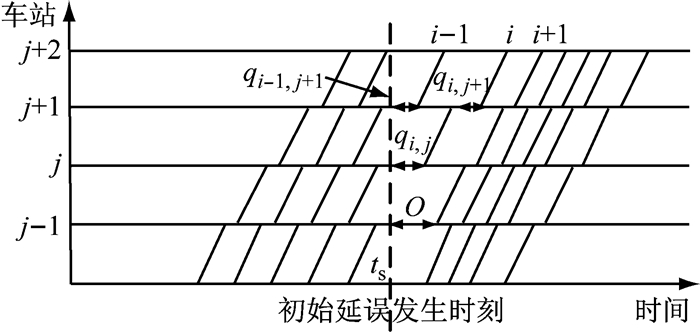
1.1 问题定义城市轨道交通一般只有两条股道供各自方向的列车分别运行.一般地,初始延误列车及其后续列车需等到延误事件排除后方能正常前行,延误期间调度员只能控制相关列车以安全间隔运行.如图 1所示,列车i+1在车站j-1发生初始延误,表现为停站时间增加O s,延误发生车站后方的列车出现“堵塞”现象,且只能依次以安全间隔“排队”,直至延误消除恢复计划运行图规定的开行间隔.
|
图 1 延误情况下扣车调整示意图 Fig.1 Sketch of the coordinated adjustment method |
初始延误发生后,延误列车i+1无法及时前行,延误地点前方区域将出现一段能力空缺,等待在前方站台的客流不断积聚,其出行时间增加,增大后续列车恢复正常运行后的客流需求压力.当列车i+1不能完全满足积聚的客流需求时,前方车站乘客进一步被留乘,由此带来连锁反应,形成延误的传播.因此,列车运行调整需要综合考虑延误地点前后列车间的运行协同、客流聚集、运行安全约束和列车能力等,协同安排各次列车的作业时刻,快速输送客流,才有助于恢复正常运营秩序.比如,将列车i分别在车站j扣停qi, js,在车站j+1扣停qi, j+1s,列车i-1在j+1站扣停qi-1, j+1s,使其延迟出站,便可将能力向后扩展,避免车站延误列车与前车间隔过大,“提早”带走一部分本将等候后续列车的乘客.以图 2为例,某一时段内,某车站乘客到达人数随时间增长,若计划发车时上车人数小于列车剩余载客能力时,将该列车的出发时刻延后一定时间,实际上车人数可相应增大.上述调整方法,本文简称为“扣车”.

|
图 2 列车运行调整对客流的作用示意图 Fig.2 The effect of train adjustment on passenger flow |
扣车能够缩短部分乘客在扣车车站的候车时间,更重要的是能够减轻延误结束后后续列车的客流压力,是延误条件下一种有效的列车运行调整方法.但是扣车后,会增加原本车内乘客的出行时间,且不能影响另一方向的运行.因此需要权衡利弊,利用有限的可扣车时间,决策扣哪些车、在哪些车站扣、扣多长时间,以使得尽量满足客流需求,从总体上减少乘客旅行时间.
1.2 问题假设结合我国城市轨道交通列车运行调度实际,本文重点研究列车运行延误条件下的运行调整问题,重大事故、自然灾害及其他突发事件所引起的线路长时间行车中断条件下的运行调整问题将另文研究.因此,给出如下假设:
(1) 列车运行满足安全行车间隔,发生延误后,列车间的次序保持不变,无越行和反向行车.
(2) 考虑可恢复的列车运行延误,初始延误结束后,列车都继续按照原停站方式载客运行,不考虑取消、增加列车以及列车跳停等,且车底交路计划不变.
(3) 初始延误列车后续列车以安全行车间隔调整,恢复至计划运行图的行车间隔时不再调整.
2 模型构建基于上述分析,延误情况下扣车调整问题主要求解初始延误列车前方列车的调整时刻表,由此建立如下整数规划模型.
2.1 参数定义表 1列出了模型的参数定义,包括输入变量和决策变量定义,除表中标注外,其他时间变量的单位都为s.
| 下载CSV 表 1 参数定义 Tab.1 Parameter definitions |
(1) 列车能力与客流需求的交互
用车内人数、上车人数和留乘人数描述列车能力与客流需求交互作用的结果.
车内人数只有在上、下车过程中发生改变,即
| $ {P_{{\rm{On}},i,j + 1}} = {P_{{\rm{On}},i,j}} - {P_{{\rm{A}},i,j}} + {P_{{\rm{B}},i,j}} $ | (1) |
下车人数PA, i, j通过车内乘客的出站信息判断,式(2)表示上车人数PB, i, j与列车停站时间、发车前的上车需求和列车剩余载客能力有关,式(3)计算留乘人数PL, i, j.发车前上车需求包括式(4)中的到达时站台上等待乘客和式(5)中的停站时间延长期间新到达乘客.
| $ {P_{{\rm{B}},i,j}} = \left\{ \begin{array}{l} {P_{{\rm{W}},i,j}} + {P_{{\rm{N}},i,j}},{P_{{\rm{W}},i,j}} + \\ \;\;\;\;\;\;{P_{{\rm{N}},i,j}} \le C - {P_{{\rm{On}},i,j}} + {P_{{\rm{A}},i,j}}\\ C - {P_{{\rm{On}},i,j}} + {P_{{\rm{A}},i,j}},反之 \end{array} \right\} $ | (2) |
| $ {P_{{\rm{L}},i,j}} = {P_{{\rm{W}},i,j}} + {P_{{\rm{N}},i,j}} - {P_{{\rm{B}},i,j}} $ | (3) |
| $ {P_{{\rm{W}},i,j}} = {P_{{\rm{L}},i - 1,j}} + \sum\limits_{k = 0}^{{t_{{\rm{d}},i,j}} - {t_{{\rm{d}},i - 1,j}}} {p_{i,j}^{\left( k \right)}} $ | (4) |
| $ {P_{{\rm{N}},i,j}} = \sum\limits_{k = 0}^{{q_{i,j}}} {p_{i,j}^{\left( k \right)}} $ | (5) |
自动售检票(AFC)系统详细记录了历史客流OD数据,包括进入车站及时间、离开车站及时间,其出行路径可通过已经成熟的客流分配模型得到,因此pi, j(k)及其出站信息与路径为已知,根据上述各式,可以量化其他参数.可见客流需求随列车的到发呈现动态变化,列车运行调整又将进一步引起客流重新分布,因此实际调整工作必须以上述交互关系为基础.
(2) 运行约束
式(6)和式(7)分别为区间运行时间和停站时间与列车到发时刻的关系.式(8)为最小行车间隔约束;式(9)为同一车站最小发到间隔约束.
| $ {t_{{\rm{a}},i,j + 1}} - {t_{{\rm{d}},i,j}} = {R_{i,j}} $ | (6) |
| $ {t_{{\rm{d}},i,j}} - {t_{{\rm{a}},i,j}} = {D_{i,j}} + {q_{i,j}} $ | (7) |
| $ {t_{{\rm{d}},i + 1,j}} - {t_{{\rm{d}},i,j}} \ge {h_{\min }} $ | (8) |
| $ {t_{{\rm{a}},i + 1,j}} - {t_{{\rm{d}},i,j}} \ge {{h'}_{\min }} $ | (9) |
(3) 调整时间约束
式(10)表示实际到站时间不早于计划到站时间;式(11)表示实际发车时间不早于计划发车时间;式(12)表明停站时间增加量为非负整数,且列车总扣车时间不能超过限制,因为不能影响另一方向的正常运营.若某列车车底还将折返后继续运行,那么这类列车总的可调整时长则不能超过其最大允许终到延误时间,若该车底不再折返,则可调整时长通过其与后一列车间的安全间隔约束得到.
| $ {t_{{\rm{a}},i,j}} - {T_{{\rm{a}},i,j}} \ge 0 $ | (10) |
| $ {t_{{\rm{d}},i,j}} - {T_{{\rm{d}},i,j}} \ge 0 $ | (11) |
| $ \sum\limits_j^N {{q_{i,j}}} \le {Q_i},{q_{i,j}} \in {{\rm{N}}^ + } $ | (12) |
本文满足客流需求的目的体现为:①使前行列车尽量多带走站台上的乘客,以减少站台乘客等待时间,表示为TW, i, j;②尽量少增加车内乘客乘车时间,表示为TR, i, j.两者组成乘客旅行时间,表示为Ti, j,三者计算如下:
| $ {T_{i,j}} = {T_{{\rm{W}},i,j}} + {T_{{\rm{R}},i,j}} $ | (13) |
| $ {T_{{\rm{W}},i,j}} = {P_{{\rm{L}},i - 1,j}}\left( {{t_{{\rm{d}},i,j}} - {t_{{\rm{d}},i - 1,j}}} \right) + k\sum\limits_{k = 0}^{{t_{{\rm{d}},i,j}} - {t_{{\rm{d}},i - 1,j}}} {p_{i,j}^{\left( k \right)}} $ | (14) |
| $ \begin{array}{l} {T_{{\rm{R}},i,j}} = \left( {{P_{{\rm{On}},i,j}} - {P_{{\rm{A}},i,j}} + {P_{{\rm{B}},i,j}}} \right){R_{i,j}} + \left( {{P_{{\rm{On}},i,j}} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {{P_{{\rm{A}},i,j}}} \right)\left( {{D_{i,j}} + {q_{i,j}}} \right) \end{array} $ | (15) |
因此,权衡对车内和站台乘客的影响,本文的优化目标为最小化全部乘客的旅行时间,即
| $ \min \sum\limits_i^M {\sum\limits_j^N {{T_{i,j}}} } $ | (16) |
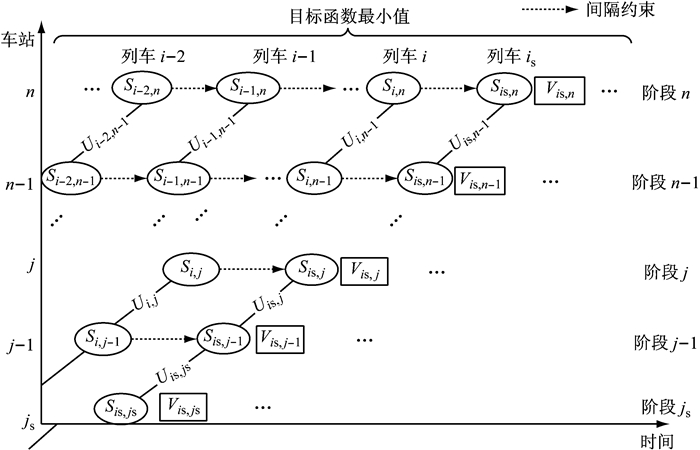
模型的关键在于确定需要调整的范围及程度.一方面,对于同一列车,其当前车站的到发时刻和车内客流状态与它在前一站的时刻和状态有关;另一方面,同一车站的多列车之间按序行车需要满足一定的间隔约束,一列车何时出发会影响后面车的时刻和站台等待客流.因此,这样的时空变化系统可以看作是车站、列车之间的状态转变过程,在每个转变过程中总是希望乘客旅行时间最小,因此需要寻找最优的转变,即最优的列车到发时刻,这与动态规划[11-12]的解题思想一致.由于涉及同列车多车站、同车站多列车两个维度的多阶段决策过程,因此需要组合的动态规划算法,而同车站多列车之间的状态转变可抽象为安全间隔约束.图 3表述了该动态规划算法的思路,包括每个车的状态转移过程和相邻列车间的联系.
|
图 3 调整前行列车的动态规划方法示意图 Fig.3 Illustration of train adjustment method using a combined dynamic programming algorithm |
认为初始延误列车的延误时长为已知,自初始延误发生时刻起至预计初始延误列车在该站发车时刻止的时段内,同一运行方向上,需要在前方车站进行停站发车作业的所有列车及相关车站构成调整区域,即满足ts≤Td, i, j≤td, is, j,其中td, is, j=Td, is, j+O为初始延误列车is在后续车站的预计发点.算法核心即为利用多少可调整时长,且如何将其合理分配给沿途各个车站,并协调相邻列车的到发时刻,使得总的效益指标达到最优.定义算法参数如下:
(1) 阶段变量为列车i在车站j;
(2) 状态变量为Si, j=(ta, i, j, Pi, j),其中Pi, j=(POn, i, j, PW, i, j),表示列车i在到达车站j时车内的乘客数和站台等待人数;
(3) 决策变量为Ui, j=qi, j,表示列车i在车站j的停站时间增加量,为本文的主要决策变量,由此可得到实际停站时间为Di, j+qi, j和发车时间为td, i, j=ta, i, j+Di, j+qi, j;
(4) 列车i在j车站采取决策Ui, j后,即得到其在下一车站到达时的状态,包括列车到达时间,车内、车外乘客数状态.则状态转移方程为
| $ {S_{i,j + 1}} = T\left( {{S_{i,j}},{U_{i,j}}} \right) $ |
其中T包含了以下意义
| $ {t_{{\rm{a}},i,j + 1}} = {t_{{\rm{a}},i,j}} + {D_{i,j}} + {q_{i,j}} + {R_{i,j}} $ |
| $ {P_{{\rm{On}},i,j + 1}} = {P_{{\rm{On}},i,j}} - {P_{{\rm{A}},i,j}} + {P_{{\rm{B}},i,j}} $ |
| $ {P_{{\rm{W}},i,j + 1}} = {P_{{\rm{L}},i - 1,j + 1}} + \sum\limits_{k = 0}^{{t_{{\rm{d}},i,j + 1}} - {t_{{\rm{d}},i - 1,j + 1}}} {p_{i,j}^{\left( k \right)}} $ |
(5) 阶段效益指标Vi, j相当于列车i在车站j调整后决定的乘客旅行时间,为目标函数的一个阶段值,即
| $ {V_{i,j}}\left( {{S_{i,j + 1}},{U_{i,j}}} \right) = {T_{i,j}} $ |
则目标函数表达为
| $ \min \sum\limits_i^M {\sum\limits_j^N {{V_{i,j}}\left( {{S_{i,j + 1}},{U_{i,j}}} \right)} } $ |
(6) 若用fi, j-1(Si, j)表示从第i车的Si, j出发,采用最优策略,到最后一列车在最后一车站乘客总的旅行时间最小.由最优化原理得最优值函数为
| $ {f_{i,j}}\left( {{S_{i,j + 1}}} \right) = \min \left\{ {{V_{i,j}}\left( {{S_{i,j + 1}},{U_{i,j}}} \right) + {f_{i,j - 1}}\left( {{S_{i,j}}} \right)} \right\} $ |
对于调整范围内的列车,始端条件fi, js-1(Si, js)是该列车在进入延误调整区域之前所决定的乘客旅行时间
关键环节在于对进入延误调整区域的列车,分析其从初始延误车站js到其终点站的状态转移过程.后行列车在前行列车的基础上进行调整,基于当前的客流分布,并满足间隔约束.基于前述模型约束与算法定义,设计如下算法步骤并用计算机编程求解:
步骤1:载入计划列车时刻表、延误信息和客流OD数据,确定各个列车在各个车站的初始状态,初始化fi, j(Si, j+1)=
步骤2:对列车i=1, …, m:
步骤2.1:对车站j=1, …, n-1:
(1) 若列车i是初始延误列车的后续列车,当还未恢复计划开行间隔,则按照最小行车间隔调整其在车站j的到发时刻,否则不调整;
(2) 若其他列车i在车站j不属于调整区域,则不调整,令ta, i, j=Ta, i, j,td, i, j=Td, i, j;
(3) 若列车i在车站j达到计划停车时间时已经满载,则不调整,qi, j=0,td, i, j=ta, i, j+Di, j;
(4) 否则,对于在调整区域内的列车i:若是初始延误列车,则ta, i, j=Ta, i, j+O,td, i, j=Td, i, j+O;若是其他列车,满足间隔约束,在车站j+1的每个可能调整时间qi, j+1条件下,遍历车站j的每个可能调整时间qi, j,每一次遍历都由上述算法参数及公式算得ta, i, j和td, i, j.
步骤2.2:针对上述(4)中每种可能情况,计算指标函数值,即
| $ {f_{i,j{\rm{\_temp}}}}\left( {{S_{i,j + 1}}} \right) = {f_{i,j - 1}}\left( {{S_{i,j}}} \right) + {V_{i,j}}\left( {{{S'}_{i,j + 1}}\left| {{S_{i,j}},{U_{i,j}}} \right.} \right) $ |
步骤2.3:更新,若fi, j_temp(Si, j+1) < fi, j(Si, j+1),则fi, j(Si, j+1)=fi, j_temp(Si, j+1),记录此刻的qi, j和td, i, j;
步骤2.4:当得到优化的fi, n-1(Si, n),即终点站n对应的最优值时,得到该列车的最优策略.根据记录的qi, j和td, i, j依次回溯找出其在各站调整后的到发时刻.
步骤3:若i=m,调整结束,转步骤4;否则i=i+1,转步骤2.1.
步骤4:得到各个列车的指标函数值,总的指标函数值以及调整后的所有列车时刻.
特别地,虽然时刻表以s为单位,但实际调度中若只调整1 s,则显得没有意义.因此,结合现场实际,设置最小的调整值e,0<e<Qi.同时,由于实际调度中调整前行列车需要兼顾站台乘客数和原本车内乘客数,两者比例可作为该站调整的参考系数.即不同车站的可调整程度可表达为ri, j=
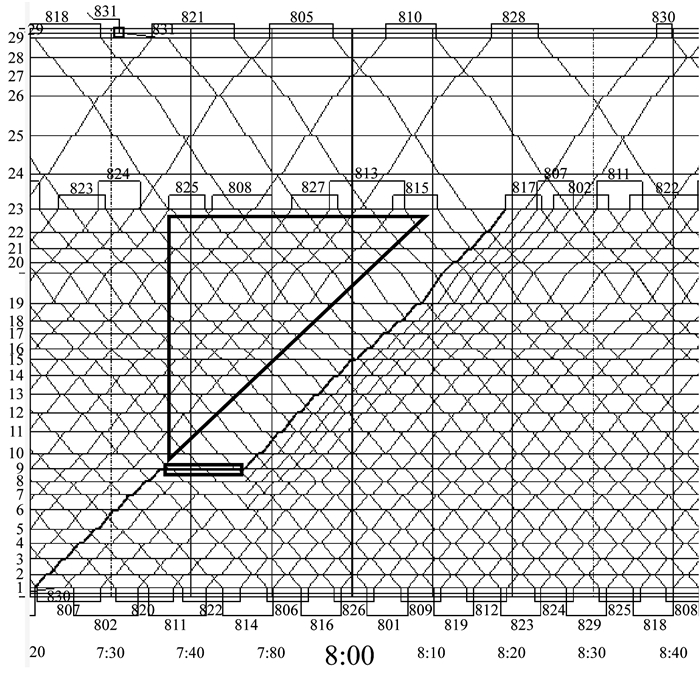
以上海地铁8号线1 d的运行图、OD数据等信息为基础进行算例分析.如图 4所示,假设上行(车站1—29)方向一列车在车站9延误10 min,该方向后续4列车被调整为追踪运行,但延误车站前方车站通过能力下降,由于正值早高峰时段,客流积压现象将较为严重,因此考虑协同调整其前行列车.为了避免28×28的OD矩阵表,采用图 5所示的弦图表示研究时段内上行方向车站之间的OD量,弦的颜色深度表明量的大小,弧的宽窄代表该站OD总量的大小.车站23之后的车站输入客流需求很小,因此这部分不算入调整区域.
|
图 4 仅调整后车的运行图 Fig.4 Train diagram with only subsequent trains adjustment on the delay |

|
图 5 OD客流量图示(7:30-8:30) Fig.5 Graphical plot of origin-destination flows |
通过匹配调整之前的列车和客流数据,可以计算得到前行列车的可调整总时长和各个车站的分担率,该算例中的各列车的Qi=210 s,最小调整时间为e=10 s,hmin=120 s,h′min =90 s.如图 6所示,利用本文模型和算法最终协同调整了前行4列车,具体结果见表 2,离初始延误列车较远的前行列车5和6没有调整.

|
图 6 协同调整后的运行图 Fig.6 Train diagram with cooperative adjustment |
| 下载CSV 表 2 前行列车在各个车站停车时间增加值 Tab.2 Added dwell time of the preceding trains at the stations |
乘客总旅行时间优化结果如表 3所示.为验证本文方法的有效性,进一步引入以下两种对比方法:①仅调整后车的方法:即只考虑利用缓冲时间调整后续列车,以安全间隔运营,渐渐恢复正常间隔;②首站调整的方法:只在延误发生后各个列车所在(或即将到达)的第一车站进行扣车,每个列车扣车时间为最大允许终到延误时间,且前车扣车时间不能多于后车.
| 下载CSV 表 3 结果对比 Tab.3 Comparison of the results |
由于存在运行延误,三种行车调整方法得到的乘客总旅行时间无疑均大于计划值,这与调度实际相符.乘客总旅行时间是该方向全天全部乘客的旅行时间之和,加之可调整范围和时长的约束,因此以小时为单位的三种方法所得总结果相差相对不显著.但本文方法结果小于其他方法,说明其有所优化;结合表 2,前行列车在相应车站的停站时间增加值较为显著,具有可操作性.而首站调整方法只考虑了在第一站扣车操作的简便性,未结合客流分布特征,导致其结果反而劣于仅调整后车方法.本文协同调整方法以满足客流需求为目的,通过考虑期待提早上车的客流,并权衡已在车内的乘客可能被增加的旅行时间,且调整方案不影响另一方向运行,由此证明了该方法的有效性和先进性.
5 结论区别于传统铁路,城市轨道交通列车运行延误下列车运行调整的首要目标是疏散客流.在延误列车后续列车以安全间隔运行直至恢复的同时,协同调整前行列车能缓解延误地点前方车站的客流积压现象.以客流需求与列车能力的动态交互及运行约束和调整限制为基础,构建的模型与算法重点解决多个前行列车在多个车站的时刻调整问题,使得优化后的运行图乘客总旅行时间最小.案例分析结果表明了模型与算法的有效性,可为实际调度调整提供一定的辅助支持.考虑结合其他调度策略(列车清客、列车救援、跳站停车等)的调整方法是进一步研究的方向.
| [1] |
路飞, 宋沐民, 田国会. 基于多智能体的地铁列车运行调整方法[J]. 中国铁道科学, 2007, 28(1): 123 LU Fei, SONG Mumin, TIAN Guohui. Method for subway operation adjustment based on multi-agent[J]. China Railway Science, 2007, 28(1): 123 |
| [2] |
柏赟, 陈垚, 陈玥, 等. 考虑列车总晚点和到发均衡性的地铁列车运行调整方法研究[J]. 交通运输系统工程与信息, 2014, 14(3): 104 BAI Yun, CHEN Yao, CHEN Yue, et al. Rescheduling of metro train timetable for delay reduction and equilibrium of trains' arrival and departure[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14(3): 104 |
| [3] |
SCHACHTEBECK M, SCHÖBEL A. To wait or not to wait-and who goes first? Delay management with priority decisions[J]. Transportation Science, 2010, 44(3): 307 DOI:10.1287/trsc.1100.0318 |
| [4] |
NIU H, ZHOU X. Optimizing urban rail timetable under time-dependent demand and oversaturated conditions[J]. Transportation Research Part C: Emerging Technologies, 2013, 36: 212 DOI:10.1016/j.trc.2013.08.016 |
| [5] |
SATO K, TAMURA K, TOMⅡ N. A MIP-based timetable rescheduling formulation and algorithm minimizing further inconvenience to passengers[J]. Journal of Rail Transport Planning & Management, 2013, 3(3): 38 |
| [6] |
KLIEWER N, SUHL L. A note on the online nature of the railway delay management problem[J]. Networks, 2011, 57(1): 28 DOI:10.1002/net.20381 |
| [7] |
乔珂, 赵鹏, 禹丹丹. 基于乘客等待时间的城市轨道交通列车运行调整模型[J]. 北京交通大学学报(自然科学版), 2014, 38(6): 27 QIAO Ke, ZHAO Peng, YU Dandan. Train regulation model of urban rail transit based on passenger waiting time[J]. Journal of Beijing Jiaotong University: Natural Science, 2014, 38(6): 27 DOI:10.11860/j.issn.1673-0291.2014.06.005 |
| [8] |
YIN J, TANG T, YANG L, et al. Energy-efficient metro train rescheduling with uncertain time-variant passenger demands: an approximate dynamic programming approach[J]. Transportation Research Part B: Methodological, 2016, 91: 178 DOI:10.1016/j.trb.2016.05.009 |
| [9] |
江志彬, 季婷婷. 基于客流影响的城市轨道交通列车运行调整策略[J]. 城市轨道交通研究, 2014, 17(1): 39 JIANG Zhibin, JI Tingting. URT train regulation strategy based on passenger flow influence[J]. Urban Mass Transit, 2014, 17(1): 39 |
| [10] |
CAPRARA A, FISCHETTI M, TOTH P. Modeling and solving the train timetabling problem[J]. Operations Research, 2002, 50(5): 851 |
| [11] |
NIU H, TIAN X, ZHOU X. Demand-driven train schedule synchronization for high-speed rail lines[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(5): 2642 DOI:10.1109/TITS.2015.2415513 |
| [12] |
CACCHIANI V, FURINI F, KIDD M P. Approaches to a real-world train timetabling problem in a railway node[J]. Omega, 2016, 58: 97 |
 2018, Vol. 46
2018, Vol. 46

