2. 同济大学 土木工程学院, 上海 200092;
3. 常州工学院 土木建筑工程学院, 江苏 常州 213002;
4. 安徽理工大学 土木建筑工程学院, 安徽 合肥 232001
2. College of Civil Engineering, Tongji University, Shanghai 200092, China;
3. Institute of Civil Engineering, Changzhou Institute of Technology, Changzhou 213002, China;
4. Institute of Civil Engineering, Anhui University of Science and Technology, Hefei 232001, China
大量的现场工程实测表明,相当一部分岩土工程中土体在工作荷载下处于小应变状态.近20年来,国内外通过高精度室内试验和现场原位测试对土体的小应变行为进行了大量的研究, 发现在小应变条件下土体刚度具有高度的非线性[1].Atkinson等[2]将应变分为3类:很小的应变,变化范围小于或等于0.001%;小应变,变化范围为0.001%~0.100%;大应变,应变范围大于0.100%.土体的剪切刚度在归一化的剪切刚度和应变的对数形成的坐标系内呈“S”形曲线,而在小应变区域内,土体的刚度将会随着应变的增加急剧减小,两者呈现非线性的关系.因此,在分析基坑问题时,有必要考虑土体刚度在小应变区域的变化特性.如果忽略小应变特性会严重低估土体的刚度,造成预计的变形偏大,无法起到应有预测的作用,同时不得不采用保守的施工来满足设计的要求,造成不必要的资源浪费.
因此准确预测基坑开挖等土体变形需要一个考虑土体小应变阶段特性的本构模型.小应变硬化模型(HSS)由Benz等[3-4]提出,这个模型在硬化模型(HS)[5]的基础上考虑了土体在小应变区域内刚度随应变的非线性变化,加入了两个小应变参数G0, ref和γ0.7.该模型可以同时考虑剪切硬化和压缩硬化,而且可以考虑剪切模量在微小应变范围内随应变衰减的行为.小应变硬化模型相比于以前的模型更好地考虑土体在应变非常小时应力相关的弹性特性,以及土体在小应变阶段时模量随应变衰减的非线性特性.徐中华等[6]对比分析了各种土体本构模型在深基坑工程中的适用性,指出HSS模型更适用于深基坑工程的精细分析.王卫东等[7]通过室内试验获得土体HS模型参数,并用反分析方法确定了土体小应变参数G0, ref、γ0.7,但没有通过室内试验实测.王浩然[8]通过参数分析表明HSS模型中对基坑变形影响最大的参数为G0, ref、γ0.7及m,其余参数影响相对很小.故本文拟用室内试验的方法测定包括G0, ref、γ0.7及m在内的全部HSS模型参数.
1 小应变模型HSS模型共包含11个HS参数和2个小应变参数,各参数定义如下:c′为土的有效黏聚力; K0为初始静止侧压力系数; m为刚度应力水平相关幂指数; E50, ref为三轴固结排水剪切试验测定的参考割线模量; Eoed, ref为标准固结试验测定的参考切线模量; G0, ref为动剪切初始模量; υur为加卸载泊松比; φ′为土的有效内摩擦角; Ψ为土的剪胀角; pref 为参考应力; Eur, ref为三轴固结排水加卸载试验测定的加卸载模量; Rf为三轴排水剪切试验测定的破坏比; γ0.7为剪切模量衰减到初始剪切模量70%时对应的剪应变.
2 试验内容 2.1 试验土样试验采用江苏常州地区3个典型土层土样,土样的基本物理指标见表 1.室内三轴试验土样直径为39.1 mm,高度为80.0 mm,标准固结试验土样直径为61.8 mm,高度为20.0 mm,共振柱试验土样直径为50.0 mm,高度为100.0 mm.
| 下载CSV 表 1 试验土样的基本物理指标 Tab.1 Physical index of the tested soil sample |
HSS模型中静止侧压力系数K0一般可以通过应力路径三轴仪试验测得; 不实测时,K0取值根据Mayne等[9]的建议基于土体的有效摩擦角φ′(φ′可由三轴固结排水剪切试验测定)和超固结比ROC(ROC可由一维固结试验测定)确定.加卸载泊松比νur可通过增加局部应变测量的三轴仪试验得到; 不实测时,可采用Brinkgreve等[10]的建议取νur=0.2.剪胀角Ψ一般可通过室内三轴试验测得; 不实测时,根据Bolton[11]的研究取值,对砂土,Ψ可取为φ′-30°, 当内摩擦角φ′小于30°时,Ψ可取为零; 对于黏性土,Ψ一般取为零.参考应力pref建议取为现场初始应力值,但大多文献取100 kPa.模型剩余参数可按本文室内试验获得,分别为:三轴固结排水剪切试验确定参数c′、φ′、Rf和E50, ref; 三轴固结排水加卸载试验确定参数Eur, ref; 标准固结试验确定参数Eoed, ref; 共振柱试验确定参数G0, ref、γ0.7和m.
2.3 试验过程 2.3.1 三轴固结排水剪切试验采用英国GDS公司生产的STDTTS应力路径三轴仪进行三轴固结排水剪切试验.为保证试样完全饱和,先将试样在饱和器中初步饱和,再进行反压饱和,直至测定的孔隙水压力系数B大于0.95.然后分别在初始有效围压100、200和300 kPa下进行固结.最后在等应变速率条件下进行排水剪切,剪切速率为0.008 mm·min-1,当轴向应变达到20%时,停止试验.
2.3.2 三轴固结排水加卸载试验三轴固结排水加卸载试验的仪器和试样饱和步骤均与三轴固结排水剪切试验相同.①~③层试样固结有效围压均为100 kPa.试验采用应力控制模块,先加载到由固结排水剪切试验确定的峰值偏应力的一半,然后再将偏应力卸载到0,最后再将偏应力不断增加直到试样剪切破坏.
2.3.3 标准固结试验标准固结试验采用常规固结仪,每层土取2个环刀试样,分别在12.5、25.0、50.0、100.0、200.0、400.0、800.0 kPa条件下进行分级加载固结,每级加载固结时间为24 h.
2.3.4 共振柱试验采用英国GDS公司生产的Stokoe型共振柱系统进行共振柱试验.试样饱和步骤与三轴固结排水剪切试验相同.①~③层土样在其现场初始有效围压下进行固结,分别为45、70和90 kPa.此外①层土样再增加3组有效围压为100、200和300 kPa的试验,③层土样增加两组围压为200、300 kPa的试验.固结完成后对试样扫频激振,确定共振频率以及相应的加速度响应,再根据振动理论确定试样的剪切模量和对应的剪应变值.然后增加激振电压(相当于激振力),测定共振时的剪应变和剪切模量,最终测定剪切模量与应变的关系.
3 试验结果 3.1 三轴固结排水剪切试验结果图 1~3给出了各土层试样在有效围压100 kPa下的应力应变关系.由图 1~3可知,在剪切初期, 各层土试样偏应力均随应变的增大而不断增加,当应变增加至某一值时应力达到峰值.①层粉质黏土试样偏应力达到峰值后,随着应变的继续增大,试样基本保持应力峰值直至试样破坏.而②、③层试样偏应力在达到峰值后明显下降,即出现应变软化现象.取峰值偏应力作为土体破坏应力值qf,连接应力应变曲线的原点和0.5qf点得到的直线斜率即为试样的参考割线模量E50, ref.本次试验确定的①~③层土的E50, ref分别为5.5、8.7和14.2 MPa.
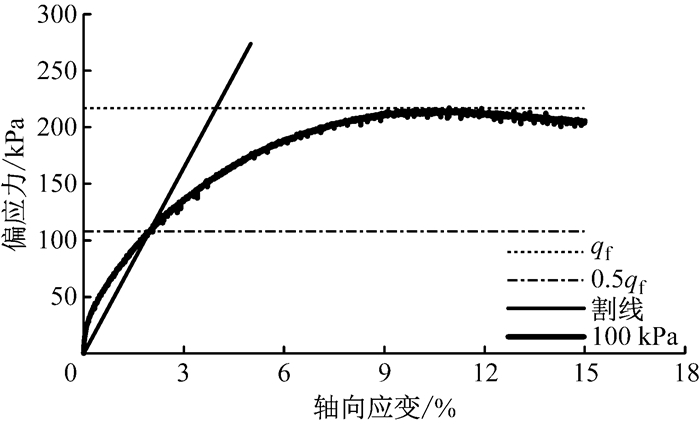
|
图 1 ① 层土试样应力-应变关系 Fig.1 Stress-strain curve of soil layer ① |

|
图 2 ② 层土试样应力-应变关系 Fig.2 Stress-strain curve of soil layer ② |

|
图 3 ③ 层土试样应力-应变关系 Fig.3 Stress-strain curve of soil layer ③ |
为获得各土层土的有效内聚力c′和有效内摩擦角φ′,又分别在200和300 kPa围压下完成各土层的三轴固结排水剪切试验.图 4~6分别为①~③层土的应力摩尔圆.基于应力摩尔圆可确定3层土的有效抗剪强度指标分别为:①层c′=6.7 kPa,φ′=29.1°; ②层c′=11.7 kPa,φ′=39.4°; ③层c′=12.5 kPa,φ′=41.4°.根据Konder[12]的建议,将各层试样的应力应变曲线拟合成双曲线函数,可得偏应力的渐近值qa,由此得到①~③层土试样的破坏比Rf分别为0.72、0.56、0.62.

|
图 4 ① 层土试样破坏时的应力摩尔圆 Fig.4 Stress Mohr circle for soil layer ① |

|
图 5 ② 层土试样破坏时的应力摩尔圆 Fig.5 Stress Mohr circle for soil layer ② |
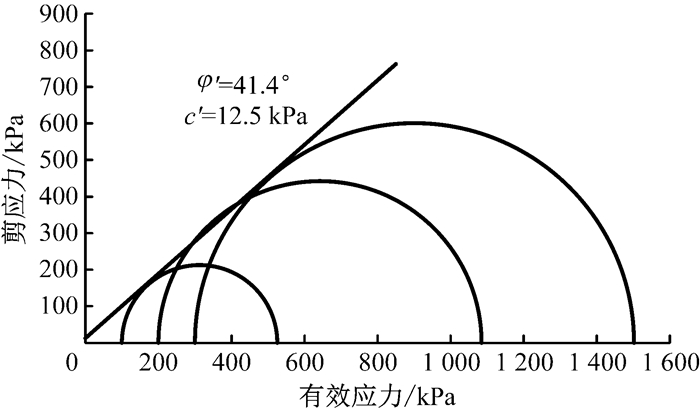
|
图 6 ③ 层土试样破坏时的应力摩尔圆 Fig.6 Stress Mohr circle for soil layer ③ |
图 7给出了①~③层土试样在围压100 kPa下三轴固结排水加卸载试验结果.由图 7可见,加载初期曲线趋势与应变控制的三轴固结排水剪切试验相同,①层土试样偏应力随应变变化最缓,③层土试样变化最快.在应力达到破坏值qf的一半时开始卸载.卸载初期轴向应变略微增大,当卸载到一定程度时,轴向应变又减小,整体上表现为卸载回弹.在再加载的过程中,初期应力应变曲线非常陡直至达到卸载前应力水平,然后加载曲线变得越来越缓,并沿初始加载曲线上升.试验曲线在加卸载段有一个明显的滞回圈,连接滞回圈两个端点,该直线斜率即为参考加卸载模量Eur, ref.最终确定①~③层土试样的Eur, ref值分别为:32.0, 48.0和88.9 MPa.

|
图 7 三轴加卸载试验应力-应变关系 Fig.7 Stress-strain curve during loading, unloading, and reloading in a triaxial test |
图 8为①~③层土试样的标准固结试验结果.从图 8可以看出,各层土样竖向应变εa随竖向荷载σv的变化趋势是相同的,初期曲线比较平缓,当竖向荷载增大的同时,曲线的斜率也变得越来越大,表明土体模量随围压的升高而变大.③层土试样的竖向变形最小,①层土试样的竖向变形相对最大.对这3条试验曲线分别用2次函数进行拟合,根据拟合函数可计算在竖向应力为100 kPa时曲线的斜率,即为参考固结切线模量Eoed, ref.最终可以得到①~③层土试样的Eoed, ref值分别为:4.8, 7.1, 12.9 MPa.

|
图 8 标准固结试验竖向应力-应变关系 Fig.8 Vertical stress-strain curves in consolidation tests |
图 9~11给出了①~③层土试样在现场初始有效围压45、70、90 kPa下动剪切模量G与剪应变的γ关系.由图 9~11可见,土样在小应变范围内均表现出明显的非线性.随着剪应变的不断增大,动剪切模量不断减小,而且衰减速率也不断增大.以图 11为例,当剪应变从6.6×10-6增加到3.8×10-4时,土体动剪切模量从64.3 MPa衰减到38.1 MPa.根据Hardin等[13]的分析,G-γ曲线可用双曲线模型描述,即1/G=a+bγ,其中a、b为常数,可基于试验数据经回归统计分析确定.当γ趋向于零时,1/G趋向与a,此时G即为初始动剪切模量或最大动剪切模量,通常用G0来表示,即G0=1/a.

|
图 9 ① 层土试样动剪切模量与应变关系 Fig.9 Dynamic shear modulus-strain curve of soil layer ① |

|
图 10 ② 层土试样动剪切模量与应变关系 Fig.10 Dynamic shear modulus-strain curve of soil layer ② |
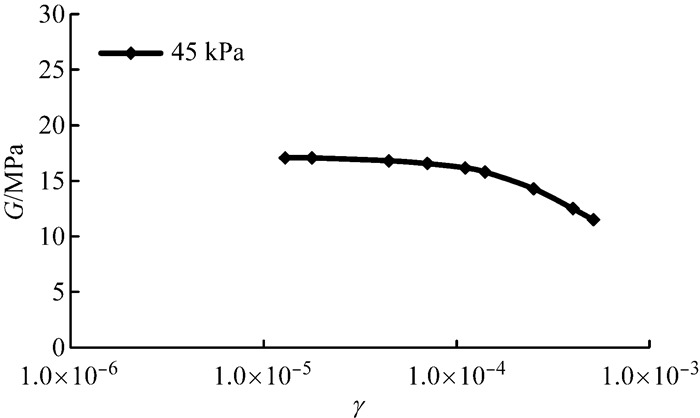
|
图 11 ③ 层土试样动剪切模量与应变关系 Fig.11 Dynamic shear modulus-strain curve of soil layer ③ |
图 12给出了③层土试样归一化后的模量退化曲线.经分析, ①~③层土试样的γ0.7分别为4.0×10-4、1.9×10-4、2.2×10-4.

|
图 12 ③ 层土试样归一化模量退化曲线 Fig.12 Normalized modulus reduction curves of soil layer ③ |
图 13和图 14分别给出了①层和③层土样在有效围压45、100、200、300 kPa和90、200、300 kPa下的动剪切模量与应变的关系.各围压下曲线整体趋势相同,相同应变下围压越大,剪切模量越大.根据双曲线模型公式进行拟合,可得到①层土各围压下初始剪切模量分别为17.1、25.7、42.1、54.8 MPa; ③层土各围压下初始剪切模量分别为64.5、107.5、142.8 MPa.进一步研究表明,在测试的应变范围内,拟合和实测的结果非常接近.经验公式如下:
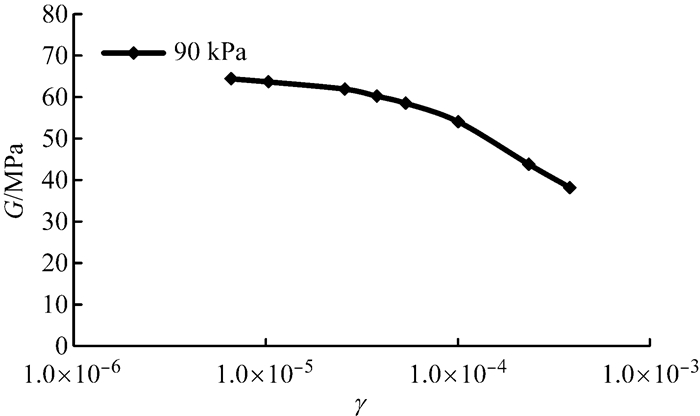
|
图 13 ① 层土试样不同围压下动剪切模量与应变关系 Fig.13 Dynamic shear modulus-strain curves of soil layer ① at different confining pressures |

|
图 14 ③ 层土试样不同围压下动剪切模量与应变关系 Fig.14 Dynamic shear modulus-strain curve of soil layer ③ at different confining pressures |
| $ {G_0} = A{\sigma ^m} $ | (1) |
式中:A为一常数,反映土体密实度、土体级配等的影响; m为应力指数,反应围压的影响.
根据式(1)即可求得①层土样的m=0.62;②层土样m值取与①层相同m=0.62;③层土样的m=0.66.最后根据式(1)和实测结果,即可得到3个土层在参考围压100 kPa下的初始剪切模量G0, ref分别为:25.7、61.8和69.1 MPa.
3.5 试验成果汇总及分析基于室内试验研究并参考相关文献,表 2给出了江苏常州地区典型土层HSS模型的全部13个参数,可供当地工程分析使用.表 3则给出了试验中的E50, ref、Eur, ref、Eoed, ref值及它们之间的比例关系.由表 3可见,同一层土样固结试验中获得的切线模量Eoed, ref最小,而加卸载割线模量Eur, ref远远大于其他两个模量.值得注意的是,这3层土的几个模量之间存在一定的关系:E50, ref与Eoed, ref的比值在1.1~1.2之间,Eur, ref与Eoed, ref的比值在6.7~6.9之间.
| 下载CSV 表 2 HSS模型参数汇总 Tab.2 Summary of parameters of HSS model |
| 下载CSV 表 3 不同模量的比例关系 Tab.3 Comparison of different modulus |
本文通过三轴固结排水剪切试验、三轴固结排水加卸载试验、标准固结试验和共振柱试验,获得了江苏常州地区典型土层HSS模型的全部参数,初步结论和建议如下:
(1) 试验确定了3个土层HSS模型的全部参数,可供本地区相关工程使用.建议利用这些参数进行变形分析并与实测数据进行比较,进一步修正模型参数.
(2) 试验结果表明,固结试验的割线模量、三轴试验的割线模量及加卸载试验的割线模量存在比较稳定的比例关系.本文建议进一步研究该比例关系,以便在实际工程中简化试验,利用一个试验模量推算出其余两个模量.
(3) 土体的小应变剪切模量表现出高度的非线性和围压相关特性,建议在当前有效应力状态下测定初始剪切模量和参考应变,然后换算到参考应力100 kPa下作为模型输入参数.
| [1] |
MAIR R J. Developments in geotechnical engineering research: application to tunnels and deep excavations[J]. Proceedings of the Institution of Civil Engineers, 1993, 93(2): 27 |
| [2] |
ATKINSON J H, SALLFORS G. Experimental determination of stress-strain-time characteristics in laboratory and in-situ tests[C]//Proceedings of 10th European Conference on Soil Mechanics and Foundation Engineering. Rotterdam: Balkema, 1991: 915-956. http://www.mendeley.com/research/experimental-determination-stressstraintime-characteristics-laboratory-situ-tests/
|
| [3] |
BENZ T. Small-strain stiffness of soils and its numerical consequences[D]. Stuttgart: University of Stuttgart, 2007.
|
| [4] |
BENZ T, SCHWAB R, VERMEER P. Small-strain stiffness in geotechnical analyses[J]. Geotechnical Engineering, 2009, 86(S1): 16 |
| [5] |
SCHANZ T, VERMEER P A, BONNIER P G. The hardening soil model-formulation and verification[M]. Amsterdam: Balkema, 1999: 281-296
|
| [6] |
徐中华, 王卫东. 敏感环境下基坑数值分析中土体本构模型的选择[J]. 岩土力学, 2010, 31(1): 258 XU Zhonghua, WANG Weidong. Selection of soil constitutive models for numerical analysis of deep excavations in close proximity to sensitive properties[J]. Rock and Soil Mechanics, 2010, 31(1): 258 |
| [7] |
王卫东, 王浩然, 徐中华. 基坑开挖数值分析中土体硬化模型参数的试验研究[J]. 岩土力学, 2012, 33(8): 2283 WANG Weidong, WANG Haoran, XU Zhonghua. Experimental study of parameters of hardening soil model for numerical analysis of excavations of foundation pits[J]. Rock and Soil Mechanics, 2012, 33(8): 2283 |
| [8] |
王浩然. 上海软土地区深基坑变形与环境影响预测方法研究[D]. 上海: 同济大学, 2012. WANG Haoran. Prediction of deformation and response of adjacent environment of deep excavation in Shanghai soft deposit [D]. Shanghai: Tongji University, 2012. |
| [9] |
MAYNE P H, KULHAWY F H. K0-OCR relationships in soils[J]. Journal of Geotechnical Engineering, 1982, 108(6): 851 |
| [10] |
BRINKGREVE R B J, BROERE W. Plaxis material models manual[R]. Delft: Delft University of Technology, 2006.
|
| [11] |
BOLTON M D. The strength and dilatancy of sands[J]. Géotechnique, 1986, 36(1): 65 DOI:10.1680/geot.1986.36.1.65 |
| [12] |
KONDER R L. Hyperbolic stress-strain response: cohesive soils[J]. Journal of Soil Mechanics and Foundation Division, ASCE, 1963, 89(1): 115 |
| [13] |
HARDIN B O, DRNEVICH V P. Shear modulus and damping in soils[J]. Journal of the Soil Mechanics and Foundations Division, 1972, 98(7): 667 |
 2018, Vol. 46
2018, Vol. 46
