随着现代科学技术的发展,复合材料以其重量轻、比强度高、比刚度高、可设计性强等特点,在航空航天、汽车、石油化工、建筑桥梁、舰船以及生物工程等领域得到了越来越广泛的应用.常用的复合材料板多为各向异性板,由于结构装配或功能方面的需求,常常需要在板中打孔,而各向异性板在不同方向呈现出不同的力学性能,对于这种开孔结构来说,特别突出的一个问题就是开孔引起的应力集中.在荷载作用下,开孔可能会对结构的承载能力、使用寿命产生严重影响,因此,精确计算出孔洞周边的应力分布对判断结构的稳定性以及采取何种加固措施等具有重要的指导意义.为此,国内外许多学者都对各向异性含孔结构进行了应力分析.
Lekhnitskii[1-2]最早采用复变函数方法,研究了带有一个椭圆孔的各向异性板在平面荷载作用下的应力计算问题.在此后很长一段时间内,只有圆孔或椭圆形孔才有精确解.近几年来,一些学者通过复变函数方法,也研究了三角形孔[3-6]、矩形孔[6-9]、某六边形孔[9]和多边形孔[10]在无穷远处作用不同荷载时的孔边应力解析解.Ukadgaonker等[11]对不规则孔的孔边应力进行了分析.但是,上述研究成果获得的解析解只有在孔边才是适用的[12],所以上述研究中的算例也只对孔边应力进行了分析,而没有涉及孔外域,因此存在一定的局限性.笔者[12]曾对这一领域进行了研究,找到了含任意孔形的正交各向异性隧洞应力计算的精确解析方法,并对马蹄形和直墙半圆拱形隧洞进行了孔边应力的分析, 但是,并未对各向异性板中含有一些不规则形状孔等更复杂的孔形进行应力解析分析,对孔边应力集中明显的位置及其孔外域的应力分析也不够全面.
为了研究各向异性板开孔结构应力分布的特殊性,本文选取具有明显尖点的某不规则形状孔和正六角形孔为例,根据带孔正交各向异性板的应力解析解,从板不同的纤维方向、开孔形状和外荷载方向几个方面分析孔边及部分孔外域的应力,并且与各向同性开孔结构进行对比,总结正交各向异性板孔边及孔外域的应力分布规律.不规则孔形在文献[11]中有讨论,但因为其解并未涉及孔外域的应力分布,本文探讨此孔形一方面是进行对比验证,更重要的是对孔外域的应力也进行研究,着重分析应力分布的规律.正六角形孔在工程中应用得也很多,但至今尚未见到其精确的分析结果,其主要原因可能是缺乏可用的高精度的正六角形映射函数.
1 基本方程和应力解析解的求解工程中常用的复合材料结构在很多场合都具有对称性,因此在很多情况下,各向异性的问题都可以化为正交各向异性的问题来讨论.复变函数中的保角变换方法是求解孔洞问题的有效工具,对于正交各向异性问题,求解时涉及3套笛卡尔坐标系:z=x+iy,z1=x+μ1y,z2=x+μ2y,通过建立3套极坐标系ζ=ρeiθ,ζ1=ρ1eiθ1,ζ2=ρ2eiθ2可以将z,z1,z2 3个物理平面的孔外域分别映射到ζ,ζ1,ζ2 3个像平面的单位圆外域,映射函数分别用z=ω(ζ),z1=ω1(ζ1),z2=ω2(ζ2)表示,其中,z=ω(ζ)可以表示为以下Laurent级数的形式[13]:
| $ z = \omega \left( \zeta \right) = R\left( {\zeta + \sum\limits_{k = 0}^\infty {{C_k}{\zeta ^{ - k}}} } \right) $ | (1) |
式中:R和Ck是代表孔的大小和孔形的常数;k为整数.当k取较大的值时,式(1)可以代表足够多的孔形.取k的最大值为n.由于3套笛卡尔坐标系z,z1,z2必须满足如下数学关系[1-2]:
| $ \left\{ \begin{array}{l} {z_1} = x + {\mu _1}y = {\gamma _1}z + {\delta _1}\bar z\\ {z_2} = x + {\mu _2}y = {\gamma _2}z + {\delta _2}\bar z \end{array} \right. $ | (2) |
式中:γ1=(1-iμ1)/2,γ2=(1-iμ2)/2,δ1=(1+iμ1)/2,δ2=(1+iμ2)/2,μ1=α1+iβ1,μ2=α2+iβ2,αk和βk(k=1, 2)是与材料性质有关的材料常数,且β1>0,β2>0.将式(1)代入式(2),并假设3套极坐标系在孔边界所对应的单位圆上满足ζ=ζ1=ζ2=σ=eiθ,可推导出z1=ω1(ζ1)和z2=ω2(ζ2)的表达式和ζ,ζ1,ζ2之间的关系如下[12]:
| $ \left\{ \begin{array}{l} {z_1} = {\omega _1}\left( {{\zeta _1}} \right) = {\gamma _1}R\left( {{\zeta _1} + } \right.\\ \;\;\;\left. {\sum\limits_{k = 0}^n {{C_k}\zeta _1^{ - k}} } \right) + {\delta _1}\bar R\left( {\frac{1}{{{\zeta _1}}} + \sum\limits_{k = 0}^n {{{\bar C}_k}\zeta _1^k} } \right)\\ {z_2} = {\omega _2}\left( {{\zeta _2}} \right) = {\gamma _2}R\left( {{\zeta _2} + } \right.\\ \;\;\;\left. {\sum\limits_{k = 0}^n {{C_k}\zeta _2^{ - k}} } \right) + {\delta _2}\bar R\left( {\frac{1}{{{\zeta _2}}} + \sum\limits_{k = 0}^n {{{\bar C}_k}\zeta _2^k} } \right) \end{array} \right. $ | (3) |
| $ \left\{ \begin{array}{l} {\gamma _1}R\left( {{\zeta _1} + \sum\limits_{k = 0}^n {{C_k}\zeta _1^{ - k}} } \right) + {\delta _1}\bar R\left( {\frac{1}{{{\zeta _1}}} + \sum\limits_{k = 0}^n {{{\bar C}_k}\zeta _1^k} } \right) = \\ \;\;\;\;{\gamma _1}R\left( {\zeta + \sum\limits_{k = 0}^n {{C_k}{\zeta ^{ - k}}} } \right) + {\delta _1}\bar R\left( {\bar \zeta + \sum\limits_{k = 0}^n {{{\bar C}_k}{{\bar \zeta }^{ - k}}} } \right)\\ {\gamma _2}R\left( {{\zeta _2} + \sum\limits_{k = 0}^n {{C_k}\zeta _2^{ - k}} } \right) + {\delta _2}\bar R\left( {\frac{1}{{{\zeta _2}}} + \sum\limits_{k = 0}^n {{{\bar C}_k}\zeta _2^k} } \right) = \\ \;\;\;\;{\gamma _2}R\left( {\zeta + \sum\limits_{k = 0}^n {{C_k}{\zeta ^{ - k}}} } \right) + {\delta _2}\bar R\left( {\bar \zeta + \sum\limits_{k = 0}^n {{{\bar C}_k}{{\bar \zeta }^{ - k}}} } \right) \end{array} \right. $ | (4) |
式(3)对任意形状的孔形都适用,式(4)对域内(|ζ|≥1)任意一点都成立.
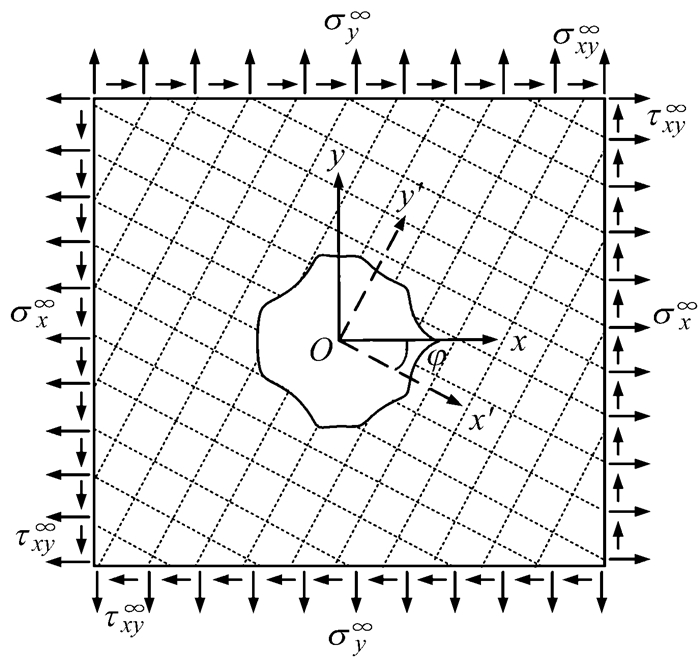
如图 1所示,考虑一个含孔正交各向异性板,承受分布于板边缘并作用在面内的力,孔形关于整体坐标系的x轴对称,局部坐标系x′Oy′沿弹性主向.如果板的尺寸远大于开孔的尺寸,并且开孔不在板边的附近,那么可以假定板无限大.除此之外,假定作用在板内的荷载远大于体力,并且无z方向的分量,此时,体力可忽略不计,问题简化成了无限域中的平面应力问题.根据平衡条件和变形协调条件可以得到应力函数F(x,y)所满足的方程[14]:
| $ \begin{array}{*{20}{c}} {{a_{22}}\frac{{{\partial ^4}F}}{{\partial {x^4}}} - 2{a_{26}}\frac{{{\partial ^4}F}}{{\partial {x^3}\partial y}} + \left( {2{a_{12}} + {a_{36}}} \right)\frac{{{\partial ^4}F}}{{\partial {x^2}\partial {y^2}}} - }\\ {2{a_{16}}\frac{{{\partial ^4}F}}{{\partial x\partial {y^3}}} + {a_{11}}\frac{{{\partial ^4}F}}{{\partial {y^4}}} = 0} \end{array} $ | (5) |
|
图 1 受面内均布荷载作用且带有任意形状孔的正交各向异性板 Fig.1 An orthotropic plate with an arbitrary shaped hole under in-plane loadings |
式(5)的解与特征方程(6)的根有关.
| $ {a_{11}}{\mu ^4} - 2{a_{16}}{\mu ^3} + \left( {2{a_{12}} + {a_{66}}} \right){\mu ^2} - 2{a_{26}}\mu + {a_{22}} = 0 $ | (6) |
式(6)的4个根必为共轭的复根,即μ1, μ1和μ2, μ2,此处的μ1,μ2与式(2)中的相同.
只讨论μ1≠μ2的情形,引入2个解析函数F1(z1)、F2(z2),则式(5)的解可以表示为
| $ F = {F_1}\left( {{z_1}} \right) + \overline {{F_1}\left( {{z_1}} \right)} + {F_2}\left( {{z_2}} \right) + \overline {{F_2}\left( {{z_2}} \right)} $ | (7) |
令Φ1(z1)=dF1(z1)/dz1,Φ2(z2)=dF2(z2)/dz2,这样,求解各向异性板平面应力问题就转化为寻找满足相应的边界条件的应力解析函数Φ1(z1)和Φ2(z2)的问题.
用Φ1(z1)、Φ2(z2)表示的应力边界条件为
| $ \left\{ \begin{array}{l} {\mathit{\Phi }_1}\left( {{z_1}} \right) + \overline {{\mathit{\Phi }_1}\left( {{z_1}} \right)} + {\mathit{\Phi }_2}\left( {{z_2}} \right) + \overline {{\mathit{\Phi }_2}\left( {{z_2}} \right)} = {f_1}\\ {\mu _1}{\mathit{\Phi }_1}\left( {{z_1}} \right) + \overline {{\mu _1}} \overline {{\mathit{\Phi }_1}\left( {{z_1}} \right)} + {\mu _2}{\mathit{\Phi }_2}\left( {{z_2}} \right) + \\ \;\;\;\;\;\;\;\overline {{\mu _2}} \overline {{\mathit{\Phi }_2}\left( {{z_2}} \right)} = {f_2} \end{array} \right. $ | (8) |
式中出现的z1、z2是孔边点.因为讨论的是带孔无限域问题,且孔边无外荷载,则f1 = f2=0,且Φ1(z1)、Φ2(z2)具有以下形式:
| $ \left\{ \begin{array}{l} {\mathit{\Phi }_1}\left( {{z_1}} \right) = {B^ * }{z_1} + \mathit{\Phi }_1^0\left( {{z_1}} \right)\\ {\mathit{\Phi }_2}\left( {{z_2}} \right) = \left( {{{B'}^ * } + {\rm{i}}{{C'}^ * }} \right){z_2} + \mathit{\Phi }_2^0\left( {{z_2}} \right) \end{array} \right. $ | (9) |
式中:实常数B*、B′*、C′*可以通过无限远处的外荷载(σx∞、σy∞、τxy∞)和与材料性质有关的常数(α1、α2、β1、β2)求出[15].
将式(3)的z1=ω1(ζ1)、z2=ω2(ζ2)代入到式(9)中后,Φ10(z1)和Φ20(z2)可整理得出如下形式:
| $ \left\{ \begin{array}{l} \mathit{\Phi }_1^0\left( {{z_1}} \right) = \mathit{\Phi }_1^0\left[ {{\omega _1}\left( {{\zeta _1}} \right)} \right] = \mathit{\Phi }_{1 * }^0\left( {{\zeta _1}} \right) = \sum\limits_{k = 0}^\infty {{a_k}\zeta _1^{ - k}} \\ \mathit{\Phi }_2^0\left( {{z_2}} \right) = \mathit{\Phi }_2^0\left[ {{\omega _2}\left( {{\zeta _2}} \right)} \right] = \mathit{\Phi }_{2 * }^0\left( {{\zeta _2}} \right) = \sum\limits_{k = 0}^\infty {{b_k}\zeta _2^{ - k}} \end{array} \right. $ | (10) |
这里的Φ1*0(ζ1)、Φ2*0(ζ2)分别为单位圆外ζ1和ζ2的解析函数,式中,ak=a1k+ia2k,bk=b1k+ib2k(k=0, …,∞),a1k、a2k、b1k、b2k为待定实数.
因在孔的边界有ζ1=σ=eiθ、ζ2=σ=eiθ,所以应力边界条件式(8)最终可以整理为如下形式:
| $ \left\{ \begin{array}{l} {\mathop{\rm Re}\nolimits} \left[ {\mathit{\Phi }_{1 * }^0\left( \sigma \right) + \mathit{\Phi }_{2 * }^0\left( \sigma \right)} \right] = \\ \;\;\;\; - {\mathop{\rm Re}\nolimits} \left[ {{B^ * }{\omega _1}\left( \sigma \right) + \left( {{{B'}^ * } + {\rm{i}}{{C'}^ * }} \right){\omega _2}\left( \sigma \right)} \right]\\ {\mathop{\rm Re}\nolimits} \left[ {{\mu _1}\mathit{\Phi }_{1 * }^0\left( \sigma \right) + {\mu _2}\mathit{\Phi }_{2 * }^0\left( \sigma \right)} \right] = \\ \;\;\;\; - {\mathop{\rm Re}\nolimits} \left[ {{\mu _1}{B^ * }{\omega _1}\left( \sigma \right) + {\mu _2}\left( {{{B'}^ * } + {\rm{i}}{{C'}^ * }} \right){\omega _2}\left( \sigma \right)} \right] \end{array} \right. $ | (11) |
根据式(3)、式(10)和式(11),采用幂级数解法.将σ-k=cos kθ-isin kθ代入式(11)的左右两边并展开,可根据sin kθ、cos kθ(k=1, ∞)前面的系数相等列出求解ak、bk的线性方程组,具体计算过程略.
所以,一旦正交各向异性板的弹性常数给定,式(6)中的系数就可以确定[15],特征方程的根可解,再根据给定的外荷载,实常数B*、B′*、C′*也可以求得.结合求解的ak、bk,再根据式(9)和式(10),解析函数Φ1(z1)、Φ2(z2)就可以求解.而笛卡尔坐标系下和正交曲线坐标系下的应力分量也可以根据下式进行求解:
| $ \left\{ \begin{array}{l} {\sigma _x} = 2{\mathop{\rm Re}\nolimits} \left[ {\mu _1^2{{\mathit{\Phi '}}_1}\left( {{z_1}} \right) + \mu _2^2{{\mathit{\Phi '}}_2}\left( {{z_2}} \right)} \right]\\ {\sigma _y} = 2{\mathop{\rm Re}\nolimits} \left[ {{{\mathit{\Phi '}}_1}\left( {{z_1}} \right) + {{\mathit{\Phi '}}_2}\left( {{z_2}} \right)} \right]\\ {\tau _{xy}} = - 2{\mathop{\rm Re}\nolimits} \left[ {{\mu _1}{{\mathit{\Phi '}}_1}\left( {{z_1}} \right) + {\mu _2}{{\mathit{\Phi '}}_2}\left( {{z_2}} \right)} \right] \end{array} \right. $ | (12) |
| $ \left\{ \begin{array}{l} {\sigma _\rho } + {\sigma _\theta } = {\sigma _x} + {\sigma _y}\\ {\sigma _\theta } - {\sigma _\rho } + 2{\rm{i}}{\tau _{\rho \theta }} = \left( {{\sigma _y} - {\sigma _x} + 2{\rm{i}}{\tau _{xy}}} \right)\frac{{{\zeta ^2}}}{{{\rho ^2}}}\frac{{\omega '\left( \zeta \right)}}{{\overline {\omega '\left( \zeta \right)} }} \end{array} \right. $ | (13) |
需要注意的是,在通常情况下,正交各向异性板已知的是局部坐标系x′Oy′下材料的主弹性常数(如图 1),由此代入式(6)求得特征方程的根也是局部坐标系下的μ′1和μ′2,当板中的2组纤维分别按照0°和-90.0°交叉布置时(记为[0°/-90.0°]s),整体坐标系与局部坐标系重合,此时,μ1=μ′1,μ2=μ′2;但当纤维角度发生旋转时,例如按照[45.0°/-45.0°]s布置,需要将此μ′1、μ′2代入式(14)中,求出整体坐标系下的μ1、μ2[1],应力求解才能进行.
| $ \left\{ \begin{array}{l} {\mu _1} = \frac{{{{\mu '}_1}\cos \varphi - \sin \varphi }}{{\cos \varphi + {{\mu '}_1}\sin \varphi }}\\ {\mu _2} = \frac{{{{\mu '}_2}\cos \varphi - \sin \varphi }}{{\cos \varphi + {{\mu '}_2}\sin \varphi }} \end{array} \right. $ | (14) |
式中:φ是局部坐标系x′Oy′与整体坐标系xOy的夹角,见图 1.
至此,对于孔的边界,由于ρ=1、ζ1=ζ2=ζ=σ=eiθ,应力分量非常容易求出,而对于ζ≠σ的孔外域点,应力求解稍微复杂一些,必须首先根据式(4)由ζ求出对应的ζ1、ζ2,再根据Φ1(z1)、Φ2(z2)进行应力求解.需要注意的是,由式(4)求出的ζ1、ζ2各有2n个解,但由于映射函数是将物理平面上的孔外域映射到像平面上的单位圆外域,在这2n个解中,只有n个解在单位圆外域.除此之外,再根据物理平面上的2个点映射到像平面上也相邻的原则,可以找出n个解中符合题意的解.
本文得出的结果是适用于任意形状孔形和任意纤维角度的精确解,只要孔的解析函数已知,就可以求出面内荷载作用下孔边及其周围的应力场.
2 算例分析和结果比较 2.1 不规则孔形的孔边切向应力分析对于带有不规则孔形的正交各向异性板,文献[11]中考虑了由石墨-环氧树脂材料(G-E)制成的具有不同纤维方向([0°/-90.0°]s,[45.0°/-45.0°]s)的复合层压板,给出的不规则孔形的映射函数系数Ck为:C3=0.06,C6=0.04,C8=0.03,C9=0.03,其他Ck均为零,特征方程的复根为:当[0°/90.0°]s时, 有μ1=0+3.640 4i,μ2=0+0.274 7i;当[45.0°/-45.0°]s时, 有μ1=-0.859 7+0.510 9i,μ2=0.859 7+0.510 9i.
为了方便进行对比验证和分析,取上述参数与文献[11]完全相同,由于讨论的是无限大平板问题,孔的大小对应力场的求解没有影响,故本文中映射函数的R值直接取为1.0.当板的无穷远处分别单独作用沿x轴或y轴方向的单向均布拉伸荷载时,即图 1中τxy∞=0,而σx∞=σ或σy∞=σ,根据上文介绍的应力解析解的求解方法,通过自编FORTRAN程序,实现该不规则孔形孔边的应力分量的计算,结果如图 2和图 3.由于孔边没有外荷载作用,所以在孔边,径向应力σρ=0,剪应力τρθ=0,故本文图中虚线绘出的都是孔边的切向应力与外荷载的比值σθ/σ的分布,其中,θ是ζ平面的极角.符号规定拉应力为正、压应力为负.

|
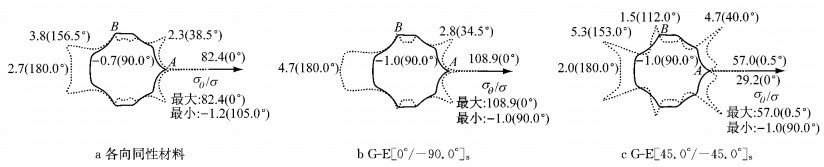
图 2 带有不规则孔形的3种材料结构在σx∞=σ单独作用下的孔边切向应力分布 Fig.2 Distribution of normalized tangential stresses for three kinds of plates with irregular shaped hole under uniaxial loading σx∞=σ |
|
图 3 带有不规则孔形的3种材料结构在σy∞=σ单独作用下的孔边切向应力分布 Fig.3 Distribution of normalized tangential stresses for three kinds of plates with irregular shaped hole under uniaxial loading σy∞=σ |
首先将图 2b、2c和图 3b、3c的结果与文献[11]进行对比验证,发现文献[11]中获得的孔边切向应力的分布规律与本文中的结果基本一致,尤其是θ=0°的点,两者得到的σθ/σ值完全相同.但是本文与文献[11]的结果最大的不同在于,图 3c中最大切向应力的数值是57.0,发生在θ=0.5°的点,但是这个最大值的点却被文献[11]忽略了.
将这2种各向异性材料与各向同性材料进行对比,如图 2和图 3,发现正交各向异性板孔边应力分布的一些特殊规律:对于各向同性材料,在2种单轴拉伸荷载作用下,孔边的最大应力集中发生在θ=0°的尖点位置A,当σx∞=σ单独作用时,在A点产生的是最大压应力,而当σy∞=σ单独作用时,在A点产生的是最大拉应力;但是对于正交各向异性材料,孔边切向应力的最大值可能发生在尖点位置,如图 3b中的尖点A,也可能发生在尖点A的临近位置,如图 3c中θ=0.5°的点.
除此之外,对于正交各向异性材料,当荷载沿x轴方向作用时(σx∞=σ),在与x轴相交的孔边2个点(A点和C点)的切向应力均为压应力,且其大小都为-σ,如图 2b、2c;当荷载沿y轴方向作用时(σy∞=σ),在与y轴相交的孔边2个点的切向应力也均为压应力,且大小也都是-σ,如图 3b、3c.而对于各向同性材料,在2种荷载作用下都没有这样的规律.但是3种材料的相同点是,当荷载作用方向与孔边尖点A的指向(x轴方向)垂直时,如图 3,最大的切向应力集中都是发生在孔边的A处尖点或其临近的孔边点.
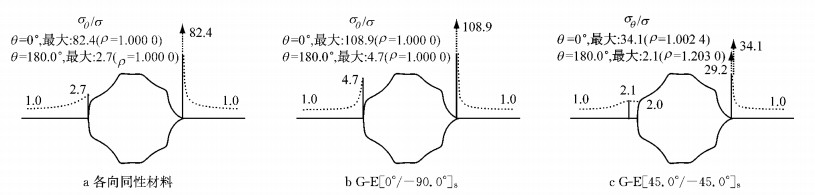
2.2 不规则孔形的孔外域切向应力分析观察图 3发现,在沿y轴方向荷载(σy∞=σ)的作用下,不规则孔形在θ=0°的孔边点其切向应力集中非常明显,为了进一步研究孔外域的应力分布情况,图 4中给出了在θ=0°、180.0°的板内,3种材料结构所对应的切向应力与外荷载的比值σθ/σ,这在文献[11]中并没有研究.
|
图 4 沿y轴单向拉伸荷载作用下(σy∞=σ)不规则孔形在θ =0°、180.0°板内点的切向应力分布 Fig.4 Distribution of normalized tangential stresses in θ=0° and 180.0° for irregular shaped hole with uniaxial loading σy∞=σ |
由图 4可以看出:各向同性材料最大切向应力产生在孔边(图 4a,ρ=1.000 0),而对于正交各向异性材料则不一定,纤维角度按[0°/-90.0°]s布置时,最大切向应力产生在孔边(图 4b,ρ=1.000 0),纤维角度按[45.0°/-45.0°]s布置时,最大切向应力产生在非常临近孔边的外部区域,如图 4c中可以清晰地看出:在ρ=1.002 4对应的孔边右侧点,σθ/σ达到最大值34.1,而在ρ=1.000 0的孔边点,σθ/σ只有29.2;在ρ=1.203 0对应的孔边左侧点,σθ/σ达到最大值2.1,而在ρ=1.000 0的孔边点,σθ/σ为2.0.
2.3 正六角形孔的孔边切向应力分析所研究的正六角形孔的映射函数系数Ck为[13]:C5=0.066 7,C11=0.010 1,C17=0.003 6,C23=0.001 8,C29=0.001 0,其他Ck均为零.材料参数的取值与上文中不规则孔完全相同,故特征方程的根也相同.R的值仍为1.0.将各向同性材料与上述2种正交各向异性材料进行对比,图 5和图 6分别用虚线绘出了沿x轴或y轴荷载作用下(σx∞=σ,σy∞=σ)正六角形孔的孔边切向应力与外荷载的比值σθ/σ的分布.

|
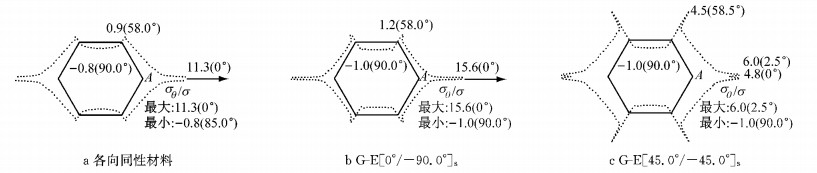
图 5 带有正六角形孔的3种材料结构在σx∞=σ单独作用下的孔边切向应力分布 Fig.5 Distribution of normalized tangential stresses for three kinds of plates with hexagon hole under uniaxial loading σx∞=σ |
|
图 6 带有正六角形孔的3种材料结构在σy∞=σ单独作用下的孔边切向应力分布 Fig.6 Distribution of normalized tangential stresses for three kinds of plates with hexagon hole under uniaxial loading σy∞=σ |
分析图 5和图 6可以看出:各向同性材料的孔边最大切向应力发生在尖点处,如图 5a中θ=60.0°的B点和图 6a中θ=0°的A点.但是对于正交各向异性材料,孔边产生最大切向应力的位置既可能是在尖点处,如图 6b的尖点A处,也可能是在尖点的附近点,如图 5b中尖点B附近θ=62.0°的点、图 5c中尖点B附近θ=59.5°的点、图 6c中尖点A附近θ=2.5°的点.除此之外,分析图 6还可以看出,当荷载作用方向与孔边尖点A的指向(x轴方向)垂直时,3种材料最大切向应力都发生在孔边A处尖点或者其临近的孔边点.这与图 3中不规则孔形的规律完全相同.
将图 2和图 3中不规则孔形的孔边应力分布与图 5、图 6中正六角形孔的结果进行对比分析发现:当3种材料结构的平板受沿y轴方向的单向拉伸时,在y轴与孔边界的交点及其附近的孔边区域,切向应力均为压应力,尤其对于2种正交各向异性板,在y轴与孔边界的交点,即θ=90.0°的点,切向应力值都是-σ;同样,当荷载是沿x轴方向拉伸时,在x轴与孔边界的交点及其附近的孔边区域,切向应力也均为压应力,而2种正交各向异性板中x轴与孔边界的交点(θ=0°的点)切向应力值也都是-σ.
2.4 孔边最大切向应力点位置的确定为了进一步研究正交各向异性板在y方向荷载σy∞=σ单独作用下孔边最大切向应力发生的位置,针对上述2种孔形,计算其他纤维角度工况下孔边的切向应力与外荷载的比值σθ/σ.不同纤维角度条件下,孔边产生最大切向应力的位置(θ角)及其最大应力值(σθ/σ)max与尖点(θ=0°)处应力值的对比见表 1.
| 下载CSV 表 1 纤维角度不同时整体坐标系下的复根μ1,μ2以及孔边最大切向应力(σθ/σ)max与尖点处(θ=0°)应力的对比 Tab.1 The complex roots μ1, μ2 in the global coordinates and the comparison of the maximum normalized tangential stress σθ/σwith the stress in the sharp corner (θ=0°) for different fiber orientation angles |
图 7给出了纤维的旋转方向和其中一种工况([10.0°/-80.0°]s)的示意图.由于孔形和荷载的对称性,纤维在[0°/-90.0°]s和[45.0°/-45.0°]s范围内的角度变化包含了纤维发生旋转时所有可能的布置情况,而不同纤维角度的布置对应的整体坐标系下特征方程的根μ1、μ2可以根据式(14)求出,结果见表 1.

|
图 7 纤维角度按[10.0°/-80.0°]s布置的示意图 Fig.7 Sketch of the fiber orientation angles at [10.0°/-80.0°]s |
由表 1可见:对于2种孔形,仅当y方向作用有荷载时,纤维角度按[0°/90.0°]s布置,最大的切向应力产生在尖点A(θ=0°);但当纤维角度稍微发生旋转时,最大切向应力的发生位置逐渐偏离A点,其中,不规则形状孔的偏离幅度较小,最远达到θ= 0.5°的点,而正六角形孔的偏离幅度最远达到θ=2.5°的点;除此之外,随着纤维角度从[0°/90.0°]s向[45.0°/-45.0°]s旋转,2种孔形对应的最大切向应力值逐渐减小.无论是不规则形状孔还是正六角形孔,正交各向异性板纤维角度的改变对孔边以及孔外域的切向应力集中都会产生很大的影响,在以后的研究中,可以针对纤维角度进行优化设计的研究,以使孔边和孔外域都获得较小的应力集中.
3 结论(1) 在单向均布荷载作用下,各向同性材料孔边产生最大切向应力的位置是尖点处,而正交各向异性材料则不一定.
(2) 当单向均布荷载的作用方向与孔边尖点的指向垂直时,纤维角度按[0°/-90.0°]s布置会使最大的切向应力产生在尖点处(θ=0°);但是随着纤维角度的旋转,最大应力点的位置逐渐偏离尖点,最大切向应力的数值也逐渐减小.
(3) 各向同性材料产生最大切向应力的位置在孔边,而正交各向异性材料则不一定,当单向拉伸荷载的方向与尖点指向垂直时,最大切向应力可能是在孔边(纤维按[0°/-90.0°]s角度布置),也可能是在孔外部的临近区域(纤维按[45.0°/-45.0°]s角度布置).
(4) 正交各向异性板切向应力的集中程度也与材料的纤维方向有很大的关系,通过调整材料纤维的方向可以获得孔边或者孔外区域较小的应力集中.
(5) 当无限平板中均布的单向拉伸荷载σ沿某坐标轴方向作用时,该坐标轴与孔边界的交点及其附近的孔边区域,切向应力均为压应力.尤其对于正交各向异性板,在该坐标轴与孔边界的交点,切向应力均为-σ.
| [1] |
LEKHNITSKⅡ S G. Anisotropic plates[M]. New York: Gordon and Breach, 1968
|
| [2] |
LEKHNITSKⅡ S G. Theory of elasticity of an anisotropic body[M]. Moscow: Mir Publishers, 1981
|
| [3] |
DAOUST J, HOA S V. An analytical solution for anisotropic plates containing triangular holes[J]. Composite Structures, 1991, 19(2): 107 DOI:10.1016/0263-8223(91)90018-T |
| [4] |
UKADGAONKER V G, RAO D K N. Stress distribution around triangular holes in anisotropic plates[J]. Composite Structures, 1999, 45(3): 171 DOI:10.1016/S0263-8223(99)00024-0 |
| [5] |
SHARMA D S. Stress distribution around circular/elliptical/ triangular holes in infinite composite plate[J]. Engineering Letters, 2012, 20(1): EL_20_1_01 |
| [6] |
REZAEEPAZHAND J, JAFARI M. Stress analysis of composite plates with non-circular cutout[J]. Key Engineering Materials, 2008, 385-387: 365 DOI:10.4028/www.scientific.net/KEM.385-387 |
| [7] |
RAO D K N, BABU M R, REDDY K R N, et al. Stress around square and rectangular cutouts in symmetric laminates[J]. Composite Structures, 2010, 92(12): 2845 DOI:10.1016/j.compstruct.2010.04.010 |
| [8] |
SHARMA D S. Stresses around polygonal hole in an infinite laminated composite plate[J]. European Journal of Mechanics-A/Solids, 2015, 54: 44 DOI:10.1016/j.euromechsol.2015.06.004 |
| [9] |
李成, 郑艳萍. 不同孔口形状对含孔复合材料板孔边应力状态影响的研究[J]. 工程力学, 2007, 24(10): 19 LI Cheng, ZHENG Yanping. Influence of different orifice figure on hole-edge stress of composite material plate with hole[J]. Engineering Mechanics, 2007, 24(10): 19 DOI:10.3969/j.issn.1000-4750.2007.10.004 |
| [10] |
PATEL N P, SHARMA D S. On the stress concentration around a polygonal cut-out of complex geometry in an infinite orthotropic plate[J]. Composite Structures, 2017, 179: 415 DOI:10.1016/j.compstruct.2017.07.037 |
| [11] |
UKADGAONKER V G, KAKHANDKI V. Stress analysis for an orthotropic plate with an irregular shaped hole for different in-plane loading conditions—Part 1[J]. Composite Structures, 2005, 70(3): 255 DOI:10.1016/j.compstruct.2004.08.032 |
| [12] |
LU A Z, ZHANG N, ZHANG X L, et al. Analytic method of stress analysis for an orthotropic rock mass with an arbitrary-shaped tunnel[J]. International Journal of Geomechanics, 2015, 15(4): 04014068 DOI:10.1061/(ASCE)GM.1943-5622.0000408 |
| [13] |
吕爱钟, 张路青. 地下隧洞力学分析的复变函数方法[M]. 北京: 科学出版社, 2007 LÜ Aizhong, ZHANG Luqing. Complex function method on mechanical analysis of underground tunnel[M]. Beijing: Science Press, 2007 |
| [14] |
萨文. 孔附近的应力集中[M]. 卢鼎霍, 译. 北京: 科学出版社, 1958. SAVIN G N. Stress concentration around holes[M]. Translated by LU Dinghuo. Beijing: Science Press, 1958. |
| [15] |
陈子荫. 围岩力学分析中的解析方法[M]. 北京: 煤炭工业出版社, 1994 CHEN Ziyin. Analytical method of rock mechanics analysis[M]. Beijing: China Coal Industry Publishing House, 1994 |
 2018, Vol. 46
2018, Vol. 46

