2. 上海城市建设设计研究总院, 上海 200125
2. Shanghai Urban Construction Design Research Institute, Shanghai 200125, China
对于超高、大跨工程结构而言,风荷载引起的结构振动可对结构的安全性造成严重威胁,风荷载是此类结构的设计控制因素[1],对风荷载的监测、分析、建模以及对结构风效应的分析,不仅是结构前期规划设计的重点难题之一,而且也是建成结构服役期安全性能评估的一项重要内容[2].
已有风功率谱从能量的频域分布角度描述了紊流脉动风的特性,它只反映了脉动风速的二阶数据特征,本质上,丢失了包括相位在内的更丰富的概率信息,难于完全还原脉动风的随机性原貌[3].因此,使用已知风功率谱产生模拟风速时程,常常需要用到谐波合成法(WAWS法、CAWS法)[4-5]或线性回归滤波器法[6],但这些方法不能同时在计算效率和计算精度上满足要求.因此,如果能采用幅值谱和相位谱的方式来表征脉动风速,不仅可以忠实地保留脉动风速的全面统计特性,从而在使用时得到更加接近真实的风速模拟时程,而且可以大大降低模拟计算的工作量.文献[7]在2007年利用实测数据拟合得到了基于Fourier的随机风幅值谱,证明了幅值谱在反映脉动风统计特性方面的优势.
由于在实测数据谱估计结果时发现相位谱在全频域范围内符合在[-π, π]上均值为零的均匀分布,故只需得到脉动风幅值谱的表达式,即可得到模拟风速时程.本文根据量纲分析法,给出一般化的风速幅值谱经验表达式,利用PSO算法结合实测风幅值谱对其参数进行估计,研究一个全面包含脉动风随机统计特性的幅值谱模型,以及此模型的3种具体使用方法.
1 脉动风的幅值谱经验表达式根据Kolmogrov理论,频域内的脉动风速功率谱可以写成如下经验表达式:
| $ S\left( {z, n} \right) = \frac{{Au_*^2{f^\gamma }}}{{n{{\left( {1 + B{f^\alpha }} \right)}^\beta }}} $ | (1) |
式中:S(z, n)表示距地面z高度处的脉动风功率谱, n为频率;A和B为常数;α,β和γ为谱的幂指数,三者满足关系式αβ-γ=2/3;u*表示摩阻速率,可由式(2)得到:
| $ {u_*} = {u_z}k/\ln \left( {{z_0}/z} \right) $ | (2) |
其中uz为距地面z高度处的脉动风平均风速, k为Von Karman常数,通常取为0.4, z0为地面粗糙度;f为莫宁(Molin)坐标,可取如下形式[8].
当
当f=1 200n/u10时,对应于Davenport功率谱.
当
根据平稳随机信号的功率谱、幅值谱定义,其单边功率谱S(z, n)与幅值谱U(z, n)的关系如下:
| $ S\left( {z, n} \right) = \frac{1}{T}E\left[{{U^2}\left( {z, n} \right)} \right] $ | (3) |
式中:T为时间,按照中国规范取600 s.
记幅值谱均值为E(U(z, n)),幅值谱标准差为Std(U(z, n)).显然,U2(z, n)、E(U(z, n))2、Std(U(z, n))2与幅值谱的均方期望值E[U2(z, n)]具有相同的量纲,也就是说,U(z, n)、E(U(z, n))、Std(U(z, n))与
| $ U\left( {z, n} \right) = \frac{{C{u_*}{f^{0.5\gamma }}}}{{\sqrt n {{\left( {1 + D{f^\alpha }} \right)}^{0.5\beta }}}} $ | (4) |
式中:C、D为待求系数;f与式(1)一致,当f取不同形式,对应于不同的脉动风幅值谱形式.摩阻速率u*和Molin坐标f均为随机变量,因此经验幅值谱U(z, n)是随机变量.可通过实测得到的幅值谱样本来拟合经验幅值谱.
2 经验风谱模型的具体表达式选取 2.1 实测脉动风速幅值谱上海地区某桥是一座公轨两用一体化双层特大桥,位于上海市黄浦江上游闵行—奉贤段.该桥的结构健康监测系统监测内容综合考虑桥梁结构特点,选择了多种监测目标,共有测点172个,其中风速风向测点有2个,分别位于塔顶与主跨跨中,其中塔顶150 m,跨中29 m(吴淞零点高程),均小于当地梯度风高度,采样频率为4 Hz,采用不间断采样方式监测作用在结构上的风速.
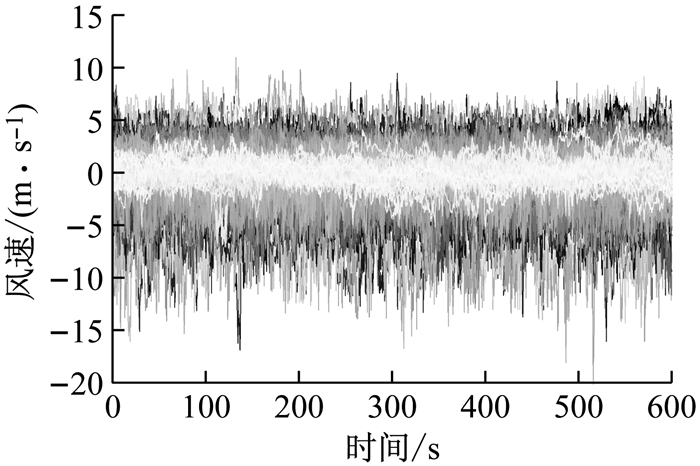
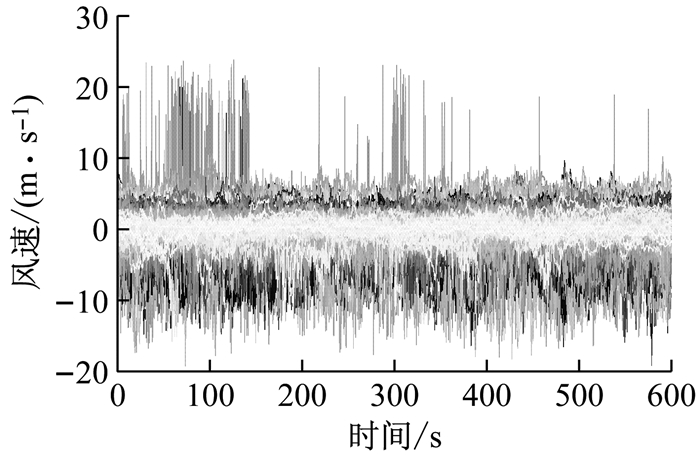
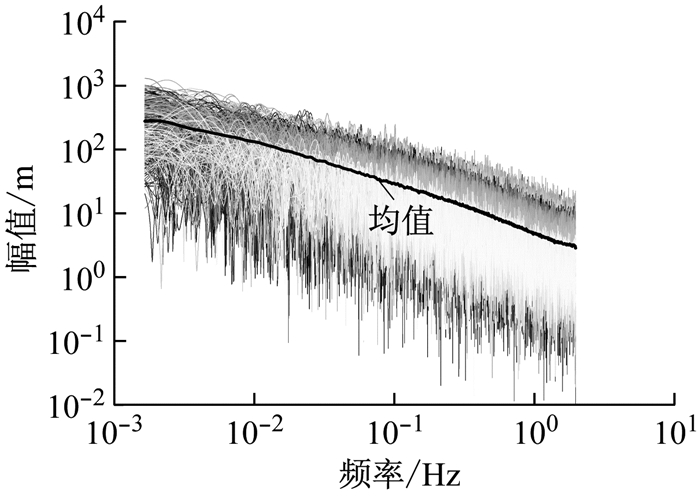
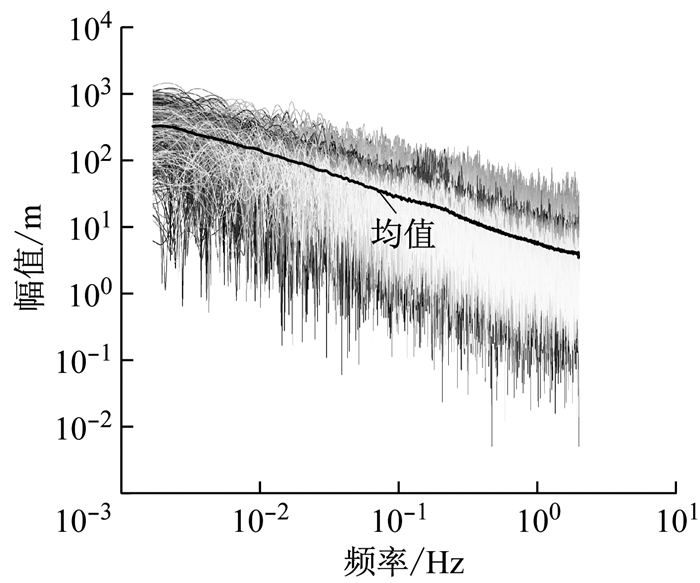
根据交通部规范文献[9]规定的10 min为平均风时距,将2016年1月份至3月份监测得到的风速数据分解为13 104个样本,每个样本包括塔顶与跨中2组数据.应用文献[10]中的方法对数据进行筛选,得到了1 014组可供应用的平稳风速数据,如图 1、图 2所示.通过矢量分解法[11]得到水平脉动风速数据,并采用APES(amplitude and phase estimation)法[12-13]估计出脉动风速的幅值谱.APES谱估计方法是一种高精度的非参数谱估计方法,通过构造观测数据的Hankel矩阵,将指定频率处的幅值问题转化为一个最佳滤波器问题,根据文献[13]给出的最佳滤波器设计,得到时程信号对应的幅值谱与相位谱估计,结果如图 3、图 4所示.
|
图 1 跨中平稳脉动风样本时程曲线 Fig.1 Time history of stationary fluctuating wind velocity in the middle of the span |
|
图 2 塔顶平稳脉动风样本时程曲线 Fig.2 Time history of stationary fluctuating wind velocity at the top of the tower |
|
图 3 跨中脉动风速幅值谱 Fig.3 Fluctuating wind velocity amplitude spectra in the middle of the span |
|
图 4 塔顶脉动风速幅值谱 Fig.4 Fluctuating wind velocity amplitude spectra at the top of the tower |
式(4)中给出的经验幅值谱具体表达形式取决于Molin坐标的表达式,可通过比较实测幅值谱的谱线与式(4)经验幅值谱的谱线来确定.但是由于式(4)中的系数均是未知的,没有办法进行直接比较.而已有的风谱模型均为功率谱形式,多数模型中的系数已通过大量研究得以确定,部分已成为规范中的标准模型.因此,可以将监测数据得到的功率谱曲线与规范中的标准风功率谱曲线进行比较,来选取合适的经验幅值谱表达形式.实测脉动风功率谱可通过式(3)求得.
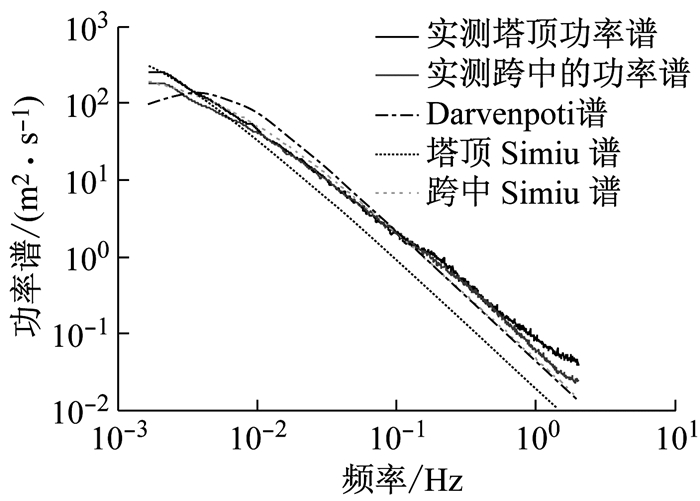
以加拿大抗风设计手册[14]采用的Davenport谱以及中国规范[9]采用的Simiu谱为例,图 5给出了上述二者谱曲线与本文监测数据得到的斜拉桥塔顶和跨中2处的脉动风功率谱的谱曲线对比情况.
|
图 5 实测脉动风功率谱与已有规范中脉动风功率谱的比较 Fig.5 Comparison between measured fluctuating wind velocity power spectra and the spectra in the specifications |
由图 5可知,实测得到的塔顶风功率谱与跨中风功率谱除了在低频和高频区各一小段内有差异外,在其余大部分频段内,二者基本吻合,这说明本桥所在地区的脉动风呈现与高度无关的特性.这不仅与Davenport谱的与高度无关的规律相同,而且,除在低频区与其有较大误差外,在其余频段二者基本吻合;而Simiu谱在理论上与高度有关,尽管其跨中功率谱与实测结果较为接近,但塔顶功率谱与实测结果相差较大.
可见,通过调整Davenport功率谱经验表达式的参数可以改善其与实测功率谱曲线的吻合程度,从而使其具备表达本地区脉动风功率谱的能力;而对于Simiu功率谱,无论对其模型参数如何调整,均不可能很好地拟合本文实测风功率谱表现出的高度无关的特性.这说明,Davenport经验功率谱形式更适于描述与本地区脉动风功率谱特性.据此可推断,Davenport形式的经验幅值谱表达式也应该更适于描述本地区脉动风的幅值谱特性.本文针对Davenport形式的经验幅值谱模型展开,用实测得到的风幅值均值谱和标准差谱来估计经验幅值谱模型的参数,以期建立适于桥址地区风场的经验幅值谱模型.
3 Davenport形式的经验幅值谱参数确定 3.1 PSO算法简介PSO(particle swam optimization)是群集智能方法的一种,由Kennedy等[15]于1995年提出,通过模拟蚁群、鸟群、鱼群等的寻径行为,从而找到问题的最优解.
PSO用于参数优化问题的具体实现方式为, 在一个d(参数个数)维目标搜索空间中,随机生成n个粒子组成的粒子群,粒子的位置表示为:xi=(xi1, xi2, …, xid), i=1, 2, …, n,粒子的速度表示为:vi=(vi1, vi2, …, vid), i=1, 2, …, n,每个粒子由位置和速度决定其飞行的速度和方向,同时由目标函数决定的适应函数来评价每个个体的优劣程度.
粒子更新方程可表示为
| $ \begin{array}{l} {v_{ij}}\left( {k + 1} \right) = {v_{ij}}\left( k \right) + {\rm{rand}}\left( {} \right) \cdot \left( {{p_{{\rm{beast}}, ij}}-x_{ij}^k} \right) + \\ \;\;{\rm{rand}}\left( {} \right) \cdot \left( {{g_{{\rm{beast}}, ij}}-x_{ij}^k} \right)\\ {x_{ij}}\left( {k + 1} \right) = {x_{ij}}\left( k \right) + {v_{ij}}\left( {k + 1} \right) \end{array} $ |
式中:k代表迭代次数,视问题复杂程度而定;rand()为0~1之间的随机数;pbest与gbest为文献[15]中定义的能反应个体最优与全局最优的解.为了保证全局搜索能力,一般都会为vij设定一个范围[16].经过若干次迭代或已满足收敛条件,即可得到参数优化问题的最优解.
3.2 Davenport经验幅值谱参数确定由于Davenport形式的经验幅值谱与高度无关,故将测得的塔顶与跨中的脉动风速幅值谱取平均后作为实测脉动风速幅值谱对其进行参数优化.
取Molin坐标的形式为f=1 200n/u10.同时,取z=10,uz=u10,将式(2)给出的摩阻速率代入式(4),可得到Davenport形式的经验幅值谱表达式
| $ U\left( n \right) = \frac{{{C_1}k{u_{10}}{{\left( {\frac{{1200n}}{{{u_{10}}}}} \right)}^{{C_3}{C_4}- 1/3}}}}{{\ln \left( {\frac{{10}}{{{z_0}}}} \right){{\left[{1 + {C_2}{{\left( {\frac{{1200n}}{{{u_{10}}}}} \right)}^{{C_3}}}} \right]}^{{C_4}}}\sqrt n }} $ | (5) |
由于与高度无关,因此可将U(z, ω)简记为U(n).同时,为了参数估计的便利,特将原式(4)中的参数C、D、γ、α和β统一改写为待识别参数C1、C2、C3和C4.
通过实测随机风幅值谱样本估计上述模型的参数,本质上是一个多参数优化问题,即寻找一组待识别参数C1、C2、C3和C4,使得拟合得到的经验幅值谱的均值与标准差均尽可能靠近实测风幅值谱均值和实测幅值谱标准差.为此,可定义谱曲线误差为
| $ \mathit{\Delta = }\left| {{{\hat U}^m}\left( n \right)-E\left( {U\left( n \right)} \right)} \right| + \left| {{{\tilde U}^m}\left( n \right)-{\rm{Std}}\left( {U\left( n \right)} \right)} \right| $ | (6) |
式中:
采用PSO算法进行若干次寻优迭代,得到的参数C1、C2、C3和C4的优化结果代入式(5),得到最终的Davenport经验幅值谱模型如下:
| $ U\left( n \right) = \frac{{601.4u_{10}^{0.6138}{n^{- 0.1138}}}}{{\ln \left( {\frac{{10}}{{{z_0}}}} \right){{\left[{1 + 19.28{{\left( {\frac{n}{{{u_{10}}}}} \right)}^{0.3846}}} \right]}^{1.8709}}}} $ | (7) |
上式给出的经验幅值谱模型由于同时满足了均值和标准差2个方面与实测风的逼近,因此该模型至少能够反映实际风幅值的一、二阶概率特性.采用该式,可以得到包括均值和标准差在内的较为全面的随机风幅值信息.这也是本文建议的经验幅值谱的第1种用法.
3.3 Davenport经验幅值均值谱与经验幅值标准差谱参数确定在实际使用中,得到随机参数u10和z0的信息较为困难,但其均值
| $ \hat U\left( n \right) = \frac{{1300 \cdot \hat u_{10}^{0.4876} \cdot {n^{0.5124}}}}{{\ln \left( {\frac{{10}}{{{{\hat z}_0}}}} \right){{\left[{1 + 47.04{{\left( {\frac{n}{{{{\hat u}_{10}}}}} \right)}^{0.4750}}} \right]}^{1.7805}}}} $ | (8) |
| $ \tilde U\left( n \right) = \frac{{2704 \cdot \hat u_{10}^{0.4029} \cdot {n^{0.5971}}}}{{\ln \left( {\frac{{10}}{{{{\hat z}_0}}}} \right){{\left[{1 + 17.82{{\left( {\frac{n}{{{{\hat u}_{10}}}}} \right)}^{0.4006}}} \right]}^{2.3225}}}} $ | (9) |
通过式(8)、式(9)也可以得到随机风场的主要概率特性,可据此模拟随机风速信号.这就是本文建议的第2种经验幅值谱使用方式,即经验幅值均值谱和经验幅值标准差谱的组合使用方式.
4 Davenport经验幅值谱的概率特性 4.1 风谱模型与实测结果的数值对比由于式(7)是用实测风幅值谱均值和幅值谱标准差拟合得到的随机模型,其随机性来自于随机变量u10和z0.拟合的效果如何,可以通过均值、标准差和指定频率线处的数据分布情况予以考察.为此,将1 014组u10和z0随机样本代入式(7),得到1 014个经验幅值谱样本,进而得到其均值和标准差.同时,直接用均值
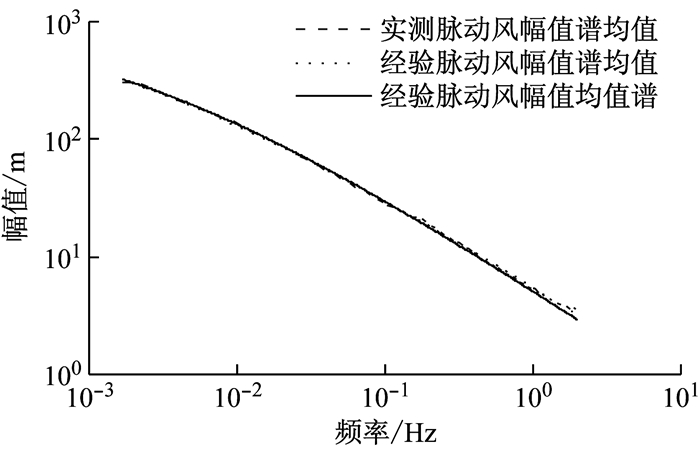
实测幅值谱均值、经验幅值谱均值和经验幅值均值谱的对比曲线如图 6给出,可见,在所有频率范围内,三者均吻合得非常好,这说明通过式(7)和式(8)均可以得到较为准确的幅值谱均值,也说明本文给出的经验幅值谱从一阶矩角度很好地逼近了实际风速幅值概率特性.
|
图 6 风谱模型与实测数据的均值对比 Fig.6 Mean value comparison between fluctuating wind velocity amplitude spectrum model and measurement result |
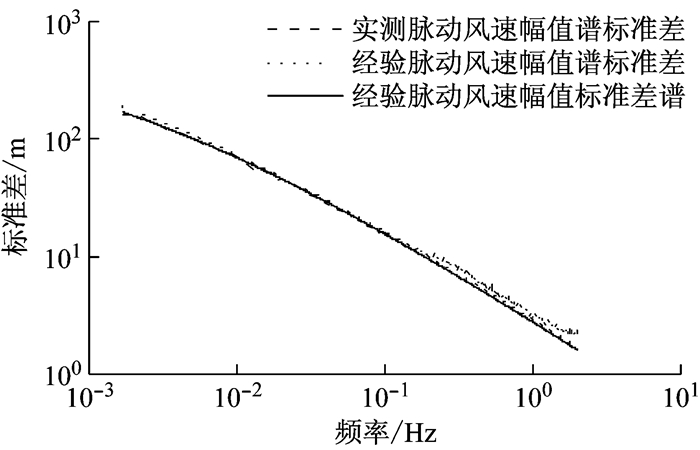
图 7给出实测幅值谱标准差、经验幅值谱标准差和经验幅值标准差谱的频域对比曲线.由图可见,三者曲线在整个频域范围内均较好地吻合.这说明,无论是采用经验幅值谱,还是采用近似的经验幅值标准差谱,均能很好地描述实际风速幅值的二阶特性.
|
图 7 风谱模型与实测数据的标准差对比 Fig.7 Standard deviation comparison of fluctuating wind velocity amplitude spectrum and measurement result |
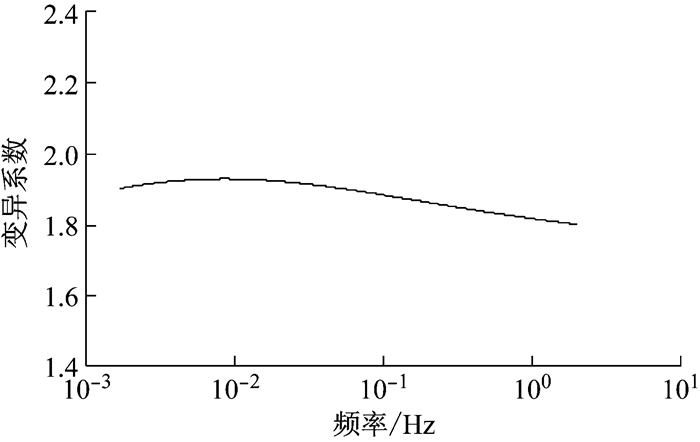
定义经验变异系数δ为经验幅值均值谱与经验幅值标准差谱的比值,其在频域的分布情况在图 8中给出.由图可以看出,δ在整个频域内基本保持不变,其平均值为1.884 7.这说明,只需通过式(8)计算得到风幅值均值谱,然后将其值除以δ,也可以近似得到相应的标准差,这就是建议的第3种经验幅值谱使用方式.
|
图 8 变异系数曲线 Fig.8 Variation coefficient curve |
进一步考察经验幅值谱的概率分布情况.图 9分别给出频率为0.005, 0.1, 1 Hz时的实测风幅值数据分布频数和经验幅值谱给出的分布频数图,3个频率分别代表低频区、中频区和高频区,图中横轴为量纲一化的幅值,定义为幅值与均值的比值,表示了风幅值的分布情况.从这3个图中可以看出,经验幅值谱给出的量纲一化的频数分布和实测风幅值频数分布较为一致,在3个频率处均为先急剧上升再急剧下降的趋势,与对数正态分布较为吻合.
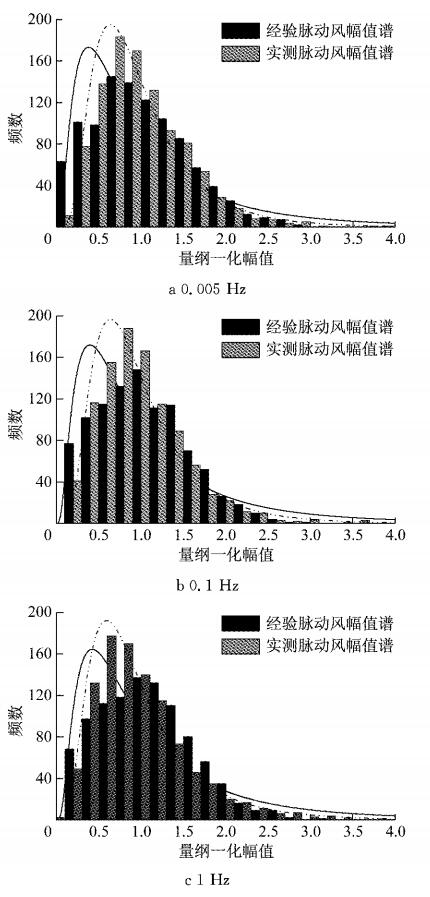
|
图 9 脉动风幅值分布频数 Fig.9 Histogram of amplitude |
为了进一步考察给出经验幅值谱的全频域取值分布情况,在每一个频率线处给出估计幅值的均值和上下1倍标准差,得到如图 10所示的曲线.可见,经验幅值谱的均值线、上下1倍标准差线在双对数坐标轴下呈现基本平行下降趋势,与实测风幅值谱的全频率分布规律一致.这说明,本文建议的经验幅值谱模型在全频率区域内能够很好地描述实际风幅值谱的概率分布规律.
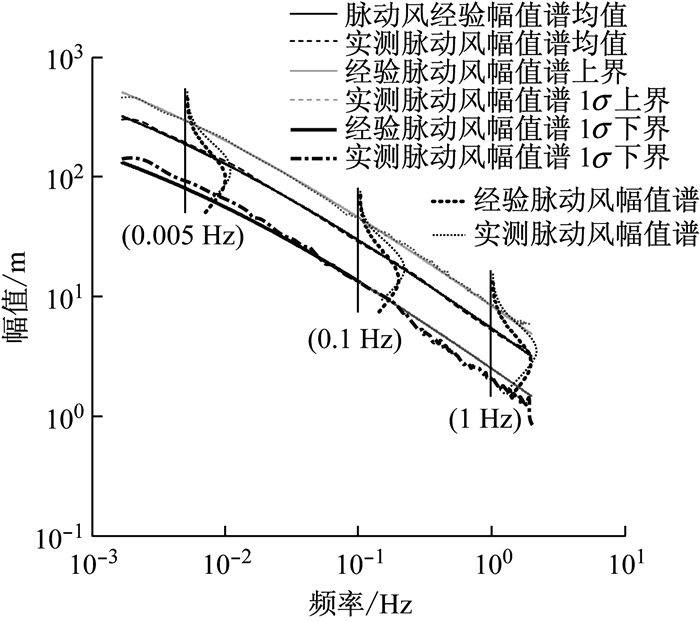
|
图 10 经验幅值谱在全频域与实测数据对比 Fig.10 Comparison between empirical amplitude spectrum and measurement result in full frequency region |
根据给出的脉动风幅值谱、幅值均值谱、幅值标准差谱以及幅值在各频率处的分布情况,脉动风速时程可表示为
| $ u\left( t \right) = \sum {U\left( n \right)\sin \left( {2{\rm{ \mathsf{ π} }}nt + {\varphi _n}} \right)} $ | (10) |
式中:φn为[-π, π]上均值为零的均匀分布;U(n)则有如下3种确定方式.
(1) 已知10 m处风速u10与地面粗糙度z0全部统计特性时,采用经验幅值谱(式(7))即可得到U(n)的概率信息.
(2) 仅知10 m处风速均值
(3) 仅知
对于工程结构风致效应分析和结构抗风设计而言,不适当的风谱模型会导致不精确的分析结果和不适当的结构设计方案.对于地区个性化的风场,采用实际监测信息建立的风谱模型,比采用规范给出的模型更具备针对性和准确性.通过量纲分析建议经验幅值谱模型,并根据实测得到的脉动风幅值谱数据,估计了Davenport经验幅值谱的具体参数;在此基础上,给出了3种具体的经验幅值谱使用方式,可供不同已知条件下风谱模型建模使用.
通过对经验幅值谱的统计特性研究,表明文中建议的随机风幅值谱模型可以从一阶矩、二阶矩和全频域统计分布方面准确描述当地风场的统计特性,弥补已有的功率谱形式的风谱模型的不足,为提高地区风荷载建模精度、改进新建结构风工程设计质量、提高既有结构抗风安全性评估的准确性提供参考.
| [1] |
DAVENPORT A G. How can we simplify and generalize wind loads?[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1995, 54(94): 657 |
| [2] |
CAMPBELL S, KWOK K C S, HITCHCOCK P A, et al. Field measurements of natural periods of vibration and structural damping of wind-excited tall residential buildings[J]. Wind & Structures An International Journal, 2007, 10(5): 401 |
| [3] |
李杰, 张琳琳. 脉动风速功率谱与随机Fourier幅值谱的关系研究[J]. 防灾减灾工程学报, 2004, 24(4): 363 LI Jie, ZHANG Linlin. A study on the relationship between turbulence power spectrum and stochastic Fourier amplitude spectrum[J]. Journal of Disaster Pnevention & Mitigation Engineering, 2004, 24(4): 363 |
| [4] |
SHINOZUKA M, JAN C M. Digital simulation of random processes and its applications[J]. Journal of Sound & Vibration, 1972, 25(1): 111 |
| [5] |
SHINOZUKA M. Simulation of multivariate and multidimensional random processes[J]. Journal of the Acoustical Society of America, 1971, 49(1): 357 |
| [6] |
SPANOS P D, MIGNOLET M P. Simulation of homogeneous two-dimensional random fields: Part Ⅱ——MA and ARMA models[J]. Journal of Applied Mechanics, 1992, 59(2S): S270 DOI:10.1115/1.2899500 |
| [7] |
李杰, 张琳琳. 实测风场的随机Fourier谱研究[J]. 振动工程学报, 2007, 20(1): 66 LI Jie, ZHANG Linlin. Research on the random Fourier spectrum of observational wind[J]. Journal of Vibration Engineering, 2007, 20(1): 66 |
| [8] |
项海帆. 现代桥梁抗风理论与实践[M]. 北京: 人民交通出版社, 2005 XIANG Haifan. Modern theory and practice on bridge wind resistance[M]. Beijing: China Communications Press, 2005 |
| [9] |
中华人民共和国交通部. 公路桥梁抗风设计规范: JTG/T D60-01—2004[S]. 北京: 人民交通出版社, 2004. Ministry of Transport of the People's Republic of China. Wind-resistent design specification for highway bridges: JTG/T D60-01—2004[S]. Beijing: China Communications Press, 2004. |
| [10] |
胡晓红, 葛耀君, 庞加斌. 上海"派比安"台风实测结果的二维脉动风谱拟合[J]. 结构工程师, 2002(2): 41 HU Xiaohong, GE Yaojun, PANG Jiabin. The fitting of 2d fluctuating wind spectrum for the actual measurement data of "PBA" typhoon in Shanghai[J]. Structural Engineers, 2002(2): 41 |
| [11] |
徐安, 傅继阳, 赵若红, 等. 土木工程相关的台风近地风场实测研究[J]. 空气动力学学报, 2010, 28(1): 23 XU An, FU Jiyang, ZHAO Ruohong, et al. Field measurements of typhoons according to civil engineering research[J]. ACTA Aerodynamica Sinica, 2010, 28(1): 23 |
| [12] |
LI J, STOICA P. An adaptive filtering approach to spectral estimation and sar imaging[J]. IEEE Transactions on Signal Processing, 1996, 44(6): 1469 DOI:10.1109/78.506612 |
| [13] |
STOICA P, LI H, LI J. A new derivation of the apes filter[J]. IEEE Signal Processing Letters, 1999, 6(8): 205 DOI:10.1109/97.774866 |
| [14] |
MEYER C, HUGLO M, PHILLIPS N C. Canadian structural design manual. National Building Code of Canada, Supplement Number 4, Publication No. NRC11530 of the National Research COUNCIL, Ottawa, Canada, 1970.
|
| [15] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]//IEEE International Conference on Neural Networks. New York: IEEE Xplore, 1995: 1942-1948.
|
| [16] |
余岭, 万祖勇, 朱宏平, 等. 基于POS算法的结构模型修正与损伤检测[J]. 振动与冲击, 2006, 25(5): 37 YU Ling, WAN Zuyong, ZHU Hongping, et al. Structural model updating and damage detection through particle swarm optimization[J]. Journal of Vibration & Shock, 2006, 25(5): 37 |
 2018, Vol. 46
2018, Vol. 46

