临床路径是医生、护士和其他人员共同制定的针对某病种所做的最适当的有顺序性和时间性的整体服务计划,目的是使患者获得最佳的服务,减少康复的延迟和资源的浪费[1].通过临床路径模型的建立和分析可以发现诊疗系统中存在的瓶颈问题,同时可以对临床路径的执行实施监控,对临床路径管理具有重大意义.临床路径执行过程中产生的事件日志中包含大量的信息,是建立临床路径模型的数据来源,因此从事件日志中挖掘相关知识,将信息形成可用的流程,并在此基础上对临床路径进行建模分析是亟待解决的问题.
对于临床路径进行建模,首先需要从事件日志中提取信息,得到完整的诊疗流程,这需要采用过程挖掘(process mining)算法发掘诊疗流程.过程挖掘是从实际事件日志中,运用过程挖掘算法,发现、监控和改进实际业务流程的思想.过程挖掘可以深入分析诊疗活动之间可能存在的关系,不遗漏事件日志中任何出现的活动,并且可以自身反复验证结果,从而得到一个完整的流程.过程挖掘思想最早由Cook等[2]提出,Agrawal等[3]将其引入工作流领域,并正式命名为过程挖掘.Herbst等[4]提出3个可以判断重名任务的过程挖掘算法,在过程挖掘上更加深入了一步.对于过程挖掘算法的研究,以Aalst等[5]提出的α算法最为全面,目前已经衍生成一系列算法:α+[6]、α++[7]、α#[8]、α*[9]以及Tsinghua-α[10]算法.α系列算法是基于工作流网络(workflow net,WF-net)的行为推理算法,该系列算法不仅可以发掘事件日志中不同活动之间的顺序、并行、因果等基础关系,同时对事件日志中存在的非自由选择、重复活动等特殊关系也有着相当完善的处理.α系列算法都是建立在事件日志中没有噪声且事件日志中活动按照有序排列的前提假设基础上.当事件日志中存在较多无规律噪声的时候,α系列算法往往会出现过拟合和准确度下降的情况.
临床路径模型是对临床路径整个流程的抽象化模型,用物理模型的方式将临床路径中诊疗活动、资源、信息等关系表达出来.临床路径模型是对诊疗流程分析的基础,也是实现临床路径管理的根本,因此模型的准确性和完整性十分重要[1].对于临床路径建模的研究主要分为2个方向:基于Petri网建模和基于UML建模.在实际的运用中,由于Petri网更加直观,更加符合使用人员的直观思维,同时Petri网是工作流最为常用的建模方法,因此对于临床路径建模研究主要集中在Petri网模型上.文献[11]将保存在数据库中的文本诊疗常规转换为工作流过程描述语言(WPDL)模型和Petri网,分析诊疗常规的实施效果,验证了模型的行为正确性.文献[12]提出利用一种临床路径典型语言PROforma对临床路径进行建模,并将临床路径转化成着色Petri网络.文献[13]提出一种基于分层赋时着色Petri网对复杂病种建立临床路径模型的方法,实现了对诊疗状态、信息流转及诊疗活动间关系的可视化监控,并基于仿真结果给出了资源配置建议.文献[14]在[13]的研究基础上做出改进,在对临床路径建模时,修改和新增部分与时间相关的参数和函数,增设费用相关变量及函数,对临床路径的住院时间和诊疗费用进行了定量分析.
综上所述,目前对于临床路径建模研究主要存在以下2个问题:第一,建模研究往往立足于已经存在的诊疗流程之上,并不能实现从事件日志中得到临床路径模型.第二,目前常用的过程挖掘算法对于噪声的控制并不好,而在实际事件日志中的噪声数据总是存在且不可控制的.因此需要首先给出一个可以消除噪声干扰并且能保证算法准确度的过程挖掘算法,再将其同Petri网模型集成,得到一个基于过程挖掘算法的临床路径Petri网.两者集成不仅可以从事件日志中直接提取知识得到完善的工作流程,而且可以将临床路径转换成临床路径Petri网络,同时保证了模型准确率和建模效率.
本文提出了一种基于统计α算法的临床路径Petri网模型,将过程挖掘算法和Petri网络进行集成,实现了对于临床路径事件日志知识抽取,得到临床路径完善的诊疗流程,并据此建立Petri网模型,进行从事件日志到Petri网模型的转换.
1 基于统计α算法的临床路径Petri网建模方案提出的基于统计α算法的临床路径Petri网建模方案如图 1所示,包括算法挖掘和建模过程两块.过程挖掘将输入的事件日志通过重名活动判别和统计α算法2个步骤得到活动关系矩阵及相关临床路径知识.建模过程将Petri网和统计α算法以及临床路径的特征集成得到临床路径Petri网模型(CP-net).接着将已经得到的活动关系矩阵和临床路径知识融入已经得到的CP-net模型中,得到针对该病种的CP-net模型,进一步可以对模型进行可达性、结构完整性和行为完整性的分析,并对该临床路径的完善程度进行考察.

|
图 1 基于统计α算法的临床路径Petri网建模方案 Fig.1 Scheme of clinical pathway Petri net modeling based on statistical α-algorithm |
过程挖掘是从大量的事件日志中挖掘活动之间的关系,得到一个由这些活动关系组成的工作流.因此,过程挖掘是实现事件日志到工作流模型的重要工具,通过过程挖掘算法对于临床路径事件日志的分析,才能得到完整的临床路径的工作流程,进而建立CP-net模型.在过程挖掘中,对于活动之间关系的定义是整个算法的基础,活动关系的定义如表 1所示[5].
| 下载CSV 表 1 活动关系定义 Tab.1 Definition of activity relations |
统计α算法以活动对为识别的噪声最小单位,在创建活动对集合Array(AC)时计算每个活动对的频率,在数据量较大时,用频率估计活动对的概率.在利用统计α算法进行活动对关系判断之前,筛选出现概率低于显著性水平的活动对,并将其从Array(AC)删除,不在最终的结果中出现.噪声在事件日志中具体有3种体现:①小概率随机活动的增加.由于该活动是低概率的,其组成的活动对必然也是低概率的,按照规则将从Array(AC)删除.②小概率活动的替换.同样地,被替换的活动是低概率的,其组成的活动对也会被删除.③小概率的活动缺失.活动对缺失会出现新的活动对,而该活动同样是低概率的,因此也会被删除,从而消除活动缺失带来的噪声影响.算法具体步骤图如2所示.
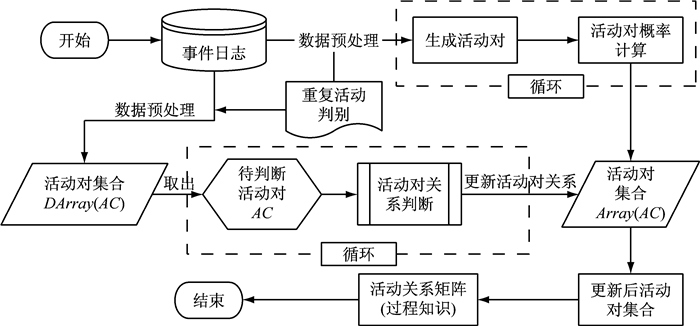
|
图 2 统计α算法流程 Fig.2 Procedure of statistical α-algorithm |
步骤1:活动对定义.统计α算法以活动对为单位,活动对的定义如下.
定义1 对于任意病种的一个事件日志W,假设有流程轨迹δi={…, Ti, Ti+1, …}W,流程轨迹中的元素按照执行时间的先后顺序排列.其中任意2个相邻的活动Ti和Ti+1及其出现的次数组成一个结构体,称为活动对(activities couple,AC).具体定义如下.
Structure活动对{
String FA,第一个活动名称(Ti);
String SA,第二个活动名称(Ti+1);
int F,出现次数=1;
String R,活动关系=顺序关系(默认);
}
步骤2:活动对概率统计.遍历事件日志中的所有流程轨迹可得一个由不同活动对组成的活动对集合,记作Array(AC).计算活动对集合Array(AC)中每个活动对的出现概率.考虑到重名活动的存在,可得活动对AC(Ti, Ti+1)的概率为
| $ P(AC({T_i}, {T_{i + 1}})) = \frac{{AC({T_i}, {T_{i + 1}}).F}}{{N{n_r}}} $ |
式中:AC(Ti, Ti+1).F为活动对AC(Ti, Ti+1)的出现次数,如果在活动对集合Array(AC)中不存在AC(Ti, Ti+1),则AC(Ti, Ti+1).F=0;N为流程轨迹数; nr=nr(Ti)+nr(Ti+1)等于活动Ti和活动Ti+1重名活动的数目总和.
步骤3:检索需要判断活动关系的活动对.对于任意病种的流程轨迹来说,顺序关系是出现次数最多的活动关系[10].对于可以确定为顺序关系的活动对,不需要对其进行二次判断.为了简化活动关系的判断流程,减少判断活动对的数目,需要对活动对进行筛选.以流程轨迹为单位,纵向比较每条预处理后的流程轨迹,排除可以确定为顺序关系的活动对,得到一个活动关系待定的活动对集合,记作DArray(AC),显然DArray(AC)
步骤4:判断活动对关系.利用统计α算法进行活动对活动关系判断时需要考察与该活动对相关的活动对,因此这里给出与之相关的2个活动对的定义,即同前活动对和转置活动对.
定义2 同前活动对:对于任意活动对AC(A, B),若存在一个活动对和它有相同的第1个活动A,第2个活动不同,则称为AC(A, B)的同前活动对,记作#AC(A, B).
定义3 转置活动对:对于任意活动对AC(A, B),若存在一个活动对的第1个活动等于它的第2个活动,第2个活动等于它的第1个活动,则称为AC(A, B)的转置活动对,记作-AC(A, B).
结合上述定义,这里给出统计α算法,如下.
Input Wd//事件日志, α//显著性水平
Output Matrix[Array(AC)]//活动关系矩阵
1. Foreach(σi in Wd)
σi←{T1, T2, …, Tj, Tj+1, …}//赋值
j : 1→σi.Length
If (AC(Ti, Ti+1) is exist)then
AC(Ti, Ti+1).F++//活动对频数
Else
AC(Ti, Ti+1).FA←Ti
AC(Ti, Ti+1).SA←Ti+1
P(AC(Ti, Ti+1))=
Array(AC).Add(AC(Ti, Ti+1))//向活动对集合中添加元素,得到原始活动对集合
2. Foreach(σ in Wd)
σi←A1, A2, …, Aj, Aj+1, …//构造轨迹
σk←B1, B2, …, Bj, Bj+1, …//构造轨迹
j : 1→σi.Length
If(Aj≠Bj)
DArray(AC).Add(AC(Aj, Aj+1))
DArray(AC).Add(AC(Aj-1, Aj))
End
Output DArray(AC)
3. Foreach (AC in DArray(AC))
AC←AC(A, B)
#AC(A, B)←AC(A, C)//同前活动对
-AC(A, B)←AC(B, A)//转置活动对
If (P(AC(A, C))> α) then
Dim AC(B, C)
If (P(AC(B, C))> α) then
If (P(AC(B, C))> α) then
B||wC
Else
B#wC
Else
B#wC
A>wB, A>wC
Else
If (P(AC(B, A))> α) then
A||wB
Else
A→wB
End.
Output Matrix[Array(AC)]//活动关系矩阵
2.2 重名活动判别规则在事件日志的某一条流程轨迹中,某一活动可能多次出现,但是每次代表的具体含义可能并不相同.因此在活动关系判断之前,需要对这类活动进行区分,为了方便描述这一类活动,这里给出2个定义.
定义4 在任一条流程轨迹中,若活动A出现一次以上,则该活动称为重名活动(cognominal activities).为了区分同一条流程轨迹中的重名活动,用记号δi(A, ni)表示在流程轨迹δi中第ni个活动A[9].
定义5 重名活动根据其具体活动内容是否相同分为2种:活动内容相同的称为重复性重名活动,简称重复活动(duplicate activities,DA); 活动内容不同的称为非重复性重名活动(homonyms activities,HA).提出重名活动判别规则是为了将重名活动区分为DA和HA,并对2类重名活动进行不同处理,以消除HA对过程挖掘的影响.
为了提高重名活动判断效率,将任意活动A的2个前驱活动TP、TPP和2个后继活动TS、TSS组成的有序集合{TPP, TP, A, TS, TSS}记作一个活动组(activities group),记作GA,并以活动组作为重名活动判别的基本单位对重名活动进行判别.
为了进一步确定重复活动的定义,这里引用Herbst等[4]对于重名活动和重复活动的定义,采用试验来探索定义.Herbst等提出的重名活动称为“非独特活动”指的是在一个模型中多次出现的具体活动.重名活动定义基于文献[9]中的定义,以整个事件日志为对象来寻找重名活动,而Herbst更加着眼于模型中的重名活动.Herbst对于重复活动的定义更加符合实际应用场景中的定义,因此本文在正式提出重复活动定义之前,通过试验将假设与Herbst的结果进行对比,确保了本文中重复活动定义的可靠性.试验采用内蒙古某三甲医院2010年3月到10月之间7个月的若干病种的事件日志数据,以活动组为单位,分析4个病种,共510条流程轨迹.通过统计发现,当2个重名活动对应的2个活动组中的元素对应相等,即活动组中的元素和元素顺序都相同时,根据Herbst等[4]对于重复活动的定义可知,这2个重名活动是重复活动的概率高达99.7%.因此可以得到以下重复活动的定义.
定义6 对于任意流程轨迹δi∈W,如果δi中存在重名活动δi(A, n), δi(A, m)∈δi,且两者对应的活动组分别为GA和G′A,若GA和G′A中除了活动A之外的其他活动对应相等,则活动δi(A, n)和活动δi(A, m)可以定义为重复活动.
定义7 对于任意流程轨迹δi∈W,如果δi中存在重名活动δi(A, n), δi(A, m)∈δi,且两者对应的活动组分别为G′A和GA,若GA和G′A中包含的除了A之外的元素相同,但元素排列顺序不同,则称为2个活动组相等,记作GA=G′A.
对于任意流程轨迹δi∈W,如果δi中存在重名活动δi(A, n), δi(A, m)∈δi,TP和TS分别是活动δi(A, n)的前驱任务和后继任务,TPP为TP的前驱活动,TSS为TS的后继活动; T′P和T′S分别是活动δi(A, m)的前驱任务和后继任务,T′PP为T′P的前驱活动,T′SS为T′S的后继活动.活动δi(A, n)和活动δi(A, m)对应的活动组分别为GA和G′A,U为重复活动集合,则有以下结论.
(1) 若GA=G′A,TP=T′P且TS=T′S,则〈δi(A, n), δi(A, m)〉
(2) 若GA=G′A,TP=T′P,TS≠T′S,TS=TSS,且TSS=T′S,则〈δi(A, n), δi(A, m)〉
(3) 若GA=G′A,TP≠T′P,TS=T′S,TP=T′PP,且TPP=T′P,则〈δi(A, n), δi(A, m)〉
(4) 若GA=G′A,TP≠T′P,TS≠T′S,TP=T′PP,TPP=T′P,TS=T′SS,且TSS=T′S则〈δi(A, n), δi(A, m)〉
(5) 若GA≠G′A,TP=T′P,TS≠T′S且TS#wT′S,则〈δi(A, n), δi(A, m)〉
(6) 若GA≠G′A,TP≠T′P,TS=T′S且TP#wT′P,则〈δi(A, n), δi(A, m)〉
(7) 若GA≠G′A,TP≠T′P,TP#wT′P,TS≠T′S且TS#wT′S,则〈δi(A, n), δi(A, m)〉
(8) 若GA≠G′A,TP≠T′P,TP#wT′P,TS≠T′S,TS=T′SS且TSS=T′S,则〈δi(A, n), δi(A, m)〉
(9) 若GA≠G′A,TS≠T′S,TS#wT′S,TP≠T′P,TP=T′PP且TPP=T′P,则〈δi(A, n), δi(A, m)〉
提出的过程挖掘算法集成了重复活动判别和统计α算法,具体算法实施步骤,如图 3所示,可以分为以下步骤:

|
图 3 基于重名活动判别和统计α算法的过程挖掘方案 Fig.3 Scheme of process mining that based on statistical α-algorithm and cognominal activity identification |
(1) 原始数据的筛选.获取数据库中结构完整、数据量较大的完备事件日志.
(2) 工作分解结构.将事件日志中的工作流按照其阶段、内容分成若干部分,从而可以减少每一部分包含的活动数目,降低算法运行时间,提高准确度.
(3) 数据预处理.将事件日志中的活动进行重命名排序操作,为重复活动判别做准备.
(4) 重复活动判别.以流程轨迹为单位,对其中出现的重名活动进行分析,根据分析结果重新修正活动命名,为活动关系识别做准备.
(5) 活动关系识别.采用本文提出的统计α算法,提取工作流程知识,分析活动之间的依赖关系,得到活动关系矩阵.
(6) 得到结果并修正.根据上一步骤中得到的活动关系矩阵,并将模型问题还原到实际问题之中.
3 基于过程挖掘算法的临床路径Petri网模型临床路径是一种特殊的工作流,工作流与Petri网有着天然的契合关系,因此建立临床路径的Petri网模型可以形象地将临床路径流程表现出来.通过Petri网可达性、完整性等属性的分析,可以分析临床路径在执行中存在的问题、可能出现的瓶颈,Petri网模型使得临床路径管理更加便捷.临床路径Petri网的定义可以在工作流网络(WF-net)[5]的基础上加以修改实现.在临床路径中,将病人看作唯一实体,病人的工作流是整个临床路径中的唯一工作流,下面给出临床路径Petri网(CP-net)的定义.
定义7 令CP-net=(P, T; F, K, W, M0),其中N=(P, T; F)是一个WF-net,称为CP-net的基网,是构成CP-net的最基本内容.P为库所集,对应病人状态.T为变迁集,对应临床诊治操作; F为流关系,F=(P×T)∪(T×P).K为N上的容量函数,规定了每个位置上的最大令牌数,该容量必须为有限值,可认为是临床路径上医生、护士、器材、药物等资源.W为流关系上的权函数,对应到临床路径之中,可以认为权函数规定了诊疗活动开展的资源等条件.M0为CP-net的初始标识,标定了病人的初始状态.WF-net是CP-net的基础,是模型的基本框架,在WF-net中包含了所有的诊疗活动、病人状态和流关系.CP-net是工作流网的拓展,把临床路径中的相关条件和资源融入其中.在进行过程挖掘时,主要还是以工作流网为对象,首先从事件日志中挖掘出工作流模型,再从事件日志和相关医疗资料中挖掘诊疗信息,最后在模型形成阶段将诊疗信息融入其中形成CP-net.
CP-net需要满足以下5条约束:
(1) 起止唯一性:有且仅有一个pi∈P满足·pi=
(2) 无孤性:不存在p∈P,使得·p∩p·=
(3) 有界性:对于
(4) 无死锁:对于
(5) 无活锁:对于最终库所po,M(po)=W(·po, po),保证最终托肯数量为零.在临床路径中一旦到达病人最终状态,不再进行该病种的任何诊疗活动.如果后续其他活动出现,则判定为路径跳转.
基于统计α算法的过程挖掘算法是建立CP-net的基础和前提,通过过程挖掘算法发掘事件日志中活动的相互关系,进而得到整个诊疗流程,形成最终的CP-net模型.本文采用的过程挖掘算法是结合了重复活动判别的统计α算法,通过将统计α算法与CP-net结合,可以使CP-net直接使用事件日志中的信息,能消除事件日志中的噪声数据,使得CP-net模型更加准确.在本文使用的统计α算法中,对于活动关系的判断以活动对为单位,因此需要首先给出活动对在CP-net中的定义.
定义8 对于CP-net=(P, T; F, K, W, M0),
定义9 对于CP-net=(P, T; F, K, W, M0),
表 1给出了过程挖掘判断的活动基本关系类型:顺序、因果、并行和选择.这些活动关系是过程挖掘算法的主要结果,因此需要先将这些关系同Petri网结合起来.这里引入工作流Petri网(WF-net)中的特殊节点AND-split/join和OR-split/join,描述活动之间关系如图 4所示.图 4a至4c分别用图形化的形式表达了顺序、并行和选择关系,对于包括因果关系的4个基本活动关系这里给出如下的定义.

|
图 4 活动关系Petri网描述 Fig.4 Description of activity relation in Petri net |
定义10 令CP-net=(P, T; F, K, W, M0),U是重复活动集合,
(1) 若a·∩·b≠
(2) 若a·∩·b=
(3) 若OR-split∈·a∩·b∧OR-join∈a·∩b·,则a#wb(选择关系)
(4) 若AND-split∈·a∩·b∧AND-join∈a·∩b·则a||wb(并行关系)
本文提出的统计α算法是以活动对为单位进行活动关系判断的算法,基于对“同前活动对”、“转置活动对”和活动对概率的计算,这里给出基于统计α算法的Petri网描述.
令W为活动集合T上的事件日志,给定显著性系数为α,统计α算法α定义如下:
(1) XW={AC(a, b)|
(2) DXW={AC(a, b)|
(3) TW={t∈T|t∈AC, AC.P≥α}
(4) Ti={t∈T|
(5) To={t∈T|
(6) PW={p(a, b)|(a, b)∈XW}∪{iW, oW},
| $ P\left( {a, b} \right) = \left\{ \begin{array}{l} 1, {\rm{ }}当\;a{ > _w}b或\;a{ \to _w}b\\ 2, 当\;a = AND{\rm{ - split}}\\ OR - {\rm{split/join}}, 当{\# _w}b \end{array} \right. $ |
(7) FW={(a, p(a, b))|a∈AC(a, b)∈DXW}∪{b, p(a, b))|b∈AC(a, b)∈DXW}∪{(a,
(8) α(W)={PW, TW, FW}
在上述定义中,XW代表着所有活动对的集合,活动对出现概率需要包含在XW之中.DXW则表示存在着差异的活动对集合,相对于上文中的DArray(AC).TW代表所有活动的集合,这些活动出现概率必须高于显著性系数,否则以噪声方式过滤掉,TW是CP-net中所有变迁的集合.Ti和To分别是流程轨迹δ∈W的起始活动和终止活动的集合,根据Ti和To设置起止库所iW和oW.PW是CP-net中所有库所的集合,P(a, b)表示变迁a和变迁b之间的库所,库所和变迁直接的连接方式如图 5所示,因此P(a, b)可能不止一个库所,当变迁a, b是顺序关系或者是因果关系时,P(a, b)的数量为一; 而当a, b是并行关系时,变迁a, b的前一个变迁为AND-split节点,此时a, b变迁与其之间则各有一个库所存在; 而当a和b是选择关系时,a和b的库所则为OR-split节点.FW是CP-net中所有流关系的集合,统计α算法得到的CP-net主网络则主要由{PW, TW, FW}三者组成.
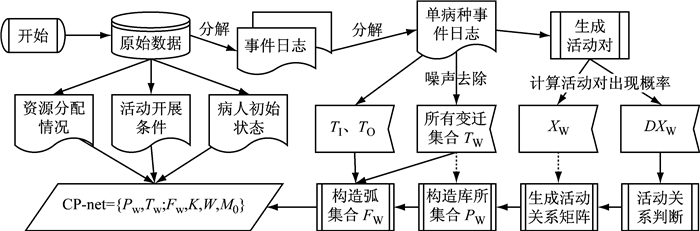
|
图 5 基于过程挖掘算法的临床路径Petri网建模过程 Fig.5 Procedure of clinical pathway modeling based on process mining |
根据上述定义,如图 5给出基于过程挖掘算法的临床路径Petri网建模步骤.
(1) 得到事件日志.从原始数据开始,首先需要获得构建CP-net必需的事件日志,这是过程挖掘的基础,也是CP-net主体网络的基本构成.
(2) 得到活动关系矩阵.对于每个单病种事件日志,首先按照定义生成活动对,得到活动对集合XW,同时计算每个活动对的出现概率,据此按照规则去除噪声数据得到变迁集合TW.接下来通过比对得到待判断活动对集合DXW以及活动每条流程轨迹的起始和终止变迁集合Ti和To.对于集合DXW,需要通过遍历该集合,利用统计α算法识别每一个活动对的活动关系,结合XW集合中已知的活动对关系,构造活动关系矩阵.
(3) 构造主网络.在得到的活动关系矩阵以及变迁集合TW基础上按照α(W)定义的第6条生成相应的库所集合PW,并由PW、TW、Ti和To得到主网络的流关系集合FW.
(4) 构造CP-net.在主网络形成之后,根据原始数据中对资源的分配得到容量函数K,根据每项诊疗活动的开展条件得到流关系的权函数W,根据病人的初始状态得到CP-net的初始标识M0,由此便得到最终的CP-net模型.
4 试验与结果分析为了验证算法和模型的有效性,试验分为2个部分,第一部分采用仿真数据分析和比较统计α算法与经典的α算法以及α+算法在准确度、拟合度和运行时间上的差异[15].同时利用其中一组数据进行建模,分析模型的可达性、结构完整性和行为完整性等指标.第二部分利用从医院采集到的真实临床数据进行建模,评价模型的可达性、结构完整性和行为完整性等指标.
4.1 仿真数据试验采用文献[16]中给出的仿真数据生成方法,生成了如表 2中的4组数据,每组数据中都包含了顺序、因果、选择和并行4种关系,分别从事件日志的轨迹长度、轨迹数目和噪声数目3个层面考察2种算法的性能表现.算法准确度和运行时间结果分别如图 6和图 7所示.
| 下载CSV 表 2 仿真数据信息 Tab.2 Details of simulate data |

|
图 6 算法准确度对比 Fig.6 Comparison of accuracy |

|
图 7 算法运行时间比较 Fig.7 Comparison of runtime |
根据图 6可以看到,不论仿真数据轨迹长度、轨迹数目和噪声数目如何变化,经典α算法和α+算法在各种参数上结果相近.统计α算法在准确度上总是好于经典α算法和α+算法,从多组试验对比来看,统计α算法准确度总是比经典α算法和α+算法高3%~4%左右,在准确度上有明显的优势.根据图 8可以看到,随着轨迹数目的增加,统计α算法在运行时间上明显优于经典α算法和α+算法; 而随着噪声数目和轨迹长度的增加,2个算法在运行时间上不相上下; 因此在第1组的试验中,大多数情况下统计α算法在运行时间上优于经典α算法.
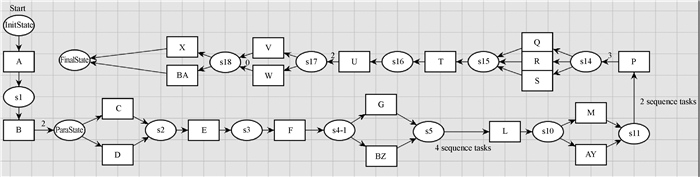
|
图 8 仿真数据Z1的Petri网模型(部分)截图 Fig.8 Petri net model of data Z1(part) |
为了分析2种算法运行时间上的差异,这里给出算法的时间复杂度分析:假设有一个轨迹数目为n、轨迹平均长度为m的事件日志,可以将该日志看作一个m×n的矩阵.对于统计α算法而言,首先需要遍历事件日志得到活动对集合Array(AC),并计算每个活动对的出现概率,此过程需循环(m-1)n次,在得到活动对集合后,计算每个活动对的具体活动关系,判断过程中不再包含循环结构,只有若干次选择结构(假设为k次),因此统计α算法的总循环次数为kn(m-1)2.而对于经典α算法而言,由于没有以活动对为基本单位,因此共需要对整个矩阵循环2次,总循环次数为n2m(m-1).因此,当轨迹程度不变时,统计α算法运行时间随着轨迹数目的增加线性增加,而经典α算法则是幂增加,在n较大时,统计α算法在运行时间上明显优于经典α算法.而在轨迹数目不变时,轨迹程度的变化对于2种算法的运行时间影响并不大.
对于过程挖掘算法评价的另一个常用指标是拟合度.拟合度用来反映过程挖掘结果模型对原始数据的拟合程度.在算法结果中噪声较多时,模型往往会出现拟合程度过高而超过100%的情况,过拟合同样是不理想的情况.拟合度越接近100%,结果越好.同样对于上述4组仿真数据进行试验,可以得到表 3中的结果.
| 下载CSV 表 3 算法拟合度对比 Tab.3 Comparison of fitness |
α系列算法由于其对噪声的消除不够,因而常常出现过拟合的问题.而统计α算法在进行活动关系判断之前,将其中的噪声进行消除,而这种消除的方式则是通过对于活动概率的统计进行的,因此,统计α算法的结果在拟合度上往往接近100%.
对第3组仿真数据进行建模试验,将算法中得到的活动关系矩阵转化为CP-net模型.对于模型的分析指标主要有3个:结构完整性、行为完整性和可达性[14].其中结构完整性衡量了模型对于有意义的活动的包含程度,越高越好; 行为完整性则是为了衡量模型中活动关系的准确性和完整性; 可达性是Petri网模型不发生死锁的衡量标准.图 8是仿真数据Z1的模型部分截图,分析模型可得到如下结果:
(1) 结构完整性.通过对模型和事件日志中活动的对比,该模型并没有包含仿真数据中出现的所有活动,根据计算,该模型的拟合度为98.2%,若对照对仿真数据Z1中噪声的设定,该模型几乎没有包含任何噪声信息,很好地消除了事件日志中的噪声.
(2) 行为完整性.这里重点考察仿真数据中添加的特殊结构.该模型由于其对于因果关系没有直接的体现,因此在因果关系方面略有不足.但是对并行、选择等关系模型都能精准地表现出来.
(3) 可达性.通过对于关键结构点的托肯分布以及变迁使能条件的分析,该模型可达率为100%.
表 4是对Z1至Z5这5个仿真数据建模分析的结果.可以看到该模型在结构完整性和可达率上都达到了一个较高的水平,行为完整性由于因果关系在模型中没有直接的展现,所以数据并不算太好,但是也达到了α系列算法的平均水平.
| 下载CSV 表 4 仿真数据Petri网建模分析结果 Tab.4 Analysis of Petri net model for data |
临床路径建模试验的数据来自内蒙古某三甲医院2010年7月到12月锁骨骨折病种的事件日志,为了减少试验的计算时间,这里选取了锁骨骨折手术监护期的数据.该部分数据流程轨迹平均长度为60,重复活动有5对,事件日志中共有156条流程轨迹.
首先,分别使用统计α算法、经典α算法和α+算法对事件日志进行分析,得到算法结果如表 5所示.可以看到,结合了重复活动判别的统计α算法在准确度上明显优于经典α算法和α+算法,同时由于统计α算法对于噪声的消除,拟合度上也没有出现过拟合的现象,总体优于经典α算法和α+算法.
| 下载CSV 表 5 算法结果对比 Tab.5 Comparison of results |
接下来利用CPN Tools软件对算法结果进行CP-net建模分析,得到图 9的CP-net模型图.分析模型可以得到如下结果:

|
图 9 锁骨骨折手术监护期临床路径Petri网模型截屏 Fig.9 The Petri net model of clavicle fracture |
(1) 结构完整性.不同于仿真数据中噪声随机的产生,该日志经过人工分析,噪声存在于事件日志中活动偶尔出现的缺失和错位,噪声量并不大,因此最终得到的模型在拟合度方面表现很好,结构完整性高达99.3%.
(2) 行为完整性.首先,该病种的事件日志中,存在着5对重名活动,模型准确地将重名活动识别出来,并分辨出其中一对为非重复性重名活动,重名活动判别准确率为100%.其次,该事件日志中存在的特殊关系较多,模型成功识别并表达出3处并行结构和2处选择结构,对于并行结构和选择结构的识别准确率为100%.对于因果关系该模型同样没有直接表现出来,属于模型欠缺的地方.通过模型还可以发现,最后一处的选择结构为2层选择结构的嵌套,对于该处的选择结构可以进行如下理解:在手术完成后并经过基本护理后,需要对病人的状态进行询问和定义,若病人状态良好让病人正常休息、正常进食即可完成整个临床路径; 若病人出现身体疼痛等生理问题,需要进行“疼痛护理”活动,为病人缓解病痛; 若病人出现心理不安,则需要进行“心理护理”活动,为病人缓解压力.总之,该模型对于特殊活动关系的反映率达到了90%.
(3) 可达性.该模型不存在死锁之处,短循环也存在着循环次数的限制,可达率为100%.
总之,基于统计α算法的临床路径Petri网络模型在结构完整性和可达性上有很好的表现.尽管在行为完整性上,对于因果关系的表达并不直接,但是因果关系在实际的临床路径执行过程中同顺序关系区别不大,因此整个模型对于实际医院的运作依然具有较好的指导意义.通过对于具有完整数据的CP-net模型进行分析,可以得到如下结果:①通过模型建立、实现从事件日志的流程重构至得到实际临床路径与标准路径中的区别,发现诊疗异常; ②通过托肯分布和弧权重分布分析,可以发现关键库所,确定关键诊疗活动,从而优化资源分配; ③通过CP-net模型最短路径搜索和实际可能性分析,优化诊疗流程,形成新的标准化临床路径.
此外,由于模型去除了噪声的干扰,整个模型可看作一个病种最基础的网络,具有极强的拓展性,在此基础上对于模型的衍生可以实现更多的功能,该模型也为临床路径的费用管理、资源调度等进一步的工作奠定基础.
4.3 显著性系数敏感性分析显著性系数是统计α算法中的重要参数,其数值直接影响最终的结果.为了确定显著性系数α对试验结果的影响,增加显著性系数敏感性分析试验.试验数据采用来自内蒙古某三甲医院2010年7月到12月正常分娩和急性阑尾炎病种的事件日志.将显著性系数分别设定在0.01~0.20之间,共5组数据.试验结果如表 6所示.
| 下载CSV 表 6 显著性系数敏感性分析结果 Tab.6 Significant level sensitivity analysis results |
从试验结果可以看出:当显著性系数较小和较大时,结果的准确度和泛化性都会明显下降; 拟合度在显著性系数较大时明显下降.具体来看,当显著性系数较小时,因果关系和选择关系识别率明显降低,出现第一类错误; 反之,当显著性系数较大时,结果受到噪声的影响明显增大,保留了较多噪声,出现较多误判的因果关系和选择关系,出现了第二类错误.需要保证敏感性系数在一个合理的范围内,一般可以设定为0.05~0.10.
5 结语针对临床路径建模提出了一套基于统计α算法的临床路径Petri网建模方法.首先给出了结合重复活动判别的统计α算法,实现了从包含噪声的事件日志中提取知识,形成完整的工作流程; 接着提出了基于统计α算法的临床路径Petri网模型,该模型很好地契合了统计α算法,实现了事件日志到Petri网模型的转化.通过仿真数据和真实的临床路径数据试验验证了统计α算法较经典α算法在准确度和运行时间方面的明显优势; 试验也证明了基于统计α算法的临床路径Petri网模型的可行性,该模型在可达性和结构完整性上表现优秀,可以用作临床路径管理的辅助工具.
| [1] |
LANG M, BVRKLE T, LAUMANN S, et al. Process mining for clinical workflows: Challenges and current limitations[J]. Studies in Health Technology & Informatics, 2008, 136: 229 |
| [2] |
COOK J E, WOLF A L. Automating process discovery through event-data analysis[C]//Proceedings of the 17th international conference on Software engineering. [S. l. ]: ACM, 1995: 73-82.
|
| [3] |
AGRAWAL R, GUNOPULOS D, LEYMANN F. Mining process models from workflow logs[C]//International Conference on Extending Database Technology. Berlin Heidelberg: Springer, 1998: 467-483.
|
| [4] |
HAMMORI M, HERBST J, KLEINER N. Interactive workflow mining-requirements, concepts and implementation[J]. Data & Knowledge Engineering, 2006, 56(1): 41 |
| [5] |
AALST W V D, WEIJTERS T, MARUSTER L. Workflow mining: Discovering process models from event logs[J]. IEEE Transactions on Knowledge & Data Engineering, 2004, 16(9): 1128 |
| [6] |
MEDEIROS A K A D, Dongen B F V, AALST W M P V D, et al. Process mining for ubiquitous mobile systems: An overview and a concrete algorithm[C]// International Workshop on Ubiquitous Mobile Information and Collaboration Systems. [S. l. ]: Springer, 2004: 151-165.
|
| [7] |
WEN L, AALST W M P V D, WANG J, et al. Mining process models with non-free-choice constructs[J]. Data Mining & Knowledge Discovery, 2007, 15(2): 145 |
| [8] |
WEN L, WANG J, SUN J. Mining invisible tasks from event logs[C]// Joint, asia-pacific web and international conference on web-age information management conference on advances in data and web management. [S. l. ]: Springer-Verlag, 2007: 358-365.
|
| [9] |
李嘉菲, 刘大有, 杨博. 过程挖掘中一种能发现重复任务的扩展α算法[J]. 计算机学报, 2007, 30(8): 1436 LI Jiafei, LIU Dayou, YANG Bo. Process mining: An extended α-algorithm to discovery duplicate tasks[J]. Chinese Journal of Computers, 2007, 30(8): 1436 |
| [10] |
WEN L, WANG J, AALST W M P V D, et al. A novel approach for process mining based on event types[J]. Journal of Intelligent Information Systems, 2009, 32(2): 163 DOI:10.1007/s10844-007-0052-1 |
| [11] |
QUAGLINI S, STEFANELLI M, LANZOLA G, et al. Flexible guideline-based patient careflow systems[J]. Artificial Intelligence in Medicine, 2001, 22(1): 65 DOI:10.1016/S0933-3657(00)00100-7 |
| [12] |
GRANDO M A, GLASSPOOL D W, FOX J. Petri nets as a formalism for comparing expressiveness of workflow-based clinical guideline languages[C]// International Conference on Business Process Management. [S. l. ]: Springer, 2008: 348-360.
|
| [13] |
赵艳丽, 江志斌, 李娜. 基于分层赋时着色Petri网的临床路径建模[J]. 上海交通大学学报, 2010(2): 252 ZHAO Yanli, JIANG Zhibing, LI Na. Modeling of clinical pathway based on hierarchical timed colored Petri net[J]. Journal of Shanghai Jiaotong University, 2010(2): 252 |
| [14] |
田燕, 马晓普, 张新刚, 等. 基于Petri网的临床路径评估与优化[J]. 计算机科学, 2013, 40(5): 193 TIAN Yan, MA Xiaopu, ZHANG Xingang, et al. Evaluation and optimization of clinical pathway based on Petri net[J]. Computer Science, 2013, 40(5): 193 |
| [15] |
WEERAPONG S, POROUHAN P, PREMCHAISWADI W. Process mining using α-algorithm as a tool: A case study of student registration[C]//2012 10th International Conference on ICT and Knowledge Engineering. Bangkok: IEEE, 2012: 213-220.
|
| [16] |
AALST W M P V D, DONGEN B F V, HERBST J, et al. Workflow mining: A survey of issues and approaches[J]. Data & Knowledge Engineering, 2003, 47(2): 237 |
 2018, Vol. 46
2018, Vol. 46
