2. 天津市市政工程设计研究院, 天津 300051
2. Tianjin Municipal Engineering Design & Research Institute, Tianjin 300051, China
工字钢混凝土桥面板组合梁桥是中小跨度桥梁最常用的组合梁形式.随着工业化建造技术的推广,少主梁及简化加劲肋形式能降低工字钢组合梁桥的综合造价,是组合梁桥发展的趋势.
国外对于组合梁桥已经有较多的实践.法国建造了世界上最多的双工字钢梁组合梁桥,文献[1]描述了这种桥梁的设计参数.新西兰经过多年的工程实践也发布了工字梁组合梁桥设计指南[2], 建议采用双工字或多工字钢梁组合梁.文献[3]介绍了德国钢混组合梁桥的应用情况,主要采用多工字钢梁.日本是采用双工字钢梁组合梁较多的国家,也编制了相应的设计指南[4-5].美国建造了大量的工字梁组合梁桥,其公路桥梁设计规范对钢梁部分从稳定、施工可行性角度规定了钢梁构造要求[6].
我国学者对钢混组合梁的设计参数进行了一些研究[7-10],但目前双工字主梁钢混组合梁应用在我国处于起始阶段,2016年安徽济祁高速公路淮河桥在我国第一次使用了这种桥型.目前我国现有的桥梁设计规范[6, 11]规定了组合梁中钢梁的构造要求,但基本是从钢桥转化来的.文献[12]介绍了国外的经验, 是目前国内设计者的主要参考资料.
设计规范和指南的重要内容之一是给出构造尺寸要求.对于工字钢梁主要包括腹板厚度tf,上翼缘板宽度ds和厚度ts,下翼缘板宽度dd和厚度td,加劲肋以及横向连系梁等参数.上述构造要求是基于满足承载能力、稳定、经济性、可施工性能要求提出来的[7-9].按照这些要求拟定尺寸,可以减少设计分析的工作量,但这些要求都是根据钢梁各部件性能独立研究得到的,有些并不合理.
本文针对中小跨径双工字钢组合梁桥,综合考虑组合梁的弯曲、局部屈曲性能、极限承载能力等性能指标,通过有限元法的参数分析,研究设计参数取值的合理性,并从钢材用量最小的角度研究双工字钢组合梁的合理梁高.
1 工字钢组合梁构造参数要求目前组合梁的设计均采用极限状态法,其特点是:当假设达到承载能力极限状态时, 对于正弯矩区,下缘钢梁受拉区完全屈服,上缘混凝土板达到抗压强度;对于负弯矩区,下缘受压区钢梁也完全屈服,上翼缘混凝土内的钢筋与钢梁受拉区全部屈服.
在架设阶段,通常钢梁除承担自重外还要承担混凝土板的自重,钢梁按照实际截面计算应力,各部分应力均应小于屈服强度,同时不发生屈曲失稳.
为了保证不在全截面屈服前发生屈曲,同时施工阶段也不发生失稳,钢梁部分必须满足一定的构造要求.各设计规范及指南的构造尺寸建议都是基于这一思路提出的.
图 1为典型的双主梁式钢板组合梁截面图.主梁断面采用直腹式双工字钢加混凝土桥面板组合截面,混凝土板和钢主梁通过栓钉连接,双工字钢梁之间采用横梁联接,形成组合体系.在设计阶段上述参数应满足相关设计规范或指南的规定[1, 5-6, 11, 13].

|
图 1 组合梁标准断面 Fig.1 Standard section of composite bridge |
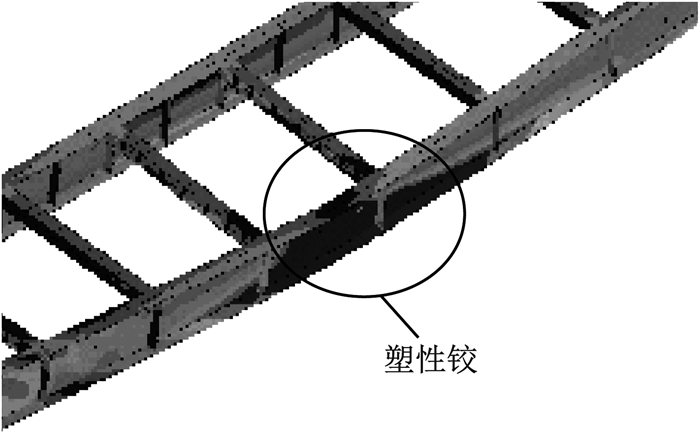
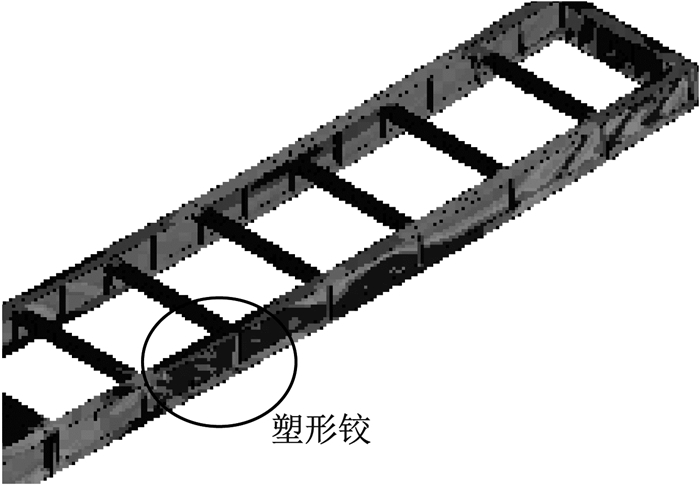
图 2为采用有限元法分析的典型双主梁组合梁极限承载状态.图 3为安装阶段钢梁可能的失稳形态,由于钢梁构造参数满足规范规定,达到承载力极限状态时在钢梁上出现屈服铰(圆圈所示),全梁不出现屈曲区域,而安装阶段的稳定系数达到7.7.
|
图 2 承载力极限状态时钢梁应力分布 Fig.2 Stress distribution in girders under strength limit state |

|
图 3 安装阶段钢梁的弹性失稳形态 Fig.3 Elastic local buckling under girder erection loading |
表 1为某一典型4×35 m连续两主梁钢板组合梁中钢梁的主要尺寸参数.双工字钢梁之间采用横梁联接,横梁间距5 m.以此结构设计为初始参数参考,对双主梁钢板组合梁桥进行设计参数的取值与优化研究.
| 下载CSV 表 1 钢梁初始参考参数 Tab.1 Initial reference parameters of steel Ⅰ girders |
采用通用有限元分析软件ANSYS空间三维有限元模型进行分析.混凝土采用Solid65单元进行模拟,采用最为常用的Hongnestad本构关系.混凝土抗压强度标准值为26.8 MPa,混凝土极限压应变取为0.003 8.混凝土破坏准则采用五参数的Willam-Warnke破坏准则.钢材采用Shell181单元,其屈服应力为345 MPa,屈服应变为εsy=0.001 6.本构关系采用双线性随动强化模型,将其本构关系简化为斜线加平直线形式.钢板梁与混凝土直接采用刚臂连接.边界条件根据连续梁的约束条件,在边支点和次边支点约束结构的竖向位移,在中支点约束结构的竖向位移、水平位移和纵向位移.收敛准则主要采用力的收敛,收敛精度默认值为0.1%.
考虑的荷载主要有两部分:①施工过程中的钢梁、混凝土板的自重和二期铺装;②车辆荷载.
Sause[14]指出:钢板梁在非组合截面状态,其尺寸设计往往受稳定控制.因此本文除了研究不同状态下的应力与变形响应外,重点分析两主梁结构体系的稳定,包括弹性稳定(一类稳定)和极限承载力(二类稳定).弹性稳定分析不考虑材料的非线性,获得结构的第一阶屈曲模态,主要采用欧拉杆原理的失稳准则.极限承载能力分析考虑材料和几何非线性,获得结构体系的极限承载力,主要采用Mises应力准则.
3 工字钢梁合理尺寸参数分析对钢梁进行参数分析,以获得构造尺寸对受力性能的影响规律.
3.1 受压翼缘板宽厚比工字钢受压翼缘除了满足强度要求外,还需要考虑屈曲稳定性,因此,各设计指南、规范[11-12, 14]均将受压翼缘的宽厚比限制在12左右.连续梁中支点下翼缘板为了抵抗使用阶段巨大的负弯矩一般都需加厚,因而不太可能屈曲.跨中截面受压上翼缘成桥阶段与混凝土板连接也不会失稳,所以失稳主要可能出现在尚未形成组合截面的安装阶段.对安装阶段跨中上翼缘进行如下分析.
3.1.1 翼缘宽厚比对稳定系数的影响在不改变截面刚度(即保持腹板及上下翼缘板的面积相同)的情况下调整跨中梁段翼缘板的宽厚比,分别建立翼缘宽厚比为8~16的对比模型,进行弹性稳定分析.图 4显示了弹性稳定系数随翼缘板宽厚比的变化.

|
图 4 不同翼缘宽厚比时施工阶段弹性稳定系数 Fig.4 Elastic stability coefficient versus flange width-thickness ratio under construction condition |
从图 4可以发现,随着翼缘宽厚比增大,钢梁在安装阶段弹性稳定系数逐渐降低.当翼缘宽厚比小于11时,弹性稳定系数趋于稳定;当宽厚比超过11时,弹性稳定系数明显下降.
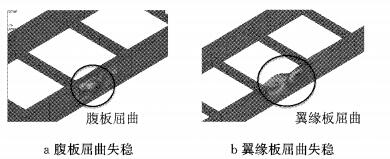
考察钢梁失稳位置,可以发现在翼缘宽厚比小于11时,即板较厚、宽度较小时,屈曲失稳均发生在腹板位置,见图 5a,因此加厚翼板对提高稳定性不起作用.而当翼缘宽厚比大于11时,屈曲发生在翼缘板位置,如图 5b所示.
|
图 5 不同翼缘宽厚比时钢梁安装阶段失稳位置 Fig.5 Buckling modes for different flange width-thickness ratio under construction condition |
从前述分析可以看出, 安装阶段钢梁的失稳会发生在翼板和腹板二者中相对薄弱的区域,片面增加翼缘板厚度会造成浪费.
分别取腹板厚度从16 mm到14、13、12、11 mm(腹板高厚比分别为110、130、140、140),对不同翼缘宽厚比下的弹性稳定系数进行如所述的对比分析.结果显示屈曲位置在腹板和翼板之间转换的临界点与翼板与腹板之间的相对厚度相关.
图 6显示了失稳形态与翼缘宽厚比和腹板高厚比的关系.在临界值附近时,翼板厚度和腹板厚度的取值比较均衡,材料最省.

|
图 6 翼缘板宽厚比随腹板高厚比的变化 Fig.6 Flange width-thickness ratio versus web depth-thickness ratio |
现有设计规范[6, 11]在不考虑腹板影响的情况下对翼缘宽厚比进行统一限制, 为12左右(Q345钢材),偏于保守.拟合图 6中的曲线,用h0/tf和d/(2t)分别代表腹板高厚比和翼缘宽厚比,可得如下关系:
| $ \frac{{d/2}}{t} = \frac{1}{{260}}{\left[{\left( {\frac{{{h_0}}}{{{t_{\rm{f}}}}}} \right)-110} \right]^2} + 11.2 $ | (1) |
式中:d为翼板的全宽;t为翼板厚度;h0为腹板高度;tf为腹板厚度.
建议翼缘板宽厚比按照如下方式选取:
(1) 腹板高厚比在110~150时,翼缘宽厚比可以根据以上经验公式(1)计算而得.
(2) 腹板高厚比小于110时,翼缘宽厚比取12.
(3) 腹板高厚比大于150时,翼缘板的宽厚比通常可以根据施工及布置剪力钉的最小要求取值.
3.2 工字钢梁腹板高厚比钢梁腹板承担剪应力,在弯矩和剪力的共同作用下产生主应力,靠近受压翼缘的主压应力区容易发生局部屈曲.因此各设计指南和规范均有腹板高厚比的限制.
腹板的局部稳定性主要与腹板的厚度相关,同时还与是否有竖向和横向加劲肋相关.对于高强度钢板,承载能力破坏时应力比较高,因此保证不失稳所需的板厚也比较大.
对于Q345钢材,如果只设竖向加劲肋,我国规范[1, 14]建议腹板的高厚比小于120,而美国和日本的规范[5-6]都建议相应强度钢材腹板的高厚比可以达到150,因此材料用量上有很大差异,按照我国规范需要更厚的腹板.
3.2.1 腹板高厚比对稳定性的影响建立不同的腹板高厚比模型进行参数分析.
在中间支点附近,腹板厚度为22 mm,高厚比约为76,远低于中国规范规定的120,但使用阶段的最大剪应力达到110 MPa,已经接近Q345钢材的抗剪允许应力125 MPa,因此支点附近的腹板厚度由剪应力设计值控制,一般不会出现局部稳定问题.
对跨中区段的腹板高厚比取90~180进行弹性稳定分析,翼板的宽厚比均取12,见表 2.即使腹板减薄到高厚比180,最大剪应力仍未超过Q345钢材的控制剪应力125 MPa,说明跨中区段抗剪强度不是设计控制因素.
| 下载CSV 表 2 不同腹板高厚比时弹性稳定系数及失稳位置 Tab.2 Elastic stability coefficient and buckling positionfor different depth-thickness ratio of web |
从表 2可以看出,架设阶段随着腹板变薄,弹性稳定系数越来越低,但是失稳位置却不相同.高厚比超过150时才表现为腹板自身屈曲失稳,腹板变厚后自身不但不会失稳,同时还能提高结构整体稳定性.
在使用阶段由于受到混凝土板的约束,因为只有腹板可能出现弹性失稳,所以钢梁的弹性稳定系数大大提高.
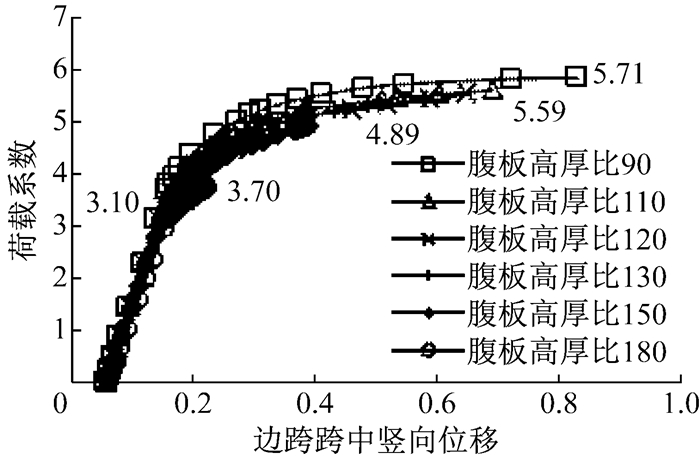
为分析腹板在使用阶段的稳定性,对上述系列组合梁桥模型进行使用阶段的极限承载能力分析,边跨跨中截面的活载-位移曲线如图 7所示.可以发现:随着腹板高厚比逐渐增高,极限的汽车活载系数逐渐降低.在各种腹板厚度下,当加载达到活载的3.15倍时进入非线性阶段,此时是从跨中截面钢梁下缘开始屈服.
|
图 7 不同腹板高厚比时荷载系数-边跨跨中竖向位移曲线 Fig.7 Load-displacement curve at mid-span under traffic loading for different web depth-thickness ratio |
此后,腹板高厚比小于130时,极限的活载加载系数为5.71~5.59,大小几乎相等,此时中间支点截面的钢梁全部屈服,全梁出现2个屈服铰而丧失承载能力,腹板厚度对极限承载力影响很小.
腹板高厚比为150及180时,极限活载加载系数分别为4.89和3.72.图 8显示了加载极限时的Mises应力.腹板在靠近中间支点的区域发生了主压应力方向的局部屈曲,与跨中截面共同形成多个屈服铰而丧失承载能力.中间支点截面虽然剪应力更大,但是腹板厚度也大,即无屈曲,也没有达到屈服应力,因此全桥承载能力比厚腹板时低.
|
图 8 跨中腹板高厚比较大时的极限状态应力 Fig.8 Ultimate stress state for thicker web thickness at mid-span |
从前面的分析可以看出:在中间支点附近截面,腹板的厚度一般由钢板抗剪强度控制;而在其他区段, 我国规范规定的腹板宽厚比偏小,造成腹板厚度大,增加了用钢量,但对稳定性并没有提高.美国和日本规范规定的宽厚比较大,腹板用钢量小,在跨中区域是安全的,而在靠近中间支点区段可能造成腹板在主应力方向失稳.
腹板在跨中梁段近支点区域的屈曲失稳并不是沿着腹板纵向形成半波屈曲,而是与腹板高度的方向呈一定的角度,这说明,腹板的受力状态受到纵向应力和剪应力的共同影响,其主压应力的方向倾斜,如图 9所示.图中,h为腹板高度;h′为腹板失稳方向长度;a为竖向加劲肋间距;σ为正应力;τ为剪应力.主压应力方向的倾斜增加了受压区的实际高度,对此区域内腹板屈曲稳定性是不利的.
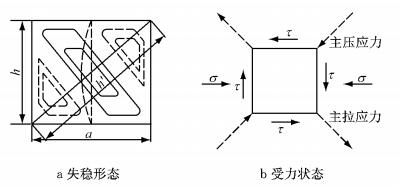
|
图 9 接近支点跨中梁段腹板屈曲失稳形态与受力状态 Fig.9 Local buckling and the corresponding stress state |
由于4分点区段是主压应力方向失稳,因此,高厚比仍可按照美日规范规定的限值取值,只要计算腹板高厚比时按照腹板中部主应力方向取斜向梁高即可.
将腹板高厚比按图 10(L为一跨跨长)所示分3个区段取值:支点区段按照抗剪强度,跨中区段腹板高厚比为150,近支点区段腹板高厚比为120(主压应力倾斜37°).计算使用阶段承载能力,几乎与原设计相同,极限状态时仍能达到图 1所示的破坏形式.
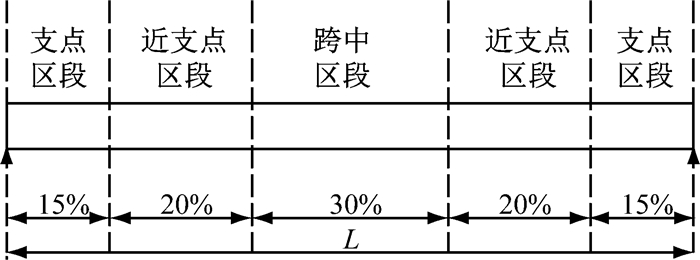
|
图 10 双工字钢梁桥腹板纵向分段示意 Fig.10 Longitudinal divisions of web for twin-I steel girders |
当工字钢梁的腹板存在稳定问题时,可以通过设置加劲肋的方式以较小的经济代价予以避免.加劲肋主要分为竖向加劲肋和纵向加劲肋,它们的布置和厚度与稳定性相关.
3.3.1 竖向加劲肋(1) 竖向加劲肋的布置.一般用加劲后腹板的纵横比来控制,即竖向加劲肋的纵向间距与上下翼缘的间距比值.对0.50、1.00、1.25、2.50、3.00进行弹性稳定分析,结果如图 11所示.随着竖向加劲肋间距的增大(从0.3增加到3.0),其稳定系数由10.6下降到2.0.当α < 1.5后不再明显下降,这时已与没有竖肋差不多.采用不同腹板厚度进行竖肋布置影响计算,其规律基本相同.因此,设置竖向加劲肋时,要使其对稳定性发挥作用,其间距不宜大于梁高的1.5~2.0倍,在此基础上,密度越大,稳定性越好.上述结论与国内外指南的推荐值相同.

|
图 11 不同竖向加劲肋间距下的弹性稳定系数 Fig.11 Elastic stability coefficients for different vertical stiffener spacing |
(2) 竖向加劲肋厚度.对竖向加劲肋厚度影响进行分析,考虑δ为8、10、12、14、16 mm等厚度变化,分析其弹性稳定性,结果如表 3所示.随着加劲肋厚度增加,安装和使用阶段的稳定系数变化微小,同时,第一阶弹性屈曲的形式和位置也没有发生变化.因此在可施工的范围内,加劲肋厚度对组合梁整体稳定性影响很小.
| 下载CSV 表 3 不同竖向加劲肋厚度下的弹性稳定系数 Tab.3 Elastic stability coefficient for different vertical stiffener thickness |
在腹板的受压区设置纵向加劲肋可提高稳定性.
3.3.2.1 纵肋的位置分别在连续组合梁的正负弯矩区的不同高度设置一道纵向加劲肋.纵向加劲肋距受压翼缘距离z分别取0.1、0.2、0.3、0.4倍梁高h,厚度取为12 mm,分析组合梁的弹性稳定性,结果如图 12所示.
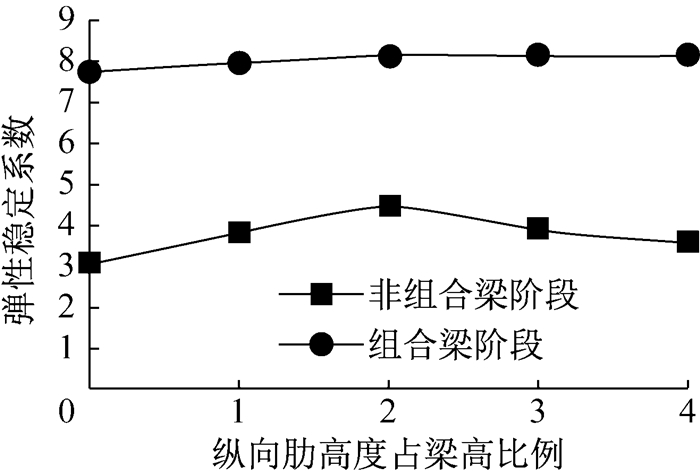
|
图 12 不同纵向加劲肋高度时的弹性稳定系数 Fig.12 Elastic stability coefficient for different longitudinal stiffener location |
纵向肋对于安装阶段有明显的影响,而且当纵肋布置在距离受压翼缘0.2倍梁高位置时效果最好.在形成组合梁的使用阶段, 纵肋对稳定性的影响很小,这是由于在组合梁阶段,中性轴位置向桥面板侧上移,钢梁受压区范围很小.因此,在安装梁阶段稳定性有保证的前提下,可以不设纵向加劲肋.
3.3.2.2 纵向加劲肋的经济性对1 700 mm净腹板高的主梁上增加一道400 mm×12 mm的纵向加劲肋,其增加的用钢量近似等于腹板厚度增加3 mm,即腹板厚度从16 mm增加到19 mm.在同等荷载条件下,其安装阶段的弹性稳定系数约为10.05,而在16 mm厚腹板上增加一道纵肋的稳定系数仅为8.12.对于中小跨径双工字钢组合梁桥,设置纵向加劲肋不如适当增加腹板厚度.
此外,纵向加劲肋一般设置在与竖向加劲肋相同的腹板面上,在竖向加劲肋处需要断开,这将增加钢梁制造的成本.
4 双工字钢组合梁桥钢梁的合理梁高在30~50 m的中等跨径范围内,双工字钢组合梁钢梁高约为跨径的1/27~1/18.
传统的组合梁桥为了减少截面的用钢量,通常采用尽量薄的腹板,由此带来的屈曲稳定问题则通过设置加劲肋进行解决,即“多加劲肋、薄腹板”设计思路.过多的加劲肋往往会增加加工成本,不适合工业化建造,从而使上述做法不一定经济.而“少加劲肋、厚腹板”可减少制造成本.2种不同的设计思路对双工字钢组合梁桥合理梁高的影响值得探讨.
以35 m跨连续组合梁桥为基础,进行梁高1 950,1 750,1 500,1 250 mm的试设计,分析梁高对组合梁桥的刚度及经济性能的影响.当梁高变化时,改变翼板的尺寸(同时满足宽厚比要求),以使上下翼缘在相同荷载下的应力相同,从而承载能力相同.在“多加劲肋、薄腹板”思路下,腹板厚度按照抗剪强度计算,稳定性通过设置加劲肋满足,而在“少加劲肋、厚腹板”思路下,只在横梁处设竖肋,腹板稳定性通过增加厚度来满足.
4.1 极限承载能力校验图 13显示了不同梁高时双工字钢组合梁桥的荷载(荷载系数)-边跨跨中竖向位移曲线.不同梁高组合梁桥达到极限承载能力状态时的荷载系数接近,说明极限承载能力基本相同.1 250 mm梁高时的极限挠度是1 950 mm时的1倍.

|
图 13 不同梁高时汽车荷载下边跨跨中竖向位移曲线 Fig.13 Load-vertical displacement curve at mid-span under traffic loading for different girder depth |
在临近破坏时,梁高为1 950 mm的双工字钢组合梁桥的钢主梁Mises应力如图 14所示.其他梁高情况类似.各梁破坏时均在跨中和支点全截面屈服(混凝土板拉裂或压碎)形成塑性铰,则为材料的强度破坏,说明所有试设计均符合极限状态破坏假定.
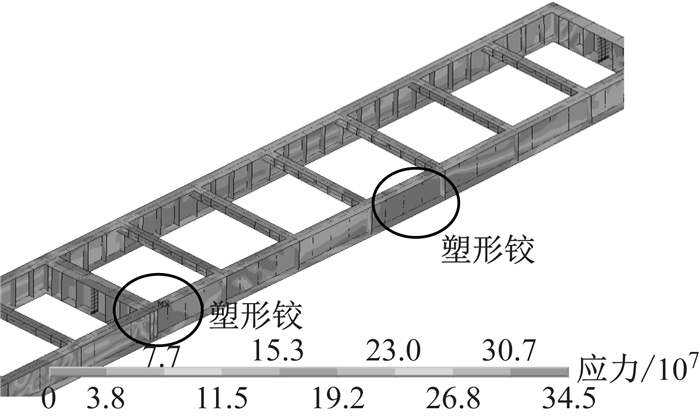
|
图 14 梁高1 950 mm的组合梁破坏时钢梁Mises应力 Fig.14 Mises stress in steel girder at failure of for girder height of 1 950 mm |
表 4为不同梁高双工字钢组合梁在各阶段的边跨跨中位移.随着梁高的降低,竖向位移显著上升,但1 250 mm梁高时的位移只比1 950 mm时增加50%.承载能力阶段如前所述, 1 250 mm时挠度比1 950 mm时增加1倍.出现这种情况是由于承载能力极限状态时的应力图是矩形的,梁高减小的效应更明显.
| 下载CSV 表 4 不同梁高组合梁不同阶段的位移 Tab.4 Displacement for different girder depths |
即使1 250 mm梁高时弹性挠度也为跨径的1/950,活载刚度也大大高于规范要求限值,梁高不是设计控制因素.
4.3 经济性能比较对上述2种不同设计思路下的不同梁高组合梁的钢梁用钢量进行统计,并将工字梁截面自身用钢量及加劲肋用钢量分开统计.图 15显示了用钢量随梁高的变化.

|
图 15 不同梁高组合梁桥用钢量 Fig.15 Steel materials for different girder depths |
由图 15a可知,采用“多加劲肋、薄腹板”对策时,随着主梁高度的降低,截面的惯性矩不断减小,矮梁截面必须在上下翼缘板增加更多的面积来满足抗弯强度要求,因此主梁截面的用钢量呈不断增加的趋势;而从屈曲稳定性能考虑,高梁截面采用了较薄的腹板,为了满足稳定性的要求,必须增加更多的加劲肋构造.由于主梁截面比例大,因此梁高越高用钢量越省.
而从图 15b可见,采用“少加劲肋、厚腹板”时,主梁工字钢截面随着主梁高度的升高,由惯性矩增加带来的翼缘板用钢量减小的好处逐渐被为了保持屈曲稳定性所增厚的腹板用钢量所抵消,因此随着主梁的高度升高到一定程度,用钢量反而增加.由于加劲肋少,其用钢量随梁高增加量较小.总用钢量在1 750 mm梁高(高跨比约为1/20)时达到最小.
“少加劲肋、厚腹板”组合梁桥最少总用钢量(152.37 kg·m-2)比“多加劲肋、薄腹板”组合梁桥同等梁高时的总用钢量(145.57 kg·m-2)稍高,如果加劲肋大大简化使得加工制造成本降低,其综合经济性可能会更好.
4.4 合理梁高取值建议在“少加劲肋”的工业化建造思路下,对于中等跨径的双工字钢组合梁桥,建议钢梁高跨比取为1/20左右.
5 结语钢混组合梁设计时一般假定钢梁达到材料的屈服强度前不出现屈曲,而截面各部件的稳定性通过构造要求来确定.目前各国的钢桥设计规范和指南均规定了一些构造要求,但是对于双主梁钢混组合梁并不完全适用.针对双工字钢混凝土桥面板组合梁桥进行系列参数设计分析,得到以下关于构造细节的结论.
(1) 由于屈曲失稳发生在钢梁最薄弱的区域,翼板与腹板保证稳定性的最小尺寸要求相互关联,分别考虑会造成材料浪费,本文提出了翼板与腹板的关联关系.
(2) 现行设计规范在整个腹板区域内采用统一的腹板高厚比限值不科学.我国规范规定的120在跨中区域偏保守,而美日规范规定的150在靠近中间支点区域有可能在主压应力方向局部失稳.建议高厚比统一按照150取值,在跨中附近截面采用实际梁高计算高厚比,而在4分点附近采用腹板中部主压应力方向的斜梁高计算高厚比.
(3) 竖向加劲肋只有在腹板纵横比小于1.5时才有明显提高腹板局部稳定性的作用.对于中小跨双工字钢组合梁桥,以纵向加劲肋防止腹板失稳的效果不如适当加厚腹板.
(4) 在“少加劲肋”的工业化建造条件下,对于中等跨径的双工字钢组合梁桥,建议钢梁的高跨比取1/20.
| [1] |
Service D'études sur les Transports. Steel-concrete composite bridges sustainable design guide[M]. [S.l.]: Service D'études sur les Transports, 2010
|
| [2] |
Raed El Sarraf, HERA, Auckland, et al. Steel-concrete composite bridge design guide[R]. [S. l. ]: NZ Transport Agency, 2013.
|
| [3] |
FALKE J. Recent developments in composite bridge building in Germany[C/CD]//Composite Construction in Steel and Concrete Ⅱ. [S. l. ]: ASCE, 2015. http://cedb.asce.org/cgi/WWWdisplay.cgi?84268
|
| [4] |
EHAB Ellobody. Finite element analysis and design of steel and steel-concrete composite bridges[M/OL]. [2015-02-01]. www.sciencedirect.com/science/book/9780124172470.
|
| [5] |
日本道路协会. 道路桥示方书.同解说[M]. 东京: 日本道路协会, 2012 Japan Road Association. Japanese bridge specifications and description for highway[M]. Tokyo: Japan Road Association, 2012 |
| [6] |
American Association of State Highway and Transportation Officials. AASHTO LRFD bridge design specifications[S]. Washington D C: American Association of State Highway and Transportation Officials, 2010.
|
| [7] |
吴冲. 我国公路简支钢板梁桥合理截面的探讨[J]. 桥梁建设, 2004(6): 35 WU Chong. Research of reasonable girder sections of simply-supported steel plate girder highway bridges in China[J]. Bridge Construction, 2004(6): 35 |
| [8] |
张静. 工字钢-混凝土组合梁桥截面设计参数优化研究[D]. 西安: 长安大学, 2007. ZHANG Jing. Research on the section parameters optimum of I-steel and concrete composite bridge[D]. Xi'an: Chang'an University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-11941-2009256895.htm |
| [9] |
张通. 简支钢板组合梁桥合理截面构造研究[D]. 西安: 长安大学, 2014. ZHANG Tong. Investigation of reasonable cross section structures for the simply supported steel-concrete composite girder [D]. Xi'an: Chang'an University, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D559009 |
| [10] |
郭超. 钢-混凝土组合梁应力分析及截面优化研究[D]. 长沙: 长沙理工大学, 2013. GUO Chao. The Research on mechanical behavior of continuous steel-concrete composite beam and reasonable section[D]. Changsha: Changsha University of Science & Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10536-1013300445.htm |
| [11] |
中华人民共和国交通运输部. 公路钢结构桥梁设计规范: JTG D64—2015. 北京: 人民交通出版社, 2015. Ministry of Transport of the People's Republic of China. Specifications for design of highway steel bridge: JTG D64—2015. Beijing: China Communications Press, 2015. |
| [12] |
刘玉擎. 组合结构桥梁[M]. 北京: 人民交通出版社, 2005 LIU Yuqing. Steel-concrete composite bridge[M]. Beijing: China Communications Press, 2005 |
| [13] |
中华人民共和国住房和城乡建设部. 钢-混凝土组合桥梁设计规范: GB50917—2013. 北京: 中国计划出版社, 2014. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for design of steel and concrete composite bridges: GB50917—2013. Beijing: China Planning Press, 2014. |
| [14] |
SAUSE R. Innovative steel bridge girders with tubular flanges[J]. Structure & Infrastructure Engineering, 2015, 11(4): 450 |
 2018, Vol. 46
2018, Vol. 46

