2. 上海机场集团技术中心,上海 201206;
3. 上海民航新时代机场设计研究院有限公司,上海 200335
2. Shanghai Airport Authority, Shanghai 201206, China;
3. Shanghai CAAC New Era Airport Design and Research Institute Co., Ltd., Shanghai 200335, China
当前我国已经进入新一轮民用机场建设高速发展阶段,我国机场飞行区道面材料以水泥混凝土为主,而影响机场水泥道面使用性能的主要问题集中在水泥板块接缝位置.在实际工程中,由于传力杆和水泥混凝土材料性能的差异,两者的接触面极易产生应力集中.蒋应军等[1]通过有限元模型发现,在轮载作用下传力杆顶部或底部存在压应力集中, 在传力杆两侧存在拉应力集中;基于Westergaard理论,Friberg[2]认为荷载作用位置下方或附近的传力杆所受剪力最大;过高的应力水平会使传力杆周围裹附的混凝土发生屈服或疲劳破坏,从而引起传力杆在面板中的松动,制约了传力杆在接缝处有效传递荷载的能力[3].
传统的传力杆分析是以Timoshenko和Lessels的论著[4]为基础的.随着日渐成熟的数值模拟技术开发和应用,有限元模拟接缝结构是研究传力杆系统力学行为较可取的手段[5].学者们提出的传力杆接缝结构数值模型层出不穷,具有代表性经典模型有以下4类:①直接连结在板单元上的Timoshenko梁单元模型[6];②直接连结在板单元上的弹簧单元模型[7];③通过弹簧单元连结板单元与梁单元的传力杆模型[8];④定义接触面的传力杆三维实体模型[9].
Mackiewicz[10]对传力杆设置了不同工况,对比分析了不同情况下杆周混凝土的力学响应,通过计算发现,混凝土的应力集中水平随着传力杆的直径和间距的增大而显著降低;尹海波等[11]通过建立基于Winkler地基假设的三维路面模型,分析得到传力杆的直径和面板厚度对于传力杆周围混凝土受力状态有较明显影响;高玉换[12]通过有限元模型,采用损伤工况多因素敏感性分析,通过计算数据得到面板厚度对板底拉应力影响显著,传力杆布设间距的影响大于传力杆直径的影响.
本文首先对三维有限元实体模型参数进行说明,包括通过压入试验确定混凝土-传力杆摩擦系数;再根据有限元计算结果,按照传力杆圆周角度依次提取杆周混凝土的力学响应,进而明确混凝土易损伤的部位,并进行传力杆失效模式分析;最后基于有限元数值模型分别分析混凝土-传力杆摩擦系数、传力杆直径、传力杆布设间距、面板厚度等因素对传力杆杆周混凝土力学响应的影响规律,为传力杆接缝形式的改良和优化提供参考依据.
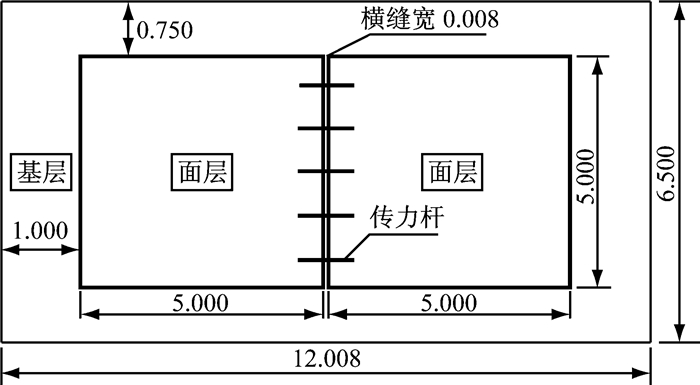
1 传力杆有限元模型的建立 1.1 结构模型建立基于ABAQUS软件建立三维有限元实体模型,道面采用2块板,每块板的平面尺寸为5 m×5 m,厚度取多种工况;接缝宽度设为8 mm.为了建模的可操作性和结构的偏安全性,不计集料嵌锁作用,传荷仅由传力杆体系完成.传力杆采用圆形钢材,长度为0.5 m,直径考虑多种工况;基层进行超宽设计,平面尺寸定为12.008 m×6.500 m,厚度为0.350 m,平面尺寸如图 1所示;面层和基层之间不考虑黏结,但需要考虑层间摩擦,国内外试验数据表明,当在半刚性基层上直接浇筑混凝土路面板时,层间摩擦系数值取5~6[13],本文模型层间摩擦系数取5;地基模型采用Winkler地基模型,地基反应模量为60 MN·m-3.
|
图 1 道面平面尺寸示意(单位:m) Fig.1 Sketch map of plane size of pavement(unit:m) |
建立的三维有限元实体模型涉及的材料分别为:水泥混凝土、水泥稳定碎石、传力杆圆钢等,各结构层材料的力学性能均采用线弹性模型来模拟,相应的表征参数为弹性(杨氏)模量E和泊松比μ,见表 1.
| 下载CSV 表 1 有限元模型材料参数 Tab.1 Material parameters of the finite element model |
荷载模型采用B737-800主起落架单轮荷载,加载方式为静态加载,建立有限元模型时为了便于划分网格和结构化建模,通常将轮印分布形状假定为矩形,荷载参数如表 2所示.
| 下载CSV 表 2 B737-800单轮荷载参数 Tab.2 Parameters of B737-800 single wheel load |
根据Tabatabaie等[14]的有限元分析结果,传力杆起传荷作用的范围是荷载作用位置向两侧各延伸面板相对刚度半径的距离,当荷载作用在板角时,起到传荷作用的传力杆数量减小了1/2,此时传力杆所受荷载同比增长了1倍,因此荷载作用在板角位置为最不利荷位.
1.3 混凝土-传力杆接触模拟传力杆的两端与混凝土的接触情况不同,一端为相互滑动,另一端为相互锚固,两端交错布置.有限元模拟锚固端接触时,以绑定约束(tie)模拟传力杆与混凝土的相互锚固;对于滑动端接触,需进行压入试验确定传力杆与混凝土之间黏结力大小.试验前需在不同长度和直径的传力杆外表面上涂一层厚度约1 mm的乳化沥青来防止传力杆与混凝土黏结,传力杆置于模具中央,在模具中浇筑混凝土,其配合比采用机场道面干硬性水泥混凝土C40的强度标准确定,配合比见表 3.
| 下载CSV 表 3 水泥混凝土试件配合比 Tab.3 Cement concrete specimen mixing ratio |
待28 d养护后取出,按传力杆和混凝土的接触面积的不同形成8种尺寸工况,如表 4所示.
| 下载CSV 表 4 传力杆尺寸 Tab.4 Dowel bar sizes |
使用YAW-3000型压力机对传力杆进行压入试验,混凝土试件放置于带孔铁块上以便传力杆向下压出,如图 2所示.

|
图 2 传力杆压入试验 Fig.2 Dowel indentation test |
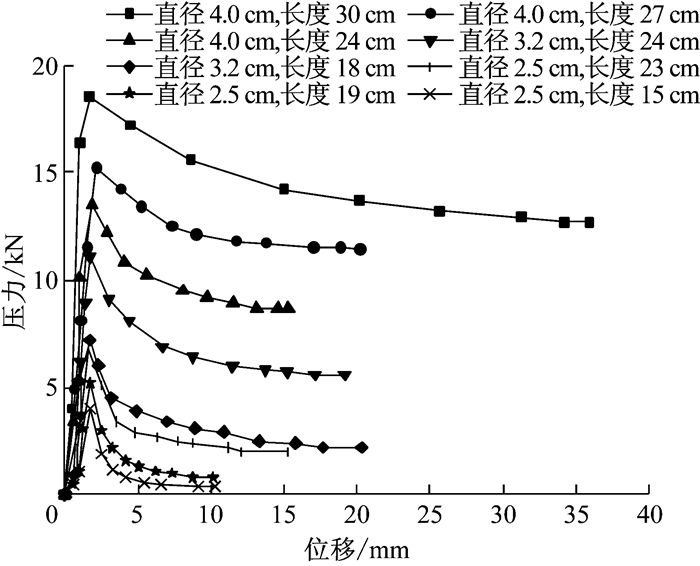
记录传力杆受压过程中的压力-位移曲线,如图 3所示.不同尺寸工况下的试件的压力-位移曲线都呈现相同的趋势:压力急剧增长,位移小幅增长,并且压力随位移近似线性增加,最后达到界面最大作用力,界面发生破坏,此时位移在2mm左右;当继续加载时,位移急剧增长,压力迅速衰减,最后收敛于某一数值.
|
图 3 压力与位移关系曲线 Fig.3 Curves of stress and displacement |
利用库伦摩擦定律(式(1))计算界面摩擦系数,其中界面剪力FS是混凝土-传力杆界面的切向作用力,取图 3曲线中各工况下的压力峰值;硬化收缩后的混凝土握裹传力杆产生界面法向压力N,计算如式(2).
| $ \mathit{\mu }{\rm{ = }}\frac{{{\mathit{F}_{\rm{S}}}}}{\mathit{N}} $ | (1) |
式中:μ为摩擦系数;FS为界面剪力,kN;N为界面法向压力,kN.
| $ \mathit{N}{\rm{ = }}\mathit{\sigma }\left( \mathit{t} \right){\rm{\cdot}}\mathit{A}{\rm{ \times 1}}{{\rm{0}}^{{\rm{ - 3}}}} $ | (2) |
式中:σ(t)为养护时间t时混凝土的收缩应力,MPa;A为传力杆和混凝土的界面接触面积,m2.
吕艳梅等[15]通过传力杆和混凝土之间的拉压平衡条件和大量试验数据,采用多系数回归分析方法,并考虑混凝土强度等级和配筋率2种影响因素,得到混凝土的收缩应力计算公式:
| $ \mathit{\sigma }\left( \mathit{t} \right){\rm{ = }}\mathit{\sigma }\left( {{\mathit{t}_{\rm{0}}}} \right){\rm{\cdot}}{\mathit{\beta }_{\rm{1}}}{\mathit{\beta }_{\rm{2}}} $ | (3) |
式中:σ(t)为养护时间t时混凝土的收缩应力,MPa;σ(t0)为混凝土基本收缩方程,σ(t0)=
当养护时间为28 d时,根据式(3)计算出混凝土的收缩应力σ(t)为0.543 MPa,将传力杆压入试验的8个压力峰值数据结合式(2)和式(3)可以计算出8个试件的传力杆和混凝土的界面库伦摩擦系数均在0.7~0.9范围内.取均值0.8作为有限元模型中传力杆滑动端和杆周混凝土的界面摩擦系数的基准值.
2 传力杆参数对杆周混凝土力学响应影响分析 2.1 影响因子及水平分析混凝土-传力杆摩擦系数、传力杆直径、传力杆布设间距和面板厚度等因子对杆周混凝土力学响应的影响规律.因子水平如表 5所示.
| 下载CSV 表 5 影响因子及水平 Tab.5 Impact factors and levels |
传力杆传荷时需要周边混凝土为其提供支撑,二者共同组成一套传力系统,因此传力杆工作时和混凝土存在相互作用,在界面上产生接触应力.在同一平面内,按应力的作用方向不同将杆周混凝土中的应力分为水平应力S22、竖向应力S33和剪应力S23.根据ABAQUS软件计算结果,提取杆周混凝土中的应力,如图 4所示,其中应力符号规定受拉为正、受压为负.

|
图 4 传力杆周混凝土应力分布云图 Fig.4 Stress distribution of concrete around dowel bar |
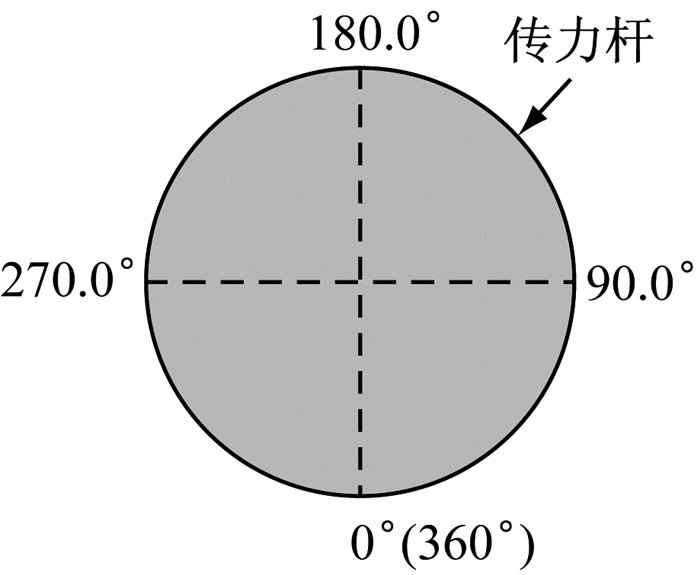
为方便表示各应力在杆周混凝土中空间位置分布,将传力杆与混凝土接触界面按圆周角度进行划分,如图 5所示,0°(360.0°)为接触界面的底部,180.0°表示其顶部.
|
图 5 传力杆与杆周混凝土圆周界面的角度位置 Fig.5 Angle position of circle interface between dowel bar and concrete around dowel bar |
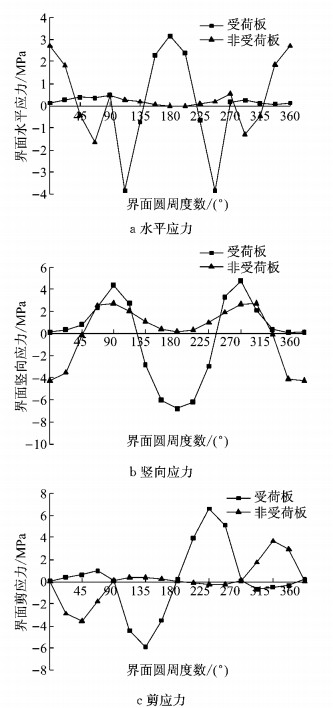
图 6表示当荷载作用在板角、影响因子采用基准值时,在受荷板和非受荷板中杆周混凝土各力学响应水平最高位置处界面应力大小按圆周角度的分布曲线.
|
图 6 杆周混凝土的力学响应 Fig.6 Mechanical response of concrete around dowel bar |
由图 6可知:对于受荷板,最大水平拉应力发生在180.0°(顶部)位置,最大水平压应力发生在112.5°位置,最大竖向拉应力发生在90.0°和270.0°(两侧)位置,最大竖向压应力发生在180.0°(顶部)位置,最大剪应力发生在135.0°和225.0°位置;对于非受荷板,最大水平拉应力发生在0°(底部)位置,最大水平压应力发生在67.5°和292.5°位置,最大竖向拉应力发生在90.0°和270.0°(两侧)位置,最大竖向压应力发生在0°(底部)位置,最大剪应力发生在45.0°和315.0°位置.
2.3 失效模式分析根据2.2节中对传力杆和杆周混凝土接触界面力学响应的提取,得到杆周混凝土中各应力最大值的位置分布,如图 7所示.

|
图 7 杆周混凝土各应力最大值位置分布 Fig.7 Maximum stress distribution of concrete around the dowel bar |
根据图 7发现,在杆周混凝土的顶面和两侧会产生较大的拉应力,尤其在圆周270.0°处,最大拉应力达到4.75Mpa,接近甚至超过混凝土的劈裂抗拉强度(3~5MPa).水泥混凝土是一种脆性材料,抗拉强度低,因此杆周混凝土的顶部和两侧极易因受拉破坏而产生裂缝.随着裂缝长度的延伸和宽度的增大,杆周混凝土与传力杆黏结性能减弱,无法为传力杆提供足够的支撑,导致传力杆传荷能力迅速降低甚至失效.另外,在杆周混凝土的顶部还会有较大的压应力产生,最大值达到6.80 MPa,在斜上方部位会有较大的剪应力,水泥混凝土虽然抗压强度大,但是经过荷载反复作用易产生疲劳破坏,导致混凝土被压碎,使得杆周混凝土对传力杆的支撑强度降低,传力杆传荷效率逐渐下降直至失效.
2.4 影响因素分析分析各因子对杆周混凝土力学响应的影响规律时,采用单因子轮换法,即改变某个影响因子的水平时,其余影响因子选用基准值;然后在建立的有限元模型基础上,对某一影响因子的不同水平进行数值计算,并提取受荷板中杆周混凝土各应力峰值;最后作图分析.
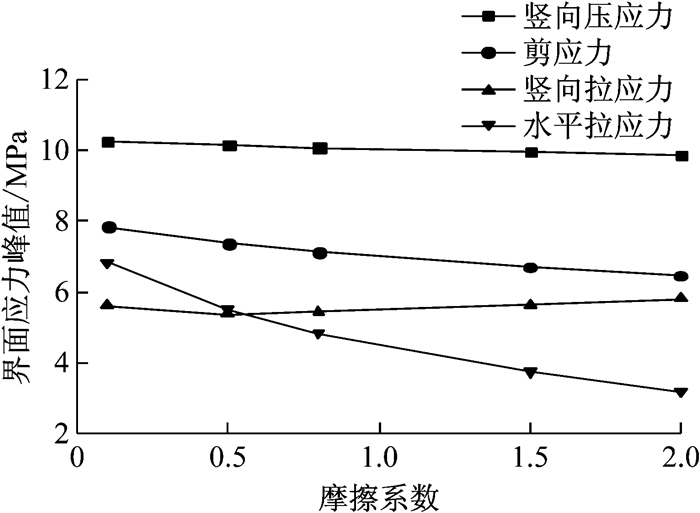
2.4.1 混凝土-传力杆摩擦系数对力学响应的影响混凝土和传力杆滑动端界面的摩擦系数直接影响杆周混凝土中力学响应的大小,而对传力杆表面采用不同的防粘防锈措施后,界面的摩擦系数不尽相同.采取的5种水平的摩擦系数分别是0.1、0.5、0.8、1.5、2.0,受荷板中杆周混凝土应力峰值的变化规律如图 8所示.
|
图 8 杆周混凝土应力峰值随摩擦系数变化规律 Fig.8 Variation law of the stress peaks of concrete around dowel bar with friction coefficient |
由图 8可知,随着水泥混凝土与传力杆摩擦系数的不断增大,杆周混凝土中的水平拉应力峰值明显减小,从6.83 MPa减小至3.18 MPa,变化了53%,但其减小幅度逐渐放缓;界面的竖向拉应力峰值呈现先减小后增大的趋势,摩擦系数在0.5时,竖直拉应力峰值最小,且与水平拉应力水平峰值接近;竖向压应力峰值几乎不受界面摩擦系数的影响;界面的剪应力略有减小,从7.84 MPa下降到6.46 MPa.
由以上分析可知,随着水泥混凝土与传力杆摩擦系数的增大,杆周混凝土水平拉应力逐渐减小,竖向拉应力先减小再逐渐增大.因此过小的摩擦系数(接近光滑接触)会使界面顶部混凝土产生过高的水平拉应力,过大的摩擦系数(接近锚固端绑定约束)会在圆周两侧产生过大的竖向拉应力.因此水泥混凝土与传力杆摩擦系数存在一个合理的取值区间,从有限元计算结果来看,摩擦系数μ取0.5~0.8区间内的值较为理想.
2.4.2 传力杆直径对力学响应的影响传力杆的横截面积直接决定了其与周围混凝土的接触面的大小,从而影响荷载作用下传力杆杆周混凝土的力学响应和损伤破坏.传力杆直径采取的5种水平分别为28、32、36、40、44 mm,受荷板中杆周混凝土应力峰值的变化规律如图 9所示.

|
图 9 杆周混凝土应力峰值随传力杆直径变化 Fig.9 Variation law of the stress peaks of concrete around dowel bar with dowel diameter |
由图 9分析可知:传力杆直径从28 mm增加到36 mm过程中,杆周混凝土各应力峰值下降幅度较大,水平拉应力峰值减小了35%,竖向拉应力峰值减小了32%,竖向压应力峰值减小了17%,剪应力峰值减小了20%;继续增大传力杆直径至44mm过程中,各应力峰值下降幅度变缓.
2.4.3 传力杆间距对力学响应的影响在水泥混凝土道面设计规范中,传力杆的布设间距是传力杆接缝设计的重要参数,布设间距的变化直接影响接缝附近的道面的各项力学响应.分别考虑传力杆布设间距为250、300、350、400、450 mm,受荷板中杆周混凝土应力峰值的变化规律如图 10所示.

|
图 10 杆周混凝土应力峰值随传力杆布设间距变化 Fig.10 Variation law of the stress peaks of concrete around dowel bar with dowel bar spacing |
由图 10分析可知:在传力杆布设间距从250 mm增加到450 mm过程中,杆周混凝土各应力峰值不断增长,且增长速度随布设间距的增加而增加,水平拉应力峰值增加了33%,竖向拉应力峰值增加了48%,竖向压应力峰值增加了35%,剪应力峰值增加了33%.
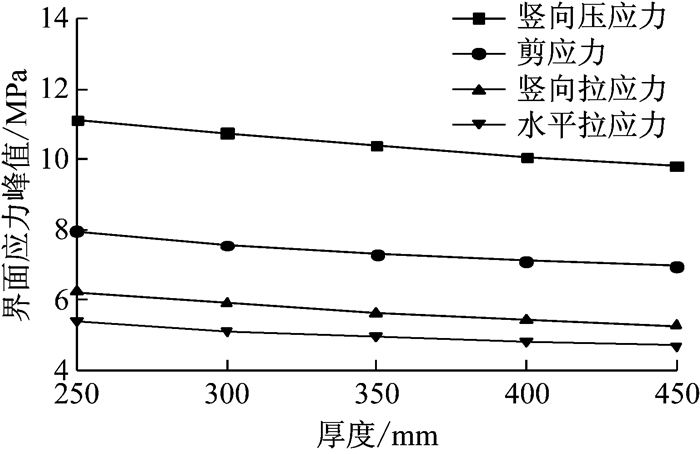
2.4.4 面层板厚度对力学响应的影响在设计新建道面时,道面厚度是需要着重考虑的.因此,讨论杆周混凝土力学响应的影响因素时,除了考虑传力杆有关的参数,道面厚度的影响也需进行研究.道面的厚度会直接影响荷载作用下的板块变形和应力,同时不同面板厚度对应不同的道面板相对刚度半径,会对传力杆接缝系统的荷载分配产生影响.选取的面板厚度分别为250、300、350、400、450 mm,受荷板中杆周混凝土应力峰值的变化规律如图 11所示.
|
图 11 杆周混凝土应力峰值随面板厚度变化规律 Fig.11 Variation law of the stress peaks of concrete around dowel bar with the thickness of slab |
由图 11分析可知,杆周混凝土各应力峰值随着面板厚度的增加而减小,且与面板厚度变化大致呈线性关系.由于面层厚度增大,使道面结构的强度增加,面层结构的变形减小,应力峰值变化量较小.
3 结论(1) 受荷板杆周混凝土顶部会产生较大的水平拉应力和竖向压应力,两侧产生较大的竖向拉应力,剪应力峰值出现在圆周斜上部.对比各个应力的最大值,受荷板均大于非受荷板.
(2) 混凝土-传力杆接触界面摩擦系数存在一个合理的取值范围,从有限元计算结果来看,摩擦系数μ取为0.5~0.8区间内的值较为理想,其受力合理.
(3) 传力杆直径增加可有效减小杆周混凝土各应力峰值,且传力杆直径从28mm增加到36mm过程中,拉应力峰值减小幅度达到30%以上.
(4) 传力杆布设间距增加会使杆周混凝土应力峰值增大,其中竖向拉应力峰值增大幅度最大,且应力峰值的增长速度随着布设间距的增加而增加.
(5) 增加面板的厚度,会少量降低杆周混凝土的各应力峰值,且各应力峰值与面板厚度变化大致呈线性关系.
| [1] |
蒋应军, 戴经梁. 传力杆与混凝土界面的接触应力[J]. 中国公路学报, 2007, 20(2): 29 JIANG Yingjun, DAI Jingliang. Contact stresses at interfaces between dowels and surrounding concrete[J]. China Journal of Highway and Transport, 2007, 20(2): 29 |
| [2] |
FRIBERG B F. Design of dowels in transverse joints of concrete pavements[J]. Transactions: American Society of Civil Engineers, 1940, 105(2081): 1076 |
| [3] |
SNYDER M B. Cyclic shear load testing of dowels in PCC pavement repairs[R]. Washington D C: Transportation Research Board, 1989.
|
| [4] |
TIMOSHENKO S, LESSELS J M. Applied elasticity[M]. Pennsylvania: Westinghouse Technical Night School Press, 1925
|
| [5] |
RIAD M Y, SHOUKRY S N, WILLIAM G W, et al. Effect of skewed joints on the performance of jointed concrete pavement through 3D dynamic finite element analysis[J]. International Journal of Pavement Engineering, 2009, 10(4): 251 DOI:10.1080/10298430701771783 |
| [6] |
TABATABAIE A M. Structural analysis of concrete pavement joints[M]. Champaign: University of Illinois at Urbana, 1978
|
| [7] |
HUANG Y H. A Computer package for structural analysis of concrete pavements[C]//The Third International Conference on Concrete Pavement Design and Rehabilitation. West Lafayette: Purdue University, 1985: 295-307.
|
| [8] |
GUO H, SHERWOOD J A, SNYDER M B. Component dowel-bar model for load transfer systems in PCC pavements[J]. Journal of Transportation Engineering, ASCE, 1995, 121(3): 289 DOI:10.1061/(ASCE)0733-947X(1995)121:3(289) |
| [9] |
SHOUKRY S N. 3D finite element modeling for pavement analysis and design[C]//The First National Symposium on 3D Finite Element Modeling for Pavement Analysis and Design. Charleston: [s. n. ], 1998: 1-92.
|
| [10] |
MACKIEWICZ P. Finite-element analysis of stress concentration around dowel bars in jointed plain concrete pavement[J]. Journal of Transportation Engineering, 2015, 141(6): 116 |
| [11] |
尹海波, 张东红, 韩建兴, 等. 传力杆对水泥混凝土面层接缝处受力状态影响分析[J]. 公路交通科技(应用技术版), 2016, 12(7): 157 YIN Haibo, ZHANG Donghong, HAN Jianxing, et al. Analysis of the mechanical condition of cement concrete slab joints influenced by dowel bars[J]. Journal of Highway and Transportation Research and Development (Applied Technology), 2016, 12(7): 157 |
| [12] |
高玉换. 基于机场水泥混凝土道面板传荷性能的传力杆设计研究[D]. 天津: 中国民航大学, 2015. GAO Yuhuan. Design research of dowel based on the load transfer performance of airport cement concrete pavement[D]. Tianjin: Civil Aviation University of China, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10059-1016776293.htm |
| [13] |
赵炜诚, 许志鸿, 黄文. 混凝土面层与贫混凝土基层的层间作用对荷载应力和弯沉的影响[J]. 中国公路学报, 2003, 16(4): 9 ZHAO Weicheng, XU Zhihong, HUANG Wen. Influence of load stress and deflection on interfacial interaction between portland concrete pavement and lean concrete base[J]. China Journal of Highway and Transport, 2003, 16(4): 9 |
| [14] |
TABATABAIE A M, BARENBURG E J, SMITH R E. Longitudinal joint systems in slipformed rigid pavements: Vol. Ⅱ-Analysis of load transfer systems for concrete pavements[R]. Champaign: Federal Aviation Administration, U. S. Department of Transportation, 1979.
|
| [15] |
吕艳梅, 刘立新, 徐有邻. 商品混凝土收缩应力试验研究[J]. 东南大学学报(自然科学版), 2005, 35(7): 144 LV Yanmei, LIU Lixin, XU Youlin. Experimental study on shrinkage stress of commercial concrete[J]. Journal of Southeast University (Natural Science Edition), 2005, 35(7): 144 |
 2018, Vol. 46
2018, Vol. 46
