2. 成都市双流区交通运输局,四川 成都 610200
2. Transportation Bureau of Shuangliu District, Chengdu 610200, China
城际铁路作为城际运输通道中新兴的出行方式,其建设运营会使运力资源在运输通道内重新配置.城际铁路的开行方案不同,会导致城际运输通道内的客流在不同的交通方式间重新分配,城际铁路列车开行频率提高能减少旅客等待时间,可吸引通道更多的客流.同时,通过客流转移到城际铁路这种绿色交通方式,其他交通方式的外部成本(包括环境污染成本、事故成本等)也随之减少,进一步减少社会总成本.在环境污染日益严重和社会对节能减排大力倡导的情况下,城际铁路作为快捷、舒适、节能、环保的交通运输方式,应合理确定列车的开行频率,提高客运服务水平,这样既吸引足够的客流增加自身效益,同时还能降低运输通道的社会总成本.
关于城际列车开行方案优化方面的研究,国内外已经取得了一系列的成果,研究主要集中于以企业运营成本最小和企业效益最大2个方面.在以企业运营成本最小为优化目标的研究中,文献[1]以运输能力和旅客需求为约束建立了非线性整数规划模型,以运营成本最小化为目标,对于列车服务频率、运行路径和编组数进行优化;文献[2]将旅客的路径选择行为描述为多商品流问题,同样以铁路企业的运营成本最小为目标函数,研究了同一路径中不同等级列车的开行方案优化模型及其算法.在以企业效益最大为优化目标的研究中,文献[3]以铁路企业效益最大化为目标,对列车开行频率和票价进行组合优化;文献[4]进一步考虑了旅客的需求,以铁路企业的效益最大化为上层目标、多类用户平衡分配为下层目标,建立了旅客列车开行方案优化的双层规划模型;文献[5]将铁路企业的效用最大化与旅客的效用最大化同时作为目标,建立开行方案多目标非线性混合整数规划模型,利用客流需求量、列车定员数、列车运输能力作为约束条件进行求解.另外在关于交通流分配模型的研究中,文献[6]将旅客乘车方案的选择描述为弹性需求下的用户平衡分配问题,从而建立弹性需求下旅客列车开行方案规划模型.综上,国内外对城际列车开行方案及开行频率优化的研究,只考虑铁路企业效益以及乘客的效益,并没有考虑各交通方式外部成本对于社会总成本的影响,不利于区域通道交通的可持续发展.因此,本文分别以铁路效益最大化与社会总成本最小化为目标,建立相应的双层规划模型,研究不同目标下客运通道内的客流分担率与城际列车开行频率的优化,为可持续发展的区域交通提供科学理论依据.
1 城际运输通道内的客流分配 1.1 城际客运通道虚拟网络将运输通道内各交通方式的路径看成一张由“节点”与“弧段”2个基本要素组成的运输通道虚拟网络,其中节点代表网络中的城市,弧段代表相应的城市之间的交通方式.节点包括3种类型,分别是车站节点、列车停车节点和列车发车节点;弧段则分为上车弧段、下车弧段、乘车弧段与停车弧段.
设G=(N, A)为运输通道网络,其符号和变量定义如下:N为网络中节点的集合, 包括车站节点、列车发车节点、列车停车节点;A为网络中弧段的集合,包括上车弧段,下车弧段、乘车弧段、停车弧段;a为网络中的某一弧段,a∈A;W为网络中所有OD(起终点)对的集合;w为网络的某一个OD对w, w∈W;kw为OD对w之间的所有交通方式,k∈{g, r, b, c},g表示城际列车,r表示普通铁路,b表示大巴,c表示小汽车;dw为OD对w之间的客运需求量;qwk为OD对w之间的某种方式的客运需求量;cwk为OD对w之间某种方式的广义出行费用;qmG为OD对w之间的城际铁路的客运需求量;Ta为弧段上a的阻抗函数;Qwl为OD对w之间的第l条路径的客流量.
1.2 基于用户均衡的交通流分配将运输通道内部不同的交通方式看成不同的路径,引入交通流分配中的用户均衡理论.运输通道内存在运输方式之间的竞争,运输方式的广义出行费用随着客流量的变化而变化,同时客流量的变化也影响广义出行费用的变化.假定不同交通方式的广义费用函数采用幂函数的形式[7],广义费用函数cwk与该交通方式客流量qwk以及效用Vwk的关系为
| $ {c_{wk}} = f\left( {{q_{wk}}} \right) = g\left( {{q_{wk}}} \right) - {V_{wk}} $ | (1) |
| $ {V_{wk}} = {\theta _1}{P_{wk}} + {\theta _2}{Y_{wk}} + {\theta _3}{E_{wk}} + {\theta _4}{R_{wk}} + {\theta _5}{S_{wk}} $ | (2) |
式中:Pwk为交通方式的票价;Twk为交通方式的旅行时间;Swk为交通方式的安全性;Ewk为交通方式等待时间;Rwk为交通方式的舒适性;g为待定参数;θ1、θ2、θ3、θ4、θ5分别为交通方式的票价、行程时间、等待时间(候车时间、出入站时间)、舒适性、安全性的权重系数[8].
建立基于用户平衡的运输通道内交通流分配模型如下.模型假设为:①城际间客流往往采用同一种直达的交通方式,因此不考虑中途换乘的情况;②暂不考虑大巴的能力限制,假设长途汽车公司的运能足够,并能及时调整运营方案;③模型假设普速铁路采用站站停开行方案,且运输能力满足普速铁路旅客的出行需求.根据用户均衡原理,建立基于用户均衡的城际通道交通流分配模型,为
| $ \min \left( {{q_{wk}}} \right) = \sum\limits_{w \in W} {\sum\limits_{k \in K} {\int_0^{{q_{wk}}} {{C_{wk}}{\rm{d}}x} } } $ | (3) |
约束条件为
| $ \sum\limits_k {{q_{wk}}} = {d_w},w \in W $ | (4) |
| $ {q_{wk}} \ge 0,\;\;\;k \in K,w \in W $ | (5) |
式(4)表示OD对w间的客流量是固定且OD对w之间各种交通方式的客流量之和等于其总的客流量.式(5)表明各种交通方式的客流量是非负的.根据上述式,可求出OD对w之间某种交通方式的客运量分担率为
| $ {p_{wk}} = \frac{{{q_{wk}}}}{{{d_w}}} $ | (6) |
由于OD间开行不同等级的城际旅客列车,因此需要将城际客流量分配到不同等级的列车,故在上式的基础上建立城际列车客流分配模型.
| $ \min \left( {{q_{wk}}} \right) = \sum\limits_a {\int_0^{{q_a}} {{C_a}\left( q \right){\rm{d}}q} } $ | (7) |
约束条件为
| $ \sum\limits_l {{q_{wl}}} = {q_{wG}},w \in W $ | (8) |
| $ {q_{wl}} \ge 0,l \in {l_w},w \in W $ | (9) |
| $ {q_a} = \sum\limits_w {\sum\limits_l {{q_{wl}}{\delta _{wal}}} } ,l \in {l_w},w \in W $ | (10) |
式中:lw表示铁路网络中w之间所有的路径的集合;qa为弧段a上的铁路客流量;Ca为弧段a的铁路出行广义费用函数;qwl为OD对w之间的第l条路径的客流量;δwal为0、-1变量, 若弧段a在OD对w之间的第l条路径上, 则δal=1, 否则δal=0.
式(8)表示OD对w间客运专线的客流量,OD对w之间所有被选择的路径流量之和等于w之间城际列车的流量.式(9)表明各条被选择的路径的客流量是非负的.
1.3 弧段阻抗函数 1.3.1 上车弧段的阻抗函数上车弧段Ta1含旅客进站时间及候车时间,候车时间长短与列车发车频率有关.旅客进站时间含排队购票或换票及进入候车室所支出的时间消耗.
| $ {T_{a1}} = \alpha \left( {{t_{a{\rm{in}}}} + {w_t}} \right) $ | (11) |
式中:tain为旅客进站时间;
以甲到丙的客流为例,因在甲站可供选择的城际列车共3种,所以甲站旅客平均等待时间为
| $ w{t_a} = 0.5/\left( {{f_1} + {f_2} + {f_3}} \right) $ | (12) |
式中:f1、f2、f3分别为城际列车1、2、3的开行频率.
1.3.2 乘车弧段的阻抗函数乘车弧段Ta2的阻抗由旅客的票价支出(由运价率和乘车距离决定)、列车运行的时间、拥挤费用以及停站时间阻抗组成.
| $ {T_{a2}} = {D_a}{P_{a1}} + \omega {t_{a{\rm{run}}}}{\left( {{q_a}/{U_a}} \right)^\theta } + \alpha \left( {{t_{a{\rm{run}}}} + {t_{a{\rm{stop}}}}} \right) $ | (13) |
式中:Da为弧段a乘客的乘车距离,即对应铁路线路的实际长度;Pal为弧段a对应的运价率,即1 km的费用;tarun为列车在弧段a上的纯运行时间;qa为弧段a的实际客流量; Ua为弧段a核定载客量;tastop代表列车在弧段a内的停站时间;ω、θ为拥挤的惩罚系数.
1.3.3 下车弧段的阻抗函数| $ {T_{a2}} = \alpha {t_{a{\rm{out}}}} $ | (14) |
式中:taout为旅客离开车站的平均出站时间.
2 开行频率的双层规划模型 2.1 双层模型建立将客流分配模型定为下层规划模型,上层规划模型分别为铁路企业运营效益最大化与运输通道社会成本最小化,通过构建双层规划模型来求出不同目标下城际列车的最优开行频率.
设城际铁路网络G(H, E)具有n个车站、m条路段,其中:H={h1, h2, …, hn}表示所有车站的集合;E={e1, e2, …, em}为所有路段的集合;DE={Dei, ei∈E}表示所有路段里程的集合,其中Dei代表路段的里程;qei为网络中路段ei的客流量;Nhi代表车站hi的始发列车能力;Nei代表路段的通行能力;CG为动车组1 km的运行成本;β=(1, 2, 3)表示不同种类的高速列车;L代表城际铁路所有路径的集合;sβL、fβL、AβL、bβL分别为等级为β的列车的行驶距离、开行频率、列车定员数和列车编组数.
2.1.1 铁路企业效益最大化当目标函数为铁路企业运营效益最大化时,双层规划的上层规划模型如下:
| $ \max {Y_1} = \sum\limits_\beta {\sum\limits_l {\sum\limits_{{e_i}} {q_\beta ^{{e_i}}{P_\beta }{D_{{e_i}}}} } } - \sum\limits_\beta {\sum\limits_l {f_l^\beta s_l^\beta b_l^\beta {C_{\rm{G}}}} } $ | (15) |
约束条件为
| $ \sum\limits_l {\sum\limits_\beta {{f_{\beta l}}} } \le {N_{{h_i}}},i \in n $ | (16) |
| $ \sum\limits_l {\sum\limits_\beta {{f_{\beta l}}} } \le {N_{{e_i}}},i \in n $ | (17) |
| $ {q_{{e_i}}} = \sum\limits_{{e_i} \in w} {{q_{wG}}} ,i \in m $ | (18) |
| $ {q_{{e_i}}} \le \sum\limits_\beta {\sum\limits_{l \in L} {{f_{\beta l}}{A_{\beta l}}} } ,i \in m $ | (19) |
| $ {q_{{e_i}{\beta _l}}} \le {f_{\beta l}}{A_{\beta l}},i \in m $ | (20) |
| $ {f_{\beta l}} \ge 0 $ | (21) |
式中:Nhi代表车站的通过能力,表示车站的到发列车数不能超过其通过能力;Nei代表路段的通过能力,表示路段上行驶的列车数不能超过路段的通过能力;式(18)代表路段ei的客流量等于通过该路段的OD客流之和;式(19)表示各路段的客流量不能大于通过该路段的所有列车的定员数之和;式(20)为路径l、等级β的高速列车在路段ei上的载客量不能超过其载客能力;式(21)为开行频率的非负约束.
2.1.2 社会总成本最小化当目标函数为社会总成本最小化时,则需要同时考虑铁路企业和大巴运营企业和小汽车的运营成本,并考虑小汽车的外部成本,使用外部成本内部化的手段来建立目标函数.铁路运营企业的运营成本为
| $ {R_{\rm{r}}} = \sum\limits_\beta {\sum\limits_l {{f_{\beta l}}{s_{\beta l}}{b_{\beta l}}{C_{rh}}} } + {f_{\rm{r}}}{s_{\rm{r}}}{b_{\rm{r}}}{C_{\rm{r}}} $ | (22) |
模型假设大巴运营公司能够随时掌握客流变化,并根据客流来调整运营策略,满足客流需求.大巴运营公司的运营成本为
| $ {R_{\rm{b}}} = \sum\limits_w {{C_{\rm{b}}}{s_{w{\rm{b}}}}{q_{w{\rm{b}}}}/{\delta _{\rm{b}}}} $ | (23) |
式中:Cb为每辆大巴1 km的运营成本;δb为大巴的平均乘客人数,人·车-1.小汽车的使用成本为
| $ {R_{\rm{c}}} = \sum\limits_w {{q_{w{\rm{c}}}}{C_{\rm{c}}}{s_w}/{\delta _{\rm{c}}}} $ | (24) |
式中:Cc为OD对w之间采用小汽车出行的旅客1 km所花费的货币成本;δc为小汽车的平均乘客人数,人·车-1.小汽车的外部成本为
| $ {R_{\rm{e}}} = \sum\limits_w {{E_{\rm{c}}}{q_{w{\rm{c}}}}{s_w}/{\delta _{\rm{c}}}} $ | (25) |
式中:Ec为汽车1 km行驶所产生的外部成本.
因此可以得到基于外部成本内部化的社会总成本最小的上层规划目标函数为
| $ \begin{array}{l} \min Y = {R_{\rm{r}}} + {R_{\rm{b}}} + {R_{\rm{c}}} + {R_{\rm{e}}} = \sum\limits_\beta {\sum\limits_l {{f_{\beta l}}{s_{\beta l}}{b_{\beta l}}{C_{rh}}} } + \\ \;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_w {{C_{\rm{b}}}{s_{w{\rm{b}}}}{q_{w{\rm{b}}}}/{\delta _{\rm{b}}}} + \sum\limits_w {{q_{w{\rm{c}}}}{C_{\rm{c}}}{s_w}/{\delta _{\rm{c}}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_w {{E_{\rm{c}}}{q_{w{\rm{c}}}}{s_w}/{\delta _{\rm{c}}}} + {f_{\rm{r}}}{s_{\rm{r}}}{b_{\rm{r}}}{C_{\rm{r}}} \end{array} $ | (26) |
其约束条件和下层模型都与上述铁路企业效益最大化的模型一致.
2.2 模型的模拟退火算法设计鉴于双层规划模型求解的复杂性,采用模拟退火算法进行求解.
模拟退火算法[8]基于对固体退火过程的模拟,用冷却进度表来控制算法的进程, 使算法在控制参数T徐徐降温并趋于零时最终求得组合优化问题的相对全局最优解.其中优化问题的一个解χ及其目标函数f(χ)分别与固体的一个微观状态χ及其能量Eχ相对应.令算法进程递减的控制参数T担当固体退火过程中温度的角色,则对于的每一取值,算法采用Metropolis接受准则,持续进行“产生新解—判断—接受或舍弃”的迭代过程而达到该温度下的平衡点.
利用模拟退火算法求解双层规划模型,具体求解步骤如下:
步骤1.设置初始温度值T0,设计温度下降比例αT,终值温度Tend;当前的温度T=T0.Markov链长度为Lk.
步骤2.产生初始解f0;判断初始解的可行性,若不可行,则进行调整,否则转步骤3,并令最优解fs=f0.
步骤3.根据当前解,利用所得模型和算法求解下层客流分配模型,获得客流在不同交通方式和城际铁路不同等级列车上的分配.
步骤4.根据客流的分配方案和初始的f0算出上层规划目标函数的值Y0,令目标函数的当前的最优值Ys=Y0.
步骤5.生成邻域解,判断新解的可行性,可行则转步骤3.算出新解和当前解的目标函数值的差值ΔY;根据接受准则计算接受概率P(ΔY, T),取在(0, 1)上均匀分布的随机数θ,P(ΔY, T)则接受新解,否则放弃新解.
步骤6.如果接受新解,则更新最优解和最优值.
步骤7.计算迭代次数n,若n<Lk,则在此温度下的迭代尚未结束,未完成一个Markov链长的迭代,转步骤5.
步骤8.判断是否满足算法的终止准则,若T>Tend,继续降温,令T=αTT,继续转步骤3,否则,算法终止,输出当前解.
3 算例研究 3.1 算例参数某城际铁路沿线有4个城市,其中A、D为城际运输通道内的大城市,也是该线路的始终点站,城市C为中型城市,城市B为小型城市,不考虑途中换乘.城市之间的距离分别为80 km、100 km和120 km.该运输通道内共有4种交通方式:城际列车、普通铁路、大巴、小汽车,其中,城际列车共有3种列车等级,站站停、大站停以及直达列车.城市之间的距离和OD对之间客流量如图 1和表 1所示.

|
图 1 城市之间的距离 Fig.1 Distance between cities |
| 下载CSV 表 1 OD对之间的客流量 Tab.1 Hourly passenger flow between OD pairs |
为了计算方便,算例中认为城市之间的距离即为城市之间高速公路、铁路的行程距离.
不同交通方式的运价率、运行速度、等待时间、安全性和舒适度(其中运价率、运行速度由沪杭通道的实际值估算得来)其数值如表 2所示.
| 下载CSV 表 3 旅客进出站及列车停站时间标准 Tab.3 Relevant time standard of passengers in and out of the station and trains stop |
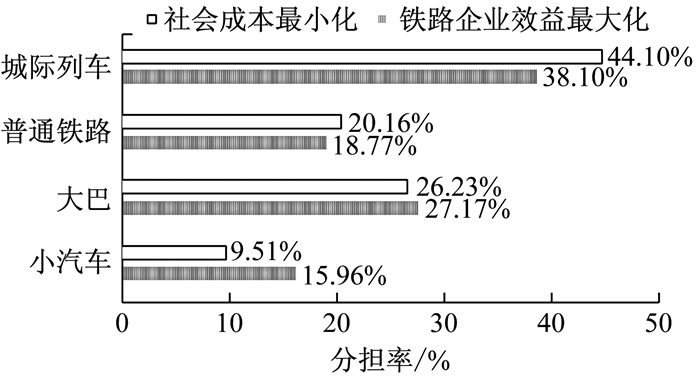
以算例中给出的线路条件、运营方案、列车等级等相关的参数为输入值,运用模拟退火算法,分别以铁路运营企业效益最大化和社会总成本最小化为目标,计算出不同目标下城际列车分担率、不同等级城际列车的开行频率以及对应的企业效益与社会成本.在铁路企业效益最大化和社会成本最小化目标下,运输通道内各交通方式分担率如图 2所示.
|
图 2 不同目标下运输通道交通方式分担率的对比 Fig.2 Comparison among sharing rate of all transport modes in transport corridor under different objectives |
可知在将上层目标从企业效益最大化改为社会成本最小化后,城际列车、普通铁路的交通分担率提高,相反,大巴、小汽车的分担率降低.城际列车和小汽车的分担率变化程度最为明显,城际列车从38.10%上升至44.10%,小汽车从15.96%下降至9.51%,这说明考虑了小汽车的外部成本以后,小汽车承担的客流向其他交通方式转移,大部分转移到了更为绿色环保的城际铁路.
根据各交通方式分担率,进一步计算得到不同目标下OD对之间不同等级城际列车客流量分别如表 5和表 6所示.
| 下载CSV 表 5 目标1下OD对间不同等级城际列车客流 Tab.5 Passenger flow between OD pairs of different-ranks trains under the first object |
| 下载CSV 表 6 目标2下OD对间不同等级城际列车客流 Tab.6 Passenger flow between OD pairs of different-ranks trains under the second object |
基于城际OD客流,计算得到不同目标下不同等级城际列车的最优开行频率以及所对应的席位利用率、企业效益与社会总成本,如表 7所示.
| 下载CSV 表 7 不同目标下的城际列车最优开行频率、企业效益与社会成本 Tab.7 Operating frequency, benefits and cost of intercity trains under different objects |
通过所得数据计算,可以得出在目标1企业效益最大化下的最优开行方案中,城际列车1、2、3的席位利用率分别为93.00%、87.25%、82.22%,而在目标2社会总成本最小化下的最优开行方案中,城际列车1、2、3的席位利用率分别下降为69.63%、74.30%、67.05%,利用率有大幅度的降低.
由以上结果,可以得出以下结论:
(1) 以社会总成本最小为目标时,由于综合考虑了小汽车外部成本的内部化,小汽车广义出行费用增加,使得小汽车的使用者向其他交通方式转移,大部分转移至城际铁路,因而城际铁路的最优开行频率增加.同时开行频率的增加会降低其广义出行费用,引起采用其他交通方式出行的旅客向城际铁路转移,城际铁路分担率的上升、其他交通方式中小汽车客流分担率的下降尤其明显.
(2) 以铁路运营企业效益最大化为目标时,城际铁路的最优开行频率比以社会总成本最小化为目标时低,各等级列车的席位利用率增大,其中直达模式的利用率达到了90%以上.以社会成本最小化为目标时,城际列车的交通分担率提高,城际列车开行的数量增加,但此时各列车的席位利用率下降,铁路企业效益也会下降.一定程度上说明此时增加城际列车开行数量并没有吸引足够的客流来弥补企业运营成本的增加.
(3) 从上表可见需要在牺牲企业效益的前提下才能够达到社会总成本最小,因此政府部门为促进运输通道内社会总成本最小化时需要适当对铁路企业进行政策优惠或补贴,使得铁路企业的开行方案在企业效益目标和社会总成本目标中达到一致.
4 结语运用乘客广义出行费用理论,考虑交通方式的外部成本,构建双层规划模型,运用用户均衡理论、采用模拟退火算法,得到不同交通方式的流量、分担率,并将城际列车的客流量分配到不同等级的列车上,求得该条件下企业的最大效益和运输通道内最小社会总成本,计算相应最优城际列车开行频率.从上述分析可知,合理的城际铁路开行频率能有效减少整个运输通道的外部成本,但增加城际铁路列车开行数量带来的企业收入并不能够弥补其随之增加的运营成本,所以政府部门在决策时应该向城际铁路这种社会效益更高的交通方式倾斜,并提供一定的补贴、优惠政策来弥补铁路企业牺牲的效益,从而使交通结构趋于节能环保,从而实现运输通道的可持续发展.
| [1] |
CLAESSENS M T, van Dijk N M, ZWANEVELD P J. Cost optimal allocation of rail passenger lines[J]. European Journal of Operational Research, 1998, 110: 474 DOI:10.1016/S0377-2217(97)00271-3 |
| [2] |
GOOSSENS Jan-Willem. Models and algorithms for railway line planning problem[D]. [S. l. ]: Open Access Publications from Maastricht University, 2004.
|
| [3] |
史峰, 罗端高, 王英姿, 等. 基于弹性需求的城市间客车开行频率与票价优化[J]. 吉林大学学报(工学版), 2009, 39(6): 1475 SHI Feng, LUO Duangao, WANG Yingzi, et al. Optimization of operating frequency and ticket price of intercity bus with elastic demand[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(6): 1475 |
| [4] |
史峰, 邓连波, 霍亮. 旅客列车开行方案的双层规划模型和算法[J]. 中国铁道科学, 2007, 28(3): 110 SHI FENG, DENG Lianbo, HUO Liang. Bi-level programming model and algorithm of passenger train operation plan[J]. China Railway Science, 2007, 28(3): 110 |
| [5] |
张拥军, 任民, 杜文. 高速列车开行方案研究[J]. 西南交通大学学报, 1998, 33(4): 400 ZHANG Yongjun, REN Min, DU Wen. Optimization of high speed train operation[J]. Journal of Southwest Jiaotong University, 1998, 33(4): 400 |
| [6] |
史峰, 周文梁, 陈彦, 等. 基于弹性需求的旅客列车开行方案优化研究[J]. 铁道学报, 2008, 30(3): 1 SHI Feng, ZHOU Wenliang, CHEN Yan, et al. Optimization study on passenger train plans with elastic demands[J]. Journal of the China Railway Society, 2008, 30(3): 1 |
| [7] |
叶玉玲, 程正. 客运走廊多模式交通条件下票价与运输需求的关系[J]. 城市轨道交通研究, 2011, 14(12): 32 YE Yuling, CHENG Zheng. Fares and transport needs on the condition of multi-mode traffic on passenger transportation corridor[J]. Urban Mass Transit, 2011, 14(12): 32 |
| [8] |
毛敏, 蒲云, 喻翔. 外部成本对城市客运交通结构的影响分析[J]. 公路交通科技, 2004, 21(11): 37 MAO Min, PU Yun, YU Xiang. Analysis of the impact of external costs on urban passenger transport system structure[J]. Journal of Highway and Transportation Research and Development, 2004, 21(11): 37 |
| [9] |
庞峰. 模拟退火算法的原理及算法在优化问题上的应用[D]. 吉林: 吉林大学, 2006. PANG Feng. The principle of SA algorithm and algorithm's application on optimization problem[D]. Jilin: Jilin University, 2006. http://cdmd.cnki.com.cn/article/cdmd-10183-2007017704.htm |
| [10] |
杨瑜, 王怀相. 高速铁路运输综合成本测算研究[J]. 铁道工程学报, 2009, 1(1): 102 YANG Yu, WANG Huaixiang. Study on comprehensive cost calculation of high speed railway transportation[J]. Journal of Railway Engineering Society, 2009, 1(1): 102 |
 2018, Vol. 46
2018, Vol. 46
