2. 同济大学 数学科学学院,上海 200092
2. School of Mathematical Sciences, Tongji University, Shanghai 200092, China
中国高速公路从2009年起平均每年增长约8 000 km,截至2016年底已达到125 373 km[1],新建高速公路主要分布于中西部山区.由于受地质地形、建设资金等因素限制,中西部山区的高速公路多数由二、三级公路改建而成,线形设计参数的设计标准较低.山区高速公路包含大量平曲线与纵坡组合的线形(以下简称组合线形),单一平曲线或竖曲线设计要素满足规范,但两者相组合则可能出现安全隐患.组合线形的驾驶风险要高于单一曲线,平曲线曲率与坡度结合更易导致驾驶员视觉感知错误从而进行有风险的操作[2-4].《公路路线设计规范》[5]和《公路工程设计标准》[6]对平曲线、纵断面有相应的定量标准,但对组合线形只有定性规定.如《公路路线设计规范》规定:设计速度大于或等于60 km·h-1的公路,应注重路线平纵组合线形设计; 长竖曲线内不宜设置小半径平曲线; 长直线不宜与坡陡或小半径且长度短的竖曲线组合.
现有的组合线形设计评估方法主要有透视图[2]、计算机仿真[7]、视距检验[6]及运行速度协调性检验[8]等.前三种方法通过绘制驾驶员视野图或进行视距校核完成评估,但缺乏车速、加减速等数据,无法反映车辆的运行特征.运行速度协调性检验通过车速差进行线形设计评估,车速变化过大会降低乘客舒适感,影响交通运行,甚至增加驾驶风险.车速差绝对值超过20 km·h-1时,线形需要调整[9-10].然而, 现有的检验方法只给出了阈值,并没有明确平纵几何特征与车速差的定量关系.明确两者的定量关系有助于对设计阶段的道路进行线形几何要素调整,对已建道路进行安全改善.
Gibreel等[11]利用雷达测速仪实地采集组合线形路段的车速,发现平曲线凹曲线的实际运行速度比传统模型预测结果高,而平曲线凸曲线则相反,说明组合线形对车速的影响比单一线形复杂.Wang等[12]对组合线形与横向加速度定量关系的研究结果表明,平曲线上坡、下坡的曲率与横向加速度正相关,坡度与横向加速度负相关, 平曲线凸曲线的长度、曲率与横向加速度正相关, 平曲线凹曲线的曲率与横向加速度正相关.大部分的研究只考虑了组合线形半径、坡长、坡度等几何设计要素,缺乏对相邻路段的研究.相邻路段几何特征可能会影响驾驶员在组合线形上的驾驶行为,如驾驶员在平曲线上坡行驶,下游路段为下坡将会影响视距,进而使其减速,车速发生变化.
基于湖南省永吉高速公路几何特征及周边地形环境等参数,利用同济大学八自由度驾驶模拟器建立虚拟场景进行实验并采集车速数据,将车速变化划分为减速、稳定车速及提速3个区间.通过多项Logistic回归模型分析组合线形及相邻路段与车速变化的定量关系.该研究有助于理解组合线形对车速变化的影响机理,为完善组合线形设计评估及设计标准提供理论基础.
1 组合线形及相邻路段几何特征提取永吉高速公路主线全长82.925 km,是湖南省“七纵九横”高速公路网中第七纵的一段,也是西北部区域通往湖北省的重要通道.地貌地形以溶蚀构造中低山地貌为主,地形起伏大,沟壑林立.选取了永吉高速公路主线中的一段,全长23.960 km,道路双侧共包含23段平曲线下坡、21段平曲线上坡.路基宽24.50 m,横断面宽10.50 m,包含3.75 m宽车道和1.50 m宽路肩,设计速度为80 km·h-1.
针对组合线形平曲线提取了进入圆曲线缓和曲线(缓和曲线1)、圆曲线及离开圆曲线缓和曲线(缓和曲线2)相应的几何特征,包含曲线长度、半径、方向等; 针对纵断面,采集了坡度、坡长、坡度差、坡度类型及变坡点位置.组合线形几何特征如图 1所示.

|
图 1 组合线形几何特征 Fig.1 Geometric characteristics of combined curves |
平曲线上坡、平曲线下坡组合线形的几何特征连续变量统计描述见表 1,几何特征离散变量统计描述见表 2.
| 下载CSV 表 1 组合线形几何特征连续变量统计描述 Tab.1 Statistical description of continuous variables of geometric characteristics of combined curves |
| 下载CSV 表 2 组合线形几何特征离散变量统计描述 Tab.2 Statistical description of discrete variables of geometric characteristics of combined curves |
为了研究相邻路段对车速变化的影响,提取了相邻路段300 m范围的几何特征,与《公路工程技术标准》[6]规定的设计速度80 km·h-1高速公路识别视距300 m一致.研究对象如图 2所示.

|
图 2 组合线形与相邻路段示意图 Fig.2 Diagram of combined curves and adjacent segments |
针对相邻路段,提取的最大、最小曲率能够反映相邻路段的转弯缓急程度, 提取的最大坡度能够体现相邻路段是急坡还是平缓路段.考虑线形设计的均衡、连续,提取了相邻路段与组合线形路段的坡度差与曲率差,如表 3所示.
| 下载CSV 表 3 相邻路段几何特征统计描述 Tab.3 Statistical description of geometric characteristics of adjacent segments |
同济大学高仿真驾驶模拟器拥有八自由度运动系统(六自由度加X轴和Y轴).模拟舱是一个封闭式刚性结构球体,中央放置了一辆去掉发动机的轿车,车内安装了轮胎、方向盘、刹车、换档的力反馈系统和数据输入输出设备,车辆后视镜由3块液晶显示屏组成,所有操作与实车完全相同.投影系统由5个投影仪组成,可视范围达到250°×40°,每个投影仪的分辨率为1 400×1 050,刷新率为60帧·s-1(见图 3).模拟器以20 Hz的频率采集实验数据.
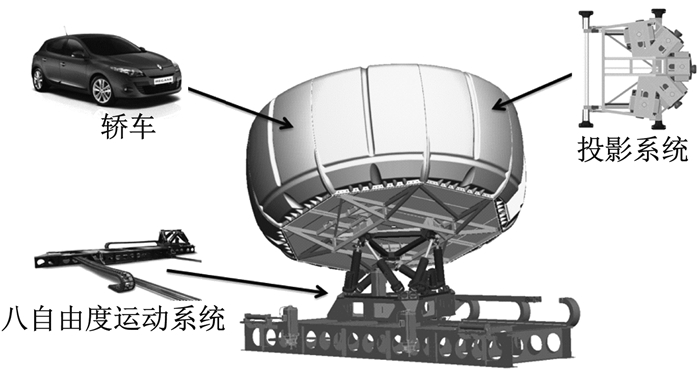
|
图 3 同济大学驾驶模拟器 Fig.3 Tongji University Driving Simulator |
驾驶模拟器于2011年建成,为了验证其有效性,在投入使用前进行了整体性能测试,内容包括模拟器眩晕、停车距离、交通标志尺寸3项测试.以超过75%参与者通过测试为标准.参与者同时通过3项测试,认为其通过了模拟器整体性能测试.模拟器眩晕测试:在15 min后对参与者进行眩晕问卷调查,该问卷主要对参与者的各种不适反应进行0~3评分(0为无不适,1为轻微不适,2为中等程度不适,3为严重不适),评分超过2以上的参与者即被认为有眩晕反应.结果显示,80%的参与者没有不适感.停车距离测试:测试参与者能否将车停在要求的停车线上.结果显示,79%的参与者通过连续刹车停车并控制在停车线2 m范围以内,通过了停车距离测试.交通标志尺寸测试:对比真实交通标志尺寸和在模拟器中显示的大小.结果显示,75%的参与者认为模拟器中显示的交通标志尺寸很真实[13].
2.2 三维虚拟驾驶场景为了确保实验环境的逼真度和数据的有效性,本研究依据永吉高速公路所处地形数据及其线形设计数据建立了三维虚拟驾驶场景.主要内容如下所述:
(1) 道路逻辑层
参与者能够在八自由度的驾驶模拟器中感受到路面的坡度、倾斜、颠簸以及车辆的加减速、转向、侧滑.本研究精确地还原了设计图中道路的平纵面设计以及道路超高.
(2) 三维环境建模
道路周边环境的逼真度会直接影响实验的准确性,本研究通过实地调研对永吉高速公路的周边地形、植被进行三维建模,并根据设计图对护坡、边坡、桥隧等进行了三维建模.
(3) 模型数据库优化
三维模型的原始文件过大会使虚拟驾驶场景在模拟器引擎中的运行发生卡顿从而影响实验效果,为了使模型运行更顺畅,对地形、道路模型进行了轻量化.为了使标志标线的显示更清晰真实,对其进行了单独建模,并优化标志标线的纹理.对光源进行了测试及优化.永吉高速公路三维虚拟驾驶场景构建过程如图 4所示.
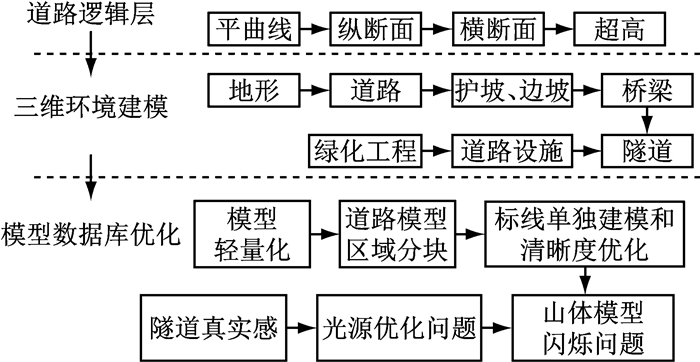
|
图 4 永吉高速公路三维虚拟驾驶场景构建过程 Fig.4 Three-dimensional scene construction process of Yongji Freeway |
实验共招募驾驶员30人,平均年龄为36.50岁,标准差为8.89岁.驾龄均值为8.30年,标准差为8.38年,其中驾龄 < 4年的占20%,≥4~10年的占56%,≥10年的占24%.根据“一周使用高速公路的次数”将驾驶员使用高速公路的频率分为4个等级:从不(几乎不使用)、偶尔(1~2次)、经常(3~4次)及一直(4次以上).30位驾驶员中经常在高速公路上开车的比例占50%.每位驾驶员的驾驶总里程不少于10 000 km,年平均里程不少于3 000 km.
3.2 实验流程实验流程主要包括以下内容:
(1) 实验准备.向驾驶员介绍实验内容及注意事项.完成个人信息、驾驶经验等基本信息采集.
(2) 模拟试驾.驾驶员进入驾驶舱,调节座椅,并熟悉舱内环境,之后进行约10 min的直行、转弯、超车及刹车等训练,熟悉模拟器操作.
(3) 正式实验.驾驶场景光线充足,路面条件干燥良好.为了减少交通环境对车速的影响,驾驶场景中不设置其他干扰车辆.由于道路双侧的几何线形不同,驾驶员需要完成双侧驾驶.
(4) 填写《眩晕不适调查问卷》.问卷通过“0为无不适、1为轻微不适、2为中等程度不适、3为严重不适”评价驾驶员有无眩晕不适症状.结果显示,30位驾驶员均无不适.
(5) 填写《驾驶模拟器场景反馈评价问卷》.问卷通过“真实、一般、不真实”3个等级评价驾驶模拟场景的真实度,如道路标志标线真实性、护栏树木真实性等,超过87%的驾驶员认为实验场景真实可靠.
3.3 数据采集提取每位驾驶员在组合线形中的车速最大值和最小值.当车速先达到最大值(v1)、后达到最小值(v2)时,车速差(Δv)为负, 反之则为正.计算公式如下所示:
| $ \Delta v = {v_2} - {v_1} $ |
车速差的平均值为0.38 km·h-1,标准差为13.82 km·h-1,最小值-41.87 km·h-1,最大值为42.30 km·h-1.95%的车速差绝对值小于20 km·h-1,5%的车速差绝对值大于20 km·h-1.车速差的分布如图 5所示.
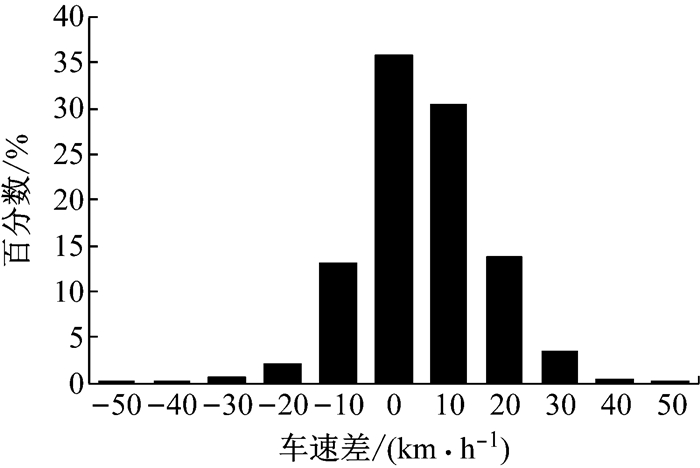
|
图 5 车速差分布 Fig.5 Distribution of speed difference |
现有的《公路项目安全性评价规范》[8]中,采用车速差绝对值20 km·h-1为阈值来评价路段的线形设计一致性.因此,本研究以20 km·h-1作为车速变化区间的划分依据,车速差小于20 km·h-1代表驾驶员减速通过组合线形路段,车速差大于20 km·h-1代表驾驶员提速通过组合线形路段,车速差绝对值在20 km·h-1内代表驾驶员车速较为平稳.
4 多项Logistic回归模型当因变量为离散型变量并多于2个类别时,可以考虑多项Logistic模型.对于具有m=2,3, …, M个类别的因变量时,以M类别作为参照组,每一个对数发生比是具体的因变量类别与参照类别的比较,模型的表达式如下所示:
| $ \begin{array}{l} {\rm{log}}\left( {\frac{{P\left( {y = 1} \right)}}{{P\left( {y = M} \right)}}} \right) = {\alpha _1} + \sum\limits_{k = 1}^K {{\beta _{1k}}{x_k}} \\ {\rm{log}}\left( {\frac{{P\left( {y = 2} \right)}}{{P\left( {y = M} \right)}}} \right) = {\alpha _2} + \sum\limits_{k = 1}^K {{\beta _{2k}}{x_k}} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {\rm{log}}\left( {\frac{{P\left( {y = m} \right)}}{{P\left( {y = M} \right)}}} \right) = {\alpha _m} + \sum\limits_{k = 1}^K {{\beta _{mk}}{x_k}} \end{array} $ |
式中:P为因变量发生的概率; αm为截距项; βmk为第k个自变量的系数,表示xk每变化1个单位,发生比变化exp(βmk)个单位; xk(k=1, 2, …, K)为组合线形及相邻组合几何设计特征变量.
本研究中,因变量为三分类变量(y=1为减速,y=2为稳定车速,y=3为提速),参照组为稳定车速,则减速行为概率模型表达式如下所示:
| $ {\rm{log}}\left( {\frac{{P\left( {y = 1} \right)}}{{P\left( {y = 2} \right)}}} \right) = {\alpha _1} + \sum\limits_{k = 1}^K {{\beta _{1k}}{x_k}} $ |
加速行为概率模型表达式如下所示:
| $ {\rm{log}}\left( {\frac{{P\left( {y = 3} \right)}}{{P\left( {y = 2} \right)}}} \right) = {\alpha _3} + \sum\limits_{k = 3}^K {{\beta _{3k}}{x_k}} $ |
设显著性水平α=0.05,当自变量的显著性检验p值小于0.05时,说明变量显著.
AIC是衡量统计模型拟合优良性的指标,值越低,说明模型拟合越好.AIC的计算公式为
| $ {\rm{AIC}} = ( - 2{\rm{ln}}L) + 2\left( {q + s} \right) $ | (1) |
式中:ln L为模型最大似然值的对数值; q为模型中自变量个数; s为因变量的类别数减1,对于文中的三分类Logistic回归模型,s=3-1=2.从式(1)可以看出,AIC能够校准模型中解释变量的数量,并不是自变量越多模型拟合度越好.如某些变量的加入会使AIC变大,模型拟合度变差,则说明模型中不应加入此变量.在使用同一组数据的前提下,可用AIC进行变量的取舍及多个模型的比选.
5 组合线形几何特征与车速变化关系分析本研究共有2个模型:模型1包含了组合线形几何特征变量,模型2包含了组合线形与相邻路段几何特征变量.若相邻路段几何特征变量显著,且模型的AIC降低,说明相邻路段对车速变化有显著影响.
5.1 组合线形的车速变化模型针对组合线形的车速变化模型,考虑了平曲线、纵坡及横断面3个方面需要分析的变量.针对平曲线考虑了半径、缓和曲线长、圆曲线长、曲线长及方向等变量,针对纵坡考虑了平均坡度、最大坡度、坡度差、坡度类型、变坡点位置等变量,针对横断面考虑了超高.
首先, 针对每一个几何特征变量分别与车速变化建立Logistic模型,分析对比其显著性; 其次, 针对显著的单一变量确定合理的组合进行建模,通过对比AIC进行变量取舍与模型优化.
组合线形的车速变化模型如表 4所示.
| 下载CSV 表 4 组合线形的车速变化模型参数估计 Tab.4 Parameter estimation of speed change model at combined curves |
由表 4可以看出,组合线形长度(L)对减速、提速皆为显著变量,参数估计系数分别为0.004 44和0.003 68.当其他变量不变时,组合线形路段越长,驾驶员减速或提速通过的概率越大.这可能是由于组合线形路段越长,驾驶员适应了线形,越容易减速或提速.
组合线形方向(D)对减速、提速皆为显著变量,参数估计系数分别为-0.362 10和-0.572 50.当其他变量不变时,相对于组合线形方向向左转弯时,驾驶员维持稳定车速的可能性更大.这可能是由于驾驶员的位置位于车子的左侧,左转时驾驶员受到的离心力小,对车速感知较好,容易维持车速.
坡度类型(Ts)在下坡时对减速不是显著变量,对提速为显著变量,参数估计系数为0.592 20.这可能是当车辆处于平曲线下坡时,受到重力影响,车速加快.
平均坡度(Sm)对减速、提速皆为显著变量,参数估计系数为0.239 80和0.330 30.当其他变量不变时,组合线形路段越陡,驾驶员越不易维持稳定车速.当处于平曲线上坡时,坡度越陡驾驶员踩油门加速的力度越大; 当处于平曲线下坡时,受到重力作用,坡度越陡车速越快,而驾驶员为了减速持续踩刹车.
5.2 组合线形加相邻路段的车速变化模型基于组合线形的车速变化模型,加入上游、下游各300 m范围的几何特征变量.建模过程与模型1类似.参数估计结果如表 5所示.
| 下载CSV 表 5 组合线形加相邻路段的车速变化模型参数估计 Tab.5 Parameter estimation of speed change model at combined curves and adjacent segments |
由表 5可以看出,上游路段与组合线形的坡度差(ΔSc, p)对减速、提速皆为显著变量,系数分别为0.351 40和0.225 20.当其他变量不变时,坡度差越大,车速差越大,驾驶员越不易维持稳定的车速.这可能是由于从上游路段驶入组合线形路段时,坡度差越大对驾驶员的视距产生了不利影响,使驾驶员不易控制车速.
下游最大曲率(Cmax, f)对减速概率是显著变量,系数为0.352 70.当其他变量不变时,随着下游路段的曲率增大,驾驶员减速通过组合线形路段的概率越大.这可能是由于驾驶员在组合线形行驶时看到下游路段曲率较大,视距受到影响或产生了紧张心理, 因此减速通过该路段.下游最大曲率(Cmax, f)对提速概率不显著,当其他变量不变时,随着下游曲率的变化,驾驶员更倾向于减速,这与Misaghi等[14]的研究结论一致.
通过对比2个模型的AIC可以看出,只包含组合线形几何特征模型的AIC为841.151, 考虑了相邻路段几何特征模型的AIC为801.584,说明加入相邻路段的几何线形特征之后模型解释度变高.在进行组合线形设计时,应考虑相邻路段的几何设计特征及两者的协调性.
6 结语本研究基于湖南省永吉高速公路几何特征及周边地形构建了三维虚拟模型,通过驾驶模拟实验采集数据,并对车速变化进行区间划分,最后采用多项Logistic回归模型建立了组合线形、相邻路段与车速变化的定量关系.
结果表明,组合线形的长度、方向、坡度类型与平均坡度是显著变量.因此,在设计阶段应注意组合线形的坡长、坡度限制,对于下坡应设置合理的车速管理措施.针对已建道路,当组合线形为长坡、陡坡及下坡时,应设置合理的标志标牌、限速措施等.
本研究还表明,上游路段与组合线形路段的坡度变化、下游路段最大曲率是显著变量.在道路设计阶段应考虑相邻路段的几何特征,与组合线形之间的过渡应自然平缓.针对已建道路,应考虑在相邻路段设置合理的标志标牌,如限速标志、警示标志等,使驾驶员在进入组合线形时能够维持较为平稳的车速.
车速变化能够反映驾驶过程的纵向稳定性,但对于组合线形设计评估和设计标准定量化还远远不够,后期会对其他车辆运行特征如横向加速度、视距等指标进行研究.
| [1] |
中华人民共和国国家统计局. 中国统计年鉴[M]. 北京: 中国统计出版社, 2016 National Bureau of Statistics of the People's Republic of China. China statistical yearbooks[M]. Beijing: China Statistical Press, 2016 |
| [2] |
Policy on Geometric Design of Highways and Streets. American association of state highway and transportation officials[R]. Washington DC: AASHTO, 2011.
|
| [3] |
HANNO D. Effect of the combination of horizontal and vertical alignments on road safety[D]. Kelowna: University of British Columbia, 2004.
|
| [4] |
PSARIANOS B, KONTARATOS M, KATSIOS D. Influence of vehicle parameters on horizontal curve design of rural highways[J]. Transportation Research Circular E-C003, 1995, 22: 1 |
| [5] |
中华人民共和国交通运输部. JTG D20—2017公路路线设计规范[S]. 北京: 人民交通出版社, 2017. Ministry of Transport of the People's Republic of China. JTG D20—2017 Design specification for highway alignment[S]. Beijing: China Communications Press, 2017. |
| [6] |
中华人民共和国交通运输部. JTG B01—2014公路工程技术标准[S]. 北京: 人民交通出版社, 2014. Ministry of Transport of the People's Republic of China. JTG B01—2014 Technical standard of highway engineering[S]. Beijing: China Communications Press, 2014. |
| [7] |
HASSAN Y, EASA S M. Effect of vertical alignment on driver perception of horizontal curves[J]. Journal of Transportation Engineering, 2003, 129(4): 399 DOI:10.1061/(ASCE)0733-947X(2003)129:4(399) |
| [8] |
中华人民共和国交通运输部. JTG/T B05—2015公路项目安全性评价规范[S]. 北京: 人民交通出版社, 2015. Ministry of Transport of the People's Republic of China. JTG/T B05—2015 Guidelines for safety audit of highway[S]. Beijing: China Communications Press, 2015. |
| [9] |
NICHOLSON A. Super-elevation, side friction, and roadway consistency[J]. Journal of Transportation Engineering, 1998, 124(5): 411 DOI:10.1061/(ASCE)0733-947X(1998)124:5(411) |
| [10] |
KRAMMES R A, RAO K S, OH H. Highway geometric design consistency evaluation software[J]. Transportation Research Record: Journal of the Transportation Research Board, 1995, 1500: 19 |
| [11] |
GIBREEL G M, EASA S M, EL-DIMEERY I A. Prediction of operating speed on three-dimensional highway alignments[J]. Journal of Transportation Engineering, 2001, 127(1): 21 DOI:10.1061/(ASCE)0733-947X(2001)127:1(21) |
| [12] |
WANG X, WANG T, TARKO A, et al. The influence of combined alignments on lateral acceleration on mountainous freeways: a driving simulator study[J]. Accident Analysis & Prevention, 2015, 76: 110 |
| [13] |
王雪松, 刘姣, 吴杏薇. 山区高速公路相邻组合路段设计安全评估[J]. 同济大学学报(自然科学版), 2016, 44(11): 1681 WANG Xuesong, LIU Jiao, WU Xingwei. Safety evaluation of adjacent combined alignments of mountain freeway[J]. Journal of Tongji University (Natural Science), 2016, 44(11): 1681 DOI:10.11908/j.issn.0253-374x.2016.11.006 |
| [14] |
MISAGHI P, HASSAN Y. Modeling operating speed and speed differential on two-lane rural roads[J]. Journal of Transportation Engineering, 2005, 131(6): 408 DOI:10.1061/(ASCE)0733-947X(2005)131:6(408) |
 2018, Vol. 46
2018, Vol. 46
