工程设计领域, 包括车身产品设计开发过程, 均趋向以产品个性化来实现高附加值的目标.因为客户个体经其认知和主观感受而对产品所作的决策和主观响应[1]存在本质的不确定性[2-3], 这种不确定性可以称之为偏好异质性.缺少对这些不确定性的研究, 势必对个性化车身产品的开发产生消极影响.因此, 工程设计理念也开始注重了解客户的偏好异质性, 并扩展传统的以定量属性(特征)为主的客户需求建模方法[4].目前国内外学者在研究个性化客户需求预测模型时认为, 某一特定客户群可以由一个个体代表, 从分析个人的评价和选择行为进而扩展到客户群整体, 是较为行之有效的方法, 即one-to-one个性化模式.然而, 诸多传统方法均难以在one-to-one个性化模式下应用[5-6], 目前常用固定系数的离散选择模型对客户的评价和选择行为进行预测, 该方法实际上是以细分客户群的平均偏好替代群体内每一客户个体的偏好, 故而难以充分表达one-to-one个性化模式下客户的偏好异质性, 即每一客户个体均具有其独特的偏好[7-8].将客户个体针对车身产品的评价和选择行为进行建模, 识别偏好异质性所在, 有助于了解个性化的客户需求, 也有助于厂商预测潜在客户的多种偏好, 并在车身产品设计或改进过程中作出相应的对策.
本文主要研究由客户个体之间偏好独特性所导致的不确定性, 即客户的偏好异质性.通过建立合适的模型, 捕获这种隐性的不确定性导致的客户个体对车身产品评价、选择行为的显性差异.离散选择模型自提出以来, 已逐渐发展成为研究个体选择行为最为有力的工具, 从最基本的多项logit模型起步, 随着研究问题的复杂化和模型设定的精细化, 目前已建构了包括一系列模型在内的较为完整的理论体系, 并在实践中广泛应用.mixed logit模型和潜在类别模型(latent class model)[9]在离散选择模型族中被广泛应用于选择者随机偏好问题.然而, 潜在类别模型在解决随机偏好差异问题时, 处理方式是由模型自动计算选择者属于每一类的概率, 从而将选择者划分为几种类别, 分别适用不同的系数.虽然与样本细分估计明显不同, 体现其“潜在性”[10], 但是归根到底还是用类别平均偏好替代类别内每一客户个体的偏好, 所以该模型在one-to-one个性化模式下, 不能有效地捕获客户个体的随机偏好.mixed logit模型[11-12]具有在效用函数可观测部分寻求异质性的特点, 并允许模型参数随可观测变量在客户个体间随机变化, 具体而言, 通过设定模型系数服从一定的分布, 可以估计出相应的分布参数, 如均值与标准差, 前者反映了平均偏好大小, 后者则反映了偏好差异的幅度.同时, mixed logit模型能够去除普通logit模型存在的三大局限:个体选择偏好具有同质性、选择集选项之间独立不相关、不可观测因素在不同时间不相关.由于mixed logit模型在极大模拟似然估计法条件下参数估计没有闭合形式解, 需要通过随机模拟进行参数估计[12], 因此运用马尔可夫链蒙特卡洛模拟方法[12], 对参数进行贝叶斯估计.本文建立面向客户偏好异质性的离散选择模型, 给出贝叶斯估计方法.根据车身产品的层次结构特点, 并在SP调查所获样本数据和参数先验分布信息基础上, 通过常用的McFadden似然比指标ρ2[13]检验拥有解释变量的模型是否优于无解释变量的模型, 比较本文所提随机系数mixed logit模型与现有固定系数模型的优劣, 阐明客户偏好异质性的所在.
1 随机系数mixed logit模型的建立客户对某款车身产品的最终选择行为, 与他对该车身产品感受直接相关, 而这些感受是主观的, 且具有一定的不确定性, 即异质性.这些隐性的偏好在客户行为上的外在显性表现也存在层次化.客户对车身的整体感受来自于外部造型, 之后会对车身布置和涉及安全性方面的车身结构属性加以考虑.在细节方面, 则会对车门开口以及进出便利性、驾乘人员在车内的空间满意程度进行主观评价.通过在稍低层次对车身诸多客户需求定性属性进行主观性和带有偏好的评价行为, 最终在高层次对车身产品整体做出选择行为.随机系数mixed logit模型是指客户针对车身产品进行选择时产生的客户效用离散表达方式.对于客户n(n=1, …, N), 选择集内车身产品选项i(i=1, …, I)产生的效用Uin表示如下:
| $ {\mathit{U}_{\mathit{in}}}{\text{ = }}{\mathit{V}_{\mathit{in}}}{\text{ + }}{\varepsilon _{\mathit{in}}} $ |
式中:Vin表示可观测效用; εin表示随机扰动效用.可观测效用Vin通过模型系数向量βn和客户需求的定性属性表示.客户最终将选择对其具有最大效用的选项.通过将客户自身属性(社会经济地位以及人口特征属性)Z引入模型, 捕获系统级偏好异质性, 而随机偏好异质性由模型的随机系数进行表达, 如下所示:
| $ \begin{gathered} {U_{in}} = {\mathit{\boldsymbol{X}}_{in}}{\mathit{\boldsymbol{\beta }}_n} + {\varepsilon _{in}} = \sum\limits_{k = 1}^K {{x_{ink}}{\beta _{nk}}} + {\varepsilon _{in}}, \hfill \\ {\mathit{\boldsymbol{\beta }}_n} = \mathit{\boldsymbol{\beta }} + \mathit{\boldsymbol{\theta Z}} + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{u}}_n} \hfill \\ \end{gathered} $ | (1) |
其中, 系数向量βn每一项可表示为
| $ {\beta _{nk}} = {\beta _k} + {\theta _k}{z_n} + {\sigma _k}{u_{nk}} = {\beta _k} + {\theta _k}{z_n} + {\sigma _k}{\rm{exp}}({\omega _k}{s_n}){\zeta _{nk}} $ | (2) |
式(1)和(2)中:Xin为关于选择集内选项、客户个体的可观测解释性变量组成的K维向量; β为客户群平均系数向量; θ为客户自身属性Z的系数向量; Γ、un为矩阵; βk为客户群平均系数, zn为客户自身属性, 表示社会经济地位, θk为zn相对大小的系数值, βk+θkzn为该模型系数分布的均值; σk为系数向量βn的元素βnk的标准差, 它捕获了随机偏好异质性的存在, 即在样本客户群内, 客户个体允许具有不同的βn, 而不是令该客户群体使用单一β; unk为方差, 呈多元正态分布, 其相关矩阵为R; sn为客户自身属性, 表示人口特征属性, ωk为sn相对大小的系数值, ζnk为随机不可观测的偏好变化.
综上所述, mixed logit模型的可观测部分可写作
| $ {V_{in}}\left( {ML} \right) = \mathit{\boldsymbol{\beta }}{\mathit{\boldsymbol{X}}_{in}} + \mathit{\boldsymbol{Z\theta }}{\mathit{\boldsymbol{X}}_{in}} + {\mathit{\boldsymbol{\beta }}_{Xn}}{\mathit{\boldsymbol{X}}_{in}} $ | (3) |
式中:βXn为随机变量.该随机变量捕获选择行为产生时客户间的随机偏好异质性, 而Zθ等则表征客户的系统偏好异质性.对于特定的βXn值, 选择i的条件概率
| $ {L_{in}}({\mathit{\boldsymbol{\beta }}_n}|{\mathit{\boldsymbol{X}}_{in}}, {\mathit{\boldsymbol{\beta }}_{Xn}}) = {\rm{exp}}({V_{in}}({\mathit{\boldsymbol{\beta }}_n}))/\sum\limits_i {{\rm{exp}}} ({V_{in}}({\mathit{\boldsymbol{\beta }}_n})) $ |
约束条件为误差项是独立同分布的极值.此时, βXn是随机变量而非特定的取值, 因此针对所有βn取值的非条件选择概率
| $ {P_n}\left( i \right) = {\smallint _{{\mathit{\boldsymbol{\beta }}_n}}}{L_{in}}({\mathit{\boldsymbol{\beta }}_n}|{\mathit{\boldsymbol{X}}_{in}}, {\mathit{\boldsymbol{\beta }}_{Xn}})f({\mathit{\boldsymbol{\beta }}_{Xn}}){\rm{d}}{\mathit{\boldsymbol{\beta }}_{Xn}} $ | (4) |
式中:f(βXn)为模型参数βXn的概率密度函数.式(4)是以βn内随机部分的概率密度作为权值, 对条件概率进行积分所得.
2 模型参数的贝叶斯估计方法上述mixed logit选择模型的闭合形式解不存在, 因此需要使用模拟方法求解, 在搜集数据的基础上进行模型估计, 本文给出贝叶斯估计方法[14-15].对于取样客户群内的客户个体n(n=1, …, N), 选择集内的选项j在时间周期t(t=1, 2, …, T)内的效用
| $ {U_{jn,t}} = {\text{ }}{\mathit{\boldsymbol{X}}_{jn,t}}{\mathit{\boldsymbol{\beta }}_n} + {\varepsilon _{jn,t}} $ |
其中, βn服从均值为b、方差为Σ的分布, 对于选择时间周期内的客户个体n, 选择的结果可表示为yn=(yn1, yn2, …, ynT), 取样客户群的选择结果为Y=(y1, y2, …, yN).客户个体n的选择概率非条件式为
| $ L({\mathit{\boldsymbol{y}}_n}|\mathit{\boldsymbol{b}}, \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}) = \smallint L({\mathit{\boldsymbol{y}}_n}|{\mathit{\boldsymbol{\beta }}_n})\phi ({\mathit{\boldsymbol{\beta }}_n}|\mathit{\boldsymbol{b}}, \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}){\rm{d}}{\mathit{\boldsymbol{\beta }}_n} $ | (5) |
式中:L(yn|b, Σ)表示mixed logit概率; φ(βn|b, Σ)表示正态密度函数, 均值为b, 方差为Σ.基于先验分布和表达式, 得到后验分布为
| $ H\left( {\mathit{\boldsymbol{b}},\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}|\mathit{\boldsymbol{Y}}} \right) \propto \prod L({\text{ }}{\mathit{\boldsymbol{y}}_n}|\mathit{\boldsymbol{b}},\mathit{\boldsymbol{ \boldsymbol{\varSigma} }})h\left( {\mathit{\boldsymbol{b}},\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}} \right) $ |
式中:h(b, Σ)为b和Σ的先验分布.然而, L(yn|b, Σ)没有闭合形式解, 因此引入βn, 得到关于b和Σ以及βn的后验分布为
| $ \begin{array}{l} H\left( {\mathit{\boldsymbol{b}},\mathit{\boldsymbol{ \boldsymbol{\varSigma} }},{\mathit{\boldsymbol{\beta }}_n}|\mathit{\boldsymbol{Y}}} \right) \propto \\ \prod\limits_n L ({\mathit{\boldsymbol{y}}_n}|{\mathit{\boldsymbol{\beta }}_n})\phi ({\mathit{\boldsymbol{\beta }}_n}|\mathit{\boldsymbol{b}},\mathit{\boldsymbol{ \boldsymbol{\varSigma} }})h\left( {\mathit{\boldsymbol{b}},\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}} \right) \end{array} $ |
其中, φ(βn|b, Σ)和)h(b, Σ)为先验分布, L(yn|βn)为mixed logit模型的似然函数.
Gibbs抽样是Metropolis-Hastings算法的一个特例, 它遍历所有参数区块, 在所有区组参数的最新抽样值条件下, 对每一候选参数进行抽样.Gibbs抽样可以从该后验分布进行抽样, 对于βn的抽样均是在其余2个参数的条件上进行的, 如下所示:
| $ H({\mathit{\boldsymbol{\beta }}_n}|\mathit{\boldsymbol{b}}, \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}, {\mathit{\boldsymbol{y}}_n}) \propto L({\mathit{\boldsymbol{y}}_n}|{\mathit{\boldsymbol{\beta }}_n})\phi ({\mathit{\boldsymbol{\beta }}_n}|\mathit{\boldsymbol{b}}, \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}) $ | (6) |
对于βn的抽样, 称为Metropolis-Hastings算法, 算法步骤如下所示:
步骤1 由βn, 0开始.
步骤2 从标准正态分布密度函数内抽样K个独立值, 并将其堆栈为向量η1.
步骤3 建立针对βn, 1的测试值
步骤4 从标准均匀分布中抽样得到u1.
步骤5 计算比值, 如下所示:
| $ F = \frac{{L({\mathit{\boldsymbol{y}}_n}|{{\mathit{\boldsymbol{\tilde \beta }}}_{n, 1}})\phi ({{\mathit{\boldsymbol{\tilde \beta }}}_{n, 1}}|\mathit{\boldsymbol{b}}, \mathit{\boldsymbol{ \boldsymbol{\varSigma} }})}}{{L({\mathit{\boldsymbol{y}}_n}|{\mathit{\boldsymbol{\beta }}_{n, 0}})\phi ({\mathit{\boldsymbol{\beta }}_{n, 0}}|\mathit{\boldsymbol{b}}, \mathit{\boldsymbol{ \boldsymbol{\varSigma} }})}} $ |
步骤6 如果u1≤F, 接受
步骤7 重复上述步骤, 可得到βt, n.
将上述过程集成进入Gibbs抽样过程, 此迭代过程如下所示:
步骤1 从正态分布N(βt-1, Σt-1/N)中抽样bt, βt-1为之前所有βn, t-1的均值.
步骤2 从N(K+N, (KI+NSt-1)/(K+N))分布中抽样Σt, 其中
步骤3 对于每一客户个体的βt, n, 由βn, t-1开始, 根据正态分布φ(βn|bt, Σt), 依照Metropolis-Hastings算法进行一次迭代获得.
上述方法均是根据另2组参数的当下值, 对一组参数进行重估计, 这就是Gibbs抽样, 最终将收敛到各组参数的正确分布.马尔可夫链蒙特卡洛模拟方法, 表示每一迭代过程的估计值是由先前的迭代所得估计值经由概率转移规则获得.这种基于贝叶斯原理的方法也可以称为层次贝叶斯估计.
3 车身产品离散选择模型的实证结合对个性化车身产品客户需求属性(特征)的定性分析, 建立层次化的、包含客户偏好异质性的层次选择模型, 并运用马尔可夫链蒙特卡洛模拟方法对参数进行贝叶斯估计, 将该方法定义为集成贝叶斯的层次选择模型, 其层次结构如图 1所示.首先客户在M2层对车身产品所具备的客户需求属性进行评价, 然后在M1层客户基于最大效用原则做出自己的车身产品选择.

|
图 1 集成贝叶斯的层次选择模型 Fig.1 Integrated Bayesian hierarchy selection model |
根据层次化的分析方法, 将离散选择及评价模型内的客户层次需求列出, 如表 1所示.为获取样本信息, 进行SP调查, 受试者为24男、24女, 具有不同的社会经济地位、人口特征属性, 即具有不同的收入水平以及身高、体重和年龄等指标.
| 下载CSV 表 1 需求属性(变量)定义及水平设定 Tab.1 Requirement attribute definition and level setting |
受试者均对选择集内4种车身产品(choice 1、2、3、4)进行评价打分, 此选择集作为受试者的初始选择集.这些评价打分行为针对车身产品的子系统, 诸如客户个体对于车身产品的造型、结构安全性、实用性等部分的评价打分.这些客户需求的主观属性再往下推一层次, 便是工程设计人员面临的设计参数, 离散选择和评价模型将这些设计参数与客户的评价和选择行为有效联系起来.表 1中, or1~or19为客户对其需求属性的评价指标, 这些指标的水平设定值可看作工程设计参数值和客户自身属性函数值.
另外, 客户自身属性包括社会经济地位和人口特征属性, 如表 2所示.这部分的属性描述了市场经由一定标准进行细分的状况, 表征了细分客户群之间存在着偏好异质性, 即系统级偏好异质性.选择过程的决策规则采用效用规则, 效用值是选项属性和受试者个体特征的函数值.效用值作为标量值, 表示受试者个体赋予选项不同属性的值, 表征受试者在不同选项之间所做的权衡.
| 下载CSV 表 2 客户社会经济地位和人口特征属性 Tab.2 Customer socioeconomic status and demographic attributes |
将未知参数的先验信息和样本信息综合, 根据贝叶斯定理, 得出后验信息, 然后根据后验信息去推断未知参数.通过迭代程序对满足条件后验分布进行Gibbs抽样, 构造出平稳分布为参数后验分布的马尔科夫链来实现对目标分布的模拟.通过WinBUGS软件可以进行模型的贝叶斯估计.
本文采用2种M1层次离散选择模型进行对比来表示方法的有效性, 如下所示:
(1) 模型1.采用固定系数β进行贝叶斯参数估计.
(2) 模型2.采用随机系数βn进行贝叶斯参数估计.
本质上, 模型1将客户群的偏好视为均值, 因此难以捕获客户个体间的偏好异质性.与之相比, 模型2能够有层次地传递不确定性, 其中随机系数能够表达客户个体的偏好差异性.从表 3可知, 模型2中对数似然值和McFadden似然比ρ02值更大, 说明随机系数模型2在固定系数模型1阐明系统偏好异质性的基础上, 能够捕获客户的随机偏好异质性, 从而进一步改善模型1的准确性, 将离散选择模型未考虑的偏好异质性囊括在内.
| 下载CSV 表 3 M1层次选择模型比较 Tab.3 M1 level selection model comparison |
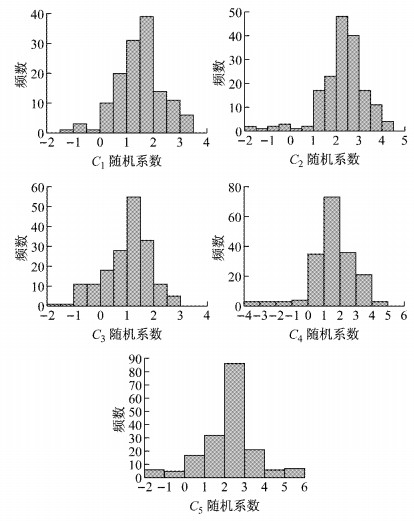
随机系数mixed logit模型2中C1~C5随机系数分布如图 2所示.这些分布呈现了客户个体偏好异质性的存在, 在社会经济地位、人口特征属性和车身产品自身属性基础上, 围绕随机系数均值随客户个体而变化, 这也就阐明了客户个体随机偏好异质性的所在, 可以认为每一客户对应的选择效用函数具有各自不同的系数.传统上, 固定系数模型是通过社会经济地位、人口特征属性将客户群进行市场细分, 以客户群平均偏好表达固定系数.引入随机系数mixed logit模型, 则可更进一步阐明客户个体间偏好异质性所在, 有效地捕获了每一客户在面对同一车身产品时, 由于偏好异质性做出不同的评价和选择行为.同时, 随机系数mixed logit模型还摆脱独立不相关假设的约束, 使不可观测效用与可观测客户属性、车身产品属性相联系, 能够表达客户偏好异质性, 因此随机系数mixed logit模型是拟合优度更好、预测效率更高的选择.
|
图 2 M1层次选择模型随机系数分布 Fig.2 Distribution of random coefficient of M1 level selection model |
本文针对one-to-one个性化模式, 分析了随机系数mixed logit模型.该模型具有在效用函数可观测部分寻求异质性的特点, 并允许模型参数随可观测变量在客户个体间系统随机变化, 同时去除了普通logit模型存在的三大局限:个体选择偏好具有同质性、选择集选项之间独立不相关、不可观测因素在不同时间不相关.根据车身产品的层次结构特点, 在客户对车身产品定性属性(特征)评价的基础上, 建立面向客户偏好异质性的离散选择模型.由于模型参数估计不具有闭合解形式, 根据SP调查所获样本数据和参数先验分布设定, 运用马尔可夫链蒙特卡洛模拟方法, 对参数进行贝叶斯估计.最后, 对比随机系数mixed logit模型与其他模型, 说明本文所提模型更能阐明个性化偏好, 即客户偏好异质性的所在, 并具有更好的模型拟合优度.因此, 本文建模方法可作为针对客户个体选择行为进行车身产品设计开发决策的辅助工具.
| [1] |
HUNG W K, CHEN L L. Effects of novelty and its dimensions on aesthetic preference in product design[J]. International Journal of Design, 2012, 6(2): 81 |
| [2] |
KHALID H M, HELANDER M G. Customer emotional needs in product design[J]. Concurrent Engineering Research and Applications, 2006, 14(3): 197 DOI:10.1177/1063293X06068387 |
| [3] |
LIN K H, SHIH L H, CHENG Y T, et al. Fuzzy product line design model while considering preference uncertainty:a case study of notebook computer industry in Taiwan[J]. Expert Systems with Applications, 2011, 38(3): 1789 DOI:10.1016/j.eswa.2010.07.106 |
| [4] |
MACDONALD E F, GONZALEZ R, PAPALAMBROS P Y. Preference inconsistency in multidisciplinary design decision making[J]. Journal of Mechanical Design, 2009, 131(3): 031009 DOI:10.1115/1.3066526 |
| [5] |
MOHAMED M S, MUSTAFA S. Kansei engineering implementation on car center stack designs[J]. International Journal of Education and Research, 2014, 2(4): 355 |
| [6] |
SHAHIN A, MOHAMMADI SHAHIVERDI S. Estimating customer lifetime value for new product development based on the Kano model with a case study in automobile industry[J]. Benchmarking:An International Journal, 2015, 22(5): 857 DOI:10.1108/BIJ-10-2013-0099 |
| [7] |
DAI Z H, SCOTT M J. Effective product family design using preference aggregation[J]. Journal of Mechanical Design, 2006, 128(4): 659 DOI:10.1115/1.2197835 |
| [8] |
杨涛, 杨育, 张东东. 考虑客户需求偏好的产品创新概念设计方案生成[J]. 计算机集成制造系统, 2015, 21(4): 875 YANG Tao, YANG Yu, ZHANG Dongdong. Generation of product innovation conceptual design schemes for considering the demand preferences of customers[J]. Computer Integrated Manufacturing Systems, 2015, 21(4): 875 |
| [9] |
GREENE W H, HENSHER D A. A latent class model for discrete choice analysis:contrasts with mixed logit[J]. Transportation Research, Part B:Methodological, 2003, 37(8): 681 DOI:10.1016/S0191-2615(02)00046-2 |
| [10] |
VARELA E, JACOBSEN J B, SOLINO M. Understanding the heterogeneity of social preferences for fire prevention management[J]. Ecological Economics, 2014, 106: 91 DOI:10.1016/j.ecolecon.2014.07.014 |
| [11] |
AKIVA M E B, LERMAN S R. Discrete choice analysis:theory and application to predict travel demand[M]. London: MIT Press, 1985
|
| [12] |
TRAIN K E. Discrete choice methods with simulation[M]. London: Cambridge University Press, 2009
|
| [13] |
MCFADDEN D. Conditional logic analysis of qualitative choice behavior[M]. Berkeley: Institute of Urban & Regional Development, 1972
|
| [14] |
茆松诗. 贝叶斯统计[M]. 北京: 中国统计出版社, 2012 MAO Songshi. Bayesian statistics[M]. Beijing: China Statistics Press, 2012 |
| [15] |
BOLSTAD W M. Understanding computational Bayesian statistics[M]. Hoboken: Wiley, 2010
|
 2018, Vol. 46
2018, Vol. 46

