目前,绝大多数燃料电池轿车均采用燃料电池加动力蓄电池(或超级电容)的电电混合动力系统结构形式[1].针对插电式燃料电池轿车,最常见的基于规则的能量管理策略可以分为基于功率平衡的恒压控制策略[2-3]和恒流控制策略[4].基于模糊逻辑控制的能量管理策略往往依靠工程经验来制定,相比基于规则的能量管理策略具有更好的能量经济性[5-6].基于规则的能量管理策略与基于模糊逻辑控制的能量管理策略都已在燃料电池轿车上进行了应用[4-5],但其能量经济性仍有待提高.为了进一步提高燃料电池轿车的能量经济性,需要对能量管理策略进行优化设计.目前,国内外对此已开展了诸多研究,包括线性二次型最优控制[7]、遗传算法[8]、确定性动态规划算法[9]、随机动态规划算法[10]等.然而,上述优化算法均存在模型复杂、计算量较大、难以实时应用的不足.基于等效氢消耗最小的控制策略[11]和基于极小值原理的优化控制[12],虽然能够实现燃料电池轿车的实时控制,但是优化的是瞬时的能量经济性,优化效果有限.因此,开发一种具有更好能量经济性与实时性的燃料电池轿车能量管理策略是亟待解决的问题.
模型预测控制(MPC)是一种在线滚动优化方法,其采用的模型简单且多样化[13].基于每一个采样时刻的对象测量值求解一个有限时域优化问题,从而得到一个预测控制序列,并将当前控制作用于对象以实现实时控制.已有学者将模型预测控制应用于油电混合动力汽车能量管理策略的开发,并证明了其能实现较好的能量经济性与实时性[14].然而,针对燃料电池轿车,模型预测控制应用于其能量管理策略开发的研究还很少.据此,本文运用模型预测控制对燃料电池轿车能量管理策略进行实时优化,改善车辆的能量经济性.基于测试数据和机理分析,建立了燃料电池轿车动力系统的数学模型.采用实车控制策略,建立了动力系统的前向仿真模型并对模型进行了验证.在此基础上,开发了模型预测控制策略.最后,通过离线仿真及硬件在环仿真试验,对所提出的模型预测控制策略的有效性进行了验证,并考察其实时性.
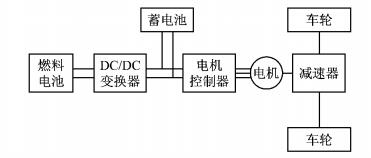
1 燃料电池轿车动力系统结构燃料电池轿车动力系统主要有燃料电池发动机单独驱动和燃料电池发动机加辅助能量源驱动2种结构形式,其中辅助能量源主要有动力蓄电池和超级电容.目前,绝大多数燃料电池轿车动力系统都采用如图 1所示的结构形式,其中燃料电池和直流/直流(DC/DC)变换器连接,DC/DC变换器和蓄电池并联共同驱动电机,最后电机带动车轮运动.这种结构具有以下优点:燃料电池作为主能源提供持续功率,动力蓄电池提供动态变化功率,并且回收再生制动能量; 动力蓄电池单独以纯电动模式驱动车辆,实现在燃料电池出现故障时的簸行回家功能.本文中燃料电池轿车采用此种结构形式.
|
图 1 燃料电池加蓄电池的动力系统结构 Fig.1 Power system structure based on fuel cell and battery |
燃料电池轿车动力系统前向仿真模型如图 2所示.本文的重点是燃料电池轿车的能量管理策略,对于燃料电池轿车模型,只需准确地反映其能耗特性即可,因此本文关注燃料电池轿车动力系统的外特性,而忽略动力元件的内部反应过程.本文采用了基于输入输出测试数据关系分析的试验建模和基于机理分析的理论建模相结合的方法.基于电压极化特性建立了质子交换膜燃料电池模型.在考虑输出动态特性和效率的基础上,DC/DC变换器和电机模型均由实际测试数据得到.锂离子动力蓄电池模型根据其实际工作特性及实车测试数据得到.以下将详细说明几个主要子模块的建模方法.

|
图 2 燃料电池轿车前向仿真模型结构 Fig.2 Forward simulation structure of fuel cell car |
在质子交换膜燃料电池工作过程中,由于存在不可逆损失,输出电压会逐渐下降.这些不可逆损失主要体现为极化电压,实际输出电压由理想电动势和极化电压共同决定,其中极化电压主要由欧姆极化电压、活化极化电压和浓度差电压组成[15].因此,质子交换膜燃料电池实际输出电压
| $ {U_{\rm{o}}} = {E_{\rm{n}}} - {U_{{\rm{act}}}} - {U_{{\rm{ohm}}}} - {U_{{\rm{con}}}} $ | (1) |
式中:Uo为单体燃料电池的实际输出电压; En为理想情况下燃料电池的开路电压; Uact为活化极化电压; Uohm为欧姆极化电压; Ucon为浓差极化电压.
燃料电池堆输出总电压
| $ {U_{\rm{s}}} = n{U_{\rm{o}}} $ | (2) |
式中:Us为燃料电池堆的实际输出电压; n为燃料电池堆所含电池单体的个数.
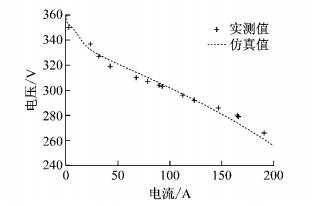
根据式(1)和式(2)建立了燃料电池的仿真模型并与测试数据进行了对比验证,结果如图 3所示.从图 3中可以看出,仿真和实测结果基本吻合,说明所建模型可用于离线仿真.
|
图 3 燃料电池仿真与实测数据比较 Fig.3 Comparison between simulation and measured data of fuel cell |
上述建立的燃料电池发动机模型作为部件模型可用于整车驱动模型中,但该模型是个复杂的非线性系统,在预测控制系统设计时需要对其进行线性化处理.假定燃料电池电堆工作温度变化不大且忽略时间常数的影响,可用如下一阶惯性环节[7]近似地表示燃料电池发动机的输入输出特性关系:
| $ {\tau _{\rm{f}}}{{\dot P}_{{\rm{f,a}}}} = {k_{\rm{f}}}{P_{{\rm{f,d}}}} - {P_{{\rm{f,a}}}} $ | (3) |
式中:τf为时间常数; Pf, a为燃料电池堆实际的输出功率; Pf, d为燃料电池堆需求的输出功率; kf为增益系数,通过参数辨识的方法得到.
2.2 锂电池模型由于Thevenin模型估计的电池端电压对电池实测电压跟随较好,能够较好地描述电池的实际工作特性[16],因此本文采用Thevenin模型作为锂电池模型.
根据某段时间内燃料电池轿车实车实时采集的锂电池电压和电流关系,运用最小二乘法递推算法对式(4)中的R0、RP、CP进行辨识并代入模型中进行仿真,得出的结果与实车电压值的比较如图 4所示.从图 4看到,所建立的锂电池仿真模型的电压值和实测值的误差率在5%以内,说明所建立的模型和辨识得到的参数是比较准确的,能够反映锂电池的实际工作情况.
| $ \left\{ \begin{array}{l} U = {U_{\rm{E}}} - {U_{\rm{P}}} - I{R_0}\\ I = {C_{\rm{P}}}\frac{{{\rm{d}}{U_{\rm{P}}}}}{{{\rm{d}}t}} + \frac{{{U_{\rm{P}}}}}{{{R_{\rm{P}}}}} \end{array} \right. $ | (4) |

|
图 4 锂电池仿真模型输出电压和实车电压比较 Fig.4 Comparison between simulation output voltage and measured voltage of lithium battery |
式中:U为锂电池端电压; UE为锂电池开路电压; UP为锂电池极化电压; I为负载电流; R0为欧姆电阻; CP为极化电容; RP为极化内阻.
2.3 DC/DC变换器模型DC/DC变换器模型由动态模型和效率模型组成,其结构如图 5所示.

|
图 5 DC/DC变换器模型结构 Fig.5 Structure of DC/DC converter model |
图 5中,ID, i为DC/DC变换器模型的输入电流,ID, o为DC/DC变换器模型的输出电流,Ub为总线电压,PD, o为DC/DC变换器模型的输出功率.
由DC/DC变换器模型的工作原理可知, DC/DC变换器模型动态响应时间较快,而且表现出较好的线性特性,因此可采用一阶环节近似表示DC/DC变换器模型输入输出之间的动态特性,如下所示:
| $ {\tau _{\rm{D}}}{{\dot I}_{{\rm{D,o}}}} = {k_{\rm{D}}}{I_{{\rm{D,i}}}} - {I_{{\rm{D,o}}}} $ | (5) |
式中:τD为DC/DC变换器模型时间常数; kD为DC/DC变换器模型增益系数,通过参数辨识的方法得到.
在实际建模中,必须考虑DC/DC变换器模型的功率(效率)损失问题.利用测试数据对效率曲线进行拟合,得到如下关系:
| $ {\eta _{\rm{D}}} = - 0.0013P_{{\rm{D,o}}}^2 + 0.1051{P_{{\rm{D,o}}}} + 96.1442 $ | (6) |
式中:ηD表示DC/DC变换器模型功率.
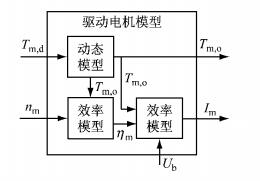
2.4 驱动电机模型同DC/DC变换器模型一样,电机模型也由动态模型和效率模型组成,其仿真模型结构简图如图 6所示.图 6中,Tm, d为电机需求转矩,Tm, o为电机输出转矩,nm为电机当前转速,Im为电机电流,ηm为电机效率.
|
图 6 驱动电机模型结构 Fig.6 Structure of drive motor model |
永磁同步电机的动态响应可以近似为一阶惯性环节[17],用线性微分方程表示为
| $ {\tau _{\rm{m}}}{{\dot T}_{{\rm{m,o}}}} = {k_{\rm{m}}}{{\dot T}_{{\rm{m,d}}}} - {T_{{\rm{m,o}}}} $ | (7) |
式中:τm为电机时间常数; km为电机增益系数.电机电流和电压与转矩和转速的关系可由下式表示:
| $ {U_{\rm{b}}}{I_{\rm{m}}} = \frac{{{T_{{\rm{m,o}}}}{n_{\rm{m}}}}}{{9550{\eta _{\rm{m}}}}} $ | (8) |
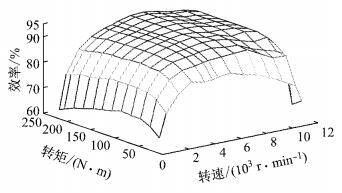
驱动电机效率模型可以根据电机当前转速和转矩给出,电机效率特性场如图 7所示.
|
图 7 电机效率特性场 Fig.7 Feature field of motor efficiency |
燃料电池轿车采用的是基于荷电状态(SOC)和锂电池电流双闭环的功率平衡实车能量管理策略[5],划分了怠速、驱动和制动3种模式,并明确了驾驶员需求功率在不同工作模式下的分配情况.据此建立的实车能量管理策略如图 8所示.图 8中:v为车速; α为踏板输入信号; Pd为驱动需求功率; Ps为制动需求功率,根据踏板开度α决定,函数关系为g; SOCl、SOCs分别为电池SOC上、下限; Pf为燃料电池需求功率,根据车速与踏板开度决定,函数关系为f; Pf, l为燃料电池输出功率上限; Pb为锂电池需求功率; Pb, d、Pb, c分别为根据双闭环控制策略得出的锂电池放电或充电功率; Pm, b、Pm, b, l分别为电机制动功率和最大制动功率; PM为机械制动功率; k1、k3为锂电池放电系数; k2、k4为锂电池充电系数.

|
图 8 实车能量管理策略 Fig.8 Energy management strategy of real car |
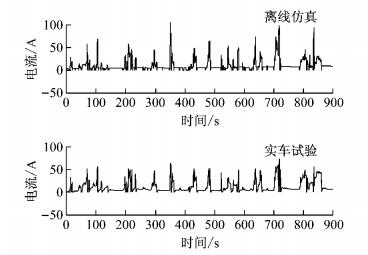
综合上述建立的系统部件模型和实车能量管理策略,搭建了燃料电池轿车动力系统闭环仿真模型, 并按照实车试验的运行工况对模型进行仿真,仿真结果同实车试验数据的对比如图 9~11所示.
|
图 9 离线仿真和实车试验DC/DC变换器电流比较 Fig.9 Comparison of DC/DC converter current between offline simulation and real test |

|
图 10 离线仿真和实车试验电机电流比较 Fig.10 Comparison of motor current between offline simulation and real test |
|
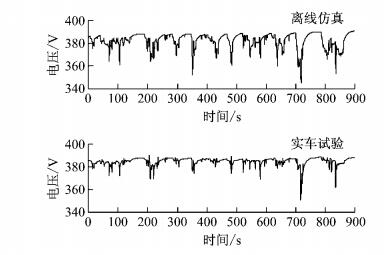
图 11 离线仿真和实车试验锂电池电压比较 Fig.11 Comparison of lithium battery voltage between offline simulation and real test |
通过比较看出,主要部件(包括DC/DC变换器和电机)的电流及锂电池的电压具有基本相同的走势和幅值,说明所建立的燃料电池轿车动力系统模型能够反映实际样车动力系统的动态特性,可以用于后续基于预测控制的能量管理策略研究.
3 燃料电池轿车模型预测控制燃料电池轿车动力系统是一个既包含了一系列连续变量的动态系统(对应着诸如燃料电池发动机、锂电池和电机等零部件的连续工作状态),又包含了随着时间的推移和系统的不断演化,在不同连续变量动态子系统之间不断切换的系统(如锂电池充电和放电,燃料电池的开启与关闭),故可称其为既包含连续变量又包含离散变量的混杂系统.
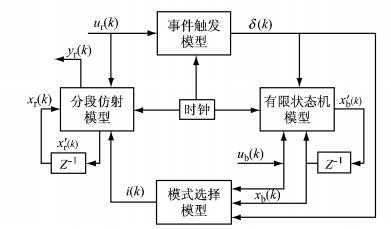
3.1 燃料电池轿车分段仿射系统架构对于混杂系统建模,具有代表性的模型有混杂自动机/petri网模型、混杂监控模型、混合逻辑动态模型和分段仿射系统模型.分段仿射系统模型在分析系统的稳定性和优化控制方面有独到之处[18],下文对燃料电池轿车动力系统的建模采用分段仿射系统的建模方法.燃料电池轿车分段仿射系统架构如图 12所示,主要包括分段仿射模型、事件触发模型、有限状态机模型和模式选择模型4个部分.
|
图 12 燃料电池轿车分段仿射系统架构 Fig.12 Piecewise affine system framework of fuel cell car |
图 12中:k为时间序列; i(k)为工作模式状态输入量,决定燃料电池轿车的工作模型; ur(k)为输入控制量,ur(k)=[ID, s(k) Im, s(k)],其中ID, s(k)为DC/DC变换器的电流设置量,Im, s(k)为电机的电流设置量; yr(k)为燃料电池轿车动力系统的输出量; xr(k)为燃料电池轿车动力系统的状态变量,xr(k)=[ID, o(k) Im, o(k) UP(k) tf(k) tb(k)],其中tf(k)为燃料电池的放电时间,tb(k)为锂电池的放电时间,Im, o(k)为电机的输出电流; x′r(k)为xr(k)前一时刻的系统状态变量; xb(k)为系统的二进制状态变量; x′b(k)为前一时刻系统的二进制状态变量; ub(k)为输入控制量的二进制状态; δ(k)为一个触发量.
根据分段仿射模型的数学定义[19],采用式(3)~(7)中的线性数学模型,可以建立如下所示的燃料电池轿车动力系统分段仿射模型:
| $ \left\{ \begin{array}{l} {x_{\rm{r}}}\left( {k + 1} \right) = {\mathit{\boldsymbol{A}}_{i\left( k \right)}}{x_{\rm{r}}}\left( k \right) + {\mathit{\boldsymbol{B}}_{i\left( k \right)}}{u_{\rm{r}}}\left( k \right)\\ {y_{\rm{r}}}\left( k \right) = {\mathit{\boldsymbol{C}}_{i\left( k \right)}}{x_{\rm{r}}}\left( k \right) \end{array} \right. $ | (9) |
其中,
| $ {\mathit{\boldsymbol{A}}_{i\left( k \right)}} = \left[ {\begin{array}{*{20}{c}} { - \frac{1}{{{\tau _{\rm{f}}}}}}&0&0&0&0\\ 0&0&{ - \frac{1}{{{\tau _{\rm{m}}}}}}&0&0\\ { - \frac{1}{{{C_{\rm{P}}}}}}&{ - \frac{1}{{{C_{\rm{P}}}{R_{\rm{P}}}}}}&{\frac{1}{{{C_{\rm{P}}}}}}&0&0\\ 0&0&0&{{a_{44}}}&0\\ 0&0&0&0&{{a_{55}}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{B}}_{i\left( k \right)}} = \left[ {\begin{array}{*{20}{c}} {\frac{{{k_{\rm{f}}}}}{{{\tau _{\rm{f}}}}}}&0\\ 0&{\frac{{{k_{\rm{f}}}}}{{{\tau _{\rm{m}}}}}}\\ 0&0\\ 0&0\\ 0&0 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{C}}_{i\left( k \right)}} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0 \end{array}} \right] $ |
系统矩阵Ai(k)中a44、a55是由状态输入量决定的,取值分别为0和1.
事件触发模型用来表示燃料电池轿车动力系统在不同输入控制和零部件状态下的触发情况,数学模型[20]表示为
| $ \delta \left( k \right) = h\left( {{x_{\rm{r}}}\left( k \right),{u_{\rm{r}}}\left( k \right),k} \right) $ | (10) |
δ(k)与系统状态变量、控制量、时间的函数关系为h,1表示触发,0表示不触发.
具体的触发由以下2组事件组成:
(1) 燃料电池发动机的开、关和功率阈值.开和关分别表示功率的输出和不输出,由输出效率和氢耗决定.功率阈值由燃料电池发动机本身性能决定.这组事件的触发情况可以表示为
| $ \delta = \left\{ \begin{array}{l} 1,\;\;\;0 < {P_{{\rm{f,d}}}} < 60\;{\rm{kW}}\;或\;{t_{\rm{f}}} > 5\;{\rm{s}}\\ 0,\;\;\;{P_{{\rm{f,d}}}} \le 0\;或\;{P_{{\rm{f,d}}}} \ge 60\;{\rm{kW}}\;或\;{t_{\rm{f}}} \le 5\;{\rm{s}} \end{array} \right. $ | (11) |
(2) 锂电池工作模式.根据当前锂电池SOC选择锂电池是处于放电模式还是充电模式.此外,从保护锂电池角度把放电时间加入触发事件的影响因素中,即若锂电池放电时间很短,则不触发此事件.这组事件的触发情况可以表示为
| $ \delta = \left\{ \begin{array}{l} 1,\;\;{\rm{SOC}} > {\rm{50\% }}\;或\;{t_{\rm{b}}} > 30\;{\rm{s}}\\ 0,\;\;{\rm{SOC}} \le {\rm{50\% }}\;或\;{t_{\rm{b}}} \le 30\;{\rm{s}} \end{array} \right. $ | (12) |
燃料电池轿车动力系统的有限状态机模型是与动力系统各零部件的二进制状态、输入控制量的二进制状态以及事件触发状态有关的函数,数学模型[19]表示为
| $ {{\dot x}_{\rm{b}}}\left( k \right) = p\left( {{x_{\rm{b}}}\left( k \right),{u_{\rm{b}}}\left( k \right),\delta \left( k \right)} \right) $ | (13) |
式中:p是关于xb(k)、ub(k)、δ(k)的函数; xb=[xb1 xb2 xb3 xb4],其中xb1表示燃料电池开启且锂电池放电,xb2表示燃料电池开启且锂电池充电,xb3表示燃料电池关闭且锂电池放电,xb4表示燃料电池关闭且锂电池充电; ub(k)=[sf(k) sb(k)]T,其中sf(k)表示燃料电池开或关的布尔量,1为开,0为关,sb(k)为锂电池充放电的布尔量,1为放电,0为充电.系统的二进制状态由如下逻辑关系得出:
| $ \begin{array}{l} {x_{{\rm{b1}}}} = {s_{\rm{f}}}\left( k \right)\& {s_{\rm{b}}}\left( k \right)\\ {x_{{\rm{b2}}}} = {s_{\rm{f}}}\left( k \right)\& !{s_{\rm{b}}}\left( k \right)\\ {x_{{\rm{b3}}}} = !{s_{\rm{f}}}\left( k \right)\& {s_{\rm{b}}}\left( k \right)\\ {x_{{\rm{b4}}}} = !{s_{\rm{f}}}\left( k \right)\& !{s_{\rm{b}}}\left( k \right) \end{array} $ | (14) |
式中:&表示逻辑与; !表示逻辑非.
动力系统的离散状态模式选择由系统的布尔状态量xb(k)、系统外的布尔输入控制量ub(k)、事件触发δ(k)共同决定,数学模型[19]表示为
| $ i\left( k \right) = q\left( {{x_{\rm{b}}}\left( k \right),{u_{\rm{b}}}\left( k \right),\delta \left( k \right)} \right) $ | (15) |
式中:q为模式选择函数.
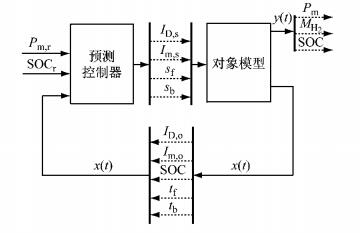
3.2 燃料电池轿车模型预测控制算法基于3.1节建立的混杂系统模型,根据模型预测控制的基本原理[13],假设Np为预测时域,Nc为控制时域,Δu为输入控制的变化量,Qj、Rj为权系数,分别表示对跟踪误差及控制量变化的抑制,yl、ys、ul、us为输出变量和控制变量边界值.建立状态预测方程、输出预测方程、优化目标函数和变量的约束条件,如式(16)~(19)所示.基于得到的预测模型以及优化目标函数,利用Matlab平台进行预测控制器的设计,预测控制器与对象模型之间的接口关系如图 13所示.
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {x\left( {k + 1\left| k \right.} \right)}\\ \vdots \\ {x\left( {k + {N_{\rm{c}}}\left| k \right.} \right)}\\ {x\left( {k + {N_{\rm{c}}} + 1\left| k \right.} \right)}\\ \vdots \\ {x\left( {k + {N_{\rm{p}}}\left| k \right.} \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{i\left( k \right)}}}\\ \vdots \\ {\mathit{\boldsymbol{A}}_{i\left( k \right)}^{{N_{\rm{c}}}}}\\ {\mathit{\boldsymbol{A}}_{i\left( k \right)}^{{N_{\rm{c}}} + 1}}\\ \vdots \\ {\mathit{\boldsymbol{A}}_{i\left( k \right)}^{{N_{\rm{p}}}}} \end{array}} \right]x\left( k \right) + \\ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{i\left( k \right)}}}\\ \vdots \\ {\sum\limits_{j = 0}^{{N_{\rm{c}}} - 1} {\mathit{\boldsymbol{A}}_{i\left( k \right)}^j{\mathit{\boldsymbol{B}}_{i\left( k \right)}}} }\\ {\sum\limits_{j = 0}^{{N_{\rm{c}}}} {\mathit{\boldsymbol{A}}_{i\left( k \right)}^j{\mathit{\boldsymbol{B}}_{i\left( k \right)}}} }\\ \vdots \\ {\sum\limits_{j = 0}^{{N_{\rm{p}}} - 1} {\mathit{\boldsymbol{A}}_{i\left( k \right)}^j{\mathit{\boldsymbol{B}}_{i\left( k \right)}}} } \end{array}} \right]u\left( {k - 1} \right) + \\ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{i\left( k \right)}}}& \cdots &0\\ {{\mathit{\boldsymbol{A}}_{i\left( k \right)}}{\mathit{\boldsymbol{B}}_{i\left( k \right)}} + {\mathit{\boldsymbol{B}}_{i\left( k \right)}}}& \cdots &0\\ \vdots &{}& \vdots \\ {\sum\limits_{j = 0}^{{N_{\rm{c}}} - 1} {\mathit{\boldsymbol{A}}_{i\left( k \right)}^j{\mathit{\boldsymbol{B}}_{i\left( k \right)}}} }& \cdots &{{\mathit{\boldsymbol{B}}_{i\left( k \right)}}}\\ {\sum\limits_{j = 0}^{{N_{\rm{c}}}} {\mathit{\boldsymbol{A}}_{i\left( k \right)}^j{\mathit{\boldsymbol{B}}_{i\left( k \right)}}} }& \cdots &{{\mathit{\boldsymbol{A}}_{i\left( k \right)}}{\mathit{\boldsymbol{B}}_{i\left( k \right)}} + {\mathit{\boldsymbol{B}}_{i\left( k \right)}}}\\ \vdots &{}& \vdots \\ {\sum\limits_{j = 0}^{{N_{\rm{p}}} - 1} {\mathit{\boldsymbol{A}}_{i\left( k \right)}^j{\mathit{\boldsymbol{B}}_{i\left( k \right)}}} }& \cdots &{\sum\limits_{j = 0}^{{N_{\rm{p}}} - {N_{\rm{c}}}} {\mathit{\boldsymbol{A}}_{i\left( k \right)}^j{\mathit{\boldsymbol{B}}_{i\left( k \right)}}} } \end{array}} \right] \cdot \\ \left[ {\begin{array}{*{20}{c}} {\Delta u\left( {k\left| k \right.} \right)}\\ \vdots \\ {\Delta u\left( {k + {N_{\rm{c}}} - 1\left| k \right.} \right)} \end{array}} \right] \end{array} $ | (16) |
| $ y\left( {k + j\left| k \right.} \right) = {\mathit{\boldsymbol{C}}_{i\left( k \right)}}\left( {k + j\left| k \right.} \right),j = 1, \cdots ,{N_{\rm{p}}} $ | (17) |
| $ \begin{array}{l} \min J\left[ {{x_{\rm{r}}}\left( k \right),u} \right] = \\ \;\;\;\;\;\sum\limits_{j = 1}^{{N_{\rm{p}}}} {\left\| {y\left( {k + j\left| k \right.} \right) - {y_{\rm{r}}}\left( {k + j\left| k \right.} \right)} \right\|_{{Q_j}}^2} + \\ \;\;\;\;\;\sum\limits_{j = 1}^{{N_{\rm{c}}} - 1} {\left\| {\Delta u\left( {k + j\left| k \right.} \right)} \right\|_{{R_j}}^2} \end{array} $ | (18) |
| $ \left\{ \begin{array}{l} {y_{\rm{s}}} \le y\left( {k + j\left| k \right.} \right) \le {y_{\rm{l}}},j = 0, \cdots ,{N_{\rm{p}}}\\ {u_{\rm{s}}} \le u\left( {k + j\left| k \right.} \right) \le {u_{\rm{l}}},j = 0, \cdots ,{N_{\rm{c}}} - 1\\ \Delta {u_{\rm{s}}} \le \Delta u\left( {k + j\left| k \right.} \right) \le \Delta {u_{\rm{l}}},j = 0, \cdots ,{N_{\rm{c}}} - 1 \end{array} \right. $ | (19) |
|
图 13 模型预测控制的控制器接口 Fig.13 Controller interface of model predictive control |
式(17)中:Ci(k)为输出向量矩阵.
图 13中,Pm, r为电机的目标功率,SOCr为锂电池的目标SOC,Pm为电机的输出功率,MH2为氢气的供给量.
3.3 燃料电池轿车动力系统模型预测控制性能仿真由于燃料电池轿车混杂系统存在多个模式,即激活模式i(k)会影响参数a44和a55的值,因此需要针对每个模式,利用3.2节的控制算法分别进行预测控制器的设计,之后将控制器和驱动系统模型进行集成.为验证提出的预测控制器的有效性,本文搭建了燃料电池轿车模型预测控制闭环仿真模型,并在欧洲经济委员会额外城市行驶(ECE-EUDC)和城市道路循环(UDDS)2种典型循环工况下对模型进行了仿真分析.在预测控制器中,采样时间为0.02 s,然后选取不同的预测时域和控制时域进行仿真.
在ECE-EUDC和UDDS 2种工况下,不同预测时域和控制时域参数的能耗仿真结果见表 1和表 2.表 3和表 4给出了模型预测控制策略与实车控制策略的能耗仿真结果.
| 下载CSV 表 1 ECE-EUDC工况不同参数下的能耗仿真结果 Tab.1 Simulation results of energy consumptions in ECE-EUDC for different parameters |
| 下载CSV 表 2 UDDS工况不同参数下的能耗仿真结果 Tab.2 Simulation results of energy consumptions in UDDS for different parameters |
| 下载CSV 表 3 ECE-EUDC工况2种策略的能耗仿真结果 Tab.3 Simulation results of energy consumptions of two strategies in ECE-EUDC |
| 下载CSV 表 4 UDDS工况2种策略的能耗仿真结果 Tab.4 Simulation results of energy consumptions of two strategies in UDDS |
从表 1和表 2可以看出,当预测时域Np相同时,控制时域Nc越大,总能耗越少.这是因为控制时域大意味着控制变量起作用的时域增大,可以得到更好的跟踪性能,使输出误差的最小化得到更大程度的满足.然而,当控制时域过大时会增加目标函数求解的维数,影响计算时长,因此减少控制时域有利于控制变量的计算.当控制时域Nc相同时,预测时域Np越大,总能耗越低,因为预测时域反映了对未来多少步输出逼近期望值的兴趣度,预测步长越多,结果就越趋于理想值,而且系统的稳定性也好,但预测时域过大同样对系统的快速性造成影响,增加控制量求解的计算量,从而影响实时性.综合上述情况,本文选取预测时域Np=10和控制时域Nc=2作为预测控制的参数.
从表 3和表 4可以看出,采用模型预测控制策略的燃料电池轿车氢燃料经济性比采用基于功率平衡的SOC闭环控制策略的能量经济性有所提高,在ECE-EUDC工况下减少了3.18%,在UDDS工况下减少了3.39%,说明了模型预测控制策略能够有效提高燃料电池轿车的能量经济性.
4 控制策略硬件在环仿真试验采用硬件在环(HIL)进行整个系统的仿真测试,能够更好地接近实车的运行情况和环境,从而更加准确地测试与评价所设计的模型预测控制策略.
4.1 燃料电池轿车HIL仿真试验方案燃料电池轿车动力系统硬件在环仿真试验平台的结构如图 14所示.PC机1、2代表用于建模、测量和标定的上位机,PC机1用于驱动系统模型的建立,PC机2用于能量管理策略模型的建立.整车控制器和MicroAutoBox则为硬件在环试验平台的硬件实物部分,相应的实物如图 15所示.

|
图 14 硬件在环仿真试验平台结构 Fig.14 Test-bed structure of HIL simulation |

|
图 15 硬件在环仿真试验平台 Fig.15 HIL simulation test-bed |
图 16和图 17所示为实车控制策略在ECE-EUDC工况下离线仿真和HIL仿真的结果对比.图 18和图 19所示为模型预测控制策略在ECE-EUDC工况下离线仿真和HIL仿真的结果对比.

|
图 16 实车控制策略电机电流比较 Fig.16 Motor current comparison of real car control strategy |
|
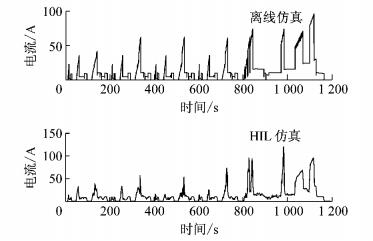
图 17 实车控制策略DC/DC变换器电流比较 Fig.17 DC/DC converter current comparison of real car control strategy |
|
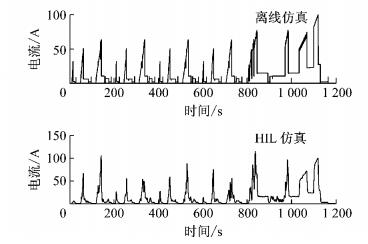
图 18 模型预测控制策略电机电流比较 Fig.18 Motor current comparison of MPC strategy |

|
图 19 模型预测控制策略DC/DC变换器电流比较 Fig.19 DC/DC converter current comparison of MPC strategy |
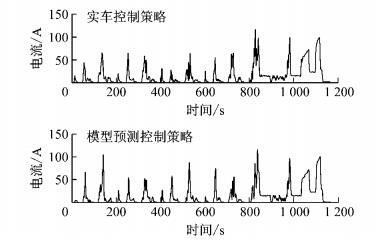
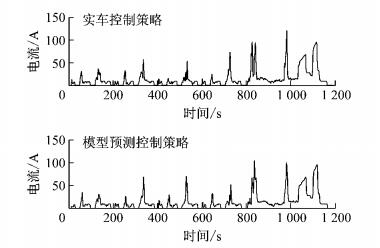
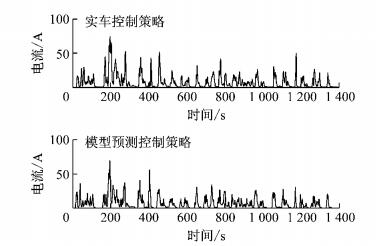
从图 16~19看出,基于实车控制策略和模型预测控制策略的离线和HIL仿真的电机与DC/DC变换器电流的走势和幅值基本相同,不同之处是由于信号受噪声等因素影响,HIL的仿真结果抖动相对较大.因此,通过HIL试验更进一步说明了所建立的驱动系统和能量管理策略模型是正确的,所提出的基于MPC的能量管理策略具有较好的实时性.在ECE-EUDC和UDDS 2种工况下, 基于搭建的硬件在环仿真试验平台, 对实车和模型预测控制策略的HIL仿真结果进行了对比和分析,ECE-EUDC工况下的结果如图 20和图 21所示,UDDS工况下的结果如图 22和图 23所示.从图 20~23可以看出,实车控制策略的零部件电流值和模型预测控制策略的零部件电流值总体趋势类似,除了极少数尖峰值外,模型预测控制策略电流值比实车控制策略电流值要小.
|
图 20 ECE-EUDC工况2种策略电机电流HIL测试结果 Fig.20 HIL test results of motor current of two strategies in ECE-EUDC |
|
图 21 ECE-EUDC工况2种策略DC/DC变换器电流HIL测试结果 Fig.21 HIL test results of DC/DC converter current of two strategies in ECE-EUDC |
|
图 22 UDDS工况2种策略电机电流HIL测试结果 Fig.22 HIL test results of motor current of two strategies in UDDS |

|
图 23 UDDS工况2种策略DC/DC变换器电流HIL测试结果 Fig.23 HIL test results of DC/DC converter current of two strategies in UDDS |
表 5和表 6给出了模型预测控制策略和实车控制策略在HIL仿真试验中能耗的测试结果对比分析.从表 5和表 6中的HIL试验结果可以看出,MPC策略的总能耗比实车控制策略在ECE-EUDC和UDDS工况下分别降低了3.07%和3.74%,这和离线仿真所得结果基本相同,进一步说明了所开发的MPC策略的有效性,同时也说明了该策略具有较好的实时性,可用于后续的实车试验.
| 下载CSV 表 5 ECE-EUDC工况2种策略能耗HIL测试结果 Tab.5 HIL test results of energy consumptions of two strategies in ECE-EUDC |
| 下载CSV 表 6 UDDS工况2种策略能耗HIL测试结果 Tab.6 HIL test results of energy consumptions of two strategies in UDDS |
(1) 搭建燃料电池轿车动力系统仿真模型,进行模型的离线仿真与实车试验验证,结果表明所搭建动力系统模型的误差在5%以内.这说明所搭建的燃料电池轿车动力系统仿真模型具有较高的精度,可应用于能量管理策略的开发.
(2) 基于模型预测控制的燃料电池轿车以有限时域内能量经济性最优为优化目标,优化有限时域内燃料电池与蓄电池的工作状态,并将当前控制作用于对象来实现实时控制,通过滚动优化提高燃料电池轿车的能量经济性.建立了燃料电池轿车动力系统的模型预测控制策略,与实车控制策略进行离线仿真对比,在ECE-EUDC工况下总能耗减少了3.18%,在UDDS工况下总能耗减少了3.39%,说明本文所提出的燃料电池轿车模型预测控制策略能够有效地提高能量经济性.
(3) 进行基于模型预测控制的能量管理策略硬件在环试验验证,与实车控制策略相比,在ECE-EUDC与UDDS工况下总能耗分别降低3.07%和3.74%,与仿真结果吻合较好,说明本文所提出的燃料电池轿车模型预测控制策略的有效性与实时性.
| [1] |
DAS H S, TAN C W, YATIM A H M. Fuel cell hybrid electric vehicles: a review on power conditioning units and topologies[J]. Renewable & Sustainable Energy Reviews, 2017, 76: 268 |
| [2] |
卢兰光, 何彬, 欧阳明高. 燃料电池城市客车能量分配算法研究[J]. 机械工程学报, 2005, 41(12): 8 LU Languang, HE Bin, OUYANG Minggao. Energy management strategies for fuel cell hybrid electric vehicle[J]. Chinese Journal of Mechanical Engineering, 2005, 41(12): 8 DOI:10.3321/j.issn:0577-6686.2005.12.003 |
| [3] |
陈超, 曹桂军, 卢兰光, 等. 功率混合型燃料电池汽车动力系统的恒压式能量分配算法[J]. 汽车工程, 2007, 29(2): 101 CHEN Chao, CAO Guijun, LU Languang, et al. Constant voltage energy distribution algorithm for power system of power-type fuel cell vehicle[J]. Automotive Engineering, 2007, 29(2): 101 |
| [4] |
钟再敏, 魏学哲, 孙泽昌. 燃料电池汽车动力总成控制策略[J]. 同济大学学报(自然科学版), 2004, 32(6): 758 ZHONG Zaimin, WEI Xuezhe, SUN Zechang. Research on control principle of fuel cell vehicle powertrain[J]. Journal of Tongji University(Natural Science), 2004, 32(6): 758 |
| [5] |
孙泽昌, 魏学哲, 钟再敏. 燃料电池汽车动力系统功率平衡控制策略[J]. 机械工程学报, 2005, 41(12): 3 SUN Zechang, WEI Xuezhe, ZHONG Zaimin. Power balance strategy of powertrain in fuel cell vehicle[J]. Chinese Journal of Mechanical Engineering, 2005, 41(12): 3 DOI:10.3321/j.issn:0577-6686.2005.12.002 |
| [6] |
ZHANG G, CHEN W, LI Q. Modeling, optimization and control of a FC/battery hybrid locomotive based on ADVISOR[J]. International Journal of Hydrogen Energy, 2017, 42: 18568 DOI:10.1016/j.ijhydene.2017.04.172 |
| [7] |
贠海涛, 孙泽昌, 万钢, 等. 燃料电池轿车动力系统线性二次型最优控制研究[J]. 汽车工程, 2007, 29(2): 112 YUN Haitao, SUN Zechang, WAN Gang, et al. A study on the linear quadratic optimal control for fuel cell car powertrain[J]. Automotive Engineering, 2007, 29(2): 112 |
| [8] |
齐占宁, 陈全世, 赵六奇. 基于遗传算法的燃料电池车控制策略优化[J]. 公路交通科技, 2004, 21(4): 93 QI Zhanning, CHEN Quanshi, ZHAN Liuqi. Optimization of FCEV's control strategies using genetic algorithm[J]. Journal of Highway and Transportation Research and Development, 2004, 21(4): 93 |
| [9] |
金振华, 欧阳明高, 卢青春, 等. 燃料电池混合动力系统优化控制策略[J]. 清华大学学报(自然科学版), 2009(2): 273 JIN Zhenhua, OUYANG Minggao, LU Qingchun, et al. Optimal control strategy for a fuel cell hybrid powertrain[J]. Journal of Tsinghua University(Science and Technology), 2009(2): 273 |
| [10] |
张炳力, 代康伟, 赵韩, 等. 基于随机动态规划的燃料电池城市客车能量管理策略优化[J]. 系统仿真学报, 2008, 20(17): 4664 ZHANG Bingli, DAI Kangwei, ZHAN Han, et al. Optimized energy management strategy for fuel cell city bus based on stochastic dynamic programming[J]. Journal of System Simulation, 2008, 20(17): 4664 |
| [11] |
RODATZ P, PAGANELLI G, SCIARRETTA A, et al. Optimal power management of an experimental fuel cell/supercapacitor-powered hybrid vehicle[J]. Control Engineering Practice, 2005, 13(1): 41 DOI:10.1016/j.conengprac.2003.12.016 |
| [12] |
ZHENG C, CHA S W. Real-time application of Pontryagin's Minimum Principle to fuel cell hybrid buses based on driving characteristics of buses[J]. International Journal of Precision Engineering and Manufacturing: Green Technology, 2017, 4(2): 199 DOI:10.1007/s40684-017-0025-y |
| [13] |
席裕庚. 预测控制[M]. 北京: 国防工业出版社, 2013 XI Yugeng. Predictive control[M]. Beijing: National Defense Industry Press, 2013 |
| [14] |
曾祥瑞, 黄开胜, 孟凡博. 具有实时运算潜力的并联混合动力汽车模型预测控制[J]. 汽车安全与节能学报, 2012, 3(2): 165 ZENG Xiangrui, HUANG Kaisheng, MENG Fanbo. Model predictive control for parallel hybrid electric vehicles with potential real-time capability[J]. Journal of Automotive Safety and Energy, 2012, 3(2): 165 |
| [15] |
AMPHLETT J C, BAUMERT R M, MANN R F, et al. Performance modeling of the Ballard mark Ⅳ solid polymer electrolyte fuel cell[J]. Journal of Electrochemical Society, 1995, 142(1): 9 DOI:10.1149/1.2043959 |
| [16] |
胡斐. 混合动力城市客车整车能量管理策略研究与开发[D]. 上海: 同济大学, 2012. HU Fei. Research and development on energy management strategies of hybrid electric bus[D]. Shanghai: Tongji University, 2012. |
| [17] |
徐衍亮. 电动汽车用永磁同步电机及其驱动系统研究[D]. 沈阳: 沈阳工业大学, 2001. XU Yanliang. Study on permanent magnet synchronous motor and its drive system in electric vehicle application[D]. Shenyang: Shenyang University of Technology, 2001. |
| [18] |
刘志林. 分段仿射系统的控制器设计及预测控制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2007. LIU Zhilin. Controller design and model predictive control approaches for piecewise affine system[D]. Habin: Harbin Institute of Technology, 2007. |
| [19] |
RODRIGUES L. Dynamic output feedback controller synthesis for piecewise-affine systems[D]. Palo Alto: Stanford University, 2002.
|
| [20] |
TORRISI F, BEMPORAD A. HYSDEL: a tool for generating computational hybrid models[J]. IEEE Transactions on Control Systems Technology, 2004, 12(2): 235 DOI:10.1109/TCST.2004.824309 |
 2018, Vol. 46
2018, Vol. 46
