中海滩浴场位于河北省秦皇岛市西部的北戴河海滨,在多种自然因素和人为因素的作用下,其岸滩长期受到侵蚀,平均宽度一度仅剩十几米,海滩坡度变陡,沙粒粗化,基岩裸露[1].海滩的侵蚀退化已演变成当今全球普遍存在的自然灾害[2],也已成为海滩防灾的重要内容,实施硬工程和软工程是海滩侵蚀防治的主要办法[3].硬工程包括修建海堤、丁坝、防波堤等一些传统的海岸建筑物,由于硬工程表现出的是对其所在海域动力环境的一种排斥并非适应环境本身,因此以人工养滩为主的软工程作为一种环境友好的工程措施得到了国内外的广泛认可[4].旅游海滩的养护工程包含硬工程和软工程相结合的养护方式,其作用机理和设计过程[5]是当前研究热点,已得到养护工程作用范围的水动力、输沙模式和地貌演变模式数学模型[6-7].近岸人工水下沙坝是软工程的一种方式,它既能削波减能,又能作为砂源对海滩持续补砂,在养滩工程中得到了充分应用[8].对于人工沙坝的相关研究主要集中在以下2个方面:人工沙坝的作用机理和人工沙坝的养滩效果.Koster [9]详细描述了水下人工沙坝的削波作用和沙坝作为砂源持续补砂的物理过程.张弛等[10]通过数学模型模拟了波浪作用下沙坝剖面形成过程. Dette等[11]通过物理实验研究了水下人工沙坝宽度对海滩养护效果的影响.ilinskasa等[12]基于泥沙的粒度组成,分析了沙坝的移动趋势并得到了沙坝的最佳养滩位置.朱金龙等[13]通过数值实验对人工沙坝的削波效果进行了对比分析.自2008年起,秦皇岛北戴河多处海滩开展了诸多人工沙坝的应用与研究.匡翠萍等[14]通过MIKE软件建立的二维潮流和波浪耦合模型预测了养滩工程对老虎石海域周围水动力环境的改变.杨燕雄等[15]通过人工沙坝的水槽实验分析研究了沙坝的形状变化,并利用整合型海岸模拟系统(SMC)模型对波流响应进行分析.
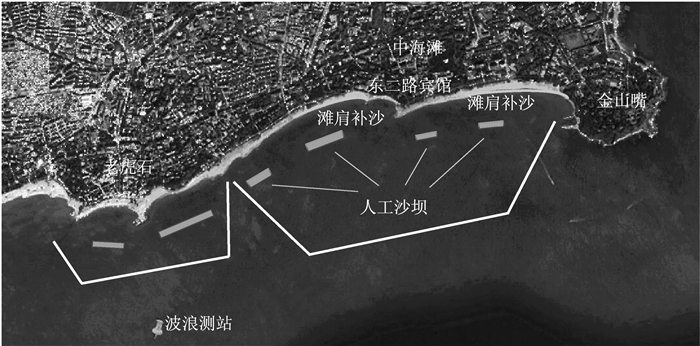
北戴河中海滩养滩工程位于北戴河老虎石东侧(见图 1),主要采用滩肩补沙与修建4座水下沙坝结合的方法.对金山嘴至东二路宾馆及东二路宾馆至老虎石公园2个岬湾进行滩肩补沙,这段岸线走向从东—西向转为东北偏东—西南偏西向,总长约1 400 m.设计平均滩肩宽度约30 m,随位置不同而异,修复后的滩肩高程达到2 m以上; 4座人工水下沙坝离岸平均约300 m,总长约800 m,坝顶高程约-0.9 m.为了详细探究人工水下沙坝的建造对中海滩海域水动力的影响,运用Delft3D软件针对该区域建立波流耦合模型,利用验证后的模型进行波流过程的模拟,并分析水动力响应特征.
|
图 1 中海滩养滩工程实施区域 Fig.1 Implementation area of Zhonghaitan beach nourishments |
Delft3D是由WL|Delft Hydraulics开发的一款由多模块集成的数值模拟软件,主要运用于模拟计算河口海岸地区的水动力、水环境、泥沙运动和岸滩演变.潮流模型的基本方程是由基于不可压缩自由表面流的三维Navier-Stokes方程和浅水假定推导而来.基于曲线正交网格进行控制方程计算,ξ和η表示水平面上正交的2个方向,σ表示垂直方向.连续性方程为
| $ \begin{array}{l} \frac{{\partial \zeta }}{{\partial t}} + \frac{1}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \left[ {\left( {d + \zeta } \right)u\sqrt {{G_{\eta \eta }}} } \right]}}{{\partial \xi }} + \frac{1}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }} \cdot \\ \;\;\;\;\;\;\;\;\frac{{\partial \left[ {\left( {d + \zeta } \right)v\sqrt {{G_{\xi \xi }}} } \right]}}{{\partial \eta }} + \frac{{\partial w}}{{\partial \sigma }} = \left( {d + \zeta } \right)\left( {{q_{{\rm{in}}}} - {q_{{\rm{out}}}}} \right) \end{array} $ | (1) |
式中:ξ为参考面以上水位; t为时间; d为参考面以下水深; u、v、w分别为ξ、η和σ方向的流速; Gηη、Gξξ为曲线正交坐标系与笛卡尔坐标系(x、y、z)之间的转换系数; qin和qout分别为单元的入流量和出流量.
ξ和η方向的动量方程为
| $ \begin{array}{l} \frac{{\partial u}}{{\partial t}} + \frac{u}{{\sqrt {{G_{\xi \xi }}} }}\frac{{\partial u}}{{\partial \xi }} + \frac{v}{{\sqrt {{G_{\eta \eta }}} }}\frac{{\partial u}}{{\partial \eta }} + \frac{w}{{d + \zeta }}\frac{{\partial u}}{{\partial \sigma }} - \\ \;\;\;\;\;\;\;\frac{{{v^2}}}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \sqrt {{G_{\eta \eta }}} }}{{\partial \xi }} + \frac{{uv}}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \sqrt {{G_{\xi \xi }}} }}{{\partial \eta }} - fv = \\ \;\;\;\;\;\;\; - \frac{{{P_\xi }}}{{\rho \sqrt {{G_{\xi \xi }}} }} + {F_\xi } + \frac{1}{{{{\left( {d + \zeta } \right)}^2}}}\frac{\partial }{{\partial \sigma }}\left[ {{\upsilon _{{\rm{mol}}}} + } \right.\\ \;\;\;\;\;\;\;\left. {\max \left( {{\upsilon _{3{\rm{D}}}},{\upsilon _{{\rm{v}},{\rm{b}}}}} \right)\frac{{\partial u}}{{\partial \sigma }}} \right] + {M_\xi } \end{array} $ | (2) |
| $ \begin{array}{l} \frac{{\partial v}}{{\partial t}} + \frac{v}{{\sqrt {{G_{\xi \xi }}} }}\frac{{\partial v}}{{\partial \xi }} + \frac{v}{{\sqrt {{G_{\eta \eta }}} }}\frac{{\partial v}}{{\partial \eta }} + \frac{w}{{d + \zeta }}\frac{{\partial v}}{{\partial \sigma }} - \\ \;\;\;\;\;\;\;\frac{{{u^2}}}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \sqrt {{G_{\eta \eta }}} }}{{\partial \eta }} + \frac{{uv}}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \sqrt {{G_{\eta \eta }}} }}{{\partial \xi }} + fu = \\ \;\;\;\;\;\;\; - \frac{{{P_\eta }}}{{\rho \sqrt {{G_{\eta \eta }}} }} + {F_\eta } + \frac{1}{{{{\left( {d + \zeta } \right)}^2}}}\frac{\partial }{{\partial \sigma }}\left[ {{\upsilon _{{\rm{mol}}}} + } \right.\\ \;\;\;\;\;\;\;\left. {\max \left( {{\upsilon _{3{\rm{D}}}},{\upsilon _{{\rm{v}},{\rm{b}}}}} \right)\frac{{\partial v}}{{\partial \sigma }}} \right] + {M_\eta } \end{array} $ | (3) |
式中:ρ为水的密度; f为柯氏力系数; υ3D为三维紊动黏滞系数,υ3D=Cμk2/ε,其中Cμ=0.09,k为湍动能,ε为紊流耗散率,采用标准k-ε紊动模型; υv, b为背景垂向黏滞系数; υmol为水的运动黏度; Pξ、Pη分别为ξ和η方向压力梯度; Fξ、Fη分别为ξ和η方向由紊动引起的雷诺应力; Mξ、Mη分别为ξ和η方向由泄流或取水、构筑物、波浪辐射应力等外部作用引起的动量变化.
采用第三代SWAN(simulating waves nearshore)波浪模型,基于波浪密度谱描述随机波,波浪频谱变化以动态频谱平衡方程描述,笛卡尔坐标系(x、y、z)下谱平衡方程为
| $ \frac{\partial }{{\partial t}}N + \frac{\partial }{{\partial x}}{c_x}N + \frac{\partial }{{\partial y}}{c_y}N + \frac{\partial }{{\partial \sigma }}{c_\omega }N + \frac{\partial }{{\partial \theta }}{c_\theta }N = \frac{S}{\omega } $ | (4) |
式中:N为波作用密度; ω为波浪相对频率; θ为波浪传播方向; cx、cy、cω和cθ分别为x、y、ω、θ方向上的波浪传播速度; S为源项,包括风生浪、耗散、非线性波和波破碎等.式(4)中第一项为波浪作用随时间的变化,第二项和第三项为波浪传播地理空间变化的影响,第四项为地形和水流造成的多普勒频移效应,第五项为因地形和水流引起的折射作用.风能输入可表示为
| $ {S_{{\rm{in}}}}\left( {\omega ,\theta } \right) = A + BE\left( {\omega ,\theta } \right) $ | (5) |
式中:A和B分别为波浪的频率、角度和风的速度、角度的函数; E(ω, θ)为能量谱密度.
综上所述,波流耦合的实现过程为:将由潮流模型计算得到的水位与流速输入波浪模型,得到新的波浪参数,同时将由波浪模型计算得到的辐射应力输入到潮流模型,得到新的水位、流速.2个模型时间步长和计算时间一致,通过数据交换实现双向耦合,最后得到波浪和潮流耦合作用下水位、流速和波高的变化.
1.2 计算范围与参数设置为保证局部流场计算符合潮流场的整体物理特征,采用大的渤海潮流模型(网格数450×350,精度1 050 m×1 050 m)和小的秦皇岛区域模型(网格数200×330,精度280 m×230 m)两重嵌套的方式进行计算(见图 2),并在小模型使用区域分解技术,划分一个子区域,包含整个中海滩浴场及其附近岬角,网格数为285×460,精度为30 m×25 m.子区域地形除近岸处坡度较陡外,整体上坡度较缓,0~2 m等深线海域坡度较大,介于11.8‰~17.2‰,2~5 m等深线海域坡度为3.2‰~3.4‰,5~10 m等深线海域坡度最小,不足1‰,介于0.94‰~0.98‰.二维计算时,垂向网格为1层; 三维计算时,垂向网格为均匀的10层.

|
图 2 大、小模型网格和子区域网格及地形 Fig.2 Mesh of big and small models and mesh and topography of subdomain |
大模型海域开边界由大连老虎滩和烟台2个潮位站所测得的潮位过程进行控制,小模型海域开边界包括西边界、东边界和南边界3条开边界以及1条岸线闭边界,其潮位条件由大模型提供,大模型初始流速为零.固边界采用不可滑移条件,并采用动边界处理滩地的干湿交换过程.干水深取0.05 m,湿水深取0.10 m,以网格中心与边界处的平均水深进行判定.小模型边界的水平紊动黏滞系数取20 m2·s-1,曼宁系数均值取0.013 5,计算时间步长取0.5 min,初始水位取平均海平面.
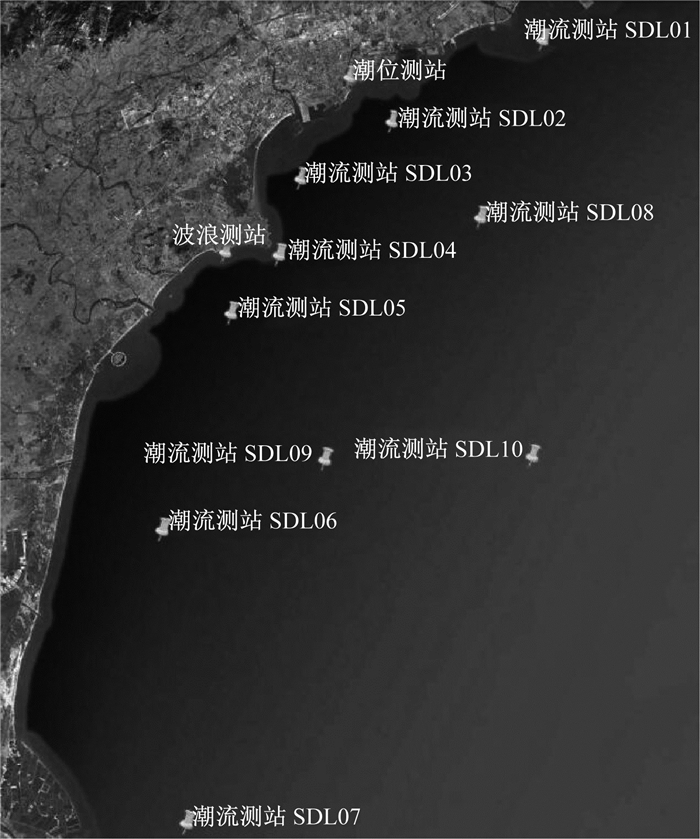
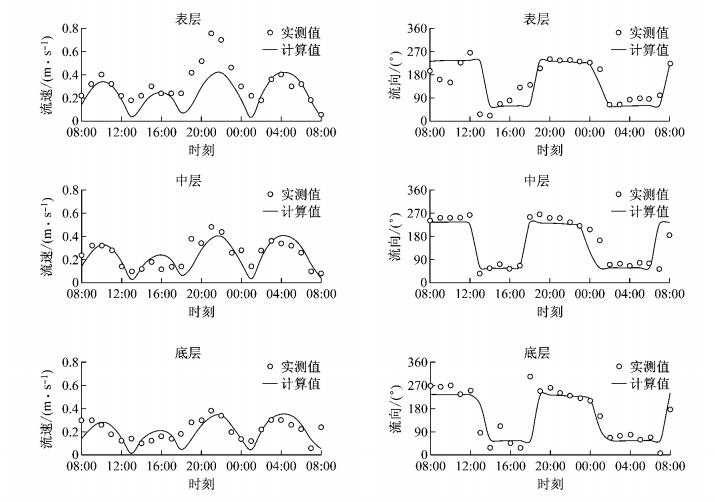
2 模型验证 2.1 潮流模型验证潮位验证采用2013年5月11日00:00至2013年5月13日00:00秦皇岛潮位站的潮位过程资料,结果表明计算潮位过程与实际潮位过程较吻合(见图 3).潮流验证采用2013年5月11日08:00至2013年5月12日08:00测站SDL01~SDL10(见图 4)的实测潮流过程资料,对比涨、落潮流速和流向的计算值与实测值,结果表明模型在水平(见图 5)和垂直(见图 6)方向上均能较好地实现潮流过程.

|
图 3 潮位过程验证 Fig.3 Validation of tidal level |
|
图 4 测站点分布 Fig.4 Position of measurement points |

|
图 5 典型测点(SDL08和SDL10)垂直方向平均流速、流向二维验证 Fig.5 Two-dimention validation of average velocity and flow direction in vertrcal direction at selected points (SDL08 and SDL10) |
|
图 6 典型测点(SDL04)垂直方向流速、流向三维验证 Fig.6 Three-dimention validation of velocity and flow direction in vertical direction at selected point (SDL04) |
根据北戴河波浪测站2013年9月至12月的资料,通过波能守恒转换,得到研究区域的条件为:常浪波高H1/3=0.29 m,对应周期T=3.96 s,波浪方向为161°; 强浪浪高H1/3=1.29 m,对应周期T=6.50 s.在潮流模型的基础上耦合波浪模型,率定得波浪测站处波高和周期分别为常浪0.29 m和3.96 s、强浪1.28 m和6.80 s,与实测一致.
2.3 模型评价为了定量评价水动力模型模拟结果的优劣,需要寻求一个评价标准来进行衡量.本文采用目前比较常用的2种评价方法——百分比偏差率法[16]和Wilmott统计学方法[17]对该模型进行评价.
百分比偏差率法计算模型的模拟结果M与实测值D之间的百分比差率,计算方法如下所示:
| $ \alpha = \frac{{\sum\limits_{i = 1}^N {\left| {{D_i} - {M_i}} \right|} }}{{\sum\limits_{i = 1}^N {{D_i}} }} \times 100 $ | (6) |
式中:α为标准化模型误差系数.α < 10时评价为极好,10≤α < 20时评价为非常好,20≤α < 40时评价为好,100>α>40时评价为差.
Wilmott统计学方法考虑了实测值和实测平均值的偏差、模型计算值和实测平均值的偏差这两者的相关程度,计算方法为
| $ s = 1 - \frac{{\sum\limits_{i = 1}^N {{{\left| {{M_i} - {D_i}} \right|}^2}} }}{{\sum\limits_{i = 1}^N {{{\left( {\left| {{M_i} - {{\bar D}_i}} \right| + \left| {{D_i} - {{\bar D}_i}} \right|} \right)}^2}} }} $ | (7) |
s代表实测值D和实测平均值
| 下载CSV 表 1 百分比偏差率法和Wilmott统计学方法评价结果 Tab.1 Evaluation results from the percentage bias method and the Wilmott statistical method |
采用验证后的水动力数学模型,分别对中海滩浴场海域人工水下沙坝建造前后的潮流场和波浪场进行模拟,并对工程前后的水动力变化进行分析和比较.
3.1 潮流场响应特征北戴河海域位于无潮点附近,水动力较弱.由于沙坝工程区域靠近岸滩,因此附近的水流流向基本与岸线或等深线平行.涨潮流为西南偏西向,落潮流为东北偏东向,潮流为典型的往复流.
图 7给出了沙坝建造前后垂直方向平均流速的变化情况(工程后平均流速减工程前平均流速).由于水下沙坝与原有水流流向基本保持平行,因此对岸滩附近海域的潮流扰动较小.整体来看,流场并未发生较大改变,小幅度的流速变化主要分布在沙坝上.涨急时刻,沙坝的顶托作用使得坝顶的流速增加最大,在沙坝C的坝顶处约增加了1.2 cm·s-1,其余沙坝的坝顶处也有不同程度的流速增加, 而在各沙坝两侧的坝脚处,流速略有减少,幅度均小于0.2 cm·s-1.落急时刻,由于潮流流速较涨急时刻更大,坝顶部的流速变化则更加显著,4座沙坝坝顶的流速变化平均为1 cm·s-1,沙坝D的坝顶处流速增加最大,达2 cm·s-1,并且由于沙坝的导流作用,使得坝体前后两侧的流速也有所增大; 沙坝坝脚处流速a涨急时刻b落急时刻的减幅较大,在沙坝C处减幅最大达2 cm·s-1,同时流速的减小幅度向沙坝间区域递减,流速减少约为0.5~1.5 cm·s-1.

|
图 7 典型时刻沙坝建造前后垂直方向平均流速差 Fig.7 Variation of average velocity at typical moment in vertical direction before and after the construction of sandbars |
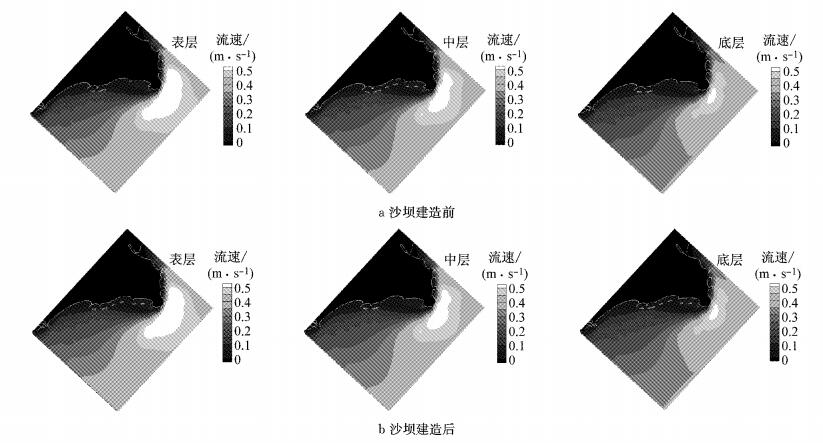
沙坝建造前后北戴河海域的三维流速场计算结果如图 8所示.整体上看,流速呈现出自表层向底层递减的趋势,人工水下沙坝的建造未对该海域的潮流动力产生明显的响应.图 9为沙坝建造前后落急时刻水下中层的流速差分布(工程后减工程前),在沙坝周围的变化幅值均在2 cm·s-1以内,与平面二维计算结果一致.
|
图 8 沙坝建造前后流速场 Fig.8 Velocity field before and after the construction of sandbars |
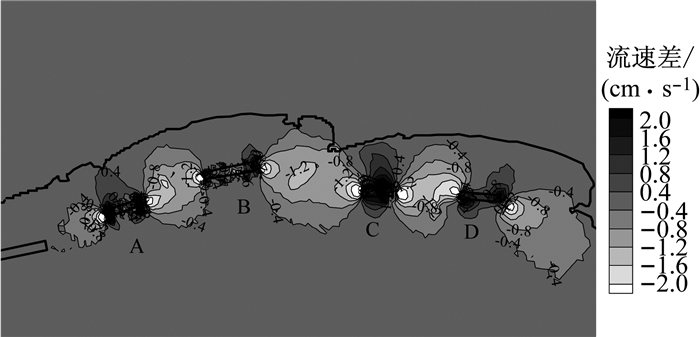
|
图 9 沙坝建造前后落急时刻中层的流速差 Fig.9 Variation of average velocity in middle layer at the moment of maximum ebb before and after the construction of sandbars |
利用验证的波流模型,分别计算了平均海平面下常浪(0.29 m)和强浪(1.29 m)组合条件下的波浪场,波浪方向为161°.在此基础上研究了波浪场对工程的响应.
在波高为0.29 m的常浪情况下,沙坝建造前后沙坝附近的波高对于工程的实施有所响应.由于波高相对于沙坝坝顶的水深较小,沙坝后区域的波浪波高变化幅度为-0.02~0.02 m,沙坝对海滩起到的掩护作用不大.
图 10给出了在波高为1.29 m的强浪作用下,沙坝建造前后的波高变化.可以看到,沙坝对强浪起到了良好的掩护作用,沙坝后掩护区的波高减少0.5~0.92 m,波高的削减幅度为50%~69%;沙坝顶部波高减小0.52~0.81 m,波高的削减幅度为49%~57%.

|
图 10 强浪作用下沙坝建造前后波高差 Fig.10 Variation of wave height in condition of strong wave before and after the construction of sandbars |
根据上述分析,水下人工沙坝具有消波作用,在相同的水深条件下,波高的减小幅度随入射波高的增大而增大,即在常浪条件下,波高的变化并不明显,而在强浪条件下,沙坝顶部和沙坝后掩护区的波高可降低约50%~70%.
4 结论(1) 中海滩浴场养滩工程海域潮流流速较小,近岸区域流向与等深线基本平行,涨潮流为西南偏西向,落潮流为东北偏东向,呈现往复流的特点.沙坝建成后,仅沙坝附近的潮流受到轻微影响,沙坝坝顶的潮流流速小幅增大,沙坝两端以及沙坝之间区域的潮流流速小幅减小.从三维流速场的计算结果来看,该海域的流速由表层至底层呈现减小趋势,在沙坝建成后,各层的流速仅有微小的变化.
(2) 沙坝建成后,沙坝附近波高有所变化.常浪作用时,沙坝起到的掩护作用不大,仅在顶部和坝后区域略有变化; 随着波浪作用的增强,波高的减小幅度也随之增大,在强浪条件下,沙坝后掩护区波高降低约50%~70%.
(3) 从总体上看,中海滩浴场的4个人工水下沙坝建成后,海域的水动力环境向着有利于海滩养护的方向发展.
| [1] |
张琳琳. 人工养滩平衡剖面及其演变的数值模拟[D]. 天津: 天津大学, 2014. ZHANG Linlin. Study on equilibrium beach nourishment profile and numerical simulation of its evolution[D]. Tianjin: Tianjin University, 2014. |
| [2] |
STEERS J A, BIRD E C F. Coastline changes: a global review[J]. Geographical Journal, 1985, 152(1): 108 |
| [3] |
赵多苍. 沙质海滩侵蚀与近岸人工沙坝防护技术研究[D]. 青岛: 中国海洋大学, 2014. ZHAO Duocang. Study on the sandy beach erosion and protection technology of the offshore artificial sand bar[D]. Qingdao: Ocean University of China, 2014. |
| [4] |
HAMM L, CAPOBIANCO M, DETTE H H, et al. A summary of European experience with shore nourishment[J]. Coastal Engineering, 2002, 47(2): 237 DOI:10.1016/S0378-3839(02)00127-8 |
| [5] |
KARASU S, WORK P A, UZLU E, et al. Beach nourishment alternative assessment to constrain cross-shore and longshore sediment transport[J]. Applied Ocean Research, 2016, 59: 459 DOI:10.1016/j.apor.2016.07.001 |
| [6] |
LARSON M, PALALANE J, FREDRIKSSON C, et al. Simulating cross-shore material exchange at decadal scale: theory and model component validation[J]. Coastal Engineering, 2016, 116: 57 DOI:10.1016/j.coastaleng.2016.05.009 |
| [7] |
BROEKEMA Y B, GIARDINO A, VAN DER WERF J J, et al. Observations and modeling of nearshore sediment sorting processes along a barred beach profile[J]. Coastal Engineering, 2016, 118: 50 DOI:10.1016/j.coastaleng.2016.08.009 |
| [8] |
庄振业, 曹立华, 李兵, 等. 我国海滩养护现状[J]. 海洋地质与第四纪地质, 2011, 31(3): 133 ZHUANG Zhenye, CAO Lihua, LI Bing, et al. An overview of beach nourishment in China[J]. Marine Geology & Quaternary Geology, 2011, 31(3): 133 |
| [9] |
KOSTER L. Humplike nourishing of the shoreface: a study on more efficient nourishing of the shoreface[D]. Delft: Delft University of Technology, 2006.
|
| [10] |
张弛, 郑金海, 王义刚. 波浪作用下沙坝剖面形成过程的数值模拟[J]. 水科学进展, 2012, 23(1): 104 ZHANG Chi, ZHENG Jinhai, WANG Yigang. Numerical simulation of wave-induced sandbar formation[J]. Advances in Water Science, 2012, 23(1): 104 |
| [11] |
DETTE H H, LARSON M, MURPHY J, et al. Application of prototype flume tests for beach nourishment assessment[J]. Coastal Engineering, 2002, 47(2): 137 DOI:10.1016/S0378-3839(02)00124-2 |
| [12] |
ŽILINSKASA G, PUPIENISB D, JARMALAVIČIUSC D. Possibilities of regeneration of Palanga coastal zone[J]. Journal of Environmental Engineering and Landscape Management, 2010, 18(2): 92 DOI:10.3846/jeelm.2010.11 |
| [13] |
朱金龙, 拾兵, 殷云珠, 等. 近岸人工沙坝对岸滩养护效果的研究[J]. 中国海洋大学学报(自然科学版), 2013, 43(5): 100 ZHU Jinlong, SHI Bing, YIN Yunzhu, et al. Study on the protective effect of off-shore artificial sandbank to beach[J]. Periodical of Ocean University of China, 2013, 43(5): 100 |
| [14] |
匡翠萍, 冒小丹, 顾杰, 等. 海域水动力对老虎石海滩养护响应关系分析[J]. 同济大学学报(自然科学版), 2014, 42(5): 689 KUANG Cuiping, MAO Xiaodan, GU Jie, et al. Analysis of hydrodynamic response to beach nourishment at Tiger-Rock Beach[J]. Journal of Tongji University (Natural Science), 2014, 42(5): 689 |
| [15] |
杨燕雄, 杨雯, 邱若峰, 等. 人工近岸沙坝在海滩养护中的应用:以北戴河养滩工程为例[J]. 海洋地质前沿, 2013, 29(2): 23 YANG Yanxiong, YANG Wen, QIU Ruofeng, et al. Application of artificial submerged sandbars to beach nourishment[J]. Marine Geology Frontiers, 2013, 29(2): 23 |
| [16] |
ALLEN J I, SOMERFIELD P J, GILBERT F J. Quantifying uncertainty in high-resolution coupled hydrodynamic-ecosystem models[J]. Journal of Marine Systems, 2007, 64(1/2/3/4): 3 |
| [17] |
WILMOTT C J. On the validation of models[J]. Physical Geography, 1981, 2(2): 184 |
 2018, Vol. 46
2018, Vol. 46
