1981年Zaitsev等[1]提出了“细观层面”的概念,将混凝土视为由骨料、界面层以及水泥胶浆组成的材料.这样既解决了宏观层面材料均质化而难以表述其随机性的难题,又避免了微观层面的海量计算.细观方法建立了混凝土材料机理研究的全新途径,同时也搭建了材料随机性与工程应用之间的桥梁,三十多年里取得了大量成果,已经成为混凝土研究,特别是化学侵蚀、随机开裂方面不可缺少的工具.
细观模型是细观研究的基础.一方面,模型要尽量准确地刻画骨料的形状和位置,服从级配分布;另一方面,还必须能够大量重复试验,通过结果统计来消除随机性波动,以便工程应用.因此,细观建模必须解决建模效率和精度的矛盾,这也关系着细观研究的发展.国内外学者投入了大量精力研究建模方法和优化途径,形成的主流方法在机理和效率上存在差异,所适用的问题也有所不同,必须科学选用.
本文通过国内外相关文献的调研,对几种主要建模方法的起源、建模流程及改进进行综述,并通过“干涉检查次数”和“最短路径比”等指标,对建模效率以及模拟效果进行对比分析,提出选用建议.
1 细观建模方法起源细观建模的关键是完成混凝土各成分的空间分布模拟,而骨料决定了界面层和水泥胶浆的分布,因此建模主要是解决骨料分布模拟的问题,包括形状模拟和级配.
早期细观建模中,采用了桁架网格模型,用骨料中心连线形成桁架网格从而进行计算,如图 1所示[2].这种模型中颗粒形状对网格形态影响不大,因此建模中也大量简化了骨料形状细节信息,普遍为圆形骨料形式.这种模型可以通过桁架内力计算模拟混凝土随机开裂,却难以实现高精度的耐久性能分析.
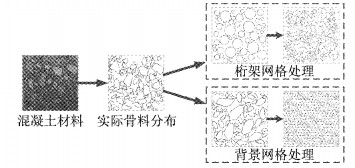
|
图 1 细观模型与计算处理示意图 Fig.1 Sketch map of meso-model and calculation processing |
Schlangen等[3]引入了背景网格处理方法,在模拟区域建立均匀分布但尺度远远小于骨料的网格,根据骨料、胶浆以及界面层空间分布,对网格单元进行属性赋值,后续计算将只基于赋值转译后的网格.该方法的原理类似于基于像素的数字图像,理论上通过调整网格尺寸可以模拟任何精度,因此骨料的复杂形状、位置等信息就会影响结果.相关的骨料形状研究也快速发展起来.目前,针对耐久性能问题的模拟方法中,骨料主要模拟为圆形、多边形或椭圆形.针对圆形骨料模型与实际碎石形状差别较大的问题,Wittmann等[4]引入形态学方法,用随机数生成多边形,使得模型更加接近实际.为了实现卵石颗粒模拟,椭圆形骨料模型也应用广泛,Zheng等[5]和Zohdi[6]对于其建模细节进行了详细研究.
实际混凝土中,骨料的大小和形状都会影响混凝土性质,因此必须借助特征参数进行整体控制.粒径是控制骨料大小的参数,对圆形骨料建模时,可通过骨料直径D控制; 对椭圆形和多边形骨料建模时,一般按同等面积圆形的原则换算为等效直径D.骨料的形状是另一个需要重点控制的参数.天然形成的砾石和卵石通常具有浑圆的粒形,破碎的岩石则具有较多的棱角且外形粗糙,而由破碎机加工的碎石则含有较多的扁平薄片状颗粒.早期采用球度(表面积与体积之比)来描述形状差异,但仍不够直观精准.Mora等[7]提出使用骨料长边与短边的长度比值β(长宽比)来替代球度,并得到广泛应用.
建模的另一个关键问题是对骨料级配和密实度进行模拟.实际工程中主要通过颗粒筛分试验控制级配.将骨料按照粒径进行筛分,然后再进行配比,以满足目标要求.建模过程中,级配模拟是利用指定密实度γ(骨料填充面积占模拟区域面积比例)来满足各种粒径骨料占比的级配要求.1980年Walraven[8]采用球形骨料模型推导出二维Fuller级配累积分布函数,实现了高精度连续级配控制.该分布函数表达形式如下所示:
| $ \begin{array}{l} {P_{2A}}\left( D \right) = 1.065\;0{\left( {\frac{D}{{{D_{{\rm{max}}}}}}} \right)^{0.5}}-0.053\;0{\left( {\frac{D}{{{D_{{\rm{max}}}}}}} \right)^{4.0}}-\\ \;\;\;\;\;\;\;0.012\;0{\left( {\frac{D}{{{D_{{\rm{max}}}}}}} \right)^{6.0}}-0.004\;5{\left( {\frac{D}{{{D_{{\rm{max}}}}}}} \right)^{8.0}} + \\ \;\;\;\;\;\;\;0.002\;5{\left( {\frac{D}{{{D_{{\rm{max}}}}}}} \right)^{10.0}} \end{array} $ | (1) |
式中:P2A表示截面内粒径小于D的骨料面积占总面积的分数;D表示颗粒粒径,对于椭圆形和多边形等复杂形状则表示同等面积等效圆直径;Dmax表示骨料最大粒径.
采用式(1)模拟只需要对函数值进行蒙特卡洛抽样,求解方程即可获得满足级配要求的粒径序列[8-9].根据大数定理,随着抽样次数不断增加,理论上模型级配会无限接近目标曲线,实际上一般由模拟区域尺寸以及密实度γ来确定目标投放面积,骨料累积面积满足要求即可.
随着形状模拟和级配问题的解决,建模的主要步骤逐渐统一,Bažant等[10]总结为以下4个步骤:①根据Walraven公式以及骨料目标密实度生成粒径序列;②随机生成骨料坐标进行区域内投放;③新投放骨料对已投放骨料进行干涉检查;④重复骨料投放流程直至骨料投放完毕.
基于上述研究,细观建模的基础基本统一.骨料形状和投放方法作为主要区别,可以划分出以下3类算法:基于生成骨料的随机投放算法、基于投放骨料的随机生长算法、基于生成骨料的单向摆放算法.各算法适用的骨料形状有所差异,部分是基于特定的形状提出的,同时算法的选用对于建模效率和计算结果都存在影响,以下将分别进行说明.
2 主要建模方法 2.1 基于生成骨料的随机投放算法该算法的基本思路是基于Walraven累积分布函数随机抽样生成满足级配的粒径序列后,随机生成投放点坐标,将骨料和投放位置进行匹配,直至完成.这类方法将骨料生成与投放相独立,因此密实度和级配模拟较好,对骨料形状的适应性强[11].基本流程如图 2所示,建模的难点在于先后投放骨料的相互干涉.
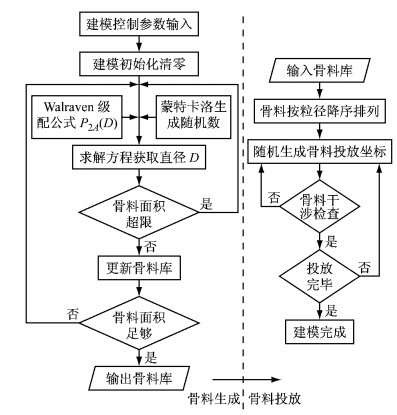
|
图 2 随机投放建模方法流程 Fig.2 Flow chart of modeling with random packing |
王宗敏[12]对圆形和多边形骨料进行了随机投放的建模方法尝试,提出探索式建模算法.在投放过程中进行3次干涉检查, 包络圆检查、角点检查、边检查,以解决骨料重叠问题.这个方法结构明确且易于实现,但在投放后期,由于大部分空间被已投放骨料占据,新投放骨料需要进行大量干涉检查,因此建模效率快速下降[13].
任志刚等[14]针对建模效率进行改进并提出了圆形搜索建模算法.只对投放点一定距离范围内骨料进行干涉检查,从而减少检查次数.
Leite等[15]结合椭圆形骨料提出了启发式微动算法.投放过程中当干涉检查不满足要求时,将骨料在原投放位置进行平移和旋转调整,在不改变骨料总体分布的基础上选取附近合适位置.如图 3所示,P8骨料的投放与P4骨料冲突,于是进行第1次平移调整,平移后与P7骨料冲突,于是又进行第2次旋转调整,最终达到合适状态.这种算法提高了投放成功率和建模效率,并且相对于探索式建模算法也容易达到更高的密实度[16].

|
图 3 启发式微动算法示意 Fig.3 Sketch map of heuristic allocation procedure |
武亮等[17]借助背景网格,提出了基于图像的投放算法.对骨料位置的元素进行赋值标记,新投放骨料时仅需检查相应的网格节点,而无需进行复杂的几何干涉判断.该算法降低了干涉检查难度,但依赖于高精度的网格划分和大规模矩阵运算,运算效率提升有限.秦川等[13]在此基础上提出了初判和细判两阶段判别方法.初判通过关键点检查来排除明显干涉状态,然后对投放骨料进行细判投放.改进后算法效率较高,但大尺度高精度建模时性能仍有所下降[18].
2.2 基于投放骨料的随机生长算法该类方法首先确定骨料基的位置,再对骨料基进行扩展,“生长”出完整形状,主要适用于多边形骨料.
高政国等[11]提出了骨料基生长算法,以三角形或四边形骨料为骨料基进行投放,干涉检查通过后进行生长,如图 4所示.当骨料棱边过长时进行延拓从而生成新的棱边,直至所有骨料投放生长完毕.由于骨料基形状简单,因此投放成功率和检查效率得到提高.该算法提高建模效率的同时骨料形态也更接近实际[19],但生长过程改变了粒径和面积,导致模型难以满足级配要求[20-21].

|
图 4 骨料基生长算法示意图 Fig.4 Sketch map of growth algorithm with aggregate base |
针对逐个骨料投放生长导致的后期运算效率降低问题,杜成斌等[22]提出了群骨料基生长算法.将所有骨料基投放完毕,再进行延拓生长,直至满足密实度要求.该算法充分利用了骨料基投放便捷、成功率高的特点,大幅提高建模效率,但级配仍然难以控制[23].
马怀发等[23]优化了有关级配控制的问题.在骨料初步生长完毕后,计算骨料面积与级配理论面积的差值并降序排列,优先对面积欠缺较大的骨料进行修正生长.该算法略微牺牲算法效率,但改善了生长算法普遍存在的级配问题.
近年来国外也出现了一些新的高效算法.Amirjanov等[24]提出了多单元骨料生长算法,引入子网格单元概念.生长过程中对与覆盖子网格单元存在交集的骨料进行检查,缩小检查范围以提升效率.如图 5所示,P8骨料侵入网格单元22和23,因此仅需对侵占这些单元的P1、P2和P6骨料进行检查即可.实际应用中该算法不仅运算效率高,还可以实现大尺度、高密实度建模.虽然目前只对圆形骨料进行尝试,还不能通用于复杂形状骨料,但是仍具有深入研究改进的价值[25].

|
图 5 多单元骨料生长算法示意图 Fig.5 Sketch map of aggregate growth algorithm with multiple cells |
综合来看,基于投放骨料的随机生长算法在一定程度上解决了建模后期效率下降的问题,但对级配的控制仍将是未来一段时间努力的方向.
2.3 基于生成骨料的单向摆放算法重力作用下,实际混凝土浇筑振捣过程中将产生骨料下沉现象,竖直截面内骨料整体向下积聚,且下部区域细骨料含量较大,这也称之为竖向堆积问题(见图 6).单向摆放算法可以很好地模拟竖向堆积现象,弥补了前两类算法的局限.
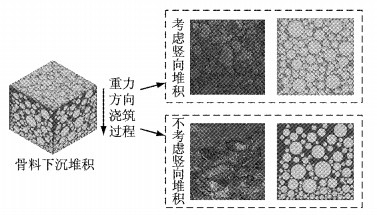
|
图 6 混凝土骨料竖向堆积效应模拟 Fig.6 Simulation of concrete aggregate with vertical accumulation |
单向逐一摆放算法的原型是1978年Cundall等[26]的砾碎石堆积离散元模型.骨料逐一从区域顶部随机水平位置下落,当接触到底部骨料时,需要翻转滑移直至到达稳定的摆放位置.这样基本实现了对竖向堆积的模拟,但忽略了水泥胶浆的影响.骨料之间没有空隙,过于向下集中,可能出现骨料紧密堆积在下部70%深度范围以内而上部30%空间完全没有骨料的情况,和真实情况差异较大.在计算效率方面,由于需要大量骨料下落模拟,因此计算效率较低[10, 27].
针对骨料空隙问题,Stankowski[28]提出中心缩放算法.在骨料内部随机选取内核中心点,投放完毕后将骨料向内部中心点进行收缩,对骨料密实度和孔隙进行调整.该算法解决了骨料紧密接触的问题,但是颗粒孔隙呈现规律带状分布[15].
针对摆放算法效率问题,很多学者提出了改进,应用较多的是Vervuurt[29]的多次尝试下落算法.该算法只进行下落摆放而无需进行骨料翻转滑移.为了防止颗粒架空失真,尝试多次随机下落,选择最低位置作为最终投放点.这样的优化避免了翻滚滑移模拟,提高了算法效率,但也容易因为小骨料无法滑移进入大粒径孔隙而出现空洞的问题[15].
唐欣薇等[30]提出分层摆放算法.对骨料进行矩形封装,利用封装箱简单的几何形状避免了复杂的干涉检查,通过封装箱的快速摆放实现了高效建模;同时,还可以通过调整骨料与封装箱间距,实现在到达指定密实度的同时不改变级配.该算法的主要问题是外包络矩形封装箱增大了骨料占用面积,降低了填充能力,不适用于细长骨料建模[31].
为了便于比较分析和工程应用,对前述建模方法的适用性进行汇总,如表 1所示.
| 下载CSV 表 1 建模方法适用性汇总 Tab.1 Applicability summary of modeling methods |
前述各种细观建模方法的算法机理、建模效率以及模拟目标有显著差别,导致骨料的最终分布形态有所差异.细观研究和方法改进中,研究者普遍关注建模方法的时间成本以及生成的模型能否满足研究需求,因此以下将从建模效率和模拟效果两方面进行探索比较.考虑到细观层面模型随机性大,比较均基于统计层面开展.
3.1 建模效率目前的各种建模方法,都在尝试通过提高投放成功率和减少干涉检查次数来提高算法效率,因此这里尝试统计和比较每颗骨料在投放过程的检查次数来比较建模效率.
对探索式建模算法、圆形搜索建模算法(属于基于生成骨料的随机投放算法)和骨料基生长算法(属于基于投放骨料的随机生长算法)进行干涉统计比较.分层摆放法(属于基于生成骨料的单向摆放算法)借助封装处理避免了干涉检查以提升效率,因此不进行干涉统计分析.
投放试验中,控制建模尺寸和粒径区间等指标不变,建立200 mm×200 mm的模型,骨料粒径控制在[3,30] mm.变化参数包括骨料形状、投放密实度γ以及长宽比β.每种算法都建模20次,统计后得到平均干涉检查次数,以消除随机性的影响.对圆形和椭圆形骨料,仅需统计判断方程执行的次数即可.多边形检查主要是棱边几何判断,检查次数受骨料形状影响较大,因此次数按棱边数折减,表达形式如下所示:
| $ {n_{{\rm{ic}}}} = \left\{ \begin{array}{l} {n_{{\rm{gc}}}}, \;\;\;\;\;\;\;\;\;\;\;\;圆形和椭圆形\\ \frac{{\sum {{n_{k, {\rm{sc}}}}} }}{{{n_{\rm{s}}}}}, \;\;\;\;\;多边形 \end{array} \right. $ | (2) |
式中:nic为最终计入的多边形检查次数;ngc为圆形和椭圆形的几何干涉检查次数;nk, sc为第k次尝试投放过程的棱边检查次数;ns为最终棱边数量.
图 7比较了各种优化算法较探索式建模算法的改进程度.相对于探索式建模算法,2种优化算法效率明显提升.骨料基生长算法效率提升3.5倍左右,圆形搜索建模算法效率提升10倍以上.骨料基生长算法前期采用骨料基投放,得益于骨料简单的几何形状,降低了干涉检查的计算量;圆形搜索建模算法预先排除不可能接触的颗粒,算法效率受搜索范围大小的影响,如样本中搜索范围占建模面积的10%左右,而在大尺度模拟中效率提升会更突出.

|
图 7 各种算法干涉检查统计(γ=30%,β=2.0) Fig.7 Statistical chart of interference check for different optimization algorithms (γ=30%, β=2.0) |
图 8统计了长宽比β为1.0和2.0时的情况,说明了各种建模方法对不同长宽比的适应性.可以看出:长宽比增大时,各种算法的干涉检查次数略有增加,但并不明显.长宽比并不是影响建模效率的主要参数.比较各种骨料形状对于长宽比调整的反应,结果表明形状的差异基本不影响效率变化,多边形投放检查次数略低于椭圆形和圆形.
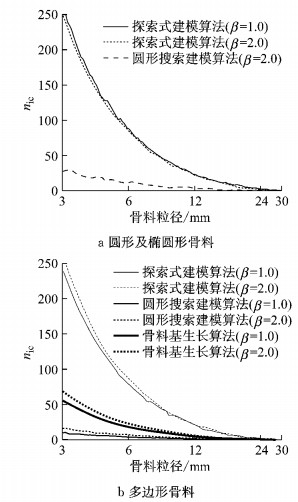
|
图 8 2种长宽比各种算法干涉检查统计(γ=30%) Fig.8 Statistical chart of interference check for different optimization algorithms with two aspect ratios (γ=30%) |
高密实度混凝土建模时,投放成功率和建模效率均会显著下降,因此高密实度情况下建模效率一直是研究重点.图 9比较了密实度为30%和60%时各种算法的建模效率.理论上密实度翻倍之后检查量也会增长1倍左右,为了直观地比较效率之间的差异,将60%密实度计算结果对半折减之后与30%密实度计算结果进行比较.结果表明:密实度增大时,探索式建模算法的效率基本不受影响;圆形搜索建模算法的效率下降较为明显,而骨料基生长算法的效率基本稳定略微提升.圆形搜索建模算法效率下降的原因在于更多的骨料进入检查范围;骨料基生长算法得益于骨料先投放后生长的逻辑,生长延拓过程成功率较高,比较适用于高密实度建模.

|
图 9 2种密实度各种算法干涉检查统计(β=2.0) Fig.9 Statistical chart of interference check for different optimization algorithms with two densities (β=2.0) |
比较高密实度时各骨料形状建模效率的差异,结果表明骨料形状对效率总体影响不大,只有圆形搜索建模算法效率下降明显,并且形状影响差异较大,其中椭圆形建模效率慢了1倍,多边形建模更为严重,慢了3倍以上.原因在于算法机理上多边形骨料只要存在角点进入检查范围就需要计算,导致效率下降更为严重.
总体来说,在不考虑竖向堆积效应的细观建模方法中,圆形搜索建模算法和骨料基生长算法要明显优于探索式建模算法;算法效率受长宽比和密实度等建模参数的影响较小;不同骨料形状之间的优化建模效率也差异不大,算法的选取主要取决于算法的适用性.
3.2 模型最短路径比工程耐久性分析普遍关注到达侵蚀临界状态的时间,为了研究局部劣化的发展过程,凭借对细观模型中骨料不可侵蚀性质以及物质传输路径扭曲的模拟,可以真实地再现混凝土中侵蚀物质的分布差异[32].因此,为了便捷高效地比较各模型的侵蚀模拟差异,选择传输路径长度作为分析依据可以一定程度上反映侵蚀寿命的长短,对于影响不大的物质局部积聚、稀释以及传输速度细微差异进行简化.
这里选择细观模型和传统宏观模型的最短路径长度比值作为计算指标,计算式为Rsp=l细观/l宏观,即可对细观模拟的效果进行比较.细观侵蚀研究中由于骨料不可侵蚀,需要计算水泥胶浆中各点到侵蚀表面的最短长度,而宏观模型中各点路径长度即为对应的侵蚀深度,如图 10a所示.细观模型的最短路径计算方法为:将模型离散化,骨料内部各点间距无穷大,胶浆各点间距则按照实际几何距离计算;利用Floyd-Warshall动态规划算法[33]进行处理,选择下部侵蚀表面为路径规划的起点,胶浆内部各点为终点;循环更新路径长度,直至胶浆内部各点路径优化完毕,即可获取最短路径分布云图.输出最短路径计算结果(见图 10),图 10中骨料孔隙颜色越浅表示对应的细观侵蚀路径越长.

|
图 10 最短路径比计算样本 Fig.10 Calculation sample of the shortest path ratio |
选取探索式建模算法和各类优化算法,包括圆形搜索建模算法、骨料基生长算法以及分层摆放算法进行比较.建模尺寸为200 mm×200 mm,骨料粒径范围为[3,30] mm,选取更易出现路径扭曲的60%高密实度,变化骨料形状和长宽比β,采用0.1 mm栅格离散处理,重复建模20次,统计各深度最短路径比的均值.
图 11比较了同样参数条件下,各算法建模最短路径比的差异.在初始侵入阶段,由于边界区域骨料级配不完整且密实度较低,路径比从1.00开始迅速增长;在侵入深度接近骨料最大粒径30 mm之后,路径比增速减缓并逐渐在一个定值上下波动.统计结果表明:圆形骨料中,分层摆放算法最短路径比稳定在1.030左右,探索式建模算法稳定在1.075左右;多边形骨料中,分层摆放算法稳定在1.070左右,而其他算法集中稳定在1.085左右.可以发现:分层摆放算法路径比与其他算法差异明显,浅层比值增长速度更为迅速,原因在于堆积侧密实度较高且细颗粒含量大,导致传输路径更易扭曲甚至受阻;随着侵蚀到达模型中部,细骨料下沉而大颗粒向上堆叠导致中上部密实度较低,路径比又逐渐下降到低于其他算法.因此,骨料下沉堆积模型与均匀随机分布模型存在较大差异,应该根据需求选择合适的算法.混凝土模拟考虑竖向堆积时,应该选择高效的骨料单向摆放算法,如分层摆放算法;不考虑竖向堆积或者骨料下沉不显著时,则应选择其他优化建模算法,如圆形搜索建模算法和骨料基生长算法.
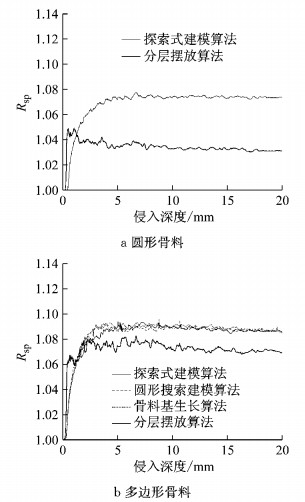
|
图 11 各种算法最短路径比(γ=60%,β=1.0) Fig.11 Shortest path ratio for different optimization algorithms (γ=60%, β=1.0) |
对比图 11a和图 11b,颗粒形状对各算法最短路径比存在影响,圆形骨料路径比普遍低于多边形骨料.一方面是因为多边形棱角细节更易造成传输路径的扭曲,另一方面多边形骨料之间的嵌挤作用使得路径扭曲更为严重.因此,必须根据实际情况选择合适的形状进行模拟.当骨料多为天然球状卵石时选择圆形和椭圆形模拟,当骨料多为人工破碎碎石时选择多边形模拟.
图 12比较了2种长宽比各算法最短路径比的差异.结果表明:长宽比对最短路径比影响显著,长宽比增大为2.0,圆形骨料变为椭圆形骨料,分层摆放算法稳定值由1.030增至1.042左右,其他算法由1.075变为1.090左右;多边形骨料建模中分层摆放算法由1.070略微下降,而其他方法由1.085变为1.105左右.随长宽比增大,骨料由卵砾石向针片状转化,嵌挤效应更为明显,导致最短路径比增大.因此,细观建模需要对实际骨料颗粒进行调研统计,根据真实形状调整长宽比参数.
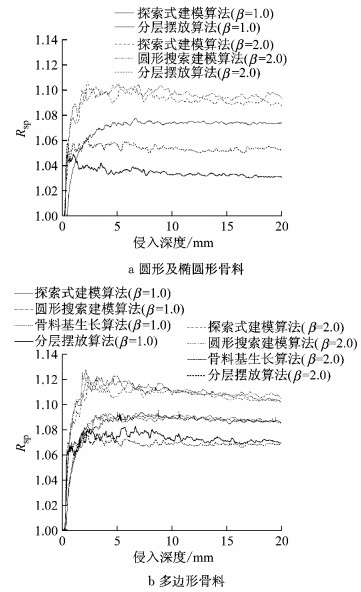
|
图 12 2种长宽比各种算法最短路径比(γ=60%) Fig.12 The shortest path ratio for different optimization algorithms with two aspect ratios (γ=60%) |
(1) 对比各类建模方法可以发现:基于生成骨料的随机投放算法结构清晰便于应用,对骨料形状适应性强,改进之后效率明显提升,适用于大尺寸建模;基于投放骨料的随机生长算法效率较高,适用于高密实度建模,但目前主要适用于多边形骨料建模,算法适应性和对于级配的调控能力还有待改进;基于生成骨料的单向摆放算法主要模拟考虑竖向堆积的分布情况,对骨料形状适应性强,但运算效率和建模细节之间的矛盾还有待优化解决.
(2) 对比分析主要参数对于建模效率和模拟效果的影响,表明当骨料由圆形或椭圆形变为多边形、密实度γ或者长宽比β增大时,模型抗侵蚀能力均显著提升.细观研究需要对实际骨料进行调研,明确建模参数以实现准确模拟分析.各方法建模效率受参数影响不大,在非耐久性细观研究中,可根据需求调整参数.
基于建模方法的综述和分析,可根据需求选择合适的研究方法,在大尺度高精度等细观研究中选择合适的建模方法.
| [1] |
ZAITSEV Y B, WITTMANN F H. Simulation of crack propagation and failure of concrete[J]. Materials and Structures, 1981, 14(5): 357 |
| [2] |
CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J]. Geotechnique, 1979, 29(1): 47 DOI:10.1680/geot.1979.29.1.47 |
| [3] |
SCHLANGEN E, VAN MIER J G M. Simple lattice model for numerical simulation of fracture of concrete materials and structures[J]. Materials and Structures, 1992, 25(9): 534 DOI:10.1007/BF02472449 |
| [4] |
WITTMANN F H, ROELFSTRA P E, SADOUKI H. Simulation and analysis of composite structures[J]. Materials Science and Engineering, 1985, 68(2): 239 DOI:10.1016/0025-5416(85)90413-6 |
| [5] |
ZHENG J J, XIONG F F, WU Z M, et al. A numerical algorithm for the ITZ area fraction in concrete with elliptical aggregate particles[J]. Magazine of Concrete Research, 2009, 61(2): 109 DOI:10.1680/macr.2007.00123 |
| [6] |
ZOHDI T I. Computational optimization of the vortex manufacturing of advanced materials[J]. Computer Methods in Applied Mechanics & Engineering, 2001, 190(46): 6231 |
| [7] |
MORA C F, KWAN A K H. Sphericity, shape factor, and convexity measurement of coarse aggregate for concrete using digital image processing[J]. Cement and Concrete Research, 2000, 30(3): 351 DOI:10.1016/S0008-8846(99)00259-8 |
| [8] |
WALRAVEN J C. Aggregate interlock: a theoretical and experimental analysis[D]. Delft: Delft University Press, 1980.
|
| [9] |
潘子超, 阮欣, 陈艾荣. 基于任意级配的二维随机骨料生成方法[J]. 同济大学学报(自然科学版), 2013, 41(5): 759 PAN Zichao, RUAN Xin, CHEN Airong. Simulation method of random aggregate in two dimension based on arbitrary gradation[J]. Journal of Tongji University (Natural Science), 2013, 41(5): 759 |
| [10] |
BAŽANT Z P, TABBARA M R, KAZEMI M T, et al. Random particle model for fracture of aggregate or fiber composites[J]. Journal of Engineering Mechanics, 1990, 116(8): 1686 DOI:10.1061/(ASCE)0733-9399(1990)116:8(1686) |
| [11] |
高政国, 刘光廷. 二维混凝土随机骨料模型研究[J]. 清华大学学报(自然科学版), 2003, 43(5): 710 GAO Zhengguo, LIU Guangting. Two-dimensional random aggregate structure for concrete[J]. Journal of Tsinghua University(Science and Technology), 2003, 43(5): 710 |
| [12] |
王宗敏. 不均质材料(混凝土)裂隙扩展及宏观计算强度与变形[D]. 北京: 清华大学, 1996. WANG Zongmin. Crack growth, computer strength and deformation of nonhomogeneous meterials (concrete)[D]. Beijing: Tsinghua University, 1996. |
| [13] |
秦川, 郭长青, 张楚汉. 基于背景网格的混凝土细观力学预处理方法[J]. 水利学报, 2011, 42(8): 941 QIN Chuan, GUO Changqing, ZHANG Chuhan. A pre-processing scheme based on background grid approach for meso-concrete mechanics[J]. Journal of Hydraulic Engineering, 2011, 42(8): 941 |
| [14] |
任志刚, 徐彬, 李培鹏, 等. 二维混凝土骨料随机生成与投放算法及程序[J]. 土木工程与管理学报, 2015, 32(1): 1 REN Zhigang, XU Bin, LI Peipeng, et al. Algorithm and program for random generation and distribution of two-dimensional concrete aggregates[J]. Journal of Civil Engineering and Management, 2015, 32(1): 1 |
| [15] |
LEITE J P B, SLOWIK V, MIHASHI H. Computer simulation of fracture processes of concrete using mesolevel models of lattice structures[J]. Cement and Concrete Research, 2004, 34(6): 1025 DOI:10.1016/j.cemconres.2003.11.011 |
| [16] |
SLOWIK V, HüBNER T, SCHMIDT M, et al. Simulation of capillary shrinkage cracking in cement-like materials[J]. Cement and Concrete Composites, 2009, 31(7): 461 DOI:10.1016/j.cemconcomp.2009.05.004 |
| [17] |
武亮, 王菁, 糜凯华. 全级配混凝土二维细观模型的自动生成[J]. 建筑材料学报, 2015, 18(4): 626 WU Liang, WANG Jing, MI Kaihua. Automatic generation of 2D mesoscale models for fully-graded concrete[J]. Journal of Building Materials, 2015, 18(4): 626 |
| [18] |
王旗华, 梁斌, 卢永刚, 等. 混凝土三相结构细观模型生成方法[J]. 混凝土, 2013(10): 49 WANG Qihua, LIANG Bin, LU Yonggang, et al. Generating approach of three-phase structure model for concrete[J]. Concrete, 2013(10): 49 |
| [19] |
高巧红, 关振群, 顾元宪, 等. 混凝土骨料有限元模型自动生成方法[J]. 大连理工大学学报, 2006, 46(5): 641 GAO Qiaohong, GUAN Zhenqun, GU Yuanxian, et al. Automatic generation of finite element model for concrete aggragate[J]. Journal of Dalian University of Technology, 2006, 46(5): 641 |
| [20] |
李运成, 马怀发, 陈厚群, 等. 混凝土随机凸多面体骨料模型生成及细观有限元剖分[J]. 水利学报, 2006, 37(5): 588 LI Yuncheng, MA Huaifa, CHEN Houqun, et al. Approach to generation of random convex polyhedral aggragate model and plotting for concrete meso-mechanics[J]. Journal of Hydraulic Engineering, 2006, 37(5): 588 |
| [21] |
杜修力, 金浏. 混凝土静态力学性能的细观力学方法述评[J]. 力学进展, 2011, 41(4): 411 DU Xiuli, JIN Liu. A review on meso-mechanical method for studying the static-mechanical properties of concrete[J]. Advances in Mechanics, 2011, 41(4): 411 DOI:10.6052/1000-0992-2011-4-lxjzJ2011-010 |
| [22] |
杜成斌, 孙立国. 任意形状混凝土骨料的数值模拟及其应用[J]. 水利学报, 2006, 37(6): 662 DU Chengbin, SUN Liguo. Numerical simulation of concrete aggregates with arbitrary shapes and its application[J]. Journal of Hydraulic Engineering, 2006, 37(6): 662 |
| [23] |
马怀发, 芈书贞, 陈厚群. 一种混凝土随机凸多边形骨料模型生成方法[J]. 中国水利水电科学研究院学报, 2006, 4(3): 196 MA Huaifa, MI Shuzhen, CHEN Houqun. A generation approach of random convex polygon aggregate model[J]. Journal of China Institute of Water Resources and Hydropower Research, 2006, 4(3): 196 |
| [24] |
AMIRJANOV A, SOBOLEV K. Optimization of a computer simulation model for packing of concrete aggregates[J]. Particulate Science & Technology, 2008, 26(4): 380 |
| [25] |
ADEKUNLE S K, AHMAD S, MASLEHUDDIN M. The effect of aggregate packing on the performance of SCC using dune sand[C]// North American Conference on the Design and Use of Self-Consolidating Concrete. Chicago: [s. n. ], 2013: 352-380.
|
| [26] |
CUNDALL P A, STRACK O D L. BALL: a program to model granular media using the distinct element method[R]. London: Dames & Moore, 1978.
|
| [27] |
TING J M, CORKUM B T, KAUFFMAN C R, et al. Discrete numerical model for soil mechanics[J]. Journal of Geotechnical Engineering, 1989, 115(3): 379 DOI:10.1061/(ASCE)0733-9410(1989)115:3(379) |
| [28] |
STANKOWSKI T. Numerical simulation of failure in particle composites[J]. Computers & Structures, 1992, 44(1): 459 |
| [29] |
VERVUURT A H J M. Interface fracture in concrete[D]. Delft: Delft University of Technology, 1997.
|
| [30] |
唐欣薇, 张楚汉. 随机骨料投放的分层摆放法及有限元坐标的生成[J]. 清华大学学报(自然科学版), 2008, 48(12): 2048 TANG Xinwei, ZHANG Chuhan. Layering diposition and FE corrdinate generation for random aggregate arrangements[J]. Journal of Tsinghua University(Science and Technology), 2008, 48(12): 2048 DOI:10.3321/j.issn:1000-0054.2008.12.006 |
| [31] |
付兵, 李建波, 林皋, 等. 基于真实骨料形状库的混凝土细观数值模型[J]. 建筑科学与工程学报, 2010, 27(2): 10 FU Bing, LI Jianbo, LIN Gao, et al. Mesosopic numerical model of concrete based on data base of real aggregate shapes[J]. Journal of Architecture and Civil Engineering, 2010, 27(2): 10 |
| [32] |
潘子超, 阮欣, 陈艾荣. 细观层面的混凝土碳化过程数值模拟[J]. 同济大学学报(自然科学版), 2012, 40(6): 900 PAN Zichao, RUAN Xin, CHEN Airong. Numerical simulation of concrete carbonation process on meso-scale[J]. Journal of Tongji University(Natural Science), 2012, 40(6): 900 |
| [33] |
张德全, 吴果林, 刘登峰. 最短路问题的Floyd加速算法与优化[J]. 计算机工程与应用, 2009, 45(17): 4 ZHANG Dequan, WU Guolin, LIU Dengfeng. Accelerated and optimized method of Floyd algorithm to find out shortest path[J]. Computer Engineering and Application, 2009, 45(17): 4 |
 2018, Vol. 46
2018, Vol. 46
