2. 同济大学 土木工程学院,上海 200092
2. College of Civil Engineering, Tongji University, Shanghai 200092, China
在多高层钢框架设计时,由于冷弯矩形钢管(RHS)截面闭合且对称,因此该种截面的钢构件比H型钢或工字型钢具有更好的承载性能.研究表明,在住宅建筑中采用钢管柱框架体系不仅可以减少用钢量,还便于构建美观的室内环境[1].然而,H型钢梁与封闭的矩形钢管柱节点难以采用传统的高强螺栓连接,这使得矩形钢管柱的使用受到限制.
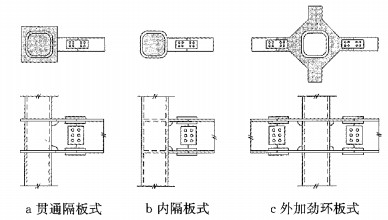
对于H型钢梁与矩形钢管柱的连接,传统的方法主要是采用焊接连接的方式,如图 1所示.这类节点通常承载力和刚度较高,一般可简化为理想刚接.然而,1994年美国Northridge地震和1995年日本阪神地震的震害调查表明,在强烈地震作用下这类刚性节点的梁上、下翼缘焊缝位置处易发生断裂现象[2-3],如图 2所示.同时,焊接的方式又使得节点现场施工人工量大,质量难以保证,不能发挥钢结构快速建造的优势.相比于焊接的刚性节点,采用端板螺栓连接节点具有施工便捷、经济高效、抗震性能好的优点.
|
图 1 H型钢梁与矩形钢管柱焊接节点 Fig.1 Welded joint of H-type steel beam and RHS column |

|
图 2 梁柱焊接节点破坏模式 Fig.2 Failure mode of beam-to-column welded connections |
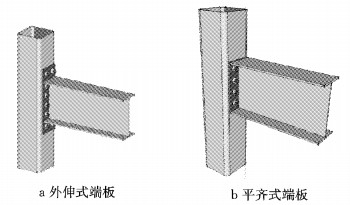
采用特殊的单向螺栓可以实现H型钢梁与封闭矩形钢管柱的螺栓连接.目前国外在工程上所使用的单向螺栓产品主要有以下3种:美国和日本的Ultra-Twist、英国的Hollo-Bolt、澳大利亚的ONESIDE Fastener.其中,应用最多的是由英国lindapter公司生产的Hollo-Bolt.国内许炎彬等[4]通过改进套筒材料和端部构造研制了国产自锁式单向螺栓,其性能与英国产品相当,但成本更低.本文研究对象也是针对H型钢梁与矩形钢管柱采用国产自锁式单向螺栓连接的节点,如图 3所示.
|
图 3 国产单向螺栓连接节点 Fig.3 Connections using domestic blind bolts |
从1993年开始,国内外学者对H型钢梁与矩形钢管柱单向螺栓连接节点进行了一系列的试验研究以及理论研究[5-23],但这些研究对于该种节点并没有给出完善的初始转动刚度理论模型和计算公式.本文基于组件法,提出了H型钢梁与矩形钢管柱端板单向螺栓连接节点初始转动刚度的理论简化模型和计算公式,并用试验结果进行了验证.
1 试验概况试验总共对12个试件进行了单调静力加载,包括6个H型钢梁与矩形钢管柱平齐式端板单向螺栓连接节点和6个外伸式端板单向螺栓连接节点.
表 1给出了H型钢梁、矩形钢管柱等试件的几何尺寸和强度等级.试件节点详图如图 4所示.试件名称中,SR代表平齐式端板连接节点,BR代表外伸式端板连接节点.螺栓采用8.8级M16国产自锁式单向螺栓,构件钢材采用Q345级.详细试验现象和结果可参见文献[24-25].
| 下载CSV 表 1 试件参数表 Tab.1 Details of specimens |

|
图 4 节点构造详图(单位:mm) Fig.4 Details of connection configurations(unit:mm) |
连接节点的初始转动刚度[26]是指节点在梁端弯矩作用下转角处于线弹性范围内时节点所具有的刚度,可用连接节点的弯矩转角关系曲线表达式在原点的一阶导数来表示,如下所示:
| $ {K_{\rm{i}}} = \frac{{{\rm{d}}M}}{{{\rm{d}}\theta }}\left| {_{\theta = 0}} \right. $ |
式中:M为作用在连接节点的弯矩;θ为连接节点的转角;Ki为连接节点的初始转动刚度.
目前,评估钢结构连接节点性能的方法主要有试验研究、数值模拟和理论分析3种,其中理论分析方法通常采用组件法.
组件法的基本原理是将节点拆分成多个基本组件,每个组件由线性或非线性的弹簧模拟,通过弹簧的串联、并联组合计算将各基本组件进行组装,从而获得节点整体的力学行为.组件法自1992年引入欧洲钢结构设计规范EC3ENV—1993-1-1,经过不断改进[27],逐渐形成了现行欧洲钢结构设计规范EC Part1-8中的节点设计方法.目前EC3中的组件法适用于纯钢结构,主要针对由欧洲热轧I或H型钢等开口截面构件或焊接组合构件组成的连接节点,对其他节点形式,并未提供相应组件的设计公式[28].
对于本文研究的H型钢梁与矩形钢管柱端板单向螺栓连接节点,同样可以借鉴EC3ENV—1993-1-1规范提出的组件法来计算它的初始转动刚度.在H型钢梁与H型柱端板单向螺栓连接节点原有组件的基础上,将与H型柱相关的组件替换成矩形钢管柱相关的组件,将普通螺栓相关的组件替换成与单向螺栓相关的组件.然后,再基于试验现象,提出H型钢梁与矩形钢管柱端板单向螺栓连接节点的简化力学模型.应用组件法计算连接节点初始转动刚度的步骤如下所示[27]:
(1) 确定对于连接刚度有贡献的组件.
(2) 计算各个相关组件的刚度.
(3) 根据各组件的刚度以及组合节点的计算模型,得到连接节点的初始转动刚度.
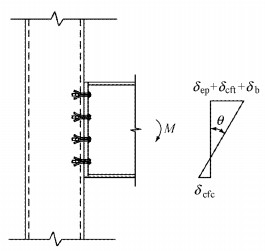
2.2 平齐式端板单向螺栓连接节点简化力学模型节点发生转动是因为节点区域的各构件在外力作用下发生了变形.由试验现象可知,对H型钢梁与矩形钢管柱平齐式端板单向螺栓连接节点,节点区域主要的变形有以下四部分(见图 5):
|
图 5 弯矩作用下平齐式端板单向螺栓节点变形模式 Fig.5 Deformation mode of flushed end-plate connection using blind bolts subjected to moment loading |
(1) 单向螺栓伸长变形(受拉区).
(2) 端板受弯变形(受拉区).
(3) 柱壁受拉变形(受拉区).
(4) 柱壁受压变形(受压区).
图 5中,δep为端板的变形,δcft为受拉钢板的变形,δb为螺栓的变形,δcfc为受压钢板的变形.
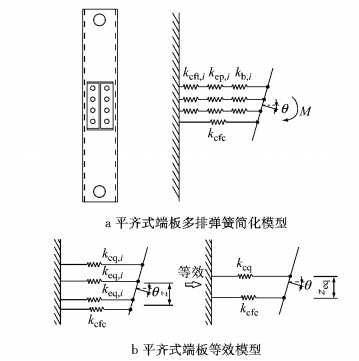
在弹性阶段,采用小变形假定,连接节点的初始转动刚度可由各组件自身的刚度计算得到.对于弯矩作用下的H型钢梁与矩形钢管柱平齐式端板单向螺栓连接节点,基于试验现象,本文提出了简化力学模型(见图 6),并遵循钢梁在受弯时符合平截面的假定.
|
图 6 平齐式端板单向螺栓节点初始转动刚度计算模型 Fig.6 Calculation model of initial rotational stiffness for flushed end-plate connection using blind bolts |
从图 6可知,当多个组件位于同一高度时,可用一个等效刚度keq, i(i表示第i排螺栓)来代替这一高度处各组件的刚度,对于受力形式相同但所处高度不同的组件,可用一个等效力臂zeq来代替原来的力臂z,从而得到不同高度处各组件的等效刚度keq.
同一个螺栓排的变形是由单向螺栓的拉伸变形、端板的弯曲变形以及柱壁的弯曲变形串联叠加组成,将3种组件各自等效为一个弹簧,则该螺栓排的等效刚度可由3个组件的刚度利用弹簧串联公式进行计算,即该螺栓排的等效刚度
| $ {k_{{\rm{eq}},i}} = \frac{1}{{\frac{1}{{{k_{{\rm{b}},i}}}} + \frac{1}{{{k_{{\rm{ep}},i}}}} + \frac{1}{{{k_{{\rm{cft}},i}}}}}} $ |
式中:kb, i为第i排螺栓处单向螺栓的抗拉刚度;kep, i为第i排螺栓处端板的抗弯刚度;kcft, i为第i排螺栓处柱壁抗拉刚度.
在弯矩M作用下,分别根据合力等效和弯矩等效(见图 6b),可以建立如下方程:
| $ {k_{{\rm{eq}}}}{z_{{\rm{eq}}}}\theta = \sum\limits_i {{k_{{\rm{ep}},i}}{z_i}\theta } $ | (1) |
| $ {k_{{\rm{eq}}}}z_{{\rm{eq}}}^2\theta = \sum\limits_i {{k_{{\rm{ep}},i}}z_i^2\theta } $ | (2) |
结合式(1)和式(2),可得
| $ {z_{{\rm{eq}}}} = \frac{{\sum\limits_i {z_i^2} }}{{\sum\limits_i {{z_i}} }} $ |
| $ {k_{{\rm{eq}}}} = \frac{{\sum\limits_i {{k_{{\rm{ep}},i}}z_i^2} }}{{z_{{\rm{eq}}}^2}} $ |
在弯矩M作用下,在zeq处由于柱壁受拉端板受弯,螺栓受拉产生的总拉伸变形
| $ {\delta _{\rm{T}}} = \frac{M}{{{z_{{\rm{eq}}}}\left( {E{k_{{\rm{eq}}}}} \right)}} $ |
式中:E为弹性模量.柱壁受压变形
| $ {\delta _{\rm{c}}} = \frac{M}{{{z_{{\rm{eq}}}}\left( {E{k_{{\rm{cfc}}}}} \right)}} $ |
因此,节点处梁柱的相对转角
| $ \theta = \frac{{{\delta _{\rm{T}}} + {\delta _{\rm{c}}}}}{{{z_{{\rm{eq}}}}}} = \frac{M}{{Ez_{{\rm{eq}}}^2}}\left( {\frac{1}{{{k_{{\rm{eq}}}}}} + \frac{1}{{{k_{{\rm{cfc}}}}}}} \right) $ |
节点的初始转动刚度
| $ {K_{\rm{i}}} = \frac{M}{\theta } = \frac{{Ez_{{\rm{eq}}}^2}}{{\frac{1}{{{k_{{\rm{eq}}}}}} + \frac{1}{{{k_{{\rm{cfc}}}}}}}} $ |
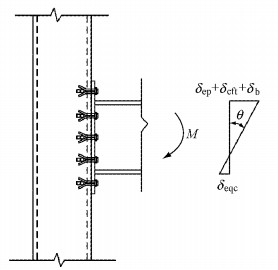
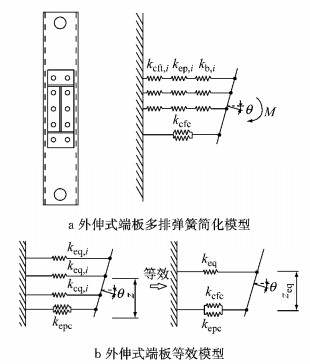
对H型钢梁与矩形钢管柱外伸式端板单向螺栓连接节点,节点区域主要的变形除了与平齐式端板单向螺栓连接节点相同的部分外,还应当考虑受压区外伸式端板的弯曲变形,如图 7所示.计算外伸式端板单向螺栓连接节点的初始转动刚度时,可采取与平齐式端板单向螺栓连接节点初始转动刚度类似的计算方法和计算假定,计算模型如图 8所示.其中,δeqc为等效受压变形.
|
图 7 弯矩作用下外伸式端板单向螺栓节点变形模式 Fig.7 Deformation mode of extended end-plate connection using blind bolts subjected to moment loading |
|
图 8 外伸式端板单向螺栓节点初始转动刚度计算模型 Fig.8 Calculation model of initial rotational stiffness for extended end-plate connection using blind bolts |
在弯矩M作用下,外伸式端板单向螺栓连接节点在zeq处由于柱壁受拉、端板受弯,螺栓受拉产生的总拉伸变形δT计算公式与平齐式端板单向螺栓连接节点的相同.
外伸式端板单向螺栓连接节点在柱壁处的受压变形
| $ {\delta _{\rm{c}}} = \frac{M}{{{z_{{\rm{eq}}}}E\left( {{k_{{\rm{cfc}}}} + {k_{{\rm{epc}}}}} \right)}} $ |
式中:kepc为受压外伸式端板抗压刚度.因此,外伸式端板单向螺栓连接节点处梁柱的相对转角
| $ \theta = \frac{{{\delta _{\rm{T}}} + {\delta _{\rm{c}}}}}{{{z_{{\rm{eq}}}}}} = \frac{M}{{Ez_{{\rm{eq}}}^2}}\left( {\frac{1}{{{k_{{\rm{eq}}}}}} + \frac{1}{{{k_{{\rm{cfc}}}} + {k_{{\rm{epc}}}}}}} \right) $ |
外伸式端板单向螺栓连接节点的初始转动刚度
| $ {K_{\rm{i}}} = \frac{M}{\theta } = \frac{{Ez_{{\rm{eq}}}^2}}{{\frac{1}{{{k_{{\rm{eq}}}}}} + \frac{1}{{{k_{{\rm{cfc}}}} + {k_{{\rm{epc}}}}}}}} $ |
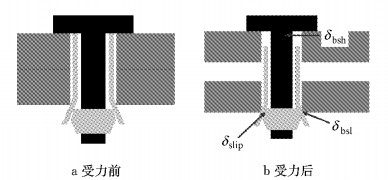
由于自锁式单向螺栓的特殊构造,在外拉力的作用下,单向螺栓的拉伸变形由三部分组成[29]:①螺杆的拉伸变形δbsh;②套筒分肢受到来自钢板和锥头的挤压变形δbsl;③在拉力作用下,螺杆与锥头作为一个整体被往上拉,产生从套筒上侧拔出的趋势,使锥头与套筒间发生相对滑移δslip.单向螺栓变形如图 9所示.
|
图 9 单向螺栓变形示意图 Fig.9 Schematic diagram of blind bolt deformation |
自锁式单向螺栓的初始拉伸刚度可以表示为这三部分的刚度串联,即:
| $ {k_{{\rm{b}},i}} = \frac{1}{{\frac{1}{{{k_{{\rm{bsh}}}}}} + \frac{1}{{{k_{{\rm{bsl}}}}}} + \frac{1}{{{k_{{\rm{slip}}}}}}}} $ |
式中:kbsh为单向螺栓螺杆抗拉刚度;kbsl为单向螺栓套筒抗拉刚度;kslip为锥头与套筒间相对滑移贡献的刚度.
螺杆的拉伸刚度可参考Eurocode 3给出的计算公式[30],如下所示:
| $ {k_{{\rm{bsh}}}} = 1.6\frac{{{A_{\rm{s}}}}}{{{L_{\rm{b}}}}} $ |
式中:As为单向螺栓螺杆横截面积;Lb为单向螺栓螺杆的有效长度。Lb可按下式计算:
| $ {L_{\rm{b}}} = {t_{{\rm{ep}}}} + {t_{{\rm{cf}}}} + {t_{{\rm{w1}}}} + {t_{{\rm{w2}}}} + \frac{1}{2}\left( {{t_{\rm{h}}} + {t_{{\rm{tc}}}}} \right) $ |
式中:tep为连接端板厚度;tcf为连接柱壁厚度;tw1为钢垫圈厚度;tw2为橡胶垫圈厚度;th为螺栓头厚度;ttc为锥头厚度.
单向螺栓外套筒抗拉刚度kbsl可按下式计算[22]:
| $ {k_{{\rm{bsl}}}} = \frac{{{t_{\rm{s}}}{A_{{\rm{slp}}}}}}{{\left[ {\nu s_1^2{C_3} - s_2^2\left( {{C_1} - \frac{\nu }{2}{C_2}} \right)} \right]\sin \alpha }} $ |
| $ {A_{{\rm{slp}}}} = \gamma \frac{{{\rm{ \mathsf{ π} }}\left( {{d_{{\rm{tcm}}}} - {d_{{\rm{tct}}}}} \right)}}{4} $ |
| $ {C_1} = {\cos ^2}\alpha \cot \alpha $ |
| $ {C_2} = \cot \alpha $ |
| $ {C_3} = \frac{1}{\nu }{\cos ^2}\alpha \cot \alpha - \frac{1}{2}\cot \alpha $ |
| $ \gamma = 1 - \frac{{8{b_{\rm{s}}}}}{{{\rm{ \mathsf{ π} }}{d_{{\rm{tct}}}}}} $ |
| $ {s_1} = \frac{{{d_{{\rm{tct}}}}}}{{2\cos \alpha }} $ |
| $ {s_2} = \frac{{{d_{{\rm{tcm}}}}}}{{2\cos \alpha }} $ |
式中:ts为套筒厚度;Aslp为充分撑开的套筒在水平面上的有效投影面积;C1、C2、C3为计算参数;γ为面积折减系数;bs为相邻套筒间开槽的宽度;dtct、dtcm分别为锥头的上部直径和中部直径;s1、s2为几何参数;α为单向螺栓充分撑开的外套筒与水平面的夹角;ν为泊松比.图 10中,s1为K点到套筒肢延长线与轴线交点的距离,s2为L点到套筒肢延长线与轴线交点的距离,qb为套筒与锥头的接触压应力,B为螺杆受到的力.

|
图 10 套筒几何参数 Fig.10 Geometric parameters of flaring sleeve |
文献[29]通过对国产自锁式单向螺栓大量的拉伸试验,给出了锥头与套筒间相对滑移对抗拉刚度的贡献,如表 2所示.
| 下载CSV 表 2 国产自锁式单向螺栓kslip试验拟合值 Tab.2 kslip test fitting value of domestic self-locked blind bolts |
对钢结构梁柱端板螺栓连接节点,Eurocode 3[30]采用等效T形件法,即将各螺栓排所在的端板与钢梁腹板的组合体简化为一T形连接件进行分析.
受拉端板的抗弯刚度kep, i可按下式计算:
| $ {k_{{\rm{ep}},i}} = \frac{{0.9{l_{{\rm{eff}}}}t_{{\rm{ep}}}^3}}{{{a^3}}} $ |
式中:leff为T形连接件受弯塑性铰线的有效长度,可根据EN 1993-1-8规定取值;tep为端板厚度;a为几何参数.对受拉区外伸式端板部分,a=ax.图 11中,e为螺栓距离梁外侧距离,bp为梁的宽度,w为螺栓水平间距,ex为螺栓距离外伸式端板上部的距离.

|
图 11 端板几何参数 Fig.11 Geometric parameters of end-plate |
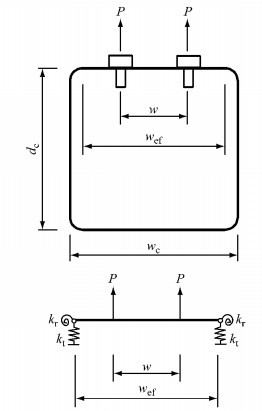
矩形钢管柱柱壁在受拉区承受螺栓拉力作用.为简化分析,将柱侧壁承受拉力作用柱壁的约束采用一转动弹簧和一轴向拉伸弹簧代替,如图 12所示.图 12中,P为作用在螺栓上的拉力,wef为有效屈服宽度,wc为矩形钢管柱宽度,dc为矩形钢管柱高度,kr为柱侧壁的转动刚度,kt为柱侧壁的轴向刚度.
|
图 12 柱壁受拉简化板模型 Fig.12 Simplified plate model of tube wall in tension |
由于矩形钢管柱侧壁连续,钢板平面内刚度远大于平面外刚度,因此轴向拉伸弹簧刚度kt可视为无限大.此时可仅考虑柱侧壁转动约束对柱壁受拉刚度的影响.
利用叠加原理,即在螺栓集中力P作用下将柱壁的面外位移视为简支板在集中力作用下的位移w1(+)与由柱侧壁刚度引起的约束弯矩作用下的位移w2(-)两部分之和,柱壁抗拉刚度[23]
| $ {k_{{\rm{cft}}}} = \frac{{{f_1}t_{{\rm{cf}}}^3}}{{w_{{\rm{ef}}}^2\cos \frac{{w{\rm{ \mathsf{ π} }}}}{{2{w_{{\rm{ef}}}}}}}} $ |
| $ {f_1} = \frac{{11.5{w_{{\rm{ef}}}}{k_{\rm{r}}} + 5.7Et_{{\rm{cf}}}^3}}{{2.024{w_{{\rm{ef}}}}{k_{\rm{r}}}{S_1} - {w_{{\rm{ef}}}}{k_{\rm{r}}} + E{S_1}t_{{\rm{cf}}}^3}} $ |
| $ {S_1} = 0.143{\left( {\frac{w}{{{w_{{\rm{ef}}}}}}} \right)^2} - 0.306\left( {\frac{w}{{{w_{{\rm{ef}}}}}}} \right) + 1.076 $ |
| $ {k_{\rm{r}}} = \frac{{4EI}}{{{d_{\rm{c}}}}}\left( {\frac{{1.5{w_{\rm{c}}} + {d_{\rm{c}}}}}{{2{w_{\rm{c}}} + {d_{\rm{c}}}}}} \right) $ |
式中:f1、S1均为计算参数.
3.4 柱壁抗压刚度矩形钢管柱柱壁在受压区承受钢梁下翼缘传递的均布荷载.与柱壁受拉刚度求解方法类似,可利用叠加原理,即在P作用下将柱壁面外位移视为简支板在均布力作用下的位移w1(-)与由柱侧壁刚度引起的约束弯矩作用下的位移w2(+)两部分之和,如图 13所示.图 13中,b为受压柱壁计算长度,u为矩形荷载区域的长度,v为矩形荷载区域的宽度,x、y为坐标轴.

|
图 13 柱壁受压部分简化力学模型 Fig.13 Simplified mechanical model for column wall in compression zone |
部分受载的简支矩形板挠度w1可由下式计算[31]得到:
| $ \begin{array}{l} {w_1} = \frac{{4qw_{{\rm{ef}}}^4}}{{D{{\rm{ \mathsf{ π} }}^5}}}\sum\limits_{m = 1,3,5, \cdots }^\infty {\frac{{{{\left( { - 1} \right)}^{\left( {m - 1} \right)/2}}}}{{{m^5}}}\sin \frac{{m{\rm{ \mathsf{ π} }}u}}{{2{w_{{\rm{ef}}}}}}\left\{ {1 - } \right.} \\ \frac{{\cosh \frac{{m{\rm{ \mathsf{ π} }}y}}{{{w_{{\rm{ef}}}}}}}}{{\cosh {\alpha _m}}}\left[ {\cosh \left( {{\alpha _m} - 2{\gamma _m}} \right) + {\gamma _m}\sinh \left( {{\alpha _m} - 2{\gamma _m}} \right) + } \right.\\ \left. {\left. {{\alpha _m}\frac{{\sinh \left( {2{\gamma _m}} \right)}}{{2\cosh {\alpha _m}}}} \right] + \frac{{\cosh \left( {{\alpha _m} - 2{\gamma _m}} \right)}}{{2\cosh {\alpha _m}}}\frac{{m{\rm{ \mathsf{ π} }}y}}{{{w_{{\rm{ef}}}}}}\sinh \frac{{m{\rm{ \mathsf{ π} }}y}}{{{w_{{\rm{ef}}}}}}} \right\} \cdot \\ \sinh \frac{{m{\rm{ \mathsf{ π} }}x}}{{{w_{{\rm{ef}}}}}} \end{array} $ | (3) |
| $ {\alpha _m} = \frac{{m{\rm{ \mathsf{ π} }}b}}{{2{w_{{\rm{ef}}}}}} $ |
| $ {\gamma _m} = \frac{{m{\rm{ \mathsf{ π} }}v}}{{4{w_{{\rm{ef}}}}}} $ |
| $ D = \frac{{Et_{{\rm{cf}}}^3}}{{12\left( {1 - {\nu ^2}} \right)}} $ |
式中:q为均布荷载,
| $ \begin{array}{*{20}{c}} {{w_{1\max }} = \frac{{4qw_{{\rm{ef}}}^4}}{{D{{\rm{ \mathsf{ π} }}^5}}}\sum\limits_{m = 1,3,5, \cdots }^\infty {\frac{1}{{{m^5}}}\sin \frac{{m{\rm{ \mathsf{ π} }}u}}{{2{w_{{\rm{ef}}}}}} \cdot } }\\ {\left\{ {1 - \frac{1}{{\cosh {\alpha _m}}}\left[ {\cosh \left( {{\alpha _m} - 2{\gamma _m}} \right) + } \right.} \right.}\\ {\left. {\left. {{\gamma _m}\sinh \left( {{\alpha _m} - 2{\gamma _m}} \right) + {\alpha _m}\frac{{\sinh \left( {2{\gamma _m}} \right)}}{{2\cosh {\alpha _m}}}} \right]} \right\}} \end{array} $ | (4) |
对矩形钢管柱,可视为b
| $ {w_1} = \frac{{12\left( {1 - {\nu ^2}} \right)Pw_{{\rm{ef}}}^3}}{{Et_{{\rm{cf}}}^3{{\rm{ \mathsf{ π} }}^4}u}}\sin \left( {\frac{{{\rm{ \mathsf{ π} }}u}}{{2{w_{{\rm{ef}}}}}}} \right) $ |
由柱侧壁刚度引起的约束弯矩作用下的位移w2(+)可由下式计算[23]:
| $ {w_2} = - \frac{{w_{{\rm{ef}}}^3{k_{\rm{r}}}P{{\left( { - 1 + {\nu ^2}} \right)}^2}\cos \left( {\frac{{\omega {\rm{ \mathsf{ π} }}}}{{2{w_{{\rm{ef}}}}}}} \right)}}{{Et_{{\rm{cf}}}^3\left[ {4.7Et_{{\rm{cf}}}^3 - 10.5{w_{{\rm{ef}}}}{k_{\rm{r}}}\left( { - 1 + {\nu ^2}} \right)} \right]}} $ |
因此,柱壁抗压刚度
| $ {k_{{\rm{cfc}}}} = \frac{P}{w} = \frac{P}{{{w_1} + {w_2}}} $ | (5) |
结合式(5),可得
| $ {k_{{\rm{cfc}}}} = {S_2}{\left( {\frac{{{t_{{\rm{cf}}}}}}{{{w_{{\rm{ef}}}}}}} \right)^3} $ |
| $ {S_2} = \frac{{\left( {4.7Et_{{\rm{cf}}}^3 + 9.555{w_{{\rm{ef}}}}{k_{\rm{r}}}} \right)u}}{{0.112\left( {4.7Et_{{\rm{cf}}}^3 + 9.555{w_{{\rm{ef}}}}{k_{\rm{r}}}} \right)\sin \frac{{{\rm{ \mathsf{ π} }}u}}{{2a}} - 0.828{k_{\rm{r}}}u\cos \frac{{wu}}{{2a}}}} $ |
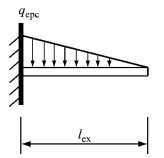
受压外伸式端板抗弯刚度的推导可采用与受压端板抗弯刚度相同的思路.将受压端板简化成一等效T形件,假设荷载P全部由该T形件承担.由于端板外侧为自由边,荷载为零,根部直接承受下翼缘传递的集中力,荷载数值最大.因此,作用在T形件上的荷载近似符合三角形分布,如图 14所示.外伸式端板根部在荷载P作用下的位移与长度为lex的悬臂板在三角形分布荷载qepc作用下的位移等效,如图 15所示.于是外伸式端板抗弯刚度的求解可转化为如图 15所示的悬臂板抗弯刚度的求解.

|
图 14 外伸式端板荷载分布 Fig.14 Load distribution of extended end-plate |
|
图 15 外伸式端板简化力学模型 Fig.15 Simplified mechanical model of extended end-plate |
由受力平衡,可得
| $ {q_{{\rm{epc}}}} = {l_{{\rm{ex}}}}{b_{{\rm{ep}}}} = P $ |
式中:qepc为三角形分布荷载最大值;lex为端板外伸部分的长度;bep为端板的宽度.
已知悬臂板在三角形分布荷载作用下的位移
| $ {\delta _{{\rm{epc}}}} = \frac{{{q_{{\rm{epc}}}}l_{{\rm{ex}}}^4}}{{30E{I_{{\rm{ep}}}}}} $ |
厚度为tep悬臂板的截面惯性矩
| $ {I_{{\rm{ep}}}} = \frac{{{b_{{\rm{ep}}}}t_{{\rm{ep}}}^3}}{{12}} $ | (6) |
结合式(6),可得
| $ {\delta _{{\rm{epc}}}} = \frac{{2Pl_{{\rm{ex}}}^3}}{{5E{b_{{\rm{ep}}}}t_{{\rm{ep}}}^3}} $ |
因此,受压外伸式端板抗压刚度
| $ {k_{{\rm{epc}}}} = \frac{{5{b_{{\rm{ep}}}}t_{{\rm{ep}}}^3}}{{2l_{{\rm{ex}}}^3}} $ |
为验证提出的H型钢梁与矩形钢管柱端板单向螺栓连接节点初始转动刚度的计算方法,对文献[24-25]中的6个平齐式端板单向螺栓连接试件和6个外伸式端板单向螺栓连接试件的初始转动刚度进行了计算,计算结果与试验结果对比见表 3和表 4.
| 下载CSV 表 3 平齐式端板单向螺栓节点试件的初始转动刚度 Tab.3 Initial rotational stiffness of flushed end- plate connection using blind bolts |
| 下载CSV 表 4 外伸式端板单向螺栓节点试件的初始转动刚度 Tab.4 Initial rotational stiffness of extended end-plate connection using blind bolts |
从表 3和表 4可以看出,本文给出的针对H型钢梁与矩形钢管柱端板单向螺栓连接节点初始转动刚度的理论公式计算结果与试验值吻合较好.
5 结论(1) 本文推导了单向螺栓抗拉刚度、受拉端板抗弯刚度、柱壁抗拉刚度、柱壁抗压刚度和受压端板抗压刚度计算式.在前人研究成果的基础上,将考虑单向螺栓与连接件孔壁之间相对滑移后的螺栓抗拉刚度引入节点初始转动刚度的计算中.对外伸式端板单向螺栓连接节点,还考虑了受压外伸式端板对节点初始转动刚度的贡献.利用组件法分别提出了平齐式、外伸式连接节点在弯矩作用下初始转动刚度的理论计算公式.
(2) 与试验结果的比较表明,本文给出的H型钢梁与矩形钢管柱端板单向螺栓连接节点初始转动刚度的计算公式与试验结果吻合较好,精度可满足工程设计的要求.
(3) 理论分析和试验结果表明,端板单向螺栓连接节点的初始转动刚度大小与端板的形式关系密切.在螺栓等级、柱壁厚度、端板厚度相同的情况下,外伸式端板连接节点的初始转动刚度约为平齐式端板连接节点的2倍.依据Eurocode 3中关于节点的分类标准进行计算可知,平齐式端板连接节点更接近铰接节点的性质,因此对于要求具有一定转动刚度的端板单向螺栓连接节点,宜采用外伸式端板连接.
| [1] |
王恒华, 曹发恒. H型钢梁与RHS柱半刚性连接节点的性能研究[J]. 建筑科学, 2009(5): 23 WANG Henghua, CAO Faheng. Research on properties for semi-rigid connections of H-section beam and RHS column[J]. Building Science, 2009(5): 23 |
| [2] |
MILLER D K. Lessons learned from the Northridge earthquake[J]. Engineering Structures, 1998, 20(4): 249 |
| [3] |
TREMBLAY R, FILIATRAULT A, BRUNEAU M, et al. Seismic design of steel buildings: lessons from the 1995 Hyogo-ken Nanbu earthquake[J]. Canadian Journal of Civil Engineering, 1996, 23(3): 727 DOI:10.1139/l96-885 |
| [4] |
许炎彬, 李国强, 张龙. 单边紧固螺栓: 201210435247. 7[P]. 2012-11-05. XU Yanbin, LI Guoqiang, ZHANG Long. One-way fastening bolt: 201210435247. 7[P]. 2012-11-05. |
| [5] |
MOURAD S. Behavior of blind bolted moment connections for square HSS columns[D]. Ann Arbor: McMaster University, 1993.
|
| [6] |
KOROL R M, GHOBARAH A, MOURAD S. Blind bolting W-shape beams to HSS columns[J]. Journal of Structural Engineering, 1993, 119(12): 3463 DOI:10.1061/(ASCE)0733-9445(1993)119:12(3463) |
| [7] |
FRANCE J E, BUICK Davison J, KIRBY P A. Strength and rotational response of moment connections to tubular columns using flowdrill connectors[J]. Journal of Constructional Steel Research, 1999, 50(1): 1 DOI:10.1016/S0143-974X(98)00235-1 |
| [8] |
FRANCE J E, BUICK D J, KIRBY P A. Strength and rotational stiffness of simple connections to tubular columns using flowdrill connectors[J]. Journal of Constructional Steel Research, 1999, 50(1): 15 DOI:10.1016/S0143-974X(98)00236-3 |
| [9] |
FRANCE J E, BUICK D J, KIRBY P A. Moment-capacity and rotational stiffness of endplate connections to concrete-filled tubular columns with flowdrilled connectors[J]. Journal of Constructional Steel Research, 1999, 50(1): 35 DOI:10.1016/S0143-974X(98)00237-5 |
| [10] |
BARNETT T C, TIZANI W, NETHERCOT D A. The practice of blind bolting connections to structural hollow sections: a review[J]. Steel & Composite Structures, 2001, 1(1): 1 |
| [11] |
TIZANI W, Al-MUGHAIRI A, OWEN J S, et al. Rotational stiffness of a blind-bolted connection to concrete-filled tubes using modified Hollo-bolt[J]. Journal of Constructional Steel Research, 2013, 80(1): 317 |
| [12] |
WANG J F, HAN L H, UY B. Hysteretic behaviour of flush end plate joints to concrete-filled steel tubular columns[J]. Journal of Constructional Steel Research, 2009, 65(8): 1644 |
| [13] |
王静峰, 张琳, 戴阳. 半刚性钢管混凝土框架梁柱端板连接抗震性能试验研究[J]. 土木工程学报, 2012, 45(11): 13 WANG Jingfeng, ZHANG Lin, DAI Yang. Seismic experimental study of end plate connections for semi-rigid concrete-filled steel tubular frames[J]. China Civil Engineering Journal, 2012, 45(11): 13 |
| [14] |
WANG J, SPENCER B F. Experimental and analytical behavior of blind bolted moment connections[J]. Journal of Constructional Steel Research, 2013, 82: 33 DOI:10.1016/j.jcsr.2012.12.002 |
| [15] |
ELGHAZOULI A Y, MALAGA-CHUQUITAYPE C, CASTRO J M, et al. Experimental monotonic and cyclic behaviour of blind-bolted angle connections[J]. Engineering Structures, 2009, 31(11): 2540 DOI:10.1016/j.engstruct.2009.05.021 |
| [16] |
LEE J, GOLDSWORTHY H M, GAD E F. Blind bolted T-stub connections to unfilled hollow section columns in low rise structures[J]. Journal of Constructional Steel Research, 2010, 66(8): 981 |
| [17] |
LEE J, GOLDSWORTHY H M, GAD E F. Blind bolted moment connection to sides of hollow section columns[J]. Journal of Constructional Steel Research, 2011, 67(12): 1900 DOI:10.1016/j.jcsr.2011.06.007 |
| [18] |
LIU Y, MALAGA-CHUQUITAYPE C, ELGHAZOULI A Y. Response and component characterisation of semi-rigid connections to tubular columns under axial loads[J]. Engineering Structures, 2012, 41(3): 510 |
| [19] |
GHOBARAH A, MOURAD S, KOROL R M. Moment-rotation relationship of blind bolted connections for HSS columns[J]. Journal of Constructional Steel Research, 1996, 40(1): 63 DOI:10.1016/S0143-974X(96)00044-2 |
| [20] |
SILVA L A P, NEVES L F N, GOMES F C T. Rotational stiffness of rectangular hollow sections composite joints[J]. Journal of Structural Engineering, 2003, 129(4): 487 DOI:10.1061/(ASCE)0733-9445(2003)129:4(487) |
| [21] |
MALAGA-CHUQUITAYPE C, ELGHAZOULI A Y. Component-based mechanical models for blind-bolted angle connections[J]. Engineering Structures, 2010, 32(10): 3048 DOI:10.1016/j.engstruct.2010.05.024 |
| [22] |
WANG Z Y, TIZANI W, WANG Q Y. Strength and initial stiffness of a blind-bolt connection based on the T-stub model[J]. Engineering Structures, 2010, 32(9): 2505 DOI:10.1016/j.engstruct.2010.04.005 |
| [23] |
PARK A Y, WANG Y C. Development of component stiffness equations for bolted connections to RHS columns[J]. Journal of Constructional Steel Research, 2012, 70: 137 DOI:10.1016/j.jcsr.2011.08.004 |
| [24] |
李国强, 段炼, 陆烨, 等. H型钢梁与矩形钢管柱外伸式端板单向螺栓连接节点承载力试验与理论研究[J]. 建筑结构学报, 2015(9): 91 LI Guoqiang, DUAN Lian, LU Ye, et al. Experimental and theoretical study of bearing capacity for extended end-plated connections between rectangular tubular columns and H-shaped beams with single direction bolts[J]. Journal of Building Structures, 2015(9): 91 |
| [25] |
李国强, 段炼, 陆烨, 等. H型钢梁与矩形钢管柱平齐式端板单向螺栓节点承载力性能[J]. 同济大学学报(自然科学版), 2018(2): 162 LI Guoqiang, DUAN Lian, LU Ye, et al. The bearing capacity for flush end-plated connections between rectangular tubular columns and H-shaped beams with single direction bolts[J]. Journal of Tongji University (Natural Science), 2018(2): 162 |
| [26] |
高婧, 石文龙, 李国强, 等. 平端板连接半刚性梁柱组合节点的初始转动刚度[J]. 工程力学, 2011, 28(3): 55 GAO Jing, SHI Wenlong, LI Guoqiang, et al. Initial rotational stiffness of semi-rigid composite beam-to-column joints with flush end plate connections[J]. Engineering Mechanics, 2011, 28(3): 55 |
| [27] |
WEYNAND K, JASPART J-P, STEENHUIS M. The stiffness model of revised annex j of Eurocode 3[C]//BJORHOVDE R, COLSON A, ZANDONINI R. Proceedings of the 3rd International Workshop on Connections. Trento: [s. n. ], 1995: 441-452.
|
| [28] |
陈颖智, 童乐为, 陈以一. 组件法用于钢结构节点性能分析的研究进展[J]. 建筑科学与工程学报, 2012, 29(3): 81 CHEN Yingzhi, TONG Lewei, CHEN Yiyi. Research developments of component method for behavior of joints in steel structures[J]. Journal of Architecture and Civil Engineering, 2012, 29(3): 81 |
| [29] |
张杰华. 钢结构用国产自锁式单向螺栓力学性能研究[D]. 上海: 同济大学, 2016. ZHANG Jiehua. Research on mechanical properties of domestic self-lock one-side bolt[D]. Shanghai: Tongji University, 2016. |
| [30] |
European Committee for Standardization (CEN). EN 1993-1-8 Eurocode 3: design of steel structures, Part 1-8 design of joints[S]. Brussels: CEN, 2005
|
| [31] |
TIMOSHENKO S, WOINOWSKY-KRIEGER S. Theory of plates and shells[M]. New York: McGraw-Hill, 1959
|
 2018, Vol. 46
2018, Vol. 46
