随着信息技术和电子商务的发展, 越来越多的制造商选择开通网络零售渠道, 如IBM、耐克、戴尔、联想等.同时, 像亚马逊、京东、当当网等这样的纯网络零售商伴随着互联网的发展活跃起来.在市场的激烈竞争下, 越来越多的零售商也纷纷开始发展电子商务业务, 如苏宁推出苏宁易购, 国美成立电子商务平台等.因此, 为了抢占市场份额, 双渠道零售商和纯网络零售商之间经常会发生价格竞争, 尤其是2012年苏宁和京东的价格战令人印象深刻.一方面, 价格竞争是不同渠道间发生冲突的重要原因, 直接影响到供应链双方的利润；另一方面, 制造商的网络零售渠道对消费者的吸引力越来越小, 因此研究双渠道零售商和纯网络零售商之间的价格竞争问题具有现实意义.

对于多渠道供应链问题, 目前已有大量研究.Chiang等^[1]研究发现, 网络电子渠道的开通, 一方面帮助传统零售商降低批发价, 另一方面在传统零售商收益出现部分降低的情况下, 整个供应链的收益获得较大改进.郭亚军等^[2]分析了双渠道环境下制造商和零售商的定价策略, 结果表明制造商采取双渠道零售策略能够诱导传统零售商降低价格, 使制造商的利润增加, 同时供应链的整体利润也增加.许传永^[3]研究了一类两层双渠道供应链的定价问题, 发现制造商的电子渠道可以拓展产品市场和满足更多客户需求, 但迫使零售商降低零售价格, 并且零售渠道的潜在威胁制衡了零售商的零售价格.Huang等^[4]发现, 在消费者没有外部选择的情况下, 开辟电子渠道并不能增加零售商利润, 传统零售商开辟电子渠道是基于竞争的需要；在消费者有其他外部选择的情况下, 传统零售商可以通过增加电子渠道扩大消费人群和实现利润增长, 消费者也将从中受益.赵连霞^[5]建立双渠道制造商和双渠道零售商的混合定价决策模型, 结果表明在保证一定补偿率的条件下, 制造商倾向于开通网络电子渠道, 网络电子渠道的开通将提升整个混合渠道供应链的绩效.

上述文献大多数是以双渠道制造商和传统零售商或双渠道制造商和双渠道零售商为背景, 研究开通网络零售渠道对供应链双方利润的影响, 但很少有文献直接研究双渠道零售商与纯网络零售商之间的价格竞争问题.Park等^[6]在考虑传统零售商、纯网络零售商及双渠道零售商等3种零售商并存的情况下, 建立了线性模型, 考虑了价格对3种零售商的影响, 但没有探究价格变动背后的原因.Wu等^[7]首次以2012年苏宁和京东的价格大战为现实背景, 构造双渠道零售商和纯网络零售商的价格博弈模型, 分析市场份额对均衡价格的影响.研究发现, 双渠道零售商是否比纯网络零售商在价格战中更有优势取决于网络渠道市场份额与传统零售渠道市场份额之比, 若双渠道零售商在市场份额上没有明显的优势, 纯网络零售商则可以在价格战中获益.

在减少或者避免渠道冲突的价格策略研究时, 以上文献中大多假设制造商占主导地位, 拥有价格决策的优先权, 或者零售商占主导地位.例如, 国内学者郑文军等^[8]假定零售商占主导地位, 研究零售商在推行线上线下同价政策的背景下, 自主开辟网络渠道的运行效果.但斌等^[9]建立了以强势零售商为主方的价格竞争主从对策博弈模型, 研究供应链成员的价格决策过程.相反, 很少有学者研究不同的定价时间策略对制造商与零售商利润产生的影响.Matsui^[10]首次研究了价格制定的时间策略对双渠道制造商和传统零售商利润的影响.研究发现, 在双渠道制造商先制定批发价、零售商后制定零售价的前提下, 双渠道制造商制定电子价格的时间应不晚于制定批发价的时间, 但此研究是以双渠道制造商和传统零售商的多渠道供应链为背景.

本文在双渠道零售商和纯网络零售商的多渠道供应链下, 假设两零售商不仅能决定各自渠道的价格, 而且能决定各自价格制定的时间, 建立以纯网络零售商为主方的Stackelberg主从对策博弈模型和以双渠道零售商为主方的Stackelberg主从对策博弈模型, 研究电子渠道的市场规模、双渠道零售商电子渠道在电子市场中所占份额对各渠道均衡价格的影响, 并分析不同定价时间策略对双方最优定价的影响.

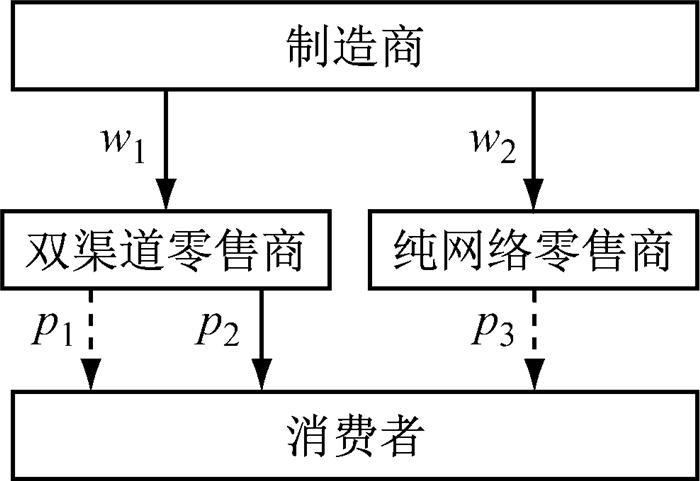
1 问题描述及模型 1.1 问题描述与假设

在由一个双渠道零售商和一个纯网络零售商组成的多渠道供应链中, 产品经过3个渠道销售给消费者, 具体如图 1所示.图 1中, 虚线代表产品销售的电子渠道, 实线代表产品销售的传统渠道.

作如下假设：

(1) 该多渠道中只销售1种产品.

(2) 产品批发价格w₁、w₂由零售商与制造商的长期合同决定, 为模型的外生变量, 且假定w₁=w₂=w.

(3) 渠道之间的交叉价格弹性系数相等, 且商品需求受自身渠道价格的影响大于竞争渠道价格的影响, 因此本文假定1>2t, 即0 < t < $\frac{1}{2}$.

本文所涉及参数如表 1所示.

1.2 模型构建

基于弹性理论的线性需求函数能够体现出不同渠道间价格差异的影响；在渠道情形较复杂的情况下, 线性需求函数更加简洁, 便于建模.因此, 结合表 1中参数, 双渠道零售商电子渠道、双渠道零售商传统渠道和纯网络零售商电子渠道的需求函数分别为

$ \begin{array}{l} {q_1} = {a_1}-{p_1} + t{p_2} + t{p_3}\\ {q_2} = {a_2}-{p_2} + t{p_1} + t{p_3}\\ {q_3} = {a_3}-{p_3} + t{p_1} + t{p_2} \end{array} $

则双渠道零售商和纯网络零售商的利润函数分别为

$ {\pi _1} = ({p_1}-w){q_1} + ({p_2}-w){q_2} $

(1)

$ {\pi _2} = ({p_3}-w){q_3} $

(2)

2 模型求解 2.1 以纯网络零售商为主方的Stackelberg主从对策博弈模型

在以纯网络零售商为主方的Stackelberg博弈中, 设纯网络零售商和双渠道零售商都是绝对理性的, 决策目标都是自身利益最大化.纯网络零售商优先做出决策, 确定p₃, 然后双渠道零售商根据p₃来确定p₁、p₂, 博弈结束.

根据逆向求解法, 可求得双渠道零售商和纯网络零售商的最优定价决策为

$ \begin{array}{l} p_1^* = \{ [{t^2}\left( {1 + t} \right) + 4(1-t-{t^2})]{a_1} + [{t^2}\left( {1 + t} \right) + \\ \;\;\;\;\;\;\;4t(1-t-{t^2})]{a_2} + 2t(1 - {t^2}){a_3} + \\ \;\;\;\;\;\;\;{B_1}\} /[8(1-{t^2})(1-t-{t^2})] \end{array} $

(3)

$ \begin{array}{l} {p_2}^* = \{ [{t^2}\left( {1 + t} \right) + 4t(1-t-{t^2})]{a_1} + [{t^2}\left( {1 + t} \right) + \\ \;\;\;\;\;\;\;\;\;4(1-t-{t^2})]{a_2} + 2t(1 - {t^2}){a_3} + \\ \;\;\;\;\;\;\;\;\;{B_1}\} /[8(1-{t^2})(1-t-{t^2})] \end{array} $

(4)

$ {p_3}^* = {\rm{ }}[t{a_1} + t{a_2} + 2\left( {1-t} \right){a_3} + 2(1-2{t^2})w\left] / \right[4(1-t-{t^2})] $

(5)

其中, B₁=2(1+t)[(1-2t²)t+2(1-t)(1-t-t²)]w.

命题1  双渠道零售商电子渠道的均衡价格p₁^*与双渠道零售商电子渠道市场规模在整个电子渠道市场规模中所占比例γ成正相关.当$\gamma \ge \frac{{-{t^3}-3{t^2} + 2t}}{{3{t^3}-3{t^2} - 6t + 4}}$时, 双渠道零售商电子渠道的均衡价格p₁^*随着电子渠道市场规模α的增大而上升; 当$\gamma < \frac{{-{t^3}-3{t^2} + 2t}}{{3{t^3}-3{t^2} - 6t + 4}}$时, 双渠道零售商电子渠道的均衡价格p₁^*随着电子渠道市场规模α的增大而下降.

证明  令a₁=αγa₀, a₂=(1-α)a₀, a₃=α(1-γ)a₀, 由式(3)及0 < t < $\frac{1}{2}$可知

$ \begin{array}{l} \frac{{\partial p_1^*}}{{\partial \gamma }} = \frac{{\partial p_1^*}}{{\partial {a_1}}}\frac{{\partial {a_1}}}{{\partial \gamma }} + \frac{{\partial p_1^*}}{{\partial {a_3}}}\frac{{\partial {a_3}}}{{\partial \gamma }} = \\ \;\;\;\;\;\;\;\;\;\frac{{3{t^3}-3{t^2}-6t + 4}}{{8(1-{t^2})(1 - t - {t^2})}}\alpha {a_0} > 0 \end{array} $

$ \begin{array}{l} \frac{{\partial p_1^*}}{{\partial \alpha }} = \frac{{\partial p_1^*}}{{\partial {a_1}}}\frac{{\partial {a_1}}}{{\partial \alpha }} + \frac{{\partial p_1^*}}{{\partial {a_2}}}\frac{{\partial {a_2}}}{{\partial \alpha }} + \frac{{\partial p_1^*}}{{\partial {a_3}}}\frac{{\partial {a_3}}}{{\partial \alpha }} = \\ \;\;\;\;\;\;\;\;\;\frac{{\;(3{t^3}-3{t^2}-6t + 4)\gamma-( - {t^3} - 3{t^2} + 2t)}}{{8(1 - {t^2})(1 - t - {t^2})}}{a_0} \end{array} $

令C₁=(3t³-3t²-6t+4)γ-(-t³-3t²+2t), 可证明, 当$\gamma \ge \frac{{-{t^3}-3{t^2} + 2t}}{{3{t^3}-3{t^2} - 6t + 4}}$时, C₁>0, 当$\gamma < \frac{{-{t^3}-3{t^2} + 2t}}{{3{t^3}-3{t^2} - 6t + 4}}$时, C₁ < 0, 又因为8(1-t²)(1-t-t²)>0, 则命题1得证.

命题2  双渠道零售商传统渠道的均衡价格p₂^*与电子渠道市场规模α成负相关.

证明  由式(4)得

$ \begin{array}{l} \frac{{\partial p_2^*}}{{\partial \alpha }} = \frac{{\partial p_2^*}}{{\partial {a_1}}}\frac{{\partial {a_1}}}{{\partial \alpha }} + \frac{{\partial p_2^*}}{{\partial {a_2}}}\frac{{\partial {a_2}}}{{\partial \alpha }} + \frac{{\partial p_2^*}}{{\partial {a_3}}}\frac{{\partial {a_3}}}{{\partial \alpha }} = \\ \;\;\;\;\;\;\;\;\left[{\frac{{(-{t^3}-3{t^2} + 2t)\gamma }}{{8(1-{t^2})(1 - t - {t^2})}}} \right. - \\ \left. {\;\;\;\;\;\;\;\;\frac{{3{t^3} - 3{t^2} - 6t + 4}}{{8(1 - {t^2})(1 - t - {t^2})}}} \right]{a_0} \end{array} $

令C₂=(-t³-3t²+2t)γ-(3t³-3t²-6t+4), 因为0 < γ < 1, -t³-3t²+2t>0, 则(-t³-3t²+2t)γ < -t³-3t²+2t, 所以C₂ < -t³-3t²+2t-(3t³-3t²-6t+4) =-4(t³-2t+1) < 0, 则命题2得证.

命题3  纯网络零售商电子渠道的均衡价格p₃^*与电子渠道市场规模α成正相关, 与双渠道零售商电子渠道市场规模在整个电子渠道市场规模中所占比例γ成负相关.

证明  由式(5)得$\begin{array}{l} \frac{{\partial p_3^*}}{{\partial \alpha }} = \frac{{\partial p_3^*}}{{\partial {a_1}}}\frac{{\partial {a_1}}}{{\partial \alpha }} + \frac{{\partial p_3^*}}{{\partial {a_2}}}\frac{{\partial {a_2}}}{{\partial \alpha }} + \frac{{\partial p_3^*}}{{\partial {a_3}}}\frac{{\partial {a_3}}}{{\partial \alpha }} = \frac{{\left( {3t-2} \right)\left( {y-1} \right)}}{{4(1-t - {t^2})}}{a_0} > 0, \\{\rm{ }} \frac{{\partial p_3^*}}{{\partial \gamma }} = \frac{{\partial p_3^*}}{{\partial {a_1}}}\frac{{\partial {a_1}}}{{\partial \gamma }} + \frac{{\partial p_3^*}}{{\partial {a_3}}}\frac{{\partial {a_3}}}{{\partial \gamma }} = \frac{{3t - 2}}{{4(1 - t - {t^2})}}\alpha {a_0} < 0 \end{array}$, 则命题3得证.

2.2 以双渠道零售商为主方的Stackelberg主从对策博弈模型

在以双渠道零售商为主方的Stackelberg博弈中, 设纯网络零售商和双渠道零售商都是绝对理性的, 决策目标都是自身利益最大化.双渠道零售商优先做出决策, 确定p₁、p₂, 然后纯网络零售商根据p₁、p₂来确定p₃, 博弈结束.

同理, 根据逆向求解法, 可求得双渠道零售商和纯网络零售商的最优定价决策为

$ {p_1}^{\prime *} = \frac{{t\left( {t + 2} \right){a_1} + (2-{t^2}){a_2} + t\left( {t + 1} \right){a_3} + {B_2}}}{{4\left( {t + 1} \right)(1-t-{t^2})}} $

(6)

$ {p_2}^{\prime *} = \frac{{(2-{t^2}){a_1} + t\left( {t + 2} \right){a_2} + t\left( {t + 1} \right){a_3} + {B_2}}}{{4\left( {t + 1} \right)(1-t-{t^2})}} $

(7)

$ {p_3}^{\prime *} = \frac{{t{a_1} + t{a_2} + (2-2t-{t^2}){a_3} + {B_3}}}{{4(1-t - {t^2})}} $

(8)

其中, B₂=(t+1)(2-t-2t²)w, B₃=(2-3t²-2t³)w.

命题4  双渠道零售商电子渠道的均衡价格p′₁与双渠道零售商电子渠道市场规模在整个电子渠道市场规模中所占比例γ成正相关, 与电子渠道市场规模α成负相关.

证明  由式(6)及0 < t < $\frac{1}{2}$可知, $\begin{array}{l} \frac{{\partial {p_1}^{\prime *}}}{{\partial \gamma }} = \frac{{\partial {p_1}^{\prime *}}}{{\partial {a_1}}}\frac{{\partial {a_1}}}{{\partial \gamma }} + \frac{{\partial {p_1}^{\prime *}}}{{\partial {a_3}}}\frac{{\partial {a_3}}}{{\partial \gamma }} = \frac{t}{{4\left( {1 + t} \right)(1 - t - {t^2})}}\alpha {a_0} > 0, \\ \frac{{\partial {p_1}^{\prime *}}}{{\partial \alpha }} = \frac{{\partial {p_1}^{\prime *}}}{{\partial {a_1}}}\frac{{\partial {a_1}}}{{\partial \alpha }} + \frac{{\partial {p_1}^{\prime *}}}{{\partial {a_2}}}\frac{{\partial {a_2}}}{{\partial \alpha }} + \frac{{\partial {p_1}^{\prime *}}}{{\partial {a_3}}}\frac{{\partial {a_3}}}{{\partial \alpha }} = \frac{{{\rm{ }}(2{t^2} + t - 2){a_0}}}{{4\left( {t + 1} \right)(1 - t - {t^2})}} + \frac{{t\gamma {a_0}}}{{4\left( {t + 1} \right)(1 - t - {t^2})}} < \\ \frac{{2{t^2} + t - 2 + t}}{{4\left( {t + 1} \right)(1 - t - {t^2})}}{a_0} = - {\rm{ }}\frac{{{a_0}}}{{1 + t}} < 0 \end{array}$, 则命题4得证.

命题5  当$\gamma \ge \frac{t}{{2-t-2{t^2}}}$时, 双渠道零售商传统渠道的均衡价格p₂^′*随着电子渠道市场规模α的增大而上升；当$\gamma < \frac{t}{{2-t-2{t^2}}}$时, 双渠道零售商传统渠道的均衡价格p₂^′*随着电子渠道市场规模α的增大而下降.

证明  由式(7)得$\begin{array}{l} \frac{{\partial {p_2}^{\prime *}}}{{\partial \alpha }} = \frac{{\partial {p_2}^{\prime *}}}{{\partial {a_1}}}\frac{{\partial {a_1}}}{{\partial \alpha }} + \frac{{\partial {p_2}^{\prime *}}}{{\partial {a_2}}}\frac{{\partial {a_2}}}{{\partial \alpha }} + \frac{{\partial {p_2}^{\prime *}}}{{\partial {a_3}}}\frac{{\partial {a_3}}}{{\partial \alpha }}\\ = {\rm{ }}\frac{{(2-t-2{t^2})\gamma {a_0}}}{{4\left( {1 + t} \right)(1-t - {t^2})}} - \frac{{t{a_0}}}{{4\left( {1 + t} \right)(1 - t - {t^2})}}. \end{array}$.当$\gamma \ge \frac{t}{{2-t-2{t^2}}}$时, $\frac{{\partial {p_2}^{\prime *}}}{{\partial \alpha }} > 0$, 当$\gamma < \frac{t}{{2-t-2{t^2}}}$时, $\frac{{\partial {p_2}^{\prime *}}}{{\partial \alpha }} < 0 $, 则命题5得证.

命题6  纯网络零售商电子渠道的均衡价格p₃^*与电子渠道市场规模α成正相关, 与双渠道零售商电子渠道市场规模在整个电子渠道市场规模中所占比例γ成负相关.

证明  由式(8)得$\begin{array}{l} \frac{{\partial {p_3}^{\prime *}}}{{\partial \alpha }} = \frac{{\partial {p_3}^{\prime *}}}{{\partial {a_1}}}\frac{{\partial {a_1}}}{{\partial \alpha }} + \frac{{\partial {p_3}^{\prime *}}}{{\partial {a_2}}}\frac{{\partial {a_2}}}{{\partial \alpha }} + \frac{{\partial {p_3}^{\prime *}}}{{\partial {a_3}}}\frac{{\partial {a_3}}}{{\partial \alpha }} \\ = {\rm{ }}\frac{{({t^2} + 3t-2)\left( {\gamma-1} \right)}}{{4(1-t - {t^2})}}{a_0} > 0, \frac{{\partial {p_3}^{\prime *}}}{{\partial \gamma }} = \\ \frac{{\partial {p_3}^{\prime *}}}{{\partial {a_1}}}\frac{{\partial {a_1}}}{{\partial \gamma }} + \frac{{\partial {p_3}^{\prime *}}}{{\partial {a_3}}}\frac{{\partial {a_3}}}{{\partial \gamma }} = \frac{{{t^2} + 3t - 2}}{{4(1 - t - {t^2})}}\alpha {a_0} < 0 \end{array}$, 则命题6得证.

3 数值试验

取t=0.25, w=10, a₀=100, γ∈[0, 1], α∈[0, 1], 进行数值试验, 可得到γ、α对两零售商最优定价策略的影响.

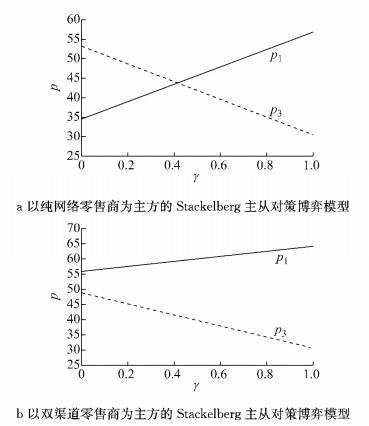
3.1 γ对定价策略的影响

γ对p₁和p₃的影响如图 2所示.在以纯网络零售商为主方和以双渠道零售商为主方的Stackelberg主从对策博弈模型中, 无论哪一方优先定价, 两零售商电子渠道的最优定价水平都随各自电子市场份额的增大而增大.

市场份额在某种程度上意味着消费者的肯定和偏好, 象征着渠道对消费者的吸引程度, 对消费者吸引力不足的渠道通常都以更低的价格经营, 吸引消费者购买.在电子商务发展的初期, 各电子商务公司纷纷通过价格战的方式来抢占市场, 如当当与亚马逊的图书销售, 京东与苏宁的价格大战.然而, 随着各电子商务公司电子渠道市场规模的逐渐扩大, 电子渠道市场不再依赖以较低的价格水平来换取销量、赢得利润, 而是逐渐将电子渠道市场的价格提高到一个更为合理的水平, 以期获得更加满意的利润.

3.2 α对定价策略的影响

如图 3a所示, 在以纯网络零售商为主方的Stackelberg主从对策博弈中, p₂随α的增大而减小, p₃随α的增大而增大, α的变动对p₁的影响与γ有关.当$\gamma < {\gamma _0}\left( {{\gamma _0} = \frac{{-{t^3}-3{t^2} + 2t}}{{3{t^3}-3{t^2} - 6t + 4}} = 0.195} \right) $时, p₁随α的增大而减小；当γ>γ₀时, p₁随α的增大而增大.

在经济学和博弈论中, Bulow等^[11]提出“战略互补”理论, 即当一个参与者采取激进的策略时, 另一个参与者也会采取激进的策略；相反, 当一个参与者采取保守的策略时, 另一个参与者也会采取保守的策略.Bulow等^[11]已证明, 在非合作博弈中, 各参与者之间的价格竞争遵从“战略互补”理论.因此, 在上述以纯网络零售商为主方的Stackelberg主从对策博弈中, 由于纯网络零售商作为领导者优先定价, 因此纯网络零售商必定会采取一个保守的定价策略—制定较高的电子渠道价格p₃, 同时双渠道零售商理应也会采取一个保守的定价策略—制定较高的电子渠道价格p₁.然而, 现实情况是, 随着电子渠道市场规模α的增大、传统零售商市场规模的缩小, 双渠道零售商作为跟随者, 为了最大化利润和扩大其电子渠道市场份额, 双渠道零售商只能采取降低p₁、p₂的定价策略.当双渠道零售商的电子渠道市场份额扩大到一定程度后, 双渠道零售商才会跟随纯网络零售商采取保守的定价策略, 逐渐提高价格p₁.这从理论上说明了苏宁要想在与处于强势地位的京东竞争中立于不败之地, 最优的定价策略是先制定电子渠道和传统渠道的全渠道低价策略, 等到抢占了一定的电子市场份额之后, 维持传统渠道的低价策略不变, 同时逐渐提高电子渠道的价格.

如图 3b 所示, 在以双渠道零售商为主方的Stackelberg主从对策博弈中, p₁随α的增大而减小, p₃随α的增大而增大, α的变动对p₂的影响与γ有关.当$\gamma < {\gamma _1}\left( {{\gamma _1} = \frac{t}{{2-t-2{t^2}}} = 0.31} \right) $时, p₂随α的增大而减小; 当γ>γ₁时, p₂随α的增大而增大.

在以双渠道零售商为主方的Stackelberg主从对策博弈中, 由于双渠道零售商作为领导者优先定价, 因此双渠道零售商可以完全预料到纯网络零售商的定价策略.双渠道零售商通过调节p₂的价格使电子渠道的价格p₁逐渐降低, 同时为了追求最优利润, 纯网络零售商理应会逐渐提高电子渠道价格p₃.然而, 现实情况是, 纯网络零售商并不会为了追求最优利润而提高电子渠道价格p₃, 相反, 为了争夺电子市场份额, 纯网络零售商会跟随双渠道零售商的定价策略, 即逐渐降低价格.因此, 京东和苏宁的价格战之所以能够发生的一个很重要的背景是, 京东并没有追求最优利润, 而是以牺牲利润的方式抢占电子市场份额, 从而采取了与苏宁相同的低价策略, 这也就能解释为什么京东在发展初期的前几个年度都是亏损.

4 结论

(1) 无论是纯网络零售商还是双渠道零售商先定价, 两零售商的电子渠道均衡价格都随各自电子渠道市场份额的增大而增大, 这是各电子商务公司在电子商务发展初期采取各种手段抢占电子渠道市场份额的原因.

(2) 当纯网络零售商拥有定价优先权时, 双渠道零售商可以先制定电子渠道和传统渠道的全渠道低价策略, 等到抢占了一定的电子渠道市场份额之后, 维持传统渠道的低价策略不变, 同时逐渐提高电子渠道的价格.当双渠道零售商拥有定价优先权时, 纯网络零售商有较大的倾向会跟随双渠道零售商采取低价策略, 因此极易发生价格战.