制动器的振动和噪声一直是学术界和工业界关注的热点[1].按照发生机理和频率,制动器的振动和噪声可以分为以下3类:①制动抖动,频率范围在100 Hz以下,是由制动力矩波动引起的强迫振动,可以通过改进设计、提高加工精度等方法抑制制动抖动[2];②制动尖叫,频率范围在1 000 Hz以上,产生的根本原因是由于制动部件模态匹配不当,采用结构修改、新的摩擦材料等能很好地控制制动抖动的产生[3];③制动颤振,频率范围在50~500 Hz,目前普遍认为其是由摩擦副动、静摩擦因数的差值引起的黏滑振动,常发生在较低的制动压力和较低的制动轮速下[4].随着自动挡汽车的加速普及和城市交通拥堵现象的日益加剧,制动颤振问题逐渐突出,用户投诉和抱怨日益激增.
目前,学术界总体上将制动颤振归结为由摩擦引起的自激振动问题,也将其理解为由动、静摩擦因数之差造成的黏滑振动现象[5].大量试验结果表明,制动器的安装刚度和阻尼[6]、悬架系统的振动传递率[7]、橡胶衬套的刚度[6]等均对制动颤振有影响.对制动颤振的研究方法主要有集中参数法、有限元法和多体动力学法.集中参数法可以反映黏滑振动的基本特征.Abdelhamid[5]最早提出了单自由度传动带模型,再现了黏滑振动极限环.在此基础上,Nakano等[8]研究了库伦摩擦条件下黏滑运动的发生机理,通过相图讨论了不同阻尼力的影响,最终建立了受2个量纲一参数控制的黏滑振动发生条件分界图,在简化模型的层面可以定量判定是否发生黏滑振动.然而,通过集中参数法所建立的模型十分简化,与试验现象差异较大.有限元法能很好地对实际摩擦副接触特性进行建模.Brecht等[9]最早建立了二维盘块有限元模型,研究了发生黏滑振动时接触压力的变化过程,同时还建立了三维制动器模型,再现了黏滑运动及其极限环特征.Tonazzi等[10]结合台架试验和有限元仿真,分析了不同相对速度和平均压力下,系统产生的不稳定黏滑运动、不稳定模态耦合以及稳定滑动等动力学现象.然而,目前有限元法大多采用简化的盘块模型,忽略了制动钳、转向节等关键部件,而且不太便于处理低频段刚体运动部件之间的柔性连接部件.制动颤振属于低频振动与噪声问题,多体动力学方法更具有优势.天合汽车集团最早利用Adams软件建立了包含后悬架总成的多体动力学模型[11],成功再现了黏滑振动现象,分析了黏滑振动的能量馈入与耗散特征.MSC公司与MTS公司合作建立了包含轮胎在内的前悬架底盘角总成刚柔耦合多体动力学模型,仿真结果可以反映发生制动颤振时系统的典型振动模式,与整车转鼓试验结果有较好的一致性[12].目前的多体动力学模型主要对制动器进行建模,而前期的研究结果表明,悬架系统既影响制动颤振的激励源,也影响传递路径特性,因此忽视悬架与制动器的关键结构特征和实际空间位置关系,势必严重影响制动颤振的仿真精度.
本文根据制动颤振发生的典型工况,设计并开展制动颤振整车试验,分析制动系统、悬架系统关键零部件的振动特征.针对包括制动器和悬架总成的底盘角系统[13],利用多体动力学方法建立汽车制动颤振的瞬态动力学模型,分析了制动颤振中关键零部件的复杂运动模式,并得到了试验验证.
1 整车道路试验与分析目前针对制动颤振开展的试验主要有简化振动摩擦台架试验、制动器惯性测功台架试验、整车转鼓试验和整车道路试验.由于整车道路试验能真实地反映零部件之间的相对运动关系,得到更为全面的振动特征,因此本文进行了整车道路试验.
1.1 试验方案本文的研究对象为配有5档自动变速器的某国产A级轿车,前后悬架均为麦弗逊式悬架,总质量在半载情况下为1 396.4 kg.试验过程中,在制动油管回路中布置了油压传感器,以测量制动油压信号; 在制动钳体、悬架减振器支柱靠近衬套点处布置了2个三向加速度传感器,以分析制动颤振的振动特性.制动钳振动加速度的X向、Y向和Z向分别是制动盘的法向、径向和切向.减振器支柱振动加速度的X向、Y向和Z向分别是整车的纵向、侧向和垂向.各传感器布置位置如图 1所示.

|
图 1 传感器布置 Fig.1 Sensor layout |
根据制动颤振发生的典型工况,要求驾驶员在将车辆开至试验场地后,低强度制动停车,挂P档后停车5 s以上,再挂D档缓慢释放刹车起步.试验中要求制动盘温度低于40 ℃,冷却液温度低于90 ℃.
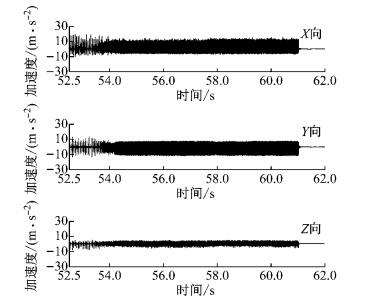
1.2 试验结果分析现有研究主要利用制动钳振动加速度评价制动颤振的发生及振动特征.试验中典型的制动钳测点振动加速度时程曲线如图 2所示.整体来看,整个过程共进行了17次制动,其中有7次制动过程中发生了明显的制动颤振.在所有制动颤振中,制动钳Z向(制动盘切向)均有较大的振动幅值,Y向(制动盘径向)次之,X向(制动盘法向)最小.

|
图 2 制动钳振动加速度时程曲线(试验) Fig.2 Vibration acceleration time history of caliper(test) |
图 3所示为图 2最后一次制动中制动钳振动加速度放大图.由图 3可知,制动颤振过程可分为以下2个阶段:52.5~54.0 s,制动钳振动幅值较大,类似于冲击效应,定义为制动颤振的A模式; >54.0~61.0 s,制动钳振动幅值较小,表现为连续且稳定的周期谐波振动,定义为制动颤振的B模式.

|
图 3 制动钳振动加速度时程曲线放大图 Fig.3 Detailed vibration acceleration time history of caliper |
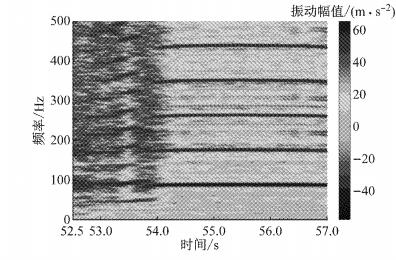
由于制动钳Z向振动最为明显,因此只对制动钳Z向振动加速度进行时频分析,如图 4所示.由图 4可知,制动颤振在时频图中也明显具有2种特性,并且时间分界点与图 3相同.在A模式中,振动频率较分散,均布于50~500 Hz范围内,具有典型的冲击特征.在B模式中,振动频率较为集中,呈现出典型的倍频特征,基频约为90 Hz,前5阶的频率成分比较突出.
|
图 4 制动钳Z向振动加速度时频图(试验) Fig.4 Time-frequency spectrum of vibration acceleration of caliper in Z direction(test) |
图 5所示为最后一次制动中悬架减振器支柱振动加速度时程曲线.由图 5可知,减振器支柱振动包含2种振动模式,其时间分界点与制动钳振动模式的分界点相同.由于减振器支柱的振动幅值小于制动钳,因此2种振动模式的幅值差与制动钳相比较小.另外,减振器支柱的X向振动幅值较大,Y向次之,Z向最小,与制动钳振动特征相似.可见,减振器支柱的振动主要是由制动钳传递的.
|
图 5 悬架减振器支柱振动加速度时程曲线 Fig.5 Vibration acceleration time history of strut |
由于减振器支柱振动加速度的X向与制动颤振的主方向一致,因此对其进行时频分析,如图 6所示.由图 6可知,减振器支柱X向振动加速度的时频特征可以分为2种模式,并且与制动钳振动加速度时频特征相似.A模式以冲击特征为主,频率分布比较均匀.B模式具有明显的倍频成份,基频为45 Hz,但振动能量较小.B模式2倍频成分与制动钳Z向振动加速度的基频相同.该结论与文献[14]中的研究结果比较一致,90 Hz的频率成分主要是由转向节的振动产生的.

|
图 6 减振器支柱X向振动加速度时频图(试验) Fig.6 Time-frequency spectrum of vibration acceleration of strut in X direction(test) |
通过以上分析可知,制动颤振包括了2种振动模式,一种以冲击特征为主,另一种以周期性谐波振动为主.这种典型的运动特征说明制动颤振不仅与制动系统有关,还与悬架等其他子系统有关.为了能够预测该现象,本文利用多体动力学方法,考虑制动器、悬架和传动系统的关键部件,建立制动颤振瞬态动力学模型.
2 底盘角刚柔耦合多体动力学建模 2.1 底盘角系统拓扑关系本文研究的底盘角系统包括制动系统、悬架系统和等效传动系统三部分.制动系统包括制动盘、摩擦衬片、制动背板、制动钳、导向销、活塞、轮毂、轴承以及转向节,所有零部件均视为刚体.在实际制动器结构中,轮毂与制动盘通过螺栓连接一起转动,摩擦衬片与制动背板黏结,保持架与转向节通过螺栓固结,因此模型中将轮毂与制动盘、制动背板和摩擦衬片(以下称为制动块)、转向节与保持架分别视为同一个刚体.悬架系统包括减振器支柱、套筒、控制臂、转向横拉杆等部件,其中控制臂和减振器支柱为柔性体.研究发现,传动系统也会影响制动颤振特性[15],但由于其结构复杂,进行实际建模既不经济也无必要,因此本文将传动系统关键部件和车身的惯量、刚度、阻尼等部件等效折算到制动盘轴线,近似模拟这些部件的动力学特性,其中传动系统的等效惯量包括发动机、变矩器、变速器、主减速器、半轴等惯量,车身则考虑了1/4车身惯量.
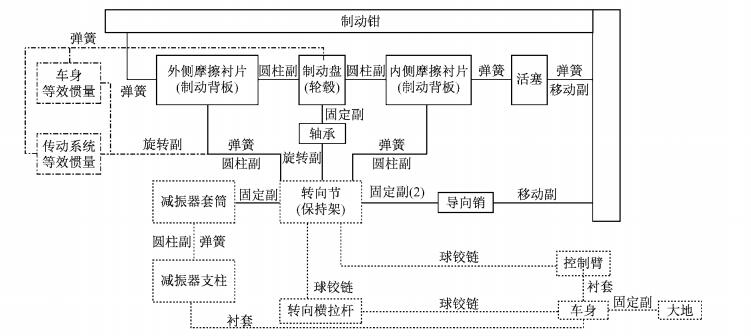
根据制动系统和悬架系统的结构特点和工作原理,建立了底盘角系统拓扑结构,如图 7所示.制动系统中,活塞与制动钳通过移动副进行约束,保证只存在沿相对运动方向上的平移自由度; 制动块与转向节(保持架)之间的约束关系为圆柱副,旋转中心为制动盘轴线,既可保证制动块绕制动盘轴线的旋转自由度,又可使制动块在制动压力下具有沿制动盘轴线的平移自由度; 内、外侧制动块通过弹簧分别与活塞和制动钳相连接; 轴承内圈与制动盘为固定约束,外圈与转向节为固定约束,内圈与外圈之间施加旋转副约束.悬架系统中,减振器支柱、控制臂前后点处通过固定副分别与相应的衬套连接,衬套与车身之间设置有衬套力,从而模拟真实衬套在相应结构中的作用; 减振器套筒与减振器支柱之间通过圆柱副约束,与转向节之间通过固定副约束; 转向横拉杆与转向节和车身间设置了球铰链约束.传动系统由设置在制动盘轴线的附加质量和惯量表示,车身惯量附加在质心位置上,它们与转向节之间采用旋转副约束.传动系统和车身与制动盘之间的刚度和阻尼分别采用一个扭转弹簧等效.
|
图 7 底盘角系统拓扑结构 Fig.7 Topology of chassis corner |
在本文的底盘角多体动力学模型中,盘块间的接触约束由法向力和切向力两部分组成.法向力由碰撞函数算法决定,如下所示:
| $ {F_{\rm{n}}} = K{\delta ^n} + C\frac{{{\rm{d}}\delta }}{{{\rm{d}}t}} $ | (1) |
式中:K为接触刚度; C为接触阻尼; n为刚度贡献指数; δ为全阻尼式穿透深度.切向力由库伦摩擦力算法决定,如下所示:
| $ {F_{\rm{f}}} = \mu {F_{\rm{n}}} $ | (2) |
式中:μ为摩擦系数.
为了能够再现制动颤振现象,摩擦系数可随相对速度变化,如下所示:
| $ \left\{ \begin{array}{l} \mu \left( {{v_{\rm{s}}}} \right) = {\mu _{\rm{s}}}\\ \mu \left( { - {v_{\rm{s}}}} \right) = {\mu _{\rm{s}}}\\ \mu \left( 0 \right) = 0\\ \mu \left( { - {v_{\rm{d}}}} \right) = {\mu _{\rm{d}}}\\ \mu \left( {{v_{\rm{d}}}} \right) = - {\mu _{\rm{d}}}\\ \mu \left( v \right) = - {\rm{sign}}\left( v \right){\mu _{\rm{d}}}, {\rm{ |}}v| > {v_{\rm{d}}}\\ \mu \left( v \right) = - {\rm{step}}\left( {|v|, {v_{\rm{d}}}, {v_{\rm{s}}}, {\mu _{\rm{d}}}, {\mu _{\rm{s}}}} \right){\rm{sign}}\left( v \right).\\ \begin{array}{*{20}{l}} {{v_{\rm{s}}} \le |v| \le {v_{\rm{d}}}}\\ \begin{array}{l} \mu \left( v \right) = {\rm{step}}(v, - {v_{\rm{s}}}, {\mu _{\rm{s}}}, {v_{\rm{s}}}, - {\mu _{\rm{s}}}), \\ - {v_{\rm{s}}} < v < {v_{\rm{s}}} \end{array} \end{array} \end{array} \right. $ | (3) |
式中:μs为静摩擦因数; μd为动摩擦因数; v为制动盘和制动块相对速度; vs为静摩擦因数滑动速度阈值; vd为动摩擦因数滑动速度阈值; step为阶跃响应函数; sign为符号函数.
摩擦系数根据制动盘块摩擦系数测试试验测得,测量装置如图 8所示,试验用车与整车道路试验相同.驾驶员缓慢踩下制动踏板并保持制动压力不变,在杠杆一端施加水平拉力对制动盘提供驱动力矩直至制动盘缓慢滑动,利用串联的拉压力传感器间接测量盘块间摩擦力的大小,结合同步测得的制动压力、活塞直径、等效摩擦半径等,重复试验20次,获得动、静摩擦因数平均值.接触刚度、接触阻尼、刚度贡献指数、穿透深度、滑动速度阈值等根据文献[16]设置,所得参数如表 1所示.

|
图 8 制动盘块摩擦系数测试试验 Fig.8 Friction coefficient test of disc and pad |
| 下载CSV 表 1 制动盘块模型接触参数 Tab.1 Parameters of disc and pad model |
本文将传动系统中驱动力矩和制动压力作为整个系统的输入,驱动力矩设置在传动系统和转向节之间的旋转副上,制动压力设置在制动钳与活塞之间,模拟真实情况下驱、制动力的施加.根据文献[17]的等效计算方法,将变速器和半轴输入输出轴的刚度和阻尼等效为传动系统的刚度和阻尼,车身的等效刚度和阻尼则是通过制动条件下K & C试验计算得到.传动系统的参数设置如表 2所示.
| 下载CSV 表 2 传动系统参数 Tab.2 Parameters of driveline system |
根据上述底盘角系统拓扑结构以及边界条件定义,建立了底盘角系统多体动力学模型,如图 9所示.

|
图 9 底盘角系统刚柔耦合多体动力学模型 Fig.9 Rigid-flexible coupling multi-body dynamics model of chassis corner |
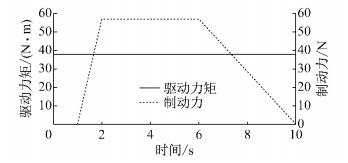
以整车道路试验中制动颤振典型工况为例,利用所建立的底盘角系统多体动力学模型进行计算.模型以驱动力矩和制动力为输入,具体参数设置如图 10所示.为了消除制动压力波动带来的影响,制动力输入模型简化了整车道路试验中油压传感器信号.驱动力矩则是考虑了发动机到驱动轴的传动比和液力变矩器特性等因素,选取涡轮转速为零时的驱动力矩值,模拟真实情况下自动挡汽车起步工况.根据整车道路试验中制动颤振时程,仿真时间设置为10 s.前期研究中发现制动颤振的振动频率可达1 000 Hz,为满足分析要求,仿真步长设置为0.000 1 s,仿真误差控制在10-5范围内,选用WSTIFF/I2型求解器计算.
|
图 10 驱动力矩、制动力输入设置 Fig.10 Input curves of drive torque and brake force |
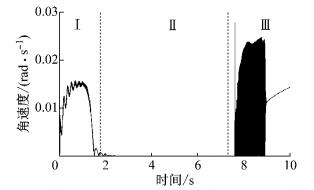
图 11为制动盘角速度随时间变化的仿真曲线.从图 11中可以看出,整个仿真过程分为以下3个阶段:
|
图 11 制动盘角速度时程曲线 Fig.11 Angular velocity time history of disc |
(1) 制动停车过程(第Ⅰ阶段).驱动力矩保持恒定,制动盘角速度从无到有后随着制动力矩的施加直至停车.
(2) 驻车制动过程(第Ⅱ阶段).驱动力矩小于制动力矩,制动盘转速为零.
(3) 制动颤振过程(第Ⅲ阶段).制动力矩略大于驱动力矩,制动盘块间产生黏滑振动现象,制动颤振现象产生.
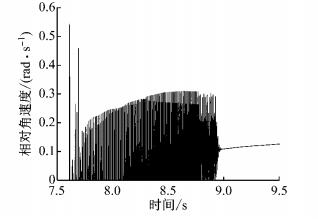
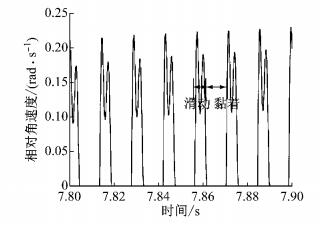
3.2 黏滑振动特征制动器的黏滑振动被认为是低速颤振的产生根源[18],该特征是制动颤振发生的重要评价标准.图 12所示为第Ⅲ阶段中制动盘块相对角速度时程曲线,可见相对角速度的幅值整体较小.为了清晰地观测到黏滑运动,将其局部放大,如图 13所示.当制动盘块间相对角速度为零时,两者处于黏着状态; 否则,两者处于滑动状态.这2种状态呈现周期性变化,表明出现了明显的黏滑振动特征.因此,第Ⅲ阶段发生了制动颤振现象.
|
图 12 制动盘块相对角速度时程曲线 Fig.12 Relative angular velocity time history of disc and pad |
|
图 13 7.80~7.90 s制动盘块相对角速度时程曲线 Fig.13 Relative angular velocity time history of disc and pad from 7.80 s to 7.90 s |
由图 12可知,制动颤振包括2种典型的振动模式.第1种模式发生在7.5~7.7 s阶段,振动幅值较大,持续时间较短,类似振动冲击效应,该运动模式与试验中发现的A模式一致.第2种模式发生在7.7~8.9 s阶段,振动幅值减小,但持续时间较长,类似于周期性谐波振动,与试验中发现的B模式相同.上述分析说明,所建立的多体动力学模型可再现试验中的制动颤振现象.
图 14为制动盘块相对角速度与制动盘角速度的相图.由图 14可知,相图中包含2种运动模式,分别与图 12中2种黏滑运动模式对应.A模式的相图表现为外侧较大的极限环,数量较为稀疏,说明这种运动模式持续时间短,进而进入B模式的极限环.B模式的相图表现为较密的极限环,并由2个环相扣而成,表明在该阶段存在2个稳定的振动频率.

|
图 14 制动盘角速度与制动盘块相对角速度相图 Fig.14 Phase diagram of disc's angular velocity and relative angular velocity of disc and pad |
制动钳和减振器支柱的振动加速度也可用于评价制动颤振现象,通过振动特性分析及仿真结果与试验特性的对比,可进一步验证模型的有效性.
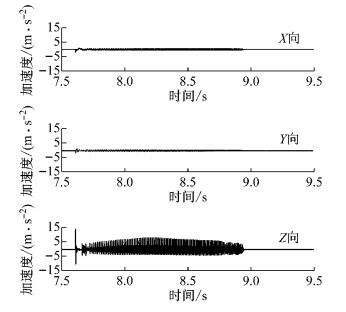
3.3.1 制动器振动特性制动钳振动特性是评价制动颤振的关键指标之一.图 15为制动钳振动加速度时程曲线.可以看出,制动钳3个方向均发生了显著振动,Z向(制动盘切向)振动幅值最大,Y向(制动盘径向)次之,X向(制动盘法向)最小.制动钳振动加速度在时域内可分为2个阶段:第1阶段从7.6 s至7.8 s,以振动冲击效应为主; 第2阶段从7.8 s至8.9 s,以周期性谐波振动为主.上述现象与整车道路试验观测到的现象是一致的.为此,第1阶段称为A模式,第2阶段称为B模式.
|
图 15 制动钳振动加速度时程曲线(仿真) Fig.15 Vibration acceleration time history of caliper(simulation) |
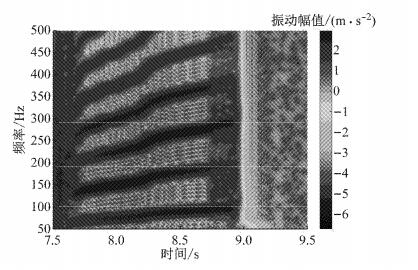
制动钳以Z向为主要振动,因此只对Z向振动特征进行分析,如图 16所示.由图 16可知,制动钳Z向振动加速度时频特性具有2种模式,时间分界点与图 15一致.A模式的频率成份较为均匀,频带较宽.B模式包含典型的倍频成份,基频范围为70~101 Hz,包含整车道路试验中90 Hz的基频.仿真中制动颤振的基频之所以变化,主要由于施加的驱动力矩与实际车辆有区别,导致仿真中制动盘的速度升高,加之摩擦系数的耦合作用,使系统的基频产生一定范围的变化.正是由于仿真与试验结果基频的差别,使得系统在500 Hz内出现了6阶主要频率,而整车道路试验中出现了前5阶的频率成份.
|
图 16 制动钳Z向振动加速度时频图(仿真) Fig.16 Time-frequency spectrum of vibration acceleration of caliper in Z direction(simulation) |
对所建立的底盘角系统进行固有特性分析,发现系统在滑动状态下第1阶固有频率为101.4 Hz,对应的振型为制动盘绕其轴线的扭转振动,如图 17所示.也就是说,当制动颤振的频率达到系统的固有频率时,两者会产生共振,打破了系统原有的黏滑振动模式,制动颤振随之消失.

|
图 17 滑动状态第1阶固有频率振型 Fig.17 First vibration mode in sliding state |
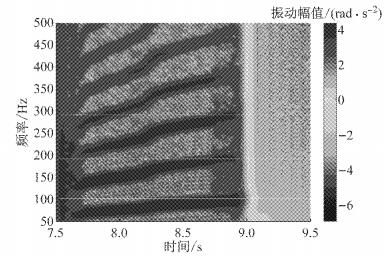
同理,本文分析了制动盘与制动块的振动特性,如图 18、19所示.制动盘与制动块的振动特性与制动钳相似,均包含A、B 2种振动模式.然而,制动盘的频率成份以第1、2阶为主,制动块的频率成份以第3、4阶为主,制动块的2个主要频率成份对应着图 14中存在的2个相扣的极限环.结合图 16可知,制动钳以前4阶频率成份为主,因此制动钳的振动特性是制动盘与制动块振动特性的综合体现.
|
图 18 制动盘角加速度时频图 Fig.18 Time-frequency spectrum of angular acceleration of disc |

|
图 19 制动块角加速度时频图 Fig.19 Time-frequency spectrum of angular acceleration of pad |
为了能够充分分析悬架系统的振动特性,选取减振器支柱、控制臂前点和后点的振动加速度进行分析, 如图 20所示.可以看出,减振器支柱和控制臂均发生了黏滑振动,其中减振器支柱的振动幅值最大,但其振动幅值仍小于制动钳的振动幅值.各点的三向振动加速度中,均是X向振动加速度幅值较大,Y向次之,Z向最小.同时,在振动过程中,包含A、B 2种振动模式,其特征与制动钳振动特性相同.上述仿真结果均与整车道路试验中观测到的现象一致.

|
图 20 悬架系统关键点振动加速度时程曲线 Fig.20 Vibration acceleration time history of key points of suspension system |
另外,对减振器支柱X向振动加速度进行时频分析,如图 21所示.可见,减振器支柱X向振动加速度时频特性与制动钳相似,包含了整车道路试验中减振器支柱的90 Hz及其倍频成份,但未出现试验中45 Hz的基频,其原因可能是由于模型中忽略了车轮及轮胎所致.

|
图 21 减振器支柱X向振动加速度时频图(仿真) Fig.21 Time-frequency spectrum of vibration acceleration of strut in X direction(simulation) |
综合制动器和悬架系统关键部件的三向振动特性可知,制动颤振传递路径包括:①制动盘→制动块→制动钳→保持架→转向节→减振器支柱→下摆臂,这是最主要的路径,表现为整车纵向振动; ②制动盘→制动块→制动钳→保持架→转向节→减振器支柱→横拉杆,这是次要路径,表现为整车侧向振动; ③制动盘→制动块→制动钳→保持架→转向节→减振器支柱→车身,这是最弱的路径,表现为整车垂向振动.这与试验中的主观感觉是一致的.在试验过程中,车辆沿纵向略有移动,发动机舱下面伴有剧烈振动,车身未有明显的垂向振动,但车内噪声明显.
4 结论(1) 开展了汽车制动颤振整车道路试验,发现制动颤振包含2种典型的振动模式,一种是幅值较大、持续时间较短的冲击振动,另一种是幅值较小、持续时间较长的周期性谐波振动.制动钳和悬架关键部件均以制动盘切向的振动特性为主.
(2) 基于多体动力学方法,考虑制动系统、悬架系统、等效传动系统的具体结构和空间位置以及制动器摩擦特性,以传动系统驱动力矩和制动压力为输入,提出了一种制动颤振瞬态动力学模型.与试验结果对比,发现该模型可再现制动颤振的主要特征,可用于制动颤振的预测与控制.
(3) 以制动盘与制动块间的黏滑运动和相图特性、制动器和悬架系统关键部件振动加速度为评价指标,分析了汽车制动颤振的瞬态动力学特性.结果表明, 制动器和悬架系统关键部件振动趋势和频率成份相似,制动钳的振动特性是制动盘与制动块振动特性的综合体现.最后, 得到了制动颤振的主要传递路径.
| [1] |
张立军, 郑一兵, 孟德建, 等. 汽车制动器摩擦颤振综述[J]. 同济大学学报(自然科学版), 2016, 44(3): 420 ZHANG Lijun, ZHENG Yibing, MENG Dejian, et al. Literature survey of friction induced automotive brake groan[J]. Journal of Tongji University (Natural Science), 2016, 44(3): 420 |
| [2] |
ABDELHAMID M K, BLASCHKE P, WANG A, et al. An overview of brake noise and vibration problems[C]//Proceeding of SPIE. Orlando: Society of Photo-Optical Instrumentation Engineers, 2001: 57-63.
|
| [3] |
LIU P, ZHENG H, CAI C, et al. Analysis of disc brake squeal using the complex eigenvalue method[J]. Applied Acoustics, 2007, 68(6): 603 DOI:10.1016/j.apacoust.2006.03.012 |
| [4] |
BRECHT J, SCHIFFNER K. Influence of friction law on brake creep-groan[C]// Brake Colloquium and Exhibition. New Orleans: SAE, 2001: 363-377.
|
| [5] |
ABDELHAMID M K. Creep groan of disc brakes[C]//SAE Noise and Vibration Conference and Exposition. Detroit: SAE, 1995: 82-87.
|
| [6] |
NEIS P D, BAETS P, OST W, et al. Investigation of the dynamic response in a dry friction process using a rotating stick-slip tester[J]. Wear, 2011, 271(9): 2640 |
| [7] |
DUNLAP K B, RIEHLE M A, LONGHOUSE R E. An investigative overview of automotive disc brake noise[R]. Detroit: SAE, 1999.
|
| [8] |
NAKANO K, MAEGAWA S. Safety-design criteria of sliding systems for preventing friction-induced vibration[J]. Journal of Sound & Vibration, 2009, 324(3/4/5): 539 |
| [9] |
BRECHT J, HOFFRICHTER W, FOHLE A. Mechanisms of brake creep groan[R]. Detroit: SAE, 1997.
|
| [10] |
TONAZZI D, FRANCESCO M, LAURENT B. Experimental and numerical analysis of frictional contact scenarios: from macro stick-slip to continuous sliding[J]. Meccanica, 2015, 50(3): 649 DOI:10.1007/s11012-014-0010-2 |
| [11] |
XU J J. Disc brake low frequency creep groan simulation using ADAMS[C]//Proceedings of the 2000 ADAMS International User Conference. Orlando: SAE, 2000: 2240-2259.
|
| [12] |
DONLEY M, RIESLAND D. Brake groan simulation for a McPherson strut type suspension[C]//SAE 2003 Noise & Vibration Conference and Exhibition. Traverse City: SAE, 2003: 1627-1636.
|
| [13] |
PURSCHER M, FISCHER P. Creep groan characterization via vehicle corner test[C]//SAE 2017 Brake Colloquium & Exhibition. Orlando: SAE, 2017: 2488-2501.
|
| [14] |
JOO K H, JEON H C, SUNG W, et al. Transfer path analysis of brake creep noise[C]//SAE 2013 Brake Colloquium & Exhibition, 31st Annual. Jacksonville: SAE, 2013: 2036-2050.
|
| [15] |
CROWTHER A R, YOON J, SINGH R. An explanation for brake groan based on coupled brake-driveline system analysis[C]//SAE 2007 Noise and Vibration Conference and Exhibition. St. Charles: SAE, 2007: 2260-2274.
|
| [16] |
MARÍN F, ALHAMA F, MORENO J A. Modelling of stick-slip behavior with different hypotheses[J]. International Journal of Engineering Science, 2012, 60: 13 DOI:10.1016/j.ijengsci.2012.06.002 |
| [17] |
CROWTHER A.R, SINGH R. Identification and quantification of stick-slip induced brake groan events using experimental and analytical investigations[J]. Noise Control Engineering Journal, 2008, 56(4): 235 DOI:10.3397/1.2955772 |
| [18] |
FUADI Z, MAEGAWA S, NAKANO K, et al. Map of low-frequency stick-slip of a creep groan[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2010, 224(12): 1235 DOI:10.1243/13506501JET834 |
 2018, Vol. 46
2018, Vol. 46

