2. 同济大学 海洋地质国家重点实验室, 上海 200092
2. State Key Laboratory of Marine Geology, Tongji University, Shanghai 200092, China
对于未爆弹(UXO)的磁异常正演, 现有研究中多使用磁偶极子场连续积分模拟有限长圆柱体, 或使用有限元方法中的立方体单元组合模拟.Zalevsky等[1]将被地球磁场磁化的UXO视作磁偶极子, 计算了3种不同高度的南北走向总磁异常梯度数据.Churchill等[2]使用COMSOL有限元分析软件计算了不同形态下UXO的磁异常, 并将求解结果与解析法椭球体模型计算结果进行了对比.Sinex[3]和Sanchez等[4]采用立方磁体单元构造了UXO和非未爆弹(non-UXO)铁构件磁异常数值分析模型.葛健等[5]使用三度体的圆柱体模型模拟航弹, 并对航弹的模量磁异常ΔT和垂直磁梯度异常进行了数值模拟和比较.郭志馗等[6]基于偶极线磁场, 在三维积分的基础上得到有限长圆柱体改进后的磁场.朱慧慧等[7]使用近似立方体单元重构地下铁质管线的几何结构, 结合磁偶极子构造法建立管道磁异常正演模型.
采用偶极线磁场模拟UXO磁异常, 计算快速简便, 但无法真实模拟未爆弹的多样化以及不规则形状, 并且适合半径远小于埋深情况下的近似; 同时考虑到未爆弹与管状物类似, 其磁性集中在外壳, 内充物质无磁性或弱磁性, 对于近地表的精细磁测, 该假设存在一定的模型误差和理论误差.使用有限元方法中的立方体单元在求解磁化率和剩余磁化强度各向异性的磁性体磁场时有优势.对于均匀磁化的磁性体, 可使用三角面元法只针对模型外形进行三角形面网格剖分计算, 从而减少立方体单元剖分法巨大的计算量.
计算效率在正演中非常重要, 迫切需要提高.虽然三角面元法相比其他正演方法有优势, 但是使用三角面元法对目标体整个表面进行剖分计算效率低, 而且三角面元法的计算量会随着网格剖分精度的增加而上升.三角面元法正演的速度很大程度上依赖于网格的剖分效率, 对于一个新的磁性体, 不需要重新剖分网格, 而是利用一个已剖分成三角网格的体积元, 在空间上插值从而构建磁性体.因此, 本文提出采用结合三角面元法和三次样条插值方法数值模拟UXO磁异常, 可以兼顾模型的精细剖分和快速计算.
1 基于三角面元法的磁异常正演方法 1.1 三角面元法正演原理与极化电介质交界面上存在面束缚电荷相似, 在磁化介质交界面上也存在面磁荷, 面磁荷密度
| $ {\sigma _{\rm{m}}} = {\mu _0}\left( {{\mathit{\boldsymbol{M}}_1} - {\mathit{\boldsymbol{M}}_2}} \right) \cdot \mathit{\boldsymbol{n}} $ | (1) |
式中:σm为磁化介质面磁荷密度; μ0为真空磁导率; M1为磁介质1的磁化强度; M2为磁介质2的磁化强度; n为界面法线方向的单位矢量, 方向从磁介质1指向磁介质2.式(1)表示磁化介质交界面上的面磁荷密度等于2种磁介质磁化强度的法向分量之差.已知磁化介质体磁荷密度ρm, 可以用直接积分法求得磁化介质的磁标势, 如下所示:
| $ {U_{\rm{m}}} = \frac{1}{{4{\rm{ \mathsf{ π} }}{\mu _0}}}\int_\mathit{\boldsymbol{V}} {\frac{{{\rho _{\rm{m}}}{\rm{d}}\mathit{\boldsymbol{V}}}}{\mathit{\boldsymbol{r}}}} + \frac{1}{{4{\rm{ \mathsf{ π} }}{\mu _0}}}\int_\mathit{\boldsymbol{S}} {\frac{{{\sigma _{\rm{m}}}{\rm{d}}\mathit{\boldsymbol{S}}}}{\mathit{\boldsymbol{r}}}} $ | (2) |
式中:Um为磁化介质的磁标势; r为计算点到磁荷的距离; ρm为磁化介质体磁荷密度, ρm=-μ0∇· M; dV为磁化介质的体积微元; dS为磁化介质的面积微元.如果磁介质磁化是分区均匀的, 因为在每种磁介质中M为常矢量, 这时式(2)中就只有面磁荷密度分布对磁标势的贡献.
根据位场关系式, 可得磁场T的面磁荷积分形式为
| $ \mathit{\boldsymbol{T}} = - {\mu _0}\frac{{\partial {U_{\rm{m}}}}}{{\partial \mathit{\boldsymbol{t}}}} = \frac{{{\mu _0}}}{{4{\rm{ \mathsf{ π} }}}}\int_\mathit{\boldsymbol{S}} {{\sigma _{\rm{m}}}\frac{{\mathit{\boldsymbol{t}} \cdot \mathit{\boldsymbol{r}}}}{{{\mathit{\boldsymbol{r}}^3}}}{\rm{d}}\mathit{\boldsymbol{S}}} $ | (3) |
式中:t是空间单位矢量.
将Um分别对x、y、z求导即可求得磁场水平x方向分量Hax, 水平y方向分量Hay和垂直方向分量Za的积分式, 如下所示:
| $ \begin{array}{l} {H_{{\rm{a}}x}} = \frac{{{\mu _0}}}{{4{\rm{ \mathsf{ π} }}}}\int_\mathit{\boldsymbol{S}} {\frac{{{\mathit{\boldsymbol{M}}_{\rm{n}}}\cos \left( {\mathit{\boldsymbol{r}},x} \right)}}{{{\mathit{\boldsymbol{r}}^2}}}{\rm{d}}\mathit{\boldsymbol{S}}} = \frac{{{\mu _0}}}{{4{\rm{ \mathsf{ π} }}}}\int_\mathit{\boldsymbol{S}} {\frac{{{\mathit{\boldsymbol{M}}_{\rm{n}}}\left( {x - \xi } \right)}}{{{\mathit{\boldsymbol{r}}^3}}}{\rm{d}}\mathit{\boldsymbol{S}}} \\ {H_{{\rm{a}}y}} = \frac{{{\mu _0}}}{{4{\rm{ \mathsf{ π} }}}}\int_\mathit{\boldsymbol{S}} {\frac{{{\mathit{\boldsymbol{M}}_{\rm{n}}}\cos \left( {\mathit{\boldsymbol{r}},y} \right)}}{{{\mathit{\boldsymbol{r}}^2}}}{\rm{d}}\mathit{\boldsymbol{S}}} = \frac{{{\mu _0}}}{{4{\rm{ \mathsf{ π} }}}}\int_\mathit{\boldsymbol{S}} {\frac{{{\mathit{\boldsymbol{M}}_{\rm{n}}}\left( {y - \eta } \right)}}{{{\mathit{\boldsymbol{r}}^3}}}{\rm{d}}\mathit{\boldsymbol{S}}} \\ {Z_{\rm{a}}} = \frac{{{\mu _0}}}{{4{\rm{ \mathsf{ π} }}}}\int_\mathit{\boldsymbol{S}} {\frac{{{\mathit{\boldsymbol{M}}_{\rm{n}}}\cos \left( {\mathit{\boldsymbol{r}},z} \right)}}{{{\mathit{\boldsymbol{r}}^2}}}{\rm{d}}\mathit{\boldsymbol{S}}} = \frac{{{\mu _0}}}{{4{\rm{ \mathsf{ π} }}}}\int_\mathit{\boldsymbol{S}} {\frac{{{\mathit{\boldsymbol{M}}_{\rm{n}}}\left( {z - \zeta } \right)}}{{{\mathit{\boldsymbol{r}}^3}}}{\rm{d}}\mathit{\boldsymbol{S}}} \end{array} $ | (4) |
式中:Mn为界面法线方向的磁化强度.最后, 根据地磁场总强度的模量差ΔT与Hax、Hay、Za之间的基本关系式计算ΔT, 如下所示:
| $ \Delta T = {H_{{\rm{a}}x}}\cos I\cos D + {H_{{\rm{a}}y}}\cos I\sin D + {Z_{\rm{a}}}\sin I $ | (5) |
式中:I是地磁倾角; D是地磁偏角.
从面磁荷积分表达式出发, 对任意形状三度体表面进行三角面元剖分.对剖分后每个三角面元, 根据三角形的3个顶点求得每个三角形磁荷面上的法向量n, 得到面磁荷密度σ= M·n, 然后通过积分运算, 可求得每个三角形磁荷面的磁位、磁场表达式(具体推导过程见文献[8-9]), 累加起来就可以得到磁性体的磁场表达式.由于磁性体表面是连续变化的, 观测点越密集, 划分重建后的模型越精确.
1.2 以球体模型为基础的正演实验球体模型是最基本的、具代表性的有限大小的地质体模型, 均匀磁化球体的外部磁场与位于球心的偶极子磁场等效, 因而球体磁场表达式有解析公式.对球体模型进行三角剖分, 计算其产生的磁异常, 对比解析解以验证三角面元法的可行性, 并对不同剖分形式下的三角面元计算结果进行分析对比.
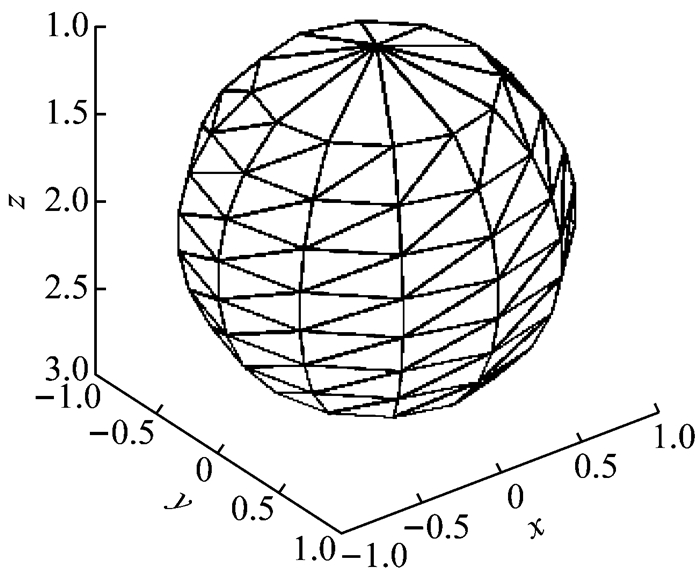
1.2.1 球体模型的剖分方法按三角面元法将球体全表面进行三角剖分, 沿垂直方向切割成若干等厚薄片, 在每层薄片上用若干个三角形来拟合薄片表面, 如图 1所示.用若干个间距相等的平行于xOy面的平面截取球体, 设截取的薄片个数为N, 在每个薄片与球体相交的圆周上等弧长间隔设立P个节点(要形成首尾相接的闭合曲面, 实际计算中需要P+1个点).对于第1个薄片, 球体上顶点与第1个薄片上各节点的连线形成P个等腰三角形, 对于球体的底层薄片同理.中间各薄片之间则能组成2P(N-3)个三角形, 如设第i层(i=2, 3, …, N-1)的第j个节点(j=1, 2, …, P)Dij点为起点, 斜线DijDi+1, j+1在四边形
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{D_{ij}}}\\ {{D_{i + 1,j}}}\\ {{D_{i + 1,j + 1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_{ij}}}&{{y_{ij}}}&{{z_{ij}}}\\ {{x_{i + 1,j}}}&{{y_{i + 1,j}}}&{{z_{i + 1,j}}}\\ {{x_{i + 1,j + 1}}}&{{y_{i + 1,j + 1}}}&{{z_{i + 1,j + 1}}} \end{array}} \right]\\ \left[ {\begin{array}{*{20}{c}} {{D_{ij}}}\\ {{D_{i + 1,j + 1}}}\\ {{D_{i,j + 1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_{ij}}}&{{y_{ij}}}&{{z_{ij}}}\\ {{x_{i + 1,j + 1}}}&{{y_{i + 1,j + 1}}}&{{z_{i + 1,j + 1}}}\\ {{x_{i,j + 1}}}&{{y_{i,j + 1}}}&{{z_{i,j + 1}}} \end{array}} \right] \end{array} $ | (6) |
|
图 1 球体三角面元剖分示意图 Fig.1 Schematic diagram of sphere division in triangular surface element |
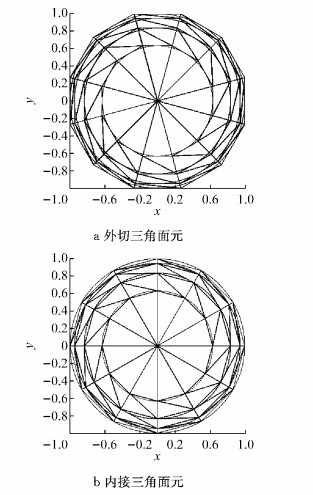
在对每层薄片的表面进行拟合时, 不同三角形剖分方式对球体表面的拟合程度不一样, 进而计算出的球体磁异常的精度也不同.根据在每个薄片与球体相交的圆周上设立的P个节点组成的多边形是圆外切多边形还是内接多边形, 可将三角面元分为外切面元和内接面元.图 2a 为一个球体被切割成9个薄片, 在每个薄片与球体相交的圆周上设立的12个节点形成的外切三角面元在xOy面上的投影, 图 2b则为球体内接面元在xOy面上的投影.
|
图 2 球体三角面元剖分投影示意图 Fig.2 Projection schematic diagram of sphere division in triangular surface element |
设球体模型的铅垂线与z轴重合, z轴向下为正方向.球体的上顶点埋深为h, 球体半径为R.球体模型的上顶点坐标为(0, 0, h), 下顶点坐标为(0, 0, h+2R).对于外切三角面元的剖分方式, 中间每一层各个节点的坐标可以表示为
| $ \begin{array}{*{20}{c}} {{x_{ij}} = \sqrt {{R^2} - {{\left( {\left( {i - 1} \right)\Delta d} \right)}^2}} \cos \left( {\left( {j - 1} \right)\Delta \theta } \right)}\\ {{y_{ij}} = \sqrt {{R^2} - {{\left( {\left( {i - 1} \right)\Delta d} \right)}^2}} \sin \left( {\left( {j - 1} \right)\Delta \theta } \right)}\\ {{z_{ij}} = h + \left( {i - 1} \right)\Delta d} \end{array} $ | (7) |
对于内接三角面元的剖分方式, 中间每一层各个节点的坐标可以表示为
| $ \begin{array}{*{20}{c}} {{x_{ij}} = \frac{{\sqrt {{R^2} - {{\left( {\left( {i - 1} \right)\Delta d} \right)}^2}} }}{{\cos \left( {2{\rm{ \mathsf{ π} }}/2P} \right)}}\cos \left( {{\rm{ \mathsf{ π} }}/P + \left( {j - 1} \right)\Delta \theta } \right)}\\ {{y_{ij}} = \frac{{\sqrt {{R^2} - {{\left( {\left( {i - 1} \right)\Delta d} \right)}^2}} }}{{\cos \left( {2{\rm{ \mathsf{ π} }}/2P} \right)}}\sin \left( {{\rm{ \mathsf{ π} }}/P + \left( {j - 1} \right)\Delta \theta } \right)}\\ {{z_{ij}} = h + \left( {i - 1} \right)\Delta d} \end{array} $ | (8) |
其中, i=2, …, N+1, j=1, …, P+1, Δθ=2π/P, Δd=2R/N.
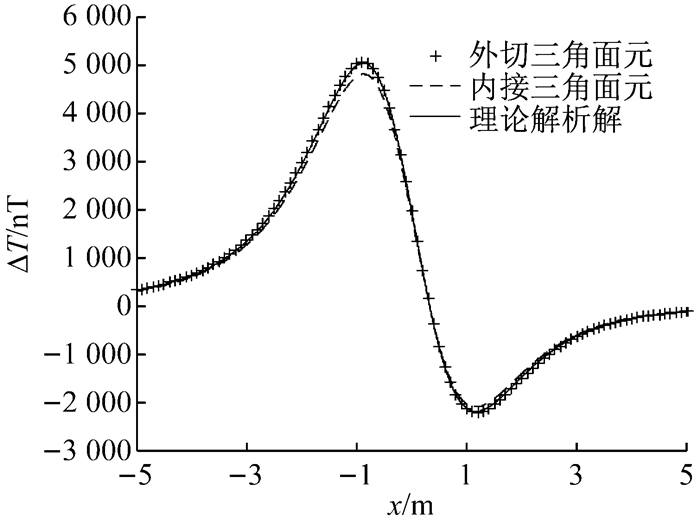
1.2.2 球体模型的正演结果通过球体模型对三角面元法进行验证.仅考虑磁性体的感应磁化强度, 并且在均匀磁化的情况下, 设地磁场强度为49 600 nT, 磁倾角为44.5°, 磁偏角为-2.5°, 磁化率为2.设球体半径为1 m, 中心点埋深为2 m, 中心位于坐标原点处.图 3所示为N=24、P=12情况下, 球体模型产生的ΔT磁异常剖面曲线.从图 3可见, 使用外切三角面元计算得到的球体磁异常曲线比使用内接三角面元计算得到的球体磁异常曲线更接近理论磁异常曲线, 与理论曲线重合.外切和内接三角面元正演得到球体磁异常的均方根误差(RMSE)分别为0.22和0.83, 这表明不同节点位置构建的外切或内接多面体模型, 会对目标磁性体磁异常正演产生一定影响.同样网格剖分下, 外切和内接三角面元对物体表面的逼近速度不同, 对球体模型而言, 外切三角面元的逼近速度更快.同时, 进一步细化剖分网格, 可以进一步提高正演精度.
|
图 3 不同方法球体磁异常剖面曲线对比 Fig.3 Comparison of section curves of spherical magnetic anomaly among different methods |
UXO大体上可以分为4类:集束弹药、普通陆战武器弹药、航空炸弹、地雷[10].UXO外壳多为铁磁性物质, 磁性参数与周围环境的差别较大, 在一定条件下能够被磁法勘探仪器所识别.然而, UXO外形差别较大.航空炸弹一般体形较大, 长度较长, 外形与圆柱体比较接近, 因此可使用均匀有限长的三度体圆柱体模拟航空炸弹; 其他几类弹药体形较小, 体长较短, 长度和埋深的比值很小, 理论和实践已经证明这几类弹药产生的磁场近似于球体所产生的磁场.常见的航空炸弹的外形往往不是标准的有限长圆柱体, 而是变径有限长圆柱体, 即沿长轴方向半径不同, 用单一有限长圆柱体的模型无法很好地近似, 但可以用不同半径的圆柱体元进行组合.
2.1 有限长圆柱体模型的剖分方法与球体的剖分方式类似, 沿圆柱体长轴方向切割成N个等厚薄片, 在每个薄片与柱体相交的圆周上等弧长地设立P个节点, 在每层薄片上用P个三角形来拟合薄片表面, 如图 4所示.对于圆柱体的顶/底面, 顶/底面圆心与第一层各节点的连线共形成P个等腰三角形, 而对于沿圆柱体长轴切割出的N个薄片, 则能组成2P(N-1)个三角面元.同样, 在对每层薄片的表面进行拟合时, 也可根据在每个薄片与柱体相交的圆周上设立P个节点组成的多边形是圆外切多边形还是内接多边形, 将三角面元分为外切面元和内接面元.

|
图 4 圆柱体三角面元剖分示意图 Fig.4 Schematic diagram of cylinder division in triangular surface element |
除此之外, 如果圆柱体各个薄片上的对应节点Dij和Di+1, j(i=1, 2, …, N, j=1, 2, …, P)位于同一条轴线上, 那么按照斜线DijDi+1, j+1分割出的三角形则为直角三角形(见图 4a).如果圆柱体各个薄片按照奇偶层交错选取节点, 则可形成等腰三角形(见图 4b).
2.2 全空间任意姿态有限长圆柱体磁异常计算方法利用三角面元法计算有限长圆柱体磁场的优势在于, 不通过旋转坐标系, 即不改变观测点坐标, 即可快速计算出有限长圆柱体在空间任意姿态(任意水平和垂直位置、任意走向、任意倾角)下的磁场, 减少了计算量, 并能保证快速稳定计算.
假设起始位置处走向0°为x轴正方向(x轴正方向为磁北, 向西为负, 向东为正), 倾角从水平投影面起算为0°(向下为正), 中心点空间位置为(0, 0, 0), 在目标位置处设走向角度为β, 倾角为α, 中心点空间位置为(x1, y1, z1).对圆柱体表面剖分出的任意一个节点Dij的三维坐标(xij, yij, zij)进行投影, 先投影到倾角方向, 再投影到走向方向, 最后平移到目标位置, 投影运算实际上是投影矩阵与坐标相乘.走向方向和倾角方向的投影矩阵分别为Tβ和Tα, 如下所示:
| $ \begin{array}{l} {\mathit{\boldsymbol{T}}_\beta } = \left[ {\begin{array}{*{20}{c}} {\cos \beta }&{ - \sin \beta }&0\\ {\sin \beta }&{\cos \beta }&0\\ 0&0&1 \end{array}} \right]\\ {\mathit{\boldsymbol{T}}_\alpha } = \left[ {\begin{array}{*{20}{c}} {\cos \alpha }&0&{\sin \alpha }\\ 0&1&0\\ {\sin \alpha }&0&{\cos \alpha } \end{array}} \right] \end{array} $ | (9) |
最终可以得到目标位置处节点Dij的坐标为
| $ \begin{array}{l} {\left( {{{x'}_{ij}},{{y'}_{ij}},{{z'}_{ij}}} \right)^{\rm{T}}} = \\ {\mathit{\boldsymbol{T}}_\beta } \times {\mathit{\boldsymbol{T}}_\alpha } \times {\left( {{x_{ij}},{y_{ij}},{z_{ij}}} \right)^{\rm{T}}} + {\left( {{x_1},{y_1},{z_1}} \right)^{\rm{T}}} \end{array} $ | (10) |
计算出每个节点的坐标后,按照一定顺序输出三角形的3个角点坐标,各个角点的输出顺序应统一为顺时针方向,计算三角面元的平面法向量时遵循右手螺旋法则.对每个三角面元产生的磁异常进行计算,将所有三角面元产生的磁异常在每一个观测点处累加,即可得到该观测点处目标体产生的磁异常
2.3 有限长圆柱体模型的正演结果设磁场参数同1.2.2节, 仅考虑磁性体的感应磁化强度且均匀磁化, 模型体各项物理参数相同, 即磁化率均为2, 半径均为0.1m, 长度均为2 m.图 5是N=20、P=36下, 采用等腰内接三角面元的计算结果.图 5a和5b是中心点平面坐标位于(1, 1)、中心点埋深1 m的有限长圆柱体在不同走向β和倾角α下的形态, 图 5c和5d是2种形态下对应的磁异常.

|
图 5 不同走向和倾角下有限长圆柱体的形态及其产生的磁场 Fig.5 Shape of finite-length cylinder in different strikes and dip angles and the corresponding magnetic field |
从图 5可以看出, 磁异常平面图中磁异常的形态与位置以及大小反映了模型体的空间位置, 比较容易标定和识别, 进而可以大致确定出UXO的走向和倾向.这一点对于在实际探测中根据探测到的磁异常形态对UXO进行空间定位有重要的理论意义.
对于中心点坐标(0, 0, 2)m的垂直有限长圆柱体, 使用3种剖分方法得到的三角面元分别计算出磁异常剖面曲线, 对比目前研究中使用偶极线磁场模拟得到的圆柱体磁异常曲线, 如图 6所示.其中, 对于三角面元法, N=20, P=36.

|
图 6 不同方法垂直有限长圆柱体磁异常剖面曲线对比 Fig.6 Comparison of section curves of vertical finite-length cylindrical magnetic anomaly among different methods |
理论上三角面元的面积和应尽可能接近圆柱体的表面积, 则计算出的圆柱体磁异常可以无限逼近真实磁异常.若以圆柱体表面积(此例中为13 194.69 cm2)和三角面元面积和之间的差值作为评判标准, 则在相同的层数和节点数目下3种剖分方式面积和如表 1所示.
| 下载CSV 表 1 圆柱体三角面元面积和与实际面积差 Tab.1 Difference between the calculated area using triangular surface element and the actual area of the cylinder |
从图 6和表 1可以看出, 在内接情况下等腰和直角三角面元对磁异常正演结果的影响较小, 但相比于等腰内接三角面元等腰外切三角面元对磁异常正演结果的影响则较大.理论上外切三角面元计算得到的圆柱体磁异常比真实值大, 而内接三角面元计算出的圆柱体磁异常比真实值小, 但从图 6可见, 采用偶极线计算得到的磁异常误差比外切三角面元计算的磁异常更大, 且该误差无法修正改进.对圆柱体模型而言, 内接三角面元的逼近速度更快, 等腰内接三角元计算出的磁异常最接近真实值.
值得注意的是, 现有的UXO磁异常计算[5-6]认为UXO内部铁磁性物质是均匀分布的, 但实际未爆物的磁性主要来源于UXO铁磁性外壳, 外壳以内爆炸物往往是弱磁性或无磁性.因此, 要进一步提高正演精度, 则必须考虑这种内部“中空”磁性结构, 只有基于表面积分法的三角面元法能够有效解决该问题.将未爆物产生的磁异常与管状磁性物产生的磁异常近似, 与相同空间位置上不同半径有限长圆柱体在观测点处产生的磁场相减, 来近似计算均匀磁化中空UXO产生的磁异常.
3 基于三次样条的UXO磁异常快速正演方法虽然使用三角面元法计算均匀磁化磁性体磁异常精度高, 但是计算不同尺寸的目标体时需要对目标体表面重复进行网格剖分.随着三角网格的细化, 计算量会提高, 导致计算效率下降.因此, 引入三次样条插值方法, 对不同长度的模型, 不需要重新剖分网格, 而是利用一个已剖分成三角网格的体积元在空间上插值构建磁性体, 进而实现UXO的磁异常快速正演.UXO模型近似为有限长圆柱体或变径有限长柱体.
正演思想可以分为以下几个步骤:
步骤1 将UXO模型磁性体沿长轴方向均匀切割为几个块体, 每个块体形态和尺寸相同或相似(不同块体可以通过通过同一块体半径变化获得).对其中一块进行上述三角面元剖分, 但对切割面不进行剖分, 因为切割面不属于目标体整体的表面.对边界块体上的端面要单独进行剖分, 并不计入以下步骤的计算.
步骤2 对每一个观测点计算出小块体在UXO腔体内任意几处以及边界位置上的磁异常.
步骤3 选取步骤2中几处位置上的磁异常值作为插值节点,以块体的切割间距进行插值.
步骤4 在每一个观测点处, 累加插值得到各个磁异常值, 并补充边界块体上的端面产生的磁异常.
3.1 三次样条插值方法基本原理Lagrange插值、Newton插值及Hermite插值等高次插值中会出现龙格(Runge)现象.分段插值虽然可以避免龙格现象, 但是分段线性插值在节点处不光滑。分段Hermite插值仅仅要求插值函数在节点上等于被插函数的一阶导数, 并且导数值往往并不已知.三次样条插值先由函数值确定导数值, 再由分段Hermite插值解决问题, 因而避免了龙格现象, 并且插值曲线光滑.
三次样条函数的定义如下所示[11]:
设对任意区间[a, b]有剖分Δ:a=l0 < l1 < … < ln=b, 如果函数S(l)满足下述条件:
(1) S(l)∈C2[a, b], 即具有连续的一阶、二阶导数, Sk, v(lk)=Sk-1, v(lk), v=0, 1, 2, k=0, 1, …, n-1.
(2) S(l)在每一个小区间[lk, lk+1]上是次数≤3的多项式, 则称S(l)为关于剖分Δ的一个三次样条函数.
(3) 设给定函数表(lq, f(lq)), q=0, 1, …, n, 若三次样条函数S(l)还满足以下插值条件:
| $ S\left( {{l_q}} \right) = f\left( {{l_q}} \right),\;\;\;q = 0,1, \cdots ,n $ |
则称S(l)为f(l)关于剖分Δ的三次样条插值函数.求取三次样条插值函数表达式, 首先以分段三次Hermite插值为基础, 满足上述条件的情况下, 从下述3种边界条件中的一种推导而来:
(1) 第一种边界条件.S′(l0)、S′(ln)已知, 即S′(l0)=f′(l0), S′(ln)=f′(ln).
(2) 第二种边界条件.S″(l0)、S″(ln)已知, 即S″(l0)=f″(l0), S″(ln)=f″(ln), 若S″(l0)=S″(ln)=0, 则称为自然边界条件.
(3) 第三种边界条件(周期边界条件).f(l)为周期函数(此时有f(l0)=f(ln)), 要求S(l)亦是周期函数, 周期为(b-a), 即取Sν(l0+)=Sν(ln-), v=0, 1, 2, 称S(l)为周期样条函数, 此时不用给出边界值.
(4) 非扭结边界.使两端点处多项式三次项系数与这两端点的邻近点的三次项系数相等, 此时不用给出边界值.
3.2 不同模型的正演结果对于半径R=0.1 m、长度L=2 m、埋深h=1m、中心点平面坐标为(0, 0) m的水平有限长圆柱体, 将其沿走向均匀切割成N=40块, 每一块都是长L/N的小圆柱体, 将每一块的中心点横坐标位置作为插值点,在空间上对应有N个插值点c1, …, cN.对每一块体进行截面节点P=12的等腰内接三角面元剖分, 在圆柱体上的对称位置任意选择n=5个型值点E1, …, E5, 对每个测点用三角面元法计算出单个块体在5个型值点处的磁场值f(Ek)(k=1, …, n)作为插值点.
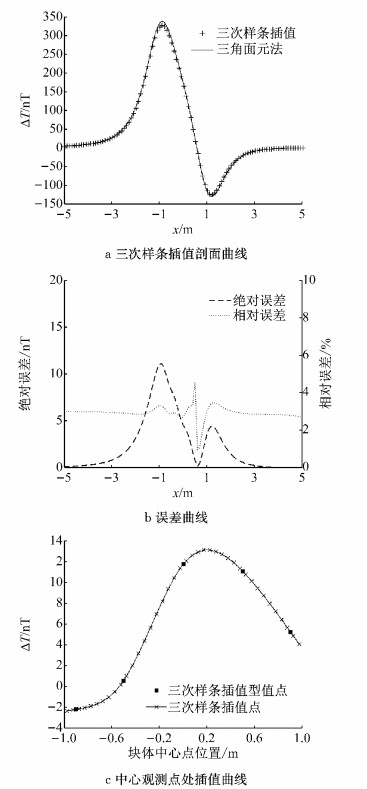
在每一个观测点上, 使用自然边界条件下的三次样条函数, 插值出块体在N个插值点处的磁场值S(ci)(i=1, …, N), 对得到的结果进行叠加, 即得到有限长圆柱体的磁场.图 7a展示了使用插值和不使用插值计算出的水平圆柱体磁异常剖面曲线对比, 图 7b展示了两者的绝对误差和相对误差分布.绝对误差分布与磁异常曲线相似, 最大值位于端点附近为11nT, 相对误差平均值约2.9%.图 7c展示了地面中心观测点处, 根据5个型值点-0.9、-0.5、0、0.5、0.9 m插值得到的磁场值, 可见插值曲线非常光滑.将40个插值点的磁场值累加, 即得到中心观测点处水平圆柱体整体的磁场值.
|
图 7 水平圆柱体磁异常三次样条插值结果 Fig.7 Results of horizontal cylindrical magnetic anomaly calculated with spline interpolation |
对于实际中许多外形更为复杂的UXO, 可以将其近似为变径有限长圆柱体模型, 即将其沿长轴均匀切割为N个长为L/N的圆柱体小块体, 每一个块体有不同的半径Ri, i=1, …, N.图 8展示了一种倾斜放置的N=40、P=12三角网构造的纺锤形UXO模型, 长度L=2 m, 中心点坐标为(0, 0, 1) m, 倾角为30°, 半径最大值为0.2 m, 半径沿长轴(x轴)方向规律变化, Ri=-xi2/8+0.2, i=1, …, N.

|
图 8 三角面元构造的变径纺锤形UXO模型 Fig.8 Fusiform UXO model with variable diameters made by triangular surface element |
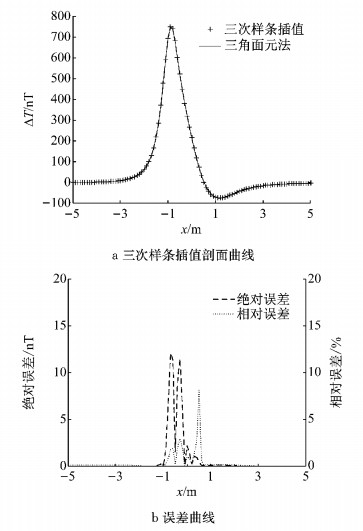
对于变径有限长圆柱体, 逐段计算每个圆柱体元产生的磁异常后叠加,计算量较大,可以用上述原理进行快速正演.插值计算过程同上述, 对于在变径有限长柱体上的对称位置任意选择n=5个型值点(-0.9、-0.5、0、0.5、0.9m), 对每个测点计算出单个块体在n个型值点处的磁场值作为插值点.在每一个观测点上, 使用自然边界条件下的三次样条函数, 插值出块体在N个插值点处的磁场值, 对得到的结果进行叠加, 即得到变径有限长圆柱体的磁场值.图 9a展示了使用插值和不使用插值计算出的变径有限长圆柱体模型磁异常曲线对比.图 9b展示了两者的绝对误差和相对误差分布, 绝对误差最大值位于端点附近, 为12 nT, 平均值为0.7 nT, 相对误差平均值为0.35%, 最大值为8%.
|
图 9 变径有限长圆柱体磁异常三次样条插值结果 Fig.9 Results of variable diameter cylindrical magnetic anomaly calculated with spline interpolation |
本文针对工程探测中遇到的地下多姿态和形态各异的均匀磁化UXO的磁正演问题, 基于面磁荷积分原理, 采用三角面元法的和三次样条插值方法, 实现了高精度快速正演模拟, 并进行了相关问题的分析.
本文提出的正演计算方法, 有较好的计算速度和正演精度, 可以模拟不规则外形以及任意空间位置下空心UXO的磁异常.该方法可进一步与反演算法结合, 以提高UXO定位的速度和准确性, 也可应用于地下复杂金属管道的磁正演.
| [1] |
ZALEVSKY Z, BREGMAN Y, SALOMONSKI N, et al. Resolution enhanced magnetic sensing system for wide coverage real time UXO detection[J]. Journal of Applied Geophysics, 2012, 84(4): 70 |
| [2] |
CHURCHILL K M, LINK C, YOUMANS C C. A comparison of the finite-element method and analytical method for modeling unexploded ordnance using magnetometer[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(7): 2720 DOI:10.1109/TGRS.2011.2174796 |
| [3] |
SINEX D B. Advancing the state of the art of UXO discrimination for total-field magnetic data[D]. Golden: Colorado School of Mines, 2006.
|
| [4] |
SANCHEZ V, LI Y G, NABIGHIAN M N, et al. Numerical modeling of higher order magnetic moments in UXO discrimination[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(9): 2568 DOI:10.1109/TGRS.2008.918090 |
| [5] |
葛健, 陆承达, 董浩斌, 等. 基于Overhauser传感器的近地表UXO磁梯度法探测技术[J]. 仪器仪表学报, 2015, 36(5): 961 GE Jian, LU Chengda, DONG Haobin, et al. The detection technology of near-surface UXO based on magnetic gradient method and Overhauser sensor[J]. Chinese Journal of Scientific Instrument, 2015, 36(5): 961 |
| [6] |
郭志馗, 陈超, 陶春辉, 等. 有限长圆柱体磁异常场全空间正演方法[J]. 地球物理学报, 2017, 60(4): 1557 GUO Zhikui, CHEN Chao, TAO Chunhui, et al. Forward modeling of magnetic anomaly of finite-length cylinder in 3D space[J]. Chinese Journal of Geophysics, 2017, 60(4): 1557 DOI:10.6038/cjg20170428 |
| [7] |
朱慧慧, 刘得军, 冯硕, 等. 基于磁偶极子构造法几何建模的铁管磁异常正演[J]. 计算机测量与控制, 2017, 25(3): 201 ZHU Huihui, LIU Dejun, FENG Shuo, et al. Magnetic dipole reconstruction geometry modeling for underground ferromagnetic pipe magnetic abnormal detection[J]. Computer Measurement and Control, 2017, 25(3): 201 |
| [8] |
吴文鹂, 管志宁, 高艳芳, 等. 重磁异常数据三维人机联作模拟[J]. 物探化探计算技术, 2005, 27(3): 227 WU Wenli, GUAN Zhining, GAO Yanfang, et al. Interactive man/computer modeling 3D body of gravity and magnetic anomaly data[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2005, 27(3): 227 |
| [9] |
管志宁. 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005 GUAN Zhining. Geomagnetic field and magnetic exploration[M]. Beijing: Geological Publishing House, 2005 |
| [10] |
李小康, 杨磊, 刘磊. 未爆弹药问题及地球物理解决方案综述[J]. 中国矿业, 2010, 19: 187 LI Xiaokang, YANG Lei, LIU Lei. Overview on unexploded ordnance problem and a solution:the geophysical scheme[J]. China Mining Magzine, 2010, 19: 187 |
| [11] |
关冶, 陆金甫. 数值方法[M]. 北京: 清华大学出版社, 2011 GUAN Ye, LU Jinfu. Numerical method[M]. Beijing: Tsinghua University House, 2011 |
 2018, Vol. 46
2018, Vol. 46
