2. 上海隧道工程有限公司,上海 200233
2. Shanghai Tunnel Engineering Co. Ltd., Shanghai 200233, China
惯用法[1]于1960年被提出,在其基础上建立的考虑接头对于结构整体刚度弱化作用的修正惯用法作为盾构隧道衬砌结构最常用的设计方法之一,已经广泛应用于国内外各类盾构隧道的设计当中.修正惯用法将实体管片刚度值乘以横向刚度有效率来考虑因接头存在对管片整体刚度的降低,并假设管片是弯曲刚度均匀的圆环,其所受荷载均为均布荷载.现阶段国内外针对盾构管片横向刚度有效率的研究几乎都基于圆形隧道展开,采用的方法主要有理论解析[2]、数值模拟[3]和模型试验[4]等.圆形隧道横向刚度有效率由于受断面尺寸、分块数量、错缝转角、螺栓强度和设计地层条件等多因素的影响,所得研究结果也不尽相同.
Wood[5]基于等分块圆形盾构衬砌结构提出管片弯曲等效刚度计算公式,并提出当管片环向接头数量在小于等于4个时衬砌结构整体刚度受接头影响很小.Lee等[6]研究发现隧道衬砌刚度受多种因素影响,并基于结构力学计算方法推导了横向刚度有效率与接头转动刚度之间的解析关系.日本盾构设计规范[1]在多个圆形管片力学试验数据的基础上,给出了横向刚度有效率建议值范围为0.6~0.8.Teachavorasinskun等[7]通过三维有限元数值模拟给出了横向刚度折减系数关于接头转动刚度和管片分块数的函数关系.封坤等[8]通过原型加载试验,提出了大断面水下盾构隧道横向抗弯刚度有效率的原型试验求解方法,得出管片结构横向刚度有效率和弯矩传递系数随荷载条件变化的规律.李晓军等[9]以上海沿江通道越江隧道工程为背景,研究大直径圆形盾构隧道横向等效刚度随埋深、地基刚度和拼装方式的变化规律.
类矩形盾构是满足双车道下立交及地铁车站等功能的市政通用型隧道衬砌结构,其内力分布和形变特征较矩形和圆形隧道更为复杂,国内外暂无设计相关规范,并缺乏类矩形盾构设计的可借鉴案例.本文基于站立式类矩形盾构管片原型加载试验,研究自重状态、设计状态和极限破坏状态下类矩形盾构管片横向刚度有效率范围、变化规律以及对侧压力系数的敏感性,并基于三维壳-弹簧模型对类矩形盾构和圆形盾构横向刚度有效率进行对比分析,证明了结构自重在反映类矩形盾构管片整体结构刚度上的重要影响,为类矩形管片的进一步优化设计以及盾构施工提供参考.
1 管片设计如图 1所示,类矩形盾构管片基于上海④号淤泥质黏土地层运营阶段进行设计,设计埋深10 m,地下水位-0.5 m,土体重度18.0 kN·m-3,运营阶段静止侧压力系数0.6,施工阶段静止侧压力系数0.7,基床系数6 000 kN·m-3,地面超载20 kPa.管片实际中心尺寸为10.2 m×7.7 m,幅宽1.2 m,厚0.5 m,采用CF50钢纤维混凝土浇筑而成.共6分块:1块封顶块(F)、2块邻接块(L1和L2)和3块标准块(B1、B2和B3).采用错缝拼装方式,块之间采用4根M30直螺栓连接,环之间采用26根M33弯螺栓连接.

|
图 1 类矩形盾构隧道管片布置图(单位:mm) Fig.1 Segmental layout of shield tunnel with a quasi- rectangular cross-section (unit: mm) |
大断面类矩形盾构管片原型加载试验将三环管片(2个半环和1个整环)错缝拼装后站立式放置于钢结构加载框架内(见图 2).管片底部铺设8组颗粒型弹性橡胶支座,该支座可模拟土体与结构之间相互作用机理.管片水土荷载通过22个轴对称并环向分布于管片外弧面的千斤顶加载点进行径向施荷,每个加载点含4个千斤顶(整环2个、半环各1个).30组纵向夹紧装置(2块夹板、4根拉杆)环向均匀分布于管片端面,以模拟管片纵向荷载并确保管片结构稳定性,每组夹紧装置夹紧力为150 t.

|
图 2 钢结构加载框架 Fig.2 Steel loading frame |
本次试验首次在大型盾构管片力学加载试验领域引入三维激光扫描设备(徕卡P40,见图 3).该设备可从左至右、从上到下对管片结构内弧面进行完整的三维坐标距测量,依次获得全面连续的全景坐标点数据,最终形成点云,降噪处理后的管片内弧面三维点云如图 4所示.

|
图 3 三维激光扫描仪 Fig.3 3D laser scanner |

|
图 4 管片内弧面三维点云视图 Fig.4 3D point cloud view of the segmental inner surface |
对经过断面选取并优化后的散点数据进行高阶多项式拟合后,可得到连续光滑的管片变形值曲线,例如自重状态下管片结构形变最终结果如图 5所示.
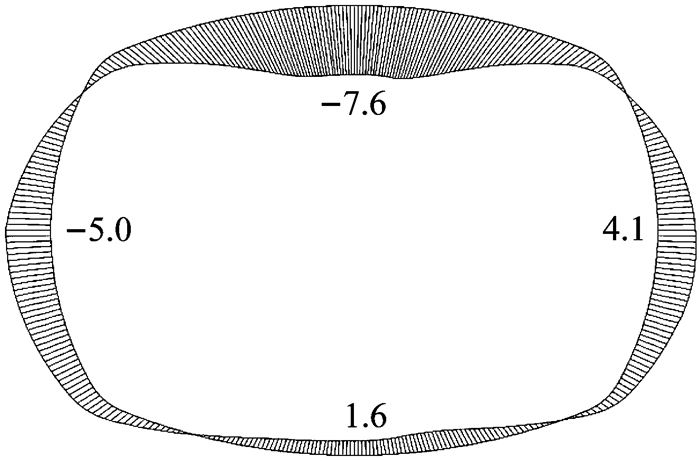
|
图 5 自重状态下管片形变图(单位:mm) Fig.5 Deformation map of segmental lining under dead weight condition (unit: mm) |
从图 5中可以看出,类矩形盾构管片形变呈竖向闭合、水平向张开的“横鸭蛋”特征.本文将管片结构在竖直对称轴和水平对称轴上的相对位移量分别命名为竖向闭合量和水平张开量.与圆形隧道不同,类矩形盾构管片竖向闭合量和水平向张开量值都较大,且后续形变增长方向同时发生在竖向和水平向.故本文同时将竖向变形和水平向变形作为衡量指标,从两个方向上综合考虑类矩形盾构衬砌结构的横向刚度有效率,并定义竖直方向的横向刚度有效率为η1,水平方向的横向刚度有效率为η2.
根据Lee等[6]基于横向变形等效原则提出的反映圆形隧道横向刚度折减的评价方法,本文通过均质梁模型的数值计算方法和参数敏感性分析,使计算得到的衬砌结构在竖向和水平向的直径变化量与原型试验结果一致,计算获得的管片等效刚度与混凝土管片刚度的比值分别为类矩形盾构隧道横向刚度有效率η1和η2.
3 结果分析 3.1 自重状态如图 5所示,自重状态下,类矩形盾构管片竖向闭合量为9.161 mm,对应横向刚度有效率η1为0.50;水平张开量为9.108 mm,对应横向刚度有效率η2为0.35.
3.2 设计状态所研究类矩形管片的设计埋深为10 m,将设计地层10 m覆土条件下类矩形盾构管片形变示于图 6.可以看出,设计状态下,类矩形盾构管片同样表现出竖向闭合、水平向张开的特征,竖向闭合量为23.80 mm,管片水平张开量为22.42 mm.自重状态下,类矩形管片竖向闭合量占运营阶段覆土10 m的38.53%,水平张开量占运营阶段覆土10 m的40.59%.由此可见,自重影响权重很大,首个“站立式”类矩形管片试验获得了以往水平放置试验无法获得的研究成果,具有重要的工程意义.

|
图 6 设计状态下管片形变图(单位:mm) Fig.6 Deformation map of segmental lining under the design condition (unit:mm) |
将设计地层条件下类矩形管片形变和横向刚度有效率随埋深增加的变化规律分别示于图 7和图 8.

|
图 7 管片形变量随埋深增加变化规律 Fig.7 Deformation values of segmental lining versus buried depths |

|
图 8 横向刚度有效率随埋深增加变化规律 Fig.8 Effective transverse rigidity ratios of segmental lining versus buried depths |
从图 7可以看出,设计地层条件下,类矩形盾构管片外荷载随埋深增加而线性增加,其竖向和水平向形变量都随隧道埋深增加呈良好的线性增加趋势,说明管片结构整体表现为弹性特征,并处于安全且具有一定承载余量的状态.
从图 8可以发现,类矩形盾构管片横向刚度有效率η1和η2随埋深增加表现出二次多项式曲线增长的趋势.究其原因,管片外荷载随覆土厚度增加而增加,环向接头两侧管片之间咬合更为紧密,接头端面混凝土的抗压和环向螺栓的抗拉性能逐渐发挥作用,接头转动刚度随之增强,管片结构整体刚度也随之增强.通过分析试验数据可知,设计工况条件下,类矩形管片竖向方向横向刚度有效率η1分布范围为0.50~0.90;水平向横向刚度有效率η2分布范围为0.21~0.49.
3.3 侧压力系数敏感性分析为进一步研究大断面类矩形盾构衬砌结构横向刚度有效率对侧压力系数的敏感性,本文将4类埋深(3、5、8、10 m)下类矩形盾构管片形变量和横向刚度有效率随侧压力系数增加的变化规律分别示于图 8和图 9.

|
图 9 形变量随侧压力系数变化规律 Fig.9 Deformation values versus lateral earth pressure coefficients |
如图 8和图 9所示,不同埋深条件下,类矩形管片竖向闭合量和水平张开量随侧压力系数增加都表现出良好的线性减小趋势,而类矩形管片两个方向上横向刚度有效率η1和η2随侧压力系数的增加而线性增加(除3 m埋深对应的η2外).分析其原因,主要是由于管片断面类矩形,同埋深条件下侧压力系数的增加,管片顶板荷载变化不大,但管片两侧荷载呈近似线性增长趋势,管片结构的弹性特征使其形变表现为两方向上线性减小特征.另外,与第3.2节结论一致,管片两侧荷载的增加同样使得类矩形盾构管片在两个方向上的结构刚度随之增强.

|
图 10 横向刚度有效率随侧压力系数变化规律 Fig.10 Effective transverse rigidity ratios versus lateral earth pressure coefficients |
本次试验将侧压力系数设为0.7,逐级增加覆土埋深(3.0、4.0、5.0、…、12.0、12.5、13.0、…、18.5 m),使管片结构达到破坏标准(裂缝宽度达到0.2 mm),以模拟类矩形盾构设计地层施工阶段极限破坏工况.将极限破坏工况下类矩形管片形变和横向刚度有效率随埋深增加的变化规律分别示于图 11和图 12.需要说明的是,试验获得的类矩形盾构管片极限埋深为18.5 m[10],考虑到试验的安全要求,当加荷至覆土16 m后将三维激光扫描仪从试验架中撤出,后续埋深对应形变数据未能捕捉完全.

|
图 11 极限破坏工况管片形变量随埋深变化规律 Fig.11 Deformation values versus buried depths in the limit failure state |
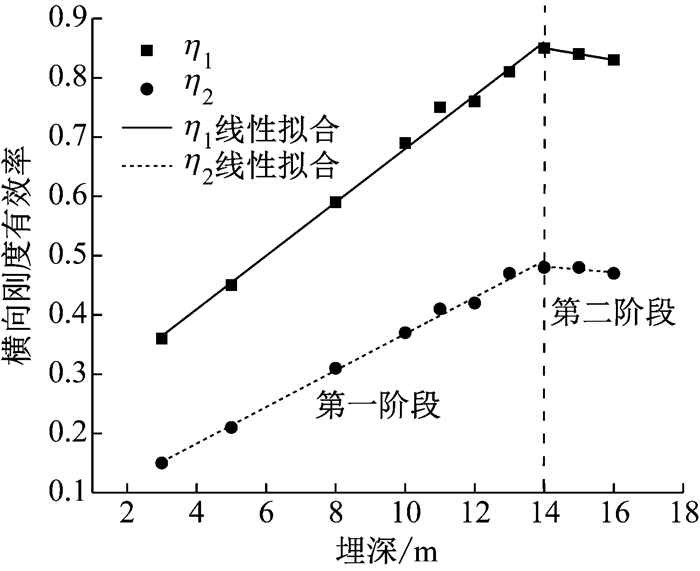
|
图 12 极限破坏工况管片横向刚度有效率随埋深变化规律 Fig.12 Effective transverse rigidity ratios versus buried depths in limit failure state |
从图 11和图 12中可以看出,类矩形管片竖向闭合量和水平向张开量以及横向刚度有效率η1和η2随埋深增加呈两阶段分线性变化趋势.第二阶段(覆土>14 m范围)管片结构竖向闭合量和水平张开量较第一阶段(覆土≤14 m)增长快,说明覆土14 m以后管片结构整体进入弹塑性阶段,由于后续埋深捕捉数据较少,暂不能断定管片形变走向,仅用线性增长趋势代之.第一阶段,横向刚度有效率η1和η2随埋深增加呈线性增长趋势,第二阶段同样由于数据量小,但随埋深继续增加表现为线性减小趋势.究其原因,一开始,随覆土厚度增加,管片结构接头转动刚度和管片结构整体性的增强使得管片结构整体刚度随之增强,但是外荷载超过一定覆土埋深后,管片接头部位整体进入弹塑性或塑性阶段,使得接头刚度减弱,管片结构整体刚度被削弱.
4 类矩形和圆形盾构管片横向刚度有效率对比分析 4.1 计算模型和计算参数为对比研究类矩形与圆形盾构管片横向刚度有效率变化特征,本文对类矩形盾构管片的设计模型进行拓展,选取外径与类矩形盾构管片横向尺寸相同(外径为10.7 m)的圆形断面,如图 13所示.

|
图 13 两类隧道横断面汇总(单位:m) Fig.13 Two types of tunnel cross-sections (unit:m) |
前期研究成果[11]已证明壳-弹簧模型可作为研究管片结构内力和形变的推荐模型,故本文运用大型有限元软件Abaqus进行壳-弹簧模型模拟分析,采用S4R壳单元模拟弹性管片实体,Spring 2单元模拟环向接头弹簧的轴向拉压、径向剪切、轴向剪切和转动特性以及纵向接头弹簧的轴向拉压、径向剪切、轴向剪切特性,Elastic Foundation模拟管片底部颗粒型弹性橡胶支座.由于未进行类矩形盾构管片环、纵向接缝力学加载试验,且类矩形盾构管片环、纵向接缝构造形式与文献[11]中青草沙输水隧道过江段管片接缝形式较为一致,故除环向接头转动刚度源于整环加载试验[11]以外,其余力学参数借鉴文献[11]所得研究成果,即纵向接缝径、切向剪切刚度为2.4×105 kN·m-1,环向接缝径、切向剪切刚度为3.0×105 kN·m-1,环、纵向接缝轴向拉压刚度为2.0×107 kN·m-1.
除断面型式不同外,圆形盾构管片其余设计参数与类矩形盾构管片一致,即:①管片分块数量不变,圆形盾构管片分块和纵向螺栓设置位置都与类矩形管片径向形成对应,衬砌环间错缝拼装且由26个纵向螺栓进行连接;②管片厚度均为0.5 m,幅宽1.2 m,采用CF50钢纤维混凝土浇筑,相同配筋;③圆形盾构管片采用与类矩形管片相同的环向和纵向接头形式,即接头弹簧模拟参数均一致,并采用相同参数的底部边界条件.最终类矩形和圆形盾构管片计算模型如图 14所示.
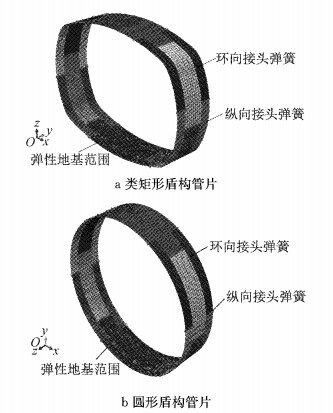
|
图 14 类矩形和圆形盾构衬砌结构数值计算模型 Fig.14 Numerical models for quasi-rectangular and circular tunnels |
试验状态下类矩形盾构管片形变量值与壳-弹簧模型计算值对比如图 15所示.可以看出,设计埋深范围内,管片结构处于弹性状态,试验值与数值计算结果较为接近,且都随隧道埋深的增加呈近似线性增长趋势,证明了壳-弹簧模型在预测盾构管片实际形变方面具有良好的指导作用.

|
图 15 形变试验值和壳-弹簧模型对比 Fig.15 Comparison of deformation results of loading tests and shell-spring model |
同等设计条件下,圆形盾构管片竖向位移U2和水平向的位移U1如图 16所示.

|
图 16 圆形隧道设计埋深下位移矢量图 Fig.16 Displacement vectors of circular shield lining structures at design depth |
从图 16可以看出,圆形盾构管片形变特征与类矩形盾构管片相反,整体表现为竖向张开、水平向闭合的“竖鸭蛋”特征.具体地,竖向形变方面,圆形盾构管片上半部分向上位移,中间位移量大于两侧,管片下半部分向下位移,中间位移量也大于两侧,管片竖向整体表现为张开状态;水平向形变方面,圆形管片两侧向各自内侧位移,中间位移量大于两侧,整体表现为水平向闭合的特征.
将3、5、8、9、10 m共5个埋深下,类矩形和圆形盾构隧道分别考虑管片结构自重和不考虑结构自重共4种情况的形变量值和横向刚度有效率η1和η2示于表 1(除考虑自重的类矩形管片相关数据源于试验,其余基于壳-弹簧模型计算获得).
| 下载CSV 表 1 两类盾构隧道不同条件下横向刚度有效率汇总 Tab.1 Summary of effective transverse rigidity ratios of two kinds of shield tunnels under different conditions |
从表 1可以对比出以下类矩形和圆形管片在形变和横向刚度有效率方面的异同点:
(1) 类矩形和圆形盾构管片虽然断面形式差异明显,但两者随覆土埋深增加的形变趋势一致,即竖向往隧道内和水平向往隧道外收敛.不同的是,圆形管片从“竖鸭蛋”逐渐往真圆形变,椭圆度随之减小,而类矩形管片继续“横鸭蛋”形变,椭圆度增加,证明了圆形隧道结构具有较优的抵抗形变的能力以及应用于深覆土的合理性.
(2) 原型整环结构试验中,考虑自重与否对类矩形和圆形管片形变的影响非常明显.不同的是,类矩形管片考虑自重时的结构形变明显大于不考虑管片结构自重的形变,两者差距随覆土埋深增加逐渐减小,证明了站立式类矩形盾构管片试验方法的科学性;相反,圆形管片不考虑自重的结构形变大于考虑自重后的管片形变,两者的差值随覆土埋深增加基本保持不变,说明传统浅覆土整环管片试验不考虑管片自重或者简化管片自重的原型试验在反映管片形变方面存在不足之处.
(3) 圆形盾构横向刚度有效率η1和η2不论考虑结构自重与否,二者值均接近0.70,且受埋深变化影响极小,说明采用修正惯用法进行圆形隧道衬砌结构设计时采用单一横向刚度有效率值是可行的.与圆形隧道相比,类矩形隧道两个横向刚度有效率之间差异较大,两者随埋深变化分布范围也较广,说明采用单一横向有效率进行类矩形盾构管片结构刚度评价和断面设计显然不够合理,须同时兼顾两方向上的横向刚度有效率.另外,考虑管片自重与否对类矩形隧道横向刚度有效率的影响非常明显,且类矩形盾构管片不考虑结构自重时两横向刚度有效率随埋深增加呈减小趋势,与考虑自重时的趋势相反,进一步证明了结构自重在反映类矩形盾构管片整体刚度上的重要性.
5 结论本文基于大断面类矩形盾构隧道衬砌结构原型加载试验和壳-弹簧模型数值计算,对类矩形盾构横向刚度有效率进行研究,主要结论为:
(1) 类矩形盾构管片自重状态和设计状态下都表现为竖向闭合、水平向张开的形变特征,且竖向闭合量和水平向张开量值接近.自重状态下类矩形管片竖向闭合量和水平向张开量占设计埋深状态的比例较大,证明浅埋类矩形盾构隧道需充分考虑自重的影响.
(2) 自重状态下,类矩形盾构管片竖直方向的横向刚度有效率η1为0.50,水平方向的横向刚度有效率η2为0.35.
(3) 设计埋深范围内,管片结构外荷载随覆土厚度增加而增加,环向接头两侧管片之间咬合更为紧密,接头端面混凝土的抗压和环向螺栓的抗拉性能逐渐发挥作用,使得接头转动刚度和管片结构整体刚度随之增强.管片结构整体表现为弹性特征,竖向和水平向形变量随隧道埋深增加呈良好的线性增加趋势,对应两方向上的横向刚度有效率随埋深增加表现出二次多项式曲线增长的趋势.
(4) 不同埋深条件下,随侧压力系数的增加,类矩形管片竖向闭合量和横向张开量都表现出良好的线性减小趋势,两方向上横向刚度有效率随着侧压力系数的增加而线性增加.
(5) 极限破坏工况条件下,类矩形管片竖向闭合量和横向张开量以及两方向上横向刚度有效率都随埋深增加呈两阶段分线性变化趋势.
(6) 基于壳-弹簧详细对比了类矩形和圆形管片形变和横向刚度有效率的异同点,证明了结构自重在反映类矩形盾构管片整体结构刚度上的重要性.
| [1] |
刘铁雄. 日本隧道标准规范(盾构篇)及解释[M]. 成都: 西南交通大学出版社, 1993 LIU Tiexiong. Japanese standard on tunnel (shield) and its interpretation[M]. Chengdu: Southwest Jiaotong University Press, 1993 |
| [2] |
彭益成, 丁文其, 闫治国, 等. 修正惯用法中弯曲刚度有效率的影响因素分析及计算方法[J]. 岩土工程学报, 2013, 35(增刊1): 495 PENG Yicheng, DING Wenqi, YAN Zhiguo, et al. Analysis and calculation method of effective bending rigidity ratio in modified routine method[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(Suppl.1): 495 |
| [3] |
黄正荣, 朱伟, 梁精华. 修正惯用法管片弯曲刚度有效率η和弯矩提高率ξ的研究[J]. 工业建筑, 2006, 36(2): 45 HUANG Zhengrong, ZHU Wei, LIANG Jinghua. Study on effective bending rigidity ratios and moment increasing rates in modified routine method[J]. Industrial Construction, 2006, 36(2): 45 |
| [4] |
孙海东. 盾构隧道管片衬砌结构刚度有效率模型试验研究[D]. 西安: 长安大学, 2012. SUN Haidong. Study on model test for effective rigidity ratio of shield-driven tunnel segments lining[D]. Xi'an: Chang'an University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10710-1013017500.htm |
| [5] |
WOOD A M M. The circular tunnel in elastic ground[J]. Geotechnique, 1975, 25(l): 115 |
| [6] |
LEE K M, GE X W. The equivalence of a jointed shield-driven tunnel lining to a continuous ring structure[J]. Journal of Canadian Geotechnical Engineering, 2001, 38(3): 461 DOI:10.1139/t00-107 |
| [7] |
TEACHAVORASINSKUN S, CHUB-UPPAKARN T. Influence of segmental joints on tunnel lining[J]. Tunnelling and Underground Space Technology, 2010, 25(4): 490 DOI:10.1016/j.tust.2010.02.003 |
| [8] |
封坤, 何川, 夏松林. 大断面盾构隧道结构横向刚度有效率的原型试验研究[J]. 岩土工程学报, 2011, 33(11): 1750 FENG Kun, HE Chuan, XIA Songlin. Prototype tests on effective bending rigidity ratios of segmental lining structure for shield tunnel with large cross-section[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(11): 1750 |
| [9] |
李晓军, 黄伯麒, 杨志豪, 等. 不同埋深下大直径盾构隧道横向刚度有效率[J]. 同济大学学报(自然科学版), 2015, 43(8): 1159 LI Xiaojun, HUANG Boqi, YANG Zhihao, et al. Lateral equivalent stiffness of large diameter shield tunnel structure at various buried depths[J]. Journal of Tongji University (Natural Science), 2015, 43(8): 1159 |
| [10] |
朱叶艇. 大断面异形盾构隧道衬砌结构力学行为研究[D]. 上海: 同济大学, 2017. ZHU Yeting. Study on the mechanical behavior of special-shaped shield lining structure with a large cross-section[D]. Shanghai: Tongji University, 2017. |
| [11] |
闫治国, 彭益成, 丁文其, 等. 青草沙水源地原水工程输水隧道单层衬砌管片接头荷载试验研究[J]. 岩土工程学报, 2011, 33(9): 1385 YAN Zhiguo, PENG Yicheng, DING Wenqi, et al. Load tests on segment joints of single lining structure of shield tunnel in Qingcaosha water conveyance project[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(9): 1385 |
 2018, Vol. 46
2018, Vol. 46
