2. 同济大学 土木工程防灾国家重点实验室,上海 200092
2. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China
作为数据分析方法的一种,聚类分析旨在将数据集合按相似程度进行分类[1].在上世纪40年代,Tryon在心理学研究中最早提出了聚类分析方法[2];在当代,通过聚类分析,互联网搜索引擎可以针对用户的查询需求将搜索结果分类分层显示[3];在地球物理科学中,聚类分析被用于影响气候的主要因素的研究[4];在分子生物学中,聚类分析在功能基因组的研究中起到重要作用[5],等等.考察应用聚类分析的动机与结果不难发现,聚类分析的主要用途在于揭示数据之间的潜在联系与内部结构,并根据这些特征结构合理地预测其他属性.由于数据之间特征组织方式的形成往往反映着特定物理背景的存在,因此聚类分析能够为物理模型勾勒出大致轮廓.显然,这种分析方法也可以应用于风工程中.
在风工程学科诞生之初,不少学者依据对自然风速观测记录的研究,建立了以功率谱密度为核心的统计分析方法[6-8].然而,尽管功率谱密度模型抓住了风速随机过程的主要特征,却并不能描述风中湍流的全部概率信息,也难以对非平稳的风速时程做出合理的反映.
为了解决传统结构动力激励建模中概率信息难以完备描述的问题,文献[9-11]提出了物理随机建模方法,明确指出物理规律是概率信息转移的轨道.对于脉动风速时程,文献[12-14]基于大气边界层能谱与零点演化时间概念给出了模拟脉动风速的随机Fourier谱模型.研究证明,该模型对实测结果的概率统计特征具有良好的刻画能力.
物理随机系统的随机性源自基本随机变量,为了合理描述脉动风速乃至结构风致响应的概率信息,需要仔细处理基本随机变量及其概率分布.应该指出:在上述随机Fourier谱模型中,对关键参数——分界波数的处理仍是粗糙的;已有工作的数据基础局限于个别风场观测台阵,模型对不同地域的适用性仍是需要研究的问题.有鉴于此,本文利用厦门风场实测记录,借助聚类分析方法,分析了随机Fourier谱中基本随机变量的分布,合理选择数据并进行建模.
1 随机Fourier谱模型物理随机系统的观点认为,物理规律是随机性传播的途径[10].如果记脉动风速沿时间t的变化为u(Θ, t),对于给定的参数Θ,就能够获得一条风速时程u(Θ, t).将该样本时程u(Θ, t)进行Fourier变换,可得到等价的描述方式
| $ \begin{array}{l} F\left( {\mathit{\Theta }, n} \right) = \left| {F\left( {\mathit{\Theta }, n} \right)} \right|{{\rm{e}}^{{\rm{i}}\varphi \left( {\mathit{\Theta }, n} \right)}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{\sqrt T }}\int_{ - \infty }^\infty {u\left( {\mathit{\Theta }, t} \right)} {{\rm{e}}^{ - {\rm{i}}2\pi \mathit{nt}}}{\rm{d}}\mathit{t} \end{array} $ | (1) |
式中:n为自然频率;T为脉动风速的总时长;|F(Θ, t)|称为幅值谱,它说明了能量在不同频率的分布;φ(Θ, t)称为相位谱,它确定了不同频率处能量在时间上的分布.
由于Θ为随机变量,上述随机Fourier谱(幅值谱与相位谱)也是随机函数.因此,只要给出幅值谱与相位谱的物理模型并确定随机参数的概率信息,就能对脉动风速随机过程进行合理的反映.
实际上,充分发展的湍流由一系列不同尺度的涡旋组成.大尺度涡旋在其与主流剪切的相互作用中吸取能量;而各尺度的涡旋又不断破碎形成更小尺度的涡旋直到黏性起主导作用的Kolmogorov尺度,在此过程中能量逐级传递;最终在黏性的作用下湍流能量耗散为大气的内能.研究指出,在与主流相互作用强烈的含能子区和能量传递达到平衡的惯性子区中,能谱密度随波数的变化呈不同幂律关系[15].据此,文献[12]提出了双线性Fourier幅值谱模型
| $ \left| {F\left( {\mathit{\Theta }, \mathit{k}} \right)} \right| = \left\{ {\begin{array}{*{20}{c}} {\sqrt {{\alpha _1}} \frac{{{u_*}}}{{{{\left( {\kappa z{k_{\rm{c}}}} \right)}^{1/3}}}}{k^{ - 1/2}}, }&{k < {k_{\rm{c}}}}\\ {\sqrt {{\alpha _1}} \frac{{{u_*}}}{{{{\left( {\kappa z} \right)}^{1/3}}}}{k^{ - 5/6}}, }&{k \ge {k_{\rm{c}}}} \end{array}} \right. $ | (2) |
式中:k为波数;z为高度;α1=0.55,为Kolmogorov常数;κ=0.4,为von Karman常数;

|
图 1 能量级串与Fourier幅值谱 Fig.1 Energy cascade and amplitude of Fourier spectrum |
在文献[13]中,分界波数可以通过涡量比值确定,但这一途径应用了比较粗糙的经验拟合方法,本质上是统计均值.本文的统计结果表明,分界波数具有较大的变异性,将其视为独立的随机变量是更合理的处理方式.即对于随机Fourier幅值谱,剪切波速u*与分界波数kc应分别作为独立随机变量.
在相位的研究方面,文献[14]建立了演化相位谱,它认为不同频率的涡旋振动速度不同,因而相位变化速度不同,通过合理猜想,这些涡旋具有相同的相位演化起点,并将共同起点时刻到实际观测时刻经历的演化时间定义为零点演化时间Te,通过幅值谱可以得到涡旋的振动速度为
| $ v\left( {\mathit{\Theta }, \mathit{n}} \right) = \sqrt {{{\left| {F\left( {\mathit{\Theta }, \mathit{n}} \right)} \right|}^2}\Delta n} $ | (3) |
式中:Δn是频率宽度.于是,对应频率n的演化相位为
| $ \mathit{\Phi }\left( {\mathit{\Theta }, n, {T_{\rm{e}}}} \right) = v\left( {\mathit{\Theta }, \mathit{n}} \right)k\left( n \right){T_{\rm{e}}} $ | (4) |
注意到零点演化时间在物理上表征了大气中旋涡相位的演化时间,它在时间尺度上一般较大,且受局部场地风环境影响较小,因此文献[14]的结果是合理的.
值得指出的是,作为风场平均风的描述,风剖面对刻画风场的宏观特性十分重要.在诸多风剖面模型中,对数律的风剖面因为有一定的理论基础且与实际结果较吻合而得到广泛的应用[16].因此,本文采用对数律作为风场平均特性的度量,即
| $ U\left( z \right) = \frac{{{u_*}}}{\kappa }{\rm{ln}}\frac{z}{{{z_0}}} $ | (5) |
式中:U(z)为高度z处的10 min平均风速;z0为地面粗糙度.
根据式(5)不难理解,风剖面的确定仅需要2个独立参数,本文采用剪切波速u*与地面粗糙度z0这一组合作为风剖面基本参数.在物理意义上加以考察,这种选择是合理的:剪切波速u*本质上反映了涡动黏性力在大气边界层中对平均风速的滞变效应,它建立起风的平均大尺度特性与高频细部结构之间联系的桥梁[6];地面粗糙度z0则将边界条件引起的底部涡旋以特征长度的方式计入风剖面,它实质上是边界条件产生的阻力对平均风速的影响[17].这样,加上分界波数kc,本文所研究的风速模型有3个基本随机变量.
2 参数识别 2.1 厦门风场观测台阵本研究小组于2014年在厦门大嶝岛(北纬24°33′9″, 东经118°19′47″)建立了一座强风观测台阵.这一台阵共有4座观测塔P1、P2、P3、P4,它们的空间布置如图 2所示.在P1塔与P4塔的10 m与20 m处安装有三维超声风速仪,在P2塔与P3塔的10 m、20 m、30 m及40 m处安装有三维超声风速仪,采样频率均为10 Hz.观测台阵周围以农业用地与灌木为主,在其四周100~200 m远处分布着多个建筑密集区,多为10 m以下民房,总体上该地区的地貌与《建筑结构荷载规范》[18]的B类地貌或C类地貌相当.在本文的分析中,采用了2015年6月28日至2015年8月19日之间的数据,经过检查,所采用数据都处于良态风环境.经过对比发现:由其他各塔的数据得出的结论与P3塔相一致,因此这里只讨论P3塔的结果.

|
图 2 风场观测台阵的布置(单位:m) Fig.2 Lay-out of the strong wind observation system (unit: m) |
本文采用最小二乘法进行参数识别.这一方法实质上是在合适的距离定义下寻找实测样本的最佳逼近.考虑实测样本y与模型y(Θ)的二范数误差
| $ J\left( \mathit{\Theta } \right) = {\left\| {y - y\left( \mathit{\Theta } \right)} \right\|_2} $ | (6) |
式中:y是观测值;y(Θ)是物理模型.参数识别结果ΘId应使式(6)取得最小值.如果将样本y与模型y(Θ)分别取为实测脉动风速的Fourier幅值谱与双线性Fourier幅值谱(式(2)),就能够识别出其基本参数剪切波速u*与分界波数kc;同理,可以进行对数律风剖面的识别.
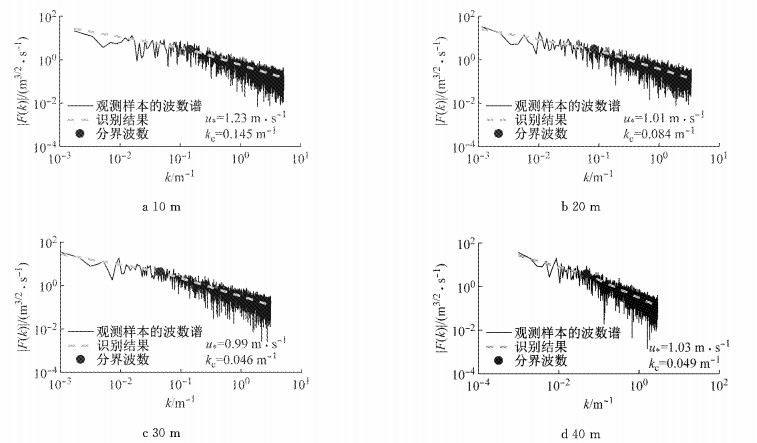
应当指出,根据脉动风速Fourier幅值谱(式(2))与风剖面(式(5))都可以识别得到剪切波速.如前所述,在Fourier谱中,剪切波速反映了考察位置处涡动黏性引起的主流剪切;而对数律中剪切波速表征了竖向剪切的平均.因此,本文先识别了各高度处Fourier幅值谱中的剪切波速;然后取其平均值作为风剖面的剪切波速进一步识别地面粗糙度.图 3和图 4是同一10 min间隔内的典型脉动风速Fourier幅值谱及风剖面的识别结果.可以看到,各高度处的剪切波速十分接近,说明这一识别方法是合理的.
|
图 3 典型波数谱与识别结果 Fig.3 Typical wave number spectrum and identification |

|
图 4 典型风剖面与识别结果 Fig.4 Typical mean wind profile and identification |
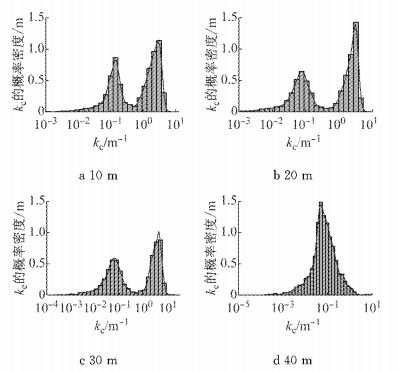
将所有识别结果作统计分析,u*、z0及kc的结果分别见图 5、图 6与图 7.与以前研究结果相比[19],关于u*识别结果的统计分布没有本质差别.但大量z0集中在10 m左右,显然不符合实际地面粗糙度分布范围;此外3个高度kc的识别结果中出现了明显的双峰特征,这表明分界波数识别结果中可能存在特有的数据结构.

|
图 5 剪切波速统计结果 Fig.5 Statistics of shear velocity |

|
图 6 地面粗糙度统计结果 Fig.6 Statistics of roughness length |
|
图 7 分界波数统计结果 Fig.7 Statistics of cut-off wave number |
为初步检验由上述识别结果得到的概率分布对风速时程基本概率信息的影响,可以考察它们所导出的功率谱密度函数并与经典谱对比.这里取Kaimal谱作为参照
| $ \frac{{nS\left( {z, n} \right)}}{{u_ * ^2}} = \frac{{200f}}{{{{\left( {1 + 50f} \right)}^{5/3}}}} $ | (7) |
式中:f=nz/U;S(z, n)为脉动风速的功率谱.注意到功率谱是样本Fourier谱的平均
| $ S\left( n \right) = 2E\left[{{{\left| {F\left( {\mathit{\Theta }, n} \right)} \right|}^2}} \right] $ | (8) |
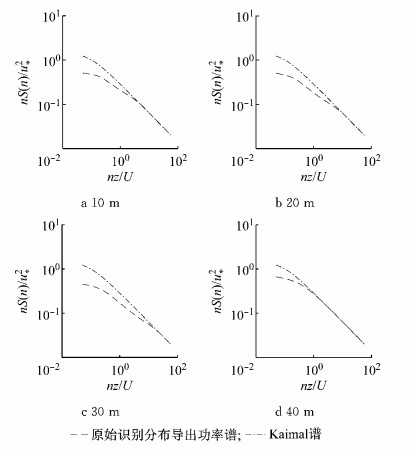
采用MATLAB中概率分布拟合的核密度估计方法,给出各高度分界波数的概率密度函数,如图 7所示.在此基础上,结合式(8)计算了由随机Fourier谱模型导出的量纲一功率谱,如图 8所示.显然,在高频段模型结果与Kaimal谱基本一致,但在中、低频段很大范围内,由分界波数直接识别结果导出的功率谱密度函数显著低于Kaimal谱.
|
图 8 由原始识别结果拟合分布导出的功率谱 Fig.8 Power spectrum density derived from statistical distribution of original identification |
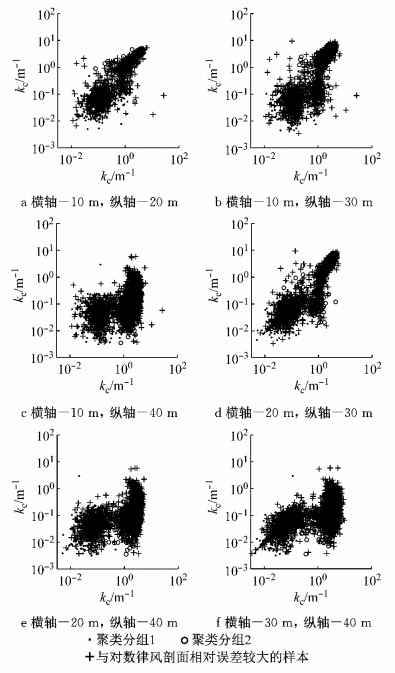
为深入研究上述问题,在图 9的各子图中作出不同高度分界波数的关系,其中各点的横、纵坐标为相应时刻不同高度分界波数.显然,任意两个高度处分界波数组成的点集都泾渭分明地分为两簇.这一特征及其原因可以通过聚类方法进行分析.
|
图 9 分界波数识别结果 Fig.9 Cluster results of cut-off wave number |
已经指出,聚类分析能够利用样本属性的相似性对样本集合进行分类.本文采用欧几里得距离作为样本相似性的描述,即:将n维点集X = {xi, i = 1, 2, …, n}中的点分成N类{Ci, i = 1, 2, …, N},使得总偏差最小,总偏差的定义为
| $ D\left( C \right) = \sum\limits_{l = 1}^N {\sum\limits_{x \in {C_l}} {{{\left\| {x - {\mu _l}} \right\|}^2}} } $ | (9) |
式中:μl是第l类的中心点;‖·‖是欧几里得距离.
一般可以使用经典的递归算法实现上述目标:
(1) 首先适当地选取N个中心点,作为各类的特征点,将集合X中的点按照距所选择的中心点的远近将其归类,接下来重复(2)与(3)的操作,直至分类最终稳定;
(2) 按上一次分类的结果重新计算N个中心点,即每一类所有点的平均值;
(3) 按新的中心点集进行分类.
根据对图 9的分析,本文分类数N取为2即可.
3.2 分界波数的聚类结果将同一时间段内、4个高度识别出的分界波数看作R4空间(每一维度代表某一高度的分界波数值)的一个点,则所有记录得到的4维分界波数数组全体构成了待聚类的点集.本文利用MATLAB中k-means函数进行聚类,聚类结果如图 9所示.显然,通过聚类分析,上节所述的分类特征得以细致地展现.需要说明的是,图 9中“ + ”代表实测风剖面与对数律风剖面相对误差大于5.5%的样本,而聚类分析只考虑相对误差小于5.5%的样本.
3.3 聚类现象原因分析可以推断,图 9中“ o ”形点集受到了外界因素的扰动.一般,风场中扰动源常有固定的空间位置,故可以在风向图中探究样本聚类的原因.
在极坐标图 10中作出各高度10 min平均风速U10与风向的关系,并用相应的记号表现上述聚类结果,对图 10的考察可以得出以下规律:

|
图 10 分界波数聚类结果与风向的关系(图中半径大小代表 10 m高、10 min平均风速,单位:m·s-1) Fig.10 Relation of cluster results to wind direction (The magnitude of radius designate 10 min mean wind speed at a height of 10 m, unit: m·s-1) |
(1) 风剖面受显著干扰的样本几乎完全集中在0°(正北)方向以及附近区域;
(2) 与其他方向比较,平均风速在0°(正北)方向有明显的凹进,说明它在此处被显著削弱;
(3) “ o ”形点集以带状形式分布在上述大相对误差样本两侧,它们一起占据了与0°(正北)方向左右约60°的范围;“·”形点集则散布在上述范围外.
综合上述结果,可以推测:当风从正南方吹来时,受到某种因素的扰动,风速被削弱,且风速受到的扰动随着风向与正北方的夹角增大而减小.考察风场观测台阵设备设施,注意到各高度处的三维超声风速仪都安装在由观测塔朝正北方向伸出约1 m左右的构件上,而且观测塔直径也在1 m左右,则有理由相信,观测塔是扰动实测记录的主要因素.
在已有的风场数据分析文献中,鲜有考虑观测设备设施对实测记录影响的工作.本文工作说明,为了获得正确合理的结论,应当重视观测系统自身带来的误差.
3.4 基于聚类分析的分界波数建模前文分析指出,将分界波数处理为随机变量是一种更合理的建模方式.为了正确地统计其概率分布,应当将上文讨论的外界扰动排除在外.据此,本文将风向在正北方向附近一定方位角内及风剖面与对数律相对误差大于5.5%的样本记录排除.由此得到的地面粗糙度的直方图见图 11,以及各高度处分界波数的对数直方图见图 12.可见,图 6的地面粗糙度异常分布及图 7分界波数的双峰分布不再存在.

|
图 11 数据筛选后的地面粗糙度统计直方图 Fig.11 Histogram of roughness length after data sieving |

|
图 12 分界波数直方图与建模 Fig.12 Histogram and modeling of cut-off wave number |
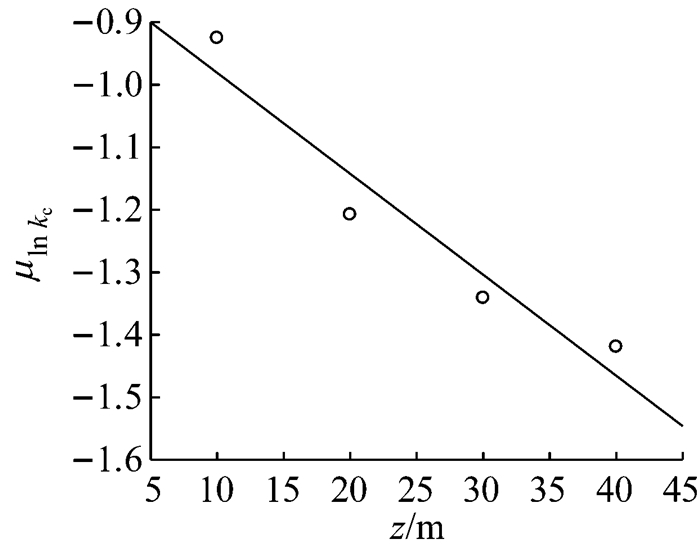
进一步考察样本筛选是否能够改善功率谱密度的模拟.采用对数正态分布对分界波数进行建模,建模结果如表 1所示.分析可见,kc对数均值μln kc与对数标准差σln kc与高度有明显的线性关系(见图 13与图 14).
| $ \begin{array}{l} {\mu _{{\rm{ln}}\;{\mathit{k}_{\rm{c}}}}} = - 0.016\;3z - 0.809\;8\\ \;\;{\sigma _{{\rm{ln}}\;{\mathit{k}_{\rm{c}}}}} = - 0.003\;6z + 0.186\;2 \end{array} $ |
| 下载CSV 表 1 分界波数建模结果 Tab.1 Modeling results of cut-off wave number |
|
图 13 分界波数对数均值与高度的关系 Fig.13 Logarithmic mean value of cut-off wave number versus height |

|
图 14 分界波数对数标准差与高度的关系 Fig.14 Logarithmic standard deviation of cut-off wave number versus height |
式中:高度z单位为m;kc单位为m-1.
按2.2节方法计算由随机Fourier谱模型导出的功率谱,并与Kaimal谱对比,如图 15所示.显然,排除异常数据后,模型功率谱与Kaimal谱在一般工程所关心的频率范围内几乎一致,证明聚类分析与样本筛选的有效性.同时,上述分析进一步验证了随机Fourier谱模型对脉动风速细部特征进行合理刻画的能力.

|
图 15 数据筛选后的参数统计分布导出的功率谱 Fig.15 Power spectrum density derived from statistical distribution after data sieving |
本文研究了脉动风速随机Fourier谱模型基本随机变量及其分布,得到以下结论:
(1) 脉动风速随机Fourier谱模型的基本随机变量包括剪切波速、地面粗糙度、分界波数以及零点演化时间.利用厦门地区实测风速记录,识别了剪切波速、地面粗糙度、分界波数.
(2) 初始识别结果中地面粗糙度分布异常;分界波数呈现双峰特征.初始识别结果的统计分布导出的功率谱密度函数明显偏离Kaimal谱.
(3) 研究发现,上述参数识别结果的异常源自风速样本的聚类特征,且与风向紧密联系.这一现象与观测装置对风场的扰动有关,因此在分析实测风场记录时,应重视风场设备设施对观测效果的影响.
(4) 依据聚类分析结果,合理地选择样本集合,进行了分界波数统计建模.由此导出的模型功率谱与Kaimal谱对比良好,这也证明了聚类分析的有效性.
| [1] |
JAIN A K. Data clustering: 50 years beyond K-means[J]. Pattern Recognition Letters, 2010, 31(8): 651 DOI:10.1016/j.patrec.2009.09.011 |
| [2] |
方开泰, 潘恩沛. 聚类分析[M]. 北京: 地质出版社, 1982 FANG Kaitai, PAN Enpei. Cluster analysis[M]. Beijing: Geological Publishing House, 1982 |
| [3] |
苍宏宇, 谭宗颖. 聚类搜索引擎发展现状研究[J]. 图书情报工作, 2009, 53(2): 125 CANG Hongyu, TAN Zongying. Research on the development situation of clustering search engine[J]. Library & Information Service, 2009, 53(2): 125 |
| [4] |
TAN P N, STEINBACH M, KUMAR V. Introduction to data mining[M]. Boston: Pearson Education Inc, 2006
|
| [5] |
BALDI P. Bioinformatics: the machine learning approach[M]. Boston: MIT Press, 2001
|
| [6] |
SIMIU E, SCANLAN R H. Wind effects on structures[M]. New York: John Wiley & Sons, 1996
|
| [7] |
COUNIHAN J. Adiabatic atmospheric boundary layers: a review and analysis of data from the period 1880-1972[J]. Atmospheric Environment, 1975, 9(10): 871 DOI:10.1016/0004-6981(75)90088-8 |
| [8] |
阎启, 谢强, 李杰. 风场长期观测与数据分析[J]. 建筑科学与工程学报, 2009, 26(1): 37 YAN Qi, XIE Qiang, LI Jie. Long-term observation and data analysis of wind field[J]. Journal of Architecture & Civil Engineering, 2009, 26(1): 37 |
| [9] |
李杰. 随机动力系统的物理逼近[J]. 中国科技论文在线, 2006, 1(2): 95 LI Jie. A physical approach to stochastic dynamical systems[J]. Sciencepaper Online, 2006, 1(2): 95 |
| [10] |
李杰. 物理随机系统研究的若干基本观点[R]. 上海: 同济大学, 2006. LI Jie. Basic views of the stochastic physical system research[R]. Shanghai: Tongji University, 2006. |
| [11] |
LI J, CHEN J. Stochastic dynamics of structures[M]. Singapore: John Wiley & Sons, 2009
|
| [12] |
李杰, 阎启. 结构随机动力激励的物理模型:以脉动风速为例[J]. 工程力学, 2009(A02): 175 LI Jie, YAN Qi. Physical models for the stochastic dynamic excitations of structures: in the case of fluctuating wind speed[J]. Engineering Mechanics, 2009(A02): 175 |
| [13] |
李杰, 阎启. 脉动风速随机Fourier波数谱研究[J]. 同济大学学报(自然科学版), 2011, 39(12): 1725 LI Jie, YAN Qi. Research on stochastic Fourier wave-number spectrum of fluctuating wind speed[J]. Journal of Tongji University(Natural Science), 2011, 39(12): 1725 |
| [14] |
LI J, PENG Y, YAN Q. Modeling and simulation of fluctuating wind speeds using evolutionary phase spectrum[J]. Probabilistic Engineering Mechanics, 2013, 32: 48 DOI:10.1016/j.probengmech.2013.01.001 |
| [15] |
KATUL G, CHU C R. A theoretical and experimental investigation of energy-containing scales in the dynamic sublayer of boundary-layer flows[J]. Boundary-Layer Meteorology, 1998, 86(2): 279 DOI:10.1023/A:1000657014845 |
| [16] |
BLACKADAR A K, TENNEKES H. Asymptotic similarity in neutral barotropic planetary boundary layers[J]. Journal of the Atmospheric Sciences, 1968, 25(6): 1015 DOI:10.1175/1520-0469(1968)025<1015:ASINBP>2.0.CO;2 |
| [17] |
DYRBYE C, HANSWN S O. Wind loads on structures[M]. Chichester: John Wiley & Sons, 1996
|
| [18] |
中华人民共和国住房和城乡建设部. 建筑结构荷载规范: GB 50009—2012[S]. 北京: 中国建筑工业出版社, 2012. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Load code for the design of building structures: GB 50009—2012[S]. Beijing: China Architecture & Building Press, 2012. |
| [19] |
LI Q S, ZHI L, HU F. Boundary layer wind structure from observations on a 325m tower[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(12): 818 DOI:10.1016/j.jweia.2010.08.001 |
 2018, Vol. 46
2018, Vol. 46

