2. 同济大学 上海市地面交通工具空气动力与热环境模拟重点实验室, 上海 201804;
3. 泛亚汽车技术中心有限公司,上海 201201
2. Shanghai Key Laboratory of Vehicle Aerodynamics and Vehicle Thermal Management Systems, Tongji University, Shanghai 201804, China;
3. Pan Asia Technical Automotive Center, Shanghai 201201, China
大涡模拟(LES)最早于1963年由Smagorinsky以亚格子应力模型的方式运用于气象学研究中[1].而后LES被逐渐应用于平面射流、绕流、燃烧、槽道流和气固两相流等多个方面,并取得了一定的研究成果.
在针对二维流动的数值仿真中,马金花等论证了LES方法对二维圆柱绕流计算的适用性[2];苑明顺等采用LES方法研究了二维圆柱绕流中三维涡量的耗散效应[3];Murakami等及Yu等的研究表明,LES对方柱绕流的预测结果更接近实际[4-5],计算结果受网格尺度及亚格子模型构建方式的影响显著[6];苏铭德的研究表明,LES对方直管内流中二次流现象的捕捉及统计平均量的解析与试验符合良好[7];杨建明等采用LES方法对方弯管内流动的仿真结果与实验数据亦符合良好[8];刘沛清等利用LES成功预测了某翼型在不同迎角下的外流场特性,并得出相应的气动力分量[9];刘宁宇等采用动力学亚格子模型研究了圆柱绕流在稳态和振荡下的尾迹流态[10]; Cheng等的研究表明,与k-ε模型相比,LES方法针对方柱绕流中所涉及的分离流及回流的预测结果更为准确[11];王兵等以自主开发的亚格子模型为基础对后台阶流的再附着过程展开研究,其计算数据与试验结果较为一致[12].
随着计算机技术的发展,以及对LES滤波方法和亚格子模型研究的深入,LES被逐步应用于求解三维湍流流动.Constantinescu等的研究发现,虽然LES和时均湍流模型(RANS)皆能准确预测出钝体绕流场的平均速度分布,但LES能更好地预测湍流动能[13];Sinisa等利用LES方法对斜背倾角为25°的Ahmed类车体外部绕流场进行数值仿真,采用不同的网格方案对气动阻力及类车体头部、上方、斜背和尾迹的流场结构进行了详细的对比分析[13-15];Eric等的研究表明大涡模拟可以得到与试验数据总体符合的结果,但Smagorinsky亚格子湍流模型不能准确预测出斜背上的分离[16];Aljure等以Ahmed类车体和Asmo类车体为对象,采用4种亚格子湍流模型对其绕流场进行数值仿真,通过与试验数据的对比,发现不同亚格子模型计算准确性存在差异[17].目前,针对绕流场结构更为复杂的三厢车体气动性能LES计算方法的研究较为罕见.
本文以MIRA三厢车体为对象,对采用LES方法解算非定常特征显著且具有大分离流动结构的近地钝体外部绕流场所涉及的迭代步数、时间步长、网格方案等影响因素开展研究; 同时分析不同亚格子湍流模型对MIRA车体所受气动力系数时均值以及车身表面压力系数时均值的计算准确性; 最终提出适用于三厢车型的LES数值仿真策略.
1 大涡模拟LES的基本思想:通过瞬时N-S方程求解大尺度涡,同时建立模型以量化小尺度涡对大尺度涡的影响,该模型即为亚格子模型(SGS).
每个流场变量φ皆被分成大尺度分量
| $ \bar \varphi \left( x \right) = \int_D {\varphi \left( {x'} \right)G\left( {x,x'} \right){\rm{d}}x'} $ | (1) |
式中:D为流动区域; x′为实际流动的空间坐标; x为过滤后大尺度空间坐标; G(x, x′)为滤波函数,决定了由N-S方程直接求解的涡尺度范围.常用的滤波函数有3种:盒式滤波函数、富氏截断滤波函数和高斯滤波函数.在本文所采用的FLUENT流体仿真平台中,有限控制体在离散的过程中隐含了过滤运算,滤波函数的表达式为
| $ G\left( {x,x'} \right) = \left\{ \begin{array}{l} \frac{1}{V},\;\;\;x' \in V\\ 0,\;\;\;\;x' \notin V \end{array} \right. $ | (2) |
式中:V是控制体体积,过滤函数相当于对物理量在控制体积上取平均值,过滤后的
| $ \bar \varphi \left( x \right) = \frac{1}{V}\int_V {\bar \varphi \left( {x'} \right){\rm{d}}x'} ,x' \in V $ | (3) |
应用式(3)的滤波函数,对质量守恒方程和瞬态N-S方程进行过滤,得到大涡模拟的控制方程
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho {{\bar u}_i}} \right) = 0 $ | (4) |
| $ \frac{\partial }{{\partial t}}\left( {\rho {{\bar u}_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho \overline {{u_i}{u_j}} } \right) = - \frac{{\partial \bar p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left( {\mu \frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}}} \right) - \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}} $ | (5) |
式中:τij为亚格子应力,该项表示了小尺度涡与大尺度涡之间的动量输运,量化了小尺度脉动对整体流场的影响.τij定义为
| $ {\tau _{ij}} = \rho \overline {{u_i}{u_j}} - \rho {{\bar u}_i}{{\bar u}_j} $ | (6) |
为了使方程组封闭,必须构造相应的亚格子模型,建立关于亚格子应力的数学表达式.对于被过滤掉的小尺度涡团,LES思想认为这部分为各向同性的耗散项.
目前比较普遍的亚格子模型皆沿用RANS方法中Boussinesq提出的涡黏假设[18],亚格子应力可以表示为
| $ {{\bar \tau }_{ij}} - \frac{1}{3}{\tau _{{\rm{kk}}}}{\delta _{ij}} = - 2{\mu _{\rm{t}}}{{\bar S}_{ij}} $ | (7) |
式中:μt为亚格子尺度的涡黏系数;
| $ {{\bar S}_{ij}} = \frac{1}{2}\left( {\frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}} + \frac{{\partial {{\bar u}_j}}}{{\partial {x_i}}}} \right) $ | (8) |
涡黏假设将对亚格子应力的求解转变为对亚格子尺度涡黏系数的求解,并发展出多种模型.本文重点研究目前常用的3种亚格子模型:DSL(dynamic smagorinsky-lilly)模型[19],WALE (wall-adapting local eddy-viscosity)模型[20]和DKE(dynamic kinetic energy subgrid-scale)模型[21].
Smagorinsky给出了最基本的亚格子模型,经Lilly改进后形成Smagorinsky-Lilly模型.该模型对亚格子尺度涡黏系数μt的计算方法为
| $ {\mu _{\rm{t}}} = \rho L_{\rm{s}}^2\left| {\bar S} \right| $ | (9) |
式中:Ls为亚格子混合长度;
| $ {L_{\rm{s}}} = \min \left( {kd,{C_{\rm{s}}}\Delta } \right) $ | (10) |
式中:k为卡门常数; d为节点到最近壁面的距离; Cs为Smagorinsky常数; Δ为过滤尺度.在研究中发现, 当Cs取为常数时该模型具有一定的局限性,于是发展出根据求解尺度动态获取Cs值的DSL模型.
在WALE亚格子尺度模型中,亚格子尺度涡黏系数的计算方法仍然沿用了混合长度的概念,计算式为
| $ {\mu _{\rm{t}}} = \rho L_{\rm{s}}^2\frac{{{{\left( {S_{ij}^{\rm{d}}S_{ij}^{\rm{d}}} \right)}^{3/2}}}}{{{{\left( {{{\bar S}_{ij}}{{\bar S}_{ij}}} \right)}^{5/2}}{{\left( {S_{ij}^{\rm{d}}S_{ij}^{\rm{d}}} \right)}^{5/4}}}} $ | (11) |
式中, Ls和Sijd的定义分别为
| $ {L_{\rm{s}}} = \min \left( {kd,{C_{\rm{w}}}{V^{1/3}}} \right) $ | (12) |
| $ S_{ij}^{\rm{d}} = \frac{1}{2}\left( {\bar g_{ij}^2 + \bar g_{ji}^2} \right) - \frac{1}{3}{\delta _{ij}}\bar g_{{\rm{kk}}}^2 $ | (13) |
式中:
DKE模型计入了亚格子尺度湍动能的输运,其亚格子尺度湍动能定义为
| $ {k_{{\rm{sgs}}}} = \frac{1}{2}\left( {\overline {u_{\rm{k}}^2} + \bar u_{\rm{k}}^2} \right) $ | (14) |
亚格子尺度涡黏系数则通过ksgs进行计算:
| $ {\mu _{\rm{t}}} = {C_{\rm{k}}}\rho \sqrt {{k_{{\rm{sgs}}}}} \Delta $ | (15) |
式中:Ck为模型系数.
2 流场仿真相关信息仿真对象为1:3缩尺比MIRA三厢车型:长(L)1 388.3 mm、宽(W)541.7 mm、高(H)473.7 mm.具体构造如图 1所示.

|
图 1 仿真模型构造 Fig.1 Structure of simulation model |
仿真空间区域,长13.88 m、宽5.42 m、高2.37 m,阻塞比1.61%;x正向为从左到右的空气流动方向, z正向垂直向上,y正向以右手螺旋定则确定,如图 2所示.
|
图 2 仿真计算区域 Fig.2 Domain of simulation |
仿真采用混合网格结构,在车身周围区域建立计算子域,采用适应性较好的四面体网格,在外围区域采用六面体网格,具体见图 3.

|
图 3 体网格布局 Fig.3 Arrangement of mesh |
将x、y、z 3个方向速度记为u、v、w,计算域入口边界设为速度入口,速度均匀分布:u=30 m·s-1、v=w=0 m·s-1.出口边界设为压力出口,表压为0 Pa.车体及地面皆采用无滑移壁面边界条件,计算域左、右两侧及顶部采用对称边界条件.按车长计算的雷诺数为Re≈2.81×106.
LES属于非稳态计算方法,在时间积分方案上保证二阶精度; 同时,采用二阶精度的空间离散格式.根据文献[22]的研究成果,以低雷诺数模型计算所得定常解作为LES计算的初始场.
MIRA车体外部绕流为充分发展的湍流流动,脉动特征显著,具有很强的时间相关性,任一点的流动参数皆为时间的函数.因此引入物理量的时均值,以便将计算值与试验值进行对比
| $ \bar \varphi = \sum\limits_{i = 1}^n {{\varphi _i}/n} $ | (16) |
式中:φi表示时刻i变量的瞬时值;
为了对变量随时间脉动的强弱程度进行评估,引入了物理量的标准差
| $ \sigma \left( {\varphi '} \right) = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left( {{\varphi _i} - \bar \varphi } \right)}^2}} }}{{n - 1}}} $ | (17) |
式中:σ(φ′)表示变量的标准差.标准差是统计意义下的物理量,数值越大表示此处脉动越剧烈.
3 仿真参数的确定依托现有计算资源,基于DSL亚格子模型,研究迭代步数、时间步长、初始场、网格数量对LES计算结果的影响规律.由于LES在近壁区域的网格策略与低雷诺数模型完全一致,故依据文献[22]的研究成果,采用车身面网格尺寸1.5 mm,体网格6 745万单元的网格方案.
3.1 时间步长内最大迭代步数在MIRA车身上选择一个监测点A,在车体尾迹区选择一个监测点B,位置如图 4所示.

|
图 4 监测点位置 Fig.4 Location of monitoring points |
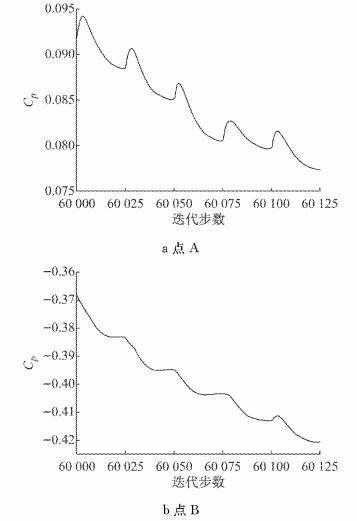
对于车体上的A点,监测其压力系数Cp随迭代步数的变化; 对于尾迹区内的B点,监测其压力系数及x、y、z3个方向的速度随迭代步数的变化.A点、B点压力系数的变化见图 5.由图可知:对于2个监测点,在任意一个时间步长内,第20次迭代后监测点的压力系数值均达到稳定.
|
图 5 压力系数变化曲线 Fig.5 Variation of Cp |
图 6给出了B点处3个方向的速度值随迭代步数的变化曲线,由图可知:在每一个时间步长内,3个方向的速度值达到稳定所需的迭代步数不同,但在20次迭代后皆达到稳定状态.为确保所有监测点都能够在时间步长内达到稳定,LES方法中每一时间步长内最大迭代步数建议为25步.

|
图 6 速度变化曲线 Fig.6 Variation of velocity |
在非定常流动计算中,当时间步长达到无穷小时,理论上数值仿真可以重现真实的流动状态,然而却不现实.由于时间步长的大小直接影响仿真精度及计算成本,故选取时间步长为5.0×10-4s、2.0×10-4s和1.0×10-4s 3种方案,分别对MIRA三厢车体绕流场进行非定常数值仿真.
在车身表面设置25个监测点,如图 7所示,并获取监测点处的压力系数随计算时间的变化数据.图 8给出了数值仿真的对比结果.由图 8可知:3种方案计算所得监测点处压力系数时均值相差较小,因此不同方案对时均结果的影响较小; 对比脉动压力系数的标准差时,发现在16号至22号监测点处3种方案计算结果的标准差最大,并存在明显差异; 1.0×10-4s方案的标准差最大,2.0×10-4s方案与5.0×10-4s方案标准差的数值彼此接近,但2.0×10-4s方案的计算成本是5.0×10-4s方案的2.5倍; 3种方案对其余18个监测点压力系数的标准差计算结果相差很小.综合考虑3种方案的计算精度和计算成本,LES方法中推荐采用5.0×10-4 s的时间步长.

|
图 7 监测点位置 Fig.7 Location of monitoring points |

|
图 8 压力系数平均值及标准差 Fig.8 Average value and standard deviation of Cp |
网格数量不仅直接决定了初始场的求解质量,而且对LES方法的计算精度及成本影响极大.本节对车身面网格尺寸1.5 mm、体网格总数6 745万单元, 以及面网格尺寸5 mm、体网格总数1 820万单元两个方案进行LES计算的对比分析.文中所涉及的测点位置见文献[22].由文献[22]可知,在MIRA三厢车体背部,5 mm网格方案的定常解不对称性显著,而1.5 mm网格方案则具有明显的对称分布特征.因此, 本节研究同时明确了初始场的不对称性对LES数值仿真结果的影响.
监测气动阻力系数CD及气动升力系数CL值,两种网格方案计算所得时均气动力系数、标准差及相对试验值的误差见表 1.由表可知,两种网格方案的时均CD值相近,仅相差0.001 3,但5 mm网格方案的CD标准差略大; 两种网格方案的时均CL值相差较大,5 mm网格方案对应的CL相对误差达到134.7%,且该方案的CL标准差也较大.由此表明:5 mm方案的准确性低于1.5 mm方案,且迭代过程的振幅较大,收敛性差于1.5 mm网格方案.
| 下载CSV 表 1 CD及CL的对比 Tab.1 Comparison of CD and CL |
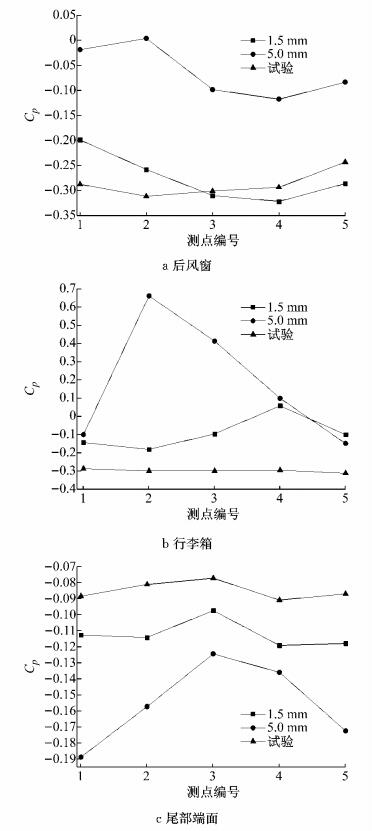
在后风窗、行李箱及尾部端面处各选择一组监测点进行详细比较.图 9给出了压力系数时均值分布结果.由图可知,在后风窗区域,由于流动的非定常性显著致使两种网格方案计算结果的对称性均不理想; 在尾部端面及底部上翘面区域,1.5 mm网格方案的对称性明显优于5.0 mm方案; 1.5 mm方案计算结果的准确性明显高于5.0 mm方案.
|
图 9 不同部位压力系数分布 Fig.9 CP distribution on each particular location |
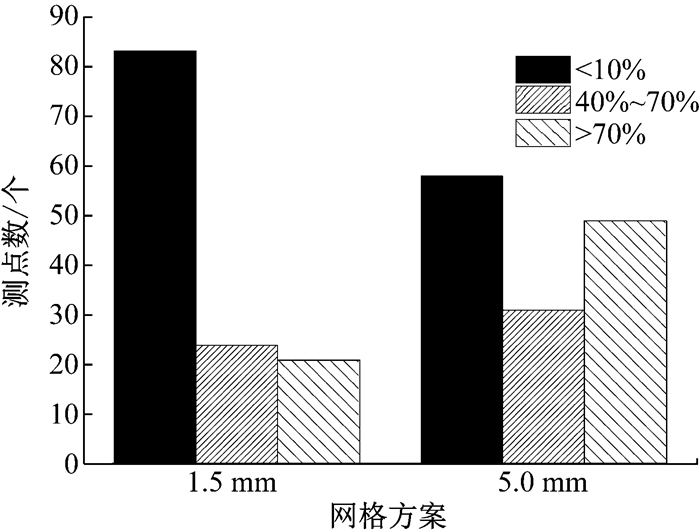
图 10给出了两种网格方案在MIRA三厢车体表面254个测压点处压力系数时均值相对于风洞试验值的误差统计结果.由图可知,1.5 mm方案的计算准确性明显高于5.0 mm方案; 在 < 10%的误差范围内,1.5 mm方案对应83个测点,5.0 mm方案仅对应58个测点; 在>70%的误差范围内,1.5 mm方案对应21个测点,5.0 mm方案则对应49个测点.综合表 1、图 9及图 10的结果可知,网格数量和初始场对LES数值计算结果的准确性影响显著,且初始场的不对称性几乎无法通过LES计算过程予以消除.
|
图 10 压力系数误差统计 Fig.10 Error statistics of CP |
通过对两种网格方案在气动力预测准确性、车身表面压力预测准确性及流场结构对称性的综合考察,面网格尺寸1.5 mm、体网格总数6 745万单元的网格方案适用于LES仿真计算.
4 湍流模型的对比基于针对LES方法的时间步长、步长内迭代步数、初始场和网格方案的研究成果,本节采用DSL模型、WALE模型和DKE模型对MIRA三厢车体气动性能进行仿真计算,通过将气动性能参数计算值与风洞试验值进行对比分析,研究3种亚格子模型的计算准确性.文中涉及的测点位置见文献[22].
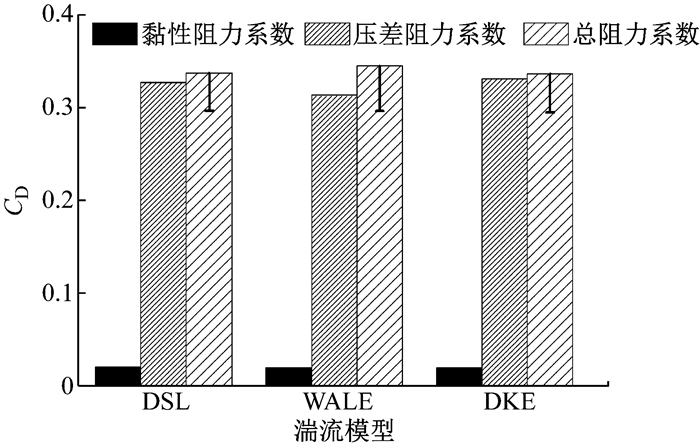
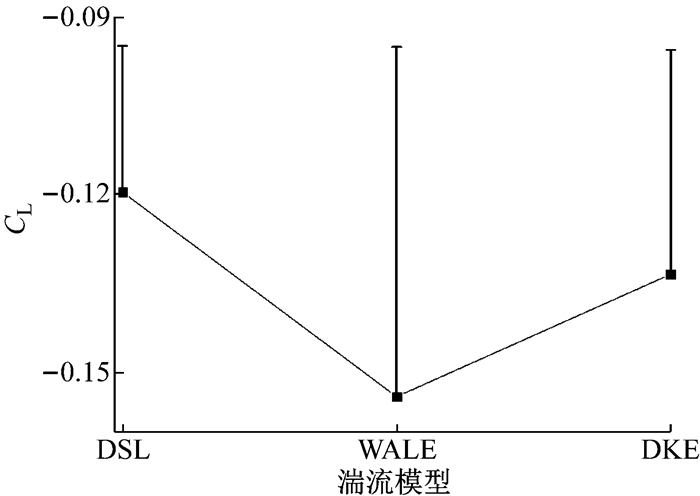
图 11为气动阻力系数时均值的对比结果,倒T线为相对于风洞试验值的误差线.由图可知:DKE模型计算的CD值为0.338,相对误差13.83%,计算准确性最高; WALE模型计算的CD值为0.345,相对误差16.32%,计算准确性最低.图 12为气动升力系数时均值的对比结果.由图可知,3种亚格子模型计算所得CL值均小于试验值; DSL模型的CL计算值为-0.119,误差最小,WALE模型的CL计算值为-0.154,误差最大.
|
图 11 3种模型气动阻力系数对比 Fig.11 Comparison of CD |
|
图 12 3种模型气动升力系数对比 Fig.12 Comparison of CL |
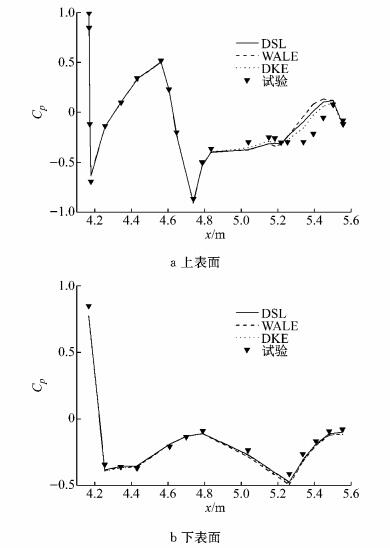
图 13显示了车身纵向对称面的压力系数分布.3种模型针对车体后风窗及行李箱上部表面(x坐标处于[5.2 m,5.55 m]范围)的压力系数计算值之间差异显著,与试验值相比DKE模型的计算准确度最高; 3种模型计算所得车身下表面压力系数之间的差异较小,预测能力相当.
|
图 13 对称面压力系数分布 Fig.13 Cp distribution on symmetry plane |
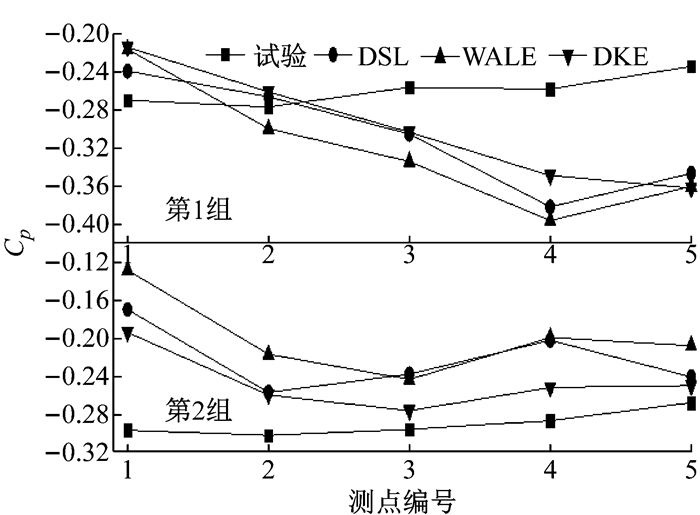
图 14显示了在后风窗表面所选取的2组共10个测点的压力系数时均值分布.由图可知,3种亚格子模型在该区域的预测结果趋势较为一致; 与试验值相比,DKE模型计算所得10个测点处的Cp值误差皆较小,DSL模型次之,WALE模型的时均值计算误差最大.
|
图 14 后风窗压力系数分布 Fig.14 Cp distribution on rear window |
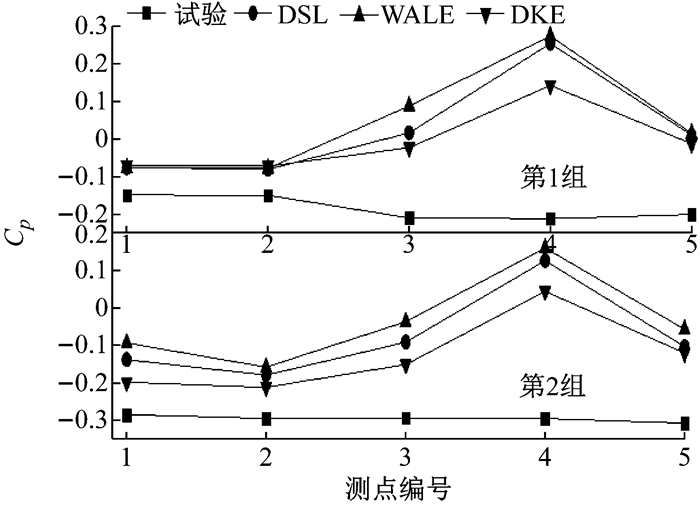
图 15给出了在行李箱表面所选取的2组共10个测点的压力系数时均值分布.由图可知,3种亚格子模型计算所得时均结果与试验值之间的趋势一致性较差; 与具体的试验值相比,DKE模型的计算准确性最高,DSL模型次之,WALE模型在该区域的计算准确性最低.
|
图 15 行李箱压力系数分布 Fig.15 Cp distribution on trunk |
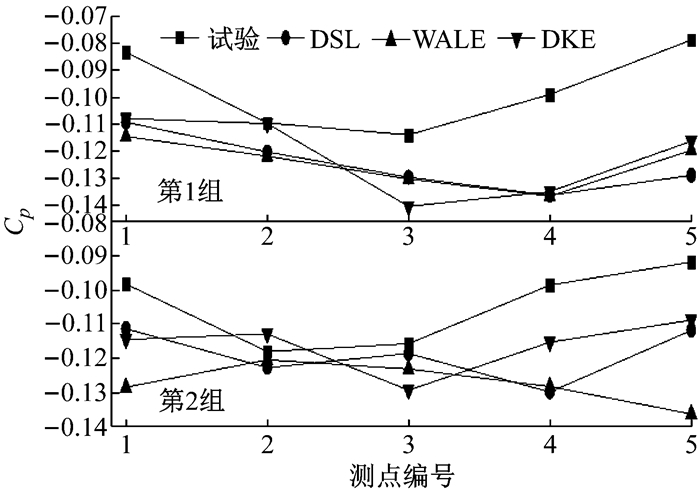
车体尾部端面所选取的10个测点处压力系数的分布如图 16所示.由图可知,3种亚格子模型中,DKE模型的计算结果与试验值之间的趋势一致性最高,DSL与WALE模型的趋势一致性相当; 与具体的试验值相比,3种模型的预测能力相当.
|
图 16 尾部端面压力系数分布 Fig.16 Cp distribution on tail end |
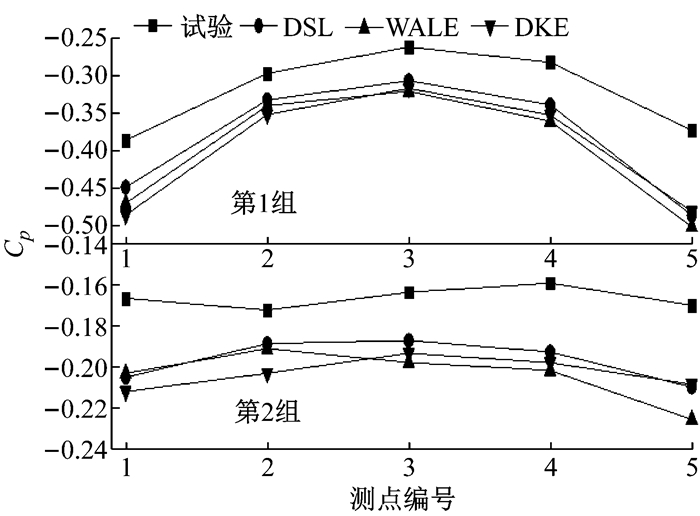
车体底部上翘面所选取的10个测点处压力系数的分布如图 17所示.由图可知,3种亚格子模型中,DSL模型的计算结果与试验值之间的趋势一致性最高,DKE与WALE模型的趋势一致性相当; 与具体的试验值相比,DSL模型的计算准确性最高,DKE与WALE模型的计算能力相当.
|
图 17 上翘面压力系数分布 Fig.17 Cp distribution on upswept surface |
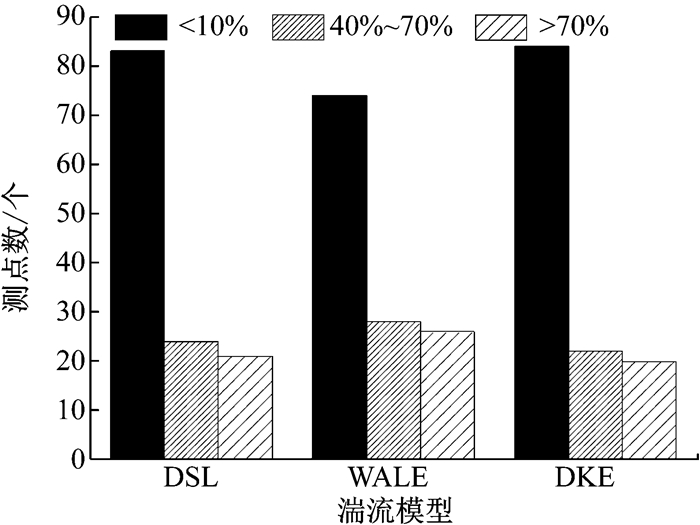
图 18给出了3种亚格子模型在MIRA三厢车体表面254个测压点处压力系数时均值相对于风洞试验值的误差统计结果.由图可知,在 < 10%的误差范围内,DKE模型的监测点数量最多; 在>70%的误差范围内,DKE模型有20个监测点,DSL模型和WALE模型分别有21个和26个监测点,这些测点主要分布在行李箱边缘和后风窗侧面区域.
|
图 18 压力系数误差统计 Fig.18 Error statistics of Cp |
(1) 应用大涡模拟法计算MIRA三厢车体的气动性能过程中,时间步长推荐值为5×10-4s,时间步长内最大迭代步数推荐值为25步,1:3缩尺比模型的面网格推荐尺寸为1.5 mm,推荐采用低雷诺数湍流模型获得定常初始场,定常初始场应具备明显的左右对称特征.
(2) 对三维性较弱的车体头部及顶部区域流动,3种亚格子模型的时均结果预测能力相当,均与试验值符合较好; 对存在地面效应和局部分离的底部区域流动,DSL模型的预测能力最强.
(3) 对三维性较强、存在大分离结构且非定常特征显著的车体后风窗、行李箱及尾部区域流动,DKE模型时均结果的计算准确性最高,WALE模型的计算准确性最低.
(4) DKE模型对CD值的计算结果最接近试验值,DSL模型对CL值的计算结果误差最小; 以车身表面254个测点处压力系数时均值为准,DKE模型的计算准确性略优于DSL模型,WALE模型的计算准确性最低.
| [1] |
SMAGORINSKY J. General circulation experiments with the primitive equations[J]. Monthly Weather Review, 1963, 91(3): 99 DOI:10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;2 |
| [2] |
马金花, 金生, 贺德馨, 等. 圆柱体绕流的数值模拟[J]. 山东建筑工程学院学报, 2001, 2(6): 45 MA Jinhua, JIN Sheng, HE Dexin, et al. Numerical simulation of fluid flow around a single circular-cylinder[J]. Journal of Shandong Institute of Architecture and Engineering, 2001, 2(6): 45 |
| [3] |
苑明顺. 高雷诺数圆柱绕流的二维大涡模拟[J]. 水动力学研究与进展(A辑), 1992(7): 614 YUAN Mingshun. Two-dimensional large eddy simulation of flow past a circular cylinder at high Reynold number[J]. Journal of Hydrodynamics (Series A), 1992(7): 614 |
| [4] |
MURAKAMI S, MOCHIDA A. On turbulent vortex shedding flow past 2D square cylinder predicted by CFD[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1995, 54(94): 191 |
| [5] |
YU D H, KAREEM A. Numerical simulation of flow around rectangular prism[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1997, 67(2): 19 |
| [6] |
童兵, 祝兵, 周本宽. 方柱绕流的数值模拟[J]. 力学季刊, 2002, 23(1): 77 TONG Bing, ZHU Bing, ZHOU Benkuan. Numerical simulation of flow around square cylinder[J]. Chinese Quarterly of Mechanice, 2002, 23(1): 77 |
| [7] |
苏铭德. 直方管内充分发展湍流的大涡模拟第一部分[J]. 空气动力学学报, 1995, 13(1): 1 SU Mingde. Larger eddy simulation of fully-developed turbulent flow in a straight duct: part Ⅰ[J]. ACTA Aerodynamica Sinica, 1995, 13(1): 1 |
| [8] |
杨建明, 吴玉林, 曹树良. 流体机械中高雷诺数流动的大涡模拟[J]. 工程热物理学报, 1998, 19(2): 184 YANG Jianming, WU Yulin, CAO Shuliang. Large eddy simulation of high Reynolds number flow in fluid machinery[J]. Journal of Engineering Thermophysics, 1998, 19(2): 184 |
| [9] |
刘沛清, 邓学蓥. 绕翼型分离流结构的数值研究[J]. 航空学报, 1997, 18(4): 2 LIU Peiqing, DENG Xueying. Numerical study of separated flows over an isolated airfoil[J]. Acta Aeronautica et Astronautica Sinica, 1997, 18(4): 2 |
| [10] |
刘宁宇, 陆夕云, 庄礼贤. 分层剪切湍流大涡模拟的一种动力学亚格子尺度模型[J]. 中国科学(A辑), 2000(2): 145 LIU Ningyu, LU Xiyun, ZHUANG LIxian. A subgrid scale model for large eddy simulation of shear turbulence[J]. Science in China (Series A), 2000(2): 145 |
| [11] |
CHENG Y, LIEN F S, YEE E, et al. A comparison of large eddy simulations with a standard k-ε Reynolds-averaged Navier-Stokes model for the prediction of a fully developed turbulent flow over a matrix of cubes[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2003, 91(11): 1301 |
| [12] |
王兵, 张会强, 王希麟, 等. 后台阶流动再附着过程的大涡模拟研究[J]. 应用力学学报, 2004, 21(3): 17 WANG Bing, ZHANG Huiqiang, WANG Xilin, et al. Investigation on the reattachment process of backward-facing step flow using large eddy simulation[J]. Chinese Journal of Applied Mechanics, 2004, 21(3): 17 |
| [13] |
CONSTANTINESCU G S, KRAJEWSKI W F, OZDEMIR C E, et al. Simulation of airflow around rain gauges: comparison of LES with RANS models[J]. Advances in Water Resources, 2007, 30(1): 43 DOI:10.1016/j.advwatres.2006.02.011 |
| [14] |
KRAJNOVIC S, DAVIDSON L. Flow around a simplified car, part 1: large eddy simulation[J]. Journal of Fluids Engineering, 2005, 127(5): 907 DOI:10.1115/1.1989371 |
| [15] |
KRAJNOVIC S, DAVIDSON L. Flow around a simplified car, part 2: understanding the flow[J]. Journal of Fluids Engineering Transactions of the Asme, 2005, 127(5): 919 DOI:10.1115/1.1989372 |
| [16] |
SERRE E, MINGUEZ M, PASQUETTI R, et al. On simulating the turbulent flow around the Ahmed body: a French-German collaborative evaluation of LES and DES[J]. Computers & Fluids, 2013, 78(12): 10 |
| [17] |
ALJURE D E, LEHMKUHL O, RODRíGUEZ I, et al. Flow and turbulent structures around simplified car models[J]. Computers & Fluids, 2014, 96(96): 122 |
| [18] |
HINZE J O. Turbulence[M]. New York: McGraw-Hill, 1975
|
| [19] |
LILLY D K. A proposed modification of the germano subgrid‐scale closure method[J]. Physics of Fluids A Fluid Dynamics, 1992, 4(4): 633 |
| [20] |
NICOUD F, DUCROS F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor[J]. Flow, Turbulence and Combustion, 1999, 62(3): 183 DOI:10.1023/A:1009995426001 |
| [21] |
KIM W W, MENON S. Application of the localized dynamic subgrid-scale model to turbulent wall-bounded flows[R]. [S. l. ]: AIAA Technical Paper, 1997.
|
| [22] |
杨志刚, 周永祥, 朱晖, 等. 低雷诺数k-ε模型钝体绕流场预测能力研究[J]. 同济大学学报(自然科学版), 2017, 45(3): 413 YANG Zhigang, ZHOU Yongxiang, ZHU Hui, et al. Comparison of low Reynolds number k-ε models in predicting complicated flow field around a bluff body[J]. Journal of Tongji University (Natural Science), 2017, 45(3): 413 |
 2018, Vol. 46
2018, Vol. 46

