2. 浙江省交通规划设计研究院,浙江 杭州 310000
2. Zhejiang Provincial Institute of Communications Planning, Design and Research, Hangzhou 310000, China
我国沿江河地区水网密布,河谷场地的中小跨径梁式桥分布广泛.结构体系上一般采用简支梁桥或连续梁桥,而基础形式以桩基础为主,分为群桩基础和桩柱式基础.桥址所在的河谷场地多包含饱和、半饱和砂土层,即存在大量的可液化土层.近些年全球各地地震频发,地震导致的土体液化所引起的桥梁震害屡有报道[1-3].震害主要有:液化引起堤岸土体侧向大变形、桥台沉陷、桩基变形、墩柱倾斜和落梁等[4-5].针对以上震害,国内外学者进行了液化场地桥梁结构的地震反应分析研究.其中多数针对单墩、单桩模型,主要包括液化场地离心机[6-8]、振动台模型试验[9-10]的模拟和液化条件下桩基础的数值分析[11-13].另外,少数研究对液化场地全桥进行了地震反应分析[14-16],但这些研究亦主要针对桥梁下部结构.相比之下,对液化场地桥梁上部结构的分析很少.王晓伟等[17]对我国典型可液化河谷场地群桩基础简支桥梁进行了地震反应分析,揭示了场地液化对该类梁桥上、下部结构各部件的地震反应规律的影响,分析结果与国内外报道的震害现象相吻合.然而,梁桥因结构体系不同、基础形式不同,在可液化河谷场地中的地震反应规律可能有差异.更重要的一点,目前我国桥梁抗震设计规范[18]对于场地液化的考虑尚不全面,因而大量已建的,特别是建造年代久远的中小跨径桥梁在场地液化情况下的地震反应特性尚不明确.换言之,场地液化对不同结构体系、基础形式的中小跨径梁桥的地震反应影响程度如何,是一个亟待解决的问题.这也是本研究的立足点.本文首先介绍二维场地-结构一体化模拟方法.然后,建立典型河谷场地的三类常见梁式桥的数值模型,包括群桩基础简支梁桥、群桩基础连续梁桥和桩柱式基础简支桥梁,进行地震反应分析,研究可液化河谷场地下不同结构体系、基础形式的梁桥地震反应规律,以及场地液化的影响程度,为液化场地已建桥梁的加固、新建桥梁的设计提供参考.
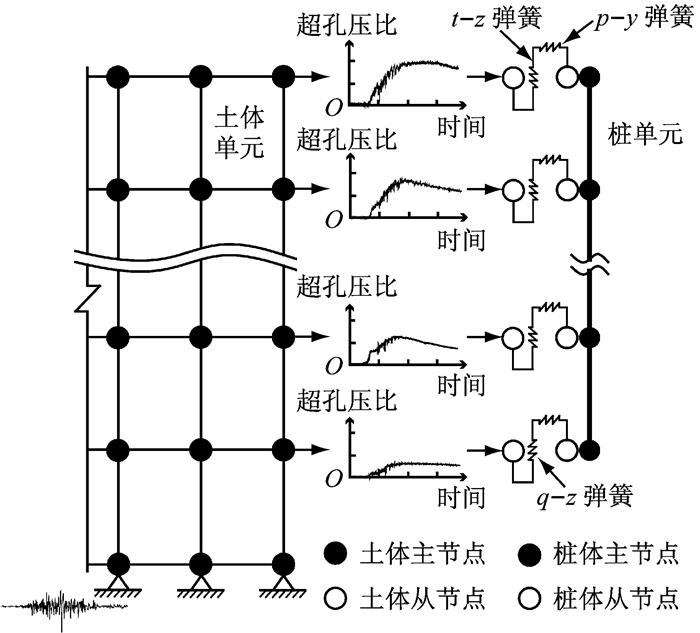
1 二维场地-结构一体化模拟方法 1.1 模拟方法概述图 1给出了二维场地-结构一体化模拟方法的图示.该方法基于有限元平台OpenSees[19].数值模型主要由土体、结构和连接单元组成.土体单元基于平面应变理论,动力方程为基于Boit土-水耦合作用理论的U-P公式[20](U为土颗粒位移、P为孔隙压力),可考虑土体液化所伴随的孔隙水压上升、有效应力下降等.结构单元可采用弹性或非线性梁柱单元模拟,具体根据所研究对象的受力情况和模型复杂程度而定.土和结构的相互作用采用土弹簧,可考虑超孔压比变化所导致的土压力峰值变化的效应,其中桩身水平向采用p-y弹簧(p为水平土抗力,y为土-桩水平相对位移),桩侧竖向摩擦采用t-z弹簧(t为桩侧摩擦力,z为土-桩竖向相对位移),桩尖竖向采用q-z弹簧(q为桩尖竖向土抗力).左、右边界土体不可排水,表层土体可排水,土体底部固定,模拟基岩面,地震动在此输入.各部件的主要特征介绍如下.
|
图 1 土-结构相互作用模拟方法 Fig.1 Modeling of soil-structure interaction |
砂土采用对孔隙水压变化较为敏感的多屈服面塑性材料本构[21],可模拟砂土在循环荷载作用下出现的剪胀、流动等现象,包括剪切大变形效应,并且特别考虑了液化引起的砂土永久剪应变循环积累效应.
黏土采用对孔隙水压变化不敏感的多屈服面塑性本构模型[22],即孔隙水压的变化对土体剪切特性的影响较小.
1.3 土-结构相互作用对于可液化砂土,桩身与土体侧向、竖向相互作用采用考虑液化影响的p-y、t-z弹簧[23-24].对于非液化黏土,土弹簧采用传统的p-y、t-z弹簧[23].由于桩尖埋深一般很深,土质较密,液化的影响很小,故桩尖与土体的竖向相互作用采用不考虑液化影响的q-z弹簧[23].
对于考虑液化的p-y、t-z弹簧,极限强度pult_liq满足下式:
| $ {p_{{\rm{ult\_liq}}}} = {p_{{\rm{res}}}} + \left( {{p_{{\rm{ult}}}} - {p_{{\rm{res}}}}} \right)\frac{{\sigma '}}{{{{\sigma '}_0}}} $ | (1) |
式中:pult为不考虑液化的桩-土相互作用力;pres为残余强度;σ′、σ′0分别为土体单元的实时、初始平均有效应力.引入土体超孔压比ru的定义,该值越大说明液化程度越高.
| $ {r_{\rm{u}}} = 1 - \frac{{\sigma '}}{{{{\sigma '}_0}}} $ | (2) |
结合式(1)可知,液化后p-y、t-z弹簧的极限强度随相邻的土体单元平均超孔压比的增大而减小,即随液化程度的加深而减小.
上述场地-结构一体化模拟方法已通过离心机试验[25]的数值模拟得到了验证,考虑到本文的简明性,具体模拟结果见文献[17, 26-28].
2 可液化河谷场地梁式桥数值模型 2.1 场地和不同形式梁桥概括在对实际工程调研的基础上,以典型的河谷软土场地三跨简支、连续梁桥为背景,基础形式包括群桩基础和桩柱式基础,共形成3组工况:
G1——群桩基础简支梁桥;
G2——群桩基础连续梁桥;
G3——桩柱式基础简支梁桥.
本文研究纵桥向地震反应规律.图 2给出了工况G1的场地和结构布置:桥梁跨径布置为3×30 m,T型截面主梁,桥墩和桩基础直径分别为1.5 m和1.2 m.图 3给出了该工况各部件的几何尺寸.桩基础埋置深度较长,伸入稳定土层的长度较长,满足现行桥梁抗震设计规范中有关液化场地桩基础埋深的要求[18];上、下部结构采用板式橡胶支座连接,两岸桥台上、左墩(P1)顶右侧布置四氟滑板式橡胶支座,其余位置布置普通板式橡胶支座.对于工况G2,P2墩设置普通板式橡胶支座,其余位置设置四氟滑板式橡胶支座.对于工况G3,与工况G1的区别在于P1、P2墩的桩基础采用桩柱式基础,桩径1.5 m,与桥墩直径相同(实际工程通常是桥墩直径与桩基础直径相同或桥墩直径稍小于桩基础直径,本文简化处理为相同直径),没有承台,桥台处桩基与工况G1相同.3组工况具有相同的土层分布,自上而下分为4层,各层土的物理性质见表 1.

|
图 2 桥梁结构布置和场地土层情况 Fig.2 Bridge structural configurations and soil layer profiles |

|
图 3 桥梁各部件截面尺寸(单位:m) Fig.3 Geometric dimensions of bridge components (unit:m) |
| 下载CSV 表 1 河谷场地的土层材料性质 Tab.1 Material properties of soil on the valley ground |
建模时取主梁、墩柱、桥台和桩基础的横桥向半结构,建立结构的二维平面模型,土体单元划分见图 2,单元厚度不超过2 m,这样的划分方式可保证高频地震波在从基底向地表的传播过程中不被过滤[15].考虑到土体材料和桩-土相互作用弹簧的高非线性特性,为提高整体有限元模型的计算收敛性和效率,桩、墩和主梁均以弹性梁柱单元模拟,后文将讨论这样的简化模拟方式的合理性.滑动支座采用理想弹塑性本构模拟,按板式橡胶支座的型号,初始刚度取6 600 kN·m-1;固定支座采用线弹性材料本构,刚度与滑动支座的初始刚度相同.为保守地获得主梁与桥台、主梁与主梁之间相对变形的地震需求,忽略主梁与桥台、主梁与主梁的碰撞,即伸缩缝未模拟.表 2列出了模型中土体本构的参数,液化后残余强度pres=0.3pult[24].桩-土、桥台-土相互作用的模拟采用上节所述结构-土相互作用模拟方法.
| 下载CSV 表 2 数值模型中各土层的本构参数 Tab.2 Parameters of soil constitutive models |
值得说明的是,对于二维场地的平面应变模型,需要通过合理选取土体单元的平面外尺寸,来近似模拟桩身对土体侧向变形的阻碍效应.本文根据研究对象的特点(直径1.2~1.5 m桩基础),对土体单元平面外尺寸作如下处理:模型两侧边界的土体模拟为远场土体(图 2),平面外尺寸取10 km,而其余土体平面外尺寸取15 m[14, 17].
基于Kramer等[29]有关液化场地边界条件处理方法的研究,本文场地边界条件为底部土体单元各节点的水平、竖向自由度约束.顶层土体可排水;对于液化场地,基底及两侧边界土体不可排水;对于非液化场地,模型基底及两侧边界可排水,同时土体渗透系数设为大值(1 m·s-1),以阻止孔隙水压的升高,避免土体液化[30].因此,上述3种梁桥形式的工况分别存在液化与非液化2种情况,共形成6个分析工况.
非线性时程反应分析中采用刚度比例阻尼,比例系数为0.006,采用Krylov-Newton算法[31]和Newmark积分方法(系数β=0.302 5、γ=0.6).
2.3 地震动采用1971年圣费尔南多地震记录作为输入,峰值加速度调整为0.5g(g=9.81 m·s-2),目的在于激发显著的液化.图 4给出了该地震动的加速度时程曲线和加速度反应谱.值得说明的是,为了得到稳定的震后反应值,将加速度时程延长10 s的零值.另外,由于模型中加速度从土层底部输入,深度较大,接近基岩,土质一般很硬,故地震波的特征周期一般很短,从加速度反应谱上可知,选用的地震动特征周期(Tg)很短,即Tg=0.16 s,满足上述要求.

|
图 4 圣费尔南多地震动 Fig.4 San Fernando ground motion |
本节首先给出液化土孔隙水压的变化,评估场地液化程度.然后从整体震后变形、桩基础变形分布、桥墩漂移率、滑动支座位移4个方面,分析可液化河谷场地中不同形式中小跨径梁式桥的地震反应规律,以及液化对此的影响程度.
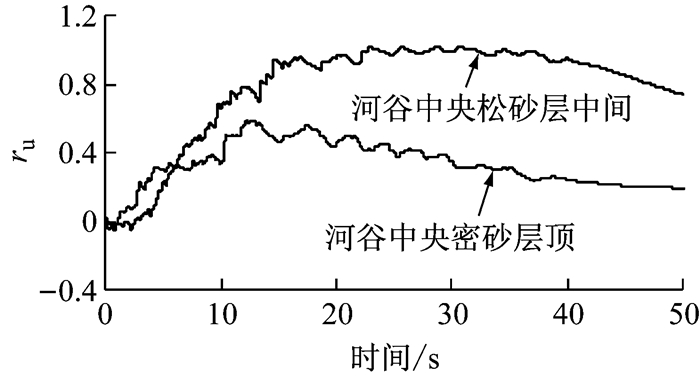
3.1 孔隙水压变化由于3组工况的场地相同,故地震下孔隙水压发展基本相同.图 5代表性地给出了场地液化情况下工况G1砂土层的孔隙水压变化.由图可见,饱和松砂层中间ru的峰值达到了1.0,说明松砂层发生了完全的液化,而密砂层顶ru的峰值约达到0.6,说明密砂层顶发生了轻微的液化.
|
图 5 砂土层孔隙水压变化 Fig.5 Buildup of pore water pressure in sand layers |
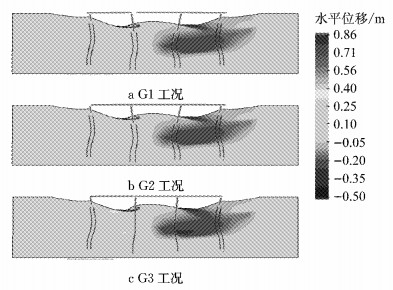
图 6给出了地震后,液化场地G1~G3工况的变形图示,通过通用前后处理程序GiD[32]得到.图中,正值代表位移向右,负值代表向左.
|
图 6 震后液化场地结构整体残余变形 Fig.6 Post-earthquake global residual deformation of liquefied ground |
由于场地条件以及地震动输入相同,各工况的场地残余变形基本一致,即河岸两侧土体向河中心方向移动,且总体上右岸土体比左岸土体变形更大,左岸最大位移为0.86 m,右岸最大位移为0.50 m.这是由于右岸的液化土层较厚,从河岸到河谷的土体累积剪切变形相对更大.对于桩基础的残余变形,无论是群桩基础,还是桩柱式基础,变形形态与土体变形趋势基本吻合,即桩基础发生同向变形,说明桩基础的变形主要是由于场地变形所引起的.比较工况G1和G3(图 6a和c),桩柱式基础的残余变形比群桩基础稍小,这是由于桩柱式基础的水平刚度比群桩基础单桩的水平刚度大.此外,各工况的桥墩P1和P2均向河岸方向倾斜,这是由于桩基础变形引起的承台(或墩底)转动所致.
3.3 液化场地桩基础的变形分布图 7给出了震后液化场地各工况的桩基础残余变形,其中图 7a给出了不同结构体系(G1、G2)桥墩P1、P2处群桩基础变形的对比,可知简支或连续的梁桥体系对桩基础震后变形的影响很小,因为这两种体系的本质区别是上部结构的惯性力差别显著,而桩基础的残余变形主要由土体的几何变形作用所引起.由图 7a可知,不同体系下群桩基础桩身最大相对变形约为0.15 m,出现在竖向标尺约-20 m处的P2墩群桩基础中(埋深约12.5 m,10倍桩径).图 7b给出了不同基础形式(G1、G3)桩基础变形.由图可知,群桩基础在黏土层下部和密砂层的变形大于桩柱式基础,这是由于群桩基础中单桩桩径较小,水平刚度较小;而群桩基础在松砂层的位移小于桩柱式基础,这是由于群桩基础的承台阻碍了桩顶的水平位移.同时,从图 7b可知,桩柱式基础的桩身最大水平相对变形也约为0.15 m,与群桩基础工况相似,这是因为桩基础的变形主要是由场地变形引起的,而不同基础形式下场地的残余变形很接近(见图 6).但最大变形位置比群桩基础工况稍浅,也就是说,桩柱式基础的变形程度稍小于群桩基础的单桩.另外,从图 7b中可推测:群桩基础承台的转角明显大于桩柱式基础在土面的转角,导致群桩基础工况(G1)的桥墩震后变形明显大于桩柱式基础工况(G3).

|
图 7 液化场地桩基础震后残余变形分布 Fig.7 Post-earthquake pile residual deformation distribution of liquefied ground |
此外,值得说明的是,以往有关桥梁地震易损性的研究中,往往采用承台的水平位移来划分损伤等级.对于与本文研究对象很相似的液化场地群桩基础的情况,Wang等[32]指出承台水平位移在7.4、11.2、26.3、39.5 cm时分别对应轻微、中度、严重、完全损伤.而本文模型中群桩基础承台的水平位移约13 cm(图 7),大致属于中度损伤,非线性程度相对而言不高.加之桩基础的变形主要由场地的位移所控制,故采用弹性单元模拟基本上是合理的.尽管如此,今后的相关研究宜考虑桩基础的非线性,以期更准确地模拟桩基础在液化场地中的抗震行为.
3.4 桥墩的漂移率图 8给出了液化和非液化情况下固定墩P2的漂移率时程曲线.这里漂移率的定义为墩顶和墩底水平位移差与墩高的比值,其中正值代表向右岸倾斜,负值代表向左岸倾斜.总体上,场地液化增加了桥墩漂移率的峰值和震后残余值.值得一提的是,对比地震动输入时程曲线(图 4),增加的10 s零值保证了稳定的残余反应值.

|
图 8 桥墩漂移率时程曲线 Fig.8 Time history of column drift ratio |
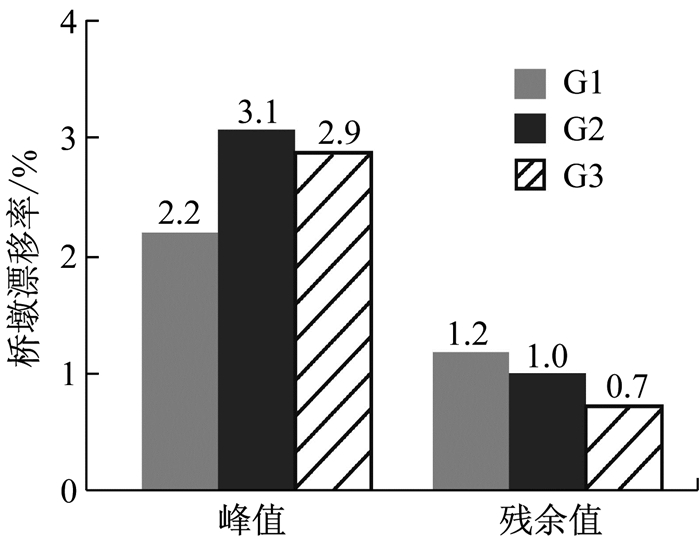
图 9给出了液化场地中,各工况P2墩漂移率的峰值和残余值的对比.值得说明的是,桥墩漂移率的峰值是由土体几何变形作用和上部结构惯性作用共同作用的结果,而残余值主要是由土体几何变形作用所决定.
|
图 9 液化场地桥墩漂移率峰值、残余值比较 Fig.9 Comparison of peak and residual values of column drift ratio of liquefied ground |
从图 9可知,工况G2(群桩基础连续梁桥)桥墩的峰值漂移率在3种桥型中最大,主要是由较大的上部结构惯性力和较大的桩身几何变形共同决定的.进一步地,对比工况G1和G2可知,较大的惯性力作用显著增加了桥墩漂移率的峰值(从2.2%提高到3.1%,约提高40%).因为由图 7a可知,G1、G2工况下群桩基础的变形基本相同,承台转角对于桥墩漂移率的贡献应当也很接近.对于桥墩漂移率的残余值,桩柱式基础工况(G3)明显小于群桩基础工况(G1、G2).这是由于漂移率的残余值主要由土体几何变形作用决定,即土体几何作用引起的承台(或墩底)的转角.
图 10给出了液化场地下工况G1和G3的桥墩漂移率和对应承台(或墩底)的转角时程曲线.值得说明的是,桥墩的漂移率是两部分的和,一是桥墩自身的相对变形,二是承台(或墩底)的转角.从图 10可知,总体上,转角对桥墩漂移率的贡献均较大,定量上看接近或超过50%,换言之,桥墩自身相对变形的贡献相对较小.对图中实、虚曲线作差可大致发现,群桩基础工况桥墩自身相对变形产生的漂移率不超过1%,而桩柱式基础工况不超过1.5%.根据以往桥梁易损性分析中有关桥墩漂移率损伤等级的研究,桥墩自身相对变形引起的漂移率在1.5%以内时,桥墩往往处于弹性或低非线性的状态[33-35].因此,本文采用弹性梁柱单元模拟桥墩大体上是合理的.具体来看,对于群桩基础工况,桥墩的漂移率与对应承台转角同步,从图 10a的数值上看,承台转动是桥墩漂移的主因,换言之,对于采用群桩基础形式的中小跨径梁式桥,应重点关注承台的转角.相比之下,对于桩柱式基础工况,墩底转角对桩柱式基础工况桥墩漂移率的贡献稍小.

|
图 10 液化场地桥墩漂移率和墩底转角时程曲线 Fig.10 Column drift ratio and rotational angle of column bottom of liquefied ground |
场地液化情况下支座和桥台处伸缩缝的位移地震反应是判断桥梁是否会发生落梁或碰撞破坏的重要指标.本节分析探讨不同形式梁式桥在非液化、液化场地中P1墩处支座以及左、右两桥台伸缩缝位移的地震反应峰值.
表 3列出了P1墩滑动支座位移峰值,其中比值大于1代表场地液化会增加支座位移反应,小于1代表场地液化会减小支座位移反应.对于非液化的情况,支座向左位移值明显大于向右位移值,而液化的情况下,工况G1、G2支座向右的位移值明显增大(分别增加197%和32%),说明群桩基础简支梁桥的中跨极易在场地液化的情况下发生落梁,这是由于G1、G2工况的P1墩向左岸倾斜严重,故而支座向右的位移增大,相应地支座向左的位移减小.因此,液化场地群桩基础简支梁桥应加强防落梁措施的设计.相比之下,工况G3支座向右位移值显著减小(40%),而向左位移仅稍有增加(5%).综上可知,桩柱式基础简支梁桥的跨中滑动支座位移受场地液化的影响较小.
| 下载CSV 表 3 P1墩滑动型支座位移峰值 Tab.3 Peak deformation of bearing on Pier P1 |
表 4列出了左、右桥台处伸缩缝伸长和缩短的峰值.比较G1和G2工况可知,无论是液化或非液化的情况,连续梁桥的伸缩缝伸长和缩短值均大于简支梁桥,说明连续梁桥比简支梁桥在桥台伸缩缝处需要更大的防止主梁和桥台发生碰撞的宽度以及更长的防止落梁的搭接长度.比较液化和非液化情况可知,场地液化时,各工况左、右桥台伸缩缝的伸长值均减小(3%~49%),说明桥台处落梁的风险在场地液化的情况下并未增加,这是由于场地液化的情况下桥台土体向河中央移动.与之相比,工况G1左、右桥台处伸缩缝缩短值显著增加(分别增加41%和78%);类似地,工况G2右桥台处伸缩缝缩短值亦有所增加(27%),说明该两类桥型在场地液化的情况下容易发生碰撞,造成桥台的损坏;相比之下,工况G3左、右桥台伸缩缝的缩短值均稍有减小.综上可知,对于所研究的3种不同形式的中小跨径梁桥,场地液化的情况下,桩柱式基础简支梁桥的落梁和碰撞风险均较小.
| 下载CSV 表 4 桥台处伸缩缝伸长、缩短的峰值 Tab.4 Expansion joint deformation at abutments |
本文针对典型可液化河谷场地的三跨梁桥,采用数值分析的方式,选取特征周期较短的0.5g圣费尔南多实测地震波作为地震输入,比较了不同结构体系(简支、连续)、不同基础形式(群桩、桩柱式)的梁式桥的地震反应规律.在该地震动作用下,得到如下结论:
(1) 如果河谷场地遭受地震液化,震后两侧土体会向河中心移动,推动桩基础发生同向变形,导致桥墩向岸边倾斜.这一趋势,基本不受结构形式影响.
(2) 场地液化后,群桩基础的承台会发生较大的残余倾角,导致群桩基础桥墩的残余漂移率会显著大于桩柱式基础桥墩.
(3) 场地液化后,群桩基础简支梁桥中跨的墩梁相对位移会显著增大,易发生落梁震害,而桩柱式基础简支梁桥的落梁风险相对较小.总体上,液化场地梁式桥应加强防落梁措施的设计.
(4) 连续梁桥的台梁相对位移较大,易发生落梁或碰撞震害,场地液化会显著增大碰撞风险;而场地液化对群桩基础简支梁桥的台梁相对位移影响更大,会显著增大碰撞风险.因此,液化场地应加强伸缩缝的设计.
(5) 总体来说,桩柱式基础桥梁受场地液化的影响较小.
鉴于本文没有考虑场地条件、地震动的变化以及桩、墩的非线性特性对桥梁地震反应的影响,后期将研究不同场地条件、不同地震波以及桩、墩非线性特性对液化场地桩基桥梁地震反应的影响.
| [1] |
徐鹏举. 可液化场地桥梁桩基础地震反应分析与简化分析方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2011. XU Pengju. Seismic response analysis and simplified method of bridge pile foundation in liquefiable ground[D]. Harbin: Harbin Institute of Technology, 2011. |
| [2] |
BHATTACHARYA S, TOKIMATSU K, GODA K, et al. Collapse of showa bridge during 1964 niigata earthquake: a quantitative reappraisal on the failure mechanisms[J]. Soil Dynamics and Earthquake Engineering, 2014, 65: 55 DOI:10.1016/j.soildyn.2014.05.004 |
| [3] |
LIN S, TSENG Y, CHIANG C, et al. Damage of piles caused by lateral spreading — back study of three cases[C]//BOULANGER R, TOKIMATSU K. Seismic Performance and Simulation of Pile Foundations in Liquefied and Laterally Spreading Ground. Davis: ASCE, 2006: 121-133.
|
| [4] |
HAMANDA M, O'ROURKE T. Case studies of liquefaction and lifeline performance during past earthquakes, volume 1, Japanese case studies[R]. New York: NCEER, 1992.
|
| [5] |
ISHIHARA K, ACACIO A, TOWHATA I. Liquefaction induced ground damage in Dagupan in the July 16, 1990 LUZON Earthquake[J]. Soils and Foundations, 1993, 33(1): 133 DOI:10.3208/sandf1972.33.133 |
| [6] |
汪明武, TOBITA T, IAI S. 倾斜液化场地桩基地震响应离心机试验研究[J]. 岩土力学与工程学报, 2009, 28(10): 2012 WANG Mingwu, TOBITA T, IAI S. Dynamic centrifuge tests of seismic responses of pile foundations in inclined liquefiable soils[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(10): 2012 |
| [7] |
CHANG D, BOULANGER R, BRANDENBERG S, et al. Dynamic analyses of soil-pile-structure interaction in laterally spreading ground during earthquake shaking[C]//BOULANGER R, TOKIMATSU K. Seismic Performance and Simulation of Pile Foundations in Liquefied and Laterally Spreading Ground. Davis: ASCE, 2006: 218-229.
|
| [8] |
ARMSTRONG R, BOULANGER R, BEATY M, et al. Liquefaction effects on piled bridge abutments: centrifuge tests and numerical analyses[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 139(3): 433 |
| [9] |
唐亮, 凌贤长, 徐鹏举, 等. 液化场地桩-土地震相互作用振动台试验数值模拟[J]. 土木工程学报, 2012, 45(增刊1): 302 TANG Liang, LING Xianzhang, XU Pengju, et al. Numerical simulation of shaking table test for seismic soil-pile interaction in liquefying ground[J]. China Civil Engineering Journal, 2012, 45(Suppl.1): 302 |
| [10] |
SU L, TANG L, LING X, et al. Pile response to liquefaction-induced lateral spreading: a shake-table investigation[J]. Soil Dynamics and Earthquake Engineering, 2016, 82: 196 DOI:10.1016/j.soildyn.2015.12.013 |
| [11] |
TANG L, MAULA B, LING X, et al. Numerical simulations of shake-table experiment for dynamic soil-pile-structure interaction in liquefiable soils[J]. Earthquake Engineering and Engineering Vibration, 2014, 13(1): 171 DOI:10.1007/s11803-014-0221-5 |
| [12] |
VALSAMIS A, BOUCKOVALAS G, CHALOULOS Y. Parametric analysis of single pile response in laterally spreading ground[J]. Soil Dynamics and Earthquake Engineering, 2012, 34(1): 99 DOI:10.1016/j.soildyn.2011.09.005 |
| [13] |
Uzuoka R, Sento N, Kazama M, et al. Three-dimensional numerical simulation of earthquake damage to group-piles in a liquefied ground[J]. Soil Dynamics and Earthquake Engineering, 2007, 27(5): 395 DOI:10.1016/j.soildyn.2006.10.003 |
| [14] |
SHIN H, ARDUINO P, KRAMER S, et al. Seismic response of a typical highway bridge in liquefiable soil[C]//ZENG D, MANZARI M, HILTUNEN D. Geotechnical Earthquake Engineering and Soil Dynamics Ⅳ. Reston: ASCE, 2008: 1-11.
|
| [15] |
ZHANG Y, CONTE J, YANG Z, et al. Two-dimensional nonlinear earthquake response analysis of a bridge-foundation-ground system[J]. Earthquake Spectra, 2008, 24(2): 343 DOI:10.1193/1.2923925 |
| [16] |
ELGAMAL A, YAN L, YANG Z, et al. Three-dimensional seismic response of Humboldt bay bridge-foundation-ground system[J]. Journal of Structural Engineering, 2008, 134(7): 1165 DOI:10.1061/(ASCE)0733-9445(2008)134:7(1165) |
| [17] |
王晓伟, 李闯, 叶爱君, 等. 可液化河谷场地简支梁桥的地震反应分析[J]. 中国公路学报, 2016, 29(4): 85 WANG Xiaowei, LI Chuang, YE Aijun, et al. Seismic demand analysis of a simply supported girder bridge in liquefied or nonliquefied ground[J]. China Journal of Highway and Transport, 2016, 29(4): 85 |
| [18] |
中华人民共和国住房与城乡建设部. 城市桥梁抗震设计规范: CJJ 166—2011[S]. 北京: 中国建材工业出版社, 2011. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Guidelines for seismic design of highway bridges: CJJ 166—2011[S]. Beijing: China Architecture and Building Press, 2011. |
| [19] |
MCKENNA F. OpenSees: a framework for earthquake engineering simulation[J]. Computing in Science and Engineering, 2011, 13(4): 58 DOI:10.1109/MCSE.2011.66 |
| [20] |
BIOT M. Theory of elasticity and consolidation for a porous anisotropic solid[J]. Journal of Applied Physics, 1955, 26(2): 182 DOI:10.1063/1.1721956 |
| [21] |
YANG Z, ELGAMAL A, PARRA E. Computational model for cyclic mobility and associated shear deformation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(12): 1119 DOI:10.1061/(ASCE)1090-0241(2003)129:12(1119) |
| [22] |
ELGAMAL A, YANG Z, PARRA E. Computational modeling of cyclic mobility and post-liquefaction site response[J]. Soil Dynamics and Earthquake Engineering, 2002, 22(4): 259 DOI:10.1016/S0267-7261(02)00022-2 |
| [23] |
BOULANGER R, CURRAS C, KUTTER B, et al. Seismic soil-pile-structure interaction experiments and analyses[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(9): 750 DOI:10.1061/(ASCE)1090-0241(1999)125:9(750) |
| [24] |
BRANDENBERG S, ZHAO M, BOULANGER R, et al. P - y plasticity model for nonlinear dynamic analysis of piles in liquefiable soil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(8): 1262 DOI:10.1061/(ASCE)GT.1943-5606.0000847 |
| [25] |
WILSON D, BOULANGER R, KUTTER B. Soil-pile- superstructure interaction at soft or liquefiable soils sites-centrifuge data report for CSP3[R]. Davis: University of California at Davis, 1997.
|
| [26] |
王晓伟, 叶爱君, 罗富元. 液化场地桩柱式基础桥梁结构地震反应的敏感性分析[J]. 工程力学, 2016, 33(8): 132 WANG Xiaowei, YE Aijun, LUO Fuyuan. Seismic response sensitivity analysis of pile supported bridge structures in liquefiable ground[J]. Engineering Mechanics, 2016, 33(8): 132 |
| [27] |
WANG X, LUO F, SU Z, et al. Efficient finite-element model for seismic response estimation of piles and soils in liquefied and laterally spreading ground considering shear localization[J]. International Journal of Geomechanics, 2017, 17(6): 6016039 DOI:10.1061/(ASCE)GM.1943-5622.0000835 |
| [28] |
WANG X, SHAFIEEZADEH A, YE A. Optimal intensity measures for probabilistic seismic demand modeling of extended pile-shaft-supported bridges in liquefied and laterally spreading ground[J]. Bulletin of Earthquake Engineering, 2018, 16(1): 229 DOI:10.1007/s10518-017-0199-2 |
| [29] |
KRAMER S, ARDUINO P, SHIN H. Using OpenSees for performance-based evaluation of bridges on liquefiable soils[R]. Berkeley: Pacific Earthquake Engineering Research Center, 2008.
|
| [30] |
SU L, LU J, ELGAMAL A, et al. Seismic performance of a pile-supported wharf: three-dimensional finite element simulation[J]. Soil Dynamics and Earthquake Engineering, 2017, 95: 167 DOI:10.1016/j.soildyn.2017.01.009 |
| [31] |
SCOTT M, FENVES G. Krylov subspace accelerated newton algorithm: application to dynamic progressive collapse simulation of frames[J]. Journal of Structural Engineering, 2010, 136(5): 473 DOI:10.1061/(ASCE)ST.1943-541X.0000143 |
| [32] |
WANG Z, DUEÑAS-OSORIO L, PADGETT J. Influence of soil-structure interaction and liquefaction on the isolation efficiency of a typical multispan continuous steel girder bridge[J]. Journal of Bridge Engineering, 2013, 19(8) |
| [33] |
LI J, SPENCER B, ELNASHAI A. Bayesian updating of fragility functions using hybrid simulation[J]. Journal of Structural Engineering, 2012, 139(7): 1160 |
| [34] |
TAVARES D, PADGETT J, PAULTRE P. Fragility curves of typical as-built highway bridges in eastern Canada[J]. Engineering Structures, 2012, 40(7): 107 |
| [35] |
KIM S, SHINOZUKA M. Development of fragility curves of bridges retrofitted by column jacketing[J]. Probabilistic Engineering Mechanics, 2004, 19(1/2): 105 |
 2018, Vol. 46
2018, Vol. 46

