2. 麦克马斯特大学 土木工程系, 汉密尔顿 L8S4L7
2. Department of Civil Engineering, McMaster University, Hamilton L8S4L7, Canada
天然形成的结构性软土与重塑软土有不同的物理力学性质,天然软土的结构性会随土体变形的发展逐渐散失,土体强度会逐渐降低,甚至会出现应变软化效应,而且天然结构性软土一般是各向异性的[1-3].因此,在对处于天然结构性软土中的工程行为进行数值模拟时用重塑软土的本构模型是不尽合理的[4-6],应该用能够反映软土的结构性的本构模型.鉴于此,国内外众多学者和研究人员提出了各种不同的描述原状结构性软黏土力学性质的本构模型[7-11].为了更好地反映原状结构性软土的力学特性,一般情况下,这些模型有很强的非线性性.模型建立完成后,必须先对其进行数值算法实现,才能将其用于工程数值计算中.因此,数值实现是从模型理论到工程应用的关键环节.对于高度非线性的弹塑性本构模型,数值实现的难度比较大.本文以考虑软土结构性的SANICLAY模型[7]为例,对高度非线性弹塑性本构模型的显式算法实现展开探讨.
常微分方程组的求解方法一般可分为隐式算法与显式算法两大类.与之对应的弹塑性模型的数值实现方法也可以分为隐式算法与显式算法两大类.当采用隐式算法时,在塑性修正步一般需要采用Newton迭代法求解回退映射非线性方程组.对于高度非线性的弹塑性本构模型,Newton迭代法所对应的Jacobian矩阵很难求出,即便求出形式也较复杂.而且Newton迭代法需要保证Jacobian矩阵是可逆的,否则无法进行求解,对于高度非线性的本构模型,这点也是很难保证的.例如,对于考虑软土结构性的SANICLAY模型,在应变硬化过渡到应变软化的阶段,Jacobian矩阵不可逆.因此,隐式算法用于高度非线性弹塑性本构模型数值实现的难度比较大.与隐式算法相比较,显式算法一般不需要迭代求解复杂的非线性方程组,因此单个增量步的计算量小,但其计算精度低,并且存在误差的积累.
对于高度非线性弹塑性本构模型,如考虑土体结构性的SANICLAY模型,当采用传统的显式算法对模型进行数值实现时,计算精度难以控制.在求解本构方程所对应的常微分方程组时,为了提高显式算法的计算精度,Sloan等[12]、Cabot等[13]、Gonzalez等[14]将向前Euler法与多步法结合使用.多步法本质上是将一个增量步分为多个增量步进行求解,实际上是减小了增量步步长,这样必然会大幅降低计算效率,而且多步法并不能完全消除传统的全显式算法所具有的误差积累和精度较低的缺点.在实际应用中,为了提高计算精度,往往会将增量步步长取得很小,这无疑会降低计算效率.
采用全显式算法进行高度非线性弹塑性本构模型的数值实现时,为提高计算效率和计算精度,本文采用四阶Dormand and Prince Runge-Kutta法[15](DPRK法)代替传统的全显式算法中的向前Euler法,并且与切平面法[16-17]相结合,形成了改进显式算法.最后,对传统的全显式算法、改进显式算法和隐式算法在计算收敛性、计算效率和计算精度方面进行了对比,得出了一些有益的结论.
1 SANICLAY模型简介在原始SANICLAY弹塑性本构模型[18]的基础上,Taiebat等[7]引入了表征土体强度和旋转硬化的内变量,以考虑随着变形的发展,结构性的逐渐散失,强度的逐渐降低和各向异性的演化.该模型的屈服函数和塑性势函数是不同的,具体如下.
1.1 弹性关系模型的弹性关系依赖于球应力p和孔隙比e,具体为
| $ \mathit{\boldsymbol{\dot \sigma }} = \mathit{\boldsymbol{C}}:{{\mathit{\boldsymbol{\dot \varepsilon }}}_{\rm{e}}} $ | (1) |
| $ \mathit{\boldsymbol{C}} = \lambda '\mathit{\boldsymbol{\delta \delta }} + 2G\mathit{\boldsymbol{I}} $ | (2) |
式中:
| $ \lambda ' = K - \frac{2}{3}G,\;\;\;\;K = \frac{{1 + e}}{k}p, $ |
| $ G = \frac{{3\left( {1 - 2\mu } \right)}}{{2\left( {1 + \mu } \right)}}\frac{{1 + e}}{k}p $ |
λ′表示拉梅常数; δ与I分别表示二阶和四阶等同张量; K、G分别表示体变模量和剪切模量; μ表示泊松比; k表示e-ln p空间内回弹线的斜率.
1.2 塑性势函数及流动法则塑性势函数
| $ \begin{array}{*{20}{c}} {\psi \left( {\mathit{\boldsymbol{\sigma }},{S_{\rm{f}}},\mathit{\boldsymbol{\alpha }}} \right) = \frac{3}{2}\left( {\mathit{\boldsymbol{s}} - p\mathit{\boldsymbol{\alpha }}} \right):\left( {\mathit{\boldsymbol{s}} - p\mathit{\boldsymbol{\alpha }}} \right) - }\\ {\left( {{M^{ * 2}} - \frac{3}{2}\mathit{\boldsymbol{\alpha }}:\mathit{\boldsymbol{\alpha }}} \right)p\left( {{p_\alpha } - p} \right)} \end{array} $ | (3) |
式中: s表示偏应力;α为表征塑性势函数旋转的张量;pα确保塑性势面过当前应力点;M*=SfM; Sf表征摩擦结构性; M通过应力罗德角θα在拉压临界状态线的斜率Me和Mc间插值确定
| $ M = \mathit{\Theta }\left( {{\theta _\alpha }} \right){M_{\rm{c}}} = \frac{{2m}}{{\left( {1 + m} \right) - \left( {1 - m} \right)\cos \left( {3{\theta _\alpha }} \right)}}{M_{\rm{c}}} $ |
其中
| $ m = \frac{{{M_{\rm{e}}}}}{{{M_{\rm{c}}}}},\;\;\;\;\cos \left( {3{\theta _\alpha }} \right) = \sqrt 6 {\rm{tr}}\left( {\mathit{\boldsymbol{n}}_\alpha ^3} \right) $ |
| $ {\mathit{\boldsymbol{n}}_\alpha } = \frac{{\mathit{\boldsymbol{\gamma }}/{\chi _\alpha } - \mathit{\boldsymbol{\alpha }}}}{{\sqrt {\left( {\mathit{\boldsymbol{\gamma }}/{\chi _\alpha } - \mathit{\boldsymbol{\alpha }}} \right):\left( {\mathit{\boldsymbol{\gamma }}/{\chi _\alpha } - \mathit{\boldsymbol{\alpha }}} \right)} }},\;\;\;\;\;\mathit{\boldsymbol{\gamma }} = \frac{\mathit{\boldsymbol{s}}}{p} $ |
χα为模型参数.将塑性势函数ψ对应力σ求导可得塑性流动方向r =∂ψ/∂σ.
1.3 屈服函数屈服函数
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {\mathit{\boldsymbol{\sigma }},{S_{\rm{i}}},{S_{\rm{f}}},{p_0},\mathit{\boldsymbol{\beta }}} \right) = \frac{3}{2}\left( {\mathit{\boldsymbol{s}} - p\mathit{\boldsymbol{\beta }}} \right):\left( {\mathit{\boldsymbol{s}} - p\mathit{\boldsymbol{\beta }}} \right) - }\\ {\left( {{N^{ * 2}} - \frac{3}{2}\mathit{\boldsymbol{\beta }}:\mathit{\boldsymbol{\beta }}} \right)p\left( {p_0^ * - p} \right)} \end{array} $ | (4) |
式中:β表示屈服函数旋转的二阶张量;p0*=Sip0; N*=SfN; p0为各向同性硬化内变量; Si表征各向同性结构性; Si和Sf均为不小于1的内变量,随着土体结构性的散失,其值逐渐趋近于1;与M相类似,N通过应力罗德角θβ在Ne和Nc之间通过插值确定
| $ \begin{array}{l} N = \mathit{\Theta }\left( {{\theta _\beta }} \right){N_{\rm{c}}} = \frac{{2n'}}{{\left( {1 + n'} \right) - \left( {1 - n'} \right)\cos \left( {3{\theta _\beta }} \right)}}{N_{\rm{c}}}\\ n' = \frac{{{N_{\rm{e}}}}}{{{N_{\rm{c}}}}},\;\;\;\;\cos \left( {3{\theta _\beta }} \right) = \sqrt 6 {\rm{tr}}\left( {\mathit{\boldsymbol{n}}_\beta ^3} \right)\\ {\mathit{\boldsymbol{n}}_\beta } = \frac{{\mathit{\boldsymbol{\gamma }}/{\chi _\beta } - \mathit{\boldsymbol{\beta }}}}{{\sqrt {\left( {\mathit{\boldsymbol{\gamma }}/{\chi _\beta } - \mathit{\boldsymbol{\beta }}} \right):\left( {\mathit{\boldsymbol{\gamma }}/{\chi _\beta } - \mathit{\boldsymbol{\beta }}} \right)} }} \end{array} $ | (10) |
χβ为模型参数.如图 1所示,在q-p平面内(其中

|
图 1 屈服函数与塑性势函数 Fig.1 Yield function and plastic potential function |
模型有Si、Sf、p0、α和β共5个内变量,对应的演化规则为
| $ {{\dot S}_{\rm{i}}} = - {k_{\rm{i}}}\left( {\frac{{1 + e}}{{\lambda - k}}} \right)\left( {{S_i} - 1} \right){{\dot \varepsilon }_{{\rm{pd}}}} = \mathit{\dot \Lambda }{{\bar S}_{\rm{i}}} $ | (5) |
| $ {{\dot S}_{\rm{f}}} = - {k_{\rm{f}}}\left( {\frac{{1 + e}}{{\lambda - k}}} \right)\left( {{S_{\rm{f}}} - 1} \right){{\dot \varepsilon }_{{\rm{pd}}}} = \mathit{\dot \Lambda }{{\bar S}_{\rm{f}}} $ | (6) |
| $ {{\dot p}_0} = \left( {\frac{{1 + e}}{{\lambda - k}}} \right){p_0}{{\dot \varepsilon }_{{\rm{pv}}}} = \mathit{\dot \Lambda }\bar p $ | (7) |
| $ \mathit{\boldsymbol{\dot \alpha }} = \mathit{\dot \Lambda }\mathit{\boldsymbol{\bar \alpha }} $ | (8) |
| $ \mathit{\boldsymbol{\dot \beta }} = \mathit{\dot \Lambda }\mathit{\boldsymbol{\bar \beta }} $ | (9) |
对应变增量塑性部分
与屈服函数相应的一致性条件
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }} = \frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}}{{\partial \mathit{\boldsymbol{\sigma }}}}:\mathit{\boldsymbol{\dot \sigma }} + \frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}}{{\partial {S_{\rm{i}}}}}{{\dot S}_{\rm{i}}} + \frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}}{{\partial {S_{\rm{f}}}}}{{\dot S}_{\rm{f}}} + }\\ {\frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}}{{\partial {p_0}}}{{\dot p}_0} + \frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}}{{\partial \mathit{\boldsymbol{\beta }}}}:\mathit{\boldsymbol{\dot \beta }} = 0} \end{array} $ |
将硬化规则式(5)~(9)代入可以得到一致性参数
| $ \mathit{\dot \Lambda } = \frac{{n:C:\dot \varepsilon }}{{n:C:r + {K_{\rm{p}}}}} $ | (11) |
其中,塑性模量
| $ {K_{\rm{p}}} = - \left( {\frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}}{{\partial {S_{\rm{i}}}}}{{\bar S}_{\rm{i}}} + \frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}}{{\partial {S_{\rm{f}}}}}{{\bar S}_{\rm{f}}} + \frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}}{{\partial {p_{\rm{0}}}}}{{\bar p}_{\rm{0}}} + \frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}}{{\partial \mathit{\boldsymbol{\beta }}}}:\mathit{\boldsymbol{\bar \beta }}} \right) $ | (12) |
考虑土体结构性的SANICLAY模型考虑的因素较全面,使得模型比较复杂,导致模型具有很强的非线性,数值实现的难度较大.结合本文第一部分可以看出,在采用显式算法对考虑土体结构性的SANICLAY模型进行数值实现的过程中,可能导致计算精度差的因素包括:①弹性关系依赖于球应力和孔隙比;②屈服函数和塑性势函数的曲率较大;③模型考虑了各向异性——旋转硬化;④硬化内变量较多,且硬化规则具有较高的非线性性.总之,一般情况下,会导致本构模型的非线性程度增加的因素都会导致显式算法的精度降低.
2.1 传统的显式算法弹塑性本构模型的显式算法数值实现主要是进行状态变量的更新.考虑土体结构性的SANICLAY模型的状态变量主要包括应力σ、应变ε、弹性应变εe、塑性应变εp、孔隙比e、表征各向同性结构性的内变量Si、表征摩擦结构性的内变量Sf、各向同性硬化内变量p0、塑性势函数和屈服函数中表征旋转硬化的内变量α与β.
弹塑性本构模型状态变量的更新一般采用应变驱动模式,所对应的基本问题为:给定满足本构模型的状态变量的初值σ(t0)、e(t0)、Si(t0)、Sf(t0)、p0(t0)、α(t0)、β(t0)以及应变历史ε(t),t∈[t0, T],求σ(t)、e(t)、Si(t)、Sf(t)、p0(t)、α(t)和β(t),使其满足如下本构方程:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot \sigma }}\left( t \right) = {\mathit{\boldsymbol{C}}_{{\rm{ep}}}}\left( t \right):\mathit{\boldsymbol{\dot \varepsilon }}\left( t \right) = \mathit{\boldsymbol{C}}\left( t \right):\left( {\mathit{\boldsymbol{\dot \varepsilon }}\left( t \right) - \mathit{\dot \Lambda }\left( t \right)\mathit{\boldsymbol{r}}\left( t \right)} \right)\\ \mathit{\boldsymbol{\dot \xi }}\left( t \right) = \mathit{\dot \Lambda }\left( t \right)\mathit{\boldsymbol{\bar \xi }}\left( t \right) \end{array} \right. $ | (13) |
其中,ξ =(Si, Sf, p0, α, β)T及ξ=(Si, Sf, p0, α, β)T分别表示硬化内变量和对应的演化方向.由此,状态变量的更新问题转化为由式(13)所组成的常微分方程组的求解问题,可以采用各种求解常微分方程组的方法求解.
当采用向前Euler法对方程(13)进行离散可以得到,在第n+1个增量步对应状态变量的更新方程为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\sigma }}_{n + 1}} = {\mathit{\boldsymbol{\sigma }}_n} + {\mathit{\boldsymbol{C}}_{{\rm{ep}}}}\left( {{\mathit{\boldsymbol{\sigma }}_n},{\mathit{\boldsymbol{\xi }}_n}} \right):\Delta {\mathit{\boldsymbol{\varepsilon }}_{n + 1}}\\ {\mathit{\boldsymbol{\xi }}_{n + 1}} = {\mathit{\boldsymbol{\xi }}_n} + \Delta \mathit{\Lambda }\left( {{\mathit{\boldsymbol{\sigma }}_n},{\mathit{\boldsymbol{\xi }}_n}} \right)\mathit{\boldsymbol{\bar \xi }}\left( {{\mathit{\boldsymbol{\sigma }}_n},{\mathit{\boldsymbol{\xi }}_n}} \right) \end{array} \right. $ | (14) |
式(14)即为传统的全显式算法所对应状态变量的更新方程.
2.2 改进显式算法考虑到传统的全显式算法所对应的向前Euler法只有一阶精度,为提高显式算法的计算效率,本文用四阶DPRK法代替向前Euler法,对方程(13)进行离散,可以得到第n+1个增量步对应状态变量的更新方程变为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\sigma }}_{n + 1}} = {\mathit{\boldsymbol{\sigma }}_n} + \frac{{31}}{{540}}\Delta {\mathit{\boldsymbol{\sigma }}_1} + \frac{{190}}{{297}}\Delta {\mathit{\boldsymbol{\sigma }}_3} - \frac{{145}}{{108}}\Delta {\mathit{\boldsymbol{\sigma }}_4} + \\ \;\;\;\;\;\;\;\;\;\;\frac{{351}}{{220}}\Delta {\mathit{\boldsymbol{\sigma }}_5} + \frac{1}{{20}}\Delta {\mathit{\boldsymbol{\sigma }}_6}\\ {\mathit{\boldsymbol{\xi }}_{n + 1}} = {\mathit{\boldsymbol{\xi }}_n} + \frac{{31}}{{540}}\Delta {\mathit{\boldsymbol{\xi }}_1} + \frac{{190}}{{297}}\Delta {\mathit{\boldsymbol{\xi }}_3} - \frac{{145}}{{108}}\Delta {\mathit{\boldsymbol{\xi }}_4} + \\ \;\;\;\;\;\;\;\;\;\;\frac{{351}}{{220}}\Delta {\mathit{\boldsymbol{\xi }}_5} + \frac{1}{{20}}\Delta {\mathit{\boldsymbol{\xi }}_6} \end{array} \right. $ | (15) |
其中,
| $ \left\{ \begin{array}{l} \Delta {\mathit{\boldsymbol{\sigma }}_i} = {\mathit{\boldsymbol{C}}_{{\rm{ep}}}}\left( {{\mathit{\boldsymbol{\sigma }}_{ni}},{\mathit{\boldsymbol{\xi }}_{ni}},\Delta {\mathit{\boldsymbol{\varepsilon }}_{n + 1}}} \right):\Delta {\mathit{\boldsymbol{\varepsilon }}_{n + 1}}\\ \Delta {\mathit{\boldsymbol{\xi }}_i} = \Delta \mathit{\Lambda }\left( {{\mathit{\boldsymbol{\sigma }}_{ni}},{\mathit{\boldsymbol{\xi }}_{ni}},\Delta {\mathit{\boldsymbol{\varepsilon }}_{n + 1}}} \right)\mathit{\boldsymbol{\xi }}\left( {{\mathit{\boldsymbol{\sigma }}_{ni}},{\mathit{\boldsymbol{\xi }}_{ni}}} \right)\\ \;\;\;\;\;\;\;\;i = 1,2, \cdots ,6 \end{array} \right. $ |
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\sigma }}_{n1}} = {\mathit{\boldsymbol{\sigma }}_n}\\ {\mathit{\boldsymbol{\xi }}_{n1}} = {\mathit{\boldsymbol{\xi }}_n} \end{array} \right. $ |
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\sigma }}_{n2}} = {\mathit{\boldsymbol{\sigma }}_n} + \frac{1}{5}\Delta {\mathit{\boldsymbol{\sigma }}_1}\\ {\mathit{\boldsymbol{\xi }}_{n2}} = {\mathit{\boldsymbol{\xi }}_n} + \frac{1}{5}\Delta {\mathit{\boldsymbol{\xi }}_1} \end{array} \right. $ |
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\sigma }}_{n3}} = {\mathit{\boldsymbol{\sigma }}_n} + \frac{3}{{40}}\Delta {\mathit{\boldsymbol{\sigma }}_1} + \frac{9}{{40}}\Delta {\mathit{\boldsymbol{\sigma }}_2}\\ {\mathit{\boldsymbol{\xi }}_{n3}} = {\mathit{\boldsymbol{\xi }}_n} + \frac{3}{{40}}\Delta {\mathit{\boldsymbol{\xi }}_1} + \frac{9}{{40}}\Delta {\mathit{\boldsymbol{\xi }}_2} \end{array} \right. $ |
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\sigma }}_{n4}} = {\mathit{\boldsymbol{\sigma }}_n} + \frac{3}{{10}}\Delta {\mathit{\boldsymbol{\sigma }}_1} - \frac{9}{{10}}\Delta {\mathit{\boldsymbol{\sigma }}_2} + \frac{6}{5}\Delta {\mathit{\boldsymbol{\sigma }}_3}\\ {\mathit{\boldsymbol{\xi }}_{n4}} = {\mathit{\boldsymbol{\xi }}_n} + \frac{3}{{10}}\Delta {\mathit{\boldsymbol{\xi }}_1} - \frac{9}{{10}}\Delta {\mathit{\boldsymbol{\xi }}_2} + \frac{6}{5}\Delta {\mathit{\boldsymbol{\xi }}_3} \end{array} \right. $ |
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\sigma }}_{n5}} = {\mathit{\boldsymbol{\sigma }}_n} + \frac{{226}}{{729}}\Delta {\mathit{\boldsymbol{\sigma }}_1} - \frac{{25}}{{27}}\Delta {\mathit{\boldsymbol{\sigma }}_2} + \frac{{880}}{{729}}\Delta {\mathit{\boldsymbol{\sigma }}_3} + \frac{{55}}{{779}}\Delta {\mathit{\boldsymbol{\sigma }}_4}\\ {\mathit{\boldsymbol{\xi }}_{n5}} = {\mathit{\boldsymbol{\xi }}_n} + \frac{{226}}{{729}}\Delta {\mathit{\boldsymbol{\xi }}_1} - \frac{{25}}{{37}}\Delta {\mathit{\boldsymbol{\xi }}_2} + \frac{{880}}{{729}}\Delta {\mathit{\boldsymbol{\xi }}_3} + \frac{{55}}{{729}}\Delta {\mathit{\boldsymbol{\xi }}_4} \end{array} \right. $ |
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\sigma }}_{n6}} = {\mathit{\boldsymbol{\sigma }}_n} - \frac{{181}}{{270}}\Delta {\mathit{\boldsymbol{\sigma }}_1} + \frac{5}{2}\Delta {\mathit{\boldsymbol{\sigma }}_2} - \frac{{226}}{{297}}\Delta {\mathit{\boldsymbol{\sigma }}_3} - \frac{{91}}{{27}}\Delta {\mathit{\boldsymbol{\sigma }}_4} + \frac{{189}}{{55}}\Delta {\mathit{\boldsymbol{\sigma }}_5}\\ {\mathit{\boldsymbol{\xi }}_{n6}} = {\mathit{\boldsymbol{\xi }}_n} - \frac{{181}}{{270}}\Delta {\mathit{\boldsymbol{\xi }}_1} + \frac{5}{2}\Delta {\mathit{\boldsymbol{\xi }}_2} - \frac{{226}}{{297}}\Delta {\mathit{\boldsymbol{\xi }}_3} - \frac{{91}}{{27}}\Delta {\mathit{\boldsymbol{\xi }}_4} + \frac{{189}}{{55}}\Delta {\mathit{\boldsymbol{\xi }}_5} \end{array} \right. $ |
式中:Δσi、Δξi分别为应力和硬化内变量的第i次修正量,并非表示应力增量Δσ和内变量增量Δξ的分量;σni、ξni分别为计算过程中所采用的修正后的应力和内变量,并非表示应力σn和内变量ξn的分量.
理论上说,显式算法经过以上改进后计算效率可以得到提高,但是其所具有的误差积累和精度较低的缺点仍无法消除,这在后文中的分析可以得到说明.造成显式算法精度低和误差积累的原因可以从显式算法的原理得到解释.显式算法是基于已知的状态变量的值直接外推下一增量步的状态变量的值,在外推过程中并没有对下一增量步的状态变量进行有效的限制.例如,外推得出的下一增量步的状态变量不一定能满足屈服函数的一致性条件.因此,通过显示算法更新后的状态变量会存在误差.同时,在本增量步的状态变量存在误差的情况下,显式算法会直接用本增量步的有误差的状态变量外推下一增量步的状态变量,显然这样会造成误差的积累.因此,提高显式算法精度的关键就在于提高每个增量步的计算精度,以减小误差的积累和传播.
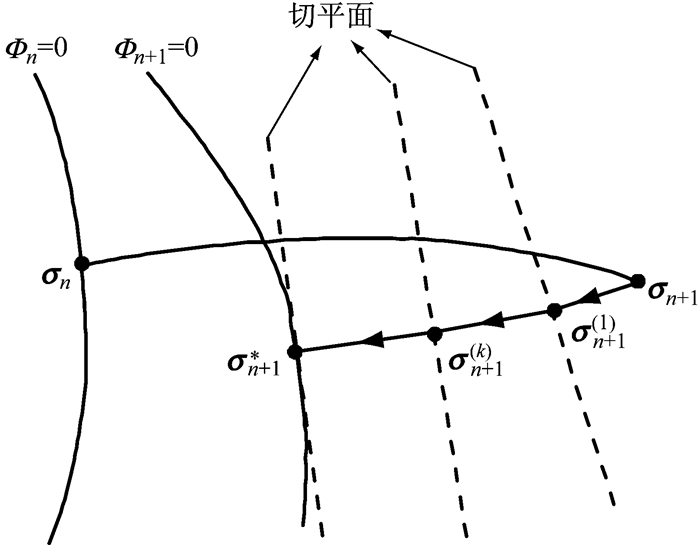
在第n+1个增量步,采用式(15)所对应的改进显式算法进行状态变量的更新,更新后的状态变量会存在误差.如图 2所示,根据更新后的状态变量得出的屈服函数值Φn+1>0,这与传统的弹塑性理论是相违背的,因此需要对更新后的状态变量进行修正.本文尝试采用切平面算法对更新后的状态变量进行修正,以提高显式算法的计算精度.具体采用的修正方程为
| $ \begin{array}{*{20}{c}} {\Delta \mathit{\Lambda }_{n + 1}^{\left( {k - 1} \right)} = \frac{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{n + 1}^{\left( {k - 1} \right)}}}{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{n + 1}^{\left( {k - 1} \right)}:\mathit{\boldsymbol{C}}_{n + 1}^{\left( {k - 1} \right)}:\mathit{\boldsymbol{r}}_{n + 1}^{\left( {k - 1} \right)} + K_{{\rm{p}}\;n + 1}^{\left( {k - 1} \right)}}}}\\ {\mathit{\boldsymbol{\sigma }}_{n + 1}^{\left( k \right)} = \mathit{\boldsymbol{\sigma }}_{n + 1}^{\left( {k - 1} \right)} - \Delta \mathit{\Lambda }_{n + 1}^{\left( {k - 1} \right)}\mathit{\boldsymbol{C}}_{n + 1}^{\left( {k - 1} \right)}:\mathit{\boldsymbol{r}}_{n + 1}^{\left( {k - 1} \right)}}\\ {\mathit{\boldsymbol{\xi }}_{n + 1}^{\left( k \right)} = \mathit{\boldsymbol{\xi }}_{n + 1}^{\left( {k - 1} \right)} + \Delta \mathit{\Lambda }_{n + 1}^{\left( {k - 1} \right)}\mathit{\boldsymbol{C}}_{n + 1}^{\left( {k - 1} \right)}} \end{array} $ | (16) |
|
图 2 切平面算法原理 Fig.2 Principle of the cutting-plane method |
其中,上标(k-1)和(k)表示修正次数.
综合本节内容可以看出,改进显式算法对传统的全显式算法做了计算效率和计算精度两方面的改进.如图 3所示,为提高计算效率而引入了DPRK法,为改善计算精度对更新后的状态变量采用切平面算法进行了修正.

|
图 3 改进显式算法框图 Fig.3 Improved-explicit algorithm |
为明确文中的改进显式算法的计算精度和计算效率,同时也为后续研究工作中采用哪种算法提出建议,笔者将显式算法、改进显式算法和隐式算法进行对比.
本文进行单个单元的计算分析以模拟原状土的三轴不排水压缩试验.具体在数值计算中采用的是8节点3维实体单元.在考虑软土结构性的SANICLAY模型中,考虑土体结构性的内变量主要包括各向同性结构性内变量Si和摩擦结构性内变量Sf,具体的模型参数取值参考文献[7].轴向初始应力σa=74.667 kPa,周向初始应力σr=37.667 kPa.采用应变控制式比例加载εa/εr=2/(-1),加载至轴向应变εa=0.150.在具体计算中,每种算法都分别考虑了增量步步长为10-1、10-2、10-3、10-4的情况.
计算结果及对比如表 1所示.表 1中,传统显式算法指的是与传统的向前Euler法相对应的显式算法,改进显式算法1指的是用四阶的DPRK法代替向前Euler法所得出的显式算法;改进显式算法2指的是用四阶的DPRK法代替向前Euler法,然后再采用切平面算法进行修正后所得出的显式算法.改进显式算法1和改进显式算法2的主要区别在于是否采用切平面算法进行精度改善.表中的收敛性可以直接反映出相应算法的收敛性,计算时间可以间接反映计算效率的高低,通过对比q-εq曲线可以反映算法的计算精度.当增量步步长为10-1时,传统显式算法、改进显式算法1、改进显式算法2会得出错误的结果,而隐式算法会不收敛.
| 下载CSV 表 1 计算结果对比 Tab.1 Comparison of calculation results |
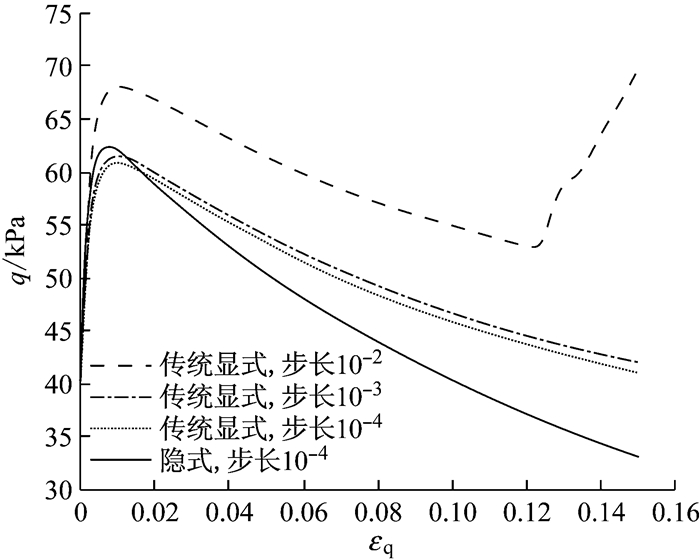
结合图 4和表 1可以看出,对传统显式算法,当增量步步长较大(如10-1和10-2)时,会得出错误的结果,只有在增量步步长较小时算法才会稳定.与隐式算法相比,即使在增量步步长取值很小(如10-4),计算时间很长的情况下,传统显式算法仍然存在误差积累,计算精度仍然较差.为了尽可能提高传统显式算法的计算精度,其增量步步长必须取得相当小,比如小于等于10-4,对应的计算时间为397.30 s,计算效率会很低.
|
图 4 传统显式算法的计算结果 Fig.4 Result of the conventional explicit algorithm |
结合图 5和表 1可以看出,对只做计算效率改进的显式算法1,当增量步步长特别大(如10-1)时会得出错误的结果,随着增量步步长的减小,计算时间大幅增加,计算趋于收敛.当增量步步长较大(如10-2)和步长较小(如10-4)时,计算精度差别不大.与传统显式算法相比,当增量步长相同时,改进显式算法1的计算效率要稍低,这是因为与改进显式算法1相对应的是DPRK法,而与传统显式算法相对应的是向前Euler法,向前Euler法显然比DPRK法计算量要小.当增量步长可以发生变化时,改进显式算法1在增量步长较大(如10-2)时即可达到与传统显式算法在增量步长较小(如10-4)时相同的精度,相应的计算时间分别为3.40 s和397.30 s.所以,整体上在变步长情况下,改进显式算法1比传统显式算法计算效率要高很多.与隐式算法相比较,改进显式算法1与传统显式算法的计算精度一样,都比较差.

|
图 5 改进显式算法1的计算结果 Fig.5 Result of improved-explicit algorithm 1 |
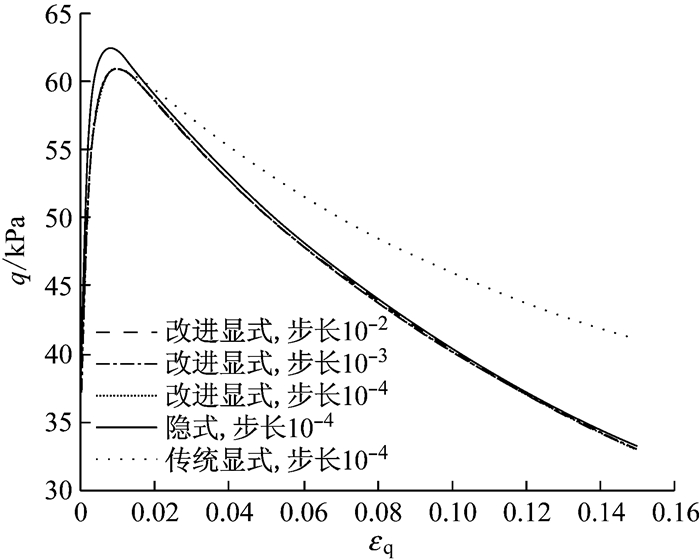
结合图 6和表 1可以看出,对做计算效率和计算精度改进的显式算法2,当增量步步长较大(如等于10-2)时,即可以得到收敛而且稳定的结果.与传统显式算法和改进的显式算法1相比较,当增量步长相同时,改进显式算法2的计算效率要低,这是因为与改进显式算法2相对应的是DPRK法,并且进行了精度修正.当增量步长可以发生变化时,改进显式算法2在增量步长较大(如10-2)时即可达到比传统显式算法在增量步长较小(如10-4)时高很多的计算精度,相应的计算时间分别为3.70 s和397.30 s.所以,整体上在变步长情况下,改进显式算法2也比传统显式算法计算效率要高很多.与传统显式算法相比较,改进显式算法2的计算精度有了极大的改善,基本不存在误差的积累,但是计算精度比隐式算法仍然略差.
|
图 6 改进显式算法2的计算结果 Fig.6 Result of improved-explicit algorithm 2 |
综合上述分析可以看出,与传统显式算法相比较,改进显示算法在计算效率和计算精度方面均有较大的改善.计算效率的提高是因为与传统显式算法对应的向前Euler法具有一阶精度,而与改进显式算法对应的DPRK法具有四阶精度.为了达到相同的计算精度,对于高阶的算法,增量步步长可以取得大一些,这样总的计算时间就会降低,计算效率就会提高.计算精度的提高是因为在每个增量步都采用切平面法对更新后的状态变量进行了修正,使其较严格地满足了屈服函数,这样即可避免误差的传递和积累.
4 多单元分析本文的算法比较是建立在简单应变路径下的单个单元分析基础之上的.然而,实际工程计算往往需要的是多单元分析的结果.多单元分析中有众多材料点,基本上每个材料点的应变路径或应力路径都是较为复杂的.因此,有必要对改进显式算法在多单元分析中的适用性进行验证分析.
以某隧道开挖工程为例进行多单元计算分析,所建立的分层土的几何模型和模型参数取值如图 7所示,所采用的SANICLAY模型参数取值参考文献[7].隧道开挖采用断面收缩法模拟,本次模拟中断面收缩率取为8‰,最后计算结果如图 8所示.这说明改进显式算法不但可用于单个单元的简单应变路径计算,而且用于工程实际中的多单元复杂应变路径或应力路径分析也是可行的.

|
图 7 几何模型及参数取值(尺寸单位:m) Fig.7 Geometric model and parameter(unit:m) |

|
图 8 Mises应力云图 Fig.8 Contour of Mises stress |
(1) 与隐式算法相比,传统显式算法虽然较为简单,但其存在误差的积累,计算精度较差,建议尽量不使用.
(2) 与传统显式算法相比,改进显式算法的计算效率和计算精度都得到大幅提高.但是,与隐式算法相比较,其计算精度仍然略差.
(3) 改进显式算法可以有效对高度非线性弹塑性本构模型进行数值实现.
本文对高度非线性弹塑性本构模型的显式算法数值实现做了一些研究工作.结合本文研究可以看出,当对计算精度要求特别高时,对高度非线性弹塑性本构模型的隐式算法实现,尤其是在不需要求Jacobian矩阵的情况下的数值实现,是极具价值的研究方向.
| [1] |
CALLISTO L, RAMPELLO S. Shear strength and small-strain stiffness of a natural clay under general stress conditions[J]. Geotechnique, 2002, 52(8): 547 DOI:10.1680/geot.2002.52.8.547 |
| [2] |
孙德安, 陈波. 结构性软土力学特性的试验研究[J]. 土木工程学报, 2011(增刊2): 65 SUN Dean, CHEN Bo. Experimental study on the mechanical behavior of structural soft clay[J]. China Civil Engineering Journal, 2011(Suppl.2): 65 |
| [3] |
JUNG Y H, FINNO R J, CHO W. Stress-strain responses of reconstituted and natural compressible Chicago glacial clay[J]. Engineering Geology, 2012, 129: 9 |
| [4] |
LIU W Z, SHI M L, MIAO L C, et al. Constitutive modeling of the destructuration and anisotropy of natural soft clay[J]. Computers and Geotechnics, 2013, 51: 24 DOI:10.1016/j.compgeo.2013.01.011 |
| [5] |
PANAYIDES S, ROUAINIA M, WOOD D M. Influence of degradation of structure on the behaviour of a full-scale embankment[J]. Canadian Geotechnical Journal, 2012, 49(3): 344 DOI:10.1139/t11-104 |
| [6] |
ROCCHI G, VACIAGO G, FONTANA M, et al. Understanding sampling disturbance and behaviour of structured clays through constitutive modelling[J]. Soils and Foundations, 2013, 53(2): 315 DOI:10.1016/j.sandf.2013.02.011 |
| [7] |
TAIEBAT M, DAFALIAS Y F, PEEK R. A destructuration theory and its application to SANICLAY model[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2010, 34(10): 1009 |
| [8] |
SUEBSUK J, HORPIBULSUK S, LIU M D. Modified structured cam clay: a generalised critical state model for destructured, naturally structured and artificially structured clays[J]. Computers and Geotechnics, 2010, 37: 956 DOI:10.1016/j.compgeo.2010.08.002 |
| [9] |
祝恩阳, 姚仰平. 结构性土UH模型[J]. 岩土力学, 2015(11): 3101 ZHU Enyang, YAO Yangping. A UH constitutive model for structured soils[J]. Rock and Soil Mechanics, 2015(11): 3101 |
| [10] |
CALLISTO L, GAJO A, WOOD D M. Simulation of triaxial and true triaxial tests on natural and reconstituted Pisa clay[J]. Geotechnique, 2002, 52(9): 649 DOI:10.1680/geot.2002.52.9.649 |
| [11] |
LIU M D, CARTER J P, AIREY D W. Sydney soil model. Ⅰ: theoretical formulation[J]. International Journal of Geomechanics, 2011, 11(3): 211 DOI:10.1061/(ASCE)GM.1943-5622.0000078 |
| [12] |
SLOAN S W, ABBO A J, SHENG D C. Refined explicit integration of elastoplastic models with automatic error control[J]. Engineering Computations, 2001, 18(1/2): 121 DOI:10.1108/02644400110365842 |
| [13] |
CABOT M L, SLOAN S W, SHENG D C, et al. Error behaviour in explicit integration algorithms with automatic sub-stepping[J]. International Journal for Numerical Methods in Engineering, 2016, 108: 1030 DOI:10.1002/nme.v108.9 |
| [14] |
GONZALEZ N A, GENS A. Evaluation of a constitutive model for unsaturated soils: stress variables and numerical implementation[C]//ALONSO E, GENS A. In Fifth International Conference on Unsaturated Soils Barcelona. Abingdon: Taylor & Francis Group, 2011: 829-836.
|
| [15] |
HAIRER E, NORSETT S P, WANNER G. Solving ordinary differential equations Ⅰ[M]. 2nd ed. Berlin: Springer-Verlag, 1993
|
| [16] |
ORTIZ M, POPOV E P. Accuracy and stability of integration algorithms for elastoplastic constitutive relations[J]. International Journal for Numerical Methods in Engineering, 1985, 21(9): 1561 DOI:10.1002/(ISSN)1097-0207 |
| [17] |
ORTIZ M, SIMO J C. An analysis of a new class of integration algorithms for elastoplastic relations[J]. International Journal for Numerical Methods in Engineering, 1986, 23(3): 353 DOI:10.1002/(ISSN)1097-0207 |
| [18] |
DAFALIAS Y F, MANZARI M T, AKAISHI M. A simple anisotropic clay plasticity model[J]. Mechanics Research Communications, 2002, 29(4): 241 DOI:10.1016/S0093-6413(02)00252-5 |
 2018, Vol. 46
2018, Vol. 46

