2. 山东省交通规划设计院, 山东 济南 250031;
3. 同济大学 先进土木工程材料教育部重点实验室, 上海 201804;
4. 上海罗洋新材料科技有限公司, 上海 200092
2. Planning and Design Institute of Shandong Province, Ji'nan 250031, China;
3. Key Laboratory of Advanced Civil Engineering Materials of the Ministry of Education, Tongji University, Shanghai 201804, China;
4. Shanghai Municipal Engineering Design Institute (Group) Co. Ltd, Shanghai 200092, China
超高性能混凝土(ultra-high performance concrete, UHPC)有着高强、抗拉、应变强化等特性,已逐渐成为学界及业界追捧的新兴混凝土材料[1].在桥梁工程中,UHPC凭借着优异的力学性能,可以在保证安全性的前提下,有效地降低梁高,减轻结构自重[1-2].同时,由于高应变强化UHPC具有出色的抗裂性能[3],应用前景广阔.2016年瑞士洛桑联邦理工大学颁布的最新UHPC设计指南[4]将UHPC分为3种类型:UO(应变软化),UA(低应变强化,强化极限应变大于1 500×10-6),UB(高应变强化,强化极限应变大于2 000×10-6).其中UO、UA、UB的应变强化抗拉强度与弹性极限抗拉强度的比值需分别大于0.7、1.1和1.2.
国内目前尚缺乏有效指导高应变强化UHPC结构设计的规范,但不少学者已经在该方面进行了较深入的研究.杨剑等[5]提出了平衡配筋率的概念,即预应力筋断裂和UHPC压碎破坏同时发生时的预应力筋配筋量,并通过试验验证了理论分析的合理性,同时在极限承载力计算中,假定梁弯拉强度为kft(ft为混凝土抗拉强度),经过试验数据对比确定了k值为0.5.邓宗才等[6]考虑高强钢筋的影响,同时对受压区UHPC引入等效矩形应力图来简化计算,发现理论值与试验值吻合程度较高.国外很多国家都已经初步建立了UHPC规范[2, 7-11].
综合国内外UHPC的研究现状,本文采用上海罗洋新材料科技有限公司提供的常温养护高应变强化型UHPC材料,将已进行的5根配筋T形截面超高性能混凝土梁弯曲性能试验成果,作为建立超高性能混凝土梁抗弯承载力计算方法的基础资料,根据试验结果建立简化的极限抗弯承载力计算模型,推导配筋T形UHPC梁抗弯承载力计算公式,并与一些国外规范提出的计算方法进行对比,为UHPC的结构应用奠定理论基础.
1 试验概况 1.1 UHPC材料制备试验材料采用的应变强化UHPC是基于最紧密堆积原理,且由计算机精确设计,可将宏观缺陷降至最低,形成高度致密的无机质基体.在常温养护条件下,具备超高强、应变强化、高耐久性、优异施工性能等特征.UHPC基体配合比见表 1.钢纤维特性见表 2.
| 下载CSV 表 1 UHPC基体配合比(质量分数) Tab.1 Mix proportion of UHPC matrix |
| 下载CSV 表 2 钢纤维特征参数 Tab.2 Characteristic parameters of steel fiber |
配筋T形截面UHPC试验梁的腹板尺寸为120 mm×300 mm,翼缘板尺寸为320 mm×60 mm,试验梁的长度为3 000 mm,为防止两端的锚固破坏,加载时两边各预留150 mm,计算跨度为2 700 mm.两侧支座处采用增大截面处理,两端各250 mm范围内为矩形截面,250~350 mm范围内截面渐变.T形试验梁的跨中截面和构造见图 1.试验梁的变化参数包括钢筋配筋率和类型,纵筋材性试验抗拉强度、试验基本参数见表 3.

|
图 1 配筋T形UHPC梁跨中截面和构造详图(单位:mm) Fig.1 Midspan cross section and structure diagram of reinforced UHPC T beam(unit:mm) |
| 下载CSV 表 3 T形梁配筋情况表 Tab.3 Reinforcement situation of T beam |
在浇筑T形试验梁时,浇筑养护完成2组(6个)100 mm×100 mm×100 mm的立方体试块,按照标准养护条件(温度20 ℃±2 ℃,湿度≥95%)养护28 d后进行立方体抗压强度试验.立方体抗压强度试验值见表 4.
| 下载CSV 表 4 UHPC立方体抗压强度 Tab.4 Compressive strength of UHPC cube |
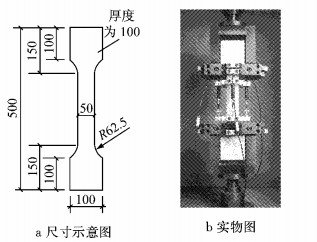
在立方体抗压强度试验过程中(特别是即将达到极限荷载前),可以听到钢纤维从基体中脱离开来的噼啪声,当立方体试块被压碎时,由于钢纤维的搭接作用,试块仍保持为一个整体.根据试验确定的UHPC立方体抗压强度标准值为(试验均值-1.645倍的标准差)fcu, k=154.6-1.645×9.8=138.5 MPa.参考Lampropoulos等[10]的试验,轴拉试件为狗骨头形,测试段尺寸为50 mm×100 mm×500 mm,轴拉试件见图 2.经试验测得轴拉应力-应变关系曲线见图 3.四点纯弯试验加载现场照片如图 4所示.
|
图 2 轴拉试件(单位:mm) Fig.2 Specimens of axial tensile(unit: mm) |

|
图 3 轴拉应力-应变曲线 Fig.3 Stress-strain of axial tensile |

|
图 4 现场加载照片 Fig.4 Loading photos onsite |
配筋T形UHPC试验梁的荷载-跨中挠度曲线见图 5.由图可知,配筋T形梁的整个受力破坏过程大致可分为3个阶段:弹性阶段、裂缝发展阶段、持荷至破坏阶段.

|
图 5 荷载-跨中挠度曲线 Fig.5 Deflection of load-midspan |
阶段Ⅰ:弹性阶段.试验加载初期,跨中纯弯段区域弯矩较小,UHPC配筋梁受力形态与均匀弹性体基本一致,荷载-挠度曲线呈直线.
阶段Ⅱ:裂缝发展阶段.随着荷载的增加,试验梁侧面出现大量微小裂缝,以微裂缝簇的方式呈现,裂缝宽度发展缓慢,且沿着梁高向上发展,受拉区进入塑性阶段的部分逐渐增多,荷载-挠度曲线斜率逐渐减小.
阶段Ⅲ:持荷至破坏阶段.纵向受拉钢筋逐渐屈服,跨中纯弯段裂缝沿梁高迅速发展且宽度增大,截面到达其极限荷载,荷载-挠度曲线斜率逐渐趋于0,当荷载-挠度曲线斜率为负时,试验梁跨中严重下挠,试验梁出现明显的主裂缝(1~3条).
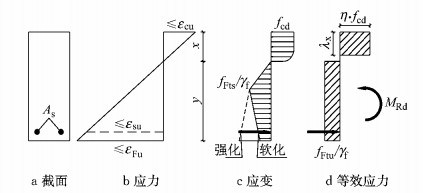
2 极限承载能力计算根据UHPC应力-应变关系,受压区混凝土未压碎,处于弹性工作状态,受拉区混凝土开裂,全截面应变及应力分布如图 6所示.图中,fy为钢筋屈服强度,As为受拉钢筋总面积,ftd为UHPC抗拉强度,b为腹板宽度,hf为翼缘高度,h为截面高度,bf为翼缘宽度,as为钢筋距底边高度,εc为UHPC应变,εy为钢筋屈服应变,εte为UHPC弹性极限应变.

|
图 6 截面受拉应力及应变分布 Fig.6 Distribution of tensile stress-strain of section |
根据UHPC试件强度试验中的6个UHPC试块结果,UHPC的抗压强度标准值可达到138.5 MPa,在进行T形配筋梁试验时发现受压区应力远达不到其抗压强度,受压区UHPC不会压碎(配筋率达4.4%).受压区处于线弹性工作状态,因此配筋T形UHPC试验梁破坏极限状态受压区按照三角形区域计算,受压区边缘的应力按UHPC轴心抗压强度fck计算.《混凝土结构设计规范》(GB 50010—2010)[12]中规定:混凝土轴心抗压强度标准值fck由立方体抗压强度标准值fcu, k经过计算确定.考虑到结构中混凝土的实体强度与立方体试件混凝土强度之间的差异,根据以往的经验,结合试验数据分析并参考其他国家的有关规定,对试件混凝土强度的修正系数取为0.88.
棱柱强度与立方强度之比αc1为:对C50及以下普通混凝土取0.76,对高强混凝土C80取0.82,中间按线性插值.C40以上的混凝土考虑脆性折减系数αc2:对C40取1.00,对高强混凝土C80取0.87,中间按线性插值[12].
| $ {f_{{\rm{ck}}}} = 0.88{\alpha _{{\rm{c1}}}}{\alpha _{{\rm{c2}}}}{f_{{\rm{cu}}, {\rm{k}}}} $ |
《混凝土结构设计规范》中混凝土强度等级最高为C80,对C80以上无明确的系数规定.依据《混凝土结构设计规范》中系数随混凝土强度线性变化的规律,对CF90~CF160进行线性外延,同时根据UHPC的材料特性对系数进行修正,各强度混凝土参数取值见表 5.
| 下载CSV 表 5 各强度纤维混凝土参数取值 Tab.5 Parameters of reinforced concrete at each strength |
根据前述fcu, k=138.5 MPa,介于CF130~CF 140之间,αc1=0.90,αc2=0.72,从而计算fck=0.88×0.90×0.72×138.5=79 MPa.
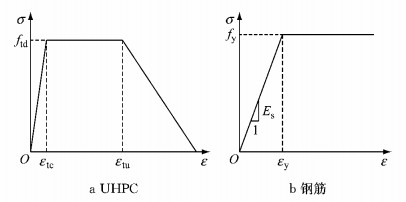
配筋T形UHPC梁正截面抗弯承载力计算与普通钢筋混凝土梁最大的不同之处,需要考虑受拉区UHPC开裂后抗拉强度对截面承载力的贡献.通过前面的分析,在设计计算时,受拉区的应力等效为矩形应力图.考虑到最终破坏时,钢筋的应变大于屈服应变,受拉区边缘的应变发展的不确定性(裂缝发展),提出受拉区UHPC等效矩形应力系数β,受拉区等效矩形拉应力为βftd.等效矩形应力系数β依据轴拉应力-应变曲线,根据受拉区合力作用点和合力值不变的原则计算求得,钢筋与UHPC的应力-应变曲线见图 7.图中,εtu为UHPC强化阶段末端应变,Es为钢筋弹性模量,εy为钢筋屈服应变.等效矩形应力系数见表 6.
|
图 7 理想受拉应力-应变关系 Fig.7 Ideal relationship between tensile stress-strain |
| 下载CSV 表 6 受拉区UHPC等效矩形应力系数β计算值 Tab.6 Equivalent rectangular stress coefficient β of UHPC of tensile region |
综合5根T形截面试验梁的计算结果,本文建议偏安全地取β=0.90.
根据图 6d截面等效应力分布,由平衡条件得到T形配筋UHPC梁的正截面抗弯承载力计算公式为
| $ {f_{\rm{y}}}{A_{\rm{s}}} + \beta {f_{{\rm{td}}}}b(h - {h_{\rm{f}}}) \le \frac{1}{2}{f_{{\rm{ck}}}}{b_{\rm{f}}}{h_{\rm{f}}} $ | (1) |
第一,若T形截面特性符合式(1),中性轴在翼缘内.压区的应力宽度均为bf,考虑腹板受拉区UHPC的抗拉作用,按下列公式进行正截面抗弯承载力计算:
| $ \begin{array}{l} {M_{\rm{u}}} = \frac{1}{3}{f_{{\rm{cd}}}}{b_{\rm{f}}}{x^2} + \frac{1}{2}\beta {f_{{\rm{td}}}}b{\left( {h - x} \right)^2} + \\ {f_{\rm{y}}}{A_{\rm{s}}}({h_0} - x) + \frac{1}{2}\beta {f_{{\rm{td}}}}({b_{\rm{f}}} - b){({h_{\rm{f}}} - x)^2} \end{array} $ | (2) |
式中:Mu为极限弯矩;x为受压区高度;h0为钢筋有效高度.
UHPC受压区高度应按下式计算:
| $\frac{1}{2}{f_{{\rm{cd}}}}bfx = {f_{\rm{y}}}{A_{\rm{s}}} + \beta {f_{{\rm{td}}}}b\left( {h - x} \right) +\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \beta {f_{{\rm{td}}}}({b_{\rm{f}}} - b)({h_{\rm{f}}} - x) $ | (3) |
第二,当不符合公式(1)时,中性轴在腹板内.应考虑截面中腹板的受压作用,其正截面抗弯承载力应按下式计算:
| $ \begin{array}{l} {M_{\rm{u}}} = {f_{\rm{y}}}{A_{\rm{s}}}\left( {{h_0} - x} \right) + \frac{1}{2}\beta {f_{{\rm{td}}}}b{\left( {h - x} \right)^2} + \\ \frac{1}{3}{f_{{\rm{cd}}}}{b_{\rm{f}}}{x^2} - \frac{1}{3}\left( {1 - \frac{{{h_{\rm{f}}}}}{x}} \right){f_{{\rm{cd}}}}({b_{\rm{f}}} - b){(x - {h_{\rm{f}}})^2} \end{array} $ | (4) |
受压区高度应按下式计算:
| $ \begin{array}{l} \frac{1}{2}{f_{{\rm{cd}}}}{b_{\rm{f}}}x - \frac{1}{2}{\mathit{f}_{{\rm{cd}}}}\left( {1 - \frac{{{h_{\rm{f}}}}}{x}} \right)\left( {{b_{\rm{f}}} - b} \right)\left( {x - {h_{\rm{f}}}} \right) = \\ \;\;\;\;\;\;\;\;\;{f_{\rm{y}}}{A_{\rm{s}}} + \beta {f_{{\rm{td}}}}b\left( {h - x} \right) \end{array} $ | (5) |
ACI 544[7]计算钢筋纤维混凝土(SFRC)梁截面抗弯承载力时考虑SFRC抗拉强度的贡献.根据传统钢筋混凝土理论的平截面假定和拉压力平衡方程,并考虑受拉区SFRC的抗拉作用,计算简图如图 8所示,计算公式及符号介绍详见文献[7].

|
图 8 ACI 544截面抗弯承载力计算方法 Fig.8 ACI 544 calculation method for flexural capacity |
Model Code 2010[8]将纤维混凝土划分为应变软化型和应变强化型两种,通过开口梁弯曲试验得到残余弯曲强度,从而建立两种类型纤维混凝土的本构模型——刚塑性模型和线弹性模型.Model Code 2010在7.7.3章节中规定,梁构件达到极限抗弯承载力的判断标准是满足下面3条准则中任何一条:①FRC受压区应变到达其极限应变;②钢筋达到其抗拉极限应变;③FRC受拉区应变达到其极限应变.计算简图如图 9所示.计算公式及符号介绍详见文献[8].
|
图 9 Model Code 2010截面抗弯承载力计算方法 Fig.9 Model Code 2010 calculation method of flexural capacity |
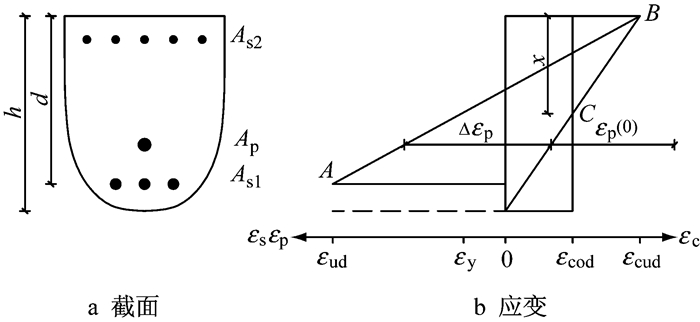
在计算截面抗弯承载力时,有如下假设:①截面在整个过程中保持为平面;②无论是受拉还是受压,钢筋中的应变均等于周围混凝土的应变;③钢筋应力由EN1991.1[13]中第3.2和第3.3条规定的设计曲线确定.计算简图如图 10所示.计算公式及符号介绍详见文献[9].
|
图 10 UHPC配筋梁截面承载力计算图示 Fig.10 Calculation icon of flexural capacity of reinforced UHPC beam |
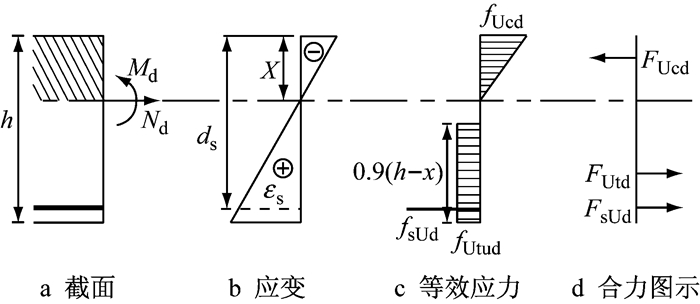
UHPC纯弯曲及含有正应力的受弯情况下的极限承载力设计值应根据图 11的承载力模型确定,考虑受拉区UHPC抗拉强度的抗弯贡献,区域高度需乘以0.9的系数.计算公式及符号介绍详见文献[4].
|
图 11 瑞士规范UHPC受弯构件正截面承载力计算图示 Fig.11 Calculation of flexural capacity of steel reinforced concrete t-shaped section |
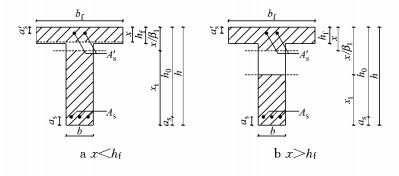
CECS 38:2004对T形配筋梁的计算方法规定如下:当受压区高度小于翼缘高度时,受压区应取宽度为bf的矩形截面,同时应考虑腹板受拉区中钢纤维混凝土的抗拉作用;当受压区高度大于翼缘高度时,应同时考虑截面中腹板的受压作用.计算简图如图 12所示.计算公式及符号介绍详见文献[11].
|
图 12 钢纤维混凝土T形截面受弯构件正截面承载力计算 Fig.12 Calculation of flexural capacity of steel reinforced concrete t-shaped section |
将各国规范和本文提出计算方法的计算值与试验值结果进行对比,结果见表 7.Mt, u为5根T形梁试验值,Mc, u1为本文提出的计算模型计算值,Mc, u2为ACI 544计算模型的计算值,Mc, u3为Model Code 2010计算值,Mc, u4为法国规范计算值,Mc, u5为CECS 38:2004计算值,Mc, u6为瑞士规范计算值.
| 下载CSV 表 7 配筋T形UHPC梁承载力各国计算值对比 Tab.7 Comparison of calculation values of reinforced UHPC T-beam flexural capacity among different methods |
从表 7分析可知:ACI 544在5个计算模型中预测结果最差,其计算值与试验值之比的平均值、标准差和变异系数分别为0.755、0.062和0.082,这是因为其抗拉强度仅考虑钢纤维与混凝土基体的黏结强度,并没有充分考虑钢纤维对基体的搭接联系作用;Model Code 2010计算方法中钢纤维混凝土开裂后的残余抗拉强度fFtu是通过三点开口梁弯曲韧性试验计算的残余抗弯强度fRi换算得到的,计算时考虑了受拉区UHPC的贡献,其计算值与试验值之比的平均值、标准差和变异系数分别为0.904、0.039和0.043;CECS 38:2004计算方法是在大量试验基础上提出的经验公式,其预测值与试验值之比的平均值、标准差和变异系数分别为0.882、0.036和0.041,该方法主要针对CF80以下纤维混凝土;法国超高性能纤维混凝土规范和瑞士UHPC规范充分考虑了受拉区UHPC的贡献,其计算值与试验值之比的平均值、标准差和变异系数分别为0.955和0.945、0.038和0.042、0.040和0.044,预测精度较高,且变异系数较低,预测结果较为稳定.本文提出计算模型的计算值与试验值之比的平均值、标准差和变异系数分别为0.968、0.030和0.031,且符合中国规范的计算原则,说明按照本文提出的配筋T形UHPC梁截面抗弯承载力计算方法准确.
4 结论(1) 相同配筋强度的T-1~T-4试验梁,随着配筋率的增加,截面极限抗弯承载力逐步增加,但配筋率达到一定程度时,极限承载力增大的幅度降低;T-5梁的极限抗弯承载力是T-2的1.2倍,说明高强钢筋的应用可以实现在低配筋率下的高承载力.
(2) 根据简化的UHPC理想本构模型,受压区应力图为三角形,受拉区应力图等效为矩形,等效系数为0.90,推导了T形配筋UHPC梁的抗弯承载力计算公式,计算值与试验值有较高的吻合度,预测结果准确.
(3) 各国纤维混凝土规范均对受拉区混凝土的贡献度有所考虑,但由于考虑纤维混凝土抗拉强度的方法存在差异,以及各国规范针对纤维混凝土的强度等级不同,各国规范的抗弯承载力计算值与试验值匹配程度有所差别.ACI 544和CECS 38:2004计算值与试验值相差较大;Model Code 2010的计算值与试验值吻合度在0.9左右;法国超高性能纤维混凝土规范及瑞士UHPC规范与本文提出方法的计算值与试验值接近度高,具有较小的标准差和变异系数.本文方法符合中国规范的计算原则.
| [1] |
GRAYBEAL B. UHPC in the U.S. highway infrastructure[J]. Indian Concrete Journal, 2014, 88(4): 84 |
| [2] |
SHI C, WU Z, XIAO J, et al. A review on ultra high performance concrete: part Ⅰ. raw materials and mixture design[J]. Construction & Building Materials, 2015, 101: 741 |
| [3] |
王俊颜, 郭君渊, 肖汝诚, 等. 高应变强化超高性能混凝土的裂缝控制机理和研究[J]. 土木工程学报, 2017, 50(11): 10 WANG Junyan, GUO Junyuan, XIAO Rucheng, et al. Study on crack control mechanism of strain-hardening ultra-high performance concrete[J]. China Civil Engineering Journal, 2017, 50(11): 10 |
| [4] |
MCS-EPFL. Ultra-high performance fibre reinforced cement-based composites (UHPFRC): construction material, dimensioning and application[S]. Zurich: Switzerland Swiss Federal Institute of Technology, 2016.
|
| [5] |
杨剑, 方志. 超高性能混凝土梁正截面承载力[J]. 中国铁道科学, 2009, 30(2): 23 YANG Jian, FANG Zhi. Normal section bearing capacity of yltra high performance concrete beam[J]. China Railway Science, 2009, 30(2): 23 |
| [6] |
邓宗才, 王义超, 肖锐, 等. 高强钢筋UHPC梁抗弯性能试验研究与理论分析[J]. 应用基础与工程科学学报, 2015, 23(1): 68 DENG Zongcai, WANG Yichao, XIAO Rui, et al. High strength reinforced UHPC beam bending performance test research and theoretical analysis[J]. Journal of Basic Science and Engineering, 2015, 23(1): 68 |
| [7] |
ACI Committee. Design considerations for steel reinforced concrete[S]. Farmington Hills: American Concrete Institue, 1999: 1-18.
|
| [8] |
International Federation for Structural Concrete. Fib model code 2010[S]. Zurich: Ernst & Sohn, 2013.
|
| [9] |
AFGC. Ultra-high performance fiber reinforced concretes interim recommendations[S]. Paris: AFGC, 2002.
|
| [10] |
LAMPROPOULOS A P, PASCHALIS S A, TSIOULOU O T, et al. Strengthening of reinforced concrete beams using ultra high performance fibre reinforced concrete (UHPFRC)[J]. Engineering Structures, 2016, 106: 370 DOI:10.1016/j.engstruct.2015.10.042 |
| [11] |
大连理工大学. 纤维混凝土结构技术规程: CECS 38: 2004[S]. 北京: 中国计划出版社, 2004. Dalian University of Technology. Technical specification for concrete structures of fiber: CECS 38: 2004[S]. Beijing: China Planning Press, 2004. |
| [12] |
中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Concrete structure design code: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2010. |
| [13] |
NARAYANAN R S. Eurocode 2—design of concrete structures[M]. Berlin: Springer Berlin Heidelberg, 2014
|
 2018, Vol. 46
2018, Vol. 46

 18
18 20
20