2. 北京交通大学 土木建筑工程学院,北京 100044
2. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China
在铁路运输中,钢轨磨耗现象一直是普遍存在并且难以解决的问题[1-3].磨耗引起钢轨型面的改变,进而会导致接触状态和系统动力性能发生变化,对列车运行稳定性、安全性及系统各部件使用寿命都会产生较大影响.通过数值仿真对磨耗进行预测,可指导相关部门有针对性地安排和优化养护维修工作,实现从发现问题后进行治理性养护到预判问题开展预防性养护的转变,有效减少养修工作量和成本,减缓磨耗发展.另外,通过磨耗发展定量预测可作为轨道结构设计的评价标准,为型面优化、结构改进提供科学指导.因此, 磨耗数值仿真具有重要研究价值,国内外学者在这方面进行了一系列的研究工作[4-13].
基于此,本文建立了车辆-轨道耦合动力学及轮轨滚动接触计算模型,在此基础上结合材料磨损理论建立轮轨磨耗预测模型,并基于MATLAB软件编制了计算程序,可实现钢轨磨耗具体分布及发展的定量预测分析.鉴于轮轨接触斑离散化网格密度参数在预测模型中具有显著的影响作用,而目前针对此问题的研究尚较少见,因此本文从接触斑黏滑区、蠕滑力分布、磨耗深度分布等角度对这一关键因素的影响机理进行了深入分析,并给出对钢轨磨耗发展速率的最终影响特征,探讨合理的接触斑网格密度取值.
1 车辆-轨道耦合动力学模型钢轨磨耗分布发展预测是在车辆-轨道耦合动力学和轮轨滚动接触分析基础上进行的,首先建立车辆轨道耦合动力学模型.
基于多体动力学理论,建立三大件式转向架重载货车车辆模型.对车体及转向架结构部件(摇枕、侧架、轴箱、轮对等)均采用六自由度刚体模拟,对车体与心盘、旁承,楔块减振器与摇枕、侧架,以及侧架与轴箱间的接触摩擦作用均采用点-面接触单元组合进行模拟,并充分考虑部件实际间隙.中央悬挂枕簧采用双线性刚度阻尼力学单元模拟.通过精细化建模确保模型尽可能与实际情况相符,如图 1所示.

|
图 1 三大件式转向架力学模型 Fig.1 Model of three-piece bogie |
轮轨接触主要基于Hertz接触理论[14]及Kalker的FASTSIM算法[15]进行计算,主要分为接触点位置探测、整体接触力学量计算(接触力、蠕滑率等), 以及接触斑局部接触力学量计算(接触应力、蠕滑应力、滑动速度分布等).
轮轨接触受力与下部轨道结构密不可分,模型充分考虑了轨道的弹性和阻尼特性,如图 2所示.图中,N1、N2分别为走行面接触点和轮缘接触点位置处的法向接触力,T1、T2分别为两接触位置处的蠕滑力,δy、δz分别为钢轨的垂、横向变形位移,Gy、Gz分别为扣件系统对钢轨的垂、横向约束反力,Cy、Cz、Dy、Dz分别为扣件系统的垂、横向刚度和阻尼,刚度阻尼参数取值基于实测结果.
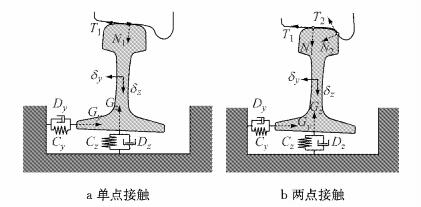
|
图 2 钢轨模型受力示意图 Fig.2 Forces of rail model |
轮轨接触计算中,为了求得法向力和蠕滑力分布,将接触斑进行离散化处理,如图 3所示.
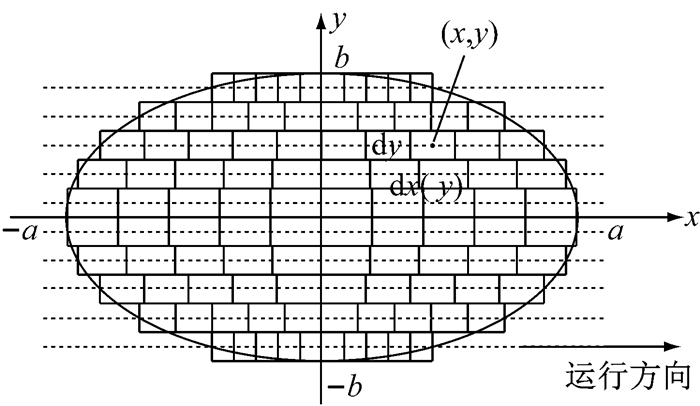
|
图 3 接触斑离散化处理 Fig.3 Discretization of contact patch |
接触斑坐标系原点位于接触斑中心,x轴、y轴分别对应轮轨接触面的纵向和横向,a、b分别为接触斑半长轴、半短轴长度.首先将接触斑沿y轴等分成ny个长条,然后将每个长条均等分为nx个矩形离散块,(x, y)为离散块中心在接触斑坐标系下的位置坐标,dy、dx(y)分别为离散块沿y方向、x方向的长度,由式(1)计算.这种划分方法可以提高接触斑边界网格分辨率和结果精确性.
| $ \left\{ \begin{array}{l} {\rm{d}}x\left( y \right) = 2a\sqrt {1 - {{\left( {y/b} \right)}^2}/{n_x}} \\ {\rm{d}}y = 2b/{n_y} \end{array} \right. $ | (1) |
接触斑经过以上离散化后,通过迭代计算求得各网格上的蠕滑力及蠕滑速度,即得接触斑蠕滑力和蠕滑速度分布,同时完成接触斑滑动、黏着区划分.通过将各网格内的蠕滑力累加得接触斑总蠕滑力.
2 钢轨磨耗分布发展预测模型基于动力学及接触模型算得的轮轨接触斑几何特性、滑动区黏着区分布以及接触法向力和蠕滑速度分布,计算接触斑内磨耗深度分布.接触斑网格划分与轮轨接触计算时保持一致.
对接触斑上每个离散单元,基于Archard材料磨损理论[16]计算磨耗体积损失,如图 4所示.
| $ \begin{array}{l} \Delta {V_{\rm{w}}}\left( {x, y} \right) = \\ {k_{\rm{w}}}\left( {x, y} \right)\frac{{p\left( {x, y} \right)\cdot {\rm{d}}x\left( y \right)\cdot {\rm{d}}y\cdot\Delta s\left( {x, y} \right)}}{H} \end{array} $ | (2) |
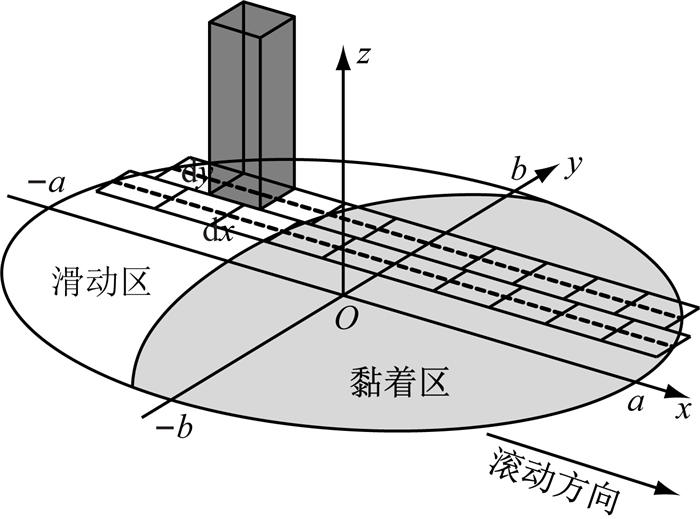
|
图 4 轮轨磨耗分布计算模型 Fig.4 Calculation model of wheel-rail wear distribution |
式中:ΔVw(x, y)为离散单元上的磨耗体积损失量;H为轮轨材料硬度;kw(x, y)为磨耗系数,根据离散单元处法向应力和相对滑动速度得到[12];Δs(x, y)为离散单元处对应的轮轨相对滑动距离;p(x, y)为离散单元中心位置法向应力.
| $ p\left( {x, y} \right) = \frac{{3N}}{{2{\rm{ \mathsf{ π} }}ab}}\sqrt {1 - {{\left( {\frac{x}{a}} \right)}^2} - {{\left( {\frac{y}{b}} \right)}^2}} $ | (3) |
式中:N为接触斑上总法向接触力.
对于轮轨相对滑动距离Δs(x, y),根据轮轨局部接触计算得到的接触斑滑动区黏着区分布,如果离散单元位于黏着区,则Δs(x, y)=0,无磨耗发生;如果离散单元位于滑动区,则
| $ \Delta s\left( {x, y} \right) = \frac{{\parallel \mathit{\boldsymbol{v}}\left( {x, y} \right)\parallel \cdot{\rm{d}}x\left( y \right)}}{{{V_0}}} $ | (4) |
| $ \begin{array}{l} \mathit{\boldsymbol{v}}\left( {x, y} \right) = {\rm{ }}{\mathit{\boldsymbol{v}}_{\rm{r}}}\left( {x, y} \right) - {\rm{ }}{\mathit{\boldsymbol{v}}_{\rm{e}}}\left( {x, y} \right) = \\ \left[ \begin{array}{l} {\xi _x} - \varphi y\\ {\xi _y} + \varphi x \end{array} \right]\cdot{V_0} - \left[ \begin{array}{l} \frac{{\partial {u_x}\left( {x, y} \right)}}{{\partial x}}\\ \frac{{\partial {u_y}\left( {x, y} \right)}}{{\partial x}} \end{array} \right]\cdot{V_0} \end{array} $ | (5) |
式中:V0为车轮滚动速度;v(x, y)为离散单元处轮轨表面相对滑动速度;vr(x, y)是刚体相对滑动速度分量; ve(x, y)是弹性变形相对滑动速度分量;ξx、ξy、φ为接触斑纵向、横向、自旋蠕滑率;ux(x, y)、uy(x, y)为离散单元处弹性变形位移.一般情况下ve(x, y)比vr(x, y)小得多,因此计算中将其忽略.
通过以上计算可以得到接触斑内每个离散单元上的磨耗体积损失ΔVw(x, y),进而可得到每个离散单元对应的磨耗深度ΔDw(x, y).
| $ \Delta {D_{\rm{w}}}\left( {x, y} \right) = \frac{{\Delta {V_{\rm{w}}}\left( {x, y} \right)}}{{{\rm{d}}x\left( y \right)\cdot{\rm{d}}y}} $ | (6) |
累加具有相同y坐标的离散单元磨耗深度,可得到接触斑内每一纵向长条上对应的磨耗深度,即得到磨耗深度沿轮轨型面的分布.
对于每一动力学积分步,通过以上计算均能得到对应的磨耗深度沿轮轨型面的分布(接触斑坐标系下),然后结合轮轨接触点位置信息将磨耗分布定位到钢轨型面坐标系下,物理意义为车轮通过当前位置钢轨时引起的钢轨型面磨耗.然后对每一积分步求平均,结果意义为车轮通过一次所引起的钢轨型面磨耗深度分布,将同侧4个车轮对应的结果相加,即得该侧钢轨在单节车辆通过一次时产生的磨耗深度分布,定义为钢轨磨耗速率cr,如图 5所示.cr为钢轨型面坐标系水平坐标yr的函数.

|
图 5 钢轨磨耗速率示意图 Fig.5 Rail wear rate |
根据以上动力学及磨耗模型的计算过程,基于MATLAB软件编制了钢轨磨耗分布发展的计算程序.
3 轮轨接触斑合理网格密度研究由前面章节可知,在车辆轨道动力学及磨耗计算过程中,轮轨接触斑离散化处理是一个关键步骤.通过将接触斑离散为一系列的单元来计算接触斑蠕滑力和蠕滑速度的分布,通过在各离散单元上应用材料磨损理论得到接触斑磨耗深度分布.接触斑离散网格密度将对计算结果和效率产生显著影响.本节基于数值试验对接触斑网格密度的影响机理和规律进行深入分析,对网格密度的合理取值进行探讨.
设置满载C80货车在直线轨道上运行,轨道不平顺采用德国低干扰谱,轮轨型面采用LM型磨耗踏面和R75重型钢轨型面,车速72 km·h-1.分别采取nx=ny=10,20,30,40,50,60的接触斑网格划分方式,计算比较不同网格密度下轮轨接触斑滑动区黏着区分布、蠕滑力分布、磨耗深度分布以及最终的钢轨磨耗发展速率情况.
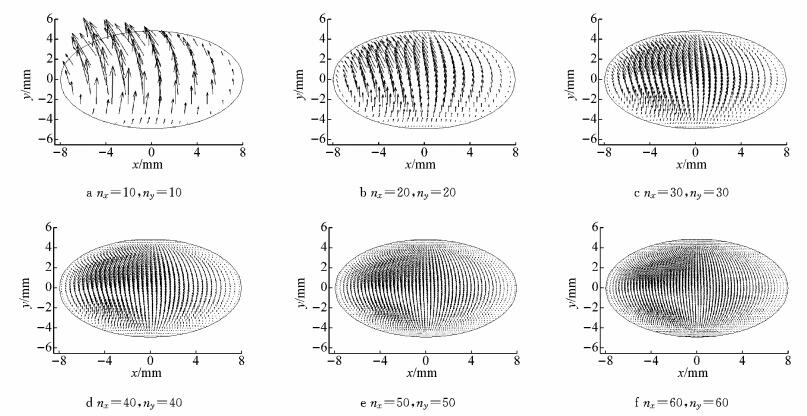
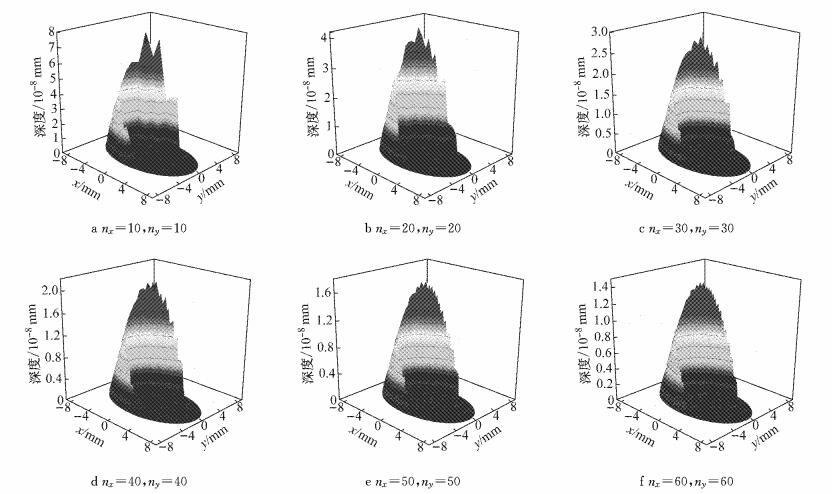
图 6给出了不同网格密度条件下,计算过程中特定积分步的导向轮对左轮与钢轨接触斑滑动、黏着区分布.图 7和图 8则分别给出了相应的接触斑蠕滑力分布及磨耗深度分布.图 9给出了不同网格密度下最终的钢轨磨耗发展速率.
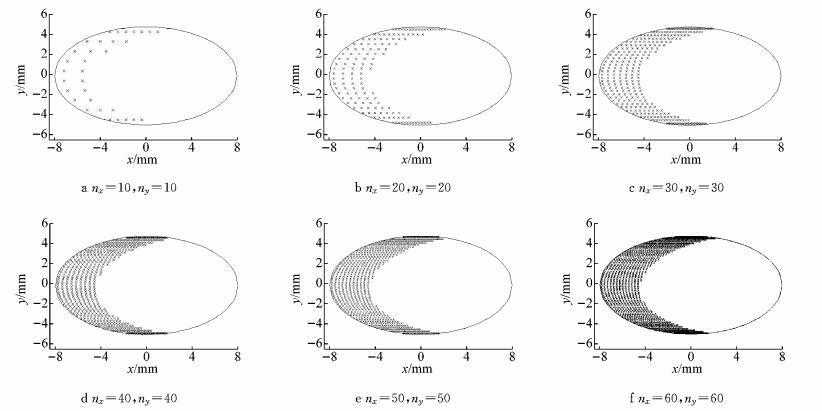
|
图 6 不同网格密度下接触斑滑动区、黏着区分布 Fig.6 Distribution of sliding and adhesion zones in contact patch at different grid densities |
|
图 7 不同网格密度下接触斑蠕滑力分布 Fig.7 Distribution of creeping force in contact patch at different grid densities |
|
图 8 不同网格密度下接触斑磨耗深度分布 Fig.8 Distribution of wear depth in contact patch at different grid densities |

|
图 9 不同网格密度下钢轨磨耗速率 Fig.9 Rail wear rate at different grid densities |
可以看出,不同接触斑网格密度条件下求得的滑动区、黏着区范围轮廓基本一致,随着网格密度的增大,接触斑内黏着区、滑动区的分布变得更为精确、连续.相应地,随着网格密度增大蠕滑力分布也更加精细化;离散网格数目越多,单个网格上的蠕滑力值越小,累加后接触斑内总的蠕滑力计算结果基本一致.
网格密度对接触斑内磨耗深度分布计算的影响较明显.在黏着区由于轮轨无相对滑动,因此磨耗为0.在滑动区不同网格密度条件下磨耗深度分布的基本特征大体一致;但网格密度较小时磨耗分布结果过于粗糙,出现很多尖锐形状突变,精度严重不足;随着网格密度的增大,接触斑内磨耗分布变化趋向稳定,越来越平滑连续.
网格密度对最终的钢轨磨耗发展速率(车辆通过一次时引起的钢轨型面磨耗深度分布)也会产生明显影响.随着网格密度的增大,钢轨磨耗速率呈减小的趋势,密度从nx=ny=10增至nx=ny=20时磨耗速率变化较明显,但继续增大密度时磨耗速率的改变非常小.可通过钢轨磨耗速率(磨耗深度分布曲线)与位置坐标轴围成的面积表征对钢轨磨耗量的影响.可以看出,随着网格密度的增加,钢轨磨耗量(面积损失速率)略有下降,但总体来看改变不显著.
综上所述,在钢轨磨耗计算中接触斑网格密度的取值总体上不会影响结果的正确性.但较小的网格密度得到的接触斑黏滑区、蠕滑力及磨耗深度分布过于粗糙,结果精确性和连续性差.增大网格密度可提高结果精度和平滑连续性,但会造成计算代价的成倍增加.当网格密度达到nx=ny=20时,钢轨磨耗速率变化趋于稳定,继续增大密度改善效果已不明显.因此,建议网格密度取为nx=ny=20,可在确保结果精度的同时拥有较高的计算效率.
4 结论本文建立了车辆-轨道耦合动力学及轮轨滚动接触分析模型,在此基础上结合Archard材料磨损理论建立了钢轨磨耗预测模型,基于MATLAB软件编制了计算程序,可实现钢轨磨耗具体分布及发展的定量预测分析.
针对预测模型中轮轨接触斑离散化网格密度的显著影响作用,率先通过数值试验从接触斑黏着滑动区、蠕滑力、磨耗深度分布等角度对这一关键因素的影响机理进行了深入分析,并给出对最终钢轨磨耗发展速率的影响,探讨接触斑网格密度的合理取值.结论如下:①网格密度不会影响结果的正确性,但较稀疏的网格得到的蠕滑力、磨耗分布过于粗糙,存在较多尖锐突变.增大网格密度可提高精确性及磨耗分布的平滑连续性,但会成倍增加计算代价.②网格密度达到20×20时,钢轨磨耗速率变化由剧烈趋于稳定,继续增大密度改善效果已不明显.因此,建议采用20×20网格密度,可在确保结果精度的同时尽可能拥有较高计算效率.
| [1] |
JIN X S. Key problems faced in high-speed train operation[J]. Journal of Zhejiang University Science A: Applied Physics & Engineering, 2014(12): 936 |
| [2] |
熊嘉阳, 邓永权, 曹亚博, 等. 重载铁路轮轨磨耗及其对安全运行的影响[J]. 西南交通大学学报, 2014(2): 302 XIONG Jiayang, DENG Yongquan, CAO Yabo, et al. Wheel-rail wear on heavy haul lines and its influences on running stability of trains[J]. Journal of Southwest Jiaotong University, 2014(2): 302 |
| [3] |
IGNESTI M, MALVEZZI M, MARINI L, et al. Development of a wear model for the prediction of wheel and rail profile evolution in railway systems[J]. Wear, 2012, 284 |
| [4] |
许玉德, 魏恺, 孙小辉, 等. 钢轨磨耗预测模型及其算法的优化[J]. 中国铁道科学, 2016, 37(4): 48 XU Yude, WEI Kai, SUN Xiaohui, et al. Prediction model and algorithm optimization for rail wear[J]. China Railway Science, 2016, 37(4): 48 |
| [5] |
周宇, 张杰, 王少锋, 等. 考虑磨耗的钢轨疲劳裂纹萌生寿命预测仿真[J]. 铁道学报, 2016, 38(7): 91 ZHOU Yu, ZHANG Jie, WANG Shaofeng, et al. Simulation on rail head crack initiation life prediction considering rail wear[J]. Journal of the China Railway Society, 2016, 38(7): 91 |
| [6] |
徐井芒. 高速道岔曲尖轨磨耗仿真分析研究[D]. 成都: 西南交通大学, 2015. XU Jingmang. Research on simulation of curved switch rail wear in high-speed turnout[D]. Chengdu: Southwest Jiaotong University, 2015. |
| [7] |
LI X, JIN X S, WEN Z F, et al. A new integrated model to predict wheel profile evolution due to wear[J]. Wear, 2011, 271: 227 DOI:10.1016/j.wear.2010.10.043 |
| [8] |
孙宇, 翟婉明. 钢轨磨耗演变预测模型研究[J]. 铁道学报, 2017, 39(8): 1 SUN Yu, ZHAI Wanming. A prediction model for rail wear evolution[J]. Journal of the China Railway Society, 2017, 39(8): 1 |
| [9] |
ARIZON J D, VERLINDEN O, DEHOMBREUX P. Prediction of wheel wear in urban railway transport: comparison of existing models[J]. Vehicle System Dynamics, 2007, 45(9): 849 DOI:10.1080/00423110601149335 |
| [10] |
PEARCE T G, SHERRATT N D. Prediction of wheel profile wear[J]. Wear, 1991, 144: 343 DOI:10.1016/0043-1648(91)90025-P |
| [11] |
ZOBORY I. Prediction of wheel/rail profile wear[J]. Vehicle System Dynamics, 1997, 28(2/3): 221 |
| [12] |
JENDEL T. Prediction of wheel profile wear-comparisons with field measurements[J]. Wear, 2002, 253: 89 DOI:10.1016/S0043-1648(02)00087-X |
| [13] |
丁军君, 李芾. 基于蠕滑机理的重载货车车轮磨耗研究[J]. 中国铁道科学, 2013, 34(4): 125 DING Junjun, LI Fu. Research on wheel wear of heavy haul freight car based on creep mechanism[J]. China Railway Science, 2013, 34(4): 125 |
| [14] |
HERTZ H. Über die berührung fester elastische Körper[J]. Journal für die reine und angewandte Mathematik, 1882, 92: 156 |
| [15] |
KALKER J J. A fast algorithm for the simplified theory of rolling contact[J]. Vehicle System Dynamics, 1982, 11(1): 1 DOI:10.1080/00423118208968684 |
| [16] |
ARCHARD J F. Contact and rubbing of flat surfaces[J]. Journal of Applied Physics, 1953, 24(8): 981 DOI:10.1063/1.1721448 |
 2018, Vol. 46
2018, Vol. 46
