基于落锤式弯沉仪(falling weight deflectometer, FWD)检测路表弯沉盆并反演结构层模量是路面结构承载能力常用的无损检测手段[1].模量反演实质上是一个最优化过程,通常以弯沉盆匹配误差最小为目标函数,采用迭代算法进行求解[2-3].
在模量反演中,理论弯沉计算模型可以是动态模型或静态模型,动态模型计算较为复杂,常用的是静态模型,如弹性层状体系模型[4].在理论弯沉计算模型中添加刚性下卧层,将模量反演计算限定在一定深度范围内,可以提高弯沉盆匹配程度.Chou[5]认为, 通过计算不同刚性层深度下的弯沉盆匹配误差,误差最小时的刚性层深度即为实际刚性层深度.Rohde等[6]通过实例分析发现, 匹配误差并不总是在实际刚性层深度时达到最小.有的学者建议将刚性层深度设置为定值,如5.0 m[7]、5.4 m[8]、5.5 m[9]和6.1 m[10],但并未考虑不同地区不同路面结构形式的差异.
刚性下卧层的设置深度对模量反演结果有较大影响,尤其是土基反演模量[11-12],而土基模量是路面结构设计和性能评价的重要参数.因此,进行面向土基反演模量的刚性层深度设置方法研究具有重要意义.本文依托北京RIOHTRACK足尺路面试验环道平台,检测不同路面结构不同层位的弯沉盆,进行刚性层深度对土基反演模量的影响分析,并提出基于土基反演模量一致性的刚性层深度设置方法.
1 逐层弯沉盆数据采集北京RIOHTRACK足尺路面环道试验铺筑了多种沥青路面结构(STR),路面结构厚度信息如表 1所示.表 1中的路面结构可能厚度组成相同,但采用不同强度的基层或不同类型的沥青混合料.对于土基类型,STR19未对土基进行处治,而其他路面结构均对土基进行了水泥稳定处治,处治厚度为20 cm,稳定土所用水泥剂量为9.5%.
| 下载CSV 表 1 路面结构层厚度及土基表面模量 Tab.1 Layer thicknesses and subgrade surface modulus of different pavement structures |
采用点对点方法进行逐层弯沉检测.首先在土基顶面进行弯沉盆数据检测,然后每加铺一层路面结构层,在相同位置重复检测弯沉盆数据.为了分析土基的应力依赖特性,采集了不同荷载水平下的土基处治前、后的弯沉盆数据,荷载水平分别为30、50和70 kN.在检测其余层位的弯沉盆数据时,荷载水平均为50 kN.FWD共有9个位移传感器,以30 cm等间隔分布,径向距离分别为0、30、60、90、120、150、180、210、240 cm.
2 基于逐层弯沉盆的土基模量反演 2.1 刚性层设置深度影响分析 2.1.1 模量反演方法模量反演实质上是一个最优化过程,通常以弯沉盆匹配误差最小为目标函数(见式(1)),采用迭代算法进行求解[2-3],比如粒子群算法、模拟退火算法等.最优化求解过程面临的主要问题是由目标函数表示的多维表面可能具有许多局部最小值.
| $ {\rm{min}}\;\mathit{E} = \sqrt {\sum\limits_{i = 1}^n {{{\left( {\frac{{{D_{{\rm{m}}\mathit{i}}} - {D_{{\rm{c}}\mathit{i}}}}}{{{D_{{\rm{m}}\mathit{i}}}}}} \right)}^2}/n} } $ | (1) |
式中:E为弯沉盆匹配误差; Dmi为路面结构第i个距离处的实际检测弯沉; Dci为路面结构第i个距离处的理论计算弯沉; n为位移传感器个数.
粒子群算法(PSO)源于对鸟群捕食的行为研究,是一种基于迭代的优化工具[13].粒子在解空间追随最优的粒子进行搜索.假定种群内有m个粒子,第i个粒子的位置和速度分别为Xi和Vi.到目前为止,该粒子所经过的个体历史最优值为Pi,种群历史最优值为Pg.则粒子i将根据式(2)和(3)更新自己的速度与位置.
| $ {\mathit{\boldsymbol{X}}_i} = {\mathit{\boldsymbol{X}}_i} + {\mathit{\boldsymbol{V}}_i} $ | (2) |
| $ {\mathit{\boldsymbol{V}}_i} = {\mathit{\boldsymbol{V}}_i} + {c_1}{\gamma _1}({\mathit{\boldsymbol{P}}_i} - {\mathit{\boldsymbol{X}}_i}) + {c_2}{\gamma _2}({\mathit{\boldsymbol{P}}_{\rm{g}}} - {\mathit{\boldsymbol{X}}_i}) $ | (3) |
式中:i=1, 2, …, m;c1和c2分别为对自身和种群的学习因子,取正常数;γ1和γ2为[0, 1]的随机数.
模拟退火算法(SA)是一种随机寻优算法,采用Metropolis抽样准则,按照一定概率接受次优解,从而有效解决了算法易陷入局部最优解的问题[13].次优解接受概率方程来自Boltzman-Gibbs分布,如式(4)所示.SA算法可以有效地防止陷入局部最优,但计算效率较低,耗时长;相反,PSO算法能较快地找到最优解,但容易陷入局部最优,两种算法互补.Dong等[13]将二者结合起来,提出了一种基于模拟退火的粒子群算法(SA-PSO),该算法既能防止陷入局部最优又能提高计算效率.
| $ P = {\rm{exp}}( - \Delta f/{T_k}) $ | (4) |
| $ \Delta f = f({\mathit{\boldsymbol{X}}_i}) - f({\mathit{\boldsymbol{P}}_i}) $ | (5) |
| $ {T_k} = {T_0}{\alpha ^k} $ | (6) |
式中:P为次优解接受概率;f(Xi)和f(Pi)分别为粒子i的适应值和种群最优适应值;Tk和T0分别为第k次迭代的模拟温度和初始温度;α为退火常数.
朱洁[4]将SA-PSO算法应用于模量反演中,研究了算法中各个参数的改变对反演结果的影响,确定了各个参数的合理取值.反演结果表明, SA-PSO算法可以高精度地反演3层结构体系的各层模量,且耗时约为2 min.因此,本文采用SA-PSO算法进行模量反演.
在模量反演时,路面结构均简化为至多3层,将所有沥青面层划分为第1层,所有水泥稳定碎石层划分为第2层,其余结构层划分为第3层.刚性层深度为土基顶面至刚性层的距离,刚性层模量取值为6 894 MPa,泊松比为0.2[4].
2.1.2 土基模量反演结果土基处治前、后的材料特性不同,以路面结构STR13和STR19为例分别分析处治土和未处治土土基的模量反演结果.STR13面层分为3层,层厚分别为4、8、12 cm,基层为2层20cm的水泥稳定碎石;STR19面层分为5层,层厚分别为4、8、12、12、12 cm,基层为1层20 cm的水泥稳定碎石.
为了区分不同层位弯沉盆反演得到的土基模量,以字母A和B分别代表沥青层和半刚性基层,以数字的增大表示层位逐渐向下.如,A1表示沥青层第1层顶面弯沉盆,B1表示半刚性基层第1层顶面弯沉盆.
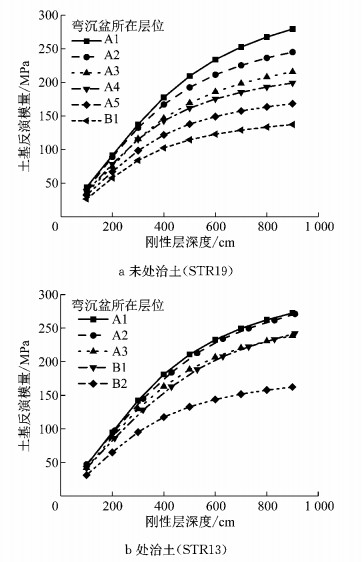
在不同刚性层深度下,基于各层顶面弯沉盆分别反演土基模量,反演结果如图 1所示.由图 1可知,随着刚性层深度的增加,土基反演模量逐渐增大,但增加趋势逐渐趋缓;随着弯沉盆检测层位上升,土基反演模量与刚性层深度的关系曲线呈上移趋势,上移幅度与刚性层深度有关,刚性层深度较浅时,上移幅度较小,刚性层深度较深时,上移幅度较大.
|
图 1 刚性层深度对土基反演模量的影响 Fig.1 Influence of rigid layer depth on subgrade back-calculation modulus |
刚性层深度可基于弯沉盆匹配误差最小原则确定或设置为定值,分别简称为匹配法和定值法.反演结果表明,各层弯沉盆的匹配误差均随着刚性层深度的增加而降低,因此匹配法的刚性层深度均设置为900 cm.定值法的刚性层深度均取值为550 cm[9].
由图 1可知,对于定值法,随着弯沉盆检测层位上升,STR13、STR19的土基反演模量均逐渐增大,变化范围分别为138~222 MPa和119~222 MPa,增加百分比分别为60%、87%;对于匹配法,STR13、STR19的土基反演模量变化范围分别为162~273 MPa和137~279 MPa,分别增大了68%、103%.表明土基逐层反演模量一致性较差,这主要是土基自身的应力依赖特性和刚性层深度设置不合理所致.
2.2 土基应力依赖特性分析 2.2.1 土基表面模量计算基于Boussinesq弯沉公式计算不同径向距离处的土基表面模量,反映了土基在不同荷载级位下的材料特性,可用于分析土基应力依赖特性.荷载中心点处和其他位置处的土基表面模量计算公式如下:
| ${E_0} = \frac{{2(1 - \mu _0^2)pa}}{{{d_0}}} $ | (7) |
| $ {E_r} = \frac{{(1 - {\mu ^2}_0)p{a^2}}}{{r{d_r}}} $ | (8) |
式中:d0和E0分别为荷载中心点处弯沉及对应土基表面模量;dr和Er分别为径向距离r处弯沉及对应土基表面模量;p和a分别为荷载压强和作用半径;μ0为土基泊松比,取值0.35.
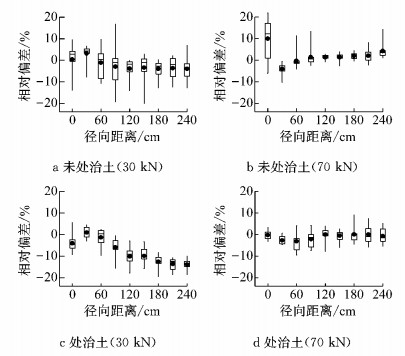
2.2.2 土基应力依赖特性分析以荷载水平50 kN对应的土基表面模量为基准,计算不同荷载水平下的模量偏差,并对不同测点的计算结果进行统计分析.图 2的箱形图为分析结果.
|
图 2 土基表面模量相对偏差的箱形图 Fig.2 Boxplot of relative deviation of subgrade surface modulus |
由图 2可知,对于未处治土,当荷载水平为30 kN时,各处的土基表面模量偏差均很小;当荷载水平为70 kN时,荷载中心点处的土基表面模量偏差较大,偏差百分比为10%,其余位置的偏差很小.对于处治土,当荷载水平为30 kN时,距离荷载中心点较远位置的土基表面模量偏差较大,极大值出现在最外侧传感器处,偏差百分比为14%;当荷载水平为70 kN时,各处的土基表面模量偏差均很小.
综上所述,不同荷载水平下的土基表面模量差异均小于20%,而基于不同层位弯沉盆的土基反演模量的变化范围在60%以上,表明土基逐层反演模量的不一致性主要是刚性层深度设置不合理造成的.刚性层深度的设置原则应当使得土基反演模量具有良好的一致性,使得基于不同层位弯沉盆的土基反演模量较为接近.
3 基于土基反演模量一致性的刚性层深度设置模型由上文分析可知,土基反演模量值随着刚性层深度的增加而增加;随着弯沉盆检测层位上升,土基反演模量值与刚性层深度的关系曲线呈上移趋势.为了使得逐层土基反演模量具有一致性,当路面厚度较厚时,刚性层深度应当设置较浅;当路面厚度较薄时,刚性层深度应当设置较深.因此,刚性层深度与路面厚度存在对应关系.首先应当确定关系模型形式,然后对模型参数进行优化.
各层厚度h和模量E并不相同,因此应当选择同一模量进行等效厚度heq计算.Ullidtz[14]认为等效厚度的计算原则是刚度保持不变,建议采用式(9)进行等效厚度换算.半刚性基层反演模量可能会大于10 GPa,因此,本文将等效模量Eeq取值为10 GPa.
| $ {h_{{\rm{eq}}}} = h{(E/{E_{{\rm{eq}}}})^{1/3}} $ | (9) |
为了确定模型形式,首先估计各个测点的土基模量值,其次确定逐层弯沉盆分别对应的刚性层深度,使得土基模量反演值与估计值相等,并计算路面等效厚度,从而得到刚性层深度与路面等效厚度的一一对应数据,即可确定刚性层深度模型形式.其中,采取径向距离为60~240 cm的土基表面模量的平均值作为各测点土基模量估计值,如表 1所示.从中可以看出,处治土和未处治土的平均土基模量分别为135 MPa和109 MPa,这反映了水泥处治与否对土基强度的影响.
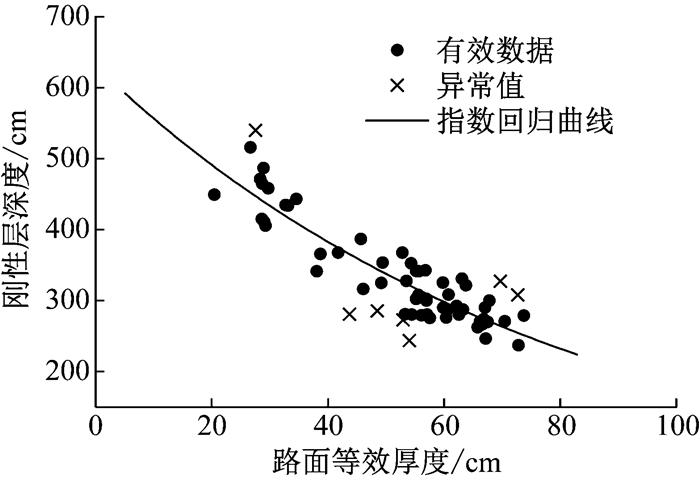
图 3为路面等效厚度Heq与刚性层深度Hrigid的散点图.由图 3可知,Heq与Hrigid具有较好的相关性,呈指数减小趋势.采用指数模型进行分析,并通过残差分析进行异常值筛选,异常值有7组,有效数据56组.指数模型回归公式如式(10)所示,相关系数为R2=0.84.表明指数模型可以很好地表征刚性层深度与路面等效厚度的相关关系.
| $\begin{array}{l} {H_{{\rm{rigid}}}} = a\;{\rm{exp}}\left( {b{H_{{\rm{eq}}}}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;630.5\;\;{\rm{exp}}( - 0.012\;48{H_{{\rm{eq}}}}) \end{array} $ | (12) |
|
图 3 刚性层深度与路面等效厚度相关性分析 Fig.3 Pavement equivalent thickness versus rigid layer depth |
以STR13为例,计算各层弯沉盆在不同刚性层深度下的路面等效厚度,得到路面等效厚度与刚性层深度之间的关系曲线,如图 4所示.并将上文确定的刚性层深度指数模型曲线(模型曲线)也绘制于图 4中.

|
图 4 模型解惟一性图示 Fig.4 Schematic diagram of unique solution obtained by model |
从图 4可以看出,关系曲线均呈现单调递减趋势;与模型曲线相比,关系曲线明显较陡,二者之间必然存在惟一的交点,这表明刚性层深度指数模型具有惟一解.
3.3 模型参数的优化确定模型参数优化确定依据土基反演模量一致性原则进行.土基模量一致性指标只需表征逐层土基反演模量的接近程度,而无需与土基模量真值进行比较.结合采集到的不同测点的逐层弯沉盆数据,土基模量一致性可用均方根变异系数Crms进行表征,计算公式如下:
| $ {C_{{\rm{rms}}}} = \sqrt {\sum\limits_{i = 1}^n {C_i^2/n} } $ | (11) |
式中:Ci为第i个测点土基反演模量的变异系数;n为测点总数.
a和b是刚性层深度指数模型的2个参数.对于土基顶面弯沉盆,其路面等效厚度Heq=0,此时其刚性层深度Hrigid=a.余欢[9]通过对不同地区的土基顶面弯沉盆进行反演分析,并与承载板法测试模量进行对比,建议土基顶面弯沉盆的刚性层深度设置为550 cm.其他学者建议刚性层深度也与550 cm较为接近,如5.0 m[7]、5.4 m[8]、6.1 m[10].因此,本文参数a取值550 cm,只对参数b进行优化.
参数b与Crms的关系曲线如图 5所示.从图 5可以看出,曲线存在极小值,当b=-0.011 30时,Crms达到极小值4.45%.当采用匹配法或定值法设置刚性层深度时,Crms分别为16.1%和14.6%.这充分表明, 刚性层深度指数模型显著提高了土基反演模量的一致性.

|
图 5 Crms与参数b的相关性 Fig.5 Crms versus parameter b |
表 2为STR13和STR19分别采用刚性层深度指数模型反演逐层弯沉盆的土基模量反演结果.其中,STR19的层2和层4在模型回归分析中被筛选为异常值,并未在表中列出.从表 2可以看出,采用指数模型设置刚性层深度后,土基逐层反演模量具有良好的一致性.
| 下载CSV 表 2 逐层土基反演模量 Tab.2 Layer-by-layer back-calculated modulus of subgrade |
在山东省某新建高速公路进行逐层弯沉盆数据采集,见表 3.表中, ω1、ω2、ω3、ω4、ω5、ω6、ω7、ω8、ω9分别为距离荷载中心点0, 203、305、457、610、914、1 219、1 524、1 829 mm处的弯沉.在模量反演时,将路面结构简化为3层,即土基、水稳碎石层、沥青层.对水稳碎石层进行钻芯取样,进行动态抗压回弹模量试验,频率为20 Hz,荷载级位为20~90 kN,得到的动态模量为20 227~21 810 MPa,因此将水稳碎石层模量反演范围设置为1 500~22 000 MPa,沥青层为1 000~10 000 MPa,土基层为30~500 MPa.
| 下载CSV 表 3 路面结构层厚度和逐层弯沉盆数据 Tab.3 Pavement structure layer thicknesses and layer-by-layer deflection basins |
分别采用定值法、反演法及本文提出的路面等效厚度法确定各层弯沉盆对应的刚性层深度,并反演各层模量,计算逐层土基反演模量的变异性,结果如表 4所示.定值法的刚性层深度均设置为550 cm,匹配法的刚性层深度设置结果均为900 cm.
| 下载CSV 表 4 刚性层设置深度及结构层反演模量 Tab.4 Setting depths of rigid layer and structural layer back-calculation modulus |
由表 4可知,对于定值法或匹配法,土基反演模量均随着弯沉盆检测层位的上升而呈现增大趋势;与定值法或匹配法相比,刚性层深度指数模型将土基反演模量变异系数从12.9%以上降低为6.9%,显著降低了土基反演模量变异性,提高了土基反演模量一致性,表明了指数模型设置的有效性.
5 结论本文在进行路面各结构层逐层弯沉盆反演土基模量时发现其一致性很差,为此建立了基于路面等效厚度的刚性层深度指数模型设置方法,显著提高了逐层土基反演模量的一致性.与其他刚性层深度设置方法相比,刚性层深度指数模型将逐层土基反演模量变异系数从12.9%以上降低为6.9%.土基反演模量一致性的提高增加了模量反演结果的可靠性,有利于模量反演技术的实际运用.
| [1] |
SUN Lijun. Structural behavior of asphalt pavements: intergrated analysis and design of conventional and heavy duty asphalt pavement[M]. Massachusetts: Butterworth-Heinemann Inc, 2016
|
| [2] |
UZAN J. Advanced backcalculation techniques[C]//The 2nd Conference on Nondestructive Testing of Pavements and Backcalculation of Moduli. West Conshohocken: ASTM International, 1994: 3-37.
|
| [3] |
GOKTEPE A B, AGAR E, LAV A H. Advances in backcalculating the mechanical properties of flexible pavements[J]. Advances in Engineering Software, 2006, 37(7): 421 DOI:10.1016/j.advengsoft.2005.10.001 |
| [4] |
朱洁. 沥青路面多层结构模量高精度反算方法研究[D]. 上海: 同济大学, 2013. ZHU Jie. Method of high-precision modulus backcalculation for multi-layer structure of asphalt pavement[D]. Shanghai: Tongji University, 2013. |
| [5] |
CHOU Y. Development of an expert system for nondestructive pavement structural evaluation[D]. Texas: Texas A & M University, 1989.
|
| [6] |
ROHDE G T, SMITH R E. Determining depth to apparent stiff layer from FWD data[R]. Texas: Texas Transportation Institute, 1991.
|
| [7] |
UZAN J, LYTTON R L, GERMANN F P. General procedure for backcalculating layer moduli[C]//The 1st Conference on Nondestructive Testing of Pavements and Backcalculation of Moduli. West Conshohocken: ASTM International, 1989: 217-228.
|
| [8] |
YUSUF M, ROQUE R. Evaluation of FWD data for determination of layer moduli of pavements[J]. Journal of Materials in Civil Engineering, 2003, 15(1): 25 DOI:10.1061/(ASCE)0899-1561(2003)15:1(25) |
| [9] |
余欢. 沥青路面半刚性基层损坏评价及刚性下卧层深度设置[D]. 上海: 同济大学, 2015. YU Huan. Damage evaluation of semi-rigid base and setting method of rigid substratum depth for asphalt pavement[D]. Shanghai: Tongji University, 2015. |
| [10] |
BUSH Ⅲ A J. Nondestructive testing for light aircraft pavements phase Ⅱ development of the nondestructive evaluation methodology[R]. Washington: Army Engineer Waterways Experiment Station Geotechnical Lab, 1980.
|
| [11] |
单景松, 黄晓明, 王鹏. 刚性层深度及层间接触状态对FWD动载响应及反算结果的影响[J]. 公路交通科技, 2007, 24(10): 16 SHAN Jingsong, HUANG Xiaoming, WANG Peng. Influence of rigid subjacent bed depth and contact status between layers on FWD dynamic reflection and back-calculation modulus[J]. Journal of Highway and Transportation Research and Developemnt, 2007, 24(10): 16 DOI:10.3969/j.issn.1002-0268.2007.10.004 |
| [12] |
谢兆星, 丛林, 郭忠印. 基于FWD弯沉盆参数的沥青路面土基模量评价方法研究[J]. 公路交通科技, 2009, 26(12): 28 XIE Zhaoxing, CONG Lin, GUO Zhongyin. Evaluation of subsoil modulus for asphalt pavement based on FWD deflection basin parameter[J]. Journal of Highway and Transportation Research and Developemnt, 2009, 26(12): 28 DOI:10.3969/j.issn.1002-0268.2009.12.006 |
| [13] |
DONG Chaojun, QIU Zulian. Particle swarm optimization algorithm based on the idea of simulated annealing[J]. International Journal of Computer Science and Network Security, 2006, 10(6): 152 |
| [14] |
ULLIDTZ P. Pavement analysis[M]. New York: Elsevier Science Publishing Company Inc, 1987
|
 2018, Vol. 46
2018, Vol. 46

