2. 上海隧道工程有限公司,上海 200232
2. Shanghai Tunnel Engineering Co., Ltd, Shanghai 200232, China
同步注浆作为环境保护和隧道稳定性控制方面的技术措施在盾构施工过程中显得极为重要,针对浆液及地层特性合理确定注浆参数是保证注浆效果的前提,而注浆参数的确定依赖于注浆理论模型的正确指导[1].目前多数注浆扩散模型的建立并不完备,注浆填充机理的理解不够充分,基于传统理论方法建立的圆环形空隙内的注浆扩散模型含有过多简化和假设[2-3],其难以精细化地描述注浆体在异形空隙中的运动充填特性和压力分布模式.有限元等数值技术利用等代层概念执行静力学(准动力学)分析,忽略了注浆过程动态效应和成环效果之间的联系,其结果很难正确指导注浆参数的确定[4].
在具有特殊断面形式的异形盾构施工中,同步注浆细观运动机制的研究尤为重要[5].本文以类矩形盾构施工中同步注浆过程为研究对象,引入光滑粒子流体动力学(smoothed particle hydrohynamics, SPH)对具有自由面流动与任意复杂几何形状物体间的相互作用进行动力学仿真,精细化地描述浆液的运动特征和填充机理.同时结合可视化大型模型试验,采用有机玻璃材料和拍摄仪器再现浆液在异形空间中的实时流淌过程并验证数值模拟的正确性.研究成果可为异形盾构同步注浆扩散过程提供必要的数值依据和试验基础.
1 SPH基本理论与材料本构 1.1 SPH方法概述光滑粒子流体动力学(SPH)法的核心实为一种插值[6].在SPH中每一个宏观物理变量(密度、压力、温度)f(x)能借助于一组无序点上的值表示成积分插值计算得到,包括函数光滑和粒子近似,其公式为
| $ f\left( x \right) = \sum\limits_{i = 1}^N {\frac{{{m_i}}}{{{\rho _i}}}f({x_i})W(x - {x_i}, h)} $ | (1) |
式中:f(x)为任意空间变量x的函数;光滑函数W(x-xi, h)又被称作插值函数; h为定义光滑函数W的影响区域的光滑长度;m,ρ分别为粒子的质量和密度;i为计算质点记号;N为质点总数.
基于流体动力学理论和离散化处理,以下给出SPH格式下的Navier-Stokes控制方程.
质量守恒方程为
| $ {\rho _i} = \frac{{\sum\limits_{j = 1}^N {{m_j}{W_{ij}}} }}{{\sum\limits_{j = 1}^N {\left( {\frac{{{m_j}}}{{{\rho _j}}}} \right){W_{ij}}} }} $ | (2) |
动量守恒方程为
| $ \frac{{{\rm{d}}\nu _i^\alpha }}{{{\rm{d}}t}} = \sum\limits_{j = 1}^N {{m_j}\frac{{\sigma _i^{\alpha \beta } + \sigma _j^{\alpha \beta }}}{{{\rho _i}{\rho _j}}}\frac{{\partial {W_{ij}}}}{{\partial x_i^\beta }}} $ | (3) |
能量守恒方程为
| $ \frac{{d{e_i}}}{{dt}} = \frac{1}{2}\sum\limits_{j = 1}^N {{m_j}\frac{{{P_i} + {P_j}}}{{{\rho _i}{\rho _j}}}\nu _{ij}^\beta \frac{{\partial {W_{ij}}}}{{\partial x_i^\beta }} + \frac{{{\mu _i}}}{{2{\rho _i}}}\varepsilon _i^{\alpha \beta }\varepsilon _j^{\alpha \beta }} $ | (4) |
式(3)~(4)中:ν为速度;t为时间;e为热能;σ为应力张量;P为压力;μ为动力黏滞系数;ε为动剪应变率;x为坐标轴符号;α和β代表不同坐标方向;i和j代表不同质点;其中i为计算质点记号;j为邻近质点记号.
1.2 注浆体材料特性通常情况下,盾构隧道同步注浆由于其浆液的水灰比在1.2~1.6之间,因此在理论分析中常基于Bingham流体模型对浆液填充过程进行描述[2-3].即当泥浆进入流动状态时,其剪应变率与剪应力之间呈非线性关系.由于Bingham模型具有剪切屈服强度的定义,本文基于等效牛顿黏度系数的概念[7],采用该模型描述注浆体的流动,表达式如下:
| $ \tau = {\eta _0}\dot \gamma + {\tau _y} $ | (5) |
式中:τ为剪应力;
采用等效黏度定义,令
| $ \eta ' = {\eta _0} + ({\tau _y}/\dot \gamma ) $ | (6) |
式中:η'为等效黏度系数.引入经典的摩尔-库伦(M-C)破坏准则τy=σntan φ+c(其中σn为正应力;φ为内摩擦角;c为黏聚力).则,式(6)可写作为
| $ \eta ' = {\eta _0} + ({\sigma _n}\tan \varphi + c)/\dot \gamma $ | (7) |
结合M-C破坏准则的Bingham流体模型便可以应用于同步注浆浆液流动分析.
2 SPH数值模拟方案与模型 2.1 SPH适应性改进及实现路径对异型空隙中的同步注浆过程进行SPH动态模拟还需考虑固壁边界的处理,特别是当该数值仿真工作的计算区域呈现相对较薄的条带状/环状分布形态时,由于在边界上或邻近边界处的粒子存在缺陷,在积分的时候会被边界截断,故而SPH方法不能完全适用于整个区域.本文采用两种类型的虚粒子来处理固定边界条件,即在固定边界上(型号Ⅰ的虚粒子)和边界外的一定领域内(型号Ⅱ的虚粒子)分别布置两层(或多层)的虚粒子[6].
另外,考虑到本文方法在一个数值模型中同时引入SPH粒子和FEM有限单元,而SPH与FEM耦合关键为最靠近有限元网格的一排SPH粒子如何顺利地将应力、应变等信息传递给FEM.比较有效的方法是将边界处SPH粒子固结与有限元网格粘结在一起,通过接触设置,被粘结的粒子将会将从其他粒子传递过来的运动方程等信息传递给有限元网格,以点-面胶结方式保证两者间的位移协调.
本次SPH模拟利用Ls-Dyna软件中的SPH引擎进行流体动力学仿真计算.异型空间中的固壁边界缺陷与流固耦合接触的处理可通过Fortran语言二次开发来实现,流变参数和受力模式以自定义的方式接入程序.仿真实现流程如图 1所示.

|
图 1 SPH适应性改进和分析流程图 Fig.1 Flow chart of SPH adaptive improvement and analysis |
本文数值模型对象依据宁波市轨道交通3号线一期工程出入段线类矩形盾构法隧道工程结构断面形式进行建模.区间推进的类矩形土压平衡盾构机外径为11.83 m×7.27 m,隧道的结构采用4段圆弧的类矩形截面,其长宽比为1.66,衬砌环共分为11块,隧道的管片外径为11.50 m×6.94 m.
数值计算几何模型采用1:1全尺寸建模,同步注浆填充环状腔体范围分别由盾尾边界、地层界面、管片外表面及尾部人工边界封闭构成.注浆材料为SPH粒子,注浆影响层和衬砌管片为FEM单元.注浆孔位布设参照标准管路设计建模,并对孔位排布顺时针编号(1~8),如图 2所示.在SPH模拟过程中,盾构机前进(盾尾边界移动)速度设置为类矩形盾构施工中的平均推进速度:3 cm·min-1.

|
图 2 同步注浆SPH数值模型 Fig.2 Numerical model of synchronous grouting for SPH |
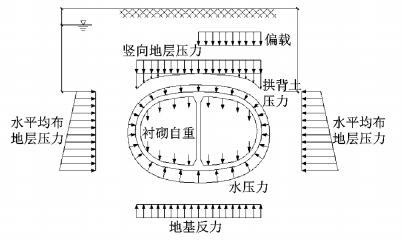
盾构同步注浆盾尾间隙腔体外的应力边界条件为埋深环境下(8~15 m)的水土压力,其中水土压力自上到下取为0.15~0.27 MPa,如图 3所示.同步注浆工艺的模拟主要通过动态生成并发射粒子实现,水土压力施加到注浆影响层外边界,粒子数最多达到100 000,粒子初始网格间距一般约10 mm.
|
图 3 类矩形盾构隧道受力分析图 Fig.3 Stress analysis sketch of quasi-rectangular shield section |
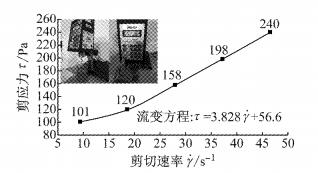
借助同济大学岩土实验室的美国博力飞可编程控制式旋转粘度计流变仪,其可测量各种牛顿/非牛顿流体的流变特性,试验流变曲线如图 4所示.
|
图 4 矩形浆流变试验和成果曲线图 Fig.4 Rheological tests and results curves of rectangular grout |
浆液材料物理力学参数见表 1.注浆施工参数则根据既有经验和研究总结,见表 2.
| 下载CSV 表 1 对应SPH模拟中的浆液计算物理参数 Tab.1 Grout physical mechanics parameters for SPH simulation |
| 下载CSV 表 2 对应SPH模拟中的注浆施工工况参数 Tab.2 Grouting construction parameters for SPH simulation |
在同步注浆SPH数值模拟中,本研究尽可能贴合实际地再现施工工况中的注浆情况,其中还包括注浆起始过程和状态的模拟.首先采用一部分粒子填充盾尾环状腔体空间,并保持一定的压力水平,类似于盾构进洞在加固区中先注满浆液的过程.然后再借助加了示踪剂的浆液颗粒对象进行正常注浆运动模拟,这些不同颜色的无网格粒子可以用来对同步注浆中浆液颗粒的细观运动机制和规律进行精细化描述,具体的计算参数见表 1和表 2.
3.1 同步注浆(浆液颗粒)整环填充规律基于SPH方法计算得到的不同时段处盾尾同步注浆整环填充规律,如图 5所示(为了可视化效果,仅给出新注入浆液不同时刻处的形态特征).

|
图 5 盾尾整环注浆动态填充规律 Fig.5 Grouting dynamic filling law of the shield tail whole loop |
从图 5中可以看出,浆液注入盾尾间隙是一个空间动态填充过程,由于注浆管路平行于隧道轴线方向,浆液颗粒从管路发射进腔体先是沿隧道纵向注入,但考虑到盾尾建筑空隙内部已填满了之前注入并保有一定压力的半流塑半凝固既有浆液层,其会给新注入浆液带来一定阻力,该阻力会造成浆液颗粒在离开出浆口一定距离后逐步转为具有环向趋势的流动,因此初始阶段各孔位所注入的浆液在出浆口附近的分布形态主要呈扇形面扩散模式为主.某时刻处浆液扩散面积和流动速率需要根据注浆参数及周围环境压力来定,由于盾尾底部的水土环境压力比顶部压力大,且相应底部的浆液注入比也较顶部少,所以同一时段内顶部注浆扩散面积更大,即底部注浆更加容易淤积在注浆孔位附近.
随注浆模拟进一步开展,浆液由压力大的地方往压力小的地方流淌,整体来看其填充规律以沿盾尾环向运动为主,受重力作用影响,盾尾肩顶部注浆孔喷出的浆液颗粒随时间增加有明显的下滑趋势;底部由于压力较大,浆液在环境阻力下未能较快向周边扩散;而在拱腰处注入的一部分浆液颗粒随拱肩处因重力作用下来的浆液一起进一步往下流淌,另一部分则因底部较大的卸荷压力而往上涌.
盾尾顶部至腰部孔位处新注入的浆液在300 s时段处已开始接触,500 s时段处就已填充饱满;而此时盾尾底部却有较大面积没有得到新注浆液填充,直到800 s时段处盾尾底部的浆液才有闭合的趋势.考虑模拟过程中无网格粒子容易产生随机波动性,浆液扩散模式并非完全对称,由此会导致浆液整体形态会产生微量的顺时针扭转变形,并造成左上方的浆液层和右下方浆液层的厚度偏大.
3.2 同步注浆(浆液颗粒)局部扩散模式(1) 顶面横断面视图
借助局部视角对注浆模拟结果进行观测可以更加精细化地展示浆液从注浆孔射出后运动特征和扩散模式的细节,基于SPH方法计算得到的不同时段处盾尾顶部同步注浆扩散模式如图 6所示,即1、8号孔位和2、7号孔位部分的注浆填充过程.

|
图 6 盾尾顶部注浆动态扩散模式 Fig.6 Grouting dynamic diffusion model at the top of shield tail |
由于盾尾顶部的周围水土压力较小,且该部位至盾尾拱肩处注浆填充率比盾尾底部至腰部的大,因此在300 s时段处顶部中间两孔的新注浆液就开始接触,而到了500~800 s时段处,顶部新注浆液已经相互充分融合,新注浆层横向分布较为均匀.图 6中两边拱肩孔位所新注浆液在500 s时段处也和顶部浆液相互接触,800 s时段处则充分闭合.从中可以看出浆液是呈椭圆弧状扩散的动态注浆过程,该椭圆弧的长轴和短轴任意时刻的长度除了受周边的环境压力影响,也跟注浆参数的选取有关.
(2) 侧部视角
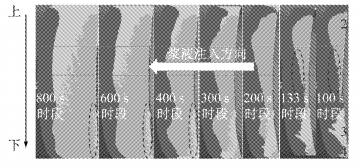
不同时段处盾尾侧面同步注浆局部扩散模式,即2、3和4号孔位(盾尾右侧3个孔位,从上到下三种颜色表示)注浆填充过程,如图 7所示.
|
图 7 盾尾侧面注浆动态扩散模式 Fig.7 Grouting dynamic diffusion model at the side of shield tail |
盾尾新注入的浆液刚开始都有各自相对独立的充填区域,其总是分布在注浆孔附近区域,即单位时间内新形成的盾尾空隙不是完全由新注入的浆液来充填(图 7中右侧虚线圆圈).盾尾当前环的注浆初始阶段(100~200 s时段内),在注浆孔一定距离外,新注入浆液尚未到达此处空间时,建筑空隙基本上依靠盾尾后方0~2环范围内尚未完全凝固的流塑状已注浆液进行挤压填充,其动力主要来自于隧道周围的水土压力、新注浆液逐渐传递来的挤压力和摩擦力,甚至盾构推进后造成的真空吸力.已注浆液填充新空隙后所损失的这部分压力和流量可由新注浆液通过逐层挤压来补充.
注浆模拟初始阶段2号和3号孔位的新注入浆液由于受到重力作用,是以非对称扇形方式扩展.在133 s时段处,2、3号孔位的新注入浆液面开始接触.随注浆模拟继续进行,在200 s时段处2号孔位注入的浆液扩散堆积在3号孔位注入的浆液扩散面前方,盾尾侧面注入的浆液易受重力影响夹裹住其他孔位的浆液一起旋转着向前运动,在模拟进行到300~400 s时段处,3号孔位新注入的部分(下侧)浆液在重力作用下向底部流动,而靠近拱腰壁面处的部分(上侧)浆液在底部较大的卸荷压力作用下会往上流淌,即此处产生了一个细微上浮通道(图 7中左侧虚线圆圈),其中浆液颗粒上涌高度取决于重力作用和卸荷压力的平衡位置.
(3) 底部视角
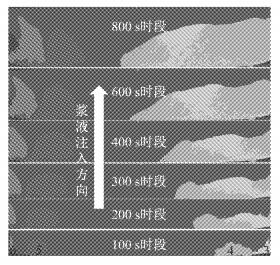
不同时段处底部注浆扩散模式如图 8所示,即4、5号孔位和3、6号孔位部分的注浆填充过程.
|
图 8 盾尾底部注浆动态扩散模式 Fig.8 Grouting dynamic diffusion model at the bottom of shield tail |
从图 8中可以看出,4、5号孔位所新注入的浆液在100~800 s时段内几乎都在出浆孔附近淤积.随时间的推移,在300 s和500 s时段处,这两个孔位所注浆液靠外侧部分会在底部较大卸荷压力作用下往外侧(向上)移动,同时也带动4、5号孔位所注浆液一部分颗粒向外运移.在800 s时段处,底部浆液可认为靠外侧部分基本融合,而完全封闭仍需时间.盾尾底部在新注入浆液量较少,且由于大阻力不易流动扩散的情况下,其空隙中间腔体更多是靠之前已经注入的既有浆液来弥补.另一方面,在管片脱出盾尾的一瞬间,底部较大的水土压力会在非常短的时间内使得周围土体快速地释放能量以及变形增加,因此盾尾底部空隙相较于其上部会更加狭小,这也是从整体扩散规律中可看出底部存留浆液要比上部稀薄的原因所在,如图 5所示.
4 可视化大型模型试验 4.1 试验系统设计试验采用上海盾构试验中心下沉式盾构掘进机综合模拟试验平台,该平台主要包括多功能模拟盾构机、组合式液压加载系统、监控测量系统、盾构推进导向系统、盾构进出洞门和洞门密封系统、吊装和运输系统、土建结构等部分.模拟土体掘进区域净空尺寸为:长度10 m、宽度7 m、深度8.5 m,在尺寸上充分考虑了边界效应的影响,试验更符合工程实际.最大土压力可模拟0.6 MPa.试验基坑由3部分组成,分别模拟盾构隧道进、出洞及区间段.坑内最大覆土深度5 m,如图 9和图 10所示.

|
图 9 试验平台示意图 Fig.9 Sketch map of test equipment |

|
图 10 试验推进现场图 Fig.10 Field picture of test propulsion |
试验土体采用分层装载方式,每层厚约0.5 m,每层应压实一遍,总体采用长臂挖机夯击,局部人工处理.可视化大型模型试验对象采用宁波轨道交通3号线类矩形盾构试验段等比例缩尺模型,模拟管片直径为1.8 m×1.1 m,接收井的端部固定在洞门上.外套筒套在模拟管片外,尺寸为1.9 m×1.2 m,套筒尾部设置注浆孔,见图 11a所示.通过始发井处回拉外套筒,尾部自接收井处开始逐渐形成盾尾间隙,同时注浆孔注浆.模拟盾构内管采用5节1.8 m×1.1 m×2 m的钢管节,1节1.8 m×1.1 m×1.5 m的有机玻璃管节作为模拟管片,见图 11b所示.本次可视化大型模型试验的土体材料为宁波原状土,浆液配合比材料、盾构机和管节形状、注浆泵及管路尺寸和布置方式、覆土环境都与实际工程一致.

|
图 11 盾尾结构和透明管片图 Fig.11 Pattern of shield tail structure and transparent segment |
试验模型中的注浆孔位安放方式与实际工程中盾构机的注浆孔位相匹配,对应数值模拟中的1~8号孔位(图 11中多出的管路布置是为了浆液堵管时备用).试验模型与盾构机注浆孔通径同为0.4 m.本次试验通过拍摄仪器记录同步注浆浆液(颗粒)的流动情况,具体采用4台高像素单反相机作为拍摄仪器,分别架设在有机玻璃管节的上部和下部,对管节4个位置的注浆填充规律和扩散模式进行全面记录,并以此来分析浆液的细观运动机制.
4.2 注浆流场运动特征为了得到更好的浆液整体填充规律和局部扩散模式,结合示踪剂的帮助来改善注浆过程中浆液的实时定位观测效果,即针对不同注浆孔位中注入的浆液分别掺入不同颜色的染色剂,如图 12所示(侧部视角).从图中可看到当盾尾刷经过后,盾尾间隙内及时注入红色(下部)和黄色(上部)浆液,浆液的充填过程是从注浆孔位附近逐渐向两侧平滑地圆弧状扩散,每个注浆孔注入的浆液都有各自相对独立的充填区域,即单位时间内新形成的盾尾空隙不是完全由新注入的浆液来充填,刚开始注入的浆液总是分布在注浆孔附近的区域.

|
图 12 盾尾侧面注浆流场特征 Fig.12 Grouting flow field characteristics in the side of shield tail |
随着试验盾构机向前推进,同步注浆浆液不断向空隙内充填,试验注浆工况可参考已有研究[8].由于埋深导致土压力分布有差异,浆液会从压力大的地方往压力小的地方流淌,盾尾处的拱顶和拱底部位主要呈扇状扩散形态,拱顶上部由于压力小,扇形面积更大,且边缘部位会向两侧移动;底部浆液扩散速率较慢,在重力作用下部分浆液会缓慢向拱底中间流淌;而盾尾侧面部位浆液则具有较复杂的运动特征,在初始类扇形扩散以后,拱腰处部分靠盾尾壁面处的浆液颗粒受卸荷压力差驱动先向上运动,压力重分布后再与拱肩处浆液逐渐混合并呈回旋状往下运动,见图 12中箭头和虚线所示.
4.3 浆液凝固形态凝固后的浆液断面形态特征能被用来反映注浆扩散规律,通过对浆液层考古测量,可以绘制凝固后的浆液横断面填充几何形态,如图 13所示.

|
图 13 凝固后的浆液横断面填充几何形态特征图 Fig.13 Geometric characteristics of coagulated grout cross-section |
根据所得数据及绘制的图像可知,在注浆管路通畅区段,浆液能够较好地填充盾尾间隙.从整个浆液凝固后的形态可以发现,肩顶部的浆液厚度远远大于底部浆液的厚度,排除因重力作用引起管片下沉的影响,更多是由于底部水土压力过大而造成的注浆困难.而对于左上顶部及侧面浆液凝固层厚度略大于右上顶部及侧面浆液凝固层厚度的现象,则是由于注浆管局部堵管所造成.基于上述两种原因,浆液在被压密后由于其不对称分布的形态使得管片产生顺时针扭转变形,就造成了右下方浆液凝固层厚度大于左下方浆液凝固层厚度,同时考虑在试验过程中抽拉外侧管片而造成的内侧管片受力不均,也可能使浆液填充整体发生一定的偏转.
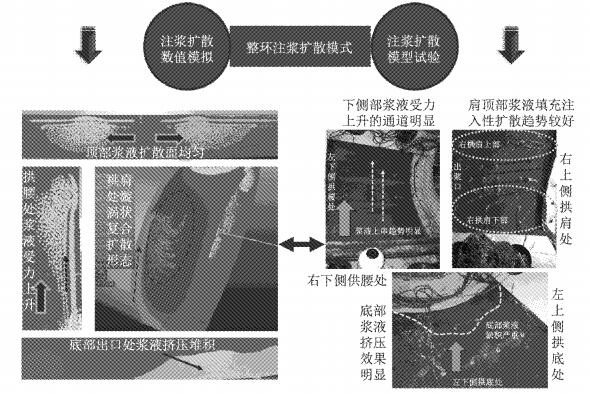
5 数值模拟与试验结果的对比验证同步注浆浆液颗粒细观运动机制的SPH模拟结果和可视化大型模型试验结果对比如图 14所示.由SPH数值计算所得到的浆液颗粒在盾尾拱顶部、拱肩部、拱腰部及拱底部任意时刻的整体填充规律与局部扩散模式和模型试验结果基本相同.
基于SPH方法的浆液颗粒运动规律数值模拟细节在于:拱顶处因压力较小使得浆液扩散面较为均匀;拱肩处浆液在重力作用下下滑趋势明显,与拱腰处部分因底部较大卸荷压力造成的上涌浆液颗粒混合而呈漩涡状复合扩散形态,同样原因也造成底部出浆口处浆液挤压淤积严重.这与模型试验中肩顶部位注入扩散形态较好,拱腰靠侧壁处有浆液受力上浮通道,以及底部浆液挤压效果显著等特征非常吻合.而同时浆液凝固后的形态对比显示数值模拟与试验结果也较为接近,由此可认为本文采用SPH方法描述的注浆精细化运动规律和扩散机制是正确的,浆液颗粒运动轨迹细节如图 15所示.
|
图 14 数值模拟和试验结果对比分析 Fig.14 Comparative analysis between numerical simulation and test results |

|
图 15 浆液颗粒细观运动轨迹示意图 Fig.15 Mesoscopic movement tracks of grout particles |
盾构隧道同步注浆填充机理以及压力分布与传播规律的准确把握需要建立在对注入浆液(颗粒)细观运动机制充分理解和认识的基础上.实际施工中同步注浆注入建筑空隙的浆液(颗粒)并非完美匹配诸多研究中的理论假设,其存在较多复杂的运动轨迹,尤其在含非常规异形断面结构的盾构工程中更加明显.传统盾构施工中的注浆研究更多的是通过浆液配比试验是否达到了需要的指标来衡量结果的好坏[9],对于浆液本身在受力极为复杂的环状空隙内的细观流动机制及其对应的填充扩散模式则关注较少,而这恰恰是诸多工程在面临上浮问题、沉降问题时束手无策根本原因.因此,可以通过更多地关注浆液细观运动规律以及凝固后的分布形态来探讨合适的注浆管位布置,上下注浆比例,甚至各个孔位不同的材料配比和加注方式等.
本文基于SPH方法分析类矩形盾构同步注浆整体填充规律及局部扩散模式,结合可视化大型模型试验结果对数值模拟进行验证,精细化地再现了浆液在异形空间中的细观运动机制,结论如下:
(1) 通过整环注浆模拟可以看出,浆液扩散模式具有纵环向相互关联的挤压填充性流动特征.考虑到类矩形盾构盾尾上下具有水平构造的特征,其盾尾间隙中的浆液流动性相比圆形盾构更低,特别是由于盾尾底部周围水土压力大的原因致使该处注浆得填充扩散效率较差,呈现挤压堆积形态.
(2) 盾尾顶部和侧面相对较好的外部水土压力环境,使得该处浆液在盾尾间隙中能够快速充填,其扩散面较为均匀.而拱腰靠近管壁处受盾尾底部上下卸荷压力差的作用有局部浆液上升通道,浆液颗粒受力上升趋势明显,其在拱肩部位压力重分布后与新注入浆液混合,再呈漩涡状往下流淌.
(3) 盾尾顶底部由于其水平构造使得此处浆液纵向扩散距离较大,而盾尾侧面的浆液受重力影响其环向流淌趋势更加明显,如此对于注浆压力扩散的推导则需考虑建立不同的模式来进行分析.
(4) 由数值模拟得到的盾尾拱顶部、拱肩处、拱腰处及拱底部任意时刻浆液的整体填充规律与局部扩散模式与模型试验结果对比非常吻合,说明本文给出的同步注浆扩散模式是合理且正确的.
| [1] |
张庆松, 张连震, 张霄, 等. 基于浆液黏度时空变化的水平裂隙岩体注浆扩散机制[J]. 岩石力学与工程学报, 2015, 34(6): 1198 ZHANG Qingsong, ZHANG Lianzhen, ZHANG Xiao, et al. Grouting diffusion in a horizontal crack considering temporal and spatial variation of viscosity[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(6): 1198 |
| [2] |
李志明, 廖少明, 戴志仁. 盾构同步注浆填充机理及压力分布研究[J]. 岩土工程学报, 2010, 32(11): 1752 LI Zhiming, LIAO Shaoming, DAI Zhiren. Theoretical study on synchronous grouting filling patterns and pressure distribution of EPB shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1752 |
| [3] |
苟长飞, 叶飞, 张金龙, 等. 盾构隧道同步注浆充填压力环向分布模型[J]. 岩土工程学报, 2013, 35(3): 590 GOU Changfei, YE Fei, ZHANG Jinlong, et al. Ring distribution model of filling pressure for shield tunnels under synchronous grouting[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(3): 590 |
| [4] |
肖广良, 李培楠, 朱雁飞, 等. 类矩形盾构施工中的SPH流体动力学应用探索[J]. 现代隧道技术, 2016, 53(增1): 181 XIAO Guangliang, LI Peinan, ZHU Yanfei, et al. Explorative research on SPH fluid dynamics applied in quasi-rectangular shield construction[J]. Modern Tunnelling Technology, 2016, 53(S1): 181 |
| [5] |
丁文其, 赵天驰, 黄德中, 等. 类矩形盾构同步注浆可视化试验技术与分析[J]. 现代隧道技术, 2016, 53(增1): 226 DING Wenqi, ZHAO Tianchi, HUANG Dezhong, et al. Analysis of synchronous grouting of quasi-rectangular shields based on visual test technology[J]. Modern Tunnelling Technology, 2016, 53(S1): 226 |
| [6] |
LIU G R, LIU M B. Smoothed particle hydrodynamics―a meshfree particle method[M]. New Jersey: World Scientific Publishing Company, 2003
|
| [7] |
黄雨, 郝亮, 谢攀, 等. 土体流动大变形的SPH数值模拟[J]. 岩土工程学报, 2009, 31(10): 1520 HUANG Yu, HAO Liang, XIE Pan, et al. Numerical simulation of large deformation of soil flow based on SPH method[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(10): 1520 DOI:10.3321/j.issn:1000-4548.2009.10.007 |
| [8] |
李刚, 庄欠伟, 黄德中, 等. 类矩形盾构同步注浆大型模型试验[J]. 现代隧道技术, 2016, 53(增1): 195 LI Gang, ZHUANG Qianwei, HUANG Dezhong, et al. Large model test for synchronous grouting of quasi-rectangular shield tunnels[J]. Modern Tunnelling Technology, 2016, 53(S1): 195 |
| [9] |
叶飞, 毛家骅, 纪明, 等. 盾构隧道壁后注浆研究现状及发展趋势[J]. 隧道建设, 2015, 35(8): 739 YE Fei, MAO Jiahua, JI Ming, et al. Research status and development trend of back-filled grouting of shield tunnels[J]. Tunnel Construction, 2015, 35(8): 739 DOI:10.3973/j.issn.1672-741X.2015.08.001 |
 2018, Vol. 46
2018, Vol. 46
