2. 天津商务职业学院 经济贸易学院, 天津 300170
2. College of Economics and Trade, Tianjin College of Commerce, Tianjin, 300170, China
基础设施在促进城市经济可持续发展、提高城市居民生活水平和减少贫富差距等方面都发挥着重要的作用[1-2].然而,我国在基础设施的建设和运营等阶段仍存在着长期利益的忽视[3]、生态环境的破坏[4]、使用寿命短[5]、运营管理水平低[6]等问题,其产生的根源在于对基础设施可持续性的忽视.因此,在决策阶段对基础设施可持续性影响因素进行识别,有利于减少基础设施建设与运营过程中可持续性问题的产生.
影响基础设施可持续性的因素来自多层次多维度.有些学者将基础设施可持续性分成三个维度进行评价和分析,即经济、社会和环境.比如,Pryn[7]、Karaca[8]、Zhang[9]、Yao[10]等从经济、社会和环境三个维度评估和分析了基础设施可持续性;Shen等[11]基于模糊集理论从经济、社会和环境三方面研究了基础设施可持续性的关键影响因素.除此之外,部分学者也从其他方面考虑了基础设施可持续性影响因素.比如,Zhou等[12]将基础可持续性分为内部可持续性和外部可持续性,考虑了项目本身的经济技术和管理水平影响因素,进而建立了项目的可持续性评估模型.Boz等[13-14]将基础设施可持续性分为产品工序和自然属性两方面,并通过专家访谈对其进行了验证分析.然而,在以往的研究中,指标权重的确定主要依赖于少数专家的主观评价值,难以克服评价结果具有较强主观性的缺点.徐选华等[15]提出了基于项目历史数据的关联度模型来评价复杂生态系统风险性.虽然该模型克服了评价方法主观性强的缺点,但仅适用于单个对象的评价,且权重模型优化不足.
基于此,本文首先通过文献回顾对基础设施可持续性影响因素进行了识别,其次对单个项目可持续性影响因素的权重进行确定.进而在考虑信息偏差、一致性和信息熵三方面因素的基础上,构建了基于关联度的基础设施可持续性多属性群决策模型.最终通过对24个公路项目进行实证分析,验证了该模型的可行性.
1 基础设施可持续性影响因素识别本文通过文献回顾[7-14],参考国内的项目竣工环境保护验收报告,将基础设施可持续性影响因素分为经济因素(ECE)、社会因素(SOE)和自然环境因素(ENE),见表 1.
| 下载CSV 表 1 基础设施可持续性影响因素及量化指标 Tab.1 Sustainability factors and quantitative indexes of urban infrastructure |
将单个基础设施可持续性影响因素看成一个群体Ω,其中包含表 1中的27个可持续性影响因素量化指标.具体定义如下:
定义1 可持续性矢量.设第i个可持续性影响因素的量化指标为q个,其中第l个量化指标对基础设施可持续性影响为vil(vil>0, l=1, 2, …, p),则称可持续矢量Vil=(vi1, vi2, …, vip)为第i个可持续性影响因素的可持续矢量.
定义2 可持续标准值矢量.设第i个可持续性影响因素中第l个量化指标的可持续标准值为vil(vil>0, l=1, 2, …, p),则称可持续标准值矢量Vil=(vi1, vi2, …, vip)为第i个可持续影响因素的可持续标准值矢量.
定义3 两个可持续性影响因素Vi和Vj之间的可持续性关联度[15]rij(Vi, Vj)表示为
| $ {r_{ij}}({\mathit{\boldsymbol{V}}_i}, {\rm{ }}{\mathit{\boldsymbol{V}}_j}) = \frac{{\left| {{\mathit{\boldsymbol{v}}_i}-{{\mathit{\boldsymbol{\bar v}}}_i}} \right|\cdot\mathit{\boldsymbol{B}}\cdot{{\left| {{\mathit{\boldsymbol{v}}_j}-{{\mathit{\boldsymbol{\bar v}}}_j}} \right|}^{\rm{T}}}}}{{{{\left\| {{\mathit{\boldsymbol{v}}_i}-{{\mathit{\boldsymbol{\bar v}}}_i}} \right\|}_2}\cdot{{\left\| \mathit{\boldsymbol{B}} \right\|}_2}\cdot{{\left\| {{\mathit{\boldsymbol{v}}_j} - {{\mathit{\boldsymbol{\bar v}}}_j}} \right\|}_2}}} $ | (1) |
其中B为第i个可持续性影响因素与第j个可持续性影响因素之间的量化指标影响关系矩阵.矩阵B由可持续影响度blkij构成,blkij表示第i个可持续性影响因素的第l个量化指标(l=1, 2, …, p)与第j个可持续性影响因素的第k个量化指标(k=1, 2, …, q)之间的影响度.
其中
定义4 基础设施两个不同阶段的可持续性影响因素权重矢量wi和wj之间的相关程度用关联度[16]ρij(wi, wj)表示为
| $ {\rho _{ij}}({\mathit{\boldsymbol{w}}_i}, {\rm{ }}{\mathit{\boldsymbol{w}}_j}) = \frac{{\left| {{\mathit{\boldsymbol{w}}_i}-\mathit{\boldsymbol{\bar w}}} \right|\cdot{{\left| {{\mathit{\boldsymbol{w}}_j}-\mathit{\boldsymbol{\bar w}}} \right|}^{\rm{T}}}}}{{{{\left\| {{\mathit{\boldsymbol{w}}_i}-\mathit{\boldsymbol{\bar w}}} \right\|}_2}\cdot{\rm{ }}{{\left\| {{\mathit{\boldsymbol{w}}_j} - \mathit{\boldsymbol{\bar w}}} \right\|}_2}}} $ | (2) |
其中,wi和wj分别是第i个阶段和第j个阶段可持续性影响因素的权重矢量.w是项目的平均权重矢量.
定义5 在计算指标综合权重过程中,引入文献中成员矢量之间的关联度均方差和矢量集一致性指标作为评价标准.相对偏差函数取得最小值时,表示每个项目权重矢量与群体综合权重偏差最小,一致性程度最高[17].据此构造成员矢量之间关联度的相对偏差函数:
| $ \begin{array}{l} f{\left( \mathit{\boldsymbol{W}} \right)_{{\rm{min}}}} = \\ {\rm{min}}\sqrt {\frac{1}{{{c_m}^2}}\sum\limits_{1 \le i \le j \le m} {{{({\rho _{ij}}({\mathit{\boldsymbol{w}}_i}, {\rm{ }}{\mathit{\boldsymbol{w}}_j})-\rho (\mathit{\boldsymbol{W}}))}^2}\rho (\mathit{\boldsymbol{W}})} } \end{array} $ | (3) |
其中
将准则权重wtr理解为第r个可持续性影响因素在准则集中所占比重,即“概率”.用Shannon信息熵[18]
| $ {H_m}(\boldsymbol{W}) =-\sum\limits_{t = 1}^m {\sum\limits_{r = 1}^n {{\boldsymbol{w}_{tr}}\ln \;{\boldsymbol{w}_{tr}}} } \; $ | (4) |
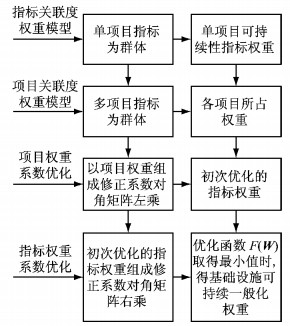
基于关联度的多属性群体决策模型构建的流程如图 1所示.
|
图 1 模型构建流程图 Fig.1 Model build flow chart |
利用关联度权重模型[15],对单个基础设施项目可持续性进行评价,得到单个项目基础设施可持续性评价指标权重.然而,一个项目得到的可持续性影响因素权重对其他各类项目的借鉴程度有限,需要考虑多个基础设施项目的综合情况.因此,在单个项目权重基础上,进一步将不同的项目看作一个群体Ψ,形成一个群体属性维度相同的多属性群决策问题.关联度多属性群体决策模型的构建具体流程如下:
(1) 运用关联度模型可得出m个项目可持续性影响因素权重,其中,第t个项目的权重矢量记为wt=(wt1, wt2, …, wtn),1≤t≤m.将m个项目可持续性影响因素的权重矢量矩阵记为:W={w1, w2, …, wt, …, wm}.
(2) 运用式(2)分别计算出两个项目之间的可持续性相关度ρij(wi, wj),形成m×m关联度矩阵.根据标准化处理公式
(3) 项目权重组成对角矩阵形成修正系数矩阵,然后右乘初始的可持续影响因素权重矩阵W,最终得到矩阵G:
| $ \begin{array}{l} \boldsymbol{G} = \left[{\begin{array}{*{20}{c}} {w_1^*}&0&0&0&0\\ 0&{w_2^*}& \cdots &0&0\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0& \cdots &0&{w_{m-1}^*}&0\\ 0&0&0&0&{w_m^*} \end{array}} \right] \cdot \\ \left[{\begin{array}{*{20}{c}} {{w_{11}}}&{{w_{12}}}& \cdots &{{w_{1, n-1}}}&{{w_{1n}}}\\ {{w_{21}}}&{{w_{22}}}& \cdots &{{w_{2, n-1}}}&{{w_{2n}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {{w_{m-1, 1}}}&{{w_{m - 1, 2}}}& \cdots &{{w_{m - 1, n - 1}}}&{{w_{m - 1, n}}}\\ {{w_{m1}}}&{{w_{m2}}}& \cdots &{{w_{m, n - 1}}}&{{w_{mn}}} \end{array}} \right] \end{array} $ | (5) |
对矩阵G每一列求均值,得到对应的项目可持续性影响因素权重值为
(4) 为了让每个项目的指标权重更好地反映综合权重,将上一步优化后得到的可持续性影响因素权重值矢量W组成对角矩阵,形成优化系数矩阵.而后,将该优化系数矩阵右乘矩阵G,得到进一步优化的权重矩阵B:
| $ \begin{array}{l} \boldsymbol{B} = \left[{\begin{array}{*{20}{c}} {{g_{11}}}&{{g_{12}}}& \cdots &{{g_{1, n-1}}}&{{g_{1n}}}\\ {{g_{21}}}&{{g_{22}}}& \cdots &{{g_{2, n-1}}}&{{g_{2n}}}\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {{g_{m-1, 1}}}&{{g_{m - 1, 2}}}& \cdots &{{g_{m - 1, n - 1}}}&{{g_{m - 1, n}}}\\ {{g_{m1}}}&{{g_{m2}}}& \cdots &{{g_{m, n - 1}}}&{{g_{mn}}} \end{array}} \right] \cdot \\ \left[{\begin{array}{*{20}{c}} {{{\bar w}_1}}&0& \cdots & \cdots &0&0\\ 0&{{{\bar w}_2}}&0& \cdots & \cdots &0\\ \vdots &0& \cdots &0& \cdots &0\\ \vdots & \vdots &0& \ddots &0&0\\ 0&0& \vdots &0&{{{\bar w}_{n-1}}}&0\\ 0&0& \cdots & \cdots &0&{{{\bar w}_n}} \end{array}} \right] \end{array} $ | (6) |
对矩阵G每一列求均值,得到对应列指标的权重值为
(5) 根据群体偏差最小以及信息熵最大原则,本研究提出权重最优化模型(7)如下:
目标函数:
| $ \begin{array}{l} F{(\mathit{\boldsymbol{W}})_{\min }} = \\ \min \sqrt {\frac{1}{{c_m^2}}\sum\limits_{1 \le i \le j \le m} {{{({\rho _{ij}}({\mathit{\boldsymbol{w}}_i}, {\rm{ }}{\mathit{\boldsymbol{w}}_j})-\rho (\mathit{\boldsymbol{W}}))}^2}/\rho (\mathit{\boldsymbol{W}})} } + \\ \sum\limits_{t = 1}^m {\sum\limits_{r = 1}^n {{\mathit{\boldsymbol{w}}_{tr}}\ln \;{\mathit{\boldsymbol{w}}_{tr}}} } \end{array} $ |
约束条件:
| $ \begin{array}{l} {{\bar w}^*}_r = \frac{{\sum\limits_{t = 1}^m {\mathit{\boldsymbol{w}}_t^*{\mathit{\boldsymbol{w}}_{tr}}} }}{m};\mathit{\boldsymbol{w}}_t^* = \frac{{{\rho _{tt}}({\mathit{\boldsymbol{w}}_t}, {\rm{ }}{\mathit{\boldsymbol{w}}_t})}}{{\sum\limits_{h = 1}^m {{\rho _{th}}({\mathit{\boldsymbol{w}}_t}, {\rm{ }}{\mathit{\boldsymbol{w}}_h})} }};\sum\limits_{r = 1}^n {{\mathit{\boldsymbol{w}}_{tr}} = 1}, \\ {w_{tr}} \ge 0;{{\bar w}^*} = \frac{{\sum\limits_{t = 1}^m {{\mathit{\boldsymbol{w}}_t}^*{\mathit{\boldsymbol{w}}_{tr}}{{\mathit{\boldsymbol{\bar w}}}_r}} }}{m};r = 1, 2, \cdots, n;t\left( h \right) = \\ 1, 2, \cdots m; \end{array} $ |
其中:W={w1, w2, …, wt, …, wm};wt=(wt1, wt2, …, wtr, …, wtn);wr*是项目可持续影响因素的最终权重值.归一化后就是基础设施可持续性影响因素的一般性权重.wtr表示第t个项目第r个可持续性影响因素的权重值,也就是wt的第r个矢量分量,所有数值均标准化后取值.
3 基础设施可持续性影响因素权重确定步骤步骤1:单个项目可持续性影响因素结构分析.
首先,运用式(1)求出两两可持续性影响因素之间的关联度rij(vi, vj),得到n×n的关联度矩阵;然后,基于可持续关联度矩阵,对可持续性影响因素群体Ω应用改进的矢量空间聚类方法进行聚类[17],可以形成p个可持续性影响因素集Ω={C1, C2, …, Cp}.
步骤2:项目不同阶段可持续性影响因素初始权重确定
求出可持续性影响因素集间的关联度Rij(Ci, Cj).最后,影响因素Vi的权重ki可以由
步骤3:可持续性影响因素权重初次优化结果
通过步骤2中方法,求解出单个项目在项目群体中所占的权重矢量,形成多项目权重矩阵W={w1, w2, …, wt, …, wm}.由模型(7)约束条件中的第2式可以求出项目可持续性影响在整个项目全生命周期中所占的权重为W*={w1*, w2*, …, wm*}.
以此权重矢量构造的对角修正矩阵左乘初始权重矩阵,得到初步优化后的权重矩阵.从而,初次优化后的指标综合权重为:W=(w1, w2, w3, …wn).
步骤4:可持续性影响因素权重再次优化结果
在初次优化的基础上,运用初次优化后的指标综合权重构造权重修正对角矩阵,对初次优化权重矩阵进行右乘,从而得到再次优化后的指标综合权重:W*=(w1*, w2*, …, wn*).通过权重最优化模型(7)计算再次优化矩阵的F(W*),f(W*),H(W*),将其与F(W),f(W),H(W)比较.
步骤5:可持续性影响因素权重迭代优化
继续对所得权重矩阵进行优化,直到当F(WZ*)趋近于某个极值最小值或者在某次优化后取得最小值时,取此时的极限权重WZ*=(w1Z*, w2Z*, w3Z*, …, wnZ*)为最优权重.
4 实证分析本文通过对24个真实的公路项目的跟踪与调查,并结合其环境评估报告、运营车流量、收费标准、公里数、运营成本等相关数据,计算和统计了表 1中的基础设施可持续性影响因素的27个量化指标,即量化指标的真实值.而影响因素量化指标的标准值则来源于历史数据的最优值或理想状态下的取值,差异值表示理想值与真实值之间的差距.最终的基础设施影响因素量化指标真实值、理想值和差异值见表 2.(因篇幅所限仅列出联兴阿城项目的计算结果).
| 下载CSV 表 2 联兴阿城段公路项目可持续性影响因素量化指标的真实值、理想值和差异值 Tab.2 The true, ideal and difference values of quantitative indexes of sustainability factors of Lian-A highway project |
根据计算单个项目可持续性影响因素之间的关联度值进行聚类,聚类结果见表 3,从而得出联兴阿城项目各因素权重见表 4.以同样的计算步骤,可得出24个项目的可持续性影响因素权重见表 5.
| 下载CSV 表 3 联兴阿城段公路项目可持续性影响因素聚类结果 Tab.3 Cluster results of sustainability factors of Lian-A highway project |
| 下载CSV 表 4 联兴阿城段公路项目可持续性影响因素的权重 Tab.4 The Weight of sustainability factors of Lian-A highway project |
| 下载CSV 表 5 24个项目的可持续性影响因素权重表 Tab.5 The weight of sustainability factors of 24 road projects |
在以上结果的基础上,以24个项目为群体Ψ,以上一步中得到的指标为准则,运用迭代的方法,按照4个步骤进行计算,优化前F(W)=223.543,经过初次优化和再次优化后F*(W)=1.229.
多次优化后F(W)min=-10.521,多次循环优化都是趋近于这个最小值.因此求解得到在F(W)最小情况下得到的基础设施可持续性影响因素的最优权重见表 6.
| 下载CSV 表 6 基础设施可持续性影响因素的一般权重值 Tab.6 Generalized weights infrastructure projects sustainability impact factors |
综合上述:(1)影响因素指标权重优化后相比优化前,F(W)大幅度下降,从223.543到-10, 521,相对偏差也大幅减小,验证了基于关联度的多属性群体决策模型的有效性; (2)得到了24个公路项目的可持续性评价指标的一般性权重.其中,对公众的影响程度、公众满意度、大气环境影响、固体废弃物、为经济发展提供便利设施等因素所占权重较大,分别达0.121、0.082、0.082、0.080、0.079,说明这些因素对公路项目可持续性的影响较大,在新建类似基础设施的项目时需重点考虑这些关键指标; (3)水环境的影响、建设资金合理性等因素所占权重相对较低,分别为0.048和0.057.水环境影响因素所占权重较低的原因在于公路的建设对水流、河流等影响较小,而建设资金合理性影响因素所占权重较低的原因在于,这些公路项目大都是政府出资建设,更为看重的是社会效益而非经济利益.
5 结论本文构建的基于关联度的多属性群决策模型,为实现在影响因素和项目数量众多的情况下对基础设施可持续性进行评价提供有效的方法.该模型通过修正系数矩阵对项目群体综合权重进行了优化,结合24个公路项目的实证分析验证了该模型的有效性.该模型的优点在于评价所需数据来源于项目建设实际历史数据和运营状况相关数据,具有一定的客观性;且能适用于影响因素复杂,数量庞大的复杂系统的评价.
| [1] |
PANDIT A, MINNE E A, LI F, et al. Infrastructure ecology: an evolving paradigm for sustainable urban development[J]. Journal of Cleaner Production, 2017, 163: S19 DOI:10.1016/j.jclepro.2015.09.010 |
| [2] |
DONG L, WANG Y, SCIPIONI A, et al. Recent progress on innovative urban infrastructures system towards sustainable resource management[J]. Resources Conservation & Recycling, 2017, 128: 355 |
| [3] |
严盛虎, 李宇, 毛琦梁, 等. 我国城市市政基础设施建设成就、问题与对策[J]. 城市发展研究, 2012, 19(5): 28 YAN Shenghu, LI Yu, MAO Qiliang, et al. The urban municipal infrastructure construction status, problem and countermeasure of china[J]. Urban Development Studies, 2012, 19(5): 9 |
| [4] |
周君. 民生视角下城市基础设施可持续建设的评价方法与协同监管[J]. 城市发展研究, 2012, 20(2): 9 ZHOU Jun. Supervision and assessment method of infrastructure sustainable construction in cities on the view of people's well-being[J]. Urban Development Studies, 2012, 20(2): 9 |
| [5] |
曾国安, 尹燕飞. 中国城镇基础设施建设和利用效率的测度与评价[J]. 中南财经政法大学学报, 2012, 194: 3 ZENG Guo'an, YIN Yanfei. Measurement and asseaament of construction and using efficiency in china's urban infrastructure[J]. Jouranl of Zhongnan University of Economics and Law, 2012, 194: 3 |
| [6] |
孙钰, 陶志梅, 姚鹏. 城市公共基础设施复合系统协调发展度研究[J]. 城市发展研究, 2015, 22(5): C24 SUN Yu, TAO Zhimei, YAO Peng. The research on the coordination development degree of the composite system of public infrastructure[J]. Urban Development Studies, 2015, 22(5): C24 |
| [7] |
PRYN M R, CORNET Y, SALLING K B. Applying sustainability theory to transport infrastructure assessment using a multiplicative ahp decision support model[J]. Transport, 2015, 30(3): 330 DOI:10.3846/16484142.2015.1081281 |
| [8] |
KARACA F, RAVEN P G, MACHELL J, et al. A comparative analysis framework for assessing the sustainability of a combined water and energy infrastructure[J]. Technological Forecasting & Social Change, 2015, 90(2): 456 |
| [9] |
ZHANG X, WU Y, SHEN L, et al. A prototype system dynamic model for assessing the sustainability of construction projects[J]. International Journal of Project Management, 2014, 32(1): 66 DOI:10.1016/j.ijproman.2013.01.009 |
| [10] |
YAO H, SHEN L, TAN Y, et al. Simulating the impacts of policy scenarios on the sustainability performance of infrastructure projects[J]. Automation in Construction, 2011, 20(8): 1060 DOI:10.1016/j.autcon.2011.04.007 |
| [11] |
SHEN L, ASCE M, WU Y, et al. Key Assessment Indicators for the Sustainability of Infrastructure Projects[J]. Journal of Construction Engineering & Management, 2011, 137(6): 441 |
| [12] |
ZHOU J, LIU Y. The method and index of sustainability assessment of infrastructure projects based on system dynamics in China[J]. Biochimica Et Biophysica Acta, 2015, 8(3): 29 |
| [13] |
BOZ M A, El-ADAWAY I H. Managing sustainability assessment of civil infrastructure projects using work, nature, and flow[J]. Journal of Management in Engineering, 2013, 30(5): 04014019 |
| [14] |
BOZ M A, El-ADAWAY I H. Creating a holistic systems framework for sustainability assessment of civil infrastructure projects[J]. Journal of Construction Engineering & Management, 2015, 141(2): 04014067 |
| [15] |
徐选华, 曹静. 大型水电工程复杂生态环境风险评价[J]. 系统工程理论与实践, 2012, 32(10): 2237 XU Xuanhua, CAO Jing. Risk evaluation for complex ecological environment of large-scale hydropower engineering[J]. Systems Engineering—Theory & Practice, 2012, 32(10): 2237 |
| [16] |
徐选华, 陈晓红. 基于矢量空间的群体聚类方法研究[J]. 系统工程与电子技术, 2005, 27(6): 1034 XU Xuanhua, CHEN Xiaohong. Research on the group clustering method based on vector space[J]. Systems Engineering and Electronic, 2005, 27(6): 1034 |
| [17] |
胡立辉, 罗国松. 改进的基于矢量空间的群体聚类算法[J]. 系统工程与电子技术, 2007, 29(3): 472 HU Lihui, LUO Guosong. Improved algorithm for group clustering based on vector space[J]. Systems Engineering and Electronic, 2007, 29(3): 472 |
| [18] |
徐泽水, 达庆利. 多属性决策的组合赋权方法研究[J]. 中国管理科学, 2002, 10(2): 84 XU Zeshui, DA Qingli. Study on method of combination weighting[J]. Chinese Journal of Management Science, 2002, 10(2): 84 |
 2018, Vol. 46
2018, Vol. 46

