2. 同济大学 土木工程防灾国家重点试验室,上海 200092
2. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China
随着经济的快速发展,高层建筑大量建造.钢筋混凝土剪力墙结构因其抗侧刚度大、承载能力高,在各类高层结构体系中占有重要的位置.国内外许多学者对联肢剪力墙进行了深入研究[1-3].在地震作用下,连梁是剪力墙结构中的主要耗能构件.但在实际工程中连梁的跨高比一般小于2,大震作用下易发生剪切破坏,形成X型交叉裂缝.例如汶川地震和智利地震中,有大量连梁遭到严重破坏[4-6].地震后很难修复,即使可以修复但修复费用较大,施工工期较长,影响地震后建筑使用功能的快速恢复,并由此带来不可预测的间接经济损失.
2009年1月,美日学者在美日地震工程第二阶段合作研究计划会议上,首次提出了“可恢复功能城市”[7],自此,可恢复功能结构成为了工程抗震的重要研究方向之一.使用可更换构件是实现结构功能可恢复的有效途径之一.在地震作用下,可更换构件首先屈服,进入塑形,耗散能量,避免主要构件破坏,震后将可更换构件更换,结构可继续使用.
近年来,国内外许多学者提出了各种可更换连梁.2007年克莱姆森大学的Fortney[8-9]首次提出“保险丝”概念——截面削弱型钢连梁,中间保险丝部分通过削减钢梁腹板厚度实现对钢梁抗剪承载力的折减,保险丝与两端钢梁的连接通过螺栓和钢板实现,震后方便拆卸.2012年,韩国首尔大学的Kim等[10]提出了一种附加复合阻尼耗能构件的钢筋混凝土连梁,加拿大多伦多大学的Lyons等[11-12]提出了一种带有粘弹性阻尼耗能部件的连梁.由于金属阻尼器性能稳定,造价低,许多学者提出了各种金属阻尼器[13-16].试验表明,金属阻尼器滞回曲线饱满,展现了良好的耗能能力.但是,在工字型截面钢阻尼器的试验中,由于加劲肋与腹板的焊缝破坏,构件性能不稳定.
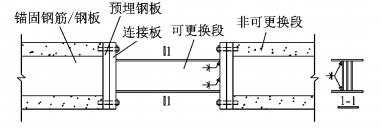
另外,设置加劲肋的腹板在加劲肋处的剪切应变增大,而没有加劲肋的腹板剪切应变均匀分布,不设置加劲肋的低屈服钢腹板的工字形钢梁有着良好的滞回性能和变形能力,当腹板高厚比不超过20时,可以避免发生平面外失稳破坏[17].基于此,本文提出一种新的可更换梁段形式,如图 1所示.通过降低可更换段的腹板高度,防止腹板平面外失稳破坏,取代传统的使用加劲肋的方法.可更换段与楼板脱开,提供了可更换的操作空间,便于耗能梁段的更换.腹板高度降低后,受剪承载力不能满足设计需要,通过设置多片腹板解决该问题.腹板选用低屈服钢,以提高可更换段的变形和耗能能力.
|
图 1 可更换连梁示意图 Fig.1 Schematic drawing of replaceable coupling beam |
本文以带可更换连梁的新型联肢剪力墙为研究对象,提出了新型剪力墙的设计方法,通过有限元分析软件ABAQUS对传统联肢剪力墙和新型联肢剪力墙进行时程分析,研究新型剪力墙的破坏模式和抗震性能,在此基础上研究了新型联肢剪力墙的变形机理,并提出了可更换段的变形与层间位移角的关系.
1 带可更换连梁的新型联肢剪力墙设计方法 1.1 设计目标带可更换连梁的联肢剪力墙的设计目标:在风振和小震作用下,连梁保持弹性,对墙肢提供约束弯矩;中震和大震作用下,连梁的可更换段首先屈曲耗能,减小剪力墙墙脚的破坏,非更换段保持弹性,震后只需要对可更换段进行更换.
1.2 刚度设计由于连梁刚度对联肢剪力墙的抗侧刚度有一定的影响,为了保证带可更换连梁的联肢剪力墙的抗侧刚度,应保证新型连梁的初始刚度没有过大削弱.根据连梁的受力特点,连梁的位移计算简图可以取半边结构,如图 2所示.图中,L为传统连梁的跨度;A为传统连梁截面面积;I为传统连梁截面惯性矩;E、G分别为传统连梁混凝土弹性模量、剪切模量;Lnr、Lr分别为新型连梁非更换段和可更换段长度;Anr、Ar分别为新型连梁非更换段和可更换段截面面积;Enr、Er、Gnr、Gr分别为新型连梁非更换段和可更换段材料的弹性模量和剪切模量;Inr、Ir分别为新型连梁非更换段和可更换段截面惯性矩.

|
图 2 连梁计算简图 Fig.2 Calculation diagram of coupling beam |
连梁的位移由弯曲变形ΔM和剪切变形ΔN两部分组成,传统连梁刚度计算如下:
| $ K = \frac{1}{{{\mathit{\Delta }_{\rm{M}}} + {\mathit{\Delta }_{\rm{V}}}}} = \frac{1}{{\frac{{{L^3}}}{{12EI}} + \frac{{kL}}{{GA}}}} $ | (1) |
式中:ΔM、ΔN分别为连梁的弯曲变形和剪切变形;k为截面剪切形状系数,矩形截面取1.2.新型连梁的刚度计算如下:
| $ \begin{array}{l} K' = \\ \frac{1}{{\frac{{L_{{\rm{nr}}}^3}}{{12{E_{{\rm{nr}}}}{I_{{\rm{nr}}}}}} + \frac{{{k_{{\rm{nr}}}}{L_{{\rm{nr}}}}}}{{{G_{{\rm{nr}}}}{A_{{\rm{nr}}}}}} + \frac{{L_{\rm{r}}^3}}{{12{E_{\rm{r}}}{I_{\rm{r}}}}} + \frac{{{k_{\rm{r}}}{L_{\rm{r}}}}}{{{G_{\rm{r}}}{A_{\rm{r}}}}} + \frac{{L_{\rm{r}}^2{L_{{\rm{nr}}}} + L_{{\rm{nr}}}^2{L_{\rm{r}}}}}{{4{E_{{\rm{nr}}}}{I_{{\rm{nr}}}}}}}} \end{array} $ | (2) |
式中:knr、kr分别为新型连梁非更换段和可更换段的截面剪切形状系数.
由于钢筋混凝土连梁的非更换段有钢板,其对非更换段的抗弯刚度和剪切刚度的贡献不可忽略,所以式(2)中非更换段的抗弯刚度和抗剪刚度如下:
| $ {E_{{\rm{nr}}}}{I_{{\rm{nr}}}} = {E_{{\rm{nrs}}}}{I_{{\rm{nrs}}}} + {E_{{\rm{nrc}}}}{I_{{\rm{nrc}}}} $ | (3) |
| $ {G_{{\rm{nr}}}}{A_{{\rm{nr}}}} = {G_{{\rm{nrs}}}}{A_{{\rm{nrs}}}} + {G_{{\rm{nrc}}}}{A_{{\rm{nrc}}}} $ | (4) |
式中:Enrc、Enrs分别为新型连梁非更换段混凝土和埋设钢板的弹性模量;Gnrc、Gnrs分别为新型连梁非更换段混凝土和埋设钢板的剪切模量;Anrc、Anrs分别为新型连梁非更换段混凝土和埋设钢板的截面面积;Inrc、Inrs分别为新型连梁非更换段混凝土和埋设钢板的截面惯性矩.计算混凝土截面面积和截面惯性矩时,扣除钢板部分.由于钢筋面积小,截面惯性矩很小,所以计算抗弯刚度和抗剪刚度时忽略钢筋部分,只考虑混凝土.
为了保证新型连梁在小震下对联肢剪力墙提供足够的约束,保证联肢剪力墙的抗侧刚度,定义刚度系数rk(新型连梁刚度K'与传统连梁刚度K的比值),不应小于0.5,不宜小于0.7[18],保证新型连梁刚度不小于传统连梁开裂后刚度,刚度系数满足式(5):
| $ {r_{k, \min }} \le {r_k} = \frac{{K'}}{K} \le 1 $ | (5) |
式中:rk, min为刚度系数最小值.
1.3 强度设计AISC[19]规定e < 1.6My/Vy,为剪切屈服型,e>2.6My/Vy,为受弯屈服型,其中,e为构件长度;My为屈服弯矩;Vy为屈服剪力.相比弯曲屈服型,剪切屈服型承载力更高,滞回曲线更饱满,耗能能力优越[20],因此可更换段设计为剪切屈服型.根据可更换段的受剪承载力与传统连梁受剪承载力相等的原则,可更换段的屈服剪力V和受弯承载力M应满足如下公式:
| $ V \le \min \left\{ {{V_{\rm{c}}}, \frac{{{M_{\rm{c}}}}}{{L/2}}} \right\} $ | (6) |
| $ M \ge \frac{{\xi V{L_{\rm{r}}}}}{2} $ | (7) |
式(6)~(7)中:V为可更换段的屈服剪力;M为可更换段的受弯承载力;ξ为弯矩增强系数,与超强系数有关,取1.5[19];Mc为传统连梁设计弯矩;Vc为传统连梁设计剪力.根据《混凝土结构设计规范》GB50010—2010[21]和《建筑抗震设计规范》GB50011—2010[22],传统连梁的设计弯矩和设计剪力如下:
| $ {M_{\rm{c}}} \le \frac{1}{{{\gamma _{{\rm{RE}}}}}}{f_{\rm{y}}}{A_{\rm{s}}}\left( {{h_0} - a{'_s}} \right) $ | (8) |
| $ {V_{\rm{c}}} \le \frac{1}{{{\gamma _{{\rm{RE}}}}}}0.2{\beta _{\rm{c}}}{f_{\rm{c}}}b{h_0} $ | (9) |
| $ {V_{\rm{c}}} \le \frac{1}{{{\gamma _{{\rm{RE}}}}}}\left( {0.42{f_{\rm{t}}}b{h_0} + {f_{{\rm{yv}}}}\frac{{{A_{{\rm{sv}}}}}}{s}{h_0}} \right) $ | (10) |
式(8)~(9)中:γRE为承载力抗震调整系数,混凝土梁受弯、受剪分别取0.75、0.85;ft、fc分别为混凝土轴心抗拉、抗压强度设计值;fy、fyv分别为纵筋和箍筋抗拉强度设计值;As为连梁纵筋截面面积;a's为受压区纵向钢筋合力点至截面受压边缘的距离;h0为连梁截面有效高度;b为连梁宽度;βc为混凝土强度影响系数,混凝土强度等级不超过C50时取0.8;Asv为箍筋截面面积;s为箍筋间距.
在中震和大震作用下,非更换段不屈服,在钢筋混凝土梁段中埋设钢板,抗剪承载力和抗弯承载力应满足如下公式:
| $ {V_{{\rm{nr}}}} \ge \xi V $ | (11) |
| $ {M_{{\rm{nr}}}} \ge \frac{{\xi VL}}{2} $ | (12) |
| $ {V_{{\rm{nr}}}} \ge \eta {V_{\rm{c}}} $ | (13) |
| $ {M_{{\rm{nr}}}} \ge \eta {M_{\rm{c}}} $ | (14) |
式(11)~(14)中:Vnr、Mnr分别为非更换段的抗剪承载力和抗弯承载力;η为承载力增强系数,根据文献[22]对连梁剪力增大系数取值的规定,抗震等级一级取1.3,二级取1.2,三级取1.1.
1.4 可更换段长度可更换段的长度与墙肢转动能力、可更换段自身变形能力等有关.可更换段长度太短,变形受到约束,长度太长,截面刚度削弱严重,所以可更换段长度的选取十分重要.在大震作用下保证可更换段不破坏,即大震下可更换段两端相对位移不大于可更换段的极限位移,满足如下关系:
| $ {\mathit{\Delta }_{\rm{r}}} = {\gamma _{\rm{r}}}{L_{\rm{r}}} \ge {\theta _{\rm{w}}}({L_{\rm{w}}} - {L_{\rm{r}}}) $ | (15) |
式中:Δr为可更换段两端的极限位移;γr为可更换段的极限转角;Lw为联肢剪力墙墙肢形心间的距离,θw为剪力墙墙肢转角.
2 新型连梁变形与层间位移角的关系可更换段长度与可更换段两端相对位移有关,简单有效地计算出可更换段两端相对位移,对可更换段的设计有着重要意义.
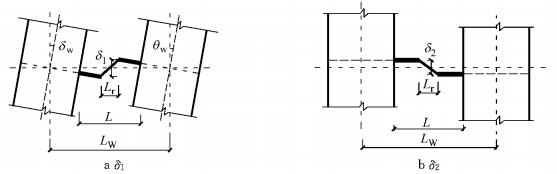
2.1 新型连梁的变形机制在计算新型连梁的变形时采用假设:忽略新型连梁的轴向变形,即同一层的墙肢水平位移相同;在同一标高处,墙肢各截面的转角和曲率分别相等,即连梁两端转角相同,连梁反弯点在梁的中点;非更换段的刚度非常大,为刚臂.新型连梁的变形主要由两部分组成:(1)墙肢弯矩作用下弯曲产生的变形δ1,(2)墙肢轴力作用下轴向变形产生的变形δ2,如图 3所示,表达式如下:
|
图 3 可更换连梁变形图 Fig.3 Deformation of replaceable coupling beam |
| $ {\delta _1} = {\theta _{\rm{w}}}({L_{\rm{w}}} - {L_{\rm{r}}}) $ | (16) |
| $ {\delta _2} = - \frac{1}{E}\left( {\frac{1}{{{A_1}}} + \frac{1}{{{A_1}}}} \right)\smallint _x^HN{\rm{d}}x $ | (17) |
式中:A1、A2分别为左、右墙肢的截面面积;N为墙肢轴力.
相比墙肢弯曲转动引起的变形,由轴力引起的变形所占比重也较小,且轴力产生的变形是有利的,为了计算简单方便,轴力引起的变形也忽略不计,则:
| $ \delta \approx {\theta _{\rm{w}}}({L_{\rm{w}}} - {L_{\rm{r}}}) $ | (18) |
剪力墙在水平荷载作用下的楼层位移由三部分组成[23],墙肢的剪切变形产生的侧移;墙肢弯曲变形产生的侧移;下部楼层结构整体弯曲变形产生的整体的转动位移,转动位移沿结构高度向上逐层累计,各层墙肢转角累积的位移也称为无害位移,该部分位移既不产生内力也不会引起非结构构件的损坏[24].根据楼层位移组成,楼层位移可表达为
| $ \begin{array}{l} \Delta {u_i} = \Delta {u_{i{\rm{m}}}} + \Delta {u_{i{\rm{v}}}} + {\Delta _i} = \Delta {{\tilde u}_{i{\rm{m}}}} + \Delta {u_{i{\rm{v}}}} + \\ \;\;\;\;\;\;{h_i}({\theta _{1{\rm{m}}}} + {\theta _{2{\rm{m}}}} + \cdots + {\theta _{i - 1, {\rm{m}}}}) \end{array} $ | (19) |
式中:Δui为第i层层间位移;Δuim、Δuiv分别为墙肢弯曲和剪切变形产生的层间位移;
| $ {\theta _i} = {\theta _{i{\rm{m}}}} + {\theta _{i{\rm{v}}}} + ({\theta _{1{\rm{m}}}} + {\theta _{2{\rm{m}}}} + \cdots + {\theta _{i - 1, {\rm{m}}}}) $ | (20) |
| $ \begin{array}{l} {\theta _{i - 1}} = \\ {\theta _{i - 1, {\rm{m}}}} + {\theta _{i - 1, {\rm{v}}}} + ({\theta _{{\rm{1m}}}} + {\theta _{{\rm{2m}}}} + \cdots + {\theta _{i - 2, {\rm{m}}}}) \end{array} $ | (21) |
式(20)~(21)中:θi为第i层层间位移角.将式(20)和式(21)相减,可得:
| $ {\theta _{i{\rm{m}}}} = {\theta _i} - {\theta _{i - 1}} + {\theta _{i - 1, {\rm{v}}}} - {\theta _{i{\rm{v}}}} $ | (22) |
由于墙肢整体变形以弯曲变形为主,剪切变形所占比重较小,当高宽比大于4时,剪切变形可以忽略.所以,墙肢转角与楼层位移角的关系可近似为
| $ {\theta _{i{\rm{m}}}} = {\theta _i} - {\theta _{i - 1}} $ | (23) |
| $ {\theta _{{\rm{1m}}}} = {\theta _1} $ | (24) |
将式(23)代入式(18),可得连梁可更换段的变形与层间位移角的关系如下:
| $ {\delta _i} = ({\theta _i} - {\theta _{i - 1}})({L_{\rm{w}}} - {L_{\rm{r}}}) $ | (25) |
将式(25)代入式(15),可更换段的长度计算公式如下:
| $ {L_{\rm{r}}} \ge ({\theta _i} - {\theta _{i - 1}})({L_{\rm{w}}} - {L_{\rm{r}}})/{\gamma _{\rm{r}}} $ | (26) |
设计一片15层的钢筋混凝土联肢剪力墙,一层层高3.6 m,其他楼层3.15 m,共47.7 m.抗震设防烈度为7度,场地类别为Ⅵ类,设计地震分组为第一组,特征周期0.9 s.左右墙肢高度分别为2 500 mm、2 400 mm,约束边缘构件形式为暗柱,墙肢尺寸和配筋见表 1.连梁跨高比为2.875,连梁尺寸及配筋见表 2.
| 下载CSV 表 1 墙肢尺寸及配筋 Tab.1 Parameters of the wall |
| 下载CSV 表 2 连梁尺寸及配筋 Tab.2 Parameters of the coupling beams |
根据提出的设计方法,金属阻尼器选用YL100钢材,腹板尺寸为13 mm×100 mm,2个腹板并联,翼缘尺寸为20 mm×100 mm,阻尼器长度为270 mm,受剪屈服力为184 kN,将传统连梁全部更换为新型连梁,带有软钢阻尼器的新型连梁与传统连梁的刚度比为0.94.
3.2 混凝土本构模型混凝土材料选用ABAQUS提供的损伤塑性模型,该模型不仅能够反映混凝土拉、压强度差异,还能模拟加载过程中由于损伤引起的刚度、强度退化以及由于裂缝闭合产生的刚度恢复等性质.该模型需要定义的参数包括混凝土损伤塑性参数、受拉应力-应变关系、受压应力-应变关系、受压损伤和受拉损伤.其中混凝土的受拉应力-应变关系和受压应力-应变关系采用现行国家标准《混凝土结构设计规范》(GB50010—2010)[21]所建议的曲线.墙肢约束边缘构件的受压应力-应变关系选用mander约束本构[25].损伤塑性模型中通过定义损伤因子d来反映材料初始(无损)弹性模量与损伤后弹性模量E之间的关系,定义如下[26]:
| $ {d_{\rm{t}}} = 1 - \frac{{{\sigma _{\rm{t}}}E_{\rm{c}}^{ - 1}}}{{\varepsilon _{\rm{c}}^{{\rm{pl}}}(1/{b_{\rm{t}}} - 1) + {\sigma _{\rm{t}}}E_{\rm{c}}^{ - 1}}} $ | (27) |
| $ {d_{\rm{c}}} = 1 - \frac{{{\sigma _{\rm{c}}}E_{\rm{c}}^{ - 1}}}{{\varepsilon _{\rm{c}}^{{\rm{pl}}}(1/{b_{\rm{c}}} - 1) + {\sigma _{\rm{c}}}E_{\rm{c}}^{ - 1}}} $ | (28) |
式中:dc和dt分别为混凝土受压、受拉损伤因子;εcpl和εtpl分别为受压、受拉塑性应变;σc和σt分别为受压、受拉应力;Ec为混凝土弹性模量.bc和bt根据文献[26]的建议,分别取0.7和0.9.
3.3 钢筋本构模型钢筋和钢材都采用双折线模型,屈服后模量Ep取为0.01Es,Es为钢筋或钢材的初始弹性模量.针对循环荷载下的钢材力学性能,强化法则采用Chaboche[27]提出的混合强化法则,包含了等向强化和随动强化两个部分.
3.4 计算模型选用通用有限元分析软件ABAQUS建模,墙体及连梁采用分层壳单元S4R,钢筋为弥散钢筋层,可更换部分的腹板选取S4R壳单元,翼缘选用梁单元B31,翼缘与腹板共节点耦合,恒荷载为5 kN·mm-2,活荷载为2 kN·mm-2,等效成节点荷载施加到剪力墙上.底部固定约束,有限元模型如图 4所示.

|
图 4 有限元模型 Fig.4 Element model |
一共有两个模型,传统联肢剪力墙结构和带可更换连梁的联肢剪力墙,分别记为TW、NW.
3.5 模态分析结果分别对两结构进行模态分析,前6阶模态分析结果见表 3,对比发现两个结构的模态振型完全一致,结构周期有一定变化,但差值较小,在2.5%以内.
| 下载CSV 表 3 前6阶模态对比 Tab.3 Characteristics of the first six natural vibration modes |
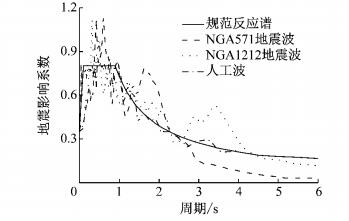
根据场地条件和结构动力特性,在PEER强震记录数据库选取了2条天然波,天然波信息见表 4.表中, EW、E均为地震波分量的代号.选用人工波生成软件Simqke,通过输入设计反应谱生成人工波.本工程抗震设防烈度为7度,多遇地震、设防地震、罕遇地震作用下的加速度峰值分别为0.35、1、2.2 m·s-2.图 5为地震波反应谱与7度小震的规范设计反应谱的对比.
| 下载CSV 表 4 所选天然地震动记录 Tab.4 Natural ground motion records |
|
图 5 加速度反应谱的对比 Fig.5 Comparison of acceleration spectrum |
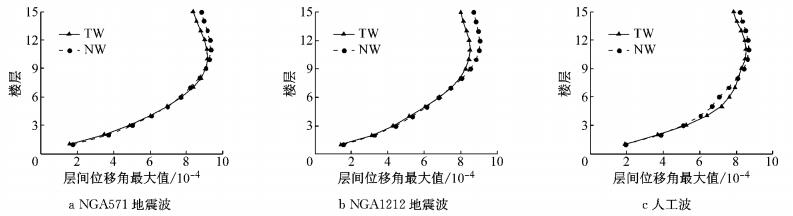
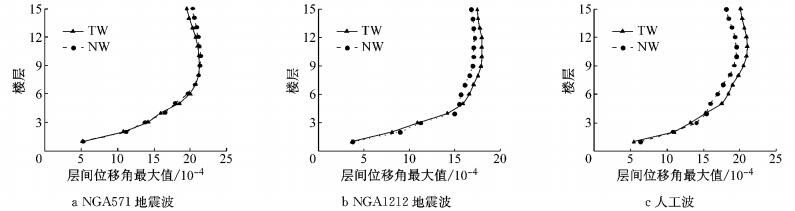
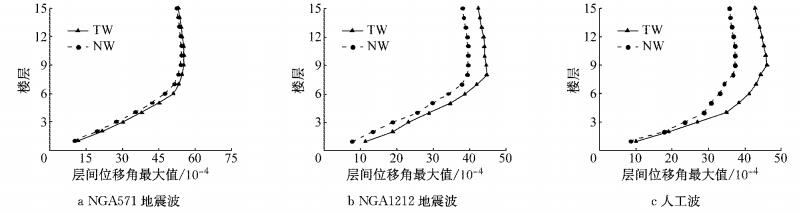
图 6~图 8分别为联肢剪力墙在多遇地震、设防地震和罕遇地震作用下的最大层间位移角.在多遇地震作用下,新型结构与传统结构的层间位移角曲线基本重合,都满足规范1/1 000的位移角限值,新型结构的层间位移角略大于传统结构,这是由于新型剪力墙中的可更换段没有屈服,新型结构的刚度略小于传统结构.在设防地震作用下,部分可更换段开始发挥作用,耗散部分地震能量,对结构的位移反应有一定控制作用.罕遇地震作用下,新型联肢剪力墙的层间位移角比传统联肢剪力墙的层间位移角有明显减小,说明新型可更换连梁在罕遇地震作用下对层间位移的控制效果好.
|
图 6 多遇地震下层间位移角 Fig.6 Inter-story drift ratio under frequent earthquake |
|
图 7 设防地震下层间位移角 Fig.7 Inter-story drift ratio under basic earthquake |
|
图 8 罕遇地震下层间位移角 Fig.8 Inter-story drift ratio under rare earthquake |
在多遇地震作用下,传统联肢墙和新型联肢墙的损伤都很小,钢筋没有屈服,可更换段在多遇地震作用下处于弹性阶段.在设防地震和罕遇地震作用下,传统连梁的损伤很大,而新型连梁的塑形变形都集中在可更换段,非更换段的损伤很小,基本处于弹性阶段.新型剪力墙中墙角损伤有一定减小.图 9为地震波NGA1212罕遇地震作用下,1~2层的损伤图.

|
图 9 罕遇作用下1~2层受压损伤图(NGA1212地震波) Fig.9 Compressive damage of 1-2 layers under rare earthquake |
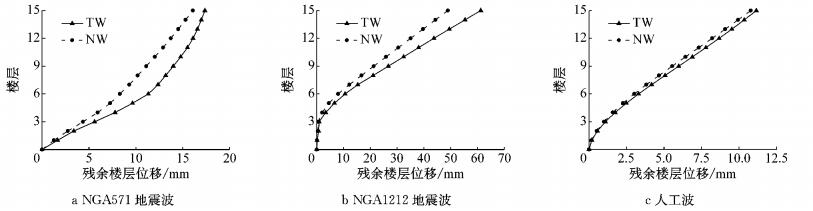
残余变形是评价结构震后可恢复性及修复工作难易程度的重要指标之一,它是结构能否实现可更换的重要影响因素之一.为了获得残余位移,地震波输入时添加了10 s的空载,让结构自由衰减.图 10为罕遇地震作用下结构的残余楼层位移对比图.由图可知,新型联肢剪力墙的残余变形明显小于传统联肢剪力墙的残余变形,为震后连梁可更换段的更换提供了便利条件.
|
图 10 残余楼层位移对比 Fig.10 Comparison of residual floor displacement |
选取NGA571地震波,分别计算带可更换连梁的新型联肢剪力墙在小震和大震下16.68 s(层间位移角最大时刻)时可更换部件的竖向位移,将有限元计算结果与式(25)计算结果进行对比,由于非更换段与可更换段的刚度比为3:1,非更换段不能假定为刚臂,将其进行修正,结果如图 11所示.由图可知,有限元分析结果与公式结算结果比较接近,说明公式正确.

|
图 11 可更换段竖向位移对比 Fig.11 Comparison of vertical displacement of the replaceable part |
(1) 本文提出了新型的可更换连梁,并进行了时程时程,分析结果表明,本文提出的可更换连梁的设计方法是合理的,能够保证新型联肢剪力墙具有足够的承载力和刚度,破坏集中在可更换段,非更换段保持弹性.
(2) 与传统联肢剪力墙相比,带可更换连梁的联肢剪力墙的抗震性能优越.两模型的结构动力特性基本一致,在小震作用下,可更换段没有屈服,为墙肢提供约束弯矩.在中震和大震作用下,塑形变形集中在可更换段,非更换段为弹性,新型联肢剪力墙的层间位移角和残余变形显著减小.本文将传统连梁全部更换,后期还需对可更换连梁布置位置及可更换连梁的参数优化进行进一步研究.
(3) 根据新型连梁的变形机制,提出了新型连梁变形与层间位移角的关系,并通过有限元分析结果进行了验证.
| [1] |
CHAALLAL O, GAUTHIER D, MALENFANT P. Classification methodology for coupled shear walls[J]. Journal of Structural Engineering, 1996, 122(12): 1453 DOI:10.1061/(ASCE)0733-9445(1996)122:12(1453) |
| [2] |
TAKAYANAGI T, SCHNOBRICH W C. Non-linear analysis of coupled wall systems[J]. Earthquake Engineering & Structural Dynamics, 1979, 7(1): 1 |
| [3] |
王社良, 陈平, 沈亚鹏. 钢筋混凝土双肢剪力墙的抗震性能[J]. 西安建筑科技大学学报, 1996, 28(4): 397 WANG Sheliang, CHEH Ping, SHEN Yapeng. On aseismic behavior of RC coupled shear walls[J]. Journal of Xi'an University of Architecture and Technology, 1996, 28(4): 397 |
| [4] |
王亚勇. 汶川地震建筑震害启示——抗震概念设计[J]. 建筑结构学报, 2008, 29(4): 20 WANG Yayong. Lessons learnt from building damages in the Wenchuan earthquake—seismic concept design of buildings[J]. Journal of Building Structures, 2008, 29(4): 20 |
| [5] |
WALLACE J W. Behavior, design, and modeling of structural walls and coupling beams—lessons from recent laboratory tests and earthquakes[J]. International Journal of Concrete Structures and Materials, 2012, 6(1): 3 DOI:10.1007/s40069-012-0001-4 |
| [6] |
KAM W Y, PAMPANIN S. The seismic performance of RC buildings in the 22 February 2011 Christchurch earthquake[J]. Structural Concrete, 2011, 12(4): 223 DOI:10.1002/(ISSN)1751-7648 |
| [7] |
NIED and NEES Consortium. Report of the seventh joint planning meeting of nees/e: defense collaborative research on earthquake engineering[R]. Berkeley: University of California at Berkeley, 2010.
|
| [8] |
FORTNEY P J, SHAHROOZ B M, RASSATI G A. Seismic performance evaluation of coupled core walls with concrete and steel coupling beams[J]. Steel and Composite Structures Journal, 2007, 7(4): 279 DOI:10.12989/scs.2007.7.4.279 |
| [9] |
FORTNEY P J, SHAHROOZ B M, RASSATI G A. Large-scale testing of a replaceable fuse steel coupling beam[J]. Journal of Structural Engineering, 2007, 133(12): 1801 DOI:10.1061/(ASCE)0733-9445(2007)133:12(1801) |
| [10] |
KIM H J, CHOI K S, OH S H, et al. Comparative study on seismic performance of conventional RC coupling beams and hybrid energy dissipative coupling beams used for RC shear walls[C/CD]//Proceedings of 15WCEE, Lisbon: [s. n. ], 2012.
|
| [11] |
LYONS R M, CHRISTOPOULOS C, MONTGOMERY M S. Enhancing the seismic performance of RC coupled wall high-rise buildings with viscoelastic coupling dampers[C/CD]//Proceedings of 15WCEE, Lisbon: [s. n. ], 2012.
|
| [12] |
MONTGOMERY M, CHRISTOPOULOS C. Experimental validation of viscoelastic coupling dampers for enhanced dynamic performance of high-rise buildings[J]. Journal of Structural Engineering, 2014, 141(5): 04014145 |
| [13] |
滕军, 马伯涛, 李卫华, 等. 联肢剪力墙连梁阻尼器地震模拟试验研究[J]. 建筑结构学报, 2010, 31(12): 101 TENG Jun, MA Botao, LI Weihua, et al. Seismic simulation test for coupling beam damper of coupled shear wall structure[J]. Journal of Building Structures, 2010, 31(12): 101 |
| [14] |
WANG T, GUO X, HE X K, et al. Experimental study on replaceable hybrid coupling beams[J]. Applied Mechanics and Materials, 2012, 166: 1779 |
| [15] |
吕西林, 陈云, 蒋欢军. 可更换连梁保险丝抗震性能试验研究[J]. 同济大学学报(自然科学版), 2013, 41(9): 1318 LU Xilin, CHEN Yun, JIANG Huanjun. Experimental study on seismic behavior of 'fuse' of replaceable coupling beam[J]. Journal of Tongji University (Natural Science), 2013, 41(9): 1318 |
| [16] |
武豪, 郭子雄, 刘阳. 基于有限元方法的震损可替换钢连梁抗震性能研究[J]. 地震工程与工程振动, 2014, 34(2): 41 WU Hao, GUO Zixiong, LIU Yang. Study on the seismic behavior of replaceable steel coupling beams with finite element method[J]. Earthquake Engineering and Engineering Dynamics, 2014, 34(2): 41 |
| [17] |
DUSICKA P, ITANI A, BUCKLE I. Cyclic behavior of shear links of various grades of plate steel[J]. Journal of Structural Engineering, 2009, 136(4): 370 |
| [18] |
中华人民共和国住房和城乡建设部. 高层建筑混凝土结构技术规程: JGJ3—2010[S]. 北京: 中国建筑工业出版社, 2010. Ministry of Housing and Urban-Rural Construction of the People's Republic of China. Technical specification for concrete structures of tall building: JGJ3—2010[S]. Beijing: China Architecture and Building Press, 2010. |
| [19] |
ANSI A. AISC 341-10 (2010). Seismic provisions for structural steel buildings[S]. Chicago: American Institute of Steel Construction, 2010.
|
| [20] |
ENGELHARDT M D, POPOV E P. On design of eccentrically braced frames[J]. Earthquake spectra, 1989, 5(3): 495 DOI:10.1193/1.1585537 |
| [21] |
中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB50010—2010[S]. 北京: 中国建筑工业出版社, 2010. Ministry of Housing and Urhan-Rural Construction of the People's Republic of China. Code for design of concrete structures: GB50010—2010[S]. Beijing: China Architecture & Building Press, 2010. |
| [22] |
中华人民共和国住房和城乡建设部. 建筑抗震设计规范: GB50011—2010[S]. 北京: 中国建筑工业出版社, 2010. Ministry of Housing and Urban-Rural Construction of the People's Republic of China. Code for seismic design of buildings: GB50011—2010[S]. Beijing: China Architecture and Building Press, 2010. |
| [23] |
邓明科, 梁兴文, 辛力. 剪力墙结构基于性能抗震设计的目标层间位移确定方法[J]. 工程力学, 2008, 25(11): 141 DENG Mingke, LIANG Xingwen, XIN Li. Determination of target story drift for RC shear wall structure in performance-based seismic design[J]. Engineering Mechanics, 2008, 25(11): 141 |
| [24] |
李坤, 史庆轩, 郭智峰, 等. 钢筋混凝土剪力墙结构受力层间位移计算及探讨[J]. 土木工程学报, 2013(增2): 86 LI Kun, SHI Anxuan, GUO Zhifeng, et al. Calculation and discussion of physical inter-story displacement for reinforced concrete shear wall structures[J]. China Civil Engineering Journal, 2013(S2): 86 |
| [25] |
MANDER J B, PRIESTLEY M J N, Park R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804 DOI:10.1061/(ASCE)0733-9445(1988)114:8(1804) |
| [26] |
BIRTEL V, MARK P. Parameterized finite element modeling of RC beam shear failure[C]//2006 ABAQUS User's Conference. Taiwan: [s. n. ], 2006: 95-108.
|
| [27] |
CHABOCHE J L. Time-independent constitutive theories for cyclic plasticity[J]. International Journal of Plasticity, 1986, 2(2): 149 DOI:10.1016/0749-6419(86)90010-0 |
 2018, Vol. 46
2018, Vol. 46


 8@200
8@200