2. 南京航空航天大学 航空宇航学院,江苏 南京 210016
2. College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
桥梁是公路交通的咽喉,其使用功能的优劣直接影响整条线路的畅通[1-2].以钢筋混凝土或预应力混凝土修建的各类桥梁占我国现役桥梁的绝大多数,其中T型截面梁具有构造简洁,并且适应现代化施工方法的要求,施工与使用过程中稳定性好,在预应力混凝土桥梁中被广泛采用.随着钢筋混凝土非线性有限元理论的逐渐成熟和完善[3-6],也有越来越多关于T梁的研究成果出现:文献[7]采用具有假定弯矩-曲率关系的分层梁单元对T梁进行了非线性分析.文献[8]对当时运行约10年的沪宁高速上某锡澄运河大桥引桥(预应力混凝土简支多梁式T梁桥)进行极限状态试验研究,其桥梁极限状态(破坏性)试验研究属于现场实桥试验破坏性研究,试验对象为目前公路桥梁中应用比较广泛的桥型,具有相当的代表性;关于实桥破坏性试验研究本身,在国内尚属空白;而对预应力混凝土简支多梁式梁桥这类桥梁的现场实桥极限状态试验研究,目前在世界范围内也属首例.文献[9]结合该座预应力混凝土多T梁桥实桥破坏性试验资料,基于实体退化壳单元,研究了多T梁桥极限承载力的计算方法.文献[10]采用不同单元对T梁进行模拟,即分别采用梁单元和分层板单元模拟T梁的梁肋和翼缘板,并对T梁进行了相应分析.文献[11]进行了预应力混凝土T梁的极限承载力等力学性能的预测评估,利用混合壳单元建立了T梁有限元计算模型,并应用非线性理论对T梁进行了分析,其中T梁中预应力钢筋采用杆单元模型.文献[12]对二根跨径25 m的装配式后张法预应力混凝土简支梁静载试验,对裂缝发展模式等进行统计分析.文献[13]通过对秦沈客运专线整体多片式T梁桥的结构空间有限元分析,进行主梁横向分析系数、主梁正应力分析、桥面板的作用分析,论述了整体多片式T梁的桥面横向应力及横截面的框架效应.此外,还有学者构造不同单元分析T梁结构行为[14-17].在钢筋混凝土非线性有限元分析中,组合式模型介于分离式和整体式之间,在单元分析时,先分别求得混凝土和钢筋对组合单元刚度矩阵的贡献,再组成一个复合的单元,这种模型能在一定程度上反映钢筋和混凝土的相互作用,其有限元离散工作量和计算规模都不大,在实际钢筋混凝土结构中便于采用,如文献[18]对平面问题的组合式模型和钢筋层对体单元刚度矩阵贡献的组合式模型进行了研究;文献[19]研究了基于体单元和梁单元的组合式模型,并用此组合式单元对钢筋混凝土结构弹性阶段进行了分析.
为此,本文基于分层壳单元和梁单元计算模式,推导预应力混凝土T梁的非线性壳梁组合单元,并建立预应力混凝土T梁的非线性有限元模型.结合已有的试验成果,考证所建立的预应力混凝土T梁的非线性壳梁组合单元模型的正确性,并对其受力性能进行研究.
1 预应力混凝土T梁的壳梁组合单元实体退化壳(图 1)中面有9个节点,图中,ν1k、ν2k、ν3k(单位向量, 上划线表示的是单位化)组成了节点k的节点坐标系,其中4个角节点为控制节点,其余5个节点的空间几何位置可由4个控制节点确定.β1k、β2k分别为绕ν2k、ν1k的转角位移,Δ1k、Δ2k分别为由β1k、β2k确定的线位移.退化壳元中9个节点的每个节点均有3个独立的线位移自由度和2个独立的转角位移自由度,转角不受中面斜率的限制,允许横向剪切变形出现[12].退化9节点壳元的节点位移为

|
图 1 退化壳单元坐标系及转角位移描述 Fig.1 Description of Coordinate system of the degenerate shell element and angular displacement of the node |
| $ {\mathit{\boldsymbol{\delta }}_k} = {[{u_k}\;\;{v_k}\;\;{w_k}\;\;{\beta _{1k}}\;\;{\beta _{2k}}]^{\rm{T}}} $ | (1) |
式中:δk为实体退化壳元节点k的节点位移列阵,uk、vk、wk为节点k在整体坐标系中的线位移.
位移场通过形函数插值可表示为[12]
| $ u = \sum\limits_{i = 1}^n {{N_i}{u_i}} + \sum\limits_{i = 1}^n {{N_i}} \frac{{{h_i}}}{2}\zeta ({\nu _{x, 1i}}{\beta _{1i}} - {\nu _{x, 2i}}{\beta _{2i}}) $ | (2) |
| $ v = \sum\limits_{i = 1}^n {{N_i}{v_i}} + \sum\limits_{i = 1}^n {{N_i}} \frac{{{h_i}}}{2}\zeta ({\nu _{y, 1i}}{\beta _{1i}} - {\nu _{y, 2i}}{\beta _{2i}}) $ | (3) |
| $ w = \sum\limits_{i = 1}^n {{N_i}{w_i}} + \sum\limits_{i = 1}^n {{N_i}} \frac{{{h_i}}}{2}\zeta ({\nu _{z, 1i}}{\beta _{1i}} - {\nu _{z, 2i}}{\beta _{2i}}) $ | (4) |
式中:u、v、w为整体坐标系下x、y、z方向的位移; n为壳元节点数; Ni为节点i的形函数; hi为节点i处壳元厚度; νx, 1i为节点i的节点坐标系ν1与x轴夹角余弦值(其余类推).
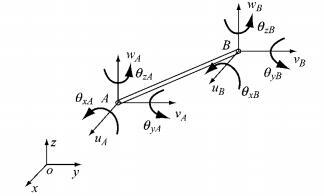
基于实体退化壳得到的分层壳单元具有良好的数值稳定性[20-21].同时文献[11]中利用大变形杆单元模拟预应力筋,利用节点线位移协调推导了一种杆壳组合单元,已对相应结构进行了全过程分析,表明在预应力混凝土梁中,预应力钢筋是梁内主要受力筋,其在梁体中考虑用组合单元处理.本文利用空间梁单元模拟预应力钢筋,根据节点线位移和转角位移协调性,推导非线性壳梁组合单元.壳梁组合单元如图 2所示,其中预应力钢筋用空间梁单元模拟如图 3所示,预应力钢筋单元节点用A和B表示.图 3中uA、vA、wA为节点A在整体坐标系下x、y、z方向的线位移,θxA、θyA、θzA为节点A在整体坐标系下绕x、y、z轴的转角位移,节点B的位移变量依此类推.

|
图 2 预应力混凝土梁的单元模型 Fig.2 Element model of the prestressed concrete beam |
|
图 3 预应力钢筋的空间梁单元 Fig.3 Spacial beam element of the prestressed reinforcement |
转角位移场通过形函数插值由式(5)~(7)表示如下:
| $ {\theta _x} = - \frac{1}{2}\sum\limits_{i = 1}^n {\frac{{\partial {N_i}}}{{\partial z}}{v_i}} + \frac{1}{2}\sum\limits_{i = 1}^n {\frac{{\partial {N_i}}}{{\partial y}}{w_i}} $ | (5) |
| $ {\theta _y} = - \frac{1}{2}\sum\limits_{i = 1}^n {\frac{{\partial {N_i}}}{{\partial x}}{w_i} + \frac{1}{2}\sum\limits_{i = 1}^n {\frac{{\partial {N_i}}}{{\partial z}}{u_i}} } $ | (6) |
| $ {\theta _z} = - \frac{1}{2}\sum\limits_{i = 1}^n {\frac{{\partial {N_i}}}{{\partial y}}{u_i}} + \frac{1}{2}\sum\limits_{i = 1}^n {\frac{{\partial {N_i}}}{{\partial x}}{v_i}} $ | (7) |
式中:θx、θy、θz为绕整体坐标系x、y、z方向的转角位移场.
利用位移插值关系式(2)~(7),则预应力钢筋单元的起点A和终点B线位移和转角位移可用退化单元的节点位移表示为
| $ \begin{array}{l} \left[ \begin{array}{l} {u_A}\\ {v_A}\\ {w_A}\\ {\theta _{xA}}\\ {\theta _{yA}}\\ {\theta _{zA}} \end{array} \right] = \\ \sum\limits_{i = 1}^n {\left[ {\begin{array}{*{20}{c}} {{N_{Ai}}}&0&0&{{N_{Ai}}\frac{{{h_i}}}{2}{\zeta _A}{\nu _{x, 1i}}}&{ - {N_{Ai}}\frac{{{h_i}}}{2}{\zeta _A}{\nu _{x, 1i}}}\\ 0&{{N_{Ai}}}&0&{{N_{Ai}}\frac{{{h_i}}}{2}{\zeta _A}{\nu _{y, 1i}}}&{ - {N_{Ai}}\frac{{{h_i}}}{2}{\zeta _A}{\nu _{y, 1i}}}\\ 0&0&{{N_{Ai}}}&{{N_{Ai}}\frac{{{h_i}}}{2}{\zeta _A}{\nu _{z, 1i}}}&{ - {N_{Ai}}\frac{{{h_i}}}{2}{\zeta _A}{\nu _{z, 1i}}}\\ 0&{ - \frac{{\partial {N_{Ai}}}}{{2\partial z}}}&{\frac{{\partial {N_{Ai}}}}{{2\partial y}}}&0&0\\ {\frac{{\partial {N_{Ai}}}}{{2\partial z}}}&0&{ - \frac{{\partial {N_{Ai}}}}{{2\partial x}}}&0&0\\ { - \frac{{\partial {N_{Ai}}}}{{2\partial y}}}&{\frac{{\partial {N_{Ai}}}}{{2\partial x}}}&0&0&0 \end{array}} \right]} \\ \left[ \begin{array}{l} {u_i}\\ {v_i}\\ {w_i}\\ {\beta _{1i}}\\ {\beta _{2i}} \end{array} \right] = \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{R}}_{Ai}}{\mathit{\boldsymbol{\delta }}_i}} \end{array} $ | (8) |
| $ \begin{array}{l} \left[ \begin{array}{l} {u_B}\\ {v_B}\\ {w_B}\\ {\theta _{xB}}\\ {\theta _{yB}}\\ {\theta _{zB}} \end{array} \right] = \\ \sum\limits_{i = 1}^n {\left[ {\begin{array}{*{20}{c}} {{N_{Bi}}}&0&0&{{N_{Bi}}\frac{{{h_i}}}{2}{\zeta _B}{\nu _{x, 1i}}}&{ - {N_{Bi}}\frac{{{h_i}}}{2}{\zeta _B}{\nu _{x, 2i}}}\\ 0&{{N_{Bi}}}&0&{{N_{Bi}}\frac{{{h_i}}}{2}{\zeta _B}{\nu _{y, 1i}}}&{ - {N_{Bi}}\frac{{{h_i}}}{2}{\zeta _B}{\nu _{y, 2i}}}\\ 0&0&{{N_{Bi}}}&{{N_{Bi}}\frac{{{h_i}}}{2}{\zeta _B}{\nu _{z, 1i}}}&{ - {N_{Bi}}\frac{{{h_i}}}{2}{\zeta _B}{\nu _{z, 2i}}}\\ 0&{ - \frac{{\partial {N_{Bi}}}}{{2\partial z}}}&{\frac{{\partial {N_{Bi}}}}{{2\partial y}}}&0&0\\ {\frac{{\partial {N_{Bi}}}}{{2\partial z}}}&0&{ - \frac{{\partial {N_{Bi}}}}{{2\partial x}}}&0&0\\ { - \frac{{\partial {N_{Bi}}}}{{2\partial y}}}&{\frac{{\partial {N_{Bi}}}}{{2\partial x}}}&0&0&0 \end{array}} \right]} \\ \left[ \begin{array}{l} {u_i}\\ {v_i}\\ {w_i}\\ {\beta _{1i}}\\ {\beta _{2i}} \end{array} \right] = \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{R}}_{Bi}}{\mathit{\boldsymbol{\delta }}_i}} \end{array} $ | (9) |
式中:NAi、NBi分别为形函数Ni在预应力筋单元起点A和终点B的值;ζA、ζB分别为预应力筋单元起点A和终点B的ζ局部坐标;RAi、RBi分别为预应力筋单元起点A和终点B的转换矩阵;δi为壳单元的节点i位移列阵.并记:δS=[uA vA wA θxA θyA θzA uB vB wB θxB θyB θzB]T,Ri=[(RAi)T (RBi)T]T,R=[R1 R2 … Rn],δC=[δ1T δ2T … δnT]T,则式(8)和式(9)可写为
| $ {\mathit{\boldsymbol{\delta }}_S} = \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{\delta }}_C} $ | (10) |
应用虚功原理[13],推得预应力筋单元对组合单元刚度矩阵的贡献如下:
| $ {\mathit{\boldsymbol{K}}_{\rm{P}}} = {\mathit{\boldsymbol{R}}^{\rm{T}}}{{\mathit{\boldsymbol{\bar K}}}_S}\mathit{\boldsymbol{R}} $ | (11) |
式中:KP为预应力筋单元对组合单元刚度矩阵的贡献;KS为整体坐标系下预应力筋单元刚度矩阵[5].壳梁组合单元刚度矩阵为
| $ {\mathit{\boldsymbol{K}}_{\rm{e}}} = \sum\limits_{k = 1}^m {{\mathit{\boldsymbol{K}}_{Ck}} + {\mathit{\boldsymbol{K}}_{\rm{S}}} + {\mathit{\boldsymbol{K}}_{\rm{P}}}} $ | (12) |
式中:Ke为组合单元刚度矩阵;m为混凝土层数,KCk为第k层混凝土的刚度矩阵;KS为普通钢筋层的刚度矩阵.
2 预应力混凝土T梁的非线性效应 2.1 混凝土的非线性描述对于混凝土的材料非线性,考虑其屈服、强化、拉伸刚化和压碎过程.本文选用Owen混凝土双参数屈服准则和Hinton压碎准则.Owen混凝土双参数屈服准则表达式为
| $ f({I_1}, {J_2}) = {(\alpha {I_1} + 3\beta {J_2})^{1/2}} = {\sigma _0} $ | (13) |
式中:I1为应力张量第一不变量;J2为应力偏量第二不变量;σ0为等效应力; α、β为材料参数,α取1.355,β取0.355.
Hinton压碎准则表达式为
| $ \varepsilon (I{'_1}, J{'_2}) = {(\alpha I{'_1} + 3\beta J{'_2})^{1/2}} = {\varepsilon _{\rm{u}}} $ | (14) |
式中:I'1为应变张量第一不变量;J'2为应变偏量第二不变量;εu为混凝土极限压应变,取为0.003 5.混凝土强化准则中的强化参数和后继屈服面由Madrid抛物线准则确定,拉伸刚化效应采用三折线模型[4].
2.2 钢筋的非线性描述本文假定普通钢筋和预应力钢筋均为力学性能是单向的理想弹塑性材料,以模拟其材料非线性特性.普通钢筋采用壳元中等效厚度的层单元考虑[13].假定每一钢筋层的力学性能是单向的,只能承受沿钢筋方向的轴向力.预应力效应的准确模拟对结构分析至关重要,本文预应力钢筋采用空间梁单元考虑[5].沿梁单元局部坐标的轴向方向,输入估算得到的有效预应力作为初始预应力,并将其处理为等效节点荷载施加于预应力混凝土梁进行结构分析.
3 非线性分析的收敛准则收敛准则一般分为:力系收敛准则和位移收敛准则.在预应力混凝土结构非线性分析中,不平衡力常可形成一些平衡力系,使得解不能单调收敛,因此采用位移收敛准则,取
| $ \frac{{{{\left\| {{\mathit{\boldsymbol{\delta }}_{i + 1}} - {\mathit{\boldsymbol{\delta }}_i}} \right\|}_2}}}{{{{\left\| {{\mathit{\boldsymbol{\delta }}_{i + 1}}} \right\|}_2}}} < \varepsilon $ | (15) |
式中:δi为第i增量步的非线性方程组迭代时的收敛解,即预应力混凝土T梁第i增量步整体位移向量;δi+1为第i+1增量步的非线性方程组迭代时的收敛解;ε为收敛容差(可取为5%).
4 算例分析 4.1 试验梁资料为研究预应力混凝土T梁的非线性受力性能,交通部第二勘查设计院进行了二根装配式后张法全预应力混凝土简支T梁的试验[12].预应力混凝土T梁尺寸如图 4所示(图中, p为荷载).采用40号混凝土,预应力钢筋采用24Φ5的冷拉碳素钢丝,极限抗拉强度1 600 MPa,控制张拉应力1 200 MPa.混凝土抗压强度36 MPa,抗拉强度3.35 MPa.混凝土弹性模量36 GPa,预应力钢筋弹性模量220 GPa.6根预应力钢筋沿T梁纵向位置坐标以及普通钢筋等构造详见文献[12].

|
图 4 预应力钢筋混凝土T梁的构造及加载方式(单位:m) Fig.4 Configuration and loading type of the prestressed reinforced concrete T beam (unit:m) |
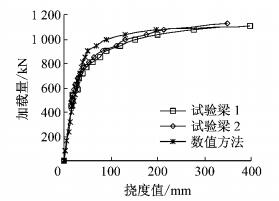
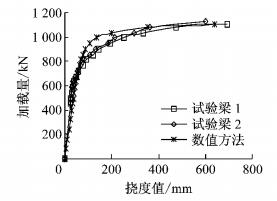
为进行预应力混凝土试验T梁非线性受力性能分析,建立非线性力学分析模型,共分176个单元,759个节点,其中壳梁组合单元48个,分层壳单元128个.对普通钢筋和混凝土均采用分层壳单元模拟,对预应力钢筋用壳梁组合单元模拟.由试验方法测得二根试验梁的极限承载力为1 104 kN和1 125.8 kN.利用本文的壳梁组合单元方法,计算得预应力混凝土T梁的极限承载力为1 100 kN.梁体1/4跨和跨中梁底的荷载-挠度曲线分别如图 5和图 6所示,典型加载步下梁的裂缝发展模式如图 7所示.
|
图 5 1/4跨荷载-挠度曲线 Fig.5 load-deflection curve of the 1/4 span |
|
图 6 跨中荷载-挠度曲线 Fig.6 load-deflection curve of the half span |

|
图 7 典型加载步下预应力混凝土T梁的裂缝发展图 Fig.7 Crack development diagram of the prestressed concrete T beam at typical loading step |
由图 5和图 6的计算结果知,本文方法与试验结果吻合程度良好,说明非线性壳梁组合单元计算方法为正确.由图 7可知,本文所得混凝土简支梁梁的裂缝发展规律与已有资料相符[9、11].本文定义“刚度折减系数”,主要描述在不同加载阶段,梁体刚度的变化情况.刚度折减系数的表达式为
| $ \beta = (1 - \frac{{{p_t}/{s_t}}}{{{p_0}/{s_0}}}) \times 100\% $ | (16) |
式中:β为梁体刚度折减系数;pt为t时刻的加载量;st为t时刻的梁跨中挠度值;pt/st为t时刻的梁割线刚度; p0/s0为梁的初始割线刚度.由图 6计算结果可知跨中刚度变化规律(刚度折减系数)见表 1.
| 下载CSV 表 1 预应力混凝土T梁跨中的刚度折减 Tab.1 Stiffness reduction in the half span of the prestressed concrete T beam |
表 1中,刚度折减系数18.19=(1-10.95/13.55)×100%.由表 1可知,在加载初期,T梁处于弹性阶段,刚度未出现明显折减.其后随着加载量增大,T梁刚度折减系数越来越大,表明其继续承受荷载的能力越来越小.本文对预应力筋采用了梁单元处理,也可以采用层单元和杆单元模拟,这在相关成果中已得到了验证[20-21].
4.3 预应力筋的应力重分布规律预应力混凝土T梁典型截面的梁底预应力钢筋的应力-荷载曲线如图 8所示.由图 8计算结果可知,接近破坏时,跨中截面的预应力筋已达1 547.02 MPa.跨中预应力筋的应力增长速度最快,1/4跨预应力筋的应力增长速度次之,1/8跨预应力筋的应力增长缓慢,而支座处预应力筋的应力-荷载曲线基本保持水平.

|
图 8 梁底预应力筋的应力-荷载曲线 Fig.8 Stress-load curve of the prestressed tendons at the bottom of the beam |
本文提出“应力重分布系数”来描述不同加载阶段应力增量对相应荷载增量的变化率与弹性阶段的应力增量对相应荷载增量的变化率之比值,分析应力的变化速度.应力重分布系数表达式为
| $ \eta = \frac{{\Delta {\sigma _t}/\Delta {p_t}}}{{\Delta {\sigma _0}/\Delta {p_0}}} $ | (17) |
式中:η为应力重分布系数;Δpt为t-1至t时段的荷载增量; Δσt为与荷载增量Δpt为t-1至t时段的应力增量; Δp0为弹性阶段的荷载增量; Δσ0为弹性阶段的应力增量.由图 8可得跨中预应力筋的应力重分布规律(应力增长率和应力重分布系数)见表 2.
| 下载CSV 表 2 预应力混凝土T梁跨中预应力筋的应力重分布 Tab.2 Stress redistribution of prestressing tendons of the half span in the prestressed concrete T beam |
表 2中,90.20=945.8-855.6;55.07=1 456.54-1 401.47;0.61=55.07/90.2;1.97=0.61/0.31.由表 2可知,随着荷载增大,预应力筋的应力增长率和重分布系数都发生一定变化,其比弹性阶段相比都有增大.在加载过程中混凝土出现裂缝及压碎后,所施加的荷载逐渐转为由预应力钢筋来承担,故与弹性阶段相比,其应力增长速度较大.
5 结语本文基于分层壳单元和梁单元计算模式,对预应力钢筋采用壳梁组合单元模拟,对普通钢筋和混凝土采用分层壳单元模拟,推导了壳梁组合单元并对预应力混凝土T梁的受力性能进行了分析.结合试验梁数据分析表明:本文推演的非线性壳梁组合单元用于此类结构分析是合适的,且所采用的Owen准则等能较为有效地描述混凝土T梁的材料非线性;预应力筋的空间预应力效应可采用空间梁单元进行较为准确地模拟;随着加载量增大,预应力混凝土T梁刚度折减系数增大,预应力钢筋的应力增长率较弹性阶段增大,直至结构失效破坏.
| [1] |
江胜华, 侯建国, 何英明. 考虑预应力损失的CFRP布加固钢筋混凝土梁正常使用极限状态可靠度研究[J]. 土木工程学报, 2015, 48(11): 36 JIANG Shenghua, HOU Jianguo, HE Yingming. Reliability research of serviceability limit states for RC beams strengthened with prestressed CFRP sheets considering prestress loss[J]. China Civil Engineering Journal, 2015, 48(11): 36 |
| [2] |
方志, 杨剑. 预应力CFRP筋混凝土T梁受力性能试验研究[J]. 建筑结构学报, 2005, 26(5): 66 FANG Zhi, YANG Jian. Experimental study on behavior of concrete T beam prestressed with CFRP tendons[J]. Journal of Building Structures, 2005, 26(5): 66 |
| [3] |
张剑, 周储伟, 俞博, 等. 预应力高性能混杂纤维增强布加固HPC梁的DNLC单元研究[J]. 复合材料学报, 2017, 34(5): 1152 ZHANG Jian, ZHOU Chuwei, YU Bo, et al. Research on DNLC element for HPC beams strengthened with high performance prestressed HFRP sheet[J]. Acta Materiae Compositae Sinica, 2017, 34(5): 1152 |
| [4] |
卢亦焱, 胡玲, 梁鸿骏, 等. CFRP布与钢板复合加固的钢筋混凝土梁受弯疲劳性能试验研究[J]. 建筑结构学报, 2015, 36(11): 64 LU Yiyan, HU Ling, LIANG Hongjun, et al. Experimental research on flexural fatigue behavior of RC beams strengthened with combination of CFRP and steel plates[J]. Journal of Building Structures, 2015, 36(11): 64 |
| [5] |
WEN Q J. Long-term effect analysis of prestressed concrete box-girder bridge widening[J]. Construction and Building Materials, 2011, 25(4): 1580 DOI:10.1016/j.conbuildmat.2010.09.041 |
| [6] |
张剑, 叶见曙, 王景全, 等. 预应力混杂碳/玻璃(C/G)纤维布加固RC梁的应力重分布[J]. 交通运输工程学报, 2017, 17(1): 45 ZHANG Jian, YE Jianshu, WANG Jingquan, et al. Stress redistribution of RC beams strengthened with prestressed hybrid carbon/glass (C/G) fiber cloth[J]. Journal of Traffic and Transportation Engineering, 2017, 17(1): 45 |
| [7] |
FRAGIACOMO M, AMADIO C, MACORINI M L. Finite-element model for collapse and long-term analysis of steel-concrete composite beams[J]. Journal of Structural Engineering, 2004, 130(3): 489 DOI:10.1061/(ASCE)0733-9445(2004)130:3(489) |
| [8] |
张宇锋. 沪宁高速公路扩建工程桥梁极限状态实桥试验研究试验[R]. 南京: 江苏省交通科学研究院, 2006. ZHANG Yufeng. Test and study on the ultimate state of the bridge in the expansion project of Hu-Ning Expressway[R]. Nanjing: Jiangsu Academy of traffic Sciences, 2006. |
| [9] |
叶见曙, 张剑, 黄剑峰. 预应力混凝土多T梁桥的极限承载力[J]. 东南大学学报(自然科学版), 2009, 39(1): 106 YE Jianshu, ZHANG Jian, HUANG Jianfeng. Analysis of ultimate loads of prestressed concrete multi-T girder bridge[J]. Journal of Southest University(Natural Science Edition), 2009, 39(1): 106 DOI:10.3969/j.issn.1001-0505.2009.01.020 |
| [10] |
WENDEL M S, RICHARD E. Nonlinear FE analysis of steel-concrete composite structures[J]. Journal of Structural Engineering, 2000, 126(6): 662 DOI:10.1061/(ASCE)0733-9445(2000)126:6(662) |
| [11] |
张峰, 叶见曙, 徐向锋. 预应力混凝土梁非线性分析单元模型[J]. 交通运输工程学报, 2007, 7(5): 68 ZHANG Feng, YE Jianshu, XU Xiangfeng. Nonlinear analysis element model of prestressed concrete beam[J]. Journal of Traffic and Transportation Engineering, 2007, 7(5): 68 |
| [12] |
杨耀铨. 跨径25米的装配式后张法预应力混凝土简支梁静载试验报告[R]. 北京: 交通部第二公路勘察设计院, 1979. YANG Yaoquan. Report on static load test of prestressed concrete simple supported beam with 25 meters span[R]. Beijing: Second Highway Survey and Design Institute of Ministry of communications, 1979. |
| [13] |
汪光庐. 整体多片式T梁结构空间分析[D]. 上海: 同济大学, 2002. WANG Guanglu. An analysis of the cross sectional frame effect of monolithic multi-piece T beam[D]. Shanghai: Tongji University, 2002. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y464822 |
| [14] |
DENG L Z, MICHEL G, ALES Z, et al. Nonlinear flexural behavior of prestressed concrete girder bridges[J]. Journal of Bridge Engineering, 2001, 6(4): 276 DOI:10.1061/(ASCE)1084-0702(2001)6:4(276) |
| [15] |
WONSEOK C, ELISA D S. Nonlinear finite-element analysis of composite steel girder bridges[J]. Journal of Structural Engineering, 2005, 131(2): 304 DOI:10.1061/(ASCE)0733-9445(2005)131:2(304) |
| [16] |
THABET A, HALDANE D. Three-dimensional simulate-on of nonlinear response of reinforced concrete members subjected to impact-loading[J]. Journal of Structure, 2000, 97(5): 689 |
| [17] |
SHEN D J, DENG S C, ZHANG J Y, et al. Behavior of reinforced concrete box beam with initial cracks repaired with basalt fiber-reinforced polymer sheet[J]. Journal of Reinforced Plastics and Composites, 2015, 34(18): 1540 DOI:10.1177/0731684415595469 |
| [18] |
吕西林, 金国芳, 吴晓涵. 钢筋混凝土结构非线性有限元理论与应用[M]. 上海: 同济大学, 1999 LV Xilin, JIN Guofang, WU Xiaohan. Nonlinear finite element theory and application of reinforced concrete structure[M]. Shanghai: Tongji University press, 1999 |
| [19] |
王家林. 钢筋混凝土结构空间有限元分析的体梁组合单元[J]. 工程力学, 2002, 19(6): 131 WANG Jialin. A brick-beam combination element for three-dimensional finite element analysis of reinforced concrete structures[J]. Engineering Mechanics, 2002, 19(6): 131 |
| [20] |
YE X, ZHANG J, MA Y, et al. Study on mechanical properties of the continuous U-shaped beam[J]. Advanced Materials Research, 2014(889-890): 1425 |
| [21] |
汪锋, 苏林, 张剑, 等. 预应力混凝土刚构U形梁的受力性能研究[J]. 新技术新工艺, 2017, 37(11): 32 WANG Feng, SU Lin, ZHANG Jian, et al. Analysis of mechanical performances of rigid frame U shaped beam[J]. New Technology & New Process, 2017, 37(11): 32 |
 2018, Vol. 46
2018, Vol. 46

